Statistical analysis of topological indices in linear phenylenes for predicting physicochemical properties using algorithms

Abstract

QSPR mathematically links physicochemical properties with the structure of a molecule. The physicochemical properties of chemical molecules can be predicted using topological indices. It is an effective method for eliminating costly and time-consuming laboratory tests. We established a QSPR between mev-degree and mve-degree-based indices and the physical properties of benzenoid hydrocarbons. To compute these indices, we designed a program using Maple software and the correlation between indices and physical properties was developed using the SPSS software. Our study reveals that the mve-degree-based sum-connectivity $(\chi ^{mve})$ and atom bond connectivity ($ABC^{mve}$) index, mev-degree-based Randić ($R^{mev}$) and Zagreb ($M^{mev}$) index are the three most significant parameters and have good prediction ability for the physicochemical properties. We examined that $R^{mev}$ predicts the molar refractivity and boiling point, ${\chi }^{mve}$ predicts the LogP and enthalpy, $ABC^{mve}$ predicts the molecular weight, $M^{mev}$ predicts the Gibb’s energy, Pie-electron energy and Henry’s law. Moreover, we computed the indices for the linear [n]-phenylen.

Introduction

From the past to the present, the link between graph theory and chemistry has come a long way. Different studies in both fields have led to very strong connections between them, which led to the creation of a field of science called chemical graph theory . Chemical graphs were first talked about in the late 18th century, when Isaac Newton’s ideas also changed the way people thought about chemistry¹. During that century, scientists learned a lot more about how atoms interact with each other, but they did not figure out what the chemical bonds were. So, the first time chemical graphs were used, they were used to show the forces between molecules and atoms that were made up¹.

John Dalton made the first atomic model in 1805. He used circles to show the different types of atoms. This model could only show the chemical positions and number of atoms in a molecule². But August Kékule showed that atoms in a molecule have both physical places and directions³. In the same way, other studies^4,5,6 give a clearer picture of how the molecular structure is shown.

In discrete mathematics, a graph shows how a set of objects, which are shown by points, are related to each other. Edges show how two things are connected to each other. Graph theory is the study of graphs. Slyvester was the first person to use the term to describe chemical structures. In chemistry, molecules are often shown as graphs, where the points and edges stand for atoms and bonds, respectively.

Quantitative structure-property relationship (QSPR) is a computer-based method that develops a relationship between the chemical structure of different mixtures (Compounds) and their activities, particularly biological activities or effects. It engages a sequence of programs to research quantitative experimental knowledge of the activities of the given compound with identified chemical designs to anticipate a relationship, model, or condition that may encourage to propose the movement of identified mixtures (compounds) with obscure activities or obscure mixtures, and their activities⁷. QSARs help to understand different aspects of varied disciplines, such as risk assessment, toxicity prediction, regulative selections, drug discovery, and lead optimization^8,9,10,11. Here we are implementing the QSARs techniques to develop a quantitative relationship between the chemical and its physicochemical properties.

A bibliometric analysis was conducted using the Scopus database, which can be accessed at www.scopus.com. The present analysis is grounded on a comprehensive examination of 986 scholarly research articles, wherein the pivotal factors of entropy and graph entropy^12,13,14 have been considered. Figure 1 displays the distribution of publications across various academic disciplines.

Figure 1

Bibliometric study of the articles written about entropy in different fields.

A bibliometric analysis was conducted to examine the research conducted in various countries pertaining to the concept of entropy, as depicted in Fig. 2.

Figure 2

Bibliographic study of studies done all over the country on the subject of entropy. The size of the circles shows how often an article appears, and the different colors show different groups of articles.

In 1947, Harold Wiener introduced the first topological index, the Wiener index, and applied this attention-grabbing index to see the physicochemical properties of a sort of alkanes called paraffin¹⁵. In 1972, I. Gutman and N. Trinajstić observed that the sum of the squares of the degree of vertices of the molecular graph gives the $\pi$-electron energy of that molecule. Later on, this sum was named “Zagreb Index”¹⁶. In 1976, Milan Randić developed a much-investigated degree-based topological index called the Randić index¹⁷. In 1987, the harmonic index appeared about some conjectures, generated by the pc program Graffiti¹⁸. In the 1990s, Estrada et al., projected a topological index named atom-bond connectivity (ABC) index, employing a Randić connectivity index modification^17,18. In 2009, galvanized by the definition of the Randić property index, Vukičević and Furtula projected a topological index named geometric-arithmetic index¹⁹. In 2009, Sum-Conductivity index was projected and eventually extended to the general sum-connectivity index²⁰. Nowadays, the topological indices (TI) are referred to as “Molecular Descriptors” because of their worldwide applications in formulating the numerical results to quantitively describe the physicochemical properties of concerned molecular structures^21,22,23.

From these indices, it’s attainable to research mathematical values and additionally investigate some chemistry of molecules. Therefore, it’s an efficient technique in avoiding valuable and long laboratory experiments. It plays a vital role in understanding the concepts of chemistry by using mathematical techniques, particularly in “QSPR” and “QSAR” investigations^24,25,26. Hayat et al.²⁸ proposed the relations to predict the enthalpy of formation and boiling point of benzenoid hydrocarbons using temperature-based indices. Sakander et al.²⁹ developed the relations to predict entropy and heat capacity benzenoid hydrocarbons using eigen-value based indices. Hayat et al.³⁰ proposed the relationship between pie electron energy and temperature indices. Similarly, they proposed the models to predict some other properties by using temperature and distance-based indices^31,32. Zhong et al., proposed the relation between physicochemical properties of Covid drugs and ve- and ev-degree based indices. They examined that ve- and ev-degree based indices showed 97.4% correlation with molecular weight and 88.6% with topological polar surface³³. After studied all these articles, we proposed the novel multiplicative version of ve- and ev-degree based indices that show significant relations with eight physicochemical properties.

In this paper, we have computed the multiplicative version of ve-degree and ev-degree. Furthermore, we have investigated the QSPR of the mve-degree and mev-degree-based indices to predict the physiochemical characteristics of benzenoid hydrocarbons.

Preliminaries

Let $G = (V;E)$ is a connected graph with edges set to E and vertices set to V. The number of edge connected with the v vertex is called degree of the v vertex, indicated by $\aleph (v)$. The v vertex’s open neighbourhood, represented by N(v), is a collection of all vertices that are close to the v vertex. The union of v vertex with open neighbourhood N(v) of v vertex is described by the closed neighbourhood of v, represented by N[v]. In^27,34, we first introduce some basic concepts about ev-degree and ve-degree.

Definition 1

The ev-degree of an edge $e = uv \in E$, denoted by $\aleph _{ev}(e)$, is the number of vertices of the union of closed neighborhoods of v and u vertex.

Observation 2.1: For any edge $e = uv \in E$ of a connected graph G

$$\begin{aligned} \aleph _{ev}(e)= \aleph _{ev}(uv)=\aleph (u)+\aleph (v)-n_e\end{aligned}$$

where $n_e$ is the no. of triangles containing edge $e = uv$.

Definition 2

The ve-degree of any vertex $v\in V$, denoted by $\aleph _{ve}(v)$, is the total edges that are incident to any vertex from the closed neighborhood of v.

Observation 2.2: For any vertex $v\in V$ of a connected graph G

$$\begin{aligned}\aleph _{ve}(v) = \sum _{v\in N(v)} \aleph (v)-n_u,\end{aligned}$$

where $n_v$ is the no. of triangles containing the vertex v.

Based upon observations 2.1 and 2.2, the multiplicative ev-degree and multiplicative ve-degree is defined as

Definition 3

For any edge $e = uv\in G(E)$ of a connected graph G, a multiplicative ev-degree denoted by mev-degree $(\aleph _{mev})$ is defined as

$$\begin{aligned} \aleph _{mev}(e)= \aleph _{mev}(uv)=\aleph (u) \aleph (v)-n_e \end{aligned}$$

where $n_e$ is the no. of triangles containing edge $e = uv$.

Definition 4

For any vertex $v\in G(V )$ of a connected graph G, a multiplicative ve-degree denoted by mve-degree $(\aleph _{mve})$ is defined as

$$\begin{aligned}\aleph _{mve}(v) = \Pi _{v\in N(v)} \aleph (v)-n_v.\end{aligned}$$

where $n_v$ is the no. of triangles containing the vertex v.

The mev-degree based Zagreb (${M}^{mev}$) index and Randić (${R}^{mev}$) index for any edge $e=uv\in E(G)$ is define as

$$\begin{aligned} {M}^{mev} = \sum _{e\in E} \aleph _{mev}(e)^2,\qquad \qquad {R}^{mev} = \sum _{e\in E} \aleph _{mev}(e)^{-\frac{1}{2}}. \end{aligned}$$

The mve-degree first Zagreb alpha ($M_1^{\alpha {mve}}$) index for any vertex $v\in V(G)$ is define as

$$\begin{aligned}M_1^{\alpha {mve}} = \sum _{v\in V} \aleph _{mve}(v)^2.\end{aligned}$$

The end vertices mve-degrees based indices for each edges, such as mve-degree based first Zagreb beta (${M}_1^{\beta {mve}}$) index, second Zagreb (${M}_2^{\beta mve}$) index, atom-bond connectivity (${ABC}^{mve}$) index, geometric-arithmetic (${GA}^{mve}$) index, Harmonic (${H}^{mve}$) index and sum-connectivity (${\chi }^{mve}$) index for each edge $uv\in E(G)$ is define as

$$\begin{aligned} {M}_1^{\beta {mve}} & = \sum _{uv\in E}(\aleph _{mve}(u)+\aleph _{mve}(v)),\qquad \qquad \qquad {M}_2^{\beta mve} \\ & = \sum _{uv\in E} (\aleph _{mve}(u)\times \aleph _{mve}(v)),\\ {ABC}^{mve} & = \sum _{uv\in E}\sqrt{\frac{\aleph _{mve}(u)+\aleph _{mve}(v)-2}{\aleph _{mve}(u)\times \aleph _{mve}(v)}},\quad \quad {GA}^{mve}\\ & = \sum _{uv\in E}\frac{2\sqrt{{\aleph _{mve}(u)\times \aleph _{mve}(v)}}}{{\aleph _{mve}(u)+ \aleph _{mve}(v)}},\\ {H}^{mve} & = \sum _{uv\in E}\frac{2}{\aleph _{mve}(u)+ \aleph _{mve}(v)},\quad \qquad \qquad \qquad {\chi }^{mve} \\ & = \sum _{uv\in E}(\aleph _{mve}(u)+ \aleph _{mve}(v))^{-\frac{1}{2}}. \end{aligned}$$

Quality testing analysis

In this section, we tells about our working and presenting methodology. In section “Algorithm”, by using Maple software, we developed a program that helps us to compute the mve- and mev degree based indices. Our program based is on adjacency matrix which can be computed by newGraph software. In section “Quantitative structure-property relationships”, we examine the relationship between physicochemical properties and indices by using SPSS software. In Fig. 3, we draw a flow chart of our working methodology.

Figure 3

Working steps in flow chart.

Benzenoid

Benzene is a parent aromatic hydrocarbon, carcinogenic and toxic. It is a naturally occurring substance and is used as a major component in spot remover, paint strippers, and also at the industrial level. Several researchers have suggested a possible benzene structure^35,36,37 but August Kekul’e suggested benzene’s recognized ring structure³⁸. According to Kekul’e, the benzene structure has six carbon atoms. In 1928, Benzene was the first cause of leukemia³⁹. In the 1950s, benzene demand was increased and acquired from coal and petroleum. Benzene is an element of crude oil and cigarette smoke and is used to make resins, synthetic fibers, and pesticides³⁹.

Figure 4 shows the molecular structures of benzenoid hydrocarbons. Each hydrogen atom only has a single chemical bond, whereas each carbon atom has a total of four chemical bonds. As a result, the hydrogen atoms can be removed from the molecule without any information being lost in the process.

Figure 4

Molecular structures of benzenoid hydrocarbons.

Algorithm

S1: Start

S2: Input: B is an adj. matrix.

S3: Output: Calculation of MVE-Degree, MEV-Degree and MVE-Degree of End Vertices.

S4: Initialize: V $\leftarrow$ no. of vertices, E $\leftarrow$ no. of edges, Conn[M] $\leftarrow$ connection matrix, D[V] $\leftarrow$ deg. of vertices, MVE$\leftarrow$mve-deg of vertices, D[MVE] $\leftarrow$ Total edges incident to the closed neighborhood vertices, MEV$\leftarrow$mev-degree of edges, D[MEV] $\leftarrow$ deg. multiplication of two connected vertices, adj[count] $\leftarrow$ Connected element, Ver[V] $\leftarrow$ Vertex list, count $\leftarrow$ 1, Bq[count] $\leftarrow$ mve-degree matrices entries, Bp[count] $\leftarrow$ mev-degree matrices entries.

S5: loop b = 1 to Vertex

S6:      For every vertex from the Ver[V].

S7:      loop c = 1 to E

S8:            count connected vertices from the matrix Conn[M].

S9:            c++

S10:      end loop

S11:      D[V] = count.

S12:      loop t = 1 to count

S13:            adj[count] = store adj. vertices

S14:            t++

S15:      end loop

S16:      loop h=1 to D[V] count

S17:            B $\times$ adj[count]

S18:            Store the outcomes of the above as MVE

S19:            h++

S20:      end loop

S21:      loop i=1 to V

S22:            loop j=1 to V

S23:                  $\sum$ of the D[V][i] with D[V][j] and multi. by $(i,j)^{th}$ entries of B.

S24:                  Store the outcomes of MEV

S25:            j++

S26:            end loop

S27:      i++

S28:      end loop

S29: end loop

S30: loop n=1 to MVE

S31:      For every vertex from the MVE

S32:      loop x=1 to MVE

S33:            count vertices from the matrix for MVE

S34:      end loop

S35:      D[MVE]=count

S36:      loop w=1 to count

S37:            Bq[count]= store vertices for MVE.

S38:            w++

S39:      end loop

S40: end loop

S41: loop i=1 to MEV

S42:      For every connected vertex from the MEV

S43:      loop j=1 to MEV

S44:            count adj. vertices from the MEV

S45:            j++

S46:      end loop

S47:      D[MEV]=count

S48:      loop k=1 to count

S49:            Bp[count]=store MEV

S50:            k++

S51:      end loop

S52: end loop

S53: loop a=1 to count

S54:      Compute the MVE-degree first Zagreb $\alpha$-Index.

S55: end loop

S56: loop b=1 to count

S57:      Compute the MEV-degree Zagreb and Randić Index.

S58: end loop

S59: loop c = 1 to E

S60:      Compute the End Vertices MVE-Degree based First and Second Zagreb $\beta$-Index, Geometric-Arithmetic, Atom-Bond Connectivity, Sum Connectivity and Harmonic Index.

S61: end loop

S62: end

Quantitative structure-property relationships

In this part, we examine the relation (QSPR) of mev-degree and mve-degree-based indices using benzenoid hydrocarbons. We use twenty to benzenoid hydrocarbons. In Table 1 the physicochemical properties and names of benzenoid hydrocarbons are given, and data taken from www.chemspider.com. The $\pi$-electron energy were calculated using Streiwieser’s and Coulson tabulation^40,41, the experimental boiling points from⁴², the enthalpy from⁴³, and the molecular weight from⁴⁴.

Table 1 The physicochemical characteristics of benzenoid hydrocarbons.

Table 2 Notations of physicochemical characteristics and statistical terms.

The symbols mentioned in Table 1 will be used instead of the names of benzenoid hydrocarbons and the notations given in Table 2 will be used physicochemical properties and statistical terms. Multiplicative ve-degree and Multiplicative ev-degree based indices are listed in Table 3.

Table 3 The computation of the indices for benzenoid hydrocarbons.

Table 4 The correlation coefficient matrix.

The results of correlation coefficients between every pair of variables are shown in Table 4. We observe that at the 1% level of significance, all of the results are very significant. It is concluded that the set of variables has a strong positive linear bivariate relationship. As the molecular theory suggests that the Pie-electron energy, enthalpy, Henry’s law, Gibb’s energy, boiling point, logP, molar refractivity and molecular weight depend on indices such as $M^{mev}$, $R^{mev}$, $M^{\alpha mve}_1$, ${M}^{\beta mve}_1$, $M^{\beta mve}_2$, $ABC^{mve}$, $GA^{mve}$, $H^{mve}$ and ${\chi }^{mve}$. We examine the perfect positive relationship of the

• boiling point with $R^{mev}$, $ABC^{mve}$, $GA^{mve}$ and ${\chi }^{mve}$,

• enthalpy with $ABC^{mve}$ and ${\chi }^{mve}$,

• Pie electron energy with $M^{mev}$, $R^{mev}$ $ABC^{mve}$, $GA^{mve}$ and ${\chi }^{mve}$,

• molecular weight with $R^{mev}$ $ABC^{mve}$, $GA^{mve}$ and ${\chi }^{mve}$,

• Gibb’s energy with $M^{mev}$, $R^{mev}$ and $GA^{mve}$,

• LogP with $ABC^{mve}$ and ${\chi }^{mve}$,

• molar refractivity with $R^{mev}$ $ABC^{mve}$, $GA^{mve}$ and ${\chi }^{mve}$,

• Henry’s law with $M^{mev}$, $R^{mev}$, ${M}^{\beta mve}_1$, $ABC^{mve}$ and $GA^{mve}$.

Similarly, some other perfect relationships exist between indices but we are developing relation between physicochemical properties and indices. As we know that the linear regression model ($P = \alpha + \beta X$) is appropriate for prediction analysis. Where P is either one of the physical characteristic of benzenoid hydrocarbons and X one of from the list of computed indices $M^{mev}$, $R^{mev}$, $M^{\alpha mve}_1$, ${M}^{\beta mve}_1$, $M^{\beta mve}_2$, $ABC^{mve}$, $GA^{mve}$, $H^{mve}$, ${\chi }^{mve}$. Now, we compute the statistical measures by taking physical characteristics as dependent variable.

Table 5 The statistical measures for boiling point.

Table 6 The statistical measures for enthalpy.

Table 7 The statistical measures for molecular weight.

Table 8 The statistical measures for Pie-electron energy.

Table 9 The statistical measures for Henry’s law.

Table 10 The statistical measures for molar refractivity.

Table 11 The statistical measures for LogP.

Table 12 The statistical measures for Gibb’s energy.

The estimated models for forecasting physical properties for a given value of any index.

$$\begin{aligned} \begin{array}{ccccccc} BP& =& 116.925 + 0.363 M^{mev}& \quad \quad \quad \quad E_H& =& - \,\,10.249 + 31.51 R^{mev} \\ BP& =& - \,\,57.560 + 54.871 R^{mev} & \quad \quad \quad \quad E_H& =& -\,\,37.611+31.343 ABC^{mve}\\ BP& =& -\,\,98.004 + 53.886 ABC^{mve}& \quad \quad \quad \quad E_H& =& 15.205+12.491 GA^{mve} \\ BP& =& -\,\,18.164 + 21.977 GA^{mve} & \quad \quad \quad \quad E_H& =& -\,\,145.983+156.489 H^{mve}\\ BP& =& -\,\,124.076 + 108.498 \chi ^{mve} & \quad \quad \quad \quad E_H& =& -\,\,55.829+63.673 \chi ^{mve} \\ \end{array}\\ \begin{array}{ccccccc} MW& =& 84.596 + 0.166 M^{mev}& \quad \quad \quad \quad E_\pi & =& 8.349 + 0.02 M^{mev}\\ MW& =& 2.427 + 25.309 R^{mev} & \quad \quad \quad \quad E_\pi & =& -\,\,0.931+2.937 R^{mev} \\ MW& =& -\,\,16.898+24.919 ABC^{mve}& \quad \quad \quad \quad E_\pi & =& -\,\,3.066+2.881 ABC^{mve}\\ MW& =& 21.173+10.11 GA^{mve} & \quad \quad \quad \quad E_\pi & =& 1.173+1.176 GA^{mve} \\ MW& =& -\,\,29.498+50.274 \chi ^{mve} & \quad \quad \quad \quad E_\pi & =& -\,\,4.467+5.803 \chi ^{mve} \\ \end{array}\\ \begin{array}{ccccccc} HL& =& 116.925 + 0.363 M^{mev}& \quad \quad \quad \quad MR& =& 26.848+0.058 M^{mev}\\ HL& =& -\,\,57.560 + 54.871 R^{mev} & \quad \quad \quad \quad MR& =& -\,\,0.773+8.696 R^{mev} \\ HL& =& -\,\,1.708+1.079 {M_1}^{\beta mve} & \quad \quad \quad \quad MR& =& -\,\,6.843+8.491 ABC^{mve}\\ HL& =& -\,\,98.004 + 53.886 ABC^{mve}& \quad \quad \quad \quad MR& =& 5.274+3.498 GA^{mve} \\ HL& =& -\,\,18.164 + 21.977 GA^{mve} & \quad \quad \quad \quad MR& =& -11.395+17.192 \chi ^{mve} \\ \end{array}\\ \begin{array}{ccccccc} LogP& =& 0.868+0.466 R^{mev} & \quad \quad \quad \quad GE& =& 95.174+0.507 M^{mev}\\ LogP& =& 0.498+0.459 ABC^{mve}& \quad \quad \quad \quad GE& =& -\,\,114.81+72.755 R^{mev} \\ LogP& =& 1.212+0.186 GA^{mve} & \quad \quad \quad \quad GE& =& -\,\,156.51+70.126 ABC^{mve}\\ LogP& =& -\,\,0.953+2.238 H^{mve}& \quad \quad \quad \quad GE& =& -\,\,70.824+29.583 GA^{mve} \\ LogP& =& 0.225+0.935 \chi ^{mve} & \quad \quad \quad \quad GE& =& -\,\,189.276+141.046 \chi ^{mve} \\ \end{array} \end{aligned}$$

In this statistical fitting process, we also obtain the correlation coefficient, R square, adjusted R square and the F statistic value for the standard error of estimate. Based on the recommendation of the International Academy of Mathematical Chemistry (IAMC), the values of $R^2 \ge 0.8$ in all models, our results are significant.

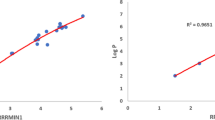
• Table 5 shows the relation between boiling point and indices. The Randić index based on multiplicative ev-degree gives the highest values of adjusted R square, R square, correlation coefficient and F statistic with boiling point. And the std. error of the estimate is small. So, we can say that the boiling point shows the best relationship with and can be predicted by the Randić index. Moreover, we can see in Fig. 5a that for boiling relation, all the point is near the fitted line.

• Table 6 shows the relation between enthalpy and indices. For enthalpy, the sum connectivity index based on multiplicative ve-degree gives the highest values of adjusted R square, R square, correlation coefficient and F statistic. The value std. error of the estimate is small for $\chi ^{mve}$. Based on the results, we can say the sum connectivity index is the best predictor of enthalpy. Moreover, all the points fall near the line, as seen in Fig. 5b.

• Table 7 shows the relationship between indices and molecular weight. The atom bond connectivity index based on multiplicative ve-degree shows significant results. The values of adjusted R square, R square and correlation coefficient are highly positive and approximately near 1. And the value of std. error of estimate is small 3.4788. We see in Fig. 5c, all the points fall near the fitted line. Based on these calculations, we can say that molecular weight can be predicted by atom bond connectivity.

• Table 8 shows the relationship between indices and Pie-electron energy. The Zagreb index based on multiplicative ev-degree shows a highly positive and best relation with Pie-electron energy. The value of the correlation coefficient is positive 1 and the values of the adjusted R square and R square are 0.999. The std. error of estimate is very small which is 0.1856. So, the Zagreb index shows significant results. However, we can predict the Pie-electron energy by the Zagreb index. Moreover, we can see in Fig. 5d, all the points fall on the line.

• Table 9 shows the relationship between Henry’s law and indices. The Zagreb index based on multiplicative ev-degree gives the highest values of adjusted R square, R square, correlation coefficient and F statistic with Henry’s law. The value of std. error of estimate is very small which is 0.137271. Moreover, we plot the graph and see that all the points fall near the fitted line, see Fig. 5e. So, we say that physical property Henry’s law can be predicted by the Zagreb index.

• Table 10 shows the relationship between indices and molar refractivity. The Randić index based on multiplicative ev-degree shows highly positive and significant results with molar refractivity. The value of the statistical measure, correlation coefficient adjusted R square and R square is positive 1. The std. error of estimate is very small which is 0.1508131. So, the Randić index shows significant results and best predictor of molar refractivity. Moreover, we can see in Fig. 5f, all the points fall on the line.

• Table 11 shows the relation between LogP and indices. For LogP, the sum connectivity index based on multiplicative ve-degree gives the highest values of adjusted R square, R square, correlation coefficient and F statistic. The value std. error of the estimate is small for $\chi ^{mve}$. Based on the results, we can say the sum connectivity index is the best predictor of LogP. Moreover, all the points fall near the line, as seen in Fig. 5g.

• Table 12 shows the relation between Gibb’s energy and indices. The Zagreb index based on multiplicative ev-degree gives the highest values of statistical measures with Gibb’s energy. And the std. error of the estimate is small. So, we can say that Gibb’s energy shows the best relationship with and can be predicted by the Zagreb index. Moreover, we can see in Fig. 5h that for Gibb’s energy relation, all the point is near the fitted line.

Figure 5

Plots of relationship measure using linear regression model between indices and physicochemical properties.

Based on the linear regression model, we can conclude that the mve-degree and mev-degree indices can accurately predict Pie-electron energy, boiling point, logP, molecular weight, Henry’s law, Gibb’s energy, molar refractivity and enthalpy. Also, we can use the above-proposed models to estimate the value of the same class of structures. Like, if we want to compute the estimated value of molar refractivity, we just calculate the value of $R^{mev}$ index and put in this model $MR= -\,0.773+8.696 R^{mev}$.

Illustration of algorithm and computation of indices for linear [n]-phenylen

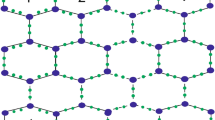
Our algorithm is based on an adjacency matrix. We will compute the mve-degree and mev-degree matrix and their corresponding indices by using the Maple algorithm. For this, we will calculate the mve- and mev-degree indices for the graph of linear [n]-phenylen. Firstly, we compute the adj. matrix of linear [n]-phenylen (P) and insert the adj. matrix in Maple. We can examine the adjacency matrix directly form the software newGraph (procedure given in⁴⁵) by drawn the structure of linear [n]-phenylen for $n=2$. The graph P have 12 vertices, the adjacency will be ordered of 12 by 12 and the Fig. 6 shows that the size of 14.

Figure 6

Structure of linear [n]-phenylen for $n=2$.

$$\begin{aligned} A=\left[ \begin{array}{llllllllllll} 0 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1 \\ 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 \\ 1 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 0\\ \end{array}\right] \end{aligned}$$

By using the adjacency matrix we will examine the mev-degree, mve-degree, and degree of vertices. We can get the degree of vertices in the form of column matrix B by adding the entries of the row

$$\begin{aligned} B =[3, 2, 2, 2, 2, 3, 3, 2, 2, 2, 2, 3] \end{aligned}$$

We can verify the degree sequence of vertices with the labeled Fig. (6). When we multiplied the adj. matrix P and degree matrix B we get a mve-degree matrix PB in column form but when we are multiplying the entries of P and B in multiplication we will multiply the non-zero entries instead of addition.

$$\begin{aligned} PB= [ 18, 6, 4, 4, 6, 18, 18, 6, 4, 4, 6, 18] \end{aligned}$$

For mev-degree, we consider two matrices $P=P_{ij}$ and $B=B_{ij}$, where i and j denoted the element of $i^{th}$ and $j^{th}$ column. When we multiply the $P_{ij}$ with $B_i \times B_j$ we get a new matrix, named L. For mev-degrees of edges we just take the non zero elements of lower or upper triangular of L.

$$\begin{aligned} L= \left[ \begin{array}{cccccccccccccc} 0 & 6 & 0 & 0 & 0 & 9 & 0 & 0 & 0 & 0 & 0 & 9 \\ 0 & 0 & 4 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 4 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 4 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 6 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 9 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 6 & 0 & 0 & 0 & 9 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 4 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 4 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 4 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 6 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array}\right] \end{aligned}$$

By using the above matrices we can compute the mve-degree and mev-degree based indices.

$$\begin{aligned} M^{mev}= & 564\\ M_1^{\alpha mve}= & 1504\\ M_1^{\beta mve}= & 296\\ M_2^{\beta mve}= & 1856\\ H^{ mve}= & \frac{501}{270}\\ R^{mve}= & \frac{13}{18}+\frac{2\sqrt{3}}{9}+\frac{\sqrt{6}}{3} \\ ABC^{mve}= & \frac{2\sqrt{66}}{9}+\frac{2\sqrt{34}}{9}+\frac{4\sqrt{3}}{3}+\frac{\sqrt{6}}{2}\\ GA^{mve}= & 6+ {2\sqrt{3}}+\frac{8\sqrt{6}}{5}+\\ \chi ^{mve}= & \frac{2}{3}+\frac{\sqrt{6}}{3}+\frac{2\sqrt{10}}{5}+\frac{\sqrt{2}}{2}\\ \end{aligned}$$

Next, we computed topological indices (the similar approach was written for $n=2$) for the structure of linear [n]-phenylen for $n=3$ given in Fig. 7.

Figure 7

Structure of linear [n]-phenylen for $n=3$.

The mve-degree and mev-degree based indices are

$$\begin{aligned} M^{mev}= & 1032\\ M_1^{\alpha mve}= & 2962\\ M_1^{\beta mve}= & 548\\ M_2^{\beta mve}= & 3800\\ H^{ mve}= & \frac{641}{270}\\ R^{mve}= & \frac{17}{18}+\frac{2\sqrt{3}}{9}+\frac{\sqrt{6}}{3}+\frac{2\sqrt{2}}{9} \\ ABC^{mve}= & \frac{2\sqrt{66}}{9}+\frac{4\sqrt{34}}{9}+\frac{4\sqrt{3}}{3}+\frac{\sqrt{6}}{2}+\frac{10\sqrt{2}}{9}\\ GA^{mve}= & 10+ {2\sqrt{3}}+\frac{8\sqrt{6}}{5}+\frac{8\sqrt{2}}{3}\\ \chi ^{mve}= & \frac{4}{3}+\frac{\sqrt{6}}{3}+\frac{2\sqrt{10}}{5}+\frac{\sqrt{2}}{2}+\frac{4\sqrt{3}}{9}\\ \end{aligned}$$

Next, we computed topological indices (the similar approach was written for $n=2$) for the structure of linear [n]-phenylen for $n=4$ given in Fig. 8.

Figure 8

Structure of linear [n]-phenylen for $n=4$.

The mve-degree and mev-degree based indices are

$$\begin{aligned} M^{mev}= & 1500\\ M_1^{\alpha mve}= & 4420\\ M_1^{\beta mve}= & 800\\ M_2^{\beta mve}= & 5744\\ H^{ mve}= & \frac{781}{270}\\ R^{mve}= & \frac{21}{18}+\frac{2\sqrt{3}}{9}+\frac{\sqrt{6}}{3}+\frac{4\sqrt{2}}{9} \\ ABC^{mve}= & \frac{2\sqrt{66}}{9}+\frac{6\sqrt{34}}{9}+\frac{4\sqrt{3}}{3}+\frac{\sqrt{6}}{2}+\frac{20\sqrt{2}}{9}\\ GA^{mve}= & 14+ {2\sqrt{3}}+\frac{8\sqrt{6}}{5}+\frac{16\sqrt{2}}{3}\\ \chi ^{mve}= & \frac{6}{3}+\frac{\sqrt{6}}{3}+\frac{2\sqrt{10}}{5}+\frac{\sqrt{2}}{2}+\frac{8\sqrt{3}}{9}\\ \end{aligned}$$

Similarly, we computed topological indices (the similar approach was written for $n=2$) for the structure of linear [n]-phenylen for $n=5$. Then, using the software Mathematica, we developed a sequence function between the similar indices values and with the help of Mathematica software we can easily computed the result for generalize structure linear [n]-phenylen for n, see Fig. 9.

Figure 9

Structure of linear [n]-phenylen for n.

mve- and mev-degree indices for the linear [n]-phenylen for n.

$$\begin{aligned} M^{mev}= & 12(39n-31)\\ M_1^{\alpha mve}= & 2(729n-706)\\ M_1^{\beta mve}= & 4(63n-52)\\ M_2^{\beta mve}= & 8(243n-254)\\ H^{ mve}= & \frac{140}{270}n+\frac{221}{270}\\ R^{mve}= & \left( \frac{4}{18}+\frac{4\sqrt{2}}{18}\right) n+\frac{2\sqrt{3}}{9}+\frac{\sqrt{6}}{3}-\frac{4\sqrt{2}}{9}+5 \\ ABC^{mve}= & \left( \frac{10\sqrt{2}}{9}+\frac{2\sqrt{34}}{9}\right) n+ \frac{2\sqrt{66}}{9}-\frac{2\sqrt{34}}{9}+\frac{4\sqrt{3}}{3}+\frac{\sqrt{6}}{2}-\frac{20\sqrt{2}}{9}\\ GA^{mve}= & \left( 4+\frac{40\sqrt{2}}{15}\right) n+\frac{8\sqrt{6}}{5}+\frac{16\sqrt{2}}{3}-\frac{80\sqrt{2}}{15}+ {2\sqrt{3}}-2\\ \chi ^{mve}= & \left( \frac{2}{3}+\frac{20\sqrt{3}}{45}\right) n- \frac{2}{3}+\frac{\sqrt{6}}{3}+\frac{2\sqrt{10}}{5}+\frac{\sqrt{2}}{2}-\frac{8\sqrt{3}}{9}\\ \end{aligned}$$

Conclusion

Topological indices predict the physicochemical properties and it’s an efficient technique to avoid long laboratory experiments. We have developed a QSPR between multiplicative ev-degree and ve-degree indices and the physical properties of benzenoid hydrocarbons. By using a linear regression model, we examined that the indices predict the physicochemical properties. We have found the following relation based on statistical measures:

• $R^{mev}$ is the best predictor of molar refractivity and boiling point,

• ${\chi }^{mve}$ seems to the best predictor of LogP and enthalpy,

• $ABC^{mve}$ is the best predictor of molecular weight,

• $M^{mev}$ is the best predictor of Gibb’s energy, Pie-electron energy and Henry’s law.

All the results were highly positive and significant but these four indices show the best relationship with the physicochemical properties of benzenoid hydrocarbons. So, these four indices can be helpful to estimate the unknown Pie-electron energy, boiling point, logP, molecular weight, Henry’s law, Gibb’s energy, molar refractivity and enthalpy of other benzene complex models. Moreover, our designed Maple-based program can be helpful for the computation of indices timely and reduce the calculation error. In addition, we have calculated mve-degree and mev-degree based indices for linear [n]-phenylen. These results will be helpful for chemical industries. In future, we propose the VIKOR analysis to ranked the drugs and chemical structures based on these indices results.