Introduction

The presence of toxic chemicals in water is a critical public health and environmental issue that poses serious risks to ecosystems and human health. Common water pollutants include heavy metals like mercury and lead, organic pollutants such as pesticides and pharmaceutical residues, and other industrial chemicals that can enter water supplies through agricultural runoff, industrial discharges, and inadequate waste management practices. The effects of these contaminants range from acute poisoning to long-term health issues like cancer, reproductive problems, and endocrine disruption. Education plays a pivotal role in addressing the challenges of water pollution by raising awareness about the sources and effects of contaminants and promoting sustainable practices1. Through formal and informal educational programs2, individuals and communities can learn about the importance of water conservation, pollution prevention, and the steps they can take to reduce their environmental footprint. Schools and universities can integrate environmental science into their curricula to equip tackle environmental challenges effectively3,4. By fostering a deeper understanding of the impacts of toxic chemicals in water and the importance of water quality, education4 can empower individuals to participate in or advocate for conservation initiatives and policy changes.

In such case of nitrophenolic compounds, defined by their benzene frameworks adorned with hydroxyl and nitro functional groups, serve as crucial precursors across various industrial realms, including but not limited to, the synthesis of herbicides, pesticides, fungicides, along with the manufacture of paints, dyes, pharmaceuticals, and explosives5. This advisory stems from their pronounced toxicity, diminished biodegradability, propensity for bioaccumulation, and oncogenic potential6,7.

The improper release of industrial wastewaters laden with nitrophenols (NPs) and their derivatives, even in minimal concentrations, poses significant risks to human health, wildlife, and plant life in aquatic ecosystems8. Regulation of phenolic compounds on different water matrices has been considered by several organizations. For example, U.S. Environmental Protection Agency establishes the maximum nitrophenol compounds level equal to 10 ng/L in natural water7,9. Moreover, the World Health Organization (WHO) establish the maximum levels of 0.009 and 0.2 mg/L for some phenolic compounds as pentachlorophenol and 2,4,6-trichlorophenol, respectively, in drinking water10.

In the case of rivers, lakes and related artificial or heavily modified water bodies, the European Union establish the maximum allowable concentrations of nonylphenol and pentachlorophenol equal to 0.002 and 0.001 mg/L, respectively11. In Mexico, The Official Mexican Standard (NOM), regulates the phenolic compounds with a maximum allowed in drinking water of 9.0 μg/L12. Previous studies have confirmed the presence of NP compounds in various environmental matrices, including groundwater13, precipitation14,15, sediment deposits16, as well as in the atmosphere and industrial discharges17.

The urgent need for effective water purification strategies has led to the exploration of biosorbents for the removal of toxic contaminants from water. This approach is not only essential for protecting environmental health but also benefits from the integration of environmental education to enhance public awareness and involvement. Biosorbents, derived from biological materials, have demonstrated significant potential in adsorbing harmful substances from water. These natural adsorbents are advantageous due to their biodegradability, cost-effectiveness, and high efficiency in binding with various contaminants including heavy metals and dyes. Studies like those by Sarkar et al.18 and Tebbutt and Woods19 highlight the effectiveness of materials like modified clays, agricultural by-products, and engineered biochar in capturing and isolating pollutants from water bodies. Sarkar et al.18 specifically reviewed the water quality management in the Ganges river, emphasizing the role of biosorbents in mitigating heavy metal pollution. They also stressed the importance of integrating environmental education to improve water resource management and enhance the sustainability of such interventions.

Environmental education plays a pivotal role in enhancing the effectiveness of environmental remediation efforts by informing and engaging the public. For instance, Papavasileiou and Mavrakis20 discussed projects implemented in Greek schools that focused on water-related issues, demonstrating how education can lead to better understanding and more proactive attitudes towards water conservation. Similarly, the work presented at the International Conference on New Water Culture by Mariolakos et al.21 used mythology to make environmental education more accessible and engaging for students, thus fostering a deeper understanding of water’s critical role in ecosystems.

Practical applications and case studies further illustrate the successful integration of biosorbents and education. The study by Sarkar et al.18 on the Ganges river utilized educational initiatives to inform and mobilize local populations about pollution control and the importance of maintaining water quality. These educational efforts are crucial in areas where industrial and agricultural activities heavily influence water quality, as they empower local communities to participate in sustainable practices.

In more recent studies, like that of Gebrekidan22, the systematic review of environmental education in Ethiopia revealed gaps in educational structures and emphasized the need for comprehensive educational frameworks to enhance environmental awareness and actions. This study highlights the necessity of embedding environmental education deeply within curriculums to cultivate a knowledgeable citizenry that can actively participate in environmental protection.

In order to remove NPs compounds or reduce its concentration from the wastewater, numerous researchers have developed various techniques such as membrane technology23,24, chemical redox6,24, adsorption24,25,26, biodegradation24,27 and bioremediation28. From the perspectives of operation, design, straightforwardness, and the ease with which adsorbent materials can be reused, the adsorption method stands out as significantly superior when contrasted with alternative approaches24. However, the use of this technique has been restricted for large-scale treatment due to the high cost of adsorbents.

During a last decade, a significant research have been dedicated to the improvement of diverse varieties of cost-effective adsorbents aimed at eliminating phenolic compounds and other pollutants from water-based solutions25,29,30. These efforts have highlighted the utilization of natural materials such as clay31, zeolite32,33, and siliceous substances34 for purification purposes. However, organic molecules removal was achieved by the modification of their external surface by surfactants32,35,36,37.

The effectiveness of bioadsorbents, including Phanerochaete chrysosporium, the fungus Pleurotus sajor-caju, and Sargassum, in eliminating chlorophenols has demonstrated that the adsorption capacity is enhanced by the increase in the number of electronegative groups present38,39.

The peak adsorption capability (qm, mmol/g) for phenol, 2-chlorophenol, 4-chlorophenol, and 2,4,6-trichlorophenol when utilizing Pleurotus sajor-caju as the adsorbent was recorded at 0.95, 1.24, 1.47, and 1.89, respectively. This highlights not only the efficacy of the adsorbent but also its potential for being reused across more than five adsorption cycles without a significant loss in capacity39. When treated with CaCl2, algal biomass was evaluated for its efficacy in removing chlorophenols, revealing that the maximum adsorption capacities (qm values) for phenol, 2-chlorophenol, and 4-chlorophenol stood at 4.6 mg/g, 79 mg/g, and 251 mg/g, respectively.

Recently, activated carbon obtained from agriculture or industry residues has become a promising adsorbent to eliminate phenolic compounds because of its availability and the cheapness of precursor material. In the literature, it was reported the use of wood-based and lignite40, olive stones41, apricot stone shells42, palm seed coat43 based-activated carbon is used for the elimination of phenolic mixes. The phenols uptake was found to be depended of various factors, such as the superficial characteristic of the activated carbon, molecular dimension, acidity and the solubility of adsorbate.

Several research44,45,46,47,48 is now available which has focused on the usage of artificial intelligence models to improve the removal percentage, and it can contribute towards sustainability49,50.

Sarang et al.51 delves into the effectiveness of a pseudo-emulsion hollow fiber strip dispersion technique in purifying industrial wastewater, with a particular emphasis on removing ethylparaben and diclofenac. This study employs an artificial neural network (ANN) as a predictive tool, estimating the success of the extraction process based on varied concentrations in the feed, carrier, and stripping phases, with extraction percentage being the key outcome measure. To assess the reliability of these models, statistical analyses such as root mean square error (RMSE) and mean absolute percentage error (MAPE) were utilized. The attainment of high regression values, 0.9956 for ethylparaben and 0.97562 for diclofenac, during the model training phase highlights the precision of the ANN in forecasting extraction outcomes. This precision suggests the method's applicability in the design and optimization of systems for treating industrial effluents.

Samadi–Maybodi et al.52 explore the removal of sarafloxacin (SRF), an antibiotic pollutant, from water bodies using a magnetized metal-organic framework (Fe3O4/MIL-101(Fe)). The study applies response surface methodology (RSM) to determine optimal conditions for the adsorption of SRF, pinpointing an initial concentration of 10 ppm, a neutral pH of 7.0, an adsorbent amount of 20 mg, and a contact time of 40 min as the ideal parameters. The adsorption phenomena were found to align more accurately with the Langmuir isotherm model. In addition, the research developed an artificial neural network (ANN) to predict the removal efficacy of SRF, utilizing the Levenberg-Marquardt algorithm for model training. This model demonstrated significant predictive strength, showcased by high determination coefficients (R2) during training (0.9995) and testing (0.9951) stages, alongside minimal mean squared errors (MSE), affirming its effectiveness as a predictive instrument for SRF adsorption rates.

El-Metwally et al.53 introduce an innovative approach employing a novel fungal system for lipase biosynthesis with the aim of converting oily residues into biodiesel, using Aspergillus flavipes MH47297 to biosynthesize lipase from Nigella sativa, a by-product of agro-industrial processes. The study examines the influence of various factors such as cultural humidity, surfactant concentration, and inoculum density on lipase production, utilizing a Box-Behnken design (BBD) and ANNs in conjunction. This marked the inaugural application of ANNs in modeling the lipase biosynthesis process via semi-solid-state fermentation (SSSF). The optimized conditions predicted by the ANN closely matched the experimental outcomes, with the ANN model demonstrating superior precision over the BBD approach. Gas chromatography analyses confirmed the successful conversion of corn oil into biodiesel, illustrating the efficacy of the lipase produced.

The investigation by Sathishkumar et al.54 explores the application of sophisticated machine learning techniques to evaluate the process of catalytic reduction in water tainted with dangerous nitrophenols and azo dyes. This study makes use of a catalyst composed of palladium oxide-nickel oxide to address pollutants like 4-nitrophenol, 2,4-dinitrophenol, 2,4,6-trinitrophenol, methylene blue, rhodamine B, and methyl orange. The effectiveness of this catalyst in diminishing these contaminants was scrutinized through experiments conducted over varying durations. To estimate the catalyst’s performance, the research applied a range of machine learning models, including linear regression, support vector machines, gradient boosted machines, random forest, and XGBoost. The evaluation of these models was based on statistical measures such as root mean squared error, mean absolute error, and mean absolute percentage error. The findings demonstrated that the model using XGBoost provided the most precise predictions for 4-nitrophenol and 2,4-dinitrophenol, the model using random forest showed the highest efficacy for 2,4,6-trinitrophenol, methylene blue, and rhodamine B, and the model using support vector machines was particularly effective in predicting the reduction of methyl orange. Notably, the catalyst achieved a 98% reduction in a mixture of azo compounds within eight minutes, indicating its strong potential for real-life applications in water purification.

In a comprehensive review by Georgin et al.55, the challenges and technological advancements in the remediation of 17β-estradiol (E2) through adsorption are explored. E2, a potent endocrine disruptor, has been shown to adversely affect aquatic biota and ecosystem health even at low concentrations. Georgin et al. identify a range of adsorbents such as graphene oxides, nanocomposites, and carbonaceous materials that have been effectively employed to remove E2 from water. The review emphasizes that the efficiency of these adsorbents is influenced by factors such as the pH and temperature of the medium, with acidic to neutral pH and ambient temperatures around 298 K being most favorable. They highlight the relevance of the Langmuir and Freundlich models in describing the adsorption isotherms, indicating predominantly low-energy, physical interactions during E2 adsorption. The review calls for the establishment of stringent national and international standards for E2 removal, pointing out the economic and sustainability challenges in implementing these technologies at a large scale. Another significant study by Ahmad et al.56 focuses on the adsorption of bisphenol A (BPA), a common pollutant from plastic production. They introduce a novel hyper cross-linked resin, ICYN-PPA, characterized by its high adsorption capacity and fast kinetics, achieving equilibrium within 350 min. This resin, synthesized from commercially available materials, shows a remarkable adsorption capacity of 112.8 mg.g−1 for BPA. Notably, ICYN-PPA’s thermal stability enhances its applicability in decontaminating BPA-laden effluents. The adsorption process, well represented by the Koble–Corrigan model, confirms the endothermic nature of the interaction, suggesting physical adsorption as the predominant mechanism. Gao et al.57 investigated the removal of 4-nitrophenol (4-NP), a toxic byproduct of petrochemical industries, using MgCo-3D hydrotalcite nanospheres. These nanospheres, synthesized via the hot solvent method, displayed a maximum adsorption capacity of 131.59 mg.g−1. The adsorption process, which predominantly involved hydrogen bonding and electrostatic interactions, adhered to the Langmuir, Redlich–Peterson, and Sips models, indicating a monolayer physical adsorption. Their study also demonstrated the excellent regeneration performance of the nanospheres, maintaining significant adsorption capacity after multiple cycles. In a study by Adebayo and Areo58, a novel composite made from coconut shell and clay was used for the adsorption of phenol and 4-nitrophenol from wastewater. This composite showed exceptionally high adsorption capacities, particularly for phenol, with a Qmax of 1665 mg.g−1. The adsorption process, analyzed through various kinetic and equilibrium models, was best described by the Avrami fractional order and Liu isotherm. The study highlights the composite’s effectiveness, achieving over 86% removal efficiency for the tested effluents, underlining its potential as a low-cost and efficient solution for treating industrial wastewater.

Khan et al.59 conduct a detailed investigation into the potential of carbon material, sourced from the remnants of domestic fireworks, to capture Hexavalent chromium (Cr(VI)) from environments, a known toxic metal. This research meticulously examines how various factors, such as the length of the adsorption period, the acidity or alkalinity (pH) of the environment, the Cr(VI) solution’s warmth, and its initial amount, impact the material's ability to adsorb the metal. To analyze, foresee, and enhance the adsorption mechanism, the study employs a sophisticated combination of response surface methodology and multiple regression analysis alongside an innovative artificial neural networks model integrated with particle swarm optimization. Findings from this integrated approach pinpoint the most effective adsorption scenario: a 94.7 min exposure period, with the Cr(VI) at 50.0 mg/L, at a temperature of 33.6 ℃, and in a highly acidic setting (pH 2). This scenario reached an apex adsorption rate of 1.37 mg.g−1. The study’s analytical comparison reveals artificial neural networks’ superiority in predicting outcomes over multiple regression analysis. Additionally, it aligns with the pseudo-first-order kinetic model in kinetic studies and identifies the Langmuir isotherm as the most accurate descriptor of this adsorption activity, indicating a primary reliance on physisorption. The thermodynamic analysis corroborates the adsorption’s beneficial, spontaneous, and heat-absorbing characteristics.

Alatrista and colleagues’ research60 systematically reviews 55 academic publications between 2011 and 2022, examining the role of metal-organic frameworks (MOFs) in phosphate adsorption processes. This comprehensive analysis indicates that the efficiency of MOFs in trapping phosphate relies on several critical elements, such as the particular variant of MOF used, its synthesis technique, any structural modifications made, and the conditions applied during its operational use. Despite the high theoretical capacity of many MOFs for phosphate adsorption, their practical application in phosphorus recovery over extended periods might be constrained due to the predominance of inner sphere complexation mechanisms. To predict the phosphate adsorption capacities effectively, the study employed machine learning techniques, particularly the use of artificial neural network (ANN) models, which took into account both operational parameters and synthesis characteristics. These models particularly emphasized the significance of the initial phosphate concentration and the use of modulator agents in the synthesis of MOFs.

Aghav and colleagues’ study61 delves into predicting the adsorption competition between phenol and resorcinol on a variety of carbonaceous materials, including activated carbon, wood charcoal, and rice husk ash, through the application of artificial neural networks. This investigation leverages a three-tiered feedforward neural network equipped with a backpropagation mechanism within MATLAB, aggregating data from 29 distinct batch experiments. Variables such as the amount of adsorbent used, initial phenol and resorcinol concentrations, the time span of contact, and the pH value were fed into the neural network to train it. The neural network then produces estimations on the efficiency of removing phenol and resorcinol. The precision of these artificial neural network predictions was rigorously evaluated using a suite of statistical indicators, including mean error, mean square error, root mean square error, and linear regression, all of which affirm the model’s reliability in foreseeing the adsorption dynamics of these substances based on experimental data.

The novelty of this work is to use Haematoxylum campechianum barks and coconut shell which are one of the most abundant agricultural wastes in Campeche State in Mexico, therefore, the work make use of local products for the removal of harmful toxins. The objective of this work is to improve the adsorption capacity of activated carbons obtained from Haematoxylum campechianum bark and coconut shell as agriculture residues for the removal of 3-Nph from aqueous solutions by varying pH solution, contact time, dosage of adsorbent, concentration of 3-Nph, and temperature. Moreover, the study is enhanced by incorporating artificial neural networks, employing deep learning techniques to formulate an empirical regression model. Subsequently, data science methodologies and genetic algorithm optimization are applied to identify the optimal variable combination for maximizing the removal percentage. This distinctive approach sets this research apart from existing literature in the field.

Materials and methods

Chemicals

3-NpH was purchased from Sigma Aldrich (C5H5NO3, MW = 139.11 g/mol, purity, 99.9%, CAS: 554-84-7). The stock solution was prepared by dissolving 1.0 g of 3-NpH in 1000 mL of deionized water and stored in a brown bottle. Solutions between 25 and 1000 mg/L used for further experiments were prepared by dilution of synthetic stock solution. 0.1 N of HCl or 0.1 N of NaOH solutions were prepared to adjust the solution pH from 3 to 8.

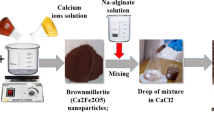
Preparation of carbonaceous material

The carbonaceous material was produced from Haematoxylum campechianum waste using the method described by Abatal et al.62. The bark of Haematoxylum campechianum was chopped, ground and sieved. The material was then washed several times with deionized water at 50 °C to remove any residues and finally dried in an oven at 70 °C for 12 h. After pre-treatment, the material was dried in a deionized water oven at 50 °C for 12 h. The material was then washed several times with deionized water at 50 °C to remove any residues.

After pre-treatment, 50 g of Haematoxylum campechianum was placed in contact with 250 ml of H3PO4 at 50 °C for 3 h (chemical activation), then the filtered solid was dried at 70 °C for 12 h. The heat treatment was carried out at 50 °C for 12 h. The heat treatment was carried out as follows: 50 g of impregnated Haematoxylum campechianum was introduced into a muffle at 500 °C for 60 min, at 10 °C/min. The sample was then cooled to 25 °C. The carbonaceous material was washed with a 5% NaHCO3 solution to remove the residual H3PO4 and then with deionized water until the pH of the filtrate reached a value of 6–7. Finally, the carbonaceous material from Haematoxylum campechianum (CM-HC) was dried at 110 °C for 12 h and then stored in a closed glass bottle and placed in a desiccator.

Characterization techniques

The point zero of charge (pHpzc) of CM-HC was determined adding 0.1 g of each adsorbent to 50 mL of NaCl 0.01 M solution at previously adjusted pH value (pHinitial). Solutions pH of were adjusted from 2 to 12 by adding a drop of 0.1 N of HCl or 0.1 N of NaOH. The sample was agitated for 24 h at ambient temperature. Then, the samples were filtered and final solution pH (pHfinal) of each solution was measured. CM-HC sample was characterized by X-Ray Diffraction methods. The X-ray patterns were collected on an APD-2000 diffractometer using CuKα radiation at room temperature in a range 2θ = 5°–70°. Surface characteristics of CM-HC sample was studied by scanning electron microscopy (SEM) technique was performed to study the superficial structure of the samples before and after adsorption.

Sorption study

In this study, removal of 3-NpH by CM-HC was carried out using batch method. For kinetic study, the experiments were done by addition a mass 0.05 g of CM-HC to 10 mL of 3-NpH at different initial concentrations in a conical tube and agitated at 200 rpm in a multitube shaker apparatus (Model CVP-0228—Cyrlab). Initial concentrations of 3-NpH were 50 mg/L, 100 mg/L and 250 mg/L and contact time was varied from 5 to 1440 min. All tests were carried out in triplicate and the mean value was used in all cases.

After each contacted time at T = 300.15 K and pH = 6, the samples were centrifuged for 5 min at 4500 rpm (Centrificient CRM Globe) in order to separate the adsorbent from aqueous phase. Before to measure the final concentrations of 3-Nph, absorbance (Abs.) of the samples with initial concentrations (Ci) of 3-Nph from 2 to 20 mg/L were measured using UV–visible spectrophotometer (Thermo Scientific Evolution 201/220) at λ = 273 nm. Calibration curve was obtained by the plotting of Abs. vs. Ci which gave a good correlation coefficient (R2 = 1).

The sorption capacity (qt, mg/g) and the removal efficiency (%) were calculated using the Eqs. (1) and (2), respectively:

$${q}_{t}=\frac{{C}_{i-}{C}_{t}}{m}V$$
(1)
$$\% removal=\frac{{C}_{i-}{C}_{t}}{{C}_{i}}*100$$
(2)

Where Ci (mg/L) is the initial concentration, Ct (mg/L) is the concentration at time t (min), qt (mg/g) is the adsorption capacity, V (L) is the volume and m (g) is the mass of the adsorbent.

Table 1 gives the experimental conditions used to investigate the effects of contact times, solution pH, temperature, and dosage of adsorbents on the removal of 3-Nph.

Table 1 Values of contact times, solution pH, temperature and adsorbent dosage parameters used for experimental process.
Full size table

Kinetic models

In order to investigate the mechanism involved in the adsorption of 3-Nph on CM-HC, experimental data were evaluated using four kinetic models, the pseudo-first order (PFO), pseudo-second order (PSO), and Elovich. The equations of PFO, PSO, and Elovich models are expressed by the Eqs. (3), (4), (5) respectively.

$${q}_{\text{t}}= {q}_{e}\left(1-\text{exp}(-{k}_{1}t\right))$$
(3)
$${q}_{\text{t}}= \frac{{k}_{2}{{q}_{e}}^{2}t}{1+{k}_{2}{q}_{e}t}$$
(4)
$${q}_{\text{t}}=\frac{1}{\beta }\text{ln}\left(1+\alpha \beta t\right)$$
(5)

Where qe (mg/g) and qt (mg/g) are the amounts of 3-Nph adsorbed at equilibrium and at time t (min) respectively. \({k}_{1}\left(\frac{1}{min}\right)\) and \({k}_{2}(\frac{g}{mgmin}\)), are the rate constants of pseudo-first, pseudo-second order, and intraparticle diffusion models respectively. β is the constant related to the extent of surface coverage (g/mg) and α is the theoretical adsorption capacity (mg/g.min).

Isotherm models

Experimental data were examined using nonlinear forms of the Langmuir, Freundlich, Temkin, and Redlich–Peterson isotherm models Eqs. (6), (7), (8), (9).

$${q}_{e}=\frac{{q}_{m}{{K}_{L}C}_{e}}{1+{{K}_{L}C}_{e}}$$
(6)
$${q}_{e}={K}_{F}{{C}_{e}}^{1/n}$$
(7)
$${q}_{e}={B}_{T}\text{ln}\left({A}_{T}{C}_{e}\right)$$
(8)
$$ q_{e} = \frac{{K_{RP} }}{{1 + \alpha_{RP} C_{e}^{\beta } }}C_{e} $$
(9)

where qe and qm are the solid phase sorbate concentration in equilibrium (mg/g), Ce is the equilibrium sorbate concentration in liquid phase (mg/L), KF is Freundlich constant (L/g) and 1/n is the heterogeneity factor. KRP (L/g), αRP (L/mg) and β are Redlich–Peterson isotherm constants. β is the exponent which lies between 1 and 0. In this study, solver add-in of Microsoft Excel was used to optimized the variance between the experimental data and predicted isotherms.

Error functions

Despite the use of coefficient of determination (R2) by many studies to provide the best fitting, the nonlinear fits of kinetic and isotherm models were analyzed against the experimental data using error functions in order to verify the suitable model for the adsorption system. In this study, six error functions including the average relative error (ARE), sum of square error (SSE), normalized standard deviation, Δq (%), Chi-square test (χ2), sum of absolute error (EABS), and root mean square error (RMSE) have been calculated employing the equations 10, 11, 12, 13, 14 and 15 respectively63.

$$ARE=\sum_{i=1}^{n}\frac{1}{N}\frac{\left|{(q}_{e,exp}-{q}_{e,cal}\right|}{{q}_{e,exp}}*100$$
(10)
$$SSE= \sum_{i=1}^{n}{{(q}_{e,exp}-{q}_{e,cal})}^{2}$$
(11)
$$\Delta q\left(\%\right)=100 \sqrt{\frac{1}{N-1}\sum_{i=1}^{n}{(\frac{{q}_{e,exp}-{q}_{e,cal}}{{q}_{e,exp}})}^{2}}$$
(12)
$${\chi }^{2}=\sum_{i=1}^{n}\frac{{{(q}_{e,exp}-{q}_{e,cal})}^{2}}{{q}_{e,cal}}$$
(13)
$$EABS=\sum_{i=1}^{n}\left|{(q}_{e,exp}-{q}_{e,cal}\right|$$
(14)
$$RMSE=100 \sqrt{\frac{1}{N-2}\sum_{i=1}^{n}{{(q}_{e,exp}-{q}_{e,cal})}^{2}}$$
(15)

where qe,exp (mg/g) is the experimental adsorption capacity obtained from the Eq. (1) and qe,cal (mg/g) is the calculated adsorption capacity obtained from the nonlinear forms of PFO and PSO kinetic models or isotherm models (Langmuir and Freundlich), and n is the number of experimental data points.

Adsorption and desorption study

The recovery of 3-Nph and the regeneration of the adsorbent material are very important in adsorption processes, sustainability and cost-effectiveness of adsorbents. For this purpose, tree adsorption/desorption cycles were carried out using NaOH solution as desorbing agent. For the adsorption step, 100 mg of CM-HC were mixed in Erlenmeyer flasks with 50 mL of 3-Nph at 100 mg/L (Ci), and stirred for 24 h at T = 300.15 K. The mixture was then filtered and the final concentration of 3-Nph (Cf) in the supernatant was determined by UV–vis spectrophotometric analysis.

The quantity of 3-Nph adsorbed after contact with AB-HC was calculated using Eq. (1).

For desorption process, 50 mL of 0.2 M NaOH was added to 3-Nph-loaded CM-HC. The mixture was agitated at 300.15 K for 24 h. After this time, the sample was filtered and the residual concentration of 3-Nph was measured.

The quantity of 3-Nph desorbed Qdes (mg/g) was calculated using this equation Eq. (16)

$${q}_{des}= \frac{{C}_{des}V}{m}$$
(16)

Where, Cdes (mg/L) is the concentration of 3-Nphafter desorption, V(L) is the volume of NaOH solution, m (g) is the mass 3-Nph-loaded CM-HC.

The regenerated CM-HC was rinsed for several time with deionized water and dried at 105 °C for 2 h before the next cycle of adsorption/desorption.

Results and discussions

Characterization of CM-HC

Figure 1 shows that the point of zero charge of CM-HC equal to 6.5. This result is similar with those obtained from other precursor materials such as Dipterocarpus alatus (pHpzc = 6.3)64, rice husk (pHpzc = 6.8)65. Therefore, when the solution pH is above than the pHpzc (pH > pHpzc), the surface of CM-HC is negatively charged and the cationic species will be preferentially removed, whereas values of pH are below than pHpzc (pH < pHpzc), the charge of the surface of CM-HC will become positive and then anionic species are preferentially attracted via electrostatic interactions66.

Fig. 1
figure 1

pHpzc of CM-HC.

Full size image

XRD diffraction pattern of CM-HC is presented in Fig. 2. It can be observed that HCAC has a semicrystalline structure related to the amorphous region between 10 and 40º corresponding to the carbonic fraction due to the preparation and characterization of activated carbons from different precursors67.

Fig. 2
figure 2

XRD pattern of CM-HC.

Full size image

Scanning electron microscope (SEM) analysis was carried out in order to investigate physical surface morphology of CM-HC. The SEM micrographs of CM-HC (Fig. 3) show that the particles of the synthesized activated carbon have a rough surface and an irregular shape with a variety of randomly distributed cavities which can provide easy access transport toward the adsorption sites68. The elemental composition of the activated carbon was performed by energy dispersive X-ray spectroscopy (EDS) is also shown in Fig. 3. In CM-HC, the material consists predominately of carbon and oxygen, the summary of these two elements to be 97.9% per weight. The rest of the composition (2.1%) corresponds to metallic fractions (Ca, K, Na and Mg).

Fig. 3
figure 3

SEM images and EDS analysis of CM-HC.

Full size image

The mean pore diameter of CM-HC calculated by BET equations were 2.1382, with a surface area of 124.15 m2/g. The difference in the surface properties can be attributed to the type of biomass precursor. Beker et al., reported that the adsorption of phenols is carried out in ulramicropores and micropore with diameters between 0.7 and 2 nm69. Therefore, it is suspected that both adsorbents can be usefully used for removal of 3-nitrophenol from aqueous solution, due to the smaller molecular diameter of 3-Nph (0.6202 nm)70.

Sorption study

Adsorption isotherms at different solution pH

The study of pH effect on the removal of 3-NpH on MC-HC was performed at ambient temperature by adjusting the solution pH of 3-Nph at 3, 6 and 8. For each solution, initial concentration was varied from 25 to 1000 mg/L.

Usually, at low pH values, anions are favorably adsorbed on the sorbent surface due to the presence of high concentration of H+ ions, while at high pH values, cations are more adsorbed on the sorbent surface as a result of high concentration of OH− ions71. In addition, it well known that the degrees of dissociation and ionization of organic compounds as well as the adsorbent surface charge depended to the pH solution72, therefore, it is important to study the effect of pH solution on the adsorption of 3-NpH on MC-HC.

Figure 4a–c show the adsorption isotherms of 3-Nph on MC-HC at initial pH 3, 6 and 8, respectively. It can be seen that the adsorption capacity increases between pH 3 and 6, and then decreases for pH 8. This suggests that, the interaction of 3-Nph with CM-HC is more favorable in the acid than alkaline medium. In previous researches, the uptake for phenols in certain pH range present a dome-shaped curve25,73, which is attributed to the change in nature of adsorbent (surface charge) and adsorbate species at different pH69.

Fig. 4
figure 4

Plot of adsorption isotherms for 3-Nph on MC-HC at (a) pH = 3, (b) pH = 6 and (c) pH = 8.

Full size image

At pH between 3 and 6, the surface of CM-HC is positively charged (pHpzc(CM-HC) = 6.7. Furthermore, in this pH range, 3-NpH mainly present as neutral species (pKa (3-Nph) = 8.3 at 298 K), however the concentration of its anionic form (C6H5NO−3) increases with increasing of solution pH and as consequently higher uptakes at pH = 6 compared to pH = 3, by means of electrostatic attractions between the surface charged positively and the anionic form of 3-NpH74,75. At pH = 8, the uptake of 3-Nph declined. This result can be attributed to the electrostatic repulsion force between the surface of CM-HC negatively charged and the abundance anionic form of 3-Nph. Previous investigations have reported similar behavior of phenol43,69,73,76, nitrophenols (2,4-dinitrophenol, 3-nitrophenl, 4-nitrophenol)42,76,77 and chlorophenols (2,4-dichlorophenol, 2-chlorophenol, 4-chlorophenol)42,76 adsorption on activated carbons.

Nonlinear equations of Langmuir, Freundlich, Temkin, and Redlich-Peterson isotherm models were used to investigate the adsorption mechanism. Table 2 shows the equation´s parameters with their respective correlation coefficients (R2).

Table 2 Langmuir, Freundlich, Temkin, and Redlich-Peterson isotherm parameters for the adsorption of 3-Nph on CM-HC at different solution pH.
Full size table

The results indicate that the Langmuir and Redlich-Peterson models were well described the adsorption data for CM-HC in the pH range studied with R2 values between 0.9805 and 0.9985 compared to Freundlich model (0.9454 ≤ R2 ≤ 0.9767) and Temkin (0.9768 ≤ R2 ≤ 0.9954). This result suggests the formation of multilayers on the adsorbent surface where the interaction between phenols and surface of carbonaceous materials is due Van der Waals’ forces and π–π interactions42. As shown in Table 2, the maximum adsorption capacities, qmax calculated from Langmuir isotherm model were 100.523, 128.625, and 87.284 mg/g, at pH = 3, 8, and 8, respectively. The values of Redlich–Peterson exponential constant, β are close to unity (0.794–0.944), this indicates that the Redlich–Peterson model reduces to the Langmuir model78.

As can be seen from Table 3, the calculated values of error functions APE, SSE, ∆q (%), χ2, EABS and RMSE from the experimental data were lowest for Langmuir and Redlich-Peterson than Temkin and Freundlich isotherms. This result proves the applicability of Langmuir and Redlich–Peterson isotherm models to describe the adsorption mechanism of 3-Nph on CM-HC.

Table 3 Values of error functions of adsorption isotherm models of 3-Nph on CM-HC at different solution pH.
Full size table

Effect of contact time on adsorption equilibrium

The study of adsorption kinetics was done at ambient temperature without any adjustment of solution pH. Figure 5a–c show respectively the adsorbed amount of 3-NpH (mg/g) by MC-HC versus contact time (min) with 3-Nph initial concentration (Ci) at 50, 100 and 250 mg/L. It can be seen that within 120 min, 80.1%, 81.7%, and 65.3% of 50, 100, and 250 mg/L of 3-NpH were removed. The higher rate of 3-Nph adsorption in this first stage can be attributed to the availability of adsorption site on the adsorbent surface79. After this time, adsorption capacity was gradually increased as increase contacted time reaching equilibrium, which varied from 180 to 360 min depending to initial 3-Nph concentration (the faster equilibrium time was found for Ci = 50 mg/L). This result can be attributed to the more availability of the uncovered surface area of the adsorbents at low solute concentrations76,80. In this study, the equilibrium time was found to be minor compared to other equilibrium times reported by other studies for the removal of phenols using different carbonaceous materials81. For Ci = 50, 100, and 250 mg/L, the adsorption capacity reached 8.97, 17.38, and 41.37 mg/g, at equilibrium time, respectively. Experimental data were analyzed using nonlinearized equations of pseudo-first-order (PFO), pseudo- second-order (PSO), and Elovich kinetic models. Table 4 displays the kinetic parameters of PFO (k1, qe), PSO (k2, qe), and Elovich (α,β) with their corresponding correlation coefficients R2.

Fig. 5
figure 5

Variation of adsorption capacity of MC-HC against contact time (min) at (a) Ci = 50 mg/L, (b) 100 mg/L and (c) 250 mg/L.

Full size image
Table 4 PFO, PSO, and Elovich kinetic parameters for different initial concentrations of 3-Nph.
Full size table

The results showed in Table 4 indicate that for Ci = 50 and 100 mg/L, pseudo-second order model displays higher coefficient regression (R2 = 0.9840, 0.9892) in comparing to pseudo-first-order (0.9043, 0.8744) and Elovich (R2 = 0.8182, 0.8839) models. Also, it can observe that the calculated adsorption capacities obtained for the PSO model (qe,cal = 9.05 and 17.26 for Ci = 50, 100 mg/L, respectively) are agree to experimental data (qe,exp = 8.97 and 17.38, mg/g for Ci = 50, 100 mg/L, respectively). As seen in Table 4, the rate constants (k2) decrease with increasing of initial concentration confirming that the adsorption process was faster for lower initial concentration. For Ci = 250 mg/L, it can be seen that the nonlinear Elovich curve pass near to experimental data (Fig. 5c). Also, Elovich model gives higher value of R2 (0.9842) compared to PFO (R2 = 0.7834) and PSO (R2 = 0.9349) suggesting that the adsorption process is controlled by chemisorption mechanism.

Elsayed et al.82 developed a biocomposite aerogel (Amf-CNF/LS) and investigated its efficacy in removing methylene blue (MB), rhodamine B (RhB), and cadmium ions (Cd2+) from synthetic wastewater. The study specifically explored the influence of contact time and stirring speed on the adsorption process. The results showed that contact time significantly impacts the adsorption capacity, with rapid increases observed within the initial minutes of exposure, suggesting a high affinity between the aerogel and contaminants. The equilibrium was quickly reached, indicating the aerogel’s efficiency in fast contaminant uptake, which is beneficial for practical wastewater treatment applications where quick removal is necessary. Stirring speed was another critical factor that influenced the adsorption efficiency. Higher stirring speeds improved the mass transfer of the adsorbate molecules to the aerogel’s surface, enhancing the adsorption rate. This adjustment helped to minimize the boundary layer around the adsorbent, facilitating faster adsorbate uptake.

As shown in Table 5, the values obtained from the six error equations considered in this study (Eq X to Eq X) are minor for PSO (for Ci = 50 and 100 mg/L) than PFO and Elovich models, while for Ci = 250 mg/L, the error function values were lower for Elovich than for PFO and PSO models. This confirms the results obtained from the nonlinear of PSO, PFO and Elovich models (R2), and agree the feasibility of PSO model (for Ci = 50 and 100 mg/L) and Elovich model (for Ci = 250 mg/L).

Table 5 Values of error functions of PFO, PSO and Elovich kinetic models of 3-Nph (Ci = 50, 100 and 250 mg/L) on CM-HC.
Full size table

Adsorption isotherms at different adsorbent dosage

The effect of adsorbent dosage on the adsorption capacity of 3-NpH was investigated at ambient temperature using isotherm experiments without modifying solution pH. In this study, dosages of adsorbent were 2, 4, 8 and 10 g/L, and initial concentrations of 3-Nph were varying from 25 to 1000 mg/L. Figure 6a–d show the equilibrium relationships between the 3-Nph concentrations in solution Ce(mg/L) and the adsorptive capacities at different dosages of CM-HC. It can be seen that for all adsorbent dose, the adsorption capacities of 3-Nph (qe (mg/g)) increase with the increasing of Ce (mg/L).

Fig. 6
figure 6

Adsorption isotherms of 3-Nph on CM-HC with dosage (a) 2 g/L, (b) 4 g/L, (c) 8 g/L and (d) 10 g/L.

Full size image

The experimental adsorption isotherms data were analyzed using nonlinear equations of Langmuir, Freundlich, Temkin, and Redlich–Peterson isotherm models. Table 6 presents the isotherm parameters with adsorbent dose from 2 to 10 g/L. The results indicate that the adsorption isotherm was depended of adsorbent dosage. According to correlation coefficients showing in Table 6, Freundlich and Redlich–Peterson isotherm models were best described to the sorption data for 2 g/L of adsorbent dose, whereas, for CM-HC dosage between 4 to 10 g/L, Langmuir and Redlich-Peterson isotherm models were well to describe the adsorption process. As seen in Table 6, it was found that the Langmuir constants KL increased from 0.309 × 10−2 to 3.9217 × 10−2 L/mg with increasing of adsorbent dosage from 2 to 10 g/L, which indicates the high affinity at low dosage of CM-HC. Additionally, it can be noted that the value of Freundlich constant 1/n (adsorption intensity) correspond to 2 g/L was lower compared than adsorbent dosages between 4 and 10 g/L, which means that the adsorption of 3-Nph is more favorably at lower adsorbent dosage. The Redlich–Peterson parameters presented in Table 6, show that for all values of adsorbent dosage, the exponent constant β is between 0 and 1, which indicates a good adsorption78. In addition, for dosage 4, 8 and 10 g/L, the values of β were close to unity (β = 1.003, 0.878, and1.0267), therefore, the Redlich–Peterson model reduces to the Langmuir model to describe the 3-Nph adsorption, whereas for dosage 2 g/L, β < 1 (β = 0.421) and αRP, KRP >> 1 (αRP = 4.604 and KRP = 18.794), then the isotherm was approaching the Freundlich form, where KRP/αRP and (1- β) are related to KF and n Freundlich parameters, respectively83.

Table 6 Langmuir and Freundlich isotherm parameters for the adsorption of 3-Nph on CM-HC at different dosages.
Full size table

Based on the values of error functions obtained by Eqs. (7), (8), (9), (10), (11), (12), it can observed from Table 7, that for adsorbent dosage 2 g/L, the Freundlich and Redlich–Peterson show the lowest values of APE, SSE, ∆q (%), χ2, EABS, and RMSE. In the case of adsorbent dosages from 4 to 10 g/L, Langmuir and Redlich–Peterson present the less values of error functions compared to Freundlich and Temkin isotherm models. These results were in agreement with the finding correlation coefficients and validate the studied isotherm models.

Table 7 Values of error functions of adsorption isotherm models of 3-Nph on CM-HC at different dosage.
Full size table

As seen in Fig. 7a, it was found that as the amount of 3-NpH (mg/g) decrease from 236.156 to 79.441 mg/g when the adsorbent dose increases from 2 to 10 g/L. This result can be attributed to the split in the flux or the concentration gradient between solute concentration in the solution and the solute84. Figure 7b, shows that the removal percentage of 3-NpH increase by the increasing of the sorbents dosage, this result can be attribute to the increase of the number of sorption site available, thus allow the increasing of removal percentage of 3-NpH85.

Fig. 7
figure 7

Effect of sorbents dosage (g/L), on the (a) amount of 3-NpH sorbed, qm (mg/g) and (b) percentage of 3-NpH removal; solution pH: 5.6.00; temperature: 297 K, agitation speed: 150 rpm; contact time: 24 h.

Full size image

Adsorption isotherms at different temperatures

Adsorption isotherms of 3-NpH at temperatures 300.15, 313.15 and 330.15 K on CM-HC are shown in Fig. 8a–c, respectively. It can be seen that the temperature has a significant effect on the removal of 3-Nph. As shown in these figures, it can observe that the adsorption capacity of CM-HC decreases with increasing of temperature confirming that the adsorption process of 3-NpH on CM-HC is controlled by an exothermic reaction. Previous studies of adsorption of phenolic compounds showed an exothermic process using oil palm shell activated carbon86, carbon black87, cattail fiber-based activated carbon88, and anaerobic granular sludge89 as adsorbents. In these studies, it was suggested that the increase of temperature may cause a breaking of attraction force between the adsorbate molecules and the active sites on the surface of carbonaceous materials leading to decrease of adsorption capacity90. The equilibrium data at temperature 300.15, 313.15 and 330.15 K were fitted using nonlinear equations of Langmuir, Freundlich, Temkin and Redlich–Peterson isotherm models. Table 8 shows the isotherm parameters with their correlation coefficients R2. It was found that for all temperatures studied, the R2 for Langmuir and Redlich-Peterson isotherm models are higher than Freundlich, Temkin isotherm models.

Fig. 8
figure 8

Adsorption isotherms of MC-HC at temperature (a) 300.15, (b) 313.15 and (c) 330.15 K.

Full size image
Table 8 Langmuir and Freundlich isotherm parameters for the adsorption of 3-Nph on CM-HC at different temperatures.
Full size table

The maximum adsorption capacities of 3-Nph on CH-HC were 128.625 107.704, and 105.441 mg/g at 300.15, 313.15 and 330.15 K, respectively. Likewise, the values of Langmuir constant KL decrease with increasing of temperature, which indicate the higher affinity at lower temperature and confirming that the adsorption of 3-Nph is an exothermic nature. Furthermore, it can be noted that the values of parameter β are close to unity, confirming that the adsorption isotherms are best approaching to Langmuir model than Freundlich model. Table 9 presents the values of error functions. It can be observed that among four studied isotherm models, the Langmuir and Redlich–Peterson isotherm showed less values, confirming that the Langmuir model is the best fitted model for the range temperature studied.

Table 9 Values of error functions of adsorption isotherm models of 3-Nph on CM-HC at different temperatures.
Full size table

Adsorption mechanisms

The proposed adsorption mechanisms of 3-Nph on CM-HC depended to the functional groups present on the surface on the adsorbent. In the recent study, we have found that the surface of CM-HC exhibits the following functional groups: OH, C=O, C–O, and C=C (aromatic ring)91. Therefore, electrostatic interaction can be carried out between the negative charge of OH, C=O, C–O groups with the positive charge of the nitrogen from 3-Nph. Also, the OH functional group may interact with the oxygen from phenol group by hydrogen bonding. Other interaction between the C=C group with the benzene from 3-nitrophenol by π–π interactions. Additionally, CM-HC has pores that may allow the 3-Nph molecules. Figure 9 shows the electrostatic interactions, hydrogen bonding, π–π interactions, and porous adsorption as a possible adsorption mechanism of 3-Nph onto CM-HC.

Fig. 9
figure 9

Adsorption mechanism of 3-Nph on CM-HC.

Full size image

Adsorption and desorption cycles

Figure 10 shows the adsorption and desorption cycles of 3-Nph onto AB-HC. It can be seen that adsorption and desorption capacities (qads and qdes) of 3-Nph has decreased. The decrease in adsorption capacity can be attributed to the possible remnant of 3-Nph on the surface of the CM-HC due to the strong interaction between adsorbate and adsorbent, and incomplete desorption of 3-Nph using NaOH. In other studies, moderate adsorption of nitrophenols was observed after the first cycle, which is attributed to the destruction of the porous structure of the activated biochar under alkaline experimental conditions. To improve the reusability of CM-HC, it is suggested to use other eluents or even temperature of aqueous solution.

Fig. 10
figure 10

Adsorption and desorption cycles of 3-Nph on CM-HC.

Full size image

Deep learning artificial intelligence framework to optimize the adsorption capacity of carbonaceous material

In this section, the focus centers on the implementation of a deep learning92 artificial intelligence (AI) algorithm utilizing an artificial neural network93. Subsequently, optimization based on a genetic algorithm94 is applied. This comprehensive procedure is executed methodically, with the initial step encompassing data visualization and description, followed by AI implementation and optimization.

Data visualization and description

Regarding data visualization and description, the entire experimental dataset is initially formatted and consolidated into a structure, as illustrated in Table 1095. Each column in this table contains variables such as time, initial concentration, pH, dosage, temperature, and the fitness function (removal percentage). Each row corresponds to an individual experimental run, mirroring the real experimental procedure, which can be resource-intensive. For instance, the execution of experiment run no. 8 required 1440 min. Despite the substantial time investment, consolidating the database at this juncture proves beneficial.

Table 10 General format of the experimental data. Data publicly available at: https://dx.doi.org/10.6084/m9.figshare.24545587.
Full size table

To elucidate the data description, violin plots (Fig. 11) are employed for each of the five variables and the removal percentage, the latter being the fitness function. The violin plot is chosen for its ability to convey data properties akin to a box and whisker plot, while also providing insights into data distribution. An alternative method for understanding data distribution is through histograms, as depicted in the scatter matrix of Fig. 12.

Fig. 11
figure 11

Violin plot of the variables and the fitness function.

Full size image
Fig. 12
figure 12

Scatter matrix with histograms between the design variables and the fitness function.

Full size image

The violin plot reveals distinctive patterns, such as a concentration of the time variable towards the upper end, aligning with the scatter matrix histogram. Furthermore, there is a noticeable concentration at the lower end, indicating durations less than 200 min. Notably, there is an abundance of experimentation for lower initial concentrations (< 200 units), a trend consistent with the scatter matrix results showcasing the highest data density in this range.

The pH variable exhibits its highest density just below the neutral point, with bottlenecks observed around pH values of 4–5 and 7. This aligns with the scatter matrix, emphasizing lower probability density at the ends compared to a peak at 6. The dosage and temperature graphs share a similar pattern, with higher probability distribution for lower dosages (< 2 units) and temperatures (< 305 K). However, as dosages and temperatures increase, the number of data points decreases.

The removal percentage’s violin plot correlates intriguingly with the histogram distribution in the scatter matrix. The highest frequency of removal percentage occurs at approximately 90 units, with a noticeable reduction in data points beyond this threshold. The upper end of the 90-unit range exhibits a more substantial data distribution compared to the lower end, suggesting a potential combination of the five design variables yielding maximum removal percentage.

It should be noted that the dataset used for the ANN analysis comprises 87 entries, which may be considered small for robust ANN applications. This limitation could potentially affect the generalizability of the model. To address this issue in future studies, we propose to expand the dataset through additional batch experiments to enhance the training process and improve the model’s accuracy and generalizability. Further, employing cross-validation methods or increasing the diversity of the data points could also contribute to more reliable ANN predictions. These steps will help in mitigating the effects of the current dataset size and provide a more robust framework for ANN applications in adsorption batch experiments.

In this phase, correlation heat maps incorporating coefficients from Pearson96, Spearman97, and Kendall98 methods have been successfully implemented and are visually represented in Fig. 13. Notably, all three heat maps exhibit a correlation coefficient of 1 along the diagonal, indicating pairwise correlations such as time-time, initial concentration with initial concentration, among others. Conversely, the data situated above or below the diagonal represents a mirrored image. Consequently, it is appropriate to focus solely on interpreting one side of the correlation heat map. The primary emphasis of this discussion is on the significance of the correlation coefficient values and the distinctions arising from the implementation of different correlation methods. It is imperative to acknowledge that, in all instances, a positively correlated coefficient is exclusively observed for time and dosage, with Pearson correlation coefficients of 0.26 and 0.38, respectively. It can be asserted that the relationship between time and the removal percentage does not exhibit a strongly positive correlation; however, dosage demonstrates a more robust positive correlation with a coefficient of 0.38. Nonetheless, this interpretation undergoes notable variations when examining the Kendall correlation, which implies that time possesses a more potent correlation coefficient with the removal percentage compared to dosage—an observation similarly noted with the Spearman method. This leads to the conclusion that the determination of whether time or dosage more significantly influences the removal percentage is inconclusive. Nevertheless, all three algorithms consistently affirm the existence of a positive relationship. The correlation coefficient of pH, as determined by all three methods, is negative. However, its value is in close proximity to zero, signifying that pH is not the most robust or influential variable affecting the removal percentage. A parallel trend is observed for temperature, displaying a negative correlation coefficient, suggesting that lower temperatures are preferable for achieving higher removal percentages. The most substantial correlation is identified for the initial concentration concerning the removal percentage, with values of −0.59 for both Pearson and Spearman correlations, and −0.45 for the Kendall correlation. This indicates that the initial concentration emerges as the most influential parameter for the removal percentage, with lower initial concentrations proving more conducive to achieving favorable outcomes.

Fig. 13
figure 13

Coefficient of correlation of Pearson, Spearman, and Kendall.

Full size image

Deep learning artificial neural network

For enhanced accuracy and mitigating multicollinearity issues within the dataset, an advanced approach involving artificial neural networks (ANNs)99 was implemented for deep learning purposes100,101. Previous attempts using traditional machine learning techniques such as multivariate regression analysis and support vector machine yielded unsatisfactory results, prompting the adoption of ANNs.

The initial ANN configuration consisted of a single hidden layer comprising 10 neurons. Architecture optimization was pursued by employing the Adam102 optimizer in Python103, within the Google Colab environment104. Despite multiple iterations, the mean square error (MSE)105 ranged between 75.8409 and 156.8976, indicating suboptimal performance.

To address this, manual iterations were conducted by varying the number of hidden layers and neurons, transitioning from a structure of 5-10-10-1 to 5-100-100-1. Unfortunately, this did not yield satisfactory results. The implementation was then transferred to MATLAB106, where the scaled conjugate method107, known for its suitability in regression fits for small and noisy datasets, was adopted.

The optimized architecture identified was 5-14-14-1 (refer to Fig. 14). This architecture includes an input layer with five variables, two hidden layers with 14 neurons each utilizing a tansig activation function, and an output layer representing the removal percentage with a linear activation function.

Fig. 14
figure 14

Optimal deep learning architecture.

Full size image

The Tansig function, or hyperbolic tangent sigmoid transfer function, is a popular activation function used in neural networks, particularly in the context of artificial neural networks (ANNs). Mathematically, it is defined as: \(tansig\left(x\right)=\frac{2}{1+{e}^{-2x}}-1\), where x represents the input to the function. This function outputs values that range from −1 to 1, making it particularly useful for modeling data that have been normalized to this range. The Tansig function is an S-shaped curve, similar to the logistic sigmoid function, but with outputs spread over a wider range on the y-axis. This characteristic allows the function to handle negative values more naturally and makes it beneficial for problems where the symmetry around zero can help in faster convergence of the learning algorithm. The use of the Tansig function in neural networks is advantageous because of its non-linear nature, which enables the network to learn complex patterns that linear models might not be able to capture. Additionally, the gradients of the Tansig function are stronger for values in the range closer to zero, which can lead to more effective and efficient training phases, especially during backpropagation where gradients are used to update the weights. In the context of our ANN model used to analyze adsorption batch experiments, employing the Tansig function as the activation helps the network in handling varying dynamics of the data while maintaining stable learning and convergence behaviors. This choice is crucial for the performance of our ANN, particularly given the constraints imposed by the relatively small size of the dataset.

The iterative adjustment of bias and weight matrices in each epoch led to the optimal values at Epoch 228 (see Fig. 15), resulting in MSE values of 4.07, 18.406, and 6.2122 for the training, testing, and total datasets, respectively (refer to Table 11).

Fig. 15
figure 15

Convergence criteria of the Mean Squared Error for the best architecture.

Full size image
Table 11 Statistical performance indicators for the best architecture.
Full size table

The coefficient of determination, corresponding to R-squared values, for training, testing, and the total dataset were 0.98759, 0.94280, and 0.98108, respectively. This confirmed the efficacy of the selected architecture and convergence criteria. The output generated from this optimized model was saved for further analysis and interpretation.

Upon establishing the architecture and statistical characteristics of the proposed artificial neural network (ANN) model, the subsequent phase involves a comprehensive graphical visualization to assess the model’s performance. While statistical indicators provide crucial insights, graphical representations offer additional nuances that may not be discernible through numerical metrics alone.

In Fig. 16a, the regression fit graph portrays the relationship between the target variable (experimental removal percentage) and the model's output (simulated removal percentage). Ideally, a perfect linear correlation between these variables signifies an impeccable goodness of fit. The linear fit equation reveals a slope of 1.00, indicating a consistent rate of change between the target and output. However, a bias of −0.56 is observed, implying a slight deviation of the y-intercept from the origin, a phenomenon rationalized by the scarcity of data points below a removal percentage of 50. Notably, the graph includes representations of both training and testing data. Strikingly, the statistical performance of the training dataset aligns more closely with the linear regression line than the testing data. Instances of substantial deviation from the regression line in the testing data caution against over-reliance on this subset for optimization, as poorly predicted points may lead to local optima47.

Fig. 16
figure 16

(a) Regression fitting for the optimal architecture. (b) Verification of the assumptions of the regression fit, including normality, independence, and homoscedasticity from left to right.

Full size image

Furthermore, adherence to key regression assumptions is imperative for robust model validation108. Figure 16b delves into the examination of normality, independence, and homoscedasticity of errors. The normality of errors is scrutinized using a QQ-plot, where the majority of data points closely adhere to the theoretical normal distribution line. However, six outlier data points, positioned at the extremes of the distribution, warrant careful consideration during the optimization phase. Independence of errors is assessed through a plot of residuals against experimental run (row number). The absence of a discernible pattern in this plot affirms the independence of errors. Intriguingly, the same six outlier data points identified earlier exhibit distinctive characteristics, emphasizing the need for meticulous handling during optimization. Finally, homoscedasticity of residuals is validated via a plot correlating predicted values with residuals. The absence of a defined pattern in this plot further confirms the homogeneity of residuals. Notably, the six outlier points exhibit unique behaviors in this context as well, underscoring their significance in the overall analysis.

In conclusion, this multifaceted graphical analysis provides a comprehensive evaluation of the ANN model’s performance, ensuring a thorough understanding of its strengths and potential limitations in addressing the research objectives.

The validation of our deep learning artificial neural network (ANN) is a critical step to ensure the reliability and accuracy of the model’s predictive capabilities. We employed a robust validation strategy that involves splitting the data into distinct sets: training, testing, and validation. This separation ensures that the model is not only trained but also fine-tuned and tested against unseen data. During the training phase, the model’s parameters are adjusted to minimize the error on the training set. Then, the validation set is used to tune the hyperparameters and prevent the model from overfitting, which is critical given the relatively small dataset. The final model’s performance is assessed on a separate test set, which provides an unbiased evaluation of its predictive power. The mean square error (MSE) and the coefficient of determination (R2) are calculated for each set to quantify the model’s accuracy and predictive performance. These metrics confirm whether the model can effectively generalize beyond the training data.

Ensuring the repeatability of our ANN model involves detailed documentation of the model architecture, including the number of layers, the type of activation functions used (e.g., Tansig), and the optimization algorithms (e.g., scaled conjugate method). The iterative process of model training is set to reproducible conditions, with fixed seeds for random number generators and consistent training-validation-test splits. This practice is vital to achieve consistent results when the model is re-run under the same conditions or by other researchers. Additionally, the robustness of the model is tested through repeated runs, where the stability of the results (such as MSE and R2 values) is checked across different iterations to ensure that the outcomes are not anomalies but reproducible findings.

Optimization using genetic algorithm

The employment of deep learning has facilitated the establishment of an empirical correlation between various tuning parameters and the fitness function, represented by the removal percentage. This correlation serves as a fitness function equation, enabling the formulation of an optimization problem. The objective of this optimization is to maximize the removal percentage by adjusting decision variables such as time, initial concentration, pH, dosis, and temperature. The decision variable bounds are defined as lower bound = [15, 50, 3, 1, 300.15] and upper bound = [1440, 250, 8, 10, 330.15]. To conform to typical optimization conventions geared towards minimization, the removal percentage is multiplied by −1. A noteworthy concern arises from the lack of a continuous dataset for digital twin modeling. Despite the high performance demonstrated during empirical modeling, the optimization process operates with a potential error margin due to the finite nature of the removal percentage (with a maximum value of 100).

The optimization problem is expressed as follows:

$$ {\text{Minimize}}: \, - {1 } \times {\text{ removal percentage subject to lower bound }} \le \, \left[ {{\text{time}},{\text{ initial concentration}},{\text{ pH}},{\text{ dosis}},{\text{ temperature}}} \right] \, \le {\text{ upper bound }}0 \, \le {\text{ removal percentage }} \le { 1}00. $$

Prior to mathematical optimization, a critical step involves visualizing the optimization data to identify potential regions for improvement. Given the multivariate nature of the data (six dimensions), a parallel coordinate plot is adopted (Fig. 17). In this plot, red lines signify a higher tendency for improved removal percentage. Analysis of the red lines indicates that lower temperatures, reduced dosis, moderate pH values, moderate initial concentration, and extended time are favorable for optimization. However, a formal algorithmic application is required to substantiate these observations.

Fig. 17
figure 17

Parallel coordinate plot.

Full size image

To address this, a single-objective genetic algorithm109 implemented in MATLAB, utilizing the ‘ga’ function, is employed for optimization. The chosen parameters include a population size of 50, a maximum of 100 generations, and parallel computing. The results of this optimization process are tabulated in Table 12.

Table 12 Optimality based upon simulation and experimentation.
Full size table

In Table 12, simulation results stemming from data-driven optimization through a deep learning algorithm are presented. Notably, the simulated maximum removal percentage reaches 100.001, a theoretically ideal value with a tolerance level of 0.001. While this represents an idealized outcome, the simulation aids in identifying decision variable combinations leading to this optimality. However, acknowledging the inherent error margin in the digital twin modeling and optimization process, it is crucial to validate the true optimality through experimentation.

A subsequent experiment, conducted under conditions aligning with the optimal points identified in simulation, yields a removal percentage of 98.77%. The percentage difference between this experimentally verified optimality and the simulated result is a mere 1.24%, demonstrating the success of applying deep learning with genetic algorithm optimization. Consequently, it is recommended to prioritize experimental optimality for robust validation.

Conclusion

It is concluded that the carbonaceous material from Haematoxylum campechianum waste (CM-CM) proved to be an effective low-cost adsorbent to remove 3-nitrophenol from aqueous solution. The experiment results show that the uptake capacity of 3-Nph by CM-HC is dependent of contact time, pH of solution, adsorbent dosage and temperature parameters. Removal of 3-Nph was found to be more favorable at pH = 6 and at T = 300.15 K. Over concentrations studied, adsorption equilibrium data showed the best fitted Langmuir model at all pH solutions, dosage of adsorbent and temperatures studied. The maximum adsorption capacity of CM-HC was calculated as 236.156 mg/g. The results of kinetic study show that for Ci (3-Nph) = 50–100 mg/L, the pseudo-second order model was best fit model to the adsorption of 3-Nph. Some other conclusions from the data analytics are following:

  1. 1.

    The relationship between time, dosage, and various environmental factors with the removal percentage is explored through correlation analysis using Pearson, Spearman, and Kendall methods. Despite differences in the strength of correlations between the methods, a consistent positive correlation exists between time and dosage with the removal percentage. The interpretation varies slightly among methods, highlighting the nuanced influence of correlation algorithms. Notably, the initial concentration emerges as the most influential parameter, emphasizing its significance in achieving favorable outcomes. The study suggests that determining whether time or dosage more significantly influences the removal percentage remains inconclusive, but the positive relationship is consistently affirmed by all three correlation algorithms.

  2. 2.

    The identified 5-14-14-1 architecture, fine-tuned over 228 epochs, demonstrated robust performance with mean squared error (MSE) values of 4.07, 18.406, and 6.2122 for training, testing, and total datasets, respectively. The coefficient of determination (R-squared) values further confirmed the efficacy of the selected architecture. The graphical analysis of the model’s performance revealed a well-fitted linear correlation between experimental and simulated removal percentages, with attention to potential pitfalls in relying solely on the testing dataset for optimization. The assessment of normality, independence, and homoscedasticity of errors provided a comprehensive understanding of the model’s strengths and limitations.

  3. 3.

    Through the approach of a single-objective genetic algorithm implemented in MATLAB, a theoretically ideal removal percentage of 100.001 was simulated, aiding in identifying decision variable combinations leading to optimality. The subsequent experimental validation under optimal conditions yielded a removal percentage of 98.77%, showcasing the success of combining deep learning with genetic algorithm optimization. However, it is emphasized that experimental validation is crucial to account for inherent error margins in digital twin modeling. The study recommends prioritizing experimental optimality for robust validation of the optimization results obtained through the integration of deep learning and genetic algorithms.

This research not only contributes to the advancement of environmental science but also offers a unique opportunity for educational innovation. By incorporating artificial neural networks, deep learning, and data science methodologies into the study of adsorption processes for pollutant removal, students can engage in cutting-edge interdisciplinary approaches. The utilization of genetic algorithm optimization adds a practical dimension to their learning experience, fostering skills in optimization and critical thinking. This innovative integration of advanced technologies provides students with valuable exposure to real-world problem-solving, preparing them for future challenges in environmental engineering and promoting a forward-looking educational model.

Overall, the combination of using biosorbents for environmental remediation and enhancing these efforts through educational programs presents a holistic approach to managing water pollution. The research underscores the importance of continuous research in biosorbent efficacy and advocates for robust educational programs that empower individuals with the knowledge and skills to make impactful environmental decisions. Future strategies should focus on expanding the availability of educational resources related to biosorbents and increasing public engagement through tailored educational programs that highlight the practical aspects of environmental stewardship (Supplementary Information).