Introduction

There has been a push in recent years to promote the distribution network's incorporation of sustainable energy sources, such as solar and wind power. To lessen the burden on converters and their ratings, this is done. "Reduced switch" refers to the fact that, in comparison to typical systems, its objectives are achieved with fewer switches. Reductions in the number of switches can have benefits including lower costs, less energy waste, and increased reliability. Like other active power filters, reduced switch SHAPF is essential to maintaining a consistent and excellent power supply in the distribution network.

Motivation

SHAPF integration with renewable energies has become increasingly significant when compared to traditional grid-tied VSC. This method has many benefits, including the capacity to keep the DCBCV constant even in the presence of load variations, enhance power quality, and increase the converter's resilience to unforeseen events. The majority of the methodologies covered in the literature currently in publication use conventional techniques like PIC as well as the sliding mode controllers (SMC), which are applied to various load types. However, in situations when consumption and the radiation from the sun vary, these methods have not been able to produce the perfect values.

Literature

The improvement of PQ in solar PV systems that are connected to the grid were equipped with a battery energy storage device to support the charging of electric vehicles (EVs) at the EV charging station (EVCS) while also meeting the energy needs of the local load1. Besides, in order to increase PQ, golden ball optimized FLC for unified power quality conditioner (UPQC) is adopted2. Next, the integrated system incorporates a fuel cell (FC), photovoltaic (PV), battery, Z-source, and Biogeography-Based Optimization (BBO) was recommended to UPQC compensator3. On other hand, the Artificial intelligence controller based controllers were developed to address PQ issues effectively4,5,6.

The novel arrangement, combined with a DC–DC boost converter and a series injection transformer, was connected to reduce the voltage strain on devices, to maximize the efficiency of the switches and to minimize losses7. Mean while four distinct compensators were employed to enhance the PQ of the system. A benchmark dataset was created in real-time, encompassing different PQ problems including swell, interruptions, sag, and harmonics8. A new mathematical model was introduced for a UPQC controlled hybrid microgrid to control the voltage and reactive power flow9. However, the impact of distributed Energy on the PQ of distribution and transmission networks was to evaluate the effects of integrating distributed ESS on enhancing PQ in certain network topologies10. The new techniques that needed for doing research and offering solutions to enhance the PQ in distribution networks are reviewed11. In addition, the sport algorithm was selected to design PI controller of UPQC to solve PQ issues12. A novel optimization approach was suggested for determining the location and size of the UPQC in the active distribution network that is connected to renewable energy sources13. On other hand, the AI based optimally designed controllers were adopted for UPQC and shunt filters powered with the renewable sources14,15,16,17,18,19,20,21,22.

Besides, the economical charger with a sensor platform was suggested by EV research employing the SIAFL-DO algorithm, MPPT functioning and battery life management are accomplished23. On other hand, an effort was done to elucidate the benefits and value for money of using high voltage transformers for protection and optimal utilization, as well as the application of computers and contemporary systems for automation24. Next, the scheduling parameters in the form of binary were suggested hybrid GHS-JGT for UC problem, while other constants are handled directly via optimal circumstances in the form of decimals25. The effectiveness of the MPPT approach was assessed under various solar irradiance scenarios, and a comparison with the traditional P&O MPPT approach was demonstrated its superiority over cutting-edge methods26.

To achieve MPPT, AI based methods was suggested in addition a single sensor based, cost-effective charging adapter for EVs27,28,29. However, the prime intention of the control technique was to feed all the generated solar power at the unity PF into the grid, which is successfully achieved by the FOGI-based method30. Nevertheless, the AI and machine learning with metaheuritic based methods was adopted for MPPT method to acquire rapid and maximal PV power with zero oscillation tracking for grid connected systems31,32,33,34.

A unique architecture was introduced numerous important innovations to improve grid-dependent PV system efficiency35. Besides, the improved active power filter and a power filter compensator were designed by optimizing the gain coefficients for the filter controllers through various metaheuristic optimization techniques36. However, by modifying the PI-multi-resonant control parameters of M-UPQC using PSO and black hole optimization approaches, the PQ has been addressed effectively37. Lastly, In a hybrid micro-grid the gain coefficients are tuned by employing metaheuristic algorithms, a novel harmonic compensation method utilizing a filter compensator device was presented38,39.

It is clearly demonstrated in Table 1 that the current literature ignores AI-based signal generation in favor of traditional techniques like SRF and pq theories. Furthermore, there seems to be a lack of focus on choosing the best gains for controller & filter variables. Moreover, while some researchers took into account the aspects of design, they failed to account for the possibility of using less number of switches for multi level converters for lowering the losses.

Table 1 State of Art of Survey.
Full size table

Highlights and contributions

  • Development of reduced switch five level VSC for SHAPF.

  • Optimal Design of SHAPF by optimal selection of filter, boost and buck boost parameters along with the selection of PIC gain values of filter and ESS with HHOA.

  • The HHOA trained NN for reference signal creation is being implemented to eliminate the need for classical conversions.

  • The suggested method seeks to increase PQ together with PF, reduce source current THD, reach a constant DCBCV faster, and provide optimal management of power. In order to show that the suggested approach is beneficial, it is tested in three different situations.

  • The suggested method seeks to increase PQ together with PF, reduce source current THD, reach a constant DCBCV faster, and provide optimal power management. In order to show that the suggested approach is beneficial, it is tested in three different cases in comparison with GA, BBO algorithms in addition with SRF, pq based PIC.

The structure of the article is as outlined below: The proposed reduced switch VSC is covered in Section "Construction and modeling", with a focus on external supplies. A thorough description of the suggested controller that uses of HHOA is given in Section "Control Technique". The investigation and outcomes are shown in Section "Simulation and Results". The draft is concluded in Section "Conclusion".

Construction and modeling

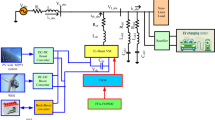
The connection of SHAPF to the DC bus in conjunction with the optimally coordinated SES, wind, and ESS is depicted in the diagram 1. In addition to ensuring DCBCV stable, the reduced switch VSC is connected in order to suppress harmonic distortions. For the cascaded H-Bridge inverter architecture to produce a 5Level output, more switches are needed. To produce pulses, the PWM circuit requires the usage of 8 switches. The two DC capacitor voltages associated in the DC link are denoted by Vdc1 and Vdc2.

This study suggests using an optimized NN control approach together with an improved switching configuration of VSC with a SHAPF. Two insulated gate bipolar transistors are employed in the Improved Reduced Switch approach for multilevel selection, and a traditional H-Bridge is utilized for polarity determination. The proposed system is shown in Fig. 1a and single-phase reduced switch multilevel inverter is shown in the Fig. 1b. Switches S1 and S2 are employed for level choice, and the other switches are utilized for polarity adjustment. The following is the operational justification behind the recommended inverter's ability to provide a 5-level output. The switching pattern is given in Table 2.

Fig. 1
figure 1

Developed SHAPF. (a) Proposed system, (b) Proposed reduced switch topology for 1phase.

Full size image
Table 2 Switching Pattern.
Full size table

It is visible from the diagram 1 that the suggested arrangement uses less switches to get a 5-level output. This means that the proposed three-phase inverter uses only six switches from the system. The circuit's size and cost can be reduced by limiting the switches. The proposed topology with a NN reference signal production strategy replaces the conventional SRF and p-q techniques to achieve increased PQ.

Design of shunt active power filter

In order to ensure the supply current free of distortion, the primary function of the SHAPF is to inject the necessary appropriate current4 by Eq. (1).

$$i_{s} = i_{l} - i_{sh}$$
(1)
$$i_{l} = \sum\limits_{n = 1}^{\infty } {i_{n} \sin } (nwt + \varphi_{n} )$$
(2)
$$V_{s} = V_{m} \sin wt$$
(3)
$$P_{L} = V_{s} *i_{l}$$
(4)

where is, il, ish, Vm, Vs, PL are represented as supply current, load current, SHAPF compensated current, maximum voltage, source voltage, and load power respectively.

The numerical value of DC capacitor Cdc is achieved by Eq. (5).

$$C_{dc} = \frac{{\pi *i_{sh} \;}}{{\sqrt 3 \omega V_{cr,pp} }}$$
(5)

The reference DCBCV \(V^{ref}_{dc}\) is chosen based on the available ratings provided by the recommended method. The optimal choice is determined by adjusting current and peak-to-peak voltage ripple (\(V_{cr,pp}\)). The filter inductor (Lsh) is determined by DCBCV \(V_{dc}\), ripple current \(I_{cr,pp}\), and switching frequency \(f_{sh}\) control, over loading factor (\(a_{f}\)) with the depth of modulation as (\(m\)) is 1 by Eq. (6)

$$L_{sh,\min } = \frac{{\sqrt 3 \;m\;V_{dc} }}{{12\;a_{f} \;f_{sh} \;I_{cr,pp} }}$$
(6)

Modeling of renewable sources

In order to provide external supply to DC bus, it is advised that the proposed converter with less switches in conjunction with solar, wind, and energy storage systems. With the help of ESS support, the DCBCV is managed by a renewable source to control changes in demand. Equation (7) offers the PL for the recommended approach.

$$P_{PV} \pm P_{BSS} + P_{W} + P_{G} = P_{L}$$
(7)

PV system

The Simulink package provided the PV model used in this study. In order to attain the required current and voltage, the photovoltaic modules are joined in series to create a string.

Equation (8) provides the output solar power, whose control system is given in Fig. 2. In this study, the perturb and observe (P & O) based maximum power point tracking approach was utilized to derive the maximum output by controlling the duty cycle DPV. However, the pulse width modulation (PWM) technique was adopted to generate the pulses to the boost converter. Here, G resembles irradiation with temperature T, LPV is the inductor value of boost converter for the PV system, PPV indicates PV power, IPV resembles PV current and voltage respectively.

$$P_{PV} = V_{PV} \times i_{PV}$$
(8)
Fig. 2
figure 2

PV control.

Full size image

Battery storage

The biggest advantage of using Li-ion battery is low discharge with minimum maintenance. Figure 3a provides the configuration of ESS with buck boost converter. Here, switches SW3 and SW2 are employed to charge/discharge the battery as per the requirement which is determined by the amount of renewable power produced taking state-of-charge of battery (SOCB) and its limits into account by Eq. (9).

$$SOCB = 80(1 + \int {i_{BS} \;} dtQ)$$
(9)
$$SOCB_{\min } \le SOCB \le SOCB_{\max }$$
(10)
Fig. 3
figure 3

Battery control with HHOA. (a) Battery at DC bus, (b) Battery controller.

Full size image

The control system that regulates the battery with HHOA optimized PI control is given in Fig. 3b. The DC reference current irefdc is obtained by reducing the difference voltage of Vdc & Vrefdc which is represented as error voltage Vdc,err with HHOA optimized PI. In the similar way the battery error reference current i*B,err obtained by the difference between irefdc and battery reference current is also estimated by the optimally selected PI. However, LB, iB, VB represents the batteries inductance, current and voltage. Table 3 provides the total power control of the system in modes of operation. Appendix gives the parameters for solar and battery systems.

Table 3 Power Control of the system.
Full size table

WEGS

The WEGS control system consists of a wind-turbine, a permanent magnet synchronous generator, a boost-converter as shown in Fig. 4. Here, VW, Iw, CW, LW, irefW are the wind voltage, current, capacitor, inductor and reference wind current. The Eq. (11) gives the available power at its output terminals.

$$P_{w} = 12\rho Av^{3} C_{p} (\lambda ,\theta )$$
(11)

where A resembles the area of the rotor turbine blades in m2, \(\rho\) indicates the air density in kg/m3, \(v\) represents wind velocity in m/s, and \(C_{p}\) gives the power coefficient of power.

Fig. 4
figure 4

WEGS controller with HHOA.

Full size image

In this work, the PMSG is selected for its cost-effective operation and maintenance. The amount of wind power produced depends on the wind speed. Later, it is converted to DC using a rectifier. Then, a DC–DC boost converter is employed to raise the voltage level, as illustrated in Fig. 4.

Control technique

By providing a suitable current, SHAF aims to minimize waveform anomalies and guarantee the uniformity of DCBCV. The suggested control plan offers: (i) HHOA trained NNC to generate reference signals. (ii) To achieve the specified goals, an HHOA-tuned PIC is created for SHAPF, WEGS, and ESS in addition to the best possible filter, buck and boost converters parameter optimization. The purpose of this work is to highlight the suggested HHOA adjusted PIC and HHOA trained NNC's control mechanism for reduced switch converter.

HHOA tuned PIC and NN

The DCBCV must be regulated and the reference current must be generated for the SHAPF to function properly. On the other hand, variations in load may result in modifications to power flow, which could impact the DCBCV's stability. The SHAPF needs to handle switching losses in order to keep things stable. As seen in Fig. 5, the inaccuracy introduced by the HHOA-based gain values chosen for the PIC is measured by calculating the difference between the set and true DCBCV using Eq. (14).

$$\Delta i_{dc} = e_{1} (t) = V^{ref}_{dc} - V_{dc} (t)$$
(12)
Fig. 5
figure 5

proposed converter with HHOA with PIC and NN.

Full size image

In order to avoid complicated SRF and pq methods, HHOA learned NNC is selected for reference production. The load currents il_abc i.e. (il_a, il_b, il_c) and Δidc obtained from HHOA optimized PIC are considered as input, while the reference currents irefsh_abci.e (irefsh_a, irefsh_b ,irefsh_c) are regarded as the target information. In this case, HHOA is adopted to train NNC. Figures 6 and 7 show the NNC's structure of organization and the HHOA NNC, respectively.

Fig. 6
figure 6

Reference signal production with HHOA-NN.

Full size image
Fig. 7
figure 7

HHOA trained NNC.

Full size image

This study is on the behavioral patterns exhibited by horses. Horses commonly exhibit grazing, hierarchy, sociability, mimicry, defense mechanism, and roaming behaviors15. This technique is derived on the six fundamental characteristics displayed by horses of varying ages. At each iteration, the horses are relocated based on Eq. (13).

$$P_{m}^{it,a} = Vl_{m}^{it,a} + P_{m}^{(it - 1),a} ,a = \alpha ,\beta ,\gamma ,\delta$$
(13)

where, “a” denotes the age group of the horse, \(P^{it,a}_{m}\) represents mth horse position, it represents current iteration, \(Vl^{it,a}_{m}\) gives the velocity vector of the horse and α gives the horses between the ages of 5 and 10, β between 10 to 15, and α denotes 15 years older horses. In order to ascertain the age of the horses, each iteration should possess a comprehensive array of responses. In this scenario, the matrix is arranged according to the most favorable ones, and 1st 10% of horses which are the top of this ordered matrix will be chosen as α horses. The β group comprises the subsequent 20% of the population. The γ and δ groups are of 30% and 40% of the left over horses. To calculate the velocity vector, quantitative methods are used to simulate the six acts performed by different groups of horses. Considering the behavior patterns mentioned, Eqs. (14)–(17) can be expressed as the different ages of horses during each cycle of the process.

$$Vl_{m}^{it,\alpha } = G_{m}^{it,\alpha } + D^{it,\alpha }$$
(14)
$$Vl_{m}^{it,\beta } = G_{m}^{it,\beta } + H_{m}^{it,\beta } + S_{m}^{it,\beta } + D^{it,\beta }$$
(15)
$$Vl_{m}^{it,\gamma } = G_{m}^{it,\gamma } + H_{m}^{it,\gamma } + S_{m}^{it,\gamma } + I_{m}^{it,\gamma } + R_{m}^{it,\gamma } + D^{it,\gamma }$$
(16)
$$Vl_{m}^{it,\delta } = G_{m}^{it,\delta } + I_{m}^{it,\delta } + R_{m}^{it,\delta }$$
(17)

Grazing (G)

The HHOA approach is used to model the grazing space for each horse. Due to the coefficient g, every horse will graze in certain regions. Horses engage in grazing behavior throughout their entire lifespan. The process of grazing is mathematically executed, following the principles outlined in Eqs. (18) and (19).

$$G^{it,a}_{m} = g_{it}^{{}} (l + r*u)(P^{(it - 1)}_{m} ),a = \alpha ,\beta ,\gamma ,\delta$$
(18)
$$g^{it,a}_{m} = w_{g} \times g_{m}^{(it - 1),a}$$
(19)

Here \(G^{it,a}_{m}\) represents motion of the ith horse. The integer "r" is a value that can range from 0 to 1, while "l" and "u" represent the lower and upper limits of the grazing space, respectively.

It is recommended that the values for "l" and "u" be set to 0.95 and 1.05, respectively, for all age groups. The coefficient g is uniformly assigned a value of 1.5 across all age ranges.

Hierarchy (H)

The tendency of a set of horses to imitate and obey the highly skilled and dominant horse is referred to as the coefficient hm in HHOA. During the middle ages of b and g, which refers to children aged 5–15 years, research have shown that horses adhere to the principle of hierarchy. The equations labeled as (20) and (21) in Sect. 3.6 can be utilized to establish this definition.

$$H^{it,a}_{m} = h^{it,a}_{m} \times (P_{lbh}^{(it - 1)} - P_{m}^{(it - 1)} )$$
(20)
$$h^{it,a}_{m} = h^{( - 1 + it),a}_{m} \times w_{h}$$
(21)

Here, \(H^{it,a}_{m}\) depicts the position of the superior equine specimen in relation to the variable of speed. The \(P_{lbh}^{(it - 1)}\) represents the rank of the top-performing horse.

Sociability (S)

Horses require socialization and have the ability to peacefully cohabit with other species. Wild horses form social groups to enhance their protection, as they are susceptible to predation. Pluralism enhances their chances of survival and facilitates their ability to escape. Horses often engage in combat because to their gregarious nature and their distinctiveness it contributes to their aggression. Horses aged 5 to 15 years exhibit a primary inclination towards being in the company of the herd, as indicated by the provided formulas: The tendency of a herd of horses to go behind the skilled and dominant horse is referred to as the coefficient hm in HHOA. During the middle ages of b and g, which refers to children aged 5–15 years, research have shown that horses adhere to the principle of hierarchy. The Eqs. (20) and (21) in Sect. 3.6 provide a definition for this.

$$S^{it,a}_{m} = s^{it,a}_{m} \left[ {\left( {\frac{1}{N}\sum\limits_{j = 1}^{N} {P^{( - 1 + it)}_{j} } } \right) - P^{( - 1 + it)}_{m} } \right],a = \beta ,\gamma$$
(22)
$$s^{it,a}_{m} = s^{( - 1 + it),a}_{m} \times \omega_{s}$$
(23)

The \(S^{it,a}_{m}\) gives the vector of social motion exhibited by the ith horse. \(s^{it,a}_{m}\) represents its orientation towards the ith group. The iteration is progressively reduced in each cycle, and N denotes the total number of horses. The s coefficient for g and b horses is determined based on these factors.

Imitation (I)

Horses imitate and learn from one other, including adopting both beneficial and detrimental behaviors, such as identifying the most favorable grazing area. The new approach incorporates the imitation behavior of horses as a significant feature, denoted as i. Equations (24) and (25) provide an explanation for the enduring tendency of young horses to imitate older ones.

$$I^{it,a}_{m} = i^{it,a}_{m} [(\frac{1}{PN}\sum\limits_{j = 1}^{pN} {P^{( - 1 + it)}_{j} } ) - P^{( - 1 + it)} ],a = \gamma$$
(24)
$$i^{it,a}_{m} = i^{( - 1 + it),a} \times \omega_{i}$$
(25)

Here, the vector of motion representing the ith horse relative to the average of the best horse at position P is denoted by \(I^{it,a}_{m}\). The reference of the horse in the direction of the group on the ith iteration is indicated by \(i^{it,a}_{m}\) , which decreases in each cycle with a parameter of \(\omega_{i}\). PN stand for the best position horses, where p is equal to 10% of the selected horses.

Defense mechanism (D)

In HOA technique, the horses' defense mechanism operates by evading horses that display inappropriate or less than ideal behaviors. This component represents their main method of defense. As said earlier, horses must either flee or engage in combat with their enemies. A protective mechanism is present in both young and adult horses throughout their whole lifespan, whenever it is feasible. In Eqs. (26) and (27), a negative coefficient indicates the presence of the horse's protective system, which serves to distance the animal from hazardous circumstances.

$$D^{it,a}_{m} = d^{it,a}_{m} [(\frac{1}{qN}\sum\limits_{j = 1}^{qN} {P^{( - 1 + it)}_{j} } ) - P^{( - 1 + it)} ],a = \gamma ,\beta ,\gamma$$
(26)
$$d^{it,a}_{m} = d^{( - 1 + it),a} \times \omega_{d}$$
(27)

The ith horse escape vector denoted as \(D^{it,a}_{m}\). The worst position of horses is given by qN and q is equal to 20% of the total number of horses and \(\omega_{d}\) represents the reduction factor per cycle.

Roam (R)

The parameter r is employed in the algorithm to simulate this kind of action, serving solely as a random displacement. Roaming is a behavior that is rarely observed in young horses and gradually diminishes as they grow older. Equations (28) and (29) illustrate the roaming variables in this process. Figure 8 displays the flowchart of the HOA algorithm.

$$R^{it,a}_{m} = r^{it,a}_{m} \partial P^{( - 1 + it)} ,a = \gamma ,\delta$$
(28)
$$r^{it,a}_{m} = r^{( - 1 + it),a}_{m} \times \omega_{r}$$
(29)
Fig. 8
figure 8

HHOA flow chart.

Full size image

Here, \(R^{it,a}_{m}\) is the velocity vector of the ith horse for a local area search and escape from local minima is represented by an arbitrary vector. The reduction factor \(\omega_{r}\) for every cycle is denoted by \(r^{it,a}_{m}\). By substituting the outcomes of Eqs. (18)–(29) into Eqs. (14)–(17), we may get the universal velocity vector. Speed of d horses between the ages of 0–5 years:

$$\begin{gathered} V^{it,\delta }_{m} = [g^{( - 1 + it),\delta }_{m} \times \omega_{g} (l + r*u)[P^{( - 1 + it)}_{m} ]] + i^{( - 1 + it),\delta }_{m} \times \hfill \\ \omega_{i} \times [(\frac{1}{PN}\sum\limits_{j = 1}^{pN} {P^{( - 1 + it)}_{j} } ) - P^{( - 1 + it)} ] + r^{( - 1 + it),\delta }_{m} \times \omega_{r} \times \partial P^{( - 1 + it)} \hfill \\ \end{gathered}$$
(30)

g horses velocity during 5–10 years:

$$\begin{aligned} V_{m}^{{it,\gamma }{}} = & [g_{m}^{( - 1 + it),\gamma } \times \omega_{g} (l + r*u)[P_{m}^{( - 1 + it)} ]] + h_{m}^{( - 1 + it),\gamma } \times \omega_{h} \times [P_{l}^{( - 1 + it)} - [P_{m}^{{( - 1 + it)}{}} ] \\ & + S_{m}^{( - 1 + it),\gamma } \times \omega_{S} \times \left[ {\left( {\frac{1}{N}\sum\limits_{j = 1}^{N} {P_{j}^{( - 1 + it)} } } \right) - P_{m}^{( - 1 + it)} } \right] + i_{m}^{( - 1 + it),\gamma } \times \omega_{im} \times \left[ {\left( {\frac{1}{PN}\sum\limits_{j = 1}^{pN} {P_{j}^{( - 1 + it)} } } \right) - P^{( - 1 + it)} } \right] \\ & + rm^{( - 1 + it),a} \times \omega_{r} \times \partial P^{( - 1 + it)} \\ \end{aligned}$$
(31)
$$\begin{aligned} V_{m}^{it,\gamma } = & [g_{m}^{( - 1 + it),\gamma } \times \omega_{g} (l + r*u)[P_{m}^{( - 1 + it)} ]] + h_{m}^{( - 1 + it),\gamma } \times \omega_{h} \times [P_{l}^{( - 1 + it)} - [P_{m}^{( - 1 + it)} ] \\ & + S_{m}^{( - 1 + it),\gamma } \times \omega_{S} \times \left[ {\left( {\frac{1}{N}\sum\limits_{j = 1}^{N} {Pj^{( - 1 + it)} } } \right) - P_{m}^{( - 1 + it)} } \right] - d_{m}^{( - 1 + it),\beta } \times \omega_{d} \times \left[ {\left( {\frac{1}{qN}\sum\limits_{j = 1}^{qN} {P_{j}^{( - 1 + it)} } } \right)P^{( - 1 + it)} } \right] \\ & + r_{m}^{( - 1 + it),a} \times \omega_{r} \times \partial P^{( - 1 + it)} \\ \end{aligned}$$
(32)

a horses velocity during 10–15 years:

$$V^{it,\alpha }_{m} = [g^{( - 1 + it),\alpha }_{m} \times (l + r*u)[P^{( - 1 + it)}_{m} ]] - d^{( - 1 + it),\alpha }_{m} \times \omega_{d} \times [(\frac{1}{qN}\sum\limits_{j = 1}^{qN} {P^{( - 1 + it)}_{j} } ) - P^{( - 1 + it)} ]$$
(33)

In this work, HHOA algorithm is selected due to its advantage which promises to deal complex, high-dimensional and multi-objective complex global optimization engineering problems. The user can tune parameters for achieving global optimal solution with fast convergence. In this case, the filter parameters, battery and shunt filter PIC gain levels, weights, and NN bias are the problem variables. As a result, each horse in HHOA is represented to indicate the variables at issue as:

$$\beta \; = \;\left[ \begin{gathered} K_{{\text{p}}} {\text{, K}}_{{\text{i}}} ,,K_{{{\text{pB1}}}} {\text{, K}}_{{{\text{iB1}}}} ,K_{{{\text{pB2}}}} {\text{, K}}_{{{\text{iB2}}}} ,K_{{{\text{pW1}}}} {\text{, K}}_{{{\text{iW1}}}} ,K_{{{\text{pW2}}}} {\text{, K}}_{{{\text{iW2}}}} , \hfill \\ wt_{1,1} ....wt_{1,5} ,...wt_{1,10} ,....wt_{2,1} ,......wt_{3,1} ,....,wt_{4,1} ........ \hfill \\ Wt_{1,1} ,....Wt_{5,1} ,...Wt_{10,1} .....,\beta_{0} ,....\beta_{5} ,....\beta_{10} ,R,L,L_{PV} ,L_{W} ,L_{B} \hfill \\ \end{gathered} \right]$$
(34)

The bonds are represented as,

$$\beta_{i(\min )} \le \beta_{i} \le \beta_{i(\max )} ;i = 1,2...n$$
(35)

The constraints and the normalized objective functions, which give each chosen objective equal weight and take into account both minimal and maximal functions, can be used to build the fitness (F).

$$\begin{aligned} MaximizeF = & \frac{1}{{1 + (obj_{1} ,obj_{2} )}} \\ obj_{1} = & MSE = \frac{1}{n}\sum\limits_{p = 1}^{m} {(O - \overline{O} )^{2} } \\ obj_{2} = & THD = \frac{{\sqrt {(I^{2}_{2} } + I^{2}_{3} + .....I^{2}_{n} )}}{{I_{1} }} \\ \end{aligned}$$
(36)

In this case, m stands for the number of instances, \(o\) and \(\overline{o}\) the output that was obtained is the needed outcome. The fundamental and harmonic components of the current are indicated by the symbols In and I1, respectively.

Simulation and results

In this work, a three-phase local distribution network was selected to evaluate the proposed approach. The parameters for the overall system configuration are detailed in the appendix. To assess the effectiveness of the method, three different test cases were chosen, each featuring various load combinations and variations in power generation from the SES and WGS. The specific details of the case studies used to evaluate the proposed system are provided in Table 4. Additionally, for each test scenario, the THD of the developed system was measured and compared with the commonly used SRF and pq techniques with PIC, as well as with GA and BBO, as shown in Table 4. The resulting waveforms for case studies 1–3 are illustrated in Figs. 8, 9, 10, depicting the following: supply/grid voltage (Vs), load voltage (Vl), DC bus capacitor voltage (Vdc), load current (il), filter injection currents (ish), supply current (is), temperature (T), and irradiation (G).

Table 4 Cases studies.
Full size table
Fig. 9
figure 9

Comparison of time (sec) to obtain steady DCBCV.

Full size image
Fig. 10
figure 10

Waveforms for case1. (a) il, ish, is, (b) Source power, PV power, T, Load power.

Full size image

In Case 1, when Load 1 and Load 2 are connected, the load current is balanced, showing a THD of 21.25% and a power factor of 0.887, though the current is non-sinusoidal and distorted. As illustrated in Fig. 10a, the developed technique successfully eliminates harmonics from the supply current. The current waveforms also exhibit a significant reduction in THD, as shown in Table 5. By incorporating the appropriate shunt currents, the THD decreased to 3.69%, and the power factor improved to 0.988—a notable improvement compared to other conventional methods and published techniques. Figure 10b demonstrates the maximum PV and wind output powers alongside grid powers under constant wind velocity and irradiance, highlighting the enhanced performance of the proposed method in power management. Additionally, the method achieved a stable DC bus voltage in under 0.03 s.

Table 5 %THD.
Full size table

The simultaneous integration of Loads 1, 2, 4, and 5 in Case 2 results in highly distorted and polluted load current, as depicted in Fig. 11a. Without a filter, the THD is measured at 16.65% and the power factor at 0.856. Figure 11a demonstrates the effectiveness of the developed approach in delivering harmonics-free current by injecting compensating currents to correct waveform distortions. This approach reduced the load current's THD to 3.76% and improved the power factor to 0.998. Additionally, Fig. 11b shows that fluctuating irradiation and wind velocity were considered, and it is evident that the HHOA-tuned PIC quickly stabilizes the DC bus voltage at a constant level, even with variations in solar and wind power. Power management was effectively handled, with the grid's support, ensuring steady electricity supply to the load.

Fig. 11
figure 11

Waveforms for case2. (a) il, ish, is, (b) Source power, PV power, T, Load power.

Full size image

In Case 3, a similar trend of increasing the power factor and decreasing the THD is observed. Due to Loads 1, 4, and 5, the load current exhibits a non-sinusoidal waveform until 0.4 s. At that point, Loads 3 and 6 are connected, leading to a non-sinusoidal waveform with unbalanced phases and an increase in current magnitude caused by the additional loads. Figure 12a illustrates the effectiveness of the proposed strategy in correcting the defects in the current waveform. Additionally, Fig. 12b shows that the recommended approach successfully maintains DC bus voltage stability under varying irradiation conditions, delivering excellent performance in power control.

Fig. 12
figure 12

Waveforms of case3. (a) il, ish, is, (b) Source power, PV power, T, Load power.

Full size image

This study involves conducting FFT analysis on all three test cases. Specifically, it focuses on the results from Test Case 3, which included the use of multiple loads in combination with an EV and an asynchronous motor. The PF and THD spectra for each scenario are shown in Figs. 13 and 14, respectively. Figure 9 displays the recorded time required to achieve stable DC bus voltage regulation across various control schemes. The data clearly indicates that the proposed HHOA-tuned PIC-based SHAPF can stabilize the DC bus voltage in less than 0.02 s. Besides, Fig. 15 exhibits the convergence plot comparison of case 1 for the developed method with respect to the standard metaheuristic algorithms like GA, BBO with the HHOA. However, it is clearly notable that GA reaches to 4.24% of THD in 54 iterations, BBO to 3.86% in 38 iterations while proposed HHOA in 18 iterations. The aforementioned discussions clearly illustrate that the suggested method is very efficient in decreasing THD, improving PF, and guaranteeing a constant DC bus voltage.

Fig. 13
figure 13

PF Comparison.

Full size image
Fig. 14
figure 14

FFT spectrum. (a) Case-1, (b) Case-2, (c) Case-3.

Full size image
Fig. 15
figure 15

Comparison of convergence characteristics for case-1.

Full size image

Conclusion

In this work, a reduced switch 5 level converter was developed for the SHAPF, along with the use of the HHOA for selecting the optimal Kp and Ki values of the PIC for the shunt, wind, and ESS controllers, as well as for the design parameters of the SHAPF, boost, and buck-boost converters. To avoid conventional transformations, an HHOA-trained NN was used for reference signal generation, enabling quick response in regulating the DCBCV, reducing THD, and improving PF. The proposed controller effectively minimized THD to within allowable limits and increased PF to nearly unity, as demonstrated by three test studies under different demand, variable irradiation, and wind velocity conditions. This approach outperformed the commonly used SRF and pq-based PIC methods. The results showed that the proposed method achieved THD values of 3.69%, 3.76%, and 4.0%, all of which are lower than those achieved by other techniques and well within IEEE standards. Additionally, the proposed system achieved stable DC bus voltage in less than 0.05 s, faster than other methods. Future research could focus on optimizing AI-based hybrid controllers and the design parameters of the model by framing the design challenge as an optimization problem and applying the latest metaheuristic optimization methods for UPQC, including the integration of hydrogen fuel cells with renewable sources.