Introduction

With the introduction of such strategic projects by China as the Belt and Road Initiative, the development of its western region, and the construction of a strong system of transportation across the country, both the scale and mileage of highways and railways have rapidly increased in recent years. Mountainous areas account for about 67% of China’s area of land1. In particular in the western hinterland that features crisscrossing mountains, transportation projects inevitably require drilling tunnels through them. Problems like the collapse and deformation of structures as well as water inrush and mudslides may frequently arise during construction for underground projects, where the hazards posed by the inrush of karst water are particularly notable2. Such issues can lead to delays in construction, damage to equipment, and the collapse of tunnels that can cause casualties and compromise the safety of construction.

To prevent such incidents, it is crucial to conduct risk assessments before construction begins. Risk evaluation is essential in rock engineering projects, such as tunnels and slopes, where complex geological environments are common. Risk assessments help identify potential geological hazards, such as faults, fractures, weak layers, and groundwater, which could affect the safety and stability of the project. Risks encountered during construction, such as soil liquefaction, collapses, and blasting accidents, can be predicted and mitigated through risk assessments. Therefore, establishing an accurate risk evaluation system for karst water inrush in tunnels during the survey and design phase is vital3,4,5. This approach helps predict water inrush disasters and implement effective prevention measures, thus providing reliable geological data for safe underground tunnel construction. Establishing an accurate system to assess the risk of inrush of karst water into tunnels based on the relevant geological information during the survey and design phases of construction projects can help prevent accidents, and can provide a reliable geological basis for the safe construction of underground tunnels6.

Xu et al.7 proposed a karst tunnel water and mud inrush risk assessment model based on the Analytic Hierarchy Process (AHP). Wang et al. used AHP to determine weights and then constructed a fuzzy comprehensive evaluation system to establish a karst water inrush risk assessment model. AHP has certain subjectivity and arbitrariness8, and the fuzzy comprehensive evaluation (FCE) method may lead to unreasonable results. To eliminate subjective uncertainty, Gao et al.9 developed a top-board drainage risk assessment model (IAHP-EWM) and a multi-factor index system, using an improved AHP and entropy weight method to determine index weights. Compared to subjective evaluation methods, the entropy weight method is more accurate and objective. However, the traditional entropy weight method neglects conflicts between indicators and has limitations, such as instability. To address this flaw, critical methods have been used to determine indicator weights while considering conflicts10 In recent years, various methods have been proposed to optimize the influence of subjective and objective weights, typically using linear and multiplicative weighting methods. These methods include the comprehensive index method11, attribute mathematical theory12, TOPSIS13, evidence theory14, set pair analysis15, matter-element analysis16, and game theory17. However, these methods cannot handle uncertainty factors and are difficult in dealing with the interrelationships and uncertainties of evaluation indicators, leading to potential subjectivity and blind spots in the results.

The innovation of this paper is as follows: it employs an improved game theory-based combinatorial weighting method. Game theory reduces subjective bias and clearly calculates the weight values for each evaluation object, avoiding deviations and inaccuracies caused by subjective weight setting. However, traditional game theory also has drawbacks, such as not ensuring the non-negativity of linear combinations. The improved game theory overcomes this flaw and is more reasonable than traditional game theory. In measuring index values, traditional measurement functions have two issues. First, the function is linear, whereas actual measurements change non-linearly. Second, traditional function curves have several inflection points, leading to discrepancies with actual conditions. Therefore, this paper improves the linear attribute measurement function using trigonometric functions, establishing a nonlinear single index measurement function.

Materials and methods

Theory and methods

AHP

The analytic hierarchy process (AHP) is a subjective method that is susceptible to subjective bias18.

To represent the importance of indicators at the same level relative to those at a higher level, a two-by-two pairwise comparison is performed by using a scale of 1 to 918.

It is also necessary to perform a consistency test on the results of calculation. If \(CR < 0.1\), the judgment matrix is considered to have passed the test of consistency; otherwise, it needs to be modified until it passes the test19. The formula is as follows:

$$ CR = \frac{{\lambda_{\max } - n}}{{\left( {n - 1} \right)RI}} $$
(1)

where \(RI\) is the indicator of stochasticity and \(n\) is the order of the matrix.

EWM

The entropy weighting method (EWM) is an objective approach to assigning weights to indicators. It does so by calculating the entropy value of each indicator and assigning it based on the degree of influence of changes in its value on the overall system. In information theory, entropy represents the degree of chaos in a given system, and serves as a measure of uncertainty in it. The larger the entropy value of a given indicator is, the smaller is its weight20.

Due to differences in the units of measurement among systems of evaluation and to eliminate the conflict between different dimensions of the assessment indicators , it is necessary to perform dimensionless adjustments to each system. Equations (2) and (3) are used to process the indicators with dimensionless. If the indicator has a positive correlation with the object to be evaluated, it is a benefit-type indicator, and Eq. (2) is used for dimensionless processing; otherwise, if the indicator has a negative correlation with the object to be evaluated, it is a cost-type indicator, and Eq. (3) is used for processing.

$$ {\text{Benefit - typeindicators}}:r_{ij} = \frac{{x_{ij} - \min \left( {X_{j} } \right)}}{{\max \left( {X_{j} } \right) - \min \left( {X_{j} } \right)}} $$
(2)
$$ {\text{Cost - typeindicators}}:r_{ij} = \frac{{\max \left( {X_{j} } \right) - x_{ij} }}{{\max \left( {X_{j} } \right) - \min \left( {X_{j} } \right)}} $$
(3)

CRITIC

The CRITIC method is an objective technique that comprehensively evaluates the importance of each indicator by assessing the comparative strength of and conflict between indicators. It considers the variability and correlation of the indicators, and does not simply determine their importance based on their magnitudes, but makes full use of the objective attributes of the data to perform a scientific assessment9

Similarly, data is standardized using formulas (2) and (3). In this process, the variability of the indicators is expressed by their standard deviation, and the conflict between indicators is represented by the correlation coefficients.

Improved game theory

To overcome the defects of the traditional method of combinatorial assignment, an improved game-theoretic method is used to reasonably derive the comprehensive weights of the sub-goals21.

The weight vector \(L\) obtained by using method is \(W\left( l \right) = \left[ {w_{l1} ,w_{l2} , \cdots ,w_{ll} } \right]\). Let any arbitrary linear combination of \(L\) weight vectors be denoted by:

$$ W = \sum\limits_{l = 1}^{L} {\alpha_{l} W\left( l \right)^{T} } $$
(4)

where \(\alpha_{l}\) is the coefficient of linear combination, \(\alpha_{l} > 0\), and \(W\) is the integrated weight vector of the sub-goals.

Based on the idea of an agglomerated model of a game, A linear combination of weight vectors for each sub-objective is applied to minimize the deviation between the integrated weight vector and the vector, \(W\left( l \right)\), and seek a compromise solution \(W^{ * }\) of integrated weights. A model is constructed to optimize the coefficients of the linear combination22.

$$ \mathop {\min }\limits_{{\alpha_{l} }} \left\| {\sum\limits_{l = 1}^{l} {\alpha_{l} W\left( l \right)^{T} } - W_{p} } \right\|_{2} \quad \left( {p = 1,2, \cdots ,L} \right) $$
(5)

According to the differential properties of matrices, the condition for the optimization of Eq. (5) is:

$$ \sum\limits_{l = 1}^{L} {\alpha_{l} W_{p} W\left( l \right)^{T} } = W_{p} W_{p}^{T} $$
(6)

Traditional game-theoretic methods cannot guarantee that the coefficients of the linear combination are greater than zero. If they are non-positive, they contradict the above assumptions. Therefore, Eq. (6) is combined with the countermeasure model to obtain a new objective function:

$$ \mathop {\min }\limits_{{\alpha_{l} }} \sum\limits_{p = 1}^{L} {\left| {\sum\limits_{l = 1}^{L} {\alpha_{l} W_{p} W\left( l \right)^{T} } - W_{p} W_{p}^{T} } \right|} $$
(7)

By drawing on the constraints of the maximum deviation in objective weights23, the constraint function is established as follows:

$$ \sum\limits_{l = 1}^{L} {\alpha^{2} } = 1\quad \alpha_{l} > 0 $$
(8)

By combining Eqs. (7) and (8), the following optimization model is constructed:

$$ \begin{gathered} \mathop {\min }\limits_{{\alpha_{l} }} \sum\limits_{p = 1}^{L} {\left| {\sum\limits_{l = 1}^{L} {\alpha_{l} \,W_{p} W\left( l \right)^{T} } - W_{p} W_{p}^{T} } \right|} \hfill \\ \sum\limits_{l = 1}^{L} {\alpha^{2} } = 1\quad \alpha_{l} > 0 \hfill \\ \end{gathered} $$
(9)

This model can be solved by establishing the Lagrangian function:

$$ L\left( {\alpha_{l} ,\lambda } \right) = \sum\limits_{p = 1}^{L} {\left| {\sum\limits_{l = 1}^{L} {\alpha_{l} \,W_{p} W\left( l \right)^{T} } - W_{p} W_{p}^{T} } \right|} + \frac{\lambda }{2}\left( {\sum\limits_{l = 1}^{L} {\alpha_{l}^{2} } - 1} \right) $$
(10)

The solution of the coefficients of combination is then determined as:

$$ \alpha_{l} = \frac{{\sum\nolimits_{p = 1}^{L} {W_{g} W\left( l \right)^{T} } }}{{\sqrt {\sum\nolimits_{l = 1}^{L} {\left( {\sum\nolimits_{p = 1}^{L} {W_{p} W\left( l \right)^{T} } } \right)^{2} } } }} $$
(11)

Normalization yields the optimized coefficients of the combination of weights:

$$ \alpha_{l}^{ * } = \frac{{\alpha_{l} }}{{\sum\nolimits_{l = 1}^{L} {\alpha_{l} } }} $$
(12)

The final comprehensive weight vector is then obtained as:

$$ W^{*} = \sum\limits_{l = 1}^{L} {\alpha_{l}^{*} \,W\left( l \right)^{T} } $$
(13)

Uncertainty measure theory

Uncertainty measure theory offers significant advantages in dealing with problems involving uncertainty. Consider a set of objects of evaluation \(R\) with \(m\) pending samples, denoted by the set of evaluation objects \(R = \left\{ {R_{1} ,R_{2} ,} \right.\left. { \cdots ,R_{m} } \right\}\). Each sample of evaluation \(R_{j} \left( {j = 1,2, \cdots ,m} \right)\) consists of \(n\) indicators that form the set of indicators \(X = \left\{ {X_{1} ,X_{2} ,} \right.\left. { \cdots ,X_{n} } \right\}\). Thus, the \(j{\text{th}}\) sample can be represented as \(R_{j} = \left\{ {r_{1j} ,r_{2j} ,} \right.\left. { \cdots ,r_{nj} } \right\}\), where \(r_{ij}\) represents the value of the \(j{\text{th}}\) sample with respect to the \(i{\text{th}}\) indicator. Assuming that each indicator of evaluation \(r_{ij}\) has \(p\) levels of evaluation, the vector space of evaluation is formulated the vector space of evaluation \(U = \left\{ {C_{1} ,C_{2} ,} \right.\left. { \cdots ,C_{p} } \right\}\) is formulated, where \(C_{k} \left( {k = 1,2, \cdots ,p} \right)\) represents the \(k{\text{th}}\) level of evaluation. Level \(k\) is higher than level \(k + 1\), as indicated by \(C_{k} > C_{k + 1}\)24.

  1. (1)

    Single-indicator uncertainty measure matrix

    Suppose \(\mu_{ijk} = \mu \left( {r_{ij} \in C_{k} } \right)\) represents the value of data item \(r_{ij}\), which belongs to the level of evaluation \(C_{k}\) If \(\mu\) simultaneously satisfies the following three conditions, it is called an uncertain measure:

    $$ 0 \le \mu \left( {r_{ij} \in C_{k} } \right) \le 1 $$
    (14)
    $$ \mu \left| {r_{ij} \in \bigcup\limits_{l}^{k} {C_{l} } } \right| = \sum\limits_{l = 1}^{k} {\mu \left( {x_{ij} \in C_{l} } \right)} $$
    (15)
    $$ \mu \left( {x_{ij} \in U} \right) = 1 $$
    (16)

    For a given sample \(R_{j}\), the single-indicator matrix of uncertain measures \(\left( {\mu_{ijk} } \right)_{n \times p}\) that is formed by the uncertain measures of various indicators is given by \(\mu_{ijk}\).

  2. (2)

    Multi-indicator uncertainty measure matrix

    If \(\mu_{jk} = \mu \left( {R_{j} \in C_{k} } \right)\) represents the degree to which sample \(R_{j}\) belongs to level of evaluation \(C_{k}\), then

    $$ \mu_{jk} = \sum\limits_{i = 1}^{n} {w_{i} \,\mu_{ijk} } \quad j = 1,2, \cdots ,m\quad k = 1,2, \cdots ,p $$
    (17)

    where \(w_{i}\) represents the weight of the \(i{\text{th}}\) indicator.

  3. (3)

    Confidence identification

    Because \(C_{k} > C_{k + 1}\), the criterion for confidence identification can be applied to determine the level of evaluation. Let \(\lambda\) be the confidence level \(\left( {\lambda \ge 0.5} \right)\)25, the typical range is 0.5–0.7. Then, the model of confidence identification can be formulated as:

    $$ K_{0} = \min \left| {K:\sum\limits_{k = 1}^{K} {\mu_{ij} > \lambda ,\,\,\,K = 1,\,2, \cdots ,p} } \right| $$
    (18)

    Then, sample \(R_{j}\) is considered to belong to the \(K_{0} {\text{th}}\) level of evaluation.

Construction of proposed model

Our model to assess the risk of inrush of karst water is based on improved game theory and uncertainty measure theory. It consists of the following main steps (Fig. 1): (1) selection of indices to assess the risk of water inrush, (2) determination of the weights of indices, (3) establishment of evaluative model, and (4) verification of its results.

Fig. 1
figure 1

Steps of the proposed model to assess the risk of water inrush.

Full size image

Determining the risk of water inrush

The engineering community commonly uses a five-level standard of classification to assess the risk of water inrush: very low risk (I), low risk (II), medium risk (III), high risk (IV), and very high risk (V)26. The division of risk into levels and their meanings are shown in Table 1.

Table 1 Standard of classification for assessing the risk of water inrush into tunnel.
Full size table

Selection of risk-related indicators of inrush water

This study focuses on karst regions in the southwest of China. When selecting indicators, a localized approach was adopted to choose those suitable for the specific research area. Therefore, I referenced Yang’s27 risk assessment system for karst water inflow in tunnels in the southwestern mountainous regions of China. From this, I selected four key aspects: rock solubility, geological structure, surface water catchment capacity, and hydrogeological factors. Based on these aspects, I identified eight risk factors: rock type, rock structure, rock mass structure, layer dip angle, rainfall infiltration coefficient, surface slope, vertical zoning of karst water, and the spatial relationship between groundwater and tunnel space.

Research on the geological conditions of karst areas and the characteristics of karst water storage and movement was utilized to identify the main factors influencing accidents in tunnel-building projects for the model. The system of indicators, which comprehensively reflects the likelihood and severity of water inrush, is divided into four primary layers. Each layer consists of several secondary layers of indicators28 (as shown in Fig. 2). The levels of risk are divided as shown in Table 2.

  1. (1)

    Rock solubility: The mineral composition and structure of carbonate rocks significantly influence the degree of karstification. The influence of the mineral composition of rocks on the development of karsts is evident from the fact that the higher the purity of the chert is, the more extensive is its karstification, and the greater is its water content. The influence of the structure of rocks on the development of karsts is complex, and is primarily reflected in how the structure controls the distribution, types, and size of pores in the original rocks29.

  2. (2)

    Geological structure: Fold axes, fold terminations, soluble and non-soluble contact zones, joints, and fissures develop in such stress-concentrated areas as faults, and create spaces for the storage and transportation of groundwater. Monocline tectonic control of the water enrichment of the karst is mainly divided into homogeneous and intercalated groups of karst layers. In the former, the karst develops in the paraphyletic layer with varying degrees of intensity, and is characterized by sinkholes and blind valleys on the surface, and by caves and underground rivers below, with the groundwater stored in these formations. The latter is constrained by water-insulating layers, with finely developed interlayer fissures in which groundwater is stored. The fold structures include oblique and dorsal oblique structures. The former favor the accumulation of karst water, and often form water-rich areas, while the latter exhibit uneven karst development but are also capable of forming water-rich zones. Fractured structures influence the accumulation of karst water mainly through fissure development, rock fragmentation, and the formation of cavern pipelines that often result in water-rich zones30.

  3. (3)

    Surface catchment capacity: The surface karst terrain facilitates the collection and seepage of surface water, while also influencing the degree of development of the underground karst and the smoothness of the channels for groundwater transport. It thus significantly impacts tunnel construction. In areas with gentle slopes and a closed karst terrain, almost all surface water infiltrates into the ground to rapidly replenish the groundwater, while conditions for surface water catchment are relatively weak in steeply inclined or open karst terrains.

  4. (4)

    Hydrogeological factors: The magnitude of risk of accidents induced by sudden water inrush into tunnels is closely related to the vertical distribution of karst water. Moreover, the groundwater level and the spatial location of the tunnel significantly influence the risk of water inrush31.

Fig. 2
figure 2

System of indices to assess the risk of water inrush into tunnel.

Full size image
Table 2 Classification of risk based on indicators of evaluation of water inrush.
Full size table

Single-indicator measurement function

According to the standards of classification and guidelines for mapping the indices of the risk of water inrush into the tunnel, Trigonometric functions were used to graph the single-indicator measurement functions32. These functions are presented in Table 3. Graphs of the single-indicator functions were plotted by using MATLAB R2022a, as shown in Fig. 3 (values of the qualitative indicators range from one to 20).

Table 3 Single-indicator measurement function for each indicator of evaluation.
Full size table
Fig. 3
figure 3

Single-indicator measurement functions for the indicators of evaluation. Graphs of the single-indicator measurement functions of (a) K11, K12, and K41, (b) K21, (c) K22, (d) K31, (e) K32, and (f) K42.

Full size image

Study area

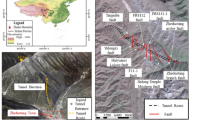
The Yunkun High-Speed Railway Salt Pit Tunnel is located at the junction of Yunlian County, Yibin City, Sichuan Province and Yanjin County, Zhaotong City, Yunnan Province. It is situated in the transitional zone between the southern edge of the Sichuan Basin and the Yungui Plateau. The overall terrain is higher in the south and lower in the north. Except for locally flat eroded basins, most of the area features rugged terrain with significant elevation differences, and the surface elevation generally ranges from 400 to 800 m. In addition to the Jinsha River flowing from east to west in the northwest, the main rivers in the survey area are the Guan River and the Baishui River, both of which flow from south to north following the terrain and eventually join the Yangtze River. Except for the Jinsha River in the northwest, which flows in the east–west direction, all major rivers in the surveyed area, including Guanhe River and Baishui River, spill into the Yangtze River from the south to the north as they follow the terrain. The Yanjin Tunnel is a single-hole tunnel with a total length of 7713 m, a maximum depth of 815 m, and a strike direction of N139° E. The exposed strata are mainly from the Permian, Ordovician, Silurian, and Cambrian, with a well-exposed bedrock. Their lithology is mainly carbonate, followed by clastic rocks, and the karst is highly developed. The geomorphology is controlled by the influence of tectonics and lithology, and exhibits prominent differences. In particular in the area occupied by soluble rock, the geomorphology and negative topography of the karst are remarkable, the degree of dissolution of the rock is high, and it enriches the groundwater. The hydrogeological profile and location of the tunnel are shown in Fig. 4.

Fig. 4
figure 4

Hydrogeological profile and location of the tunnel.

Full size image

The engineering context of Yanjin Tunnel was considered, and five of its sections were selected for analysis. (DK294 + 433 to DK295 + 198; DK295 + 198 to DK295 + 987; DK295 + 987 to DK298 + 700; DK300 + 092 to DK300 + 458; DK300 + 458 to DK301 + 748). According to the geological background of each section in conjunction with field investigation and other information, data on the indices for these five sections were obtained, as presented in Table 4.

Table 4 Classification of risk of indicators of water inrush.
Full size table

Results

Results of proposed method

The AHP was employed to determine the subjective weights of the indicators, while the EWM and CRITIC methods were used to calculate their objective weights. These weights were then integrated using the improved game-theoretic method to establish the comprehensive weight of each indicator33, as detailed in Table 5.

Table 5 Comprehensive weights of indicators to assess the risk of water inrush.
Full size table

Calculation of single-indicator measurement matrix

Data on each index from Table 4 was substituted into the corresponding functions to calculate the indices, shown in Fig. 2, and obtain the single-indicator measurement matrix \(\left[ {\mu_{ijk} } \right]\)\(\left( {i = 1,2, \cdots ,5} \right)\) of the five sections of the tunnel. The matrix for DK294 + 433 to DK295 + 198 is provided as an example.

$$ \left[ {\mu_{ijk} } \right] = \left( {\begin{array}{*{20}l} 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {0.5} \hfill & {0.5} \hfill \\ \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {0.794} \hfill & {0.206} \hfill \\ \end{array} } \right) $$

Calculation of multi-indicator measurement vector and confidence criteria

The comprehensive weights from Table 6 and the single-indicator measurement matrix were used. \(\left[ {\mu_{ijk} } \right]\)\(\left( {i = 1,2, \cdots ,5} \right)\), derived in section “Calculation of single-indicator measurement matrix”, in Eq. (17) to calculate the multi-indicator measurement vector. The confidence level was calculated using the criterion of confidence. Similarly, using DK294 + 433 to DK295 + 198 as an example. The results of the evaluation are shown in Table 6.

$$ \begin{aligned} \left[ {C_{k} } \right] & = \left( {\begin{array}{*{20}l} {0.1655} \hfill & {0.0962} \hfill & \cdots \hfill & {0.1657} \hfill & {0.1160} \hfill \\ \end{array} } \right)\left( {\begin{array}{*{20}l} 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {0.5} \hfill & {0.5} \hfill \\ \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {0.794} \hfill & {0.206} \hfill \\ \end{array} } \right) \\ & = \left( {\begin{array}{*{20}l} {0.1519} \hfill & {0.0109} \hfill & {0.4594} \hfill & {0.1402} \hfill & {0.2375} \hfill \\ \end{array} } \right) \\ \end{aligned} $$
Table 6 Evaluation of risk of water inrush based on uncertainty measure theory.
Full size table

According to the confidence recognition principle, \(\lambda\) with a value of 0.5 and based on Eq. (18), when \(K_{0} = 3\) then \(0.1519 + 0.0109 + 0.4594 = 0.6222 > 0.5\), and the risk level for DK294 + 433 to DK295 + 198 is classified as moderate risk (III).

Discussion

The grade of risk of water inrush in the five tunnel sections was assessed based on the proposed method. These results,along with a comparison with other methods, are shown in Table 7.

Table 7 Evaluation of risk of inrush water by using different methods.
Full size table

Based on the records from the construction site and the estimation of inflow volumes, the records should reflect whether there will be casualties and property damage. For sections where inflow occurs, records are kept, and the inflow volume is estimated. The on-site observation results are summarized in Table 7, which shows that the comprehensive unknown measurement evaluation results are consistent with the on-site observations. Compared to the THK and AHP methods, the consistency of this method is 40% and 60%, respectively.

Sections DK295 + 198 to DK295 + 987, and DK295 + 987 to DK298 + 700 of the tunnel were found to be at a medium risk (III) of water inrush. These sections contained strata from the Middle and Lower Silurian and Ordovician in the north flank of the backslope, and the area was dominated by chert and muddy dolomite, which was loose and watery. The enclosing rock belonged to grade IV, and the difference between the level of groundwater and the elevation of the tunnel was significant, such that it could have been inundated with a medium amount of water. Section DK300 + 092 to DK300 + 458 was at a higher risk of water inrush (IV). It contained strata from the Middle and Lower Ordovician, with a negative topography of the karst on the surface. The region was dominated by chert and muddy chert as well as dolomite and muddy dolomite. The enclosing rock belonged to grade IV, with highly soluble rocks that could lead to erosion, and concentrated karst pipelines and karst storage space underground. This rendered large-scale water inrush more likely to occur.

Conclusions

  1. (1)

    The relationships among the indices of evaluation were considered to obtain subjective weights using the analytic hierarchy process, and objective weights were obtained through the entropy weighting method and the CRITIC method. Subsequently, optimal weights were calculated using an improved game-theoretic method. The linear measurement function was then optimized using trigonometric functions based on uncertainty measure theory to achieve the final evaluation. This method can comprehensively and objectively evaluate the risk of water inrush into tunnels during their construction.

  2. (2)

    Eight factors related to the risk of water inrush were extracted from four aspects: the solubility of rock, geological structure, capacity for surface catchment, and hydrogeological factors. These factors in turn included the type and structure of rock, its inclination, coefficient of rainfall infiltration, slope of the ground, vertical zoning of karst water, and spatial location of the groundwater and tunnel. A system was established to assess the risk of karst water inrush during tunnel construction by considering interactions between the indicators in the evaluation system.

  3. (3)

    The results of evaluation of the Yanjin Tunnel by using the proposed method showed that it can objectively reflect the situation on the ground, and can minimize the influence of subjective factors on the outcomes. Compared with the traditional linear measurement function, the trigonometric functions used in our method can better reflect the actual status of the tunnel. Our model thus provides a feasible method to assess the risk of inrush of karst water into tunnels, and has important guiding significance for the relevant engineering projects.