Higgs decay and CP violation phase in the CPV TNMSSM

Abstract

In this study, we calculate the Higgs mass matrix and explore the limitations of the minimum conditions of the scalar potential on parameter degrees of freedom in the CP violation TNMSSM. We discuss the contributions of some parameters to Higgs mass, and their impact on the strength of Higgs decay signals in different decay channels $h\rightarrow$ $\gamma \gamma$, $h\rightarrow$ $VV$ $(V=W,Z)$ and $h\rightarrow$ $f\bar{f}$ $(f=b,c,\tau )$.

Introduction

The Standard Model (SM) of electroweak and strong interactions of elementary particles has achieved great success in the last century^1,2. The Higgs particle was observed in 2012, which means that all particles in the SM have been discovered^3,4. On the other hand, the SM also has some disadvantages, for example, its inability to explain neutrino oscillations^5,6 and the asymmetry of matter and antimatter in the universe, as well as can not provide the candidates for dark matter. Therefore, some extended models of SM have been proposed in an attempt to explain these issues.

The Minimal Supersymmetric Standard Model (MSSM) is a well-known new physics model⁷, which has been extensively studied by physicists in the past few decades. However, the MSSM also has some unexplained problems⁸, such as the hierarchical and $\mu$ term problems, and physicists have proposed some extended models of the MSSM. The extension of the MSSM by addition a gauge singlet which is coupled to Higgs doublets (NMSSM) has been proposed to solve the $\mu$ term problem⁹. The TNMSSM introduce a forbidden bare $\mu$ term, and an effective $\mu$ term is generated by the vacuum expectation value of the singlet. However, all the couplings in the NMSSM being perturbative up to the GUT scale also does not polish up the little gauge hierarchy problem^{10,11,12,13,14,15}. Fortunately, the next-to-minimal supersymmetric standard model with triplets (TNMSSM) is proposed by Kaustubh Agashe et al. , which combines the advantages of NMSSM and TMSSM^16,17. Compared with the MSSM, the TNMSSM introduces a gauge singlet and two $SU(2)_{L}$ triplets with hypercharge $Y=0$, which can validly solve the little gauge hierarchy and $\mu$ term problems in MSSM. In addition, the TNMSSM can give neutrinos a small mass by introducing Majorana mass term without the need to introduce right-handed neutrinos^16,18, which is cannot in the MSSM and NMSSM.

The violation of CP was first observed in neutral kaon decay experiments and strongly validated in B-meson decay experiments^19,20. In addition to particle physics, CP violation (CPV) also provides a possible explanation for the asymmetry of matter and antimatter in the universe²¹. The Higgs interactions play an important role in mediating CPV, for example, CP is broken explicitly in the SM by complex Yukawa couplings of the Higgs boson to quarks. There are literatures indicating, in models that expand the Higgs sector, such as SUSY and MSSM, CP symmetries of those theories are broken spontaneously^22,23.

The existence of Higgs boson has been confirmed, but further research is needed on its properties. In this paper, we consider the contributions of one-loop effective potential²⁴ and two-loop leading-log radiative correction^25,26 to Higgs mass, and calculate the mass matrix of Higgs boson in CPV TNMSSM and explore the reduction of parameter degrees of freedom by the minimum conditions of the scalar potential in Chapter $\textrm{II}$. The concrete theoretical expressions of Higgs decay are presented in Chapter $\textrm{III}$. It is found in the calculation that CPV appears in the tree level Higgs mass matrix in the CPV TNMSSM, which is absent in MSSM²⁷. In numerical analysis, we find that the appearance of CPV in the tree level Higgs mass matrix has negative contributions to Higgs boson mass and greatly limits the range of parameter selection. Then we conduct a numerical analysis of the signal strength of Higgs decay in different decay channels in Chapter $\textrm{IV}$. We observe the effects of tan$\beta$, $M\lambda$ (modulus of $\lambda$), tan$\beta '$ and M$\lambda _{T}$ (modulus of $\lambda _{T}$) on signal strengths when $\lambda _{T}$ and $\chi _{d}$ were selected as different phase angles and M$\chi _{d}$ (modulus of M$\chi _{d}$) and Re$A_{u}$ (real part of $A_{u}$) were selected as different values. We note that because triplets have no coupling with fermions in the Lagrangian , the signal strengths of $h\rightarrow$ $f\bar{f}$ $(f=b,c,\tau )$ are almost unaffected when the phase angle of $\lambda _{T}$ changes. In addition, in Chapter $\textrm{IV}$, we also calculate the electric dipole moments of neutrons and electrons, the contribution of doubly charged particles to Higgs decay, and the mass spectrum of doubly charged particles. In Chapter $\textrm{V}$, we discuss the results of the article.

THE Higgs sector in the CPV TNMSSM

The TNMSSM

Some literature has investigated B meson rare decays²⁸, Higgs boson decays h $\rightarrow$ MZ²⁹, and transition magnetic moment of Majorana neutrinos¹⁸ in the TNMSSM. These studies indicate that the TNMSSM is capable of making good predictions for B meson decay and neutrino transition magnetic moment, and provides valuable information for the experimental exploration of rare Higgs decays. In addition, M.A. Ouahid et al.studied the phenomenology of neutrinos and doubly charged Higgs in flavored-TNMSSM³⁰.

Compared to the MSSM, the TNMSSM has an additional gauge singlet S and two $SU(2)_{L}$ triplets T and $\bar{T}$. The superpotential of Higgs sector and Yukawa sector in TNMSSM are given as follows, respectively

$$\begin{aligned} W_{\text {Higgs}}= & {} \lambda \widehat{S}\widehat{H}_{u}^{T}\cdot \widehat{H}_{d}+\lambda _T\widehat{S}tr(\widehat{\bar{T}} \widehat{T})\nonumber \\{} & {} +\frac{k}{3} \widehat{S}^3+\chi _{u}\widehat{H}_{u}^{T}\cdot \widehat{\bar{T}} \widehat{H}_{u}+\chi _{d}\widehat{H}_{d}^{T}\cdot \widehat{T}\widehat{H}_{d},\end{aligned}$$

(1)

$$\begin{aligned} W_{\text {Yukawa}}= & {} h_u\widehat{Q}^{T}\cdot \widehat{H}_u\widehat{U} -h_d\widehat{Q}^{T}\cdot \widehat{H}_d\widehat{D} \nonumber \\{} & {} -h_l\widehat{L}^{T}\cdot \widehat{H}_d\widehat{E}, \end{aligned}$$

(2)

where $\lambda$, $\lambda _T$, $\kappa$, $\chi _{u}$ and $\chi _{d}$ are dimensionless. The field contents of the TNMSSM are given in Table 1. The singlet S, doublets $H_{u}$, $H_{d}$ and triplets T, $\bar{T}$ are given respectively by

$$\begin{aligned}{} & {} H_u=(H^+_u,H^0_u),H_d=(H^0_d,H^-_d), \nonumber \\{} & {} T =\begin{pmatrix} T^-/\sqrt{2} &{} -T^{--}\\ T^0&{}-T^-/ \sqrt{2} \end{pmatrix}, \end{aligned}$$

(3)

$$\begin{aligned}{} & {} \bar{T} =\begin{pmatrix} \bar{T}^+/\sqrt{2} &{} -\bar{T}^{0}\\ \bar{T}^{++}&{}-\bar{T}^+/ \sqrt{2} \end{pmatrix}, \nonumber \\{} & {} H^0_u =(v_u+\phi _u+ia_u)/\sqrt{2},H^0_d=(v_d+\phi _d+ia_d)/\sqrt{2},\nonumber \\{} & {} T^0 =(v_t+\phi _t+ia_t)/\sqrt{2},S=(v_s+\phi _s+ia_s)/\sqrt{2},\nonumber \\{} & {} \bar{T}^0=(v_{\bar{t}}+\phi _{\bar{t}}+ia_{\bar{t}})/\sqrt{2}, \end{aligned}$$

(4)

where $v_{u},v_{d},v_{s},v_{t}$ and $v_{\bar{T}}$ are vacuum expectation value (VEV) of singlet S, doublets $H_{u}$ and $H_{d}$, triplets T and $\bar{T}$, respectively. Traditionally, tan$\beta$ and tan$\beta '$ are can defined by tan$\beta \equiv v_{u}/v_{d}$ and tan$\beta '\equiv v_{t} /v_{\bar{t}}$. There is a relationship between VEV in SM and VEV in TNMSSM¹⁶

$$\begin{aligned} v^2=v_{u}^2+v_{d}^2+4v_{t}^2+4v_{\bar{t}}^2. \end{aligned}$$

The soft supersymmetry-breaking Lagrangian reads

$$\begin{aligned} -\mathcal {L}_{ {\text {soft} }}=\,&m_{H_{u}}^{2}\left| H_{u}\right| ^{2}+m_{H_{d}}^{2}\left| H_{d}\right| ^{2}+m_{S}^{2}|S|^{2} +m_{T}^{2} {\text {tr}}\big (|T|^{2}\big ) \nonumber \\&+\,m_{\bar{T}}^{2} {\text {tr}}|\bar{T}|^{2}+m_{Q}^{2}|\widetilde{Q}|^{2} +m_{U}^{2}|\widetilde{U}|^{2}+m_{D}^{2}|\widetilde{D}|^{2} \nonumber \\&+\,m_{L}^{2}|\widetilde{L}|^{2}+m_{E}^{2}|\widetilde{E}|^{2}+\big (A_{h_{u}} \widetilde{Q} \cdot H_{u} \widetilde{U}\nonumber \\&-A_{h_{d}} \widetilde{Q} \cdot H_{d} \widetilde{D}-A_{h_{l}} \widetilde{L} \cdot H_{d} \widetilde{E} +A S H_{u} \cdot H_{d}\nonumber \\&+A_{T} S {\text {tr}}(T \bar{T}) +\frac{A_{k}}{3} S^{3} +A_{u} H_{u} \cdot \bar{T} H_{u}\nonumber \\&+A_{d} H_{d} \cdot T H_{d}+ h.c.\big )\nonumber \\&+\frac{1}{2}\big (M_{1}\lambda _{\widetilde{B}\widetilde{B}}+M_{2}\lambda _{\widetilde{W}\widetilde{W}}+M_{3}\lambda _{\widetilde{g}\widetilde{g}}+h.c.\big ). \end{aligned}$$

(5)

Table 1 The field content of the TNMSSM.

The potential and Higgs mass

In the supersymmetry theory, scalar supersymmetry potentials are given in the following way

$$\begin{aligned} V_{0}=\frac{1}{2} D^{a} D^{a}+F_{i}^{\star } F_{i}, \end{aligned}$$

F and D are two auxiliary functions

$$\begin{aligned}{} & {} F_{i} =\partial W / \partial A_{i}, \\{} & {} D^{a} =g A_{i}^{\star } T_{i j}^{a} A_{j}. \end{aligned}$$

In the $\overline{\text {MS}}$ scheme, the CPV effective potential is determined by²⁷

$$\begin{aligned} V_{\text {eff}}=V_0+V_1, \end{aligned}$$

$V_0$ is the tree level potential, $V_1$ is the one-loop level effective potential with²⁴

$$\begin{aligned}{} & {} V_1=\frac{3}{32\pi ^2} \sum _{q=t,b,c}\Bigg [\sum _{i=1,2} m_{\widetilde{q}_{i}}^{4} \Bigg (\ln \frac{m_{\widetilde{q}_{i}}^{2}}{Q^2} -\frac{3}{2}\Bigg )\nonumber \\{} & {} \quad \quad \;\;-2 m^4_{q}\Bigg (\ln \frac{m^2_{q}}{Q^2} -\frac{3}{2}\Bigg )\Bigg ], \end{aligned}$$

(6)

where $m_q$ is the q quark mass, and $m_{\widetilde{q}}$ is the $\widetilde{q}$ squark mass and Q is the renormalization scale at TeV order.The mass matrix of squarks is given by

$$\begin{aligned} m_{\widetilde{q}}^{2}= \begin{pmatrix} m_{\widetilde{q}_{L} \widetilde{q}_{L}^{*}} &{} m_{\widetilde{q}_{R} \widetilde{q}_{L}^{*}}^{\dagger }\\ m_{\widetilde{q}_{L} \widetilde{q}_{R}^{*}}&{} m_{\widetilde{q}_{R} \widetilde{q}_{R}^{*}} \end{pmatrix}, \end{aligned}$$

where the matrix elements for up-type squarks are

$$\begin{aligned} m_{\widetilde{u}_{L} \widetilde{u}_{L}^{*}}=\,&\frac{1}{12}\big (g_{1}^{2}-3g_{2}^{2}\big )\big (H_{u}^{0,*}H_{u}^{0}-H_{d}^{0,*}H_{d}^{0}+2H_{T}^{0,*}H_{T}^{0}\\&-2H_{\bar{T}}^{0,*}H_{\bar{T}}^{0}\big )+\frac{1}{2}\big (2m_{Q}^{2}+h_{u}^{\dagger }h_{u}H_{u}^{0,*}H_{u}^{0}\big ),\\ m_{\widetilde{u}_{L} \widetilde{u}_{R}^{*}}=\,&A_{h_{u}}H_{u}^{0}+h_{u}\big (2H_{d}^{0,*}H_{\bar{T}}^{0,*}\chi _{u}^{*}-H_{d}^{0,*}H_{s}^{0,*}\lambda ^{*}\big ),\\ m_{\widetilde{u}_{R} \widetilde{u}_{R}^{*}}=\,&-\frac{1}{3}g_{1}^{2}\big (H_{u}^{0,*}H_{u}^{0}-H_{d}^{0,*}H_{d}^{0}+2H_{T}^{0,*}H_{T}^{0}\\&-2H_{\bar{T}}^{0,*}H_{\bar{T}}^{0}\big )+\frac{1}{2}\big (2m_{u}^{2}+h_{u}^{\dagger }h_{u} H_{u}^{0,*} H_{u}^{0}\big ), \end{aligned}$$

the matrix elements for down-type squarks are

$$\begin{aligned} m_{\widetilde{d}_{L} \widetilde{d}_{L}^{*}}=\,&\frac{1}{12}\big (g_{1}^{2}+3g_{2}^{2}\big )\big (H_{u}^{0,*}H_{u}^{0}-H_{d}^{0,*}H_{d}^{0}+2H_{T}^{0,*}H_{T}^{0}\\&-2H_{\bar{T}}^{0,*}H_{\bar{T}}^{0}\big )+\frac{1}{2}\big (2m_{Q}^{2}+h_{d}^{\dagger }h_{d}H_{d}^{0,*}H_{d}^{0}\big ),\\ m_{\widetilde{d}_{L} \widetilde{d}_{R}^{*}}=\,&A_{h_{d}}H_{d}^{0}+h_{d}\big (2H_{u}^{0,*}H_{T}^{0,*}\chi _{d}^{*}-H_{u}^{0,*}H_{s}^{0,*}\lambda ^{*}\big ),\\ m_{\widetilde{d}_{R} \widetilde{d}_{R}^{*}}=\,&\frac{1}{6}g_{1}^{2}\big (H_{u}^{0,*}H_{u}^{0}-H_{d}^{0,*}H_{d}^{0}+2H_{T}^{0,*}H_{T}^{0}-2H_{\bar{T}}^{0,*}H_{\bar{T}}^{0}\big )\\&+\frac{1}{2}\big (2m_{d}^{2}+h_{d}^{\dagger }h_{d}H_{d}^{0,*}H_{d}^{0}\big ). \end{aligned}$$

The mass of squarks can be obtained through

$$\begin{aligned} m_{\widetilde{u}_{1,2}}^{2}=\,&\frac{1}{2}\Big [m_{\widetilde{u}_{L} \widetilde{u}_{L}}+m_{\widetilde{u}_{R} \widetilde{u}_{R}} \\&\pm \sqrt{\big (m_{\widetilde{u}_{L} \widetilde{u}_{L}}-m_{\widetilde{u}_{R} \widetilde{u}_{R}}\big )^{2}-4m_{\widetilde{u}_{L} \widetilde{u}_{R}} m_{\widetilde{u}_{R} \widetilde{u}_{L}}}\Big ],\\ m_{\widetilde{d}_{1,2}}^{2}=\,&\frac{1}{2}\Big [m_{\widetilde{d}_{L} \widetilde{d}_{L}}+m_{\widetilde{d}_{R} \widetilde{d}_{R}} \\&\pm \sqrt{\big (m_{\widetilde{d}_{L} \widetilde{d}_{L}}-m_{\widetilde{d}_{R} \widetilde{d}_{R}}\big )^{2}-4m_{\widetilde{d}_{L} \widetilde{d}_{R}} m_{\widetilde{d}_{R} \widetilde{d}_{L}}}\Big ]. \end{aligned}$$

The elements of Higgs mass matrix can be calculated by the following formula on the basis ($\phi _{d},\phi _{u},\phi _{s},\phi _{t},\phi _{\bar{t}},a_{d},a_{u},a_{s},a_{t},a _{\bar{t}}$)

$$\begin{aligned} m_{h_{ij}}^{2}= \left\langle \frac{V_{eff}}{\phi _{i}\phi _{j}} \mid _{\phi _{i,j}=\phi _{d},\phi _{u},\phi _{s},\phi _{t},\phi _{\bar{t}},a_{d},a_{u},a_{s},a_{t},a _{\bar{t}} } \right\rangle . \end{aligned}$$

It is found in the calculation that CPV appears in the tree level Higgs mass matrix in the CPV TNMSSM, namely $m_{h_{ij}}\ \text {and}\ m_{h_{ji}}\ne 0(\phi _{i}=\phi _{d},\phi _{u},\phi _{s},\phi _{t},\phi _{\bar{t}}\ \text {and}\ \phi _{j}=a_{d},a_{u},a_{s},a_{t},a _{\bar{t}})$, which is absent in MSSM. In this paper, we consider the contributions of quarks (t,b,c) and squarks (stop, sbottom, scharm) to Higgs mass.

In addition, the Goldstone can be analytically obtained through $Z^{\dagger }M_h Z$ , where Z is the unitary matrix defined as

$$\begin{aligned} Z= & {} \frac{1}{v}\left( \begin{array}{cccccc} v_{5\times 5} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} {v_{d}} &{} {v_{u}} &{} 0 &{} 2 {v_{t}} &{} -2 {v_{\bar{t}}} \\ 0 &{} -{v_{u}} &{} {v_{d}} &{} 0 &{} 2 {v_{\bar{t}}} &{} 2 {v_{t}} \\ 0 &{} 0 &{} 0 &{} v &{} 0 &{} 0 \\ 0 &{} -2 {v_{t}} &{} -2 {v_{\bar{t}}} &{} 0 &{} {v_{d}} &{} -{v_{u}} \\ 0 &{} 2 {v_{\bar{t}}} &{} -2 {v_{t}} &{} 0 &{} {v_{u}} &{} {v_{d}} \\ \end{array} \right) , \end{aligned}$$

(7)

$$\begin{aligned} v_{5\times 5}= & {} \left( \begin{array}{cccccc} v &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} v &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} v &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} v &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} v\\ \end{array} \right) . \end{aligned}$$

Moreover, we also consider the contribution of two-loop radiative correction to the Higgs boson mass^25,26,31

$$\begin{aligned}&\Delta m_{h}^{2}=\frac{3m_{t}^{4}}{4\pi ^{2}v^{2}}\Bigg [\frac{1}{16\pi ^{2}}\Bigg (\frac{3m_{t}^{2}}{2v^{2}}-32\pi \alpha _{3}\Bigg )\big (\widetilde{t}^{2}+\widetilde{X}_{t}\widetilde{t}\big )\Bigg ]\nonumber \\&\widetilde{t}=Log\frac{M_{S}^{2}}{m_{t}^{2}},\qquad \qquad \widetilde{X}_{t}=\frac{2\widetilde{A}_{t}^{2}}{M_{S}}\Bigg (1-\frac{\widetilde{A}^{2}_{t}}{12M_{S}^{2}}\Bigg ) \end{aligned}$$

(8)

where $\alpha _{3}$ is the strong coupling constant, $M_{S}$ =$\sqrt{m_{\widetilde{t}_{1}}m_{\widetilde{t}_{2}}}$, $\widetilde{A}_{t}=A_{h_{u}}-\left| \mu \right|$ cot$\beta$, $m_{\widetilde{t}_{1}}$ and $m_{\widetilde{t}_{2}}$ denote the stop masses and $A_{h_{u}}$ is the trilinear Higgs stop coupling.

Here we provide the mass matrices of doubly charged particles in TNMSSM. The mass matrix of the doubly charged Higgs $m_{h^{\pm \pm }}$ is

$$\begin{aligned} m_{h^{\pm \pm }}^{2}={} & {} \left( \begin{array}{cccccc} m_{T^{--}T^{--,*}} &{} m_{T^{++,*}T^{--,*}}^{*} \\ m_{T^{--}T^{++}} &{} m_{T^{++,*}T^{++}} \\ \end{array}\right) . \end{aligned}$$

(9)

where

$$\begin{aligned} m_{T^{--}T^{--,*}}=\,&\frac{1}{2}v_{s}^{2}|\lambda _{T} |^{2}\\&-\frac{1}{4}\big (g_{1}^{2}-g_{2}^{2}\big )\big (v_{u}^2-v_{d}^2+2v_{t}^2-2v_{\bar{t}}^2\big )+m_{\bar{t}}^{2},\\ m_{T^{--}T^{++}}=\,&\frac{1}{2}\big (\lambda _{T}\big (v_{u}v_{d}\lambda ^{*}+v_{t}v_{\bar{t}}\lambda _{T}\big )-\big (v_{s}\lambda _{T}k^{*}+\sqrt{2}A_{T}\big )\big ),\\ m_{T^{++,*}T^{++}}=\,&\frac{1}{2}v_{s}^{2}|\lambda _{T} |^{2}\\&-\frac{1}{4}\big (g_{1}^{2}-g_{2}^{2}\big )\big (v_{u}^2-v_{d}^2+2v_{t}^2-2v_{\bar{t}}^2\big )+m_{\bar{t}}^{2}. \end{aligned}$$

The mass matrix of the doubly chargino $m_{\chi ^{\pm \pm }}$ is

$$\begin{aligned} m_{\chi ^{\pm \pm }\chi ^{\pm \pm }}=\frac{1}{\sqrt{2}}v_{s}|\lambda _{T}|. \end{aligned}$$

(10)

CP violation and phase angle

Consider $Ae^{i\theta _{A}}Be^{i\theta _{B}}Ce^{i\theta _{C}}$ is a term in Lagrangian, A, B, C are parameters or fields in Laragian, because $ABCe^{i(\theta _{A}+\theta _{B}+\theta _{C})}=Ae^{i\theta _{A}}Be^{i\theta _{B}}Ce^{i\theta _C}$, we can absorb all the phase angles of the fields into the coupling coefficient through redefining $e^{i\theta _{i}}=e^{i\theta _{A}}e^{i\theta _B}e^{i\theta _C}$. Because all phase angles are undetermined, it is sufficient and reasonable to only add phase angles to the coupling coefficient. In this paper, we use $MA_{i}e^{i\theta _{i}}$ to represent complex parameters $A_{i}$, $MA_{i}$ is modulus of complex parameters $A_{i}$.

The total tadpoles are given by:

$$\begin{aligned}{} & {} T_{\phi _i}=\left\langle \frac{V_{\text {eff}}}{\phi _{i}} \right\rangle =T_{\phi _i}^{0}+T_{\phi _i}^{1},\nonumber \\{} & {} \phi _{i}=\phi _{d},\phi _{u},\phi _{s},\phi _{t},\phi _{\bar{t}},a_{d},a_{u},a_{s},a_{t},a _{\bar{t}}, \end{aligned}$$

(11)

where

$$\begin{aligned}{} & {} T_{\phi _i}^{0}=\left\langle \frac{V_{0}}{\phi _{i}} \mid _{\phi _{i}=\phi _{d},\phi _{u},\phi _{s},\phi _{t},\phi _{\bar{t}},a_{d},a_{u},a_{s},a_{t},a _{\bar{t}} } \right\rangle \\{} & {} T_{\phi _i}^{1}=\left\langle \frac{V_{1}}{\phi _{i}} \mid _{\phi _{i}=\phi _{d},\phi _{u},\phi _{s},\phi _{t},\phi _{\bar{t}},a_{d},a_{u},a_{s},a_{t},a _{\bar{t}} } \right\rangle , \end{aligned}$$

$T_{\phi _i}^{0}$ and $T_{\phi _i}^{1}$ are given in the appendix A. Due to the requirement of vanishing tadpole equations, the degrees of freedom of the parameters can be reduced, i.e. $m_{i}^{2}$ ($i=H_{u},H_{d},S,T$ and $\bar{T}$) disappear in the main diagonal elements of the Higgs mass matrix, and the imaginary parts of the five parameters $A_{i}$ ($A_{i}$=$A_{u}$, $A_{d}$, $A_{k}$, $A_{T}$, $A_{h_{u}}$) will be reduced. The reduced imaginary parts of those parameters are present in the appendix A (A1–A5).

THE 125 Higgs decays

The Higgs boson is a mixed state of CP-even and CP-odd components in CPV theory, differentiate from the SM Higgs boson, both of the two final states appear and could be distinguished from each other by detecting photon polarization³².

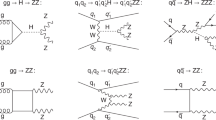
The Higgs are mainly produced by gluon pairs fusion in LHC experiments^33,34. The one loop diagrams with virtual top quarks have the most significant contribution to the leading order (LO). In new physics (NP), one-loop diagrams containing virtual squarks also contribute to the LO. In this section, we use H to denote CP-even Higgs and A to denote CP-odd Higgs. The decay widths of CP-even Higgs to gluon pairs $H\rightarrow gg$ and CP-odd Higgs to gluon pairs $A\rightarrow gg$ are given respectively by^{35,36,37,38,39,40}:

$$\begin{aligned} \Gamma _{\text {NP}}(H\rightarrow gg)= & {} \frac{G_{F}\alpha _{s}^{2}m_{H}^{3}}{64\sqrt{2}\pi ^{3}}\Bigg | \sum _{q}g_{Hqq}A_{1/2}^{H}(x_{q}) \nonumber \\{} & {} +\sum _{\tilde{q}}g_{H \tilde{q} \tilde{q}} \frac{m_{Z}^{2}}{m_{\tilde{q}}^2}A_{0}^{H}(x_{\tilde{q}})\Bigg | ^{2},\end{aligned}$$

(12)

$$\begin{aligned} \Gamma _{\text {NP}}(A\rightarrow gg)= & {} \frac{G_{F}\alpha _{s}^{2}m_{A}^{3}}{64\sqrt{2}\pi ^{3}}\Bigg | \sum _{q}g_{Aqq}A_{1/2}^{A}(x_{q})\Bigg | ^{2} \end{aligned}$$

(13)

The LO contributions to the decay Higgs to diphoton come from the one-loop diagrams. In the NP, all of the fermions, W boson and these supersymmetric partners contribute to Higgs to diphoton decay. The partial widths of CP-even Higgs and CP-odd Higgs bosons decay into diphoton are given by^{33,41,42,43,44,45,46}:

$$\begin{aligned} \Gamma _{\text {NP}}(H\rightarrow \gamma \gamma )={} & {} \frac{G_{F}\alpha _{s}^{2}m_{H}^{3}}{128\sqrt{2}\pi ^{3}}\Bigg | \sum _{f}N_{c}Q_{f}^{2}g_{Hff}A_{1/2}^{H}\big (x_{f}\big ) \nonumber \\{} & {} +\sum _{\tilde{f}}N_{c}Q_{\tilde{f}}^{2}g_{H \tilde{f} \tilde{f}} \frac{m_{Z}^{2}}{m_{\tilde{f}}^2}A_{0}^{H}\big (x_{\tilde{f}}\big ) ^{2}\nonumber \\{} & {} +\sum _{i=1}^{3}g_{HH_{i}^{+}H_{i}^{-}}\frac{m_{Z}^{2}}{m_{H_{i}^{\pm }}^{2}}A_{0}^{H}\big (x_{H_{i}^{\pm }}\big )\nonumber \\{} & {} +\sum _{j=1}^{2}Q_{H_{j}^{++}}^{2}g_{HH_{j}^{++}H_{j}^{--}}\frac{m_{Z}^{2}}{m_{H_{j}^{\pm \pm }}^{2}}A_{0}^{H}\big (x_{H_{j}^{\pm \pm }}\big )\nonumber \\{} & {} +\sum _{k=1}^{3}g_{H\chi _{k}^{+}\chi _{k}^{-}}\frac{m_{W}}{m_{\chi _{k}^{\pm }}}A_{1/2}^{H}\big (x_{\chi _{k}^{\pm }}\big )\nonumber \\{} & {} \,+Q_{\chi ^{++}}^{2}g_{H\chi ^{++}\chi ^{--}}\frac{m_{W}}{m_{\chi ^{\pm \pm }}}A_{1/2}^{H}\big (x_{\chi ^{\pm \pm }}\big )\nonumber \\{} & {} \,+g_{HWW}A_{1}^{H}(x_{W})\Bigg |^{2},\end{aligned}$$

(14)

$$\begin{aligned} \Gamma _{\text {NP}}(A\rightarrow \gamma \gamma )= & {} \frac{G_{F}\alpha _{s}^{2}m_{A}^{3}}{128\sqrt{2}\pi ^{3}}\Bigg | \sum _{f}N_{c}Q_{f}^{2}g_{Aff}A_{1/2}^{A}\big (x_{f}\big )\nonumber \\ {}{} & {} +\sum _{k=1}^{3}g_{A\chi _{k}^{+}\chi _{k}^{-}}\frac{m_{W}^{2}}{m_{\chi _{k}^{\pm }}^{2}}A_{1/2}^{A}\big (x_{\chi _{k}^{\pm }}\big )\nonumber \\{} & {} \,+Q_{\chi ^{++}}^{2}g_{A\chi ^{++}\chi ^{--}}\frac{m_{W}^{2}}{m_{\chi ^{\pm \pm }}^{2}}A_{1/2}^{A}\big (x_{\chi ^{\pm \pm }}\big )\Bigg | ^{2}, \end{aligned}$$

(15)

where $x_{i}=m_{h}^{2}/\big (4m_{i}^{2}\big )$, $A_{1}^{H}(x)$, $A_{\frac{1}{2}}^{H}(x)$, $A_{0}^{H}(x)$ and g(x) are given by⁴⁷

$$\begin{aligned}{} & {} A_{1}^{H}(x)=-\big [2x^{2}+3x+3(2x-1)g(x)\big ]/x^{2},\nonumber \\{} & {} A_{\frac{1}{2}}^{H}(x)=2[x+(x-1)g(x)]/x^{2},\nonumber \\{} & {} A_{0}^{H}(x)=-(x-g(x))/x^{2},\nonumber \\{} & {} A_{1/2}^{A}(x)=2g(x)/x,\nonumber \\{} & {} g(x)={\left\{ \begin{array}{ll} \arcsin ^{2}\sqrt{x},&{}x\le 1\\ -\frac{1}{4}\Bigg [\ln \frac{1+\sqrt{1-1/x}}{1-\sqrt{--1/x}}-i\pi \Bigg ]^{2},&{}x> 1 \end{array}\right. } \end{aligned}$$

(16)

The partial widths of CP-even Higgs bosons decay into vector boson pairs $H$ $\rightarrow$ $VV$ $(V = W, Z)$ are given by^{48,49,50,51,52,53,54,55}:

$$\begin{aligned} \Gamma _{\text {NP}}(H\rightarrow WW)= & {} \frac{3e^{4}m_{H}}{512\pi ^{3}s_{W}^{4}}\left| g_{HWW}\right| ^{2} F\Bigg (\frac{m_{W}}{m_{H}}\Bigg ),\end{aligned}$$

(17)

$$\begin{aligned} \Gamma _{\text {NP}}(H\rightarrow ZZ)= & {} \frac{e^{4}m_{H}}{2048\pi ^{3}s_{W}^{4}c_{W}^{4}}\Bigg (7-\frac{40}{3}s_{W}^{2}+\frac{160}{9}s_{W}^{4}\Bigg )\nonumber \\{} & {} \times \left| g_{HZZ}\right| ^{2}F\Bigg (\frac{m_{Z}}{m_{H}}\Bigg ), \end{aligned}$$

(18)

with

$$\begin{aligned} F(x)=\,&-(1-x^{2})\Bigg (\frac{47}{2}x^{2}-\frac{13}{2}+\frac{1}{x^{2}}\Bigg )\\&-3(1-6x^{2}+4x^{4})\ln {x}\\&+\frac{3(1-8x^{2}+20x^{4})}{\sqrt{4x^{2}-1}} \arccos \Bigg (\frac{3x^{2}-1}{2x^{3}}\Bigg ) \end{aligned}$$

CP-odd Higgs A is uncoupled with vector bosons in tree-level.

In the Born approximation, the partial decay widths of CP-even and CP-odd Higgs bosons decay into fermion pairs are given by^35,49:

$$\begin{aligned} \Gamma _{\text {NP}}(H\rightarrow f\bar{f})= & {} \frac{N_{c}G_{F}m_{f}^{2}m_{H}}{4\sqrt{2}\pi }\left| g_{Hff} \right| ^{2}\beta _{f}^{3},\end{aligned}$$

(19)

$$\begin{aligned} \Gamma _{\text {NP}}(A\rightarrow f\bar{f})= & {} \frac{N_{c}G_{F}m_{f}^{2}m_{A}}{4\sqrt{2}\pi }\left| g_{Aff} \right| ^{2}\beta _{f},\nonumber \\ \beta _{f}= & {} \Bigg (1-\frac{4m_{f}^{2}}{m_{H,A}^{2}}\Bigg )^{\frac{1}{2}} \end{aligned}$$

(20)

In the CPV TNMSSM, the concrete expressions for $g_{Hff}$, $g_{H\widetilde{f}\widetilde{f}}$, $g_{HH^{+}H^{-}}$, $g_{HH^{++}H^{--}}$, $g_{H\chi ^{+}\chi ^{-}}$, $g_{H\chi ^{++}\chi ^{--}}$, $g_{HVV}$, $g_{Aff}$, $g_{A\chi ^{+}\chi ^{-}}$ and $g_{A\chi ^{++}\chi ^{--}}$ appeared in Eqs. (6–9, 11–14) are given in the appendix B.

The signal strengths for the Higgs decay channels are⁵⁶

$$\begin{aligned} \mu _{\gamma \gamma ,VV}^{ggF}= & {} \frac{\sigma _{\text {NP}}(ggF)}{\sigma _{\text {SM}}(ggF)}\frac{BR_{\text {NP}}(h\rightarrow \gamma \gamma ,VV)}{BR_{\text {SM}}(h\rightarrow \gamma \gamma ,VV)},(V=W,Z)\nonumber \\ \mu _{f\bar{f}}^{VBF}= & {} \frac{\sigma _{\text {NP}}(VBF)}{\sigma _{\text {SM}}(VBF)}\frac{BR_{\text {NP}}(h\rightarrow f\bar{f})}{BR_{\text {SM}}(h\rightarrow f\bar{f})},(f=b,c,\tau ) \end{aligned}$$

(21)

The Higgs production cross sections can be simplified through

$$\begin{aligned} \frac{\sigma _{\text {NP}}(ggF)}{\sigma _{\text {SM}}(ggF)}\approx{} & {} \frac{\Gamma _{\text {NP}}(h\rightarrow gg)}{\Gamma _{\text {SM}}(h\rightarrow gg)},\\ \frac{\sigma _{\text {NP}}(VBF)}{\sigma _{\text {SM}}(VBF)}\approx{} & {} \frac{\Gamma _{\text {NP}}(h\rightarrow VV)}{\Gamma _{\text {SM}}(h\rightarrow VV)}, \end{aligned}$$

the ratios of the signal strengths from the Higgs decay channels can be reduced as

$$\begin{aligned} \mu _{\gamma \gamma }^{ggF}={} & {} \frac{\Gamma _{\text {SM}}}{\Gamma _{\text {NP}}}\frac{\Gamma _{\text {NP}}(h\rightarrow gg)}{\Gamma _{\text {SM}}(h\rightarrow gg)}\frac{\Gamma _{\text {NP}}(h\rightarrow \gamma \gamma )}{\Gamma _{\text {SM}}(h\rightarrow \gamma \gamma )}\nonumber \\ \mu _{VV}^{ggF}={} & {} \frac{\Gamma _{\text {SM}}}{\Gamma _{\text {NP}}}\frac{\Gamma _{\text {NP}}(h\rightarrow gg)}{\Gamma _{\text {SM}}(h\rightarrow gg)}\frac{\Gamma _{\text {NP}}(h\rightarrow VV)}{\Gamma _{\text {SM}}(h\rightarrow VV)}\nonumber \\ \mu _{f\bar{f}}^{VBF}={} & {} \frac{\Gamma _{\text {SM}}}{\Gamma _{\text {NP}}}\frac{\Gamma _{\text {NP}}(h\rightarrow VV)}{\Gamma _{\text {SM}}(h\rightarrow VV)}\frac{\Gamma _{\text {NP}}(h\rightarrow f\bar{f})}{\Gamma _{\text {SM}}(h\rightarrow f\bar{f})}, \end{aligned}$$

(22)

where $\Gamma _{\text {NP}}$ = $\sum _{f}$ $\Gamma _{\text {NP}}$($h$ $\rightarrow$ $f\bar{f}$) + $\sum _{V}$ $\Gamma _{\text {NP}}$($h$ $\rightarrow$VV) + $\Gamma _{\text {NP}}$($h$ $\rightarrow$ $gg$) + $\Gamma _{\text {NP}}$($h$ $\rightarrow$ $\gamma$ $\gamma$), represents the NP total decay width of physical Higgs.

Numerical analysis

We study the mass and decay of the lightest Higgs boson $h^{0}$ in CPV TNMSSM in this section. After considering the experimental limitations, the scalar lepton masses larger than 700 GeV, and chargino masses larger than 1100 GeV⁵⁷, the parameters in CPV TNMSSM were selected as

$$\begin{aligned}{} & {} \ v_{s}=1\ \text {TeV},\ M_{1}=1\ \text {TeV},\ M_{2}=1\ \text {TeV},\nonumber \\{} & {} Q=1\ \text {TeV},\ \text {M}k=0.9,\ \text {M}\chi _{u}=0.3,\nonumber \\{} & {} \text {M}A=0.8\ \text {TeV},\ \theta _{\lambda }=0.02,\ \theta _{k}=0.05,\nonumber \\{} & {} \theta _{\chi _{u}}=\pi /3,\ \theta _{A}=0.01,\ \text {Re}A_{d}=0.5\ \text {TeV},\nonumber \\{} & {} \text {Re}A_{k}=-0.5\ \text {TeV},\ \text {Re}A_{T}=0.5\ \text {TeV},\nonumber \\{} & {} A_{h_{d}}=A_{h_{l}}=\text {Re}A_{h_{u}}=0.2\ \text {TeV},\nonumber \\{} & {} m_{Q}^{2}=m_{\bar{u}}^{2}=m_{\bar{d}}^{2}=m_{L}^{2}=m_{\bar{e}}^{2}=1.8\ \text {TeV}^{2}. \end{aligned}$$

(23)

where Re$A_{i}$ are the real parts of $A_{i}$ ($A_{i}=A_{u}$, $A_{d}$, $A_{k}$, $A_{T}$, $A_{h_{u}}$), M$A_{j}$ are the modulus of $A_{j}$ ($A_{j}=\lambda _{T}$, k, $\chi _{u}$, $\chi _{d}$, A), and $\theta _{A_{k}}$ are the CP phase of $A_{k}$ ($A_{k}=\lambda$, k, $\chi _{u}$, A), respectively.

Due to the CP violation appears in the tree-level Higgs mass matrix which leads to a negative contribution to Higgs mass and the value of $v_{s}$ is large, the selection ranges of phase angles for $\lambda$, k and A are strictly limited.

Fig. 1

(a) The variation of the mass of $h^{0}$ with tan$\beta$ when $\theta _{\lambda _T}$ is selected as different phase angles. (b) The variation of the mass of $h^{0}$ with M$\lambda$ when $\theta _{\chi _{d}}$ is selected as different phase angles.

From the superpotential equations (1) and (2), it can be simply inferred that due to the vacuum expectation value $v_{t}$ and $v_{\bar{t}}$ are very small compared to the vacuum expectation value $v_{u}$, $v_{d}$ and $v_{s}$, the parameters that have no coupling with S, $H_{u}$ and $H_{d}$ are not sensitive to the influence of higgs mass and decay signal strengths. Moreover, because of the value of $v_{s}$ is very large, some parameters such as $\chi _{u}$, k, A and $A_{k}$ are too sensitive to higgs mass, resulting in the inability to observe those impacts on the decay signal strengths within suitable parameter ranges. After considering the above factors, we select the parameters that are sensitive to signal strengths and analyse the results.

Fig. 2

(a) The variation of the mass of $h^{0}$ with tan$\beta '$ when M$\chi _{d}$ is selected as different values. (b) The variation of the mass of $h^{0}$ with M$\lambda _{T}$ when Re$A_{u}$ is selected as different values.

We adopt the parameters as follow

$$\begin{aligned}{} & {} 6\le \text {tan}\beta \le 50,\ 0.2\le \text {M}\lambda \le 0.6,\nonumber \\{} & {} 0.3\le \text {tan}\beta '\le 6,\ 0.35\le \text {M}\lambda _{T}\le 1,\nonumber \\{} & {} \theta _{\lambda _{T}}=0,\ \pi /4,\ \pi /3\ \text {and}\ \pi /2,\nonumber \\{} & {} \theta _{\chi _{d}}=0,\ \pi /3,\ \pi /2,\ \pi ,\nonumber \\{} & {} \text {M}\chi _{d}=0.5,\ 0.6,\ 0.7,\ 0.8,\nonumber \\{} & {} \text {Re}A_{u}=-400,\ -500,\ -600,\ -700, \end{aligned}$$

(24)

We explore the effects of these parameters on the Higgs mass and consider the limitations of experiments on Higgs mass, further explore their effects on Higgs decay signal strengths. In Figs. 1, 3 and 5, we adopt tan$\beta '$ = 1.5, M$\lambda _{T}$ = 0.9, M$\chi _{d}$ = 0.8 and Re$A_{u}$ = − 500, in Figs. 2, 4 and 6, we adopt tan$\beta$ = 10, $\theta _{\lambda _{T}}$ = $\pi$/6, M$\lambda$ = 0.4 and $\theta _{\chi _{d}}$ = 0.8.

In Fig. 1a and b, we select M$\lambda$ = 0.4, $\theta _{\chi _{d}}=\pi /3$ when observing the effects of tan$\beta$ and $\theta _{\lambda _{T}}$ on $h^0$ mass, select tan$\beta$ = 10, $\theta _{\lambda _T}=\pi /6$ when observing the effects of $M\lambda$ and $\theta _{\chi _{d}}$ on $h^0$ mass. In Fig. 2a and b, we select M$\lambda _{T}$ = 0.9, Re$A_{u}=-500$ when observing the effects of tan$\beta '$ and M$\chi _{d}$ on $h^0$ mass, select tan$\beta '$ = 1.5, M$\chi _{d}=0.8$ when observing the effects of $M\lambda _{T}$ and Re$A_{u}$ on $h^0$ mass.

We take the parameter ranges to accept 124 GeV $\le m_{h^{0}}\le$ 126.5 GeV and study the impacts of these two sets of parameters on signal strengths.After considering the experimental data of Higgs mass, these parameter spaces are further limited

$$\begin{aligned}{} & {} 8\le \text {tan}\beta \le 50,\ 0.35\le \text {M}\lambda \le 0.55,\nonumber \\{} & {} 0.5\le \text {tan}\beta '\le 5,\ 0.45\le \text {M}\lambda _{T}\le 0.8, \end{aligned}$$

(25)

We analyse signal strengths within the new parameter ranges.

Fig. 3

(a) The variation of neutron EDM with $\theta _{\chi _{d}}$ and $\theta _{\lambda _{T}}$. (b) The variation of neutron EDM with M$\lambda$ when $\theta _{\lambda _{T}}$ is selected as different values. (c) the variation of neutron EDM with tan$\beta '$ when M$\chi _{d}$ is selected as different values. (d) The variation of neutron EDM with M$\lambda _{T}$ when Re$A_{u}$ is selected as different values.

Fig. 4

(a) The variation of electron EDM with $\theta _{\chi _{d}}$ and $\theta _{\lambda _{T}}$. (b) The variation of electron EDM with M$\lambda$ when $\theta _{\lambda _{T}}$ is selected as different values. (c) The variation of electron EDM with tan$\beta '$ when M$\chi _{d}$ is selected as different values. (d) The variation of electron EDM with M$\lambda _{T}$ when Re$A_{u}$ is selected as different values.

In addition, the selection of complex parameters, especially the phase angle, is strongly limited by the electric dipole moments (EDM) of electrons and neutrons. To further verify the rationality of these parameters, we calculated the electric dipole moments of electrons and neutrons using some unique parameters of TNMSSM. These results are presented in Figs. 3 and 4.

The effective Lagrangian for spin-$\frac{1}{2}$ particles EDMs can be written as

$$\begin{aligned} \mathcal {L}_{I}^{\text {EDM}}=-\frac{i}{2}d_{f}\bar{\psi }\sigma _{\mu \nu }\gamma _{5}\psi F^{\mu \nu } \end{aligned}$$

Similarly, the effective Lagrangian for spin-$\frac{1}{2}$ particles EDMs can be written as

$$\begin{aligned} \mathcal {L}_{I}^{\text {CEDM}}=-\frac{i}{2}\widetilde{d}_{q}^{C}\bar{q}\sigma _{\mu \nu }\gamma _{5}T^{a}q G^{\mu \nu a}. \end{aligned}$$

The concrete formulas of EDMs and CEDMs can be seen in^{58,59,60,61,62}. The research by T.Ibrahim et al. shows that the main factors affecting fermion EDM are the phase of the fermion field , vector Superfields, Higgs field, and the coupling parameters between Higgs fields⁵⁸. Due to the fact that this article only considers the phase of parameters related to Higgs decay, and $\lambda$ and $\chi _{u}$ have already been selected, only the phase of $\chi _{d}$ and $\lambda _{T}$ needs to be considered.

The experimental limitations for neutron and electron EDM are $d_{n}<0.18\times 10^{25}$ and $d_{e}<0.11\times 10^{28}$, respectively, which are denoted by blue dashed lines in the Figs. 3 and 4. Due to the influence of $\lambda$ and $\chi _{u}$ not being equal to 0, the EDM of electrons and neutrons is not equal to 0 when $\chi _{d}$ and $\lambda _{T}$ are equal to 0. When $\lambda _{T}$ changes, the EDM of electrons and neutrons does not change. This is because singlet and triplets are not coupled with fermions. The calculation results are in good agreement with experimental limits, leading us to believe that these parameters are appropriate.

Fig. 5

(a, b) The variation of the signal strength $\mu ^{ggF}_{\gamma \gamma }$ and $\mu ^{ggF}_{VV}$ with tan$\beta$ when $\theta _{\lambda _{T}}$ is selected as different phase angles. (c, d) The variation of the signal strength $\mu ^{ggF}_{\gamma \gamma }$ and $\mu ^{ggF}_{VV}$ with M$\lambda$ when $\theta _{\chi _{d}}$ is selected as different phase angles.

Fig. 6

(a, b) The variation of the signal strength $\mu ^{ggF}_{\gamma \gamma }$ and $\mu ^{ggF}_{VV}$ with tan$\beta '$ when M$\chi _{d}$ is selected as different values. (c, d) The variation of the signal strength $\mu ^{ggF}_{\gamma \gamma }$ and $\mu ^{ggF}_{VV}$ with M$\lambda _{T}$ when Re$A_{u}$ is selected as different values.

Fig. 7

(a, b) The variation of the signal strength $\mu ^{VBF}_{bb}$, $\mu ^{VBF}_{\tau \tau }$ and $\mu ^{VBF}_{cc}$ with tan$\beta$ when $\theta _{\lambda _T}$ is selected as different phase angles. (c, d) The variation of the signal strength $\mu ^{VBF}_{bb}$, $\mu ^{VBF}_{\tau \tau }$ and $\mu ^{VBF}_{cc}$ with M$\lambda$ when $\theta _{\chi _{d}}$ is selected as different phase angles.

Fig. 8

(a, b) The variation of the signal strength $\mu ^{VBF}_{bb}$, $\mu ^{VBF}_{\tau \tau }$ and $\mu ^{VBF}_{cc}$ with tan$\beta '$ when M$\chi _{d}$ is selected as different values. (c, d) The variation of the signal strength $\mu ^{VBF}_{bb}$, $\mu ^{VBF}_{\tau \tau }$ and $\mu ^{VBF}_{cc}$ with M$\lambda _{T}$ when Re$A_{u}$ is selected as different values.

When different phase angles for $\lambda _{T}$ and $\chi _{d}$ are selected, $\mu ^{ggF}_{\gamma \gamma }$ in Fig. 5a and b first increases and then decreases, and reaches its maximum at tan$\beta$ = 12 and $M\lambda$ = 0.47, $\mu ^{ggF}_{VV}$ in Fig. 5a and d first increases and then decreases, and reaches its maximum at tan$\beta$ = 14 and $M\lambda$ = 0.46, respectively. According to the datas provided in PDG⁵⁷, $\mu ^{exp}_{\gamma \gamma }$ = 1.10 ± 0.07^63,64,65,66, $\mu ^{exp}_{WW}$ = 1.19 ± 0.12^65,66, $\mu ^{exp}_{ZZ}$ = 1.01 ± 0.07^65,67,68, the maximum error between the experimental data and the theoretical prediction of $\mu _{\gamma \gamma }$ is about 1$\sigma$ and of $\mu _{WW}$ is less than 1$\sigma$ and of $\mu _{ZZ}$ is approaching 2.5$\sigma$.

When different vlaues for M$\chi _{d}$ and Re$A_{u}$ are selected, $\mu ^{ggF}_{\gamma \gamma }$ gradually increasing in Fig. 6a and gradually decreasing in Fig. 6b, $\mu ^{ggF}_{VV}$ gradually increasing in Fig. 6c and gradually decreasing in Fig. 6d, respectively. Because the value of $v_{d}$ is relatively small compared to $v_{u}$ when tan$\beta$=10, the effects of M$\chi _{d}$ on signal strengths are insensitive, so that $\mu ^{ggF}_{\gamma \gamma }$ and $\mu ^{ggF}_{VV}$ remain almost unchange when M$\chi _{d}$ changes. According to the datas provided in PDG, the maximum error between the experimental data and the theoretical prediction of $\mu _{\gamma \gamma }$ is about 1.1$\sigma$ and of $\mu _{WW}$ is less than 0.8$\sigma$ and of $\mu _{ZZ}$ is approaching 2.4$\sigma$.

When different phase angles for $\lambda _{T}$ and $\chi _{d}$ are selected, $\mu ^{VBF}_{bb}$ and $\mu ^{VBF}_{\tau \tau }$in Fig. 7a and b gradually decreasing, $\mu ^{VBF}_{cc}$ in Fig. 7c and d gradually increasing. According to the datas provided in PDG⁵⁷, $\mu ^{exp}_{bb}$ = 0.98 ± 0.12^65,66,69,70, $\mu ^{exp}_{cc}$ = 37 ± 20^71,72, and $\mu ^{exp}_{\tau \tau }$ = $1.15_{-0.15}^{+0.16}$^65,66,73, the maximum error between the experimental data and the theoretical prediction of $\mu _{bb}$ is about 1.6$\sigma$, of $\mu _{cc}$ is less than 1.5$\sigma$ and of $\mu _{\tau \tau }$ is much less than 1$\sigma$. When different phase angles of $\lambda _T$ are selected, $\mu ^{VBF}_{bb}$, $\mu ^{VBF}_{\tau \tau }$and $\mu ^{VBF}_{cc}$ remain almost unchanged, because the Higgs singlet and triplets are uncoupled with fermions in the Lagrangian.

When different vlaues for M$\chi _{d}$ and Re$A_{u}$ are selected, $\mu ^{ggF}_{\gamma \gamma }$ almost unchange in Fig. 8a and b, $\mu ^{ggF}_{VV}$ almost unchange in Fig. 8d and only slightly reduce in Fig. 8c. This meets our expectation because these parameters are uncoupled with fermions in the Lagrangian.

We calculated $\Gamma _{\text {NP}}(h\rightarrow \gamma \gamma )$ after ignoring the contribution of doubly charged particles $\Gamma _{\text {NP}}^{\text {no doubly}}(h\rightarrow \gamma \gamma )$ and compared it with $\Gamma _{\text {NP}}(h\rightarrow \gamma \gamma )$ to quantify the contribution of two charged particles to the decay $h\rightarrow \gamma \gamma$.These results are presented in Fig. 9. The $\textrm{C}_{\text {doubly}}$ in Fig. 9 is defined by

$$\begin{aligned} \text {C}_{\text {doubly}}=\frac{\Gamma _{\text {NP}}(h\rightarrow \gamma \gamma )-\Gamma _{\text {NP}}^{\text {no doubly}}(h\rightarrow \gamma \gamma )}{\Gamma _{\text {NP}}(h\rightarrow \gamma \gamma )}. \end{aligned}$$

Fig. 9

(a) The variation of $\textrm{C}_{\text {doubly}}$ with tan$\beta$ when $\theta _{\lambda _{T}}$ is selected as different phase angles. (b) The variation of $\textrm{C}_{\text {doubly}}$ with M$\lambda$ when $\theta _{\chi _{d}}$ is selected as different phase angles. (c) The variation of $\textrm{C}_{\text {doubly}}$ with tan$\beta '$ when M$\chi _{d}$ is selected as different values. (d) The variation of $\textrm{C}_{\text {doubly}}$ with M$\lambda _{T}$ when Re$A_{u}$ is selected as different values.

Due to the large mass of the doubly charged Higgs, its contribution to the decay width is small. For the doubly charged chargino, because the vacuum expectation values of triplets are very small, its contribution to the decay width is also small.

We calculate the masses of the lightest doubly charged Higgs boson $h^{++}$ and doubly charged chargino $\chi ^{++}$, and compared them with experimental results. The analytical expressions for the mass of doubly charged Higgs boson and doubly charged chargino are given in Eqs. (9) and (10), and the numerical results are shown in Figs. 10 and 11.

Fig. 10

(a) The variation of the mass of $h^{++}$ with tan$\beta$ when $\theta _{\lambda _T}$ is selected as different phase angles. (b) The variation of the mass of $h^{++}$ with M$\lambda$ when $\theta _{\chi _{d}}$ is selected as different phase angles. (c) The variation of the mass of $h^{++}$ with tan$\beta '$ when M$\chi _{d}$ is selected as different values. (d) The variation of the mass of $h^{++}$ with M$\lambda _{T}$ when Re$A_{u}$ is selected as different values.

Fig. 11

The variation of the mass of $\chi ^{++}$ with M$\lambda _{T}$.

The limitation of the experiment is that $m_{h^{++}}$ > 1080 GeV^74,75,76, we mark it with a blue dashed line in the Fig. 10. From the Eq. (10), it can be seen that the mass of $m_{\chi ^{++}}$ depends only on $\lambda _{T}$.

Conclusion

As an extended model of MSSM, the TNMSSM introduces a new gauge singlet S and two $SU(2)_{L}$ triplets T, $\bar{T}$. The neutral parts of Higgs singlet, two Higgs doublets($H_{d}$ and $H_{u}$) and two Higgs singlets mix together, which constitute a $10\times 10$ mass squared matrix of Higgs boson after considering CP violation. After considering the contributions of one-loop effective potential and two-loop radiative correction, we obtain complete Higgs mass matrix and the lightest Higgs $h^{0}$ with a mass $m_{h^{0}}$ near 125 GeV in Chapter II. We show concrete theoretical expressions of the Higgs decay in Chapter III, and provide the concrete expressions of $g_{Hff}$, $g_{H\widetilde{f}\widetilde{f}}$, $g_{HH^{+}H^{-}}$, $g_{HH^{++}H^{--}}$, $g_{H\chi ^{+}\chi ^{-}}$, $g_{H\chi ^{++}\chi ^{--}}$, $g_{HVV}$, $g_{Aff}$, $g_{A\chi ^{+}\chi ^{-}}$ and $g_{A\chi ^{++}\chi ^{--}}$ in the appendix B.

We explore the limitations of the minimum conditions of the scalar potential on the degrees of freedom of parameters and present the relevant results in the appendix A. After considing the minimum conditions of the scalar potential in the CPV TNMSSM model, we reduce five parameters $m_{i}^{2}$ ($i=H_{u}$, $H_{d}$, S, T and $\bar{T}$) and the imaginary parts of the five parameters $A_{i}$ (A$_{i}$ = $A_{u}$, $A_{d}$, $A_{k}$, $A_{T}$, $A_{h_{u}}$) . In Chapter IV, after considering limitations of the minimum conditions of the scalar potential and Higgs mass, we obtain a set of parameters and calculate the signal strengths of Higgs decay in different decay channels $h\rightarrow$ $\gamma \gamma$, $h\rightarrow$ $VV$ $(V=W,Z)$ and $h\rightarrow$ $f\bar{f}$ $(f=b,c,\tau )$ , and compare them with experimental results in PDG, where $\mu ^{VBF}_{\gamma \gamma }$, $\mu ^{VBF}_{WW}$ and $\mu ^{VBF}_{\tau \tau }$ match the experimental data very well. Compared to the SM, the theoretical calculations of new physics better conform to the experimental results. In addition, the calculation result of the signal strengths $\mu _{ff}^{VBF}$ of $h\rightarrow f\bar{f}$ are almost the same when $\theta _{\lambda _{T}}$ takes different values, we analyze that this is because the triplets are uncoupled with fermions in the Lagrangian. Moreover, we explore the effects of some parameters that beyond the MSSM on Higgs mass and decay signal strengths, such as tan$\beta '$, $\theta _{\chi _{d}}$, $\theta _{\lambda _{T}}$, M$\chi _{d}$ and M$\lambda _{T}$. From the Chapter IV, it can be seen that $\theta _{\chi _{d}}$ and M$\lambda _{T}$ are sensitive to Higgs decay signal strengths. In addition, in Chapter $\textrm{IV}$, we calculate the EDM of electrons and neutrons, as well as the mass spectrum of doubly charged particles, which well meet the experimental limitations. We also discuss the contribution of doubly charged particles to Higgs decay in the “Numerical analysis” Section. Due to the large mass of $h^{++}$ and small $v_{t}$, the contribution of doubly charged particles to Higgs decay is relatively small. We look forward to more experimental measurements of these decays in the future, which will be beneficial for understanding more about the properties of Higgs boson.