Introduction

Advancements in minimally invasive robotic surgical systems have expanded the gold standards in healthcare and medicine1. These advancements are leading to reduced tissue trauma and faster recovery times, which reduces hospitalization time and increased comfort of patients after critical surgeries2. Conventional robotic arm-based surgical systems, such as the da Vinci®, are commonly used in such surgeries3. These devices employ bulky, contact-based end-effectors, which limits possible miniaturization of the current technology. In addition, due to the physical connections to the robot arm, surgeries such as bile duct surgery, which requires complex maneuvers, can be challenging and invasive with such conventional robotic technologies.

Magnetic actuation could be a pivotal technology for ultra-minimally invasive surgeries. Systems for steering untethered magnetic devices may empower surgical robotic systems to operate deep within patients with even further minimization of tissue damage because they obviate the need for making physical contact with the end effector4,5,6,7. To capitalize on the potential benefits of magnetic actuation, researchers have developed unique magnetic devices aimed at controlling particles8, robots9, and devices10. At the microscale, magnetic particles have been steered with magnetic fields to perform local drug delivery targeting tumors11,12. At the centimeter scale, magnetic capsule endoscopy (MACE) devices have actively steered imaging devices in the gastrointestinal tract to improve diagnostic data collection, and future advances aim to enable targeted therapeutic capabilities13,14,15. Similarly, magnetic catheter guidance is another established discipline where magnetic fields provide improved manipulation capabilities and accuracy for steering the distal tip of the catheter, reducing tissue damage caused by the catheter-based procedures16,17,18. Magnetic navigation systems from Stereotaxis Inc.19 and Aeon Scientific20 also have each demonstrated clinical relevance in cardiovascular interventions.

Surgeries require a variety of tool-tissue interactions, including tissue cutting, tissue manipulation, and tissue penetration. Each of these tasks requires significant force. While surgical robotic arms are able to readily supply newton-scale forces and control multiple tools independently, comparable tasks are not easily accomplished with magnetic robots. Recent work has demonstrated potential mechanical surgical applications. Onaizah and Diller have demonstrated cutting with magnetic untethered robots21, Mair et al. have demonstrated tissue penetration with magnetic needles22, and Rahmer et al. have shown drilling to pass through the tissues5. In addition to the research efforts, Levita Magnetics® has demonstrated tissue manipulation with magnetic fields to apply constant forces on certain organs in the abdomen to ease the operations and allow a larger workspace for surgeons23.

Electromagnetic actuation systems are commonly used for remote force/torque delivery onto magnetic tools. There are various considerations to optimize an electromagnetic actuation system, including workspace size, spatial magnetic field addressability, single or multi-tool controllability, and force and torque requirements. To generate refined spatial control, an array of engineered magnetic field-generating systems have been devised. Magnetic manipulation systems are composed of electromagnets, permanent magnets, or combinations thereof, with individual magnets being either fixed or movable24. An array of such systems have been proposed for particle-based drug delivery25, as well as magnetically driven medical devices26. Notable research-scale electromagnet systems include OctoMag27 and its variants12,28,29, OmniMag30,31,32, and MPI-based systems33 that are designed for generating a magnetic field and its gradients in a versatile manner for proof-of-concept demonstrations. The strong gradients in the fringe field of an MRI instrument can also be used to generate strong forces and torques34,35, but limitations exist due to the constant nature of the gradients created by superconducting coils in its fringe field. To overcome the challenge of the weak forces for surgical applications, Erin et al. have developed an MPACT-Needle which is capable of exerting strong forces at miniaturized needle scales by utilizing impact forces generated by magnetic fields36. However, to further meet the needs of surgical applications, the ability to control multiple agents independently is essential37. Additionally, the magnetic agents need to receive strong forces; for instance, a needle usually requires more than 1 N to penetrate liver tissue38. Therefore, it is crucial for an electromagnetic actuation system to generate sufficient field articulation to enable the simultaneous control of multiple agents, along with strong forces through magnetic gradients.

Here we present details on our Variable Outer Radius Individually Addressable Coil Stacks (VORIACS) system (shown in Fig. 1), which aims to supply stronger fields and gradients for the manipulation of objects in the micrometer to centimeter scale range. By using genetic algorithms for optimizing coil design for magnetic field gradients within the power limit constraints and by implementing a novel stacked tri-coil configuration, the VORIACS system is capable of creating the strongest magnetic pulling force as yet presented for systems having decimeter-scale workspaces. VORIACS can generate 1.85–6.08 times greater forces than their solenoid counterparts by using the same electrical power. In a particular example, we have experimentally shown that VORIACS can create more than \(5\times\) stronger forces at a given point as compared to a non-optimized solenoid configuration system such as the MagnetoSuture™39. Moreover, with 12 independently controlled coils, VORIACS has sufficient degrees of freedom (DoF) and workspace variability to simultaneously control multiple agents. In what follows, we present our method of optimization, coil manufacturing, field mapping characterization, and experimental results which demonstrate high-force generation.

Fig. 1
figure 1

Variable Outer Radius Individually Addressable Coil Stacks (VORIACS) utilizes concentric three coils per coil-unit-set to exert strong magnetic forces and to articulate the magnetic fields within a compact footprint. This electromagnetic actuation system is utilized for successfully actuating a magnetic clinical needle for difficult-to-penetrate 2% agarose gel.

Full size image

Methods

Electromagnetic coils are typically solenoid-shaped large inductors. The current passing through the electromagnets generate magnetic fields. This magnetic field can be adjusted by controlling the current amplitude and direction applied to each coil.  Combinations of individually addressable coils can be used to further tune the strengths, directions, and spatial gradients of local magnetic fields. Here we summarize background information regarding magnetic fields and actuation forces, introduce the fundamentals of magnetic field simulation, and lay out our approach for coil design optimization using genetic algorithms. We then describe our system integration approach for generating the VORIACS system hardware, concluding with our approach to characterizing our system.

Magnetic fields and actuation forces

The magnetic fields generated by different electromagnets are superimposable. In other words, the magnetic fields and their gradients can be linearly combined to yield the total magnetic field at any location. Externally applied magnetic fields exert forces and torques on rigid magnetic bodies. This induced action enables the wireless manipulation and control of magnetic objects. The magnetization vector of an object, \({{\textbf {M}}_m}\), is a three-dimensional (3D) vector that represents the unit volume magnetic strength of this object. Typically, it is assumed to be homogeneous throughout the volume and constant for hard magnetic materials. For such an object, the magnetic pulling forces, \(\textbf{F}_m\), and torques, \(\textbf{T}_m\), acting on a magnetic body can be represented by the following:

$$\begin{aligned} \textbf{T}_m&= V_m(\textbf{M}_m\times \textbf{B}) , \end{aligned}$$
(1)
$$\begin{aligned} \textbf{F}_m&= V_m(\textbf{M}_m\cdot \nabla )\textbf{B}, \end{aligned}$$
(2)

where \(V_m\) is the magnetic volume strength of the magnetic body, \(\textbf{M}_m\), is the unit magnetization vector of the magnetic body, and \(\textbf{B}\) is the applied external magnetic field vector.

The magnetic torque exhibits a linear relationship with the strength of magnetic field \(\textbf{B}\), while the magnetic pulling force similarly scales linearly with the magnetic field gradient, \(\nabla \textbf{B}\). The actuation forces also exhibit a linear scaling with \(V_m\). However, larger \(V_m\) often implies an increase in the size of the magnetic device and, in surgical settings, a corresponding increase in induced damage to surrounding tissues. In many scenarios, the aim is to accomplish the surgical task with the smallest useful tool possible. Consequently, it is advantageous to aim for manipulating the smallest possible device while striving for maximizing \(\textbf{B}\) and \(\nabla \textbf{B}\).

Magnetic field calculations via single current loop integration

The simulation is designed to calculate the magnetic field and its gradient strength at any given distance along the concentric center axis of the circular windings of an electromagnetic coil. The Biot–Savart Law provides a mathematical framework to calculate the magnetic field at any given point due to an arbitrary current passing through a wire, and it can be expressed as follows:

$$\begin{aligned} \textbf{dB}_{grad} = \frac{{\mu _0 }}{{4\pi }}\frac{{Id{\varvec{\ell }} \times {\varvec{\hat{r}}}}}{{r^2}} \end{aligned}$$
(3)

where \(\mu _0\) is the permeability of vacuum constant, I is the current passing through the wire, \(d{\varvec{\ell }}\) is the infinitesimal length element of the physical wire, \(\varvec{\hat{r}}\) is the 3D unit vector pointing from the coil wire towards to the target point in space, and r is the distance between the coil wire and the target point the magnetic field is evaluated at.

In the case of an ideal circular loop, the magnetic field along the loop’s normal axis (\(\hat{\textbf{i}}\)) can be calculated using this law, which can be expressed as follows:

$$\begin{aligned} \textbf{B}_{loop} = \frac{\mu _0 I R^2}{2(x^2+R^2)^{3/2}}\hat{\textbf{i}}, \end{aligned}$$
(4)

where R is the radius of the coil loop and x is the distance from the coil center to the point, where the magnetic field is being evaluated.

For a coil with N number of total windings, the corresponding magnetic field can be calculated by integrating Eq. (4) over each winding as:

$$\begin{aligned} \textbf{B}_{coil} = \sum _{i=1}^N{\frac{\mu _0 I R_i^2}{2(x_i^2+R_i^2)^{3/2}}\hat{\textbf{i}}}, \end{aligned}$$
(5)

The simulation solves Eq. (5) for any given coil shape to find the magnetic field at any given point along the center axis of the windings. The magnetic field gradient is obtained by taking the discrete spatial derivative of the magnetic field. Solving Eq. (5) for the field at the locations \(x_i + x_\epsilon\) and \(x_i - x_\epsilon\) yields the magnetic field gradient by the given formula below:

$$\begin{aligned} \textbf{B}_{grad} = \mu _0 I \sum _{i=1}^N\left( {\frac{R_i^2}{2((x_i - x_\epsilon )^2+R_i^2)^{3/2}} - \frac{R_i^2}{2((x_i + x_\epsilon )^2+R_i^2)^{3/2}}}\right) \frac{1}{2\epsilon }\hat{\textbf{i}}, \end{aligned}$$
(6)

where \(\epsilon\) is the infinitesimal spatial displacement. By providing any values for \(x_i\) and \(R_i\), it is possible to simulate coil shapes at any length and any diametrically geometrical variation as long as the windings are concentric.

Coil design optimization

The design optimization study aims to identify the optimal coil parameters, specifically coil shape and wire gauge. The optimization goal is to maximize \(\textbf{B}_{grad}\) presented in Eq. (6) at a specified target location. The optimization problem is also subjected to constraints stemming from geometrical, physical, and electrical limits. This process focuses explicitly on amplifying the magnetic pulling force on a magnetic object achieved via the use of a three-coil concentrically stacked configuration.

Design problem

Every single loop is concentrically positioned along the center axis of a hypothetical coil within the minimum and maximum physical limits in the coil geometry. For any winding distribution, the magnetic field gradient for every single loop is calculated via Eq. (4), and then integrated to find the overall magnetic gradient field strength via Eq. (5) and field gradients via Eq. (6) of the candidate design. The magnetic gradient strength varies depending on each winding positioning and the wire gauge being used. This magnetic gradient field maximization problem can be formulated as

$$\begin{aligned} \textrm{f}(X_0)=\mathop {\mathrm {arg\,max}}\limits _{\textbf{W}} |\textbf{B}_{grad}(\textbf{W}, X_0)|, \end{aligned}$$
(7)

\(X_0\) is the distance from the coil; \(\textbf{W}=\{\phi _{s}, \phi _{m}, \phi _{l}, N_{s}, N_{m}, N_{l}, L_{s}, L_{m}, L_{l}\}\subset \mathbb {R}^9\) represents the set of design parameters. \(\phi _{s}, \phi _{m}, \phi _{l}\) represent copper wire diameters for small, medium, and large coils with their values ranging from 0.573 mm (23 AWG) to 3.264 mm (4 AWG). \(N_{s}, N_{m}, N_{l}\) represent numbers of windings per row in small, medium, and large coils with their values ranging from 20 to 1000. \(L_{s}, L_{m}, L_{l}\) represents the coil lengths for small, medium, and large coils with their values ranging from 10 to 50 mm. In this design, the position of \(X_0\) is set at the workspace center, as illustrated in Fig. 2b. Table 1 provides the optimized coil properties. The overall coil design can be completely defined by combining Fig. 2 and Table 1. The workspace of VORIACS is a square with a side length of 10 cm surrounded by coils. The optimization function is evaluated at the center of the workspace, which is set at 52 mm along the coil axis. This positioning takes into account the 2 mm thickness of the inner coil frame wall used in the manufacturing process.

Figure 2
figure 2

The optimization of the coil configuration in the VORIACS aims to maximize the magnetic field gradients with the space and power constraints of the three concentric coils. Subfigure (a) represents the optimized unit-coil-set. As shown in subfigure (b), the target position for the magnetic gradient optimization is 52 mm away from the coil surface.

Full size image
Table 1 The physical and electrical properties of the optimzmized coil designs that maximize the magnetic pulling force at the center of the workspace. By finding the optimization-driving parameters for wire gauge and winding location, the other design-driven coil parameters in this table can be calculated.
Full size table

Design constraints

The constraints of this problem come from electrical power and physical size limitations. Regarding the electrical power, the power constraint per coil is 2 kW power with 60 V and 33 A ratings, which is limited due to the 2 kW power limit that can be consumed through a standard 110 V outlet when it is consumed at its full electrical power. Also, due to the laboratory’s electrical power capacity and the available physical space, every two coils are powered by the same power supply. The combined power consumption of these two coils adheres to this 2 kW total power constraint. This drives each individual coil design to have a resistance of 1.8 \(\Omega\). To satisfy this constraint, our optimization algorithm selects the wire gauge and the coil shape together. The wire gauge is selected from the American Wire Gauge (AWG) standard. It is incorporated into the design optimization problem as a discrete parameter, with a range spanning from 8 to 23 AWG. Wire gauge and overall wire length together constitutes the resistance of each coil segment. To utilize the power supplies to their fullest output capabilities (60 V and 33 A), the resistance of the each electromagnetic coil should be designed to have resistance of approximately 1.82 \(\Omega\). Therefore, the power supply-related design constraints are the major factor that affect the wire gauge and overall wire length results as well as the overall geometry of the electromagnet. Heavy insulation is selected to enhance wire durability, which adds additional thickness to them. All wire specifications are acquired from the wire manufacturer (MWS Wire, Oxnard, CA). The windings are implemented as discrete row and layer count to reduce the feature space of possible configurations for the subsequent optimization search. This electrical resistance condition to be satisfied can be given as

$$\begin{aligned} R_1(\textbf{W}) = R_2(\textbf{W}) = R_3(\textbf{W}) = 1.8 \Omega , \end{aligned}$$
(8)

where \(R_1\), \(R_2\), \(R_3\) are the resistance of three stacked coils.

The physical dimensions constraint is required for our coils to be within the manufacturability specifications and provides an upper limit to the size of the coils we can have. The coil design strategy involves three distinct coils, arranged in a front-to-back stacking configuration with varying wire gauges and windings. This arrangement forms one coil stack. All three coils are designed with the same inner diameter (ID) to accommodate a single, cylindrical iron core, which can fit inside all of them. The cylindrical diameter of the iron core is set at 85 mm to facilitate a near-uniform magnetic field within the 100 mm \(\times\) 100 mm workspace. Consequently, the ID of the coils is set to match this at 85 mm. The coil stacks are arranged in a cubical pattern, placing four coil stacks on a single plane. This configuration imposes a physical constraint on the system, limiting the coil windings from extending beyond a 45-degree line from the corner of the 100 mm \(\times\) 100 mm workspace. The maximum outer diameter (OD) of the largest coil winding is set to 200 mm, as there are diminishing returns on field strength with respect to additional weight and material costs.

Genetic algorithm for optimized coil stacks

Since our optimization problem is a highly nonlinear, multi-dimensional problem, we utilized a genetic algorithm (GA) optimization method40. For the initial search, the population size, mutation rate, and the number of generations of the genetic algorithm are set as \(6 \times 10^{6}\), 0.18, and 50 generations, respectively. The feature space spans \(8.9 \times 10^{12}\) configurations. When the best solution to this initial search is found, the assumption is made that this solution will be, at worst, a local minimum near the global minimum due to the GA’s search principal for the optimal solution. Therefore, the feature space is constrained to \(7.4 \times 10^{9}\) configurations around the local minimum and the search is repeated with a population size and generation count of \(3 \times 10^{6}\) and 20, respectively, to ensure that the best coil configuration is found. The resulting optimized set of parameters suggested by the genetic algorithm is provided in Table 1. The visualized coil design with the optimized parameters are provided in Figs. 2 and 3. Figure 2 depicts winding-level coil details for each of the three coils in a VORIACS, labels each VORIACS sub-coil, and provides dimensions for the stack. Additionally, Fig. 2 depicts the target location for magnetic gradient optimization. Figure 3 shows VORIACS stacks assembly, workspace, and core insertion apparatus. The machined aluminum frames are used in the system for their efficient heat dissipation properties, allowing the application of high power without causing system overheating. Each coil set is named North, East, South, and West to identify these coils individually.

Figure 3
figure 3

The optimized coil design provides a compact structure with tapered winding as shown in (a). (b) Iron core is designed to be at the center of the electromagnetic coil to intensify the magnetic field generated by the coils.

Full size image

VORIACS system stack manufacturing

Coil supports are machined from 6061-T6 aluminum (Xometry, Gaithersburg, MD), and custom designed based on results from the genetic algorithm. Small, medium, and large coils have identical inner diameters but differ in outer diameter, wire gauge, and windings profile as presented in Table 1. Idealized final profiles for each coil are shown in Fig. 2. Coils are wound using an automated winding tool (Acme Mechatronics, AEH-01), and windings are held together with a high-temperature cyanoacrylate adhesive (GorillaPro™ CA500RT). Small, medium, and large coil assemblies are held together by threaded rods passing through the centers of the coils, located between the magnetic wire windings and the iron cores. All fasteners are non-magnetic stainless steel 316 (SS316). Each three-coil assembly shares a single iron core (ASTM A848 Type 1-Soft Magnetic Iron), housed inside of a 3D printed removable core-holder (ABS). Three-coil assemblies are connected to one another along cardinal coordinate axes using aluminum mounting brackets with SS316 fasteners.

System components

Actuator design, power distribution, and computational power are the main components of the system design for VORIACS. Specifically, the actuator design is the most crucial and novel stage for system integration. The tri-coil concentric design is proposed by the optimization algorithm, and the electromagnetic coils are manufactured accordingly. The modular design of this system allows every individual coil to be attached and detached individually.

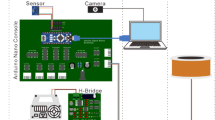
As shown in Fig. 4, coils are controlled by motor controllers (Roboclaw, 2x60AHV) operated in two-channel mode. Six motor controllers, powered by six AC-DC converters (SL Power, TF3000A60K), are used to allow for the individual control of the coils. The power supplies provide 60 V maximum voltage for all coils. When two coils are connected to the same power supply, their total combined power must not exceed 2 kW. This design strategy is aimed at optimizing the output of a single coil within the constraints of the power supply. Electrical chokes are used to protect signal transmission from electromagnetic interference. A computer interface with motor controllers is provided via two Arduino Uno boards. PacketSerial serves as the controlling mode for motor controller, and MATLAB on the PC is used to communicate with the Arduino board. The average time taken by one control loop is less than 0.1 s.

Figure 4
figure 4

(a) Illustrates the hardware connections of the entire system. (b) Details the connections of all coils to the power supplies. To be able to exert the highest amount of power, 6 individual power supplies are being used to power 6 motor controllers. Each motor controller is responsible for driving 2 electromagnetic coils that are of the same size but belong to the adjacent coil sets. The combined total power of these two coils must not exceed 2 kW.

Full size image

Magnetic field characterization

Magnetic field measurements of the constructed coil stack are conducted in the XY plane with a Gauss meter in a custom, 3D printed square grid array, as shown in Fig. 5. The grid and probe sheath help to locate the probe precisely and allow for up to \(24 \times 24\) measurements, but only \(11 \times 12\) measurements are taken spaced 8mm apart. The sensor locations within the probe are noted, allowing for 2D, cubic interpolation to yield an accurate map of the fields at nearly any location despite the actual 8 mm measurement resolution.

Figure 5
figure 5

The magnetic field generated by each coil is characterized by using a gaussmeter and a square grid array designed to position the probe tip precisely. (a) The experimental stage for measurements. The use of an iron core increases the magnitude of magnetic field and axial component of gradients measured by 1.9 times as shown in (b). By using the measured values from each coil, we can simulate the total magnetic field by linearly superimposing the magnetic field contribution from each coil to estimate the magnetic field generated as shown in (c).

Full size image

While 4 coil stacks are used for XY manipulation as observed in Fig. 3, only one coil stack (consisting of three individually addressable coils) is powered for magnetic field gradient and magnetic field measurements shown in Fig. 5b,c. The results of Fig. 5 are collected with the coils powered to 3% of their full power , then linearly scaled to simulate the full power of the system at 33A. Figure 5b presents the scaled results of the magnetic field and gradient from both measurements and calculations based on physical models. The measurements closely match the model-based results, validating the accuracy of the model. To demonstrate the linear scaling with current, magnetic field measurements at the center of the workspace are also conducted with input currents ranging from 3 to 27 A, with measurement increments of 3 A. Fitting the results to a linear model yields an R-squared value of 0.9823 (further details regarding the data can be found in Supplementary Information Document). This suggests that even with an iron core, the field magnitude is linearly proportional to the input currents, within our range of applied current values.

Measurements are collected both with and without an iron core boosting the field strength. Figure 5b demonstrates that the use of an iron core increases the magnitude of magnetic field and axial component of gradients by a factor of 1.9. A second-order interpolation calculated in MATLAB is applied to the measured magnetic field data spaced 0.1 mm apart, matching the step size used in the simulations, to derive the magnetic field gradients at any point.

Manipulability analysis

It is important to know the limits of any magnetic manipulation system in terms of its ability to control the field and its gradient at different points in space. In other words, we assess the VORIACS system’s ability to control the field and its gradient at different points for any pose (position and orientation) of the magnetic body that is being manipulated. We restrict the analysis to a single plane in the workspace, though the analysis can be extended to three-dimensional space. The most common method used to generate desired magnetic field and desired magnetic force at any given point in the workspace involves computing an inverse mapping between forces and torques and applied currents. More precisely, to generate desired forces (\(F_{des}\)) and desired fields (\(B_{des}\)), the set of desired coil currents \(I_c\) can be computed as shown in Eq. (9)

$$\begin{aligned} \underbrace{\begin{bmatrix} F_{des} \\ B_{des} \end{bmatrix}}_{\beta }= \underbrace{\begin{bmatrix} \overline{\textbf{F}} \\ \overline{\textbf{B}} \end{bmatrix}}_{\alpha }I_c , \quad \implies I_c = \alpha ^{\dagger }\beta \end{aligned}$$
(9)

where \(\overline{\textbf{F}}\) and \(\overline{\textbf{B}}\) provide a pose-dependent map between applied currents, and magnetic force \(F_m\) and magnetic field vector \(\textbf{B}\), respectively. In the plane, the size of the matrix \(\alpha\), which relates forces and torques to currents, is \(4 \times\) n, where n is the number of independent coils. Hence, to analyze the benefits of having individually addressable coils in each axis, we compare the computation of coil current vector \(I_c\) for two cases. The first case assumes that each set of concentric coils has the same coil current, representative of conventional electromagnetic coil arrays, where each coil set consists of a single solenoid. This case will be referred to as VORIACS with a non-individually addressable coil on each side. In this case, we get n as four. The second case is for our VORIACS system, where each coil is individually addressable, which yields n to be twelve (three for each of the four coil stacks). Note that the size of \(I_c\) is n \(\times\) 1.

Results

As a result of multi-parameter optimization of the 3-coil-stacked electromagnetic coils for maximized force throughput, we analyze quantitative and qualitative experiments to demonstrate the ultra-strong magnetic forces generated via VORIACS. We compare our system with other published electromagnetic actuation systems to demonstrate the added benefit of our design strategy. Additionally, we discuss how variable outer diameter, individually addressable coils can provide better control in the workspace, as compared with the more simple singe-coil version of the system.

Force output of a single coil stack

To validate the strength of the VORIACS for force exertion, we create one quantitative and one qualitative experiment. In the quantitative experiment, we target to quantify the force output of a cylindrical permanent magnet by using a single coil stack. In the qualitative experiment, we experiment with the penetration performance of a magnetized surgical suture needle into an agarose gel at different concentrations.

Force validation with permanent magnets

In this experiment, a cylindrical magnet composed of disc magnets is utilized. The magnet has a length of 10 mm and a diameter of 7 mm. To measure the exerted force via visual displacement, we have created a spring-based measurement setup. As shown in Fig. 6, the force measurement setup consists of plastic springs (equivalent spring rate = 0.232 N/mm) and cylindrical Neodymium-Iron-Boron (NdFeB) permanent magnets making a single magnetic unit placed within a clear Polyethylene tube attached to the iron-core holder within the one coil set. The setup includes the iron core to augment the magnetic field strength of the single coil stack. Further, the spring-magnet-tube assembly is kept perfectly aligned with the center of the coil to optimize the interaction between magnetic fields generated by the coil stack and the magnetic field of the permanent magnet. Since the permanent magnet is aligned along the axis of the coil set, the magnetic field applies a pulling force with zero torque.

Figure 6
figure 6

Magnetic force experiments are conducted by using a NdFeB permanent magnet and a nonmagnetic spring. Full magnetic-pulling power is exerted onto the small, medium, and large coils, respectively. The gray rectangle indicates the coil is off while the orange rectangle indicates the coil is turned on and at the maximum power. Powering all the coils at the maximum power yields 1.673 N pulling force as demonstrated on the right-most image.

Full size image

To measure the force, the intended coil stack is powered up to full power, and the resulting deflection in the spring caused due to attraction force is measured using the millimeter scale on the tube. Force is then calculated using the simple spring equation. The force generated on the permanent magnet within the tube is measured for four distinct cases to characterize the force contribution from each individual coil (in each case, the coil(s) used is operated at full power of 2 kW): (1) Solely Small Coil, (2) Solely Medium Coil, (3) Solely Large Coil, (4) All three coils (one coil-unit).

To accurately calculate the force generated, the deflection of the spring is measured by counting the number of pixels and considering the pixel-to-mm conversion scale from Fig. 6. As illustrated in Fig. 6, the small coil, medium coil, and large coil can add 0.325 N, 0.622 N and 0.654 N on the magnet, respectively. These values are consistent with the gradient magnitudes they generate: 745 mT/m, 1425 mT/m, and 1499 mT/m for small, medium, and large coils, respectively, as calculated using the magnet parameters. By generating a magnetic gradient magnitude of 3834 mT/m, the force output from the entire coil stack is 1.673 N, which is a 4.5% increase from taking the sum of the individual force outputs of the coils. This increased force measurement is mainly due to the fact that the stack’s cumulative pulling force progressively moves the magnet attached to the spring very slightly closer to the gradient-generating coils during the experiment.

Force measurements with rod and needle

Two experiments were conducted to demonstrate the magnetic forces generated by a single coil stack using the same setup employed for force validation. An 18-8 stainless steel rod, measuring 6.35 mm in diameter and 9.53 mm in length, and a 14 gauge needle, 50 mm in length, filled with an N52 NdFeB permanent magnet (1.5 mm in diameter, 40 mm in length) were used in the tests. The results, displayed in Fig. 7, illustrate VORIACS’s capability to exert significant magnetic force on both hard and soft magnets from a distance. A slight sub-millimeter distance difference occurs between the magnets and steel rod due to the difference in the size, applied force and corresponding spring compression amount. Such a sub-millimeter difference at more than 18 mm distance from the coil results in negligible magnetic gradient change. The forces can be further increased by utilizing all coils and changing the pulling direction to the diagonal of the workspace.

Figure 7
figure 7

The box and whisker plot illustrate all magnetic force measurements with a single coil stack in maximum power input. Magnets and steel rods are tested in a single position, while needles are tested in three different positions. For each position, five measurements are recorded. Notably, the standard deviations are less than 0.006 N, while the uncertainty is less than 0.02 N.

Full size image

Penetration experiments with a clinical suture needle

Two agarose gel penetration experiments are conducted using a single coil stack operating at full power. Agarose gel’s concentrations for the experiments are 1.5% and 2%, as the 1.5% concentration resembles the rigidity of nerve and liver tissues, while the 2% concentration resembles the rigidity of endothelium and lung tissues41,42. As depicted in Fig. 8, the same needle used in the force measurement is placed inside the needle.

Figure 8
figure 8

Multiple time instances of an agarose gel penetration experiment where a needle is placed directly below and aligned with the center axis of the coil stack. A 14G suture needle can penetrate to a 2.0% agarose gel by traveling 24.3 mm within 21 s with gradient pulling. Such an agarose gel concentration is considered to have rigidity similar to endothelium, lung, and liver organs in the human body. For this experiment, only the North coil stack is powered at full capacity for each of its three individual coils.

Full size image

For the 1.5% agarose gel, the average penetration speed is measured to be 2.50 mm/s. Simulating the magnetic field from the coils based on the Biot-Savart laws suggests that the force exerted on the needle ranged from 0.24 to 0.38 N (2963–4691 mT/m magnetic gradient magnitude). In the case of the 2.0% agarose gel, the average penetration speed was measured to be 1.16 mm/s, with the force on the needle ranging from 0.19 to 0.36 N (2346–4444 mT/m magnetic gradient magnitude). Notably, the speeds in both tests exhibit a gradual increase as the needle approaches the coils. An additional test is conducted using 2.5% agarose gel. However, the needle is unable to penetrate the 2.5% gel. In contrast to the MagnetoSuture system, which was only able to penetrate 0.5% agarose gel under similar conditions39, the current experiments demonstrate improved penetration capabilities through stronger magnetic gradients.

Field strength comparison with Similar Electromagnetic Actuation Systems

The VORIACS system is developed based on the MagnetoSuture™ system39, with both systems having the same workspace size, cooling method, and similar coil inner diameter.

However, the VORIACS system is capable of generating a gradient strength of 3768 mT/m at the center of the workspace, which is the strongest magnetic gradient strength to our knowledge at such a large workspace. Also the pulling force is \(5.3 \times\) greater than that of the MagnetoSuture™ system. Importantly, the VORIACS system achieves these improvements in pulling force by implementing optimized coil-driver design, adding independently controlled coils along each axis, and increasing the power consumed by \(6.5 \times\) that consumed by the MagnetoSuture™ system. The gradient-to-power ratio of VORIACS is 0.314 mT/(mW), which is similar to the MagnetoSuture™ system. To emphasize the impact of the stacked coil design, we compared the magnetic gradient strengths of VORIACS with those of its single-coil solenoid counterparts, maintaining identical subcoil properties. These results are presented in Table 2. To obtain these results, we used our coil geometry calculator to determine the total windings that yield equivalent outer diameter results matching VORIACS’s geometry. We then applied the identical power to calculate the corresponding field gradient. The geometry of individually addressable stacked coils further enables the VORIACS system to produce unique and specialized magnetic fields that cannot be generated by the other systems in the literature.

Table 2 Comparison between the VORIACS’s magnetic gradient strengths with those of its single-coil solenoid counterparts.
Full size table

Table 3 shows a comparison between the VORIACS and other similar electromagnetic actuation systems that have been developed. It can be observed that most electromagnetic actuation systems listed have a maximum center gradient strength that is approximately half or less of that generated by the VORIACS. The VORIACS’s workspace size and maximum power also exceed many of them.

Table 3 Comparison between the VORIACS and other similar electromagnetic actuation systems. The VORIACS is the strongest electromagnetic system to be used in magnetic robot manipulation in the literature in terms of magnetic force delivery at a decimeter-scale workspace.
Full size table

The BatMag system43 is capable of generating a high gradient strength level that is comparable to the VORIACS. However, the size of its workspace is only about 0.043 of that of the VORIACS, which may not be sufficient for many experiments. Schonewille et al.’s system44 and Niu et al.’s system45, on the other hand, have larger workspace but maximum gradient strength that are less than 0.09 and 0.07 of the one generated by the VORIACS respectively, which limits the force exertion capabilities. Rahmer et al.’s system5 is capable of generating a comparable maximum gradient magnitude and offers a larger workspace. However, this gradient strength is only achievable in the vertical direction. In other directions, their system can only reach approximately 25% of this maximum value.

Field articulation and multi-magnet polarity control

Individually addressable concentric coils can be used to generate complex magnetic field distributions compared to their single-solenoid counterparts. Such a complex distribution could be used to control multiple magnetic objects simultaneously. In this experiment, four individual coils are used, consisting of two small and large coils on two opposite coil stacks. Three ring-magnets are placed on three poles along the center axis of the coils. The pole allows the ring magnets to rotate freely but does not allow them to translate and keeps their location fixed. Due to the small volume of magnets, the magnetic field generated by the magnets does not interfere with each other when placed at a distance.

Considering the binary polarity of ring magnets, there are 8 total configurations. As depicted in Fig. 9a, all of the 8 possible polarity configurations with 3 ring magnets are achieved. We refer to the polarity state where the red side is pointing up as 0, while the state where the blue side is pointing up as 1. Figure 9b shows the simulation field of input currents corresponding to the 0-1-0 and 0-1-1 configurations, which is found to be consistent with the results obtained from the actual test. Such a configuration could not be accomplished if a non-addressable magnet stack (single-solenoid) is used at each side due to the continuity property of magnetic fields. Thanks to the concentric design, addressing the polarity of each of the three ring magnets individually is made possible.

Figure 9
figure 9

Three ring magnets polarized radially can be oriented at any binary orientation within the workspace of the VORIACS as shown in (a). The magnetic current values needed to accomplish such configurations are calculated by using our simulation platform as shown in (b).

Full size image

Manipulability results

We have selected a circular path trajectory with a radius of 20 mm, shown in Fig. 10a to showcase the determination of desired forces and torques for two cases (VORIACS with hypothetically non-individually addressable coil stacks on each of the four sides, and VORIACS). The circular trajectory is divided into 360 equally spaced points, and we compute \(I_c\) using Eq. (9) at each point on the circular trajectory with the magnitude of \(F_{des}\) set to 4 mN, and the magnitude of \(B_{des}\) set to 1 mT. The direction of the desired force and field is always tangential to the given point on the circular path. Figure 10b depicts the sum of \(I_c\) computed for both cases. It shows the spike in coil currents at certain locations on the trajectory for the first case due to the \(\alpha\) matrix being close to singular. It is observed that the coil currents for the VORIACS are significantly below the absolute electrical current limit of 33 A for the entire trajectory for the prescribed forces and torques, (as seen in Fig. 10c,d).

Figure 10
figure 10

We have chosen a circular path to depict the magnetic field manipulability in a plane using VORIACS. (a) A circular trajectory with 360 points. At each point, the desired force and field directions are tangential to the circle (b) Comparison between sum of absolute coil currents between the VORIACS and a corresponding four coil system with small, medium, and large coils considered as a single unit. (c) Depiction of required absolute coil currents (if the small, medium, and large coils on each side were powered as a single unit) to generate 4 mN force and 1 mT field in the tangential direction at each point on the circular trajectory. (d) Depiction of required absolute coil currents (for the VORIACS) to generate 4 mN force and 1 mT field in the tangential direction to the circle at each point on the circular trajectory. The plot depicts how the required coil currents at each point on the trajectory are well within the bounds of 33 A per coil.

Full size image

This comparison shows the benefits of VORIACS in determining currents from desired forces and torques to generate a circular trajectory. To show the benefits afforded for any trajectory, for every point in a grid with 0.5 mm spacing, and for all magnetic body orientations at intervals of \(\hbox {1}^{\circ }\), we investigate the improvement in the conditioning of the \(\alpha\) matrix.

Figure 11a,b show the difference in maximum condition number over all magnetic body orientations at any given point in a 2D plane for non-individually addressable VORIACS and our VORIACS system, respectively. It is observed that the maximum condition number for at least one magnetization orientation exceeds the threshold for nearly every point in the workspace for the non-addressable VORIACS. This suggests that there may exist no trajectory where all poses avoid singularities, or it requires complex trajectory planning of a magnetic object to ensure a feasible mapping to currents exists from desired forces/torques for hypothetical non-individually adressable VORIACS design. On the other hand, the maximum condition number for any angle is at most about 8% of the threshold for the VORIACS system. This suggests that a well-defined relationship between desired forces/torques and currents exists for the VORIACS system to facilitate control of a single magnetic object everywhere in the domain, regardless of its pose.

Figure 11
figure 11

(a) The maximum 2-norm condition number of the orientation-dependent linear map between coil currents and forces and torques is taken over all possible magnetization vector orientations at every point in the workspace for VORIACS with non-individually addressable coils on each stack. (b) Corresponding contour for VORIACS where each coil is addressed individually, even within a stack. It can be seen that allowing each coil to be individually addressable greatly reduces the maximum condition number (32 is maximum on (b)), allowing us to solve for coil currents to achieve a desired force and torque everywhere on the workspace at every orientation.

Full size image

Discussion and conclusion

Magnetic medical robotics is aimed to improve surgical outcomes by offering new instruments that are smaller than currently used instruments and can be wirelessly manipulated. However, magnetic field-based manipulation of such small instruments will require the generation of strong, controllable fields and gradients across the surgical workspace to meet the exerted force/torque requirements of medical procedures such as navigating deep in tissues and clinical suturing. Here, we present a novel electromagnetic actuation system, VORIACS, to bring a large amount of magnetic force by optimizing the coil design for force delivery and stacking the electrical power of the electromagnetic coils together. We experimentally demonstrate the system’s ability to apply strong gradients to surgical tools via quantitative force measurements and qualitative penetration experiments. In addition, we explore the added advantage of the complex magnetic field articulation of such a system.

Increasing the maximum force also indicates the possibility of reducing the size of the magnetic end-effectors, allowing for ultra-minimally invasive surgeries. The presented VORIACS system reduces the limited-resource challenge for the force/miniaturization trade-off, however, there are still many challenges ahead.

The VORIACS system is currently designed for planar magnetic robot manipulation purposes. The optimization and manufacturing techniques can be extended without difficult alterations to 3D by adding top and bottom coils along the gravity direction. Such an alteration would require a total of 18 coils with 9 power supplies and 9 motor controllers. While the system improves the applicable force, the full assembly of all eighteen coils leaves the workspace occluded and difficult to reach. As such, the removal of one coil stack is required for the placement of an agent in the workspace. While detriments exist, the VORIACS geometry with potential 3D expansion have the potential to expand the controllability and available force for the manipulation of small magnetic agents in 3D.

It should be noted that even though the design space we present is fairly flexible and large, there are some design decisions to limit the overall design space. For example, ‘total number of coil segments’ and ‘the relative-configuration of the segments’ may present as additional design variables that may yield stronger gradients when the optimization is considered together. Due to the possible design and manufacturing challenges, in this study, we pre-selected these parameters as 3-coil segments that are positioned concentrically along the axial direction of the coils. In future studies, we plan to investigate possible improvement over this proposed coil system by including additional design parameters as a variable in our optimization.

Maintaining the operating temperature of the electromagnetic coil systems may become challenging for electromagnetic actuation systems with high electrical power consumption. Thanks to the aluminum framing in our system, even fan-based air cooling is effective, but for extended use at high capacity, we will use pump-based water cooling. In future work, we will work on embedding the VORIACS system into an actively circulated cooling water.

One major physical challenge in generating much stronger fields is the coil resistance and the energy loss due to the coil resistance. Introducing a super-cooled electromagnet would result in very low electrical resistance in the coil, allowing for pushing much higher coil currents and stronger magnetic forces as demonstrated by Leclerc et al.46. Such reductions in resistances would also require redesign of the coils and power supplies so as to account for the changing resistance with power supplies capable of appropriate voltage and current output capabilities.

Dynamically changing the magnetic field at a high rate may become challenging for such large field-generating systems. Since these coils have large inductance, similar to having a high-inertia in mechanical components, ramping the coil currents and magnetic fields up and down introduces a larger slew time than the smaller electromagnetic coils with lower inductance. Therefore, the inductance vs. magnetic field dynamics should be considered together. As one potential solution and future work of this study, over-driving electromagnetic coils via autonomous powering algorithms could allow the electromagnetic coils to track the desired coil currents swiftly despite their large inductance values.

Easing these limitations via effective electromagnetic coil designs technology and combining multi-coil powering strategy would push their current potential, and allow for tinier end-effectors, stronger forces, and larger workspaces for human-scale operations, resulting in such systems to be practically useful for clinical requirements with the accompanying advantage of ultra-minimally invasive surgeries with untethered tool tips. There are still many challenges ahead toward versatile magnetic robot navigation in the human body. Solving all of the practical challenges to sufficient levels for first-in-human studies may require this technology to improve multi-dimensionally, especially in the fields such as magnetic tool and actuator design, integrating high-rate noninvasive imaging modalities, and bio-compatible robot designs.