Sensitivity analysis and compensation for tooth surface deviation of spiral bevel gear machine tool

Abstract

To analyze the quantitative mapping relationship between the geometric errors of the five-axis CNC machine tool and the tooth surface deviation of spiral bevel gears, and identify the key geometric errors that affect the machining deviation of the spiral bevel gear tooth surface, a sensitivity analysis method for tooth surface machining deviation of spiral bevel gear based on screw theory and EFAST method is proposed. Firstly, the machining model of the spiral bevel gear tooth surface based on the five-axis CNC machine tool is established. Then, the geometric error transfer model of the machine tool is established based on the screw theory. Combined with the EFAST global sensitivity analysis method, the key geometric errors that affect tooth surface deviation are identified. Finally, the reliability and effectiveness tests are performed by comparing the results to the local sensitivity analysis method and simulating compensation for the key geometric errors. The result of compensation shows that the tooth surface deviation is reduced significantly according to global sensitivity analysis. The feasibility of applying sensitivity analysis to control the tooth surface deviation of spiral bevel gears has been demonstrated.

Introduction

Spiral bevel gears are widely used in the automotive, mining, and aviation industries, due to their high transmission efficiency, robust bearing capacity, stable transmission, and compact structure¹. The accuracy of gear transmission is directly impacted by the precision of gear machining, which is essential to the service life, safety, and dependability of mechanical equipment, and the accuracy of the gear is affected by the accuracy of the gear processing machine tool. Of all errors that affect the machining accuracy of machine tools, the geometric errors and thermal deformation errors of machine tools account for roughly 60–70%². The geometric errors are more stable and measurable than thermal deformation errors³. Therefore, in order to improve the machining accuracy of gears economically and efficiently, it is of significance to establish the geometric errors model and identify the key geometric errors that affect the tooth surface accuracy.

The establishment of the geometric errors model is the basis for key geometric errors identification. The main methods include multi-body system theory, homogeneous coordinate transformation, and screw theory⁴. On the basis of an error model, combined with sensitivity analysis methods, the influence weight of the geometric error is quantified, and the key geometric error is identified. Sensitivity analysis methods mainly include local sensitivity analysis methods and global sensitivity analysis methods, such as the matrix differential method, factor perturbation method, Morris method, Sobol method, and EFAST method⁵. In recent years, some scholars have conducted related research. Chen et al.⁶ established the volumetric error model of a five-axis machine tool with the configuration of RTTTR and conducted a sensitivity analysis by calculating partial differentials. The analysis results were successfully utilized in the design and production of a five-axis ultra-precision machine tool. Cai et al.⁷ established the precision model based on the multi-body system theory. They analyzed the sensitivity of geometric error parameters of the machine tool by using the matrix differential method and identified the geometric error items of main parts. Li et al.⁸ established the error model of a three-axis machining center based on multi-body system theory and the homogeneous coordinate transformation method. They determined the sensitivity coefficient of geometric errors to machining errors using the matrix differential method and identified the key geometric errors that affect machining accuracy. Shih⁹ established a sixth-order polynomial for the motion parameters of each axis of the machine tool. Shih added the disturbance amount into the first-order coefficient of the motion parameter polynomial for each axis, that is, the perturbation is applied to each motion axis. Shih discovered that the alteration of the first-order coefficient significantly impacted the accuracy of the tooth surface and then drew tooth surface error topology diagrams for each axis under the same disturbance amount. Through analyzing the topology diagrams, the sensitivity of each axis to the disturbance amount change could be determined. Cheng et al.¹⁰ proposed a sensitivity analysis method based on the product of exponential screw theory and the Morris approach for global sensitivity analysis of the volumetric machining accuracy of a five-axis machine tool. They identified the key geometric errors that have a significant influence on machining accuracy and used the analysis results to adjust the machine components. Zou et al.¹¹ established a measurement error model for the five-axis measuring machine using the homogeneous coordinate transformation. They employed the Sobol global sensitivity analysis method was used to quantify the influence of geometric errors on the measurement results. Wu et al.¹² constructed the forward kinematic chain solution and the volumetric error model for vertical machining centers using screw theory. The identified and analysis the 13 key geometric errors of vertical machining centers through global sensitivity analysis. Liu et al.¹³ established a volumetric error model for the dual-spindle ultra-precision drum roll lathe by combining the homogeneous transfer matrix and multi-body system theory. They utilized the improved Sobol method to identify the sensitivity of geometric error components of the lathe. Guo et al.¹⁴ established a comprehensive volumetric error model of a five-axis machine tool by using multi-body system theory and the homogeneous coordinate transformation method. They determined the influence of geometric error items on machine tool accuracy and conducted error compensation by applying the EFAST global sensitivity analysis method.

Screw theory is widely used in the field of robotics for tasks such as trajectory planning, motion control, error modeling, and more. Compared with the traditional homogeneous coordinate transformation modeling method based on multi-body system theory, the screw theory does not require to establish the local coordinate system for each component in the modeling process. Instead, it only needs to establish a global reference coordinate system, which simplifies the modeling complexity and workload¹⁵. The Extended Fourier Amplitude Sensitivity Test (EFAST) method combines the better efficiency of FAST with Sobol’s capacity to compute total effects and was proposed by SALTELLI¹⁶. It is an effective global sensitivity analysis method that has been successfully applied in agriculture, meteorology, and other fields^17,18. To quantitatively analyze the key geometric errors affecting the machining accuracy of spiral bevel gears, this paper proposes a sensitivity analysis method for spiral bevel gear tooth surface deviation based on screw theory and the EFAST method. Firstly, the tooth surface processing model of the spiral bevel gear for the five-axis CNC machine tool is established. Based on the motion transfer relationship of the machine tool, the geometric errors transfer model is established between the machine tool’s geometric errors and the tooth surface deviation. Then, the sensitivity coefficients of machine tool geometric errors to tooth surface deviation are calculated using the EFAST method, and the key geometric errors are identified. Finally, the key geometric errors are compensated, and the changes in tooth surface deviation are compared to verify the effectiveness of the sensitivity analysis. This paper provides theoretical guidance for the manufacture of high-precision spiral bevel gears and machine tools.

CNC machining model of spiral bevel gear

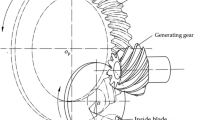
The structural diagram of the spiral bevel gear CNC machine tool is shown in Fig. 1. The X-axis, Y-axis, and Z-axis represent the three translational axes of the machining tool. The A-axis represents the rotation axis of the workpiece gear, the B-axis represents the root cone angle swing axis, and the C-axis represents the cutter shaft. For Gleason bevel gears, the C-axis generates rotary cutting motion, which is independent of tooth surface formation. Through the linkage of the X-axis, Y-axis, Z-axis, A-axis, and B-axis, the tooth surface of the Gleason bevel gear can be obtained¹⁹.

Fig. 1

The structural diagram of the five-axis CNC machine tool.

Fig. 2

Machining coordinate diagram of the five-axis CNC machine tool.

According to the coordinate transformation relationship in Fig. 2, the spatial transformation matrix M_C from the tool to the workpiece gear can be expressed as follows:

$${{\varvec{M}}_C}=\left[ {\begin{array}{*{20}{c}} 1&0&0&0 \\ 0&{\cos {\varphi _a}}&{\sin {\varphi _a}}&0 \\ 0&{-\sin {\varphi _a}}&{\cos {\varphi _a}}&0 \\ 0&0&0&1 \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} 1&0&0&{-{C_d}} \\ 0&1&0&0 \\ 0&0&1&0 \\ 0&0&0&1 \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {\cos {\varphi _b}}&0&{\sin {\varphi _b}}&0 \\ 0&1&0&0 \\ {-\sin {\varphi _b}}&0&{\cos {\varphi _b}}&0 \\ 0&0&0&1 \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} 1&0&0&{{C_x}} \\ 0&1&0&{{C_y}} \\ 0&0&1&{-{C_z}} \\ 0&0&0&1 \end{array}} \right]$$

(1)

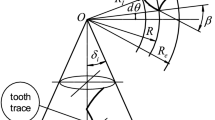
The space transformation matrix M_C is determined by φ_a, φ_b, C_x, C_y, and C_z. φ_a represents the rotation angle of the workpiece gear on the CNC machine tool. φ_b denotes the installation angle of the workpiece gear on the machine tool. C_x, C_y, and C_z represent the distances from the O_e to the O_n along the X-axis, Y-axis, and Z-axis directions respectively. C_d represents the distance from the O_g to the O_h. As shown in Fig. 2, the five quantities represent the relative positions of the two rotary axes and the three translational axes of the CNC machine tool²⁰. The tooth surface equation r_g can be obtained by combining the spatial transformation matrix M_C from the A-axis to the C-axis with the tool equation r_t²¹, as shown in the following:

$${{\varvec{r}}_g}={{\varvec{M}}_C} \cdot {r_t}\left( {u,\theta } \right)$$

(2)

$${{\varvec{r}}_t}(u,\theta )=\left[ {\begin{array}{*{20}{c}} {{r_{tx}}} \\ {{r_{ty}}} \\ {{r_{tz}}} \\ 1 \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} {({r_0} \pm u\sin \alpha )\cos \theta } \\ {({r_0} \pm u\sin \alpha )\sin \theta } \\ { - u\cos \alpha } \\ 1 \end{array}} \right]$$

(3)

Where r₀ represents the nominal radius of the cutter head. u and$\theta$represent the cutter head parameters. α represents the tooth profile angle of the tool. Symbols + and - represent the cutting concave surface of the outer blade and the convex surface of the inner blade, respectively.

Establishment of geometric errors transfer model based on screw theory

Screw theory

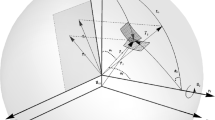
As shown in Fig. 3, according to the Chasles theorem, the motion of any rigid body can be achieved by rotating around and moving along an axis. This combined motion is called screw motion²². The motion screw is expressed by Eq. (4).

Fig. 3

Schematic diagram of spinor motion.

$$\varvec{\xi}={\left[ {\begin{array}{*{20}{c}} {\varvec{v}}&\varvec{\omega} \end{array}} \right]^\text{T}}$$

(4)

Where $\varvec{\omega}={\left[ {\begin{array}{*{20}{c}} {{\omega _1}}&{{\omega _2}}&{{\omega _3}} \end{array}} \right]^{\text{T}}}$ denote the unit vector in the rotation direction and ${\varvec{v}}={\left[ {\begin{array}{*{20}{c}} {{v_1}}&{{v_2}}&{{v_3}} \end{array}} \right]^{\text{T}}}$ denote the unit vector in the moving direction.

The motion screw can be further expressed in matrix form as follows:

$$\hat{\boldsymbol{\xi}} =\left[ {\begin{array}{ll} \hat{\boldsymbol{\omega}} &{\boldsymbol{v}} \\ 0&0 \end{array}} \right]$$

(5)

Where $\hat{\varvec{\omega}}$ is an antisymmetric matrix of $\varvec{\omega}$, which can be calculated as follows:

$$\hat{\varvec{\omega}} =\left[ {\begin{array}{*{20}{c}} 0&{ - {\omega _3}}&{ - {\omega _2}} \\ {{\omega _3}}&0&{ - {\omega _1}} \\ { - {\omega _2}}&{{\omega _1}}&0 \end{array}} \right]$$

(6)

When the rigid body moves, $\varvec{\omega}=0$, the exponential matrix is expressed as follows:

$${\varvec{T}}={\text{e}^{\hat{\varvec{\xi}} \theta }}=\left[ {\begin{array}{*{20}{c}} {{{\varvec{I}}_{3 \times 3}}}&{{\varvec{v}}\theta } \\ 0&1 \end{array}} \right]$$

(7)

When the rigid body rotates, $\varvec{\omega} \ne 0$, the exponential matrix is expressed as follows:

$${\varvec{T}}={\text{e}^{\hat{\varvec{\xi}} \theta }}=\left[ {\begin{array}{*{20}{c}} {{\text{e}^{\hat{\varvec{\omega}} \theta }}}&{(I - {\text{e}^{\hat{\varvec{\omega}} \theta }})(\varvec{\omega} \times {\varvec{v}})+\varvec{\omega}{\varvec{\omega}^\text{T}}{\varvec{v}}\theta } \\ 0&1 \end{array}} \right]$$

(8)

Where ${{\text{e}}^{\hat{\varvec{\omega}} \theta }}$ can be expanded using the trigonometric series method as follows:

$${\text{e}^{\hat{\varvec{\omega}} \theta }}=I+\hat{\varvec{\omega}} \text{s}\text{i}\text{n}\theta +{\hat{\varvec{\omega}} ^2}(1 - \text{c}\text{o}\text{s}\theta )$$

(9)

The exponential matrix ${\varvec{T}}={{\text{e}}^{\hat{\xi} \theta }}$ of the motion screw can be used to represent the positional relationship of the rigid body from the initial position to the final one. For a system with n rigid bodies in series, the position transformation matrix of the end coordinate system relative to the reference coordinate system can be expressed in the form of an exponential product as follows²³:

$${{\varvec{g}}_n}(\theta )={\text{e}^{{{\hat{\varvec{\xi}} }_1}{\theta _1}}}{\text{e}^{{{\hat{\varvec{\xi}} }_2}{\theta _2}}}{{\text{e}}^{{{\hat{\varvec{\xi}} }_3}{\theta _3}}} \cdot \cdot \cdot {{\text{e}}^{{{\hat{\varvec{\xi}} }_n}{\theta _n}}}{{\varvec{g}}_n}(0)$$

(10)

Where ${{\varvec{g}}_n}(\theta )$$(n=1,2,3 \cdot \cdot \cdot )$represents the position transformation matrix of the end coordinate system relative to the reference coordinate system with the displacement parameter$\theta$. ${{\varvec{g}}_n}(0)$ means the initial state of${{\varvec{g}}_n}(\theta )$, which is a constant matrix and can be omitted in the calculation process.

Geometric errors analysis

Due to geometric errors that occurred during the manufacturing and installation process of the motion axes of the five-axis CNC machining tool, the actual position of each motion axis will deviate from the ideal one, which results in the tooth surface deviation error of the spiral bevel gear after machining process²⁴.

Each axis of the machine tool includes six errors, three linear errors, and three angular errors²⁵. As shown in Fig. 4(a)(b), taking the motion of the Z-axis and the B-axis as examples, δ represents linear error, while ε represents angular error. The error variable is distinguished by two subscripts: the first represents the direction of the error, and the second represents the corresponding axis. So, δ_yZ represents the linear error of the Z-axis in the y-direction, and ε_αB represents the angular error of the B-axis in the α-direction. The three linear errors of the Z-axis and B-axis include δ_xZ, δ_yZ, δ_zZ, and δ_xB, δ_yB, δ_zB. Similarly, the three angular errors are ε_αZ, ε_βZ, ε_γZ and ε_αB, ε_βB, ε_γB. Therefore, the total geometric errors of the five-axis CNC machine tool are 30 items.

Fig. 4

Geometric error diagram of motion axis. (a) Geometric errors of the Z-axis. (b) Geometric errors of the B-axis.

The five-axis CNC machine tool consists of three linear axes and two rotational axes. To facilitate the sensitivity analysis, the geometric errors are numbered as shown in Table 1.

Table 1 Geometric errors and corresponding numbers of the five-axis CNC machine tool.

Screw representation of geometric errors

There are five types of motion screws in the five-axis CNC machine tool: (1) Moving along the X-axis, (2) Moving along the Y-axis, (3) Moving along the Z-axis, (4) Rotating around the A-axis, (5) Rotating around the B-axis. The ideal motion screws for each axis are shown in Table 2, where “Q” (Q = X-axis, Y-axis, Z-axis, A-axis, B-axis) denotes the axis of motion, and a, b, and c denote the ideal displacement along the X-axis, Y-axis, and Z-axis, while d and e denote the ideal rotation angles around the A-axis and B-axis.

Table 2 Ideal motion screws for each axis of the CNC machine tool.

The Y-axis is chosen as an example, and the ideal motion screw of the Y-axis is as follows:

$${\varvec{\xi}_\text{Y}}={(\varvec{\nu},\varvec{\omega})^{\text{T}}}={\left[ {\begin{array}{*{20}{c}} 0&b&0&0&0&0 \end{array}} \right]^{\text{T}}}$$

(11)

Where $\varvec{\nu}={\left[ {\begin{array}{*{20}{c}} 0&b&0 \end{array}} \right]^{\text{T}}}$, $\varvec{\omega}={\left[ {\begin{array}{*{20}{c}} 0&0&0 \end{array}} \right]^{\text{T}}}$, the ideal exponential matrix of the Y-axis is as follows:

$${{\text{e}}^{\mathop {\hat{{\varvec{\xi}}_\text{Y}}} {\theta _\text{Y}}}}=\left[ {\begin{array}{*{20}{c}} {{{\varvec{I}}_{3 \times 3}}}&{{\varvec{v}}\theta } \\ 0&1 \end{array}} \right] =\left[ {\begin{array}{*{20}{c}} 1&0&0&0 \\ 0&1&0&b \\ 0&0&1&0 \\ 0&0&0&1 \end{array}} \right]$$

(12)

The transformation matrices ${\text{e}^{\mathop {\hat{{\varvec{\xi}}_\text{X}}} {\theta _\text{X}}}}$, ${{\text{e}}^{\mathop {\hat{{\varvec{\xi}}_\text{Z}}} {\theta _\text{Z}}}}$, ${{\text{e}}^{\mathop {\hat{{\varvec{\xi}}_\text{A}}} {\theta _\text{A}}}}$ and ${{\text{e}}^{\mathop {\hat{{\varvec{\xi}}_\text{B}}} {\theta _\text{B}}}}$ for other axes can be obtained similarly.

If the geometric errors of the machine tool are considered, the motion errors of each axis can be represented by three sets of motion screws as shown in Table 3, where P (P = x, y, z, α, β, γ) represents the direction of motion, and Q (Q = X-axis, Y-axis, Z-axis, A-axis, B-axis) denotes the axis of motion.

Table 3 Error motion screws of each axis of the CNC machine tool.

Considering the X-axis as an example, the error motion screw of the X-axis in the x-direction is as follows:

$${\varvec{\xi}_{x\text{X}}}={({\varvec{\nu}_x},{\varvec{\omega}_x})^{\text{T}}}={\left\lceil {\begin{array}{*{20}{c}} {{\delta _{x\text{X}}}}&0&0&{{\varepsilon _{\alpha \text{X}}}}&0&0 \end{array}} \right\rceil ^{\text{T}}}$$

(13)

where ${\varvec{\nu}_x}={\left[ {\begin{array}{*{20}{c}} {{\delta _{x\text{X}}}}&0&0 \end{array}} \right]^{\text{T}}}$ and ${\varvec{\omega}_x}={\left[ {\begin{array}{*{20}{c}} {{\varepsilon _{\alpha \text{X}}}}&0&0 \end{array}} \right]^{\text{T}}}$.

Similarly,

$${\varvec{\xi}_{y\text{X}}}={({\varvec{\nu}_y},{\varvec{\omega}_y})^{\text{T}}}={\left[ {\begin{array}{*{20}{c}} 0&{{\delta _{y\text{X}}}}&0&0&{{\varepsilon _{\beta \text{X}}}}&0 \end{array}} \right]^{\text{T}}}$$

(14)

$${\varvec{\xi}_{z\text{X}}}={({\varvec{\nu}_z},{\varvec{\omega}_z})^{\text{T}}}={\left[ {\begin{array}{*{20}{c}} 0&0&{{\delta _{z\text{X}}}}&0&0&{{\varepsilon _{\gamma \text{X}}}} \end{array}} \right]^{\text{T}}}$$

(15)

The exponential form of the error motion screw in the x-direction of the X-axis is as follows:

$${{\text{e}}^{{{\hat{\xi} }_{x\text{X}}}{\varepsilon _{\alpha \text{X}}}}}=\left[ {\begin{array}{*{20}{c}} 1&0&0&0 \\ 0&{\cos {\varepsilon _{\alpha \text{X}}}}&{ - \sin {\varepsilon _{\alpha \text{X}}}}&0 \\ 0&{\sin {\varepsilon _{\alpha \text{X}}}}&{\cos {\varepsilon _{\alpha \text{X}}}}&0 \\ 0&0&0&1 \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} 1&0&0&{{\delta _{x\text{X}}}} \\ 0&1&0&0 \\ 0&0&1&0 \\ 0&0&0&1 \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} 1&0&0&{{\delta _{x\text{X}}}} \\ 0&{\cos {\varepsilon _{\alpha \text{X}}}}&{ - \sin {\varepsilon _{\alpha \text{X}}}}&0 \\ 0&{\sin {\varepsilon _{\alpha \text{X}}}}&{\cos {\varepsilon _{\alpha \text{X}}}}&0 \\ 0&0&0&1 \end{array}} \right]$$

(16)

${{\text{e}}^{{{\hat {\varvec{\xi}}}_{y\text{X}}} {\varepsilon _{\beta \text{X}}}}}$ and ${\text{e}^{{{\hat {\varvec{\xi}}}_{z\text{X}}} {\varepsilon _{\gamma \text{X}}}}}$can be calculated in the same way.

${\text{e}^{{{\hat {\varvec{\xi}}}_{\text{X}e}}\;{\theta _{\text{X}e}}}}$ is used to represent the error transformation matrix, which consists of three sets of error motion screws related to the X-axis. It is expressed as follows:

$$\begin{aligned}&{\text{e}^{{{\hat {\varvec{\xi}}}_{\text{X}e}}\;{\theta _{\text{X}e}}}} ={\text{e}^{{{\hat {\varvec{\xi}}}_{x\text{X}}} {\varepsilon _{\alpha \text{X}}}}} \cdot {\text{e}^{{{\hat {\varvec{\xi}}}_{y\text{X}}} {\varepsilon _{\beta \text{X}}}}} \cdot {\text{e}^{{{\hat {\varvec{\xi}}}_{z\text{X}}} {\varepsilon _{\gamma \text{X}}}}}\\ & =\left( {\begin{array}{*{20}{c}} {\cos ({\varepsilon _{\beta \text{X}}})\cos ({\varepsilon _{\gamma \text{X}}})}&{ - \cos ({\varepsilon _{\beta \text{X}}})\sin ({\varepsilon _{\gamma \text{X}}})}&{\sin ({\varepsilon _{\beta \text{X}}})}&{{\delta _{x\text{X}}}+\sin ({\varepsilon _{\beta \text{X}}}){\delta _{z\text{X}}}} \\ {\cos ({\varepsilon _{\gamma \text{X}}})\sin ({\varepsilon _{\alpha \text{X}}})\sin ({\varepsilon _{\beta \text{X}}})+\cos ({\varepsilon _{\alpha \text{X}}})\sin ({\varepsilon _{\gamma \text{X}}})}&{\cos ({\varepsilon _{\alpha \text{X}}})\cos ({\varepsilon _{\gamma \text{X}}}) - \sin ({\varepsilon _{\alpha \text{X}}})\sin ({\varepsilon _{\beta \text{X}}})\sin ({\varepsilon _{\gamma \text{X}}})}&{ - \sin ({\varepsilon _{\alpha \text{X}}})\cos ({\varepsilon _{\beta \text{X}}})}&{\cos ({\varepsilon _{\alpha \text{X}}}){\delta _{y\text{X}}} - \cos ({\varepsilon _{\beta \text{X}}})\sin ({\varepsilon _{\alpha \text{X}}}){\delta _{z\text{X}}}} \\ {\sin ({\varepsilon _{\alpha \text{X}}})\sin ({\varepsilon _{\gamma \text{X}}}) - \cos ({\varepsilon _{\alpha \text{X}}})\cos ({\varepsilon _{\gamma \text{X}}})\sin ({\varepsilon _{\beta \text{X}}})}&{\sin ({\varepsilon _{\alpha \text{X}}})\cos ({\varepsilon _{\gamma \text{X}}})+\cos ({\varepsilon _{\alpha \text{X}}})\sin ({\varepsilon _{\beta \text{X}}})\sin ({\varepsilon _{\gamma \text{X}}})}&{\cos ({\varepsilon _{\alpha \text{X}}})\cos ({\varepsilon _{\beta \text{X}}})}&{\sin ({\varepsilon _{\alpha \text{X}}}){\delta _{y\text{X}}}+\cos ({\varepsilon _{\beta \text{X}}})\cos ({\varepsilon _{\alpha \text{X}}}){\delta _{z\text{X}}}} \\ 0&0&0&1 \end{array}} \right)\end{aligned}$$

(17)

The geometric error transformation matrices ${\text{e}^{{{\hat {\varvec{\xi}}}_{\text{Y}e}}\;{\theta _{\text{Y}e}}}}$, ${\text{e}^{{{\hat {\varvec{\xi}}}_{\text{Z}e}}\;{\theta _{\text{Z}e}}}}$, ${\text{e}^{{{\hat {\varvec{\xi}}}_{\text{A}e}}\;{\theta _{\text{A}e}}}}$ and ${\text{e}^{{{\hat {\varvec{\xi}}}_{\text{B}e}}\;{\theta _{\text{B}e}}}}$ for other axes can be obtained using the same method.

Establishment of geometric errors transfer model

A geometric error transfer model of the five-axis CNC machine tool is established in this paper based on screw theory. The topological structure of the machine tool is illustrated in Fig. 5. The motion chain from the tool to the workpiece is as follows: Tool – Y-axis – X-axis – Bed – Z-axis – B-axis – A-axis – Gear. Under ideal conditions, the theoretical tooth surface equation can be expressed in the form of an exponential product, as shown in Eq. (18).

Fig. 5

Topology diagram of machine tool.

$${{\varvec{r}}_g}={\text{e}^{{{\hat {\xi }}_\text{A}}{\theta _\text{A}}}} \cdot {\text{e}^{{{\hat {\xi }}_\text{B}}{\theta _\text{B}}}} \cdot {\text{e}^{{{\hat {\xi }}_\text{Z}}{\theta _\text{Z}}}} \cdot {\text{e}^{{{\hat {\xi }}_\text{X}}{\theta _\text{X}}}} \cdot {\text{e}^{{{\hat {\xi }}_\text{Y}}{\theta _\text{Y}}}} \cdot {{\varvec{r}}_t}$$

(18)

Under the influence of the combined linear errors and angular errors of the motion axes, the relative position of the workpiece and the tool will deviate from the theoretical one. The actual tooth surface equation ${\varvec{r}}_{g}^{e}$ can be expressed in the form of an exponential product in the following equation:

$${\varvec{r}}_{g}^{e}={\text{e}^{{{\hat {\varvec{\xi}}}_\text{A}}{\theta _\text{A}}}} \cdot {\text{e}^{{{\hat {\varvec{\xi}}}_{\text{A}e}}{\theta _{\text{A}e}}}} \cdot {\text{e}^{{{\hat {\varvec{\xi}}}_\text{B}}{\theta _\text{B}}}} \cdot {\text{e}^{{{\hat {\varvec{\xi}}}_{\text{B}e}}{\theta _{\text{B}e}}}} \cdot {\text{e}^{{{\hat {\varvec{\xi}}}_\text{Z}}{\theta _\text{Z}}}} \cdot {\text{e}^{{{\hat {\varvec{\xi}}}_{\text{Z}e}}{\theta _{\text{Z}e}}}} \cdot {\text{e}^{{{\hat {\varvec{\xi}}}_\text{X}}{\theta _\text{X}}}} \cdot {\text{e}^{{{\hat {\varvec{\xi}}}_{\text{X}e}}{\theta _{\text{X}e}}}} \cdot {\text{e}^{{{\hat {\varvec{\xi}}}_\text{Y}}{\theta _\text{Y}}}} \cdot {\text{e}^{{{\hat {\varvec{\xi}}}_{\text{Y}e}}{\theta _{\text{Y}e}}}} \cdot {{\varvec{r}}_t}$$

(19)

The tooth surface is discretized into 15 × 9 grid points. The coordinate values for the grid points can be determined to calculate the error K_f (f = 1, 2, …, 135) of grid points between the actual tooth surface and the theoretical one. Subsequently, the tooth surface deviation value K can be expressed by summing the absolute values of the errors of each grid point in the following equation:

$$K=\sum\limits_{{f=1}}^{{135}} {\left| {{K_f}} \right|}$$

(20)

The 30 geometric errors of the machine tool are used as input values, and the tooth surface deviation value K is utilized as the output result to assess the degree of deviation. The model of the machine tool’s geometric errors to the gear tooth surface deviation can be expressed as:

$$K=y{\text{(}}{x_1},{x_2}, \cdot \cdot \cdot {x_{30}}{\text{)}}$$

(21)

Global sensitivity analysis of geometric errors

Analysis process of EFAST method

EFAST is a variance-based global sensitivity analysis method that is independent of any assumptions about the model structure²⁶. It has the characteristics of requiring fewer model evaluations and provides a good approximation of nonlinear systems. When a feasible input parameter range is provided, the EFAST method offers a way to estimate the expected value E and variance V of the model output, as well as the contribution of input parameters and their interactions to the variance. Sensitivity analysis methods typically focus on three main aspects: models or systems, input parameters, and output results. According to Eq. (21), the analysis process of the EFAST method is shown in Fig. 6. Each error item has a certain range of variations and distribution forms, and all error items constitute a multidimensional parameter space²⁷.

Fig. 6

The process diagram of the EFAST method.

Based on Weyl’s theorem, the primary concept of the EFAST method is to transform the k-dimensional integral into a one-dimensional integral according to the following Eq. (22).

$$E(K) =\int_{{{\Omega ^k}}} {y(x)p(x)dx}$$

(22)

Where the expected value of the output E(K) is obtained through the k-dimensional integration ${\Omega ^k}$ of the product of the joint probability density function of the model y(x) and p(x) in the input space. A unique frequency ${\omega _i}$ is assigned to each input parameter x_i, and then transformed according to the following function:

$${x_i}=\frac{1}{2}+\frac{1}{\pi }\arcsin (\sin ({\omega _i}s+{\varphi _i}))$$

(23)

Where φ_i is a random phase uniformly selected in $[0,2\pi )$, and s is a scalar in the range of $( - \pi ,\pi )$. For different values of s, all factors change along a scan input space ${\Omega ^k}$ curve. The oscillation x_i depends only on its corresponding frequency ${\omega _i}$. The output of the model is periodic and combined with different frequencies of input ${\omega _i}$, regardless of the model f(x). Therefore, if the parameter i has a strong influence on the model, the oscillation output ${\omega _i}$ will have a high amplitude.

According to Eq. (23), $K=y{\text{(}}{x_1},{x_2}, \cdot \cdot \cdot {x_{30}}{\text{)}}$can be transformed into the following formula:

$$K=y(s)=y[{X_1}(\sin {\omega _1}s),{X_2}(\sin {\omega _2}s),{X_3}(\sin {\omega _3}s) \cdot \cdot \cdot {X_{30}}(\sin {\omega _{30}}s)]$$

(24)

The formula for E(K) can be expressed as follows:

$$E( K) =\int_{{ - \pi }}^{\pi } {y(s)ds}$$

(25)

The total variance V(K) of the output of the y(s) model in the formula can be approximated by Fourier analysis as follows:

$$V(K)=\frac{1}{{2\pi }}\int_{{ - \pi }}^{\pi } {{y^2}(s)ds - {E^2}(K)} \approx 2\sum\limits_{{j=1}}^{N} {(A_{j}^{2}+B_{j}^{2}} )$$

(26)

For the set of odd frequencies, the integral range of the y(s) can be reduced from $( - \pi ,\pi )$ to $( - \pi /2,\pi /2)$, and the number of required model operations can be halved. The calculation of Fourier coefficients ${A_j}$ and ${B_j}$ are demonstrated in the following equations:

$${A_j}=\frac{1}{{{N_s}}}\left\{ {y({s_{{N_0}}})+\sum\limits_{{q=1}}^{{{N_q}}} {\left[ {y({s_{{N_0}+q}})+y({s_{{N_0} - q}})} \right]} \times \cos (j\frac{\pi }{{{N_s}}}q)} \right\}$$

(27)

$${B_j}=\frac{1}{{{N_s}}}\left\{ {\sum\limits_{{q=1}}^{{{N_q}}} {\left[ {y({s_{{N_0}+q}}) - y({s_{{N_0} - q}})} \right]} \times \sin (j\frac{\pi }{{{N_s}}}q)} \right\}$$

(28)

$${V_i}(K)=2\sum\limits_{{p=1}}^{M} {(A_{{p{\omega _i}}}^{2}+B_{{p{\omega _i}}}^{2}} )$$

(29)

$${V_{ci}}(K)=2\sum\limits_{{p=1}}^{M} {(A_{{p{\omega _{\sim i}}}}^{2}+B_{{p{\omega _{\sim i}}}}^{2}} )$$

(30)

Where N_s represents the number of calculations, N₀=(N_s+1)/2 and N_q=(N_s-1)/2. M is the maximum harmonic number to be considered.${A_{p{\omega _{\sim i}}}}$ and ${B_{p{\omega _{\sim i}}}}$ are Fourier coefficients without the parameter x_i. V_i represents the variance of the model output when the parameter x_i acts alone. V_ci is the variance of the model output when the remaining error items of x_i is not included.

In order to measure the influence of a single error x_i on the output variance, the ratio S_i of V_i to the total variance V is called the first-order sensitivity coefficient of the error x_i. The size of the first-order sensitivity coefficient reflects the degree of influence of the error item on the tooth surface deviation when acting independently. Due to the mutual coupling between the error items, the global sensitivity coefficient S_Ti is introduced to measure the influence of the error x_i itself and its coupling with other input error items on the output variance. Then the first-order sensitivity coefficient S_i and global sensitivity coefficient S_Ti of parameter x_i are calculated in the following equations:

$${S_i}=\frac{{{V_i}(K)}}{{V(K)}}$$

(31)

$${S_{Ti}}=1 - \frac{{{V_{ci}}(K)}}{{V(K)}}$$

(32)

Sensitivity analysis results

To use EFAST for global sensitivity analysis, the distribution range of the geometric errors should be determined. Since the machine tool exhibits numerous geometric errors and the actual measurement process is complex, the primary objective of this paper is to validate the feasibility of the proposed theory. This paper adopts the geometric error range of the machine tool from existing literature and scales it²⁸. Assuming that the linear error range is 0 ~ 15 μm and the angular error range is 0 ~ 0.015 deg, with the geometric error items being uniformly distributed. The geometric error range is inputted into the program for sensitive calculation, resulting in the derivation of first-order and global sensitivity coefficients for 30 geometric errors. The data is obtained by rounding the original data to retain five decimal points, and the results are presented in Table 4. Subsequently, the data is utilized in drawing software to generate a sensitivity analysis radar diagram, as shown in Fig. 7.

Table 4 First-order and global sensitivity coefficients.

Fig. 7

The comparison between the first-order and global sensitivity coefficients.

Figure 7 illustrates the distribution of the first-order and global sensitivity coefficients regarding the influence of geometric errors on the tooth surface deviation of the spiral bevel gear. The numbers 1 to 30 denote the sequence numbers of the geometric error items, while the numbers 0 to 0.27 represent the sensitivity coefficient values of the corresponding geometric error items. The following conclusions can be obtained:

• (1) It can be observed that the first-order and global sensitivity coefficients of each geometric error to spiral bevel gear tooth surface deviation are greater than 0, which have the same distribution and change trends. The larger the sensitivity coefficient, the greater the influence of the geometric error on the tooth surface deviation. The relationship between the first-order and global sensitivity coefficients is undetermined. When the global sensitivity coefficient surpasses the first-order sensitivity coefficient, it indicates that the coupling effect between the error item and other error items amplifies the influence of the error item on the tooth surface deviation. Conversely, when the global sensitivity coefficient is lower than the first-order sensitivity coefficient, it indicates that the coupling effect between the error item and other error items diminishes the influence of the error item on the tooth surface deviation. However, the coupling mechanism between the error items is not clear, indicating that the coupling among the error items is complex.

• (2) According to Reference¹⁶, the sum of the first-order or global sensitivity coefficients should be close to 1. Assuming that the sum of the sensitivity coefficients of the 30 geometric errors is 1, and the sensitivity coefficients of each error are equal, the coefficients are approximately 0.033. Therefore, the geometric error item with a sensitivity coefficient greater than 0.03 is considered as the key geometric error item. To comprehensively consider the coupling effect between the error items, this paper chooses the global sensitivity coefficient as the evaluation index. Consequently, there are 12 key geometric error items, including 8 linear geometric error items δ_xX, δ_yX, δ_xY, δ_yY, δ_xZ, δ_xA, δ_xB, δ_yB, corresponding to error serial numbers 1, 2, 7, 8, 13, 19, 25, and 26, respectively, and 4 angular geometric error items ε_βX, ε_γX, ε_αY, ε_βY, corresponding to error serial numbers 5, 6, 10, and 11, respectively. Upon comparison with the first-order sensitivity coefficients, the error items with strong coupling are δ_yX, δ_yY and δ_yB, with corresponding serial numbers are 2, 8, and 26.

• (3) The sensitivity coefficient of the angular geometric error item ε_γX is the largest, indicating it is the most critical error. By summing the sensitivity coefficients of each motion axis, it is evident that the X-axis is the most sensitive motion axis of the machine tool. To improve the machining accuracy of the gear tooth surface more effectively, the 12 identified key geometric errors should be compensated for in a targeted manner. Simultaneously, when compensating for geometric errors, special attention should be given to the most sensitive error item ε_γX and the most sensitive X-axis.

• (4) The theory proposed in this paper can be extended to other gear manufacturing processes, such as the hobbing and the power skiving. However, this paper only focuses on the influence of the geometric error on the tooth surface deviation. It is important to note that there are multiple sources of errors, including thermal error, force error and others, during actual processing of the machine tool. Future research should comprehensively consider the influence of these errors on tooth surface deviation.

Comparison and compensation of sensitivity analysis results

Comparison of key geometric errors identification results

To validate the reliability of the key geometric errors identified by the EFAST sensitivity analysis method, the local sensitivity analysis method based on factor perturbation method is applied. The size of the local sensitivity coefficient reflects the degree of influence of the error item on the tooth surface deviation when acting independently. The comparison is performed by changing one parameter within the geometric errors range while keeping the other parameters constant. The parameter sensitivity coefficient S is calculated as follows:

$$S=\frac{1}{{n - 1}}\sum\limits_{{i=1}}^{{n - 1}} {\frac{{\left( {{K_{i+1}} - {K_i}} \right)/{K_a}}}{{\left( {{x_{i+1}} - {x_i}} \right)/{x_a}}}}$$

(33)

Where K_i+1 and K_i are the i + 1 and i model output values, respectively. K_a is the mean of the two output values. x_i+1 and x_i are the i + 1 and i model input values, respectively. x_a is the average value of the two input values. The larger the |S|, the higher the sensitivity of the parameter.

According to Eq. (33), the local sensitivity coefficients of 30 geometric errors are calculated and then obtained by rounding the original data to retain five decimal points, as shown in Table 5. The data is imported into the drawing software to generate the sensitivity analysis radar diagram, as shown in Fig. 8. Compared with those obtained using the EFAST method, the distribution trend of the sensitivity results is largely consistent. This consistency confirms the reliability of the EFAST sensitivity analysis.

Table 5 Local sensitivity coefficient.

Fig. 8

The comparison among first-order, global and local sensitivity coefficients.

Simulation compensation of key geometric errors

To validate the effectiveness of the global sensitivity analysis results obtained from the EFAST method. The simulation compensation is conducted to assess the influence of the identified key errors on the tooth surface deviation. In the simulation compensation, the initial errors for each axis of the machine tool are set to their maximum values within the range, with linear errors at 15 μm and angular errors at 0.015 deg. Given that it is impossible to completely eliminate geometric errors during the manufacturing process, it is assumed that the maximum values for linear and angular key geometric error items are 4 μm and 0.0034 deg respectively after compensation. The values of the other geometric error items remain unchanged. The absolute error values of tooth surface deviation at 135 grid points before and after compensation are illustrated in Figs. 9 and 10(a)(b).

Fig. 9

The absolute error values of 135 grid points before and after the key error items compensation. (unit: mm)

Fig. 10

Tooth surface deviation topology diagram before and after the key error items compensation. (a) Topology diagram of tooth surface deviation before the key error items compensation. (unit: mm). (b) Topology diagram of tooth surface deviation after the key error items compensation. (unit: mm)

From Figs. 9 and 10(a)(b), it can be observed that the absolute error values of each grid point have decreased significantly after compensating for the identified key error items. The value K of tooth surface deviation before and after compensating for the key error items is calculated, as shown in Table 6 After the key geometric error items are compensated, the tooth surface deviation value K is reduced from 0.58802 mm to 0.1363 mm, and the tooth surface deviation reduction rate is 76.82%. The tooth surface deviation is significantly reduced, which further verifies the effectiveness of the key geometric error items identified by the EFAST sensitivity analysis method, and also proves the strong correlation between the key geometric error items of the machine tool and the gear tooth surface accuracy. The relevant gear parameters used in this paper are shown in Table 7.

Table 6 The tooth surface deviation value before and after the key error items compensation. (unit: mm)

Table 7 Gear geometry parameters.

Conclusion

Due to the complex relationship between the geometric errors and tooth surface deviation in the five-axis CNC spiral bevel gear machine tool, a key geometric errors identification method based on screw theory and the EFAST method is proposed. This method can reliably and effectively identify the key geometric error items that affect the tooth surface deviation. The main conclusions are as follows:

• (1) According to the principles of tooth surface forming and based on the screw theory, the error transfer model from the machine tool to the gear workpiece is established. This model reveals the quantitative mapping law between the geometric errors of the machine tool and the tooth surface deviation of the spiral bevel gear.

• (2) According to the error transfer model, the EFAST method is utilized to quantitatively calculate the first-order sensitivity coefficient and global sensitivity coefficient of each geometric error item. This method identifies the key geometric error items that significantly influences the tooth surface deviation, and ensures error traceability.

• (3) After compensating for the key geometric error items, the deviation of each grid point is significantly reduced, and the tooth surface deviation value is significantly reduced, demonstrating the feasibility of reducing the tooth surface deviation by compensating for the key geometric error items of the machine tool. This provides theoretical guidance for reducing the gear tooth surface deviation and enhancing the accuracy of the machine tool.