Coati optimization algorithm based Deep Convolutional Forest method for prediction of atmospheric and oceanic parameters

Abstract

Droughts and floods are examples of extreme weather events that can result from changes in ocean temperature. Ocean temperature is a key component of the global open sea system. Currently, real-time sea surface temperature (SST) forecasts are generated by numerical models based on physics principles and influenced by boundary and initial conditions. These models generally perform better over large areas than at specific locations. To address this and improve prediction accuracy, particularly in high-precision areas, the Coati Optimization Algorithm-based Deep Convolutional Forest (COA-DCF) method is proposed. This optimization approach is utilized to train the Deep Convolutional Forest (DCF) classifier, which then applies the prediction strategy. The COA-DCF method forecasts ocean surface temperature anomalies by considering key variables such as SST, Sea Surface Height (SSH), soil moisture, and wind speed, using historical data ranging from 1 to 10 days across six different locations. The proposed method achieves improved accuracy with low Root Mean Square Error (RMSE) and Mean Absolute Error (MAE) values, and a high Pearson’s correlation coefficient (r) of 0.493, 0.487, and 0.4733, respectively, thereby enhancing the overall performance of the deep learning model.

Introduction

Satellite remote sensing data sets have greatly contributed to ocean studies. However, due to the challenge of electromagnetic radiation penetrating water, most of these datasets are limited to the ocean’s surface⁷. Despite advancements in deep ocean data mining, driven by large-scale in-situ observation programs like the Argo buoy¹¹, existing subsurface observational datasets still need enhancement to meet the demands of research into the fundamental dynamics of the oceans⁴⁰. Further investigation into the ocean’s depths is essential, as most significant oceanographic events occur below the surface^2,5,14,25,39. Moreover, the majority of the additional heat added to Earth’s climate system in recent decades has been absorbed by the oceans⁴⁹, making the study of internal ocean heating a crucial aspect of addressing global warming^6,34.

Recent research^9,16,17,31 has shown that the warming of the upper ocean reflects recent increases in sea surface temperatures (SST). Changes in the ocean system significantly influence atmospheric circulation and global climate²⁴. Temperature differences between land and water can lead to air-sea interactions, potentially causing severe weather and climate phenomena, such as storm swells⁴⁴ and super typhoons²⁷. Additionally, changes in ocean temperature affect monsoon circulation and precipitation, influencing both interannual and interdecadal climatic variations in the region¹⁸. Model-based studies suggest that the El Niño-Southern Oscillation (ENSO) and La Niña may be linked to upper ocean warming¹⁹. However, due to a lack of subsurface data, only a few studies have explored this area. Since air-sea interactions have less impact on subsurface temperatures compared to SST, interannual variability in subsurface temperatures is often more pronounced. Therefore, investigating the ocean’s thermal structure is crucial, as it plays a significant role in climatic patterns. Although satellites cannot directly observe deep ocean layers, information about the subsurface can be inferred from surface measurements^15,19,22. Surface satellite remote sensing data can be used to estimate subsurface conditions through statistical modeling^{10,21,28,29,30,46}.

Changing environmental factors, such as cyclone intensity, are accounted for by incorporating both oceanic and atmospheric features into calculations of general environmental variables. However, tropical cyclones (TC) exhibit distinct characteristics at different stages of their development. Consequently, various changes are reported due to the interaction of oceanic factors, distributional characteristics, and atmospheric variables. These fluctuations impact heat transfer between the ocean and atmosphere, influencing sea surface temperatures (SST). Research has revealed that the roles of the North Atlantic Oscillation (NAO) and the Arctic Oscillation (AO) are more complex than previously thought.

Additionally, multidecadal variability in SST is evident in the Pacific Decadal Oscillation (PDO) in the North Pacific Ocean and the Atlantic Multidecadal Oscillation (AMO) in the North Atlantic Ocean, significantly affecting Arctic sea ice melting. The Arctic ecosystem is particularly vulnerable to these changes. Sea ice is essential for controlling the energy transfer between the ocean and atmosphere, and its melting modifies the structure of the upper Arctic Ocean. As a result of the interaction of ice, sea, and air, anomalies in Arctic surface temperatures arise. These alterations alter the temperature differential between the polar and mid-latitude regions and weaken the westerly winds in the mid-latitudes^41,47.

To increase prediction accuracy, this study uses the Deep Convolutional Forest (COA-DCF) technique, which is based on the Convolutional Optimisation Algorithm and targets both atmospheric and oceanic components. Key factors that serve as forecast inputs for the model are wind velocity, soil moisture, rainfall index, and sea surface temperature (SST). First, technical indicators such as the trend detection index (TDI), simple moving average (SMA), and commodity channel index (CCI) are extracted from these input values. These indicators help to smooth out short-term oscillations and reveal trends based on data from the ocean and atmosphere. In order to increase the dimensionality of the data and improve the prediction performance of the model, the extracted features are subjected to data augmentation.

Oversampling is used to do this, adding new, artificial data points to the dataset to make it more complete. The Deep Convolutional Forest (DCF), which combines the advantages of deep learning and decision trees to handle complicated interactions within the data, is one of the deep learning classifiers that receives the enriched, high-dimensional dataset. With the use of the COA-DCF optimisation technique, the classifier is adjusted to produce predictions based on the supplemented dataset that are more accurate and guarantee that the model is well calibrated. This method efficiently analyses and forecasts results from complicated atmospheric and marine data by fusing deep learning with sophisticated data processing techniques.

The key contributions of this research are as follows:

• 1. A COA-DCF model is introduced, capable of capturing the spatial and temporal dependencies of sea surface temperature (SST), enabling a more accurate and comprehensive prediction of SST fields.

• 2. The proposed method has been shown to be an effective approach in predicting root mean square error (RMSE), correlation coefficient (r), and mean absolute error (MAE) for SST fields within a specific region, using time series satellite data.

• 3. This study also presents a straightforward yet efficient averaging technique within the COA-DCF model, demonstrating superior performance over the SVR, LSTM, AdaBoost, and ArDHO models in predicting sea surface temperature.

The structure of the paper is as follows: Sect. 2 provides a foundational overview of the research. Section 3 details the proposed COA-DCF method for predicting subsurface temperature fields. Section 4 discusses the research findings, and the final section addresses the implications and potential future research directions.

Literature review

In the past few years, air-sea interactions at intermediate latitudes have received more attention, which is indicative of a general increase in research on the North Pacific Oscillation (NPO). Climate change significantly impacts the local weather and ecosystem in East Asia and North America, thereby exerting a substantial influence on the NPO^45,47. Global climate is influenced by ocean-atmospheric circulation patterns, which are influenced by ocean thermal conditions, mostly represented by water temperature^4,37.

In order to find latent relationships between variations in the intensity of tropical cyclones and their spatial distribution, Wang et al. created a 3D convolutional neural network (CNN) model⁴¹. This model does not require specific cyclone settings; instead, it relies only on observable environmental patterns to extract deep hybrid characteristics for forecasting strength fluctuations from TC (tropical cyclone) imagery. The precision of the model was enhanced by the use of data augmentation approaches, but at the expense of a reduced model lifetime.

Sarkar et al. used an LSTM classifier to improve numerical prediction outputs³³. This method showed that the learning-based LSTM performed better in feature extraction from the sample space than other approaches by successfully using various statistical measures based on correlation values. Test findings suggest that this approach has potential as a forecasting tool³².

To replicate rainfall properties, Im et al. created a regional climate model with higher resolution¹³. By incorporating physical models into conventional systems, performance was enhanced, though at the cost of increased computation time. Using time series data, pattern recognition, and correlation measures, He et al. presented an updated version of the particle swarm optimisation (PSO) technique¹². Although it produced an inaccurate forecast, the use of a support vector machine (SVM) to identify the most pertinent patterns from the gathered data improved convergence, especially for long-term series.

To address issues of portability, robustness, and biases in feature selection, Wolf et al. created a machine-learning ensemble model⁴³. Using seasonal trends and temporal correlations, this model was able to accurately predict sea surface temperature (SST) features with a low computational resource requirement.

Xiao et al. first introduced the LSTM-AdaBoost method for predicting sea surface temperature (SST)⁴⁶. By incorporating a deep learning classifier into the algorithm, this approach significantly reduced prediction error and improved results. Polynomial regression was used to model the time series data; however, long-term and spatial-temporal forecasting were not addressed.

Zhang et al. employed a gated recurrent neural network (RNN) with a Gated Recurrent Unit (GRU) layer to capture the temporal patterns of SST⁵⁰. The predictions were made using a fully connected layer. This method was highly reliable and effectively captured the SST trend, though it was occasionally affected by weather fluctuations.

Ye et al. proposed partial least squares regression (PLSR) to forecast sea ice concentration (SIC) variability in key regions⁴⁹. This statistical model accurately predicted sea variation and achieved a high absolute value. Despite its utility in predictions, it exhibited poor predictability and contributed to systematic inaccuracies, prompting the development of a backpropagation neural network (BPNN)-based method for SST prediction.

In response, we developed a COA-DCF model to forecast SST using historical data. Performance is evaluated through root mean square error (RMSE), Pearson’s correlation coefficient (r), and mean absolute error (MAE). However, the research should have incorporated high-resolution data. The SST predictions were refined using a feedback connection network, achieving the best performance in prediction accuracy. Additionally, a two-stacked BPNN was developed to further enhance forecast precision.

Proposed COA-DCF method for atmospheric and oceanic prediction

Fig. 1

Schematic view of proposed COA-DCF based method.

The study of the linkages between the atmospheric and oceanic systems has provided considerable impetus to the recent surge in the application of machine learning to predict climate change. This project is one of the most sophisticated and difficult problems in science and technology today. This paper presents a research project that uses the Deep Convolutional Forest (DCF), which is based on COA, to develop a prediction model that is useful for evaluating oceanic and atmospheric data. Technical indicators are first extracted from the input parameters to provide features like the Trend Detection Index (TDI), Commodity Channel Index (CCI), and Simple Moving Average (SMA). After extracting these features, an enhanced dataset is created by applying oversampling to the data.

The COA algorithm is then used to train the DCF classifier, which is then used to generate predictions. Figure 1 depicts the suggested COA-DCF approach.

COA methodology

The COA technique is based on coatis’ behaviour modelling. The metaheuristic COA algorithm treats coatis as members of the population⁸. Coati locations in the search space influence choice variable values. Thus, coatis in the COA may solve the situation. Equation (1) describes the COA implementation’s random initialization of the coatis’ search space location.

$$\:{S}_{i}:{s}_{ij}={l}_{j}+rand*\left({u}_{j}-{l}_{j}\right),\:i=\text{1,2},\dots\:P\:and\:j=\text{1,2},\dots\:.Q$$

(1)

$$\:M=\left[\begin{array}{c}{M}_{\begin{array}{c}1\\\: \vdots \end{array}}\\\:{M}_{\begin{array}{c}i\\\: \vdots \end{array}}\\\:{M}_{P}\end{array}\right]=\left[\begin{array}{ccc}{M}_{\begin{array}{c}11\cdots\:\\\: \vdots \end{array}}&\:{M}_{\begin{array}{c}1j\\\: \vdots \end{array}}\dots\:&\:{M}_{1Q}\\\:{M}_{\begin{array}{c}i1\cdots\:\\\:\vdots \end{array}}&\:{M}_{\begin{array}{c}ij\\\:\vdots \end{array}}\dots\:&\:{M}_{\begin{array}{c}iQ\\\: \vdots \end{array}}\\\:{M}_{P1\cdots\:}&\:{M}_{Pj}\dots\:&\:{M}_{PQ}\end{array}\right]$$

(2)

The mentioned equation pertains to the determination of the position of the$\:{\:i}^{th}$ coati within the search space, wherein $\:{s}_{ij}$ denotes the value of the $\:{\:j}^{th}$ decision variable. The variables P and Q represent the number of coatis and decision variables, respectively. Additionally, $\:r$and is a random real number that falls within the interval of [0, 1], while $\:{l}_{j}$ and $\:{u}_{j}$ correspond to the lower and upper bounds of the$\:{\:j}^{th}$ decision variable. The population matrix $\:M$ is utilized as a mathematical representation in Eq. (2) of the coati population in the COA.

The allocation of potential solutions across decision variables results in the computation of distinct values for the problem’s objective function. The aforementioned values are exhibited through the utilization of Eq. (3).

$$\:f=\left[\begin{array}{c}{f}_{\begin{array}{c}1\\\: \vdots \end{array}}\\\:{f}_{\begin{array}{c}i\\\: \vdots \end{array}}\\\:{f}_{P}\end{array}\right]=\left[\begin{array}{c}\begin{array}{c}f\left({S}_{1}\right)\\\: \vdots \end{array}\\\:\begin{array}{c}f\left({S}_{i}\right)\\\: \vdots \end{array}\\\:f\left({S}_{P}\right)\end{array}\right]$$

(3)

The vector $\:f$ represents the objective function obtained, while $\:{f}_{i}$ denotes the objective function value obtained from the $\:{\:i}^{th}$ coati.

In metaheuristic algorithms, like the COA algorithm, the value of the objective function is used to assess the quality of a potential solution. Therefore, the member of the population that leads to the identification of the ideal value for the objective function is known as the optimal member of the population. The potential solutions are updated while the algorithm iterations continue on, which results in the optimal member of the population being updated simultaneously with each iteration.

Exploration phase (hunting and attacking strategy)

In the initial stage of improving the coatis’ population within the exploration area, their behaviour is modeled after their approach to hunting iguanas. This model represents a pack of coatis scaling a tree to get to an iguana and frighten it. Certain coatis display their hunting instincts by congregating under the tree and biding their time until the iguana descends to the ground. The coatis then launch an ardent chase to get the iguana down on the ground. This method demonstrates the COA’s capacity for comprehensive exploration across the problem-solving space by enabling coatis to move to different areas within the search space. The optimal population member is thought to be positioned where the iguana is according to the COA design. Additionally, it’s thought that half of the coatis ascend the tree, and the other half waits below for the iguana to descend. Equation (4) describes the mathematical simulation of the coatis climbing out of the tree.

$$\:{S}_{i}^{x1}:{s}_{ij}^{x1}={s}_{ij}+rand*\left({I}_{j}-J*{s}_{ij}\right),\:for\:i=\text{1,2},\dots\:,\raisebox{1ex}{$P$}\!\left/\:\!\raisebox{-1ex}{$2$}\right.and\:j=\text{1,2},\dots\:.,Q$$

(4)

Upon descending, the iguana is placed at a stochastic location within the exploration domain. Coatis on the ground then move within the simulated search space according to Eqs. (5) and (6), which determine their new positions based on random assignments.

$$\:{I}^{G}:{I}_{j}^{G}={l}_{j}+rand*\left({u}_{j}-{l}_{j}\right),\:j=\text{1,2},\dots\:.,Q$$

(5)

$$\:{S}_{i}^{x1}:{s}_{ij}^{x1}=\left\{\begin{array}{c}{s}_{ij}+rand*\left({I}_{j}^{G}-J*{s}_{ij}\right),\:\:\:if\:{f}_{{I}^{G}}<{f}_{i}\\\:{s}_{ij}+rand*\left({I}_{j}-{I}_{j}^{G}\right),\:\:\:\:\:\:\:\:\:Otherwise\end{array}\right.$$

(6)

If the new position of each coati results in an improved value for the objective function, the update is considered acceptable. If not, the coati will remain in its previous position. This update condition applies to values of $\:i$ ranging from 1 to P and is simulated using Eq. (7).

$$\:{S}_{i}=\left\{\begin{array}{c}{S}_{i}^{x1},\:\:\:if\:{f}_{i}^{x1}<{f}_{i}\\\:{S}_{i},\:\:\:Otherwise\end{array}\right.$$

(7)

In this context, $\:{S}_{i}^{x1}$denotes the newly calculated position of the the i^th coati, with $\:{s}_{ij}^{x1}$ representing its $\:{j}^{th}$ dimension and $\:{f}_{i}^{x1}$ representing the corresponding objective function value. The variable $\:rand$ is a random real number within the interval [0,1]. The term “Iguana” refers to the position of the best member in the search set {1,2}. The position of the iguana on the ground, $\:{I}_{j}^{G}$, is randomly generated, where $\:{I}_{j}^{G}$, represents as $\:{I}_{j}^{G}$ for its jth dimension. Additionally, J is an integer randomly selected from the set {1,2}, and $\:{f}_{{I}^{G}}$ represents the objective function value at the iguana’s position.

Exploitation phase (the procedure of fleeing out of the way of a predator)

The mathematical modeling of the second phase of updating the coatis’ positions in the search space is inspired by their natural behaviour in response to predator encounters and their evasion tactics. When a predator attacks a coati, the animal quickly moves away from its current location. These strategic movements result in the coati remaining close to its original position, demonstrating the coati’s ability to perform a local search effectively, as per the COA.

The acceptability of the newly computed position depends on whether it improves the objective function’s value. This criterion is simulated using Eq. (8).

$$\:{S}_{i}=\left\{\begin{array}{c}{S}_{i}^{x2},\:\:\:if\:{f}_{i}^{x2}<{f}_{i}\\\:{S}_{i},\:\:\:\:\:Otherwise\end{array}\right.$$

(8)

In the second phase of COA, the new position $\:{S}_{i}^{x2}$ for the i^th coati is computed based on its $\:{j}^{th}$ dimension $\:{s}_{ij}^{x1}$ and objective function value $\:{f}_{i}^{x2}$​. This calculation incorporates a random number ($\:rand$) and the iteration counter ($\:t$). Additionally, the local lower bound ($\:{l}_{j}$) and local upper bound ($\:{u}_{j}$) of the jth decision variable decision variable, as well as the overall lower bound ($\:{l}_{j}$) and upper bound ($\:{u}_{j}$) for the same variable, are considered.

Deep Convolutional Forest for parameter prediction

Predictions for atmospheric and oceanic parameters are then produced by feeding the augmented data into the Deep Convolutional Forest (DCF) classifier. In atmospheric prediction, deep learning classifiers have shown to be especially successful. To generate its predictions, the DCF classifier makes use of the updated data. The recommended COA algorithm is utilised for the classifier’s training, though. Researchers frequently use data augmentation to get around the requirement for a lot of training samples for deep learning classifiers. To satisfy the needs of the classifier, this procedure produces several data samples.

A popular method in research to fulfil the demand for a high number of training samples for deep learning classifiers is data augmentation. This approach guarantees that the classifier has a varied and sufficient collection of samples, which improves its learning and predicting skills by producing several versions of the original data.

As shown in Fig. 2, the DCF model uses a cascade mechanism that was influenced by deep forest and neural network designs³⁸. According to this method, each level processes and sends its output to the level after it, which creates its own results and sends them on. Based on the processed data, each level generates a probability. These probabilities are merged with feature maps to provide input for the subsequent step. Calculating the average probability from the last level and choosing the maximum average as the forecast outcome yields the final classification.

The main factor affecting the model’s difficulty level is its accuracy. When an accuracy plateau is reached, the Dynamic Cascade Forward (DCF) algorithm ends its iterative process, in contrast to deep neural networks that have a set number of hidden layers. This happens when the accuracy of the validation data increases, creating new levels until a suitable degree of precision is attained. It is possible to apply the DCF methodology to datasets of different sizes, even small-scale datasets. The system’s capacity to modify its complexity by stopping the training process when acceptable precision levels are reached accounts for this adaptability.

Fig. 2

Architecture of DCF method.

The convolutional layer, classification layer, and pooling layer are the three fundamental parts of each level of the DCF model. Four primary classifiers comprise the classification layer: two highly randomised trees and two randomised forests. The pooling layer is essential for lowering overfitting in the suggested model, whereas the convolutional layer manages feature extraction.

The reason DCF works so well is that it combines the best aspects of bagging and boosting. These methods each have a different use in terms of lowering bias and variation. In bagging, a group of ineffective learners are trained concurrently, and the final model score is calculated by averaging their performances. Boosting, on the other hand, educates weak learners in a sequential manner, with each learner trying to outperform its predecessor.

The DCF model uses an aggregate of all the forests’ classification layer outputs to represent bagging. The basic classifier used by DCF is Random Forest; the average of the model is obtained by summing the predictions made by each decision tree separately. DCF also includes boosting by consistently adding new stages, each of which fixes the flaws of the one before it. With this strategy, DCF can take advantage of the advantages of both boosting and bagging.

Convolution operation

In the convolutional layer of the neural network, convolution is performed on an input matrix, followed by the application of the Rectified Linear Unit (ReLU) activation function to extract hidden features from the textual input. Let $\:X\in\:{\mathbb{S}}^{n\times\:m}$ be the input matrix, where $\:n$ represents the number of samples and $\:m$ is the dimensionality of each sample vector. A filter $\:X\in\:{\mathbb{S}}^{m\times\:d}$ is then applied to the input, resulting in a feature vector $\:V$ with a dimension of $\:n-d+1$, commonly referred to as a feature map. Here, $\:d$ refers to the size of the kernel’s area of interest. Equations (9–11) illustrate the process for deriving the feature vector, assuming $\:d$ equals 2.

$$X = \left[ \begin{array}{llll} {{I_{11}}} \hfill & {{I_{12}}} \hfill & \cdots \hfill & {{I_{1m}}} \hfill \\ {{I_{21}}} \hfill & {{I_{22}}} \hfill & \cdots \hfill & {{I_{2m}}} \hfill \\ \vdots \hfill & \vdots \hfill & {} \hfill & \vdots \hfill \\ {{I_{n1}}} \hfill & {{I_{n2}}} \hfill & \cdots \hfill & {{I_{nm}}} \hfill \\ \end{array} \right]$$

(9)

$${K_f} = \left[ \begin{array}{ll}{{K_{11}}} \hfill & {{K_{21}}} \hfill \\ {{K_{12}}} \hfill & {{K_{22}}} \hfill \\ \vdots \hfill & \vdots \hfill \\ {{K_{1m}}} \hfill & {{K_{2m}}} \hfill \\ \end{array} \right]$$

(10)

$$X \circledast {K_f} = V \to \left[ \begin{array}{ll} {{K_{11}}} \hfill & {{K_{21}}} \hfill \\ {{K_{12}}} \hfill & {{K_{22}}} \hfill \\ \vdots \hfill & \vdots \hfill \\ {{K_{1m}}} \hfill & {{K_{2m}}} \hfill \\ \end{array} \right]$$

(11)

The feature vector $\:V$ of length $\:(n\:-\:2\:+\:1)$ is obtained by applying the convolution operator ⊛. Each element in the resulting vector is computed using the following formula:

$${V_1} = {I_{11}}{K_{11}} + {I_{12}}{K_{12}} + \cdots + {I_{1m}}{K_{1m}} + {I_{21}}{K_{21}} + {I_{22}}{K_{22}} + \cdots + {I_{2m}}{K_{2m}}$$

(12)

$${V_2} = {I_{21}}{K_{21}} + {I_{22}}{K_{22}} + \cdots + {I_{2m}}{K_{1m}} + {I_{31}}{K_{21}} + {I_{32}}{K_{22}} + \cdots + {I_{3m}}{K_{2m}}$$

(13)

$${V_i} = {I_{\left( {n - 1} \right)1}}{K_{11}} + {I_{\left( {n - 1} \right)1}}{K_{12}} + \cdots + {I_{\left( {n - 1} \right)m}}{K_{1m}} + {I_{n1}}{K_{21}} + {I_{n2}}{K_{22}} + \cdots + {I_{nm}}{K_{2m}}$$

(14)

The ReLU activation function is applied to the feature vector $\:V$. As described in Eqs. (12–14), ReLU processes each value $\:{V}_{i}$ by returning the value itself if it is positive. If the value is negative, ReLU returns zero, effectively selecting the maximum value between $\:{V}_{i}$ and zero.

The convolutional layer’s output is transformed into a set of feature maps by applying several filters. This is because each filter generates only one feature map $\:{\widehat{V}}_{i}$ of length $\:(n\:-\:2\:+\:1)$ that contains only positive values.

$$\:{\widehat{V}}_{i}=\text{m}\text{a}\text{x}(0,\:{V}_{i})$$

(15)

Pooling operation

In deep learning, pooling is a popular method for lowering the dimensionality of feature maps. The input is divided into non-overlapping sections, and for each region, a summary statistic—like the maximum or average value—is computed. By doing this, the model’s parameter count is lowered, overfitting is avoided, and significant data features are preserved. The DCF model’s pooling layer uses pooling to downsize sample feature maps, which lowers the possibility of overfitting, according to Akhtar et al. (2020)¹.

By choosing a subset of features from a wider set, pooling makes the model simpler by combining the filter outputs and lightening the computational load on later processing steps. By addressing model complexity and lowering data noise, it aids in the mitigation of overfitting. An early termination mechanism included in the DCF model stops training as soon as performance starts to decline.

There are three ways that pooling can be applied: average, min, and max. Since max-pooling chooses the biggest value from each region to represent the feature map’s primary feature, it is typically recommended. In max-pooling, the output dimension matches the input dimension, and each element $\:{\stackrel{\sim}{V}}_{i}\:$represents the maximum value of its corresponding feature map, which can be computed using Eq. (16).

$$\:{\stackrel{\sim}{V}}_{i}=\text{m}\text{a}\text{x}\left({\widehat{V}}_{i}\right)$$

(16)

Ultimately, the features extracted from the convolutional and pooling layers are passed through the classification layer.

Fitness function

The optimal solution is determined using a fitness evaluation, where the goal is to achieve the minimum value. The fitness function is calculated using a specific expression.

$$\:F=\frac{1}{\omega\:}\sum\:_{i=1}^{\omega\:}{\left(Z-{\stackrel{\sim}{V}}_{i}\right)}^{2}$$

(17)

The fitness measure is represented by $\:F$, while $\:Z$ denotes denotes the target output. The total number of training samples is specified by $\:\omega\:$, and $\:{\stackrel{\sim}{V}}_{i}$​ represents the classification result from the deep learning classifier.

These steps are repeated iteratively until the optimal solution is obtained. Algorithm 1 provides the pseudo-code for the developed COA-DCF.

Algorithm 1

COA-DCF procedure.

Dataset description

These observational SST datasets are provided by NOAA in the USA and are collected using the AVHRR infrared satellite. Among NOAA’s products, the OISST version 2 dataset is notable for its large sample size and near-surface readings. This dataset is particularly well-suited for short-term modeling projections as it accounts for diurnal variations in SST. The dataset features a grid resolution of 0.25° by 0.25°, allowing for detailed weekly and monthly evaluations (https://www.esrl.noaa.gov/psd/data/gridded/data.noaa.oisst.v2.html).

Acquisition of input atmospheric and oceanic parameters

The deep learning classifier is utilized for the prediction of atmospheric and oceanic parameters. For the prediction process, this study incorporates a comprehensive set of meteorological and oceanic variables, including soil moisture, wind velocity and direction, sea level height (SLH), and sea surface temperature (SST).

Sea Surface temperature (SST) SST is a key climate and weather parameter derived from microwave radiometers on satellites, widely recognized as a reliable indicator of global productivity, pollution, and climate change. This measurement is typically obtained using the infrared bands of optical satellites. SST serves as a crucial climatic variable for monitoring continuous climate variations and understanding the broader climate system.

Annual India Rainfall Index (AIRI) AIRI consists of annual rainfall data organized in a time series format. It provides evidence of climate variability in India, offering insights into the region’s changing climate patterns.

Wind Velocity/Speed Wind velocity at two meters above the ground level represents wind speed at pedestrian height, directly influencing thermal comfort through air ventilation. In the atmospheric context, wind velocity is calculated using the Cartesian coordinate system on a spherical surface. The minimum wind speed that initiates particle movement is referred to as the threshold velocity.

Sea Level Height (SLH) SLH is a critical global ocean climate parameter obtained using tidal gauges. It represents the sea surface height measured relative to an ellipsoid reference point. Although SLH is not well-observed in the Arctic region, it plays a vital role in understanding the global ocean circulation patterns.

Soil moisture Soil moisture refers to the amount of water retained within the soil, primarily influenced by soil properties, precipitation, and temperature. It is the key variable controlling the exchange of water and heat energy between the atmosphere and the ground surface, largely through processes like plant transpiration and evaporation.

$$D = \left\{ {P_{1} ,P_{2} ,...P_{i} ,...,P_{n} } \right\}; \quad 1 \le i \le n$$

(18)

where, $D$ indicates dataset, $P$ denotes atmospheric and oceanic data, $P_{i}$ denotes $i^{th}$ data, and $n$ indicates total number of data.

Extraction of technical indicators

To extract technical indicators such as CCI (Commodity Channel Index), SMA (Simple Moving Average), and TDI (Trend Detection Index), the relevant input data $P_{i}$ is selected from the dataset and processed in the technical indicators extraction phase⁵⁵. Technical indicators are heuristic or pattern-based signals derived from price, open interest, or trade volume of an asset. These indicators are crucial for predicting soil and atmospheric moisture, as they use historical data to forecast future parameters. Below is an explanation of the technical indicators derived from the atmospheric and oceanic parameters:

CCI: Commodity channel index is the term used to describe the data's cyclical turns. This indicator is described as follows:

$$ f_{3} = \frac{{S^{a} - f_{6} \left( {S^{a} } \right)}}{{0.015\sum\limits_{l = 1}^{m} {\left| {S_{a - l + 1} - f_{6} \left( {S^{a} } \right)} \right|/m} }} $$

(19)

where, $f_{3}$ specifies CCI indicator with the dimension of $\left[ {1 \times 1} \right]$.

SMA: It is calculated by taking into account the average statistics for a specific time frame. It's calculated as

$$ f_{6} = \frac{1}{m}\sum\limits_{l = 0}^{m} {B_{a - l} } $$

(20)

where, $B_{a}$ indicates close price on the day $a$, $m$ signifies input window length, and $f_{6}$ represents SMA with the size of $\left[ {1 \times 1} \right]$.

TDI: It is employed to determine the beginning and end of a trend. It can be used in conjunction with other indicators or as a standalone indication. It is depicted as $f_{7}$ having the dimensions of $\left[ {1 \times 1} \right]$. In order to produce the augmentation result, the technical indicators that were collected from the data are sent to the data augmentation phase. On the other hand, the technical indicators that were taken out of the data are described as $f$ having a dimension of $\left[ {1 \times 7} \right]$ such that $f = \left\{ {f_{1} ,...,f_{7} } \right\}$, respectively.

Data augmentation by oversampling method

Each technical feature undergoes data augmentation once technical indicators have been extracted from the data, which increases the dimensionality of the data. Therefore, in order to produce a feature result with big sized dimensions, each feature is fed independently to the data augmentation module. By adding data at random, it is a significant technique used to enhance diversity and volume. By employing the training data’s minimum and maximum feature index values as the threshold values for creating data samples, the oversampling approach produces the augmented output.

Every technical characteristic with a dimension $\left[ {U \times V} \right]$ is permitted to proceed to the data augmentation phase, whereupon the oversampling model procedure generates an augmented result as $A$ with the dimension of $\left[ {M \times V} \right]$ such that $M > U$. Nevertheless, after the data augmentation process, the RSI indicator with size $\left[ {1 \times 1} \right]$ produces an enhanced result with dimensions of $\left[ {50,000 \times 1} \right]$ created by the oversampling technique.

As a result, the outcome with size $\left[ {1 \times 1} \right]$ of is produced by the TRIX indication with size of $\left[ {50,000 \times 1} \right]$. Likewise, the technical indicators—CCI, Williams %R, ATR, SMA, and TDI—each possessing a dimension of $\left[ {1 \times 1} \right]$ that produces an enlarged outcome with the dimension of $\left[ {50,000 \times 1} \right]$ for each feature, correspondingly. As a result, the enhanced result's entire dimension is provided as $\left[ {50,000 \times 7} \right]$, each. The augmented data is fed into the classifier as input to create the prediction mechanism, and its size is larger than that of the original training set.

Experimental setup and result analysis

For each location’s SST forecast trial, datasets for the COA-DCF, SVR, AdaBoost, ArDHO, and LSTM models were prepared with a maximum input sequence length of 40 observations. The trial interval was determined, with 70% of the new data used for training and the remaining 30% reserved for testing. During training, 5% of the training data was further partitioned for validation.

Comparisons were made among the LSTM, SVR, AdaBoost, ArDHO, and COA-DCF models using stacking generalization to demonstrate that averaging their predictions is the most effective strategy. The COA-DCF model was constructed using the following procedures:

• 1. Base Learners Training: The training dataset was divided into three distinct sets, each containing an equal number of unique examples.

• 2. Training and Validation: Each set was used once as the validation set, while the other two sets served as training data. This process was repeated until each set had been used for validation.

• 3. Prediction Generation: After training, predictions were generated using the trained base learners for the remaining set.

Referring to Fig. 3, the predictions were integrated, and the target SST was forecasted at a higher level.

Fig. 3

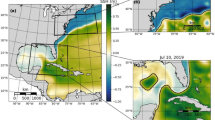
Estimated temperature based on sea surface temperature in six locations (L1, L2, L3, L4, L5, L6) (https://skepticalscience.com/print.php?n=4180).

Depending on the resolution of satellite observations, images display the specifics of sea-surface temperature distributions. The resolution in the infrared is much higher (1 km) than it is in the microwave (about 25 km). Various data plots can be created by using the data range provided and latitude and longitude information. (https://psl.noaa.gov/mddb2/makePlot.html?variableID=2701)

Fig. 4

Root Mean Square Error (RMSE) prediction of LSTM, SVR, AdaBoost, ArDHO, and COA-DCF in six locations for 1–10 days.

Fig. 5

Pearson’s correlation coefficient (r) prediction of LSTM, SVR, AdaBoost, ArDHO, and COA-DCF in six locations for 1–10 days.

Table 1 Mean Absolute Error (MAE) prediction of LSTM, SVR, AdaBoost, ArDHO, and COA-DCF in six locations for 1–10 days.

Figure 4 shows the root-mean-square error (RMSE) of predictions generated using the five methods: LSTM, SVR, AdaBoost, ArDHO, and COA-DCF, across various prediction horizons. When comparing performance across six different locations and the full forecast range, COA-DCF outperforms LSTM, SVR, AdaBoost, and ArDHO. However, there is no clear superiority between LSTM and SVR at any of the six tested locations or across the forecast ranges.

To further quantify and compare the accuracy of the predicted SSTs, Pearson’s correlation coefficient (r) was calculated, and the results are displayed in Fig. 5. The ‘r’ values are all statistically significant, as shown in the table. The results indicate that the observed and predicted SSTs exhibit a linear relationship, which weakens as the forecast horizon extends from 1 to 10 days.

In all six location and prediction horizon comparisons, SVR and LSTM demonstrated lower r values compared to BPNN. Additionally, the r values for ArDHO were either lower than or comparable to those for COA-DCF across all prediction horizons from L1 to L6.

Fig. 6

Mean Absolute Error (MAE) prediction of LSTM, SVR, AdaBoost, ArDHO, and COA-DCF in six locations.

Table 1; Fig. 6 present the mean absolute error (MAE) for predictions generated using the five methods: LSTM, SVR, AdaBoost, ArDHO, and COA-DCF, across all prediction horizons. COA-DCF consistently outperforms LSTM, SVR, AdaBoost, and ArDHO across all prediction horizons and six locations.

Currently, mathematical models based on physics-based hypotheses, subject to boundary and initial conditions, are capable of generating real-time SST estimates over larger geographic areas compared to models tailored to specific locations.

The results indicate the proposed COA-DCF model outperforms the other models for 10 days successively and in all 6 locations. The performance is evaluated on two metrics- the errors and the correlation coefficient. The performance not degrading for 10 consecutive days is an indication that the methodology systematically discovers the optimum parameter in the search space at all intermediate steps. In meteorology this is a significant development because the deterministic function that governs the time series in unknown. Neither the numerical nor the statistical models are characterized to determine this equation. The prediction is based on modelling the regression curve to the best possible estimation. In such a process the models tend to deviate from the time series in a spatial or temporal region of prediction and then come back to the trajectory in another region. No model systematically predicts better than the others. This is one reason why Multi Model Ensemble (MME) (Krishnamurthy and others, 2001) works in numerical modelling domain⁵⁶. The system dynamics is captured by one model at one time or location and by another model at an entirely different time or space. The errors of individual models are neutralised by such ensemble.

The present study indicates that statistical models of the tune described above are capable of making better predictions at all temporal and spatial domains. Consequently the need for ensemble forecasting can be done away with thus saving computational time and cost.

Conclusion

Surface water temperature is a critical indicator of global ocean health and can significantly influence or exacerbate droughts, floods, and other severe weather conditions, as well as impact oceanic systems and global warming. To generate accurate daily SST predictions, it is recommended to use the back-propagation neural network model, a machine learning technique that leverages an ensemble of diverse predictors. This ensemble approach uses averaging to mitigate the weaknesses of individual predictors while capitalizing on their strengths, thus providing state-of-the-art performance.

We train and evaluate the proposed COA-DCF method using daily SST data from the AVHRR sensor satellite at six locations. Across nearly all forecast ranges, from one to ten days, and using various metrics such as RMSE, correlation coefficient (r), and MAE, COA-DCF consistently outperforms LSTM, SVR, AdaBoost, and ArDHO. This location-specific SST forecasting method has the potential to enhance maritime activity planning and safety.

With advances in high-performance computing, researchers will soon be able to explore both extended SST forecasts and spatiotemporal SST predictions over larger regions. Additionally, the proposed technique could be applied to forecast other important marine, atmospheric, and environmental variables, including sea surface height (SSH), sea surface velocity (SSV), and sea surface wave (SSW).