Introduction

KOA is a common degenerative disease among middle-aged and elderly populations, characterized by joint pain, swelling, and impaired mobility. The occurrence of OA greatly reduces the quality of life for older adults and has a high disability rate1,2,3. With the aging population, the incidence of KOA is increasing year by year, with a prevalence rate of up to 50% in people over 60 years old, making it a significant public health problem. UKA has gained popularity as an excellent treatment option for patients with unicompartmental knee osteoarthritis. It offers less trauma but better knee joint dynamic recovery compared to total knee arthroplasty, as it preserves more anatomical functions. Numerous studies have reported excellent long-term survival rates and postoperative limb function after UKA4,5,6. However, the progression of lateral compartment osteoarthritis (LCOA) remains a major drawback of UKA. Other common issues include polyethylene (PE) liner wear, aseptic loosening, femorotibial instability, tibial fractures, and infection. Progression of LCOA due to altered cartilage stress patterns is the main concern7. The wear of the lateral compartment is attributed to abnormal cartilage stress, which is often related to lower limb alignment and the position of the unicompartmental prosthesis. Lower limb alignment, especially the mechanical axis of the lower limb, is associated with UKA. Several finite element studies on medial UKA have provided suggestions for postoperative lower limb alignment and unicompartmental prosthesis positioning, but their results vary. Ma et al. developed finite element models with 13 different femoral prosthesis positions: the standard position, 3° and 6° of varus and valgus angulation, and 1 mm, 3 mm, and 5 mm of medial and lateral translations. They analyzed stress variations in different regions below the tibial component and suggested that coronal tilt of the femoral component over 6° could significantly increase the stress on the PE surface, while varus angulation over 6° could significantly increase the stress on the cartilage surface. For the femoral component, they recommended placing it at the distal center of the femoral condyle8. Douiri conducted a retrospective study on the clinical outcomes and radiographic positioning of two groups of patients after medial UKA: residual varus axis alignment group and neutral mechanical axis alignment group. The residual varus axis alignment group had significantly higher KOOS scores and global NewIKS scores than the neutral mechanical axis alignment group. Residual varus axis alignment after medial UKA significantly improved knee joint functional scores at 2 years postoperatively, with better physical activity and recreational activities9. Wen et al. studied eight 3D models, which included three different lower limb alignment states: 3° of varus tilt, neutral alignment, and 3° of valgus tilt, as well as four different tilt angles of the tibial component: 4°, 2° of varus tilt, neutral alignment, and 2° and 4° of valgus tilt. Their FEA concluded that a slight varus alignment (undercorrection) of the lower limb could be a preventive measure for lateral compartment osteoarthritis after medial UKA, and a neutral or slightly valgus alignment on the coronal plane of the tibial component could be the optimal positioning for UKA10,11. In addition, Kennedy conducted a retrospective study on the overall clinical outcomes and postoperative alignment of 100 cases of medial UKA. Better outcomes were achieved when the mechanical axis fell within the central area (Zone C) or slightly medially (Zone 2) of the knee joint12. Another study analyzed the relationship between tibiofemoral alignment and failure in 246 cases of medial UKA. The preoperative tibiofemoral angle changed from a mean of 0.4° varus to 5.4° valgus, with an average correction angle of 5.8°. In a follow-up period of an average of 7 years and 5 months, both knee and functional scores significantly improved in all groups, regardless of the tibiofemoral angle. However, a significant difference in cumulative survival rates of the implants was observed between groups, with the highest survival rate found in the group with tibiofemoral valgus angles of 4° to 6°13. There have been some studies on the impact of lower limb alignment on medial UKA. However, there is a lack of in-depth research on the effects of different lower limb alignments on this procedure. In vivo biomechanical research is difficult to perform, which is why FEA has become a popular method for achieving a thorough biomechanical analysis and replacing the limitations of in vivo biomechanics. Therefore, this study uses simulation technology to establish a finite element model of medial UKA and analyze the impact of different lower limb alignments on this procedure.

Method

Establishment of a three-dimensional model of the knee joint

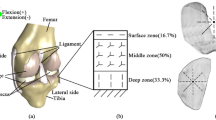
we selected MR and CT data of healthy adult male (26 years old, height 170 cm, weight 70 kg) knee joints to establish a complete FEA model of the knee joint. After the procedure, the raw data was exported in DICOM format and imported into pre-processing software Mimics 22.0 (Materialise NV, Leuven, Belgium). Based on the physiological structure of the knee joint, bones, ligaments, menisci, and cartilage were extracted layer by layer on a two-dimensional plane to create an initial intact knee joint model. The knee joint model was then exported and saved in STL format. It was subsequently imported into medical reverse engineering software Geomagic Wrap 2021 (3D Systems, America), where various functions such as mesh doctoring, manifold creation, cutting, and removal were applied to process different parts of the knee joint. NURBS surfaces were generated and exported in STP format. The resulting model was imported into finite element pre-processing software Hyperworks 21.0 (Altair Corporation, USA) for meshing and contact setup. To better simulate the biomechanics of the knee joint, the mesh was refined at ligament attachment points, menisci, and articular cartilage. The average edge lengths of the menisci, cartilage, and bones were 0.7 mm, 0.9 mm, and 1.6 mm, respectively, with shared nodes between menisci, cartilage, and ligaments. To better replicate the original structure of the knee joint, the bones, ligaments, menisci, cartilage, and other immovable components are combined into a unified whole, forming a binding relationship. For components that can only slide, frictional contact is set up. There are four contact relationships established: femoral cartilage with tibial cartilage, femoral cartilage with patellar cartilage, femoral cartilage with meniscus, and tibial prosthesis with polyethylene liner. The contact relationships are set as frictional contact, with a friction coefficient of 0.07 for the tibial prosthesis and polyethylene liner, and a friction coefficient of 0.1 for the other frictional contacts. This establishes a complete finite element model of the knee joint14,15 (Fig. 1: Generated using Mimics 22.0 (Materialise NV, Leuven, Belgium))

Fig. 1
figure 1

A complete finite element model of the knee joint.

Full size image

Building UKA finite element model and material assignment

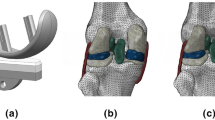
Using the current mainstream third-generation Oxford UKA with a fixed medial bearing platform for three-dimensional modeling, the model includes the femoral component, tibial component, and polyethylene liner. Each component was scanned separately using a three-dimensional scanner(SHINING EinScan Pro 2X V2) and imported into Geomagic Wrap 2021. The reverse reconstruction function was used to generate a three-dimensional model that includes the femoral component, polyethylene liner, and tibial component. The complete UKA model was combined with the complete knee joint model to simulate the standard UKA surgical process. The femur and tibia were cut and the components were placed. After the components were placed, the model was moved to fill the appropriate gaps to simulate bone cement. The complete UKA original model was saved in STL format and imported into Hyperwork 2020 for meshing. Using its mesh function, contacts and common nodes were sequentially established to complete the construction of the UKA finite element model, which was then saved in INP format. Ansys 2021 r1 was used for material assignment. Ligaments are tissues that respond to tension rather than compression. To better reflect the properties of the ligaments in the finite element model, they are considered to be isotropic and hyperelastic materials, representing their nonlinear stress-strain relationship, expressed by an incompressible Neo-Hookean behavior. Its energy density function is.

$$\Psi {\text{ }} = {\text{ C}}_{{\text{1}}} \times {\text{ }}({\text{I}}_{{\text{1}}} - {\text{3}}) ,$$

where C1 is the initial shear modulus and I1 is the first modified invariant of the right Cauchy-Green strain tensor. The C1 values for the lateral collateral ligament, medial collateral ligament, anterior cruciate ligament, and posterior cruciate ligament are 6.06, 6.43, 5.83, and 6.06 MPa, respectively8,16. The meniscus is defined as a transversely isotropic material, and the rest of the knee joint tissue structure is defined as a linear elastic isotropic material. Reference to previous finite element biomechanical studies of the knee joint was used to assign values to the elastic modulus and Poisson’s ratio for each structure in the knee joint, which were then verified11,17,18 (Fig. 2)

Fig. 2
figure 2

Material properties of different structures.

Full size image

Definition of lower limb alignments and boundary conditions

The hip-knee-ankle line defines the position of the mechanical axis, which needs to be measured in the anterior-posterior projection and in full-length standing X-rays. It is considered the gold standard for measuring the lower limb alignment as it accurately measures the mechanical tibiofemoral angle and assesses limb deformities. The mechanical axis of the lower limb, also known as the Mikulicz line, is drawn by connecting a point at the center of the femoral head to a point at the center of the ankle. The physiological position of this line is on average 4 ± 2 mm medial to the center of the knee. Any deviation from this physiological range, such as an outward extension of the line, is called varus, and if the line extends inward, it is called valgus. The deviation value is measured in millimeters and is referred to as the mechanical axis deviation (MAD)19. In this experiment, starting from the midpoint of the knee joint and directed toward the medial side of the knee joint, points were marked at 1 mm intervals to simulate the Mikulicz line passing through different points of the knee joint, resulting in a total of 60 different finite element models of the knee joint. The medial side was recorded as + MAD, and the lateral side was recorded as -MAD. The tibia was fixed, and the coordinates XYZ and -X-Y-Z of the distal fibula were constrained while the femur was defined as a solid entity. A remote point and remote force were set, coupling all nodes on the surface of the femur. The remote point was set at the center of the femoral head, and the remote force was directed vertically downward with a load of 1000 N to simulate a complete biomechanical analysis on a complete knee joint20,21. The finite element model was subsequently modified sequentially to ensure the accuracy of the experiment and to minimize deviations. Throughout the entire experimental process, except for the different lower limb alignments, all other load conditions and parameter settings remained consistent (Fig. 3: Generated using Ansys 2021 R1 (Ansys, Inc., Canonsburg, Pennsylvania, United States))

Fig. 3
figure 3

Connections: Tibial cartilage (A) to femoralcartilage (A), meniscus (D) to femoral cartilage (D), patellar cartilage (B) to femoral cartilage (B), and femoral prosthesis (C) to PE (C).

Full size image

Knee joint model validation

To ensure the accuracy of the established finite element model of the knee joint, it is necessary to validate the model. Validation method 1 involves applying a 1 kN load along the axis of the lower limb and observing the distribution, peak values, and load ratios of forces in the medial and lateral regions of the knee joint, including the cartilage and meniscus. Validation method 2 simulates the Lachman test on the knee joint. By modifying the applied boundary conditions, the femur is completely restrained, allowing only anterior-posterior motion in the coronal plane, and a 134 N anterior load is applied to the proximal tibia. The distance of anterior tibial displacement is observed. By comparing the results of these two validation methods with previous research, if the experimental results closely match the findings of previous studies, it indicates that the model is reasonable and can be used for further experimental research8,22.

Data collection and calculation of tibial implant periprosthetic fracture risk

The collected data includes stress on the insert, stress on the lateral meniscus, stress on the lateral femoral cartilage, stress on the tibial cartilage, contact area between the femoral implant and the insert, and contact area between the medial and lateral femoral cartilage.For the calculation of the periprosthetic fracture risk around the tibial implant, the Risk of Fracture (ROF) criterion is utilized. ROF is calculated by dividing the maximum principal strain (ε) within the bone by the limit of elastic strain. This criterion distinguishes between tensile and compressive loading states, and a high ROF value in a localized region indicates a higher risk of fracture23,24.

$$\begin{aligned} ROF = & \,\,\varepsilon /0.0073{\text{ if tensile}}{\text{.}} \\ & \varepsilon /0.0104{\text{ if compressive}}. \\ \end{aligned}$$

ROI setting: To quantitatively evaluate the maximum principal strain/limit of elastic strain within the bone, we defined four regions of interest (ROI) on the inner side of the proximal tibia. ROI 1 is located on the innermost side of the proximal tibia, and ROI 2–4 are sequentially positioned outward with a spacing of 12 mm. ROI 4 is located on the outer side slightly away from the center of the knee joint (Fig. 3: Generated using Ansys 2021 R1 (Ansys, Inc., Canonsburg, Pennsylvania, United States))

Results

Validation results of the model’s effectiveness

The normal knee joint model was validated and found to converge after loading. The established model consisted of a total of 95,660 nodes and 350,972 elements. To validate the effectiveness of the finite element model, the simulation results were compared with experimental results. Validation method 1: By comparing the stress on the medial and lateral femoral cartilage, meniscus, and tibial cartilage, the validation results showed that the peak equivalent stress on the surface of the medial tibial cartilage and lateral tibial cartilage were 1.47 MPa and 1.27 MPa, respectively. The peak equivalent stress on the surface of the medial femoral cartilage and lateral femoral cartilage were 1.15 MPa and 1.06 MPa, respectively. The peak equivalent stress on the surface of the medial meniscus and lateral meniscus were 1.33 MPa and 1.34 MPa, respectively. The contact area between the medial and lateral compartments was 4.25 × 102 mm2 and 3.98 × 102 mm2, respectively. The load distribution between the medial and lateral compartments was 56.21% and 43.79%, respectively. The stress, contact area, and load distribution were consistent with previous studies25,26,27. Validation method 2: By comparing the tibial anterior translation distance, the validation results showed that the anterior translation distance of the tibial plateau was 5.04 mm, which is very close to the research results of Pena, Gabriel, Fox, and others. The experimental model established was effective and can be used for experimental research16,28,29.

Equivalent stress changes in the lateral compartment and meniscus

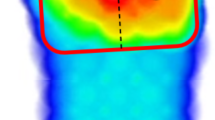
Figure 4 shows the stress changes in the main structures of the lateral compartment and meniscus in the finite element models of 60 different positions of the Mikulicz line. As the Mikulicz line shifts inward from the midpoint of the knee joint, the lower limb load mainly concentrates in the lateral compartment. The stress values of the lateral meniscus, tibial cartilage, and femoral cartilage gradually decrease from MAD 0 mm to + MAD 30 mm. The stress reduces from 1.62 MPa, 1.83 MPa, and 1.19 MPa to 1.14 MPa, 0.49 MPa, and 0.87 MPa, respectively, with reductions of 29.63%, 73.22%, and 26.89%. On the other hand, the stress in the medial PE liner gradually increases from 16.06 MPa to 21.82 MPa, with an increase of 26.40%. The increase in stress in the medial compartment is inversely proportional to the decrease in stress in the lateral compartment.As the Mikulicz line shifts outward from the midpoint of the knee joint, the lower limb load mainly concentrates in the lateral compartment. The stress values of the lateral meniscus, tibial cartilage, and femoral cartilage gradually increase from MAD 0 to -MAD 30. The lateral meniscus, tibial cartilage, and femoral cartilage experience increases of 5.62 MPa, 4.75 MPa, and 2.28 MPa, respectively, with increases of 246.91%, 159.56%, and 91.60%. Meanwhile, the stress in the medial PE liner gradually decreases and directly drops to 0.056 MPa, showing a significant decrease. It can be observed that there is a significant decrease in stress in the medial compartment and a substantial increase in stress in the lateral compartment. When the Mikulicz line moves outward, the stress in the lateral compartment starts to increase obviously. When -MAD > 15 mm, the increases in stress for the lateral meniscus, tibial cartilage, and femoral cartilage are 182.41%, 101.27%, and 65.22% respectively, with about two-thirds of the reduction occurring thereafter (Figs. 5 and 6 )

Fig. 4
figure 4

When MAD=0, the vertical load on the knee joint is 1000N. A represents the stress distribution map of theanterior cruciate ligament, B represents the stress distribution map of the lateral meniscus, C represents the stressdistribution map of the medial tibial plateau, and D represents the stress distribution map of the lateral femoralcondyle cartilage.

Full size image
Fig. 5
figure 5

Locations of four regions of interests defined in the study.

Full size image
Fig. 6
figure 6

Different equivalent stress in PE under different Mikulicz lines.

Full size image

The maximum principal strain/elastic strain limit values of ROI

In 60 different positions of the Mikulicz line in a finite element model, the ROI 1 and ROI 2 show the maximum principal strain changes during the inward displacement process of the Mikulicz line from the midpoint of the knee joint. ROI 3 and ROI 4 exhibit less obviously fluctuations, with their maximum principal strains roughly increasing proportionally. The maximum principal strain value of ROI 1 increases from 2000 to 14,800, a 640% increase. The maximum principal strain values of ROI 2, ROI 3, and ROI 4 increase from 1600, 600, 2000 to 13,600, 3200, and 3000 respectively, with increases of 750%, 433%, and 50%. The noticeable changes in ROI 1 and ROI 2 occur after + MAD > 10 mm. The calculation of their maximum principal strain/elastic strain limit values can be seen in Fig. 6. On the other hand, during the outward displacement process of the Mikulicz line from the midpoint of the knee joint, the maximum principal strains of ROI 1, ROI 2, ROI 3, and ROI 4 decrease, showing a roughly inverse relationship, but the overall decrease is small (Figs. 7, 8 and 9).

Fig. 7
figure 7

Different equivalent stress in meniscus, tibial cartilage, femoral cartilage under different Mikulicz lines.

Full size image
Fig. 8
figure 8

Different ROF in different ROI under different Mikulicz lines.

Full size image
Fig. 9
figure 9

Different maximum principal strain in different ROI under different Mikulicz lines.

Full size image

Discussion

Based on a validated normal knee joint three-dimensional finite element model and referencing the state-of-the-art Oxford Third Generation UKA implant, we established a standard knee joint after unilateral single-compartment UKA and created three-dimensional finite element models of UKA with different Mikulicz lines. This was done to investigate the impact of different lower limb alignments on medial UKA. Although the benefits of UKA in terms of postoperative range of motion and preservation of normal functional movement are well recognized, the progression of LCOA, polyethylene liner wear, aseptic loosening, femorotibial instability, periprosthetic fractures, etc., pose challenges to the development of UKA4,30,31.

This article constructs a model of UKA using FEA technology, which includes all bone, meniscus, ligament, and cartilage structures. To simulate the difficult-to-model ligament structure, a hyper-elastic rubber material was used, which better simulates the physiological structure of the knee joint compared to linear or spring ligaments, reproducing the biomechanical changes of the knee joint. Different Mikulicz lines are constructed based on the definition of MAD value, incrementing by 1 mm, centered on the intercondylar eminence of the knee joint, to conduct mechanical analysis. The design scheme can be used to study the effect of different lower limb alignments on medial UKA19,32,33. In this study, we focused on exploring the impact of different lower limb alignments on stress distribution following UKA using FEA. The aim of the research was to reveal trends and patterns in stress distribution, rather than to compare differences between groups, hence statistical analysis was not required. By precisely simulating different alignments of the lower limbs, we were able to directly observe and analyze the distribution of stress across various parts of the knee joint. This understanding allows us to grasp the potential effects of these changes on the outcomes of UKA surgery. This approach enables us to delve into the biomechanical foundations of surgical design and planning without relying on statistical methods to support our findings.

The article presents research findings suggesting that the Mikulicz line has a significant impact on the short- and long-term function of the joint after UKA. As the Mikulicz line moves inward toward the knee joint, the risk of tibial component-related fractures increases, especially when the Mikulicz line extends beyond the medial edge of the tibial plateau. The load in the medial compartment is represented by the adduction moment applied on the knee joint, which is directly proportional to the value of MAD. In other words, MAD is directly proportional to the ROF34,35.Schileod conducted a study and proposed that the maximum principal strain criterion can accurately identify the risk level of failure and the location of fracture in finite element models. The maximum principal strain is directly proportional to the ROF36. Pegg and Stoddart utilized the maximum principal strain criterion to predict the risk of fracture associated with UKA and conducted scientific validation23,24. According to our research findings, when the Mikulicz line is moved from the midpoint of the knee joint to the medial edge of the tibial plateau, the maximum ROF increases by 7.5 times. This increase is particularly significant when + MAD (> 10 mm) is present. These findings suggest that controlling the Mikulicz line within 10 mm inside the midpoint of the knee joint is an important measure to prevent tibial implant fractures in clinical practice. Previous studies have shown that critical strain thresholds for tensile strain exceeding 2500µε and compressive strain exceeding 4000µε may lower bone remodeling capacity, leading to bone degeneration. Additionally, bone strains below 100µε, caused by the stress shielding effect, can induce disuse remodeling and result in bone loss32. When + MAD > 10 mm, a high-strain state has already been reached. Continuing to increase this strain can lead to bone degeneration and accelerate the process. In finite element models where the Mikulicz line is located outside the midpoint of the knee joint, the risk of tibial implant fracture decreases as the Mikulicz line moves further away from the knee joint midpoint, showing a inverse correlation between MAD and ROF. While the risk of tibial implant fracture is reduced, this does not necessarily translate into clinical benefits, as the outward shift of the Mikulicz line causes stress shielding-induced bone loss in the medial tibial region, while also increasing external compartment stress, thus increasing the incidence of lateral compartment osteoarthritis.

The incidence of lateral compartment osteoarthritis is initiated by the degeneration of cartilage and meniscus, and the distribution of forces in the lower limb is one important factor that accelerates this degeneration. In our experiments, as the Mikulicz line moves from the medial edge to the lateral edge of the knee joint, the stress and load on the lateral compartment gradually increase, and the magnitude of this increase is much greater than the reduction in tibial implant fractures. Therefore, it is not advisable to move the Mikulicz line to the lateral side of the knee joint. The lower limb distribution of forces is closely related to the changes in tibial plateau subchondral bone and cartilage. Abnormal distribution of forces can result in stress concentration and an increase in subchondral bone density relative to cartilage, which can lead to further degeneration of cartilage. The further the Mikulicz line deviates from the normal range, the higher the incidence of lateral compartment osteoarthritis37,38. Wen investigated the influence of lower limb alignment on the stress and load distribution of the lateral compartment in UKA through FEA. In the knee joint model with 3 degrees of varus alignment, the contact stress and load percentage in the lateral compartment significantly increased. Specifically, the stress in the femoral cartilage reached 3.45 MPa, while in the tibial cartilage it reached 3.35 MPa10. Similar results were obtained from this study. Once the Mikulicz line exceeds the midpoint of the knee joint and deviates outward, the primary structural stress in the lateral compartment rapidly increases. In a study of 3351 cases of UKA, the average hip-knee-ankle angle at a 4-month follow-up after surgery for cases requiring revision due to progression of lateral compartment osteoarthritis was (− 0.3 ± 3.6°), while the average hip-knee-ankle angle for matched cases without revision was (4.4 ± 2.6°)39,40. In a study on the relationship between lower limb alignment and postoperative failure in UKA, Kim et al. found a significant correlation between postoperative tibiofemoral angle and implant failure rate. The survival rate was highest in the group with 4°-6° of varus alignment in the tibiofemoral angle, but when the varus alignment exceeded 10°, it predicted a lower survival rate13. We know that in UKA, the lower limb alignment is determined by the contact point height between the medial condyle of the femur and the tibial component. This is influenced by factors such as implant design, level of proximal tibial resection, ligament stability, preoperative deformity, implant thickness, and surgical technique40,41. Therefore, it is important to carefully select appropriate implants and perform precise bone resection based on the patient’s preoperative condition and surgical planning in order to achieve the optimal postoperative lower limb alignment as much as possible42.

As implant technology has improved, the wear of PE liners has decreased, but PE liner wear remains an important factor leading to revision surgery after UKA. The stress on the surface of the PE liner is significantly higher than that on the lateral tibial cartilage and meniscus, due to differences in the parameters of cartilage and polyethylene. The elastic modulus of polyethylene is about 60 times that of cartilage, so under the same load conditions, the deformation of PE is much smaller than that of the meniscus and cartilage. According to the law of conservation of energy, cartilage with greater deformation can convert more stress into elastic potential energy, so the stress on the lateral compartment is much lower than that on the polyethylene18,43. In our experiment, when the Mikulicz line is shifted towards the medial side of the knee joint, the Equivalent stress of the PE increases, but the increase is relatively small compared to the increase in stress on the lateral compartment when the Mikulicz line is shifted towards the lateral side of the knee joint. If we only consider the stress variation of the PE and do not consider the manufacturing process of the PE or tibial fractures beneath the tibial implant, it seems reasonable to have the Mikulicz line located on the medial side of the knee joint. However, in reality, we have to consider tibial fractures beneath the tibial implant and the manufacturing process of the PE. Therefore, it is a reasonable choice to position the Mikulicz line 10 mm medially or slightly laterally from the midpoint of the knee joint.

The amount of correction during UKA depends on the size of the deformity and the position of the rotational and angular centers. Intra-articular deformities can be easily corrected through surgical intervention and are ideal indications for UKA. The challenging deformities that are difficult to control are those originating from the metaphysis and outside of the knee joint. These deformities are the key factors influencing the lower limb alignment44. Under the circumstance of significant extra-articular deformity when considering factors such as osteoporosis, bone loss, and high body weight, the decision to perform a total knee replacement instead of a medial UKA should be given priority if the postoperative Mikulicz line is significantly far away from the knee center. To assess the optimal position of the Mikulicz line, the tibial plateau is divided into several regions (0, 1, 2, C, 3, 4, 5) based on the classification by Kennedy and White. The region of the tibial plateau that the line connecting the center of the femoral head and the center of the ankle joint passes through is observed. Good functional recovery and low revision rates can be achieved if the Mikulicz line is located at the center of the knee (region C) or slightly medial to the center (region 2) during follow-up after surgery12,45. Our research has also yielded similar results. When the Mikulicz line is located 10 mm medial to the knee joint center or with a slight deviation to the lateral side of the knee joint center, there is a relatively lower risk of tibial component subsidence, lower lateral compartment stress, and lower implant loading.

However, this research also has some limitations. The FEA is only a computer-simulated, in vitro biomechanical study, which has some differences from in vivo biomechanics. Compared with the complex human knee joint, the model established by the computer is simplified and cannot accurately replicate all the changes that occur in the human knee joint. Nevertheless, the model established in the experiment has been validated to accurately replicate the mechanical changes in the knee joint, and the FEA method allows for quantitative analysis. Therefore, the conclusions from the experiment can still reflect the actual situation to a certain extent.

Conclusion

This study demonstrates that the different limb alignments have a profound impact on the functional outcomes of medial UKA in both the short-term and long-term. When the Mikulicz line is located 10 mm medial to the knee joint center or with a slight deviation to the lateral side of the knee joint center, there is a relatively lower risk of tibial component subsidence, lower lateral compartment stress, and lower implant loading. Therefore, during medial UKA, it is important to use appropriate surgical techniques, including bone resection and implant selection, to optimize the positioning of the Mikulicz line, in order to achieve good functional outcomes with low implant-related complications.