Introduction

Depth maps generated from RGB images provide information about the distance of objects from the camera. Thus, depth estimation plays a fundamental role in computer vision such as 3D reconstruction1, augmented2 reality, autonomous driving3, and robotics4. Monocular depth estimation refers to estimating depth from a single image, which does not require additional complicated equipment and professional techniques. However, it is an ill-posed problem as each two-dimensional image can be projected from an infinite number of different three-dimensional scenes5. Additionally, occlusions, texture loss, and changes in lighting conditions may result in the uncertainty of depth estimation.

The traditional methods of depth estimation from images mainly consist of two steps: manually designed feature extraction and depth information obtained by triangulation6,7. These methods are efficient in some cases, but they are complex and require extensive post-processing, and cannot adapt to complex scenes. Recently, many works have adopted deep learning (DL) techniques to directly regress the depth maps with good performance8,9,10. It is possible to learn complex mapping relationships between image features and depth from large amounts of training images annotated with per-pixel ground-truth depth like KITTI11 and NYU Depth V212.

In deep learning, considering the parameter count and computational efficiency, 3 × 3 or 1 × 1 convolutional kernels are commonly used to extract feature information. However, they exhibit limited capability in extracting global feature information due to the small receptive fields. To obtain a large receptive field, Inception v213 was proposed for single crop evaluation on the ILSVR 2012 classification, in which a 5 × 5 convolutional kernel was replaced by two layers of 3 × 3 convolution. Also, the ASPP module can provide a large receptive field and enhance the extraction of contextual information by employing convolutional kernels with different dilation rates to convolve the image. More importantly, the U-shape network has received the most attention in classification tasks14,15, because the network can construct enriched feature maps by replacing pooling operators with up-sampling operators.

The deeper networks bring challenges such as the vanishing and exploding gradient problems, which were solved until the introduction of the ResNet16, and it was first applied to the encoder for improving feature extraction. Although the framework of the encoder and the decoder has achieved significant progress, the repeated up-sampling operations in the decoding process fail to fully utilize underlying features extracted by the encoder, resulting in the degradation of high-frequency features in the depth map. Moreover, there are inaccurate depth values between object boundaries.

Aiming at above problems, this paper presents the LapUNet for the monocular depth estimation, in which the encoder adopts the ResNeXt10117, and the decoder is constructed with the novel DLRU module. The DLRU module based on the U-shape structure can collect the high-frequency features by fusing dynamic Laplacian residual into the process of upsampling. Moreover, the residual is dynamically learnable due to the addition of convolutional operation after downsampling. Unlike the direct concatenation of the two sides of U-net14, the DLRU module incorporates the dynamic Laplacian residual into U-shape network to capture the entire frequency features. The main contributions of this paper can be summarized as follows:

  1. (1)

    LapUNet based on the framework of the encoder-decoder is proposed for monocular depth estimation, and the decoder is constructed with the novel DLRU module, in which the Laplacian residual is obtained with the U-shape structure rather than simple downsampling and upsampling. Also, learnable parameterized convolutional layers are introduced into the process of Laplacian residuals collection, which enables the Laplacian residuals to adjust their representations for better capturing high frequency features by dynamic learning.

  2. (2)

    The ASPP module is introduced to capture multi-scale contextual information through multi-scale atrous convolutions and global pooling. Additionally, a depth map fusion module is designed to merge features from depth maps at different scales, enabling the final depth map to contain more detailed information.

  3. (3)

    Various experimental results on the KITTI and NYU Depth V2 datasets show that the estimated depth by the proposed method has more object information and clearer edges than other previous works. Especially, the efficiency of the estimated depth maps is further highlighted by the application to 3D reconstruction and target ranging.

The structure of the upcoming paper is outlined as follows: The second section provides an overview of related work in monocular depth estimation. The third section elaborates on the proposed method, including the detailed design of the DLRU module and the depth residual multi-level decoding scheme. The fourth section describes our experimental setup and results analysis. Finally, the fifth section concludes and provides prospects for future work. We believe that our novel approach will contribute significantly to the advancement of research and practical applications in the field of monocular depth estimation.

Related work

Early monocular depth estimation primarily relied on techniques such as image matching and manually designed features. Torralba and Oliva18 proposed to infer the scale and absolute mean depth of a scene by recognizing spectral magnitude properties. Considering the global context of the whole image, Saxena19 proposed the trained Markov random field (MRF) model to infer the depth. Karsch20 used the similarity of spectral coefficients to find the candidate depth and refine the depth with a SIFT flow-based mechanism. In the work21, a high-order conditional random field (CRF) model with field of experts (FoE) is proposed for depth estimation. In22, the cluster-based learning scheme was exploited to select the optimal depth from training samples in a coarse-to-fine manner. However, traditional monocular depth estimation techniques usually require high-contrast scenes, and cannot reconstruct depth in textureless regions. Moreover, they suffer from limited generalization capabilities for non-experimental scenarios and restricted applicability.

With the powerful capability of deep learning for image classification and segmentation, various deep neural networks such as convolutional neural networks (CNNs)5, recurrent neural networks (RNNs)23, variational auto-encoders (VAEs)24 and generative adversarial networks (GANs)25 have been used for monocular depth estimation. For example, Eigen5 firstly proposed a two-stage CNN-based model which predicted the coarse result of the depth image based on the deeply stacked CNN and refined local details by using the second CNN stream. With the relatively good performance of the CNN-based approach for depth estimation in26, various encoder-decoder architectures have been developed. Liu27 proposed a hybrid depth estimation method with the CNN and CRF, which extracted the relevant features from an RGB image through CNN and improved the smoothness and edge preservation of adjacent super pixel blocks by using CRF. Cao28 transformed the depth estimation problem into a pixel-level classification task by use of a deep residual network. On the other hand, Fu29 viewed depth estimation as a regression problem using the ASPP module for encoding features. Aiming to address the difficulty of fully utilizing underlying properties of well-encoded features, Song30 proposed a simple but effective scheme by incorporating the Laplacian pyramid into the decoder architecture. However, the improvement is limited due to the unchanging (static) Laplacian residuals. For more effective guidance of densely encoded features to the desired depth prediction, Lee31 proposed to utilize novel local planar guidance layers located at multiple stages in the decoding phase. To reduce the computation complexity of CRFs optimization, Yuan32 built a bottom-up-top-down structure, where this neural window FC-CRFs (fully-connected CRFs) module served as the decoder, and a vision transformer served as the encoder. To achieve better-generalized performance, Bae et al.33 proposed a self-supervised monocular depth estimation method based on MonoFormer. Lu and Chen34 improved depth estimation accuracy by jointly estimating depth and optical flow in dynamic scenes. Aiming at virtual and real-world water scenes, Lu and Chen35 presented an intra-frame-supervised depth estimation via specular reflection. To learn single-view depth estimation from videos, Gonzalez Bello et al.36 proposed self-supervised monocular depth estimation method based on positional shift depth variance and adaptive disparity quantization. To further improve self-supervised monocular depth estimation, Zhang et al.37 adopted self-reprojection mask, self-statistical mask and self-distillation consistency loss, which can effectively handle anomalous pixels to protect the reprojection and mitigate the ill-posed nature of monocular depth estimation. In the work38, the PROMOTION method was introduced for accurately estimating the depth of an object in motion. To enhance the model’s robustness against real-world disturbances in depth estimation tasks, Cheng et al.39,40 developed a novel technique for synthesizing 2D images that adhere to real-world constraints. Aiming at various motion tasks, ProtoFormer41 was proposed to enhance the understanding of dynamic scenes in depth estimation.

Deep neural networks based on the encoder-decoder architecture have achieved significant success in depth estimation. However, they often lose high-frequency image features due to the inefficient decoding scheme, resulting in blurry artifacts at the depth boundary. To address this issue, we propose the novel DLRU module to construct the decoder for progressively restoring depth boundaries via various scales.

Methods

In this section, we introduce the proposed DLRU module, and then construct the LapUNet based on the encode and decode structure using DLRU modules, and finally describe the loss function.

Dynamic laplacian residual U module

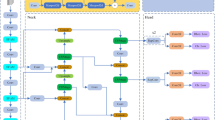
To aggregate multiscale local and global features, the DLRU module is proposed for depth estimation. As shown in Fig. 1, the DLRU module adopts the U-shape structure and consists of 9 convolutional blocks, which are divided into three categories, namely, ordinary convolutional block, downsampling convolutional block and upsampling convolutional block. The DLRU module with depth T (\(T={{1}},2,3,4\)) has T downsampling convolutional blocks, Tupsampling convolutional blocks, and \(9 - 2T\) ordinary convolutional blocks, of which one is located at bottom of the U-shape structure, and the rest are evenly distributed on both sides. The input feature X is transformed to depth features \({D_{T - 1}}, \cdots ,{D_t}, \cdots ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {D_0}\) (\(0 \leqslant t \leqslant T - 1\)) with different resolutions through T downsampling convolutional blocks, and\({D_T}=X\). Similarly, different resolution depth maps \({U_1},{\kern 1pt} {\kern 1pt} \cdots ,{\kern 1pt} {\kern 1pt} {U_t},{\kern 1pt} {\kern 1pt} {\kern 1pt} \cdots ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {U_T}\)(\(1 \leqslant t \leqslant T\)) are output through T upsampling convolutional blocks, and \({U_0}\) is the input of upsampling convolutional blocks.

Fig. 1
figure 1

The structure of the DLRU module.

Full size image

The decoding process usually repeats simple upsampling operations to recover the original resolution. However, this may lead to the loss of high-frequency feature information. Aiming at this problem, dynamic Laplacian residual is introduced into the U-shape structure. Unlike the ordinary Laplacian residual, which is defined as

$${R_t}={D_t} - Up({D_{t - 1}}){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1 \leqslant t \leqslant T$$
(1)

where \({R_t}\) is the Laplacian residual, and \({D_t}\) is obtained by downsampling the original input image to \(1/{2^{T - t}}\), \(Up(\cdot )\) is the upsampling operation. Obviously, the residuals are obtained with simple downsampling and upsampling.

The proposed dynamic Laplacian residual in Fig. 1 is descripted as follows

$${R_t}=\left\{ \begin{gathered} {D_t} - Up({U_{t - 1}}+{R_{t - 1}}){\text{ 2}} \leqslant t \leqslant T \hfill \\ {D_t} - Up({U_0}){\text{ }}t=1{\text{ }} \hfill \\ \end{gathered} \right.$$
(2)

It is worth mentioning that \({D_t}\) in Eq. (2) is obtained with downsampling, convolution, batch normalization, and ReLU activation operations. Hence, the proposed residual \({R_t}\) in Eq. (2) is influenced not only by the features from downsampling and upsampling but also by the upsampled Laplacian residual from the previous layer. Thus, the DLRU module can supplement high-frequency features through the upsampled Laplacian residual from the previous layer. Furthermore, the Laplacian residual is refined through a parametric convolution layer, which helps capture high-frequency features more effectively.

Architecture of LapUNet

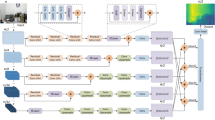
The overall framework of the proposed LapUNet model is illustrated in Fig. 2. The encoder gradually reduces the size of the feature map through convolution and pooling, which can extract high-level abstract features. The decoder progressively recovers back from the high-dimensional features to the low-dimensional space. It merges features from different layers of the encoder with those of the current decoder, refining the feature representation of the decoder.

ResNeXt101-based feature extraction

The encoder adopts the ResNeXt101 network17 with 4 layers due to the good performance in computer vision. The original image with a spatial resolution of H×W is taken as input, and through the stride convolution operation, the spatial resolution of maps is reduced by half in the ResNeXt101 network. Hence, the spatial resolution at each layer is H/2×W/2, H/4×W/4, H/8×W/8, and H/16×W/16, respectively. In addition, the convolutional layer (Conv1) is added into the encoder, and its detailed architecture is shown in Table 1.

Table 1 Detailed architecture of the encoder.
Full size table

Dynamic laplacian residual U-shape (DLRU) decoder with ASPP

The decoder is constructed with DLRU modules, ASPP modules, adaptive depth maps fusion module and convolutional layers, as depicted in Fig. 2. The decoder consists of five layers, namely, level 1, level 2, level 3, level 4 and level 5, and at each level, we use DLRU modules (DLRU-4, DLRU-3, DLRU-2, DLRU-1) and a convolutional block, respectively. As mentioned before, “4”, “3”, “2” and “1” represent the depth of DLRU. It is worth mentioning that the reason for the fifth layer without the DLRU module is that further sampling of these feature maps leads to loss of useful context information due to too small resolution of feature maps. Figure 3 shows the output of each layer, and it is obvious that the depth maps from level 5 to level 2 are progressively restored from coarse to fine scales, and the depth map at level 1 preserves more local details.

Fig. 2
figure 2

The structure of the proposed LapUNet.

Full size image
Fig. 3
figure 3

Depth residuals recovered at each layer of the proposed LapUNet.

Full size image

Rather than resampling, the ASPP module can capture image context at multiple scales by using multiple parallel atrous convolutional layers with different sampling rates. Hence, ASPP modules are introduced to the first and fifth layers. On the one hand, RGB image in the first layer is not fed into the ResNeXt101 network for feature extraction, and thus the feature map is large. To increase the receptive field, an ASPP module is introduced to the first layer. On the other hand, to capture more dense contextual information, we add another ASPP module to the fifth layer.

In the decoding process, the DLRU module fuses the encoded features of the current layer and the output of the DLRU of the previous layer, and depth maps with different spatial resolution can be obtained by DLRU modules (DLRU-4, DLRU-3, DLRU-2, DLRU-1) and a convolutional block. To obtain good quality depth maps, the depth map fusion module, which consists of a concatenation operation and upsampling, is used for combining high and low frequency features from these depth maps with different spatial resolution.

Loss function

Considering that depth information tends to be densely concentrated in close areas and sparsely distributed in distant areas, the scale-invariant mean squared error5 is introduced as loss function, which is defined as

$$L(y,{y^*})=\frac{1}{n}\sum\limits_{{i=1}}^{N} {d_{i}^{2} - \frac{\lambda }{{{n^2}}}(} \sum\limits_{{i=1}}^{N} {{d_i}} {)^2}$$
(3)

where \({d_i}=\log {y_i} - \log y_{i}^{*}\) represents the difference between the estimation \({y_i}\) and ground truth \(y_{i}^{*}\) at pixel i, N denotes the total number of valid pixels, and \(\lambda\) is the balancing factor. Obviously, the higher value of the balancing factor reflects more focusing on minimizing the variance of the error, and the balancing factor is set to 0.85 in our simulation. During the training process, as ground truth is often incomplete (e.g., sparse LiDAR maps used in KITTI), we employ a method of masking invalid points. This means that the loss is computed only for the valid points with ground truth.

Experiments

Dataset

The KITTI and NYU Depth V2 are widely used outdoor and indoor scene datasets for monocular depth estimation. The KITTI dataset contains various road configurations from different driving situations by employing Lidar, and the acquired images have the resolution of 1242 × 375 pixels. According to the split strategy5, 23,488 images from the 32 scenes are selected as the training set, while 697 images from remaining 29 scenes are selected as the testing set. Following the official guidelines of the KITTI dataset, the upper bound of depth is set to 80 m. The NYU Depth V2 dataset includes 120 K pairs of RGB and depth images by using Kinect sensors under 464 different indoor scenes. The resolution of RGB and depth images are 640 × 480 pixels. Also, adopting the same split strategy, we select 20,630 images from 249 scenes for training and 654 images from 215 scenes for testing. To fairly compare our method with other existing methods, RGB and depth images are cropped to the size of 561 × 427.

Comparative experiments

The deep learning model was implemented on the PyTorch framework with an NVIDIA GTX 2080ti GPU. The model is trained for 40 epochs with a batch size of 4 due to the GPU memory limit of single-card training. The Adam W optimizer is employed with an initial learning rate of 0.0001 and a final learning rate of 0.00001. The encoder and decoder have the weight decay factor of 0.0005 and 0, respectively. The momentum is set to 0.90. The ResNeXt101 network for encoding utilizes pre-trained weights based on the ILSVRC dataset42. To enhance the generalization of the model, random horizontal flip with the probability of 0.5 and random rotation between − 5 and 5° are added for data preprocessing during the training. Additionally, a scale factor in the range of (0.9, 1.1) was randomly selected to adjust the brightness, color, and gamma values of input color images.

The proposed model is evaluated on KITTI and NYU Depth V2 datasets from qualitative and quantitative points of view. Figure 4 shows the estimated depth on the KITTI dataset, and it can be seen that the depth maps estimated by our method exhibit higher clarity with fewer artifacts and contain more detailed depth structures with well localized depth edges. Thus, visualization results demonstrate the superiority of the proposed model in capturing edges and details. Especially the areas marked with green and red dashed boxes show significant improvement of the proposed model. For example, the proposed method can effectively capture small objects such as railings and poles on the road, and the estimated depth maps show clear boundaries and rich detail information. In contrast, the estimated depth maps by the other methods are lack of details and edges. Thus, the proposed method provides sharp depth boundaries.

Fig. 4
figure 4

Qualitative depth results on the KITTI dataset.

Full size image

In the case of indoor scene, as depicted in Fig. 5, it can be observed that our proposed model not only has clearer depth edges but also more detailed depth structures. In particular, complex texture variations result in depth variations in previous methods while our method can accurately predict the depth boundaries even with complex object shapes. For example, as shown in the first row of Fig. 5, previous methods in26 and30 were unable to estimate the towel rack, whereas the method proposed in this paper accurately predicted the outline of the towel rack. Moreover, the proposed method demonstrates fine reconstruction of textures, edges, and other complex features in the depth maps of the chair, bookshelf, and sofa.

Fig. 5
figure 5

Qualitative depth results on the NYU Depth V2 dataset.

Full size image

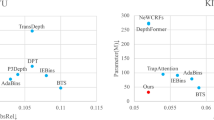
In order to quantitatively analyze the network, we introduced RMSE (root mean squared error), RMSLE (root mean squared logarithmic error), AbsRel (absolute relative error), SqRel (square relative error) and threshold accuracy \(\delta\) as evaluation criteria, and the results are presented in Tables 2 and 3, respectively. It is evident that the proposed method achieved better performance on the two datasets and Lapdepth model by song et al.30 is ranked 2nd compared with previous leading approaches. Almost all errors of our method are reduced by over 5% in comparison with the Lapdepth. Specifically, the RMSE, RMSLE, AbsRel, SqRel of the KITTI dataset are decreased by 8.14%, 6.59%, 6.78%, 5.66%, respectively, and the RMSLE, AbsRel on the NYU Depth V2 dataset are reduced markedly, up to 19.1% and 25.5%, respectively. Also, the results show that the proposed method obtain the best accuracy on the two datasets. Especially the accuracy “\(\delta <1.25\)” on the NYU Depth V2 dataset increases by 4.29%. All this demonstrates the superiority of the proposed method.

Table 2 Quantitative evaluation of the KITTI dataset with various monocular depth estimation methods.
Full size table
Table 3 Quantitative evaluation of the NYU depth V2 dataset with various monocular depth estimation methods.
Full size table

Furthermore, to demonstrate computational efficiency, the model size and single-frame runtime of the proposed method are compared with existing methods. As shown in Table 4, the proposed method has the smallest model size, even slightly outperforming the Lapdepth30. As for the running time, our model is slightly inferior to the Lapdepth and DORN29, but it demonstrates the best performance on KITTI and NYU datasets.

Table 4 The model size and running time.
Full size table

Ablation experiment

To further demonstrate the effectiveness of each key component in the proposed architecture, i.e., the decoder based on the DLRU module and ASPP block, all ablation experiments are conducted on the KITTI dataset by removing a specific component from the proposed framework. The experiment results are presented in Table 5, and some visualization examples of estimated depth maps on KITTI are shown in Fig. 6.

Table 5 Performance analysis of the proposed method on the KITTI dataset with different decoder structures.
Full size table
Fig. 6
figure 6

Comparison results on the KITTI dataset with different decoder structures.

Full size image

Obviously, when the DLRU and ASPP are removed, or the dynamic Laplacian residuals are replaced with traditional Laplacian residuals, the performance of the models deteriorates in terms of these metrics. In particular, the model without the DLRU has large errors compared to the proposed model, and the SqRel is increased by 29%. Also, compared to the model utilizing the traditional Laplacian operator, the proposed model performs well due to the DLRU. In Fig. 6, it can be seen that the depth maps estimated by our model are clearer and more detailed. These results confirm the contributions of both the DLRU and ASPP components. In the reconstruction of the depth maps, the dynamic Laplace residuals is advantageous for restoring both global information and local details of the depth map, and the ASPP plays a positive role in enriching the depth map with more detailed information.

In addition, we conducted a series of benchmark experiments by replacing the ResNeXt101 with four mainstream frameworks (i.e., MobileNetV2, VGG19, ResNet-101, and DenseNet-161) in the case of keeping other settings unchanged. The comparison results are presented in Table 6. As for the model size, the MobileNetV2 is the lightest among all models. The proposed model based on the ResNeXt101 has moderate model size, but has the best performance in terms of the error and accuracy.

Table 6 Performance of the proposed method on the NYU dataset using different encoders.
Full size table

Application

To explore potential applications of the estimated depth maps, we recovered some indoor scenarios by projecting the 2D pixels of the color images into 3D space. Figure 7 shows the estimated depth maps and the projected 3D point clouds from different views. The 3D reconstructions obtained by the proposed approach are close to the scene structure compared to those obtained by Laina et al.26. Obviously, as for our method, the whole structures of indoor scenarios are successfully reconstructed, and the floors, sofas and beds keep flat, which is consistent with real appearance. Instead, these point clouds from the method by Laina et al.26 have more lacks and discontinuities, as shown in the red box of Fig. 7. The 3D comparison results in Fig. 7 further prove the effectiveness of the proposed method.

Fig. 7
figure 7

Visualization of 3D point clouds on the NYU Depth V2 Dataset.

Full size image

To further verify the effectiveness of the proposed method, the estimated relative depth is converted into absolute distance by the mapping relationship between the estimated depth and the true distance. In this simulation, we collect some new outdoor images in the real world and apply the LapUNet model to these unseen images. The estimated depth maps are shown in Fig. 8, where the red points with known actual distance are used for finding the conversion relationship between relative depth and absolute distance, and the green dots are used for testing. For simplicity, linear function is used for depicting the relationship between the relative depth and the absolute distance, namely,

$$D=k\hat {D}+b$$
(4)

where \(\hat {D}\) and D represent the relative depth and the absolute distance, respectively, and k, b are the calibration parameters, whose values are determined using the least squares method.

Fig. 8
figure 8

The RGB images and the estimated depth maps in unseen scenes.

Full size image

Figure 9. shows the fitting curve, we can conclude that most red points are in the straight line, which verifies the effectiveness of linear fitting. Also, the testing points (green points) in Fig. 9 are roughly on the fitted straight line. Moreover, to quantitatively evaluate the effectiveness, the absolute error and relative error of the testing points are shown in Table 7; Fig. 10, and it can be seen that all the estimated distances based on the proposed LapUNet are closest to true distances compared with other methods such as LapDepth30 and Monodepth235. Especially the relative error based on our method is less than 6%, while the maximum relative error based on the other methods are more than 15%. All this verifies the superiority and practicality of the proposed method. It is worth mentioning that the error gradually increases with the increase of measurement distance, which is consistent with theory.

Fig. 9
figure 9

The fitting line between the relative depth and the absolute distance.

Full size image
Fig. 10
figure 10

The mean of absolute and relative errors of the estimated distances with different methods.

Full size image
Table 7 Comparison of predicted results with different methods.
Full size table

Conclusions

In this paper, the LapUNet based on encoder-decoder framework is proposed for monocular depth estimation. In the proposed model, the great innovation is to construct the decoder with the novel DLRU module, which helps the model capture high-frequency features effectively through introducing dynamic Laplacian residual. In addition, the ASPP module and the depth map fusion module are introduced to capture image context and combine high and low frequency features from depth maps with different spatial resolution, respectively. Extensive experiments on KITTI and NYU Depth V2 datasets show that the LapUNet has moderate model size and the best performance in terms of the error and accuracy in comparison with existing methods. Notably, 3D reconstruction and target ranging based on the estimated depth maps further prove the effectiveness of our proposed method. Our model is expected to be applied in the fields of autonomous driving, robotics, and AR/VR systems. However, there remain some limitations to be overcome, such as the speed and the model size. In the future, we will explore some lightweight architectures to improve the speed and decrease the model size.