Data-driven solutions and parameter estimations of a family of higher-order KdV equations based on physics informed neural networks

Abstract

Physics informed neural network (PINN) demonstrates powerful capabilities in solving forward and inverse problems of nonlinear partial differential equations (NLPDEs) through combining data-driven and physical constraints. In this paper, two PINN methods that adopt tanh and sine as activation functions, respectively, are used to study data-driven solutions and parameter estimations of a family of high order KdV equations. Compared to the standard PINN with the tanh activation function, the PINN framework using the sine activation function can effectively learn the single soliton solution, double soliton solution, periodic traveling wave solution, and kink solution of the proposed equations with higher precision. The PINN framework using the sine activation function shows better performance in parameter estimation. In addition, the experiments show that the complexity of the equation influences the accuracy and efficiency of the PINN method. The outcomes of this study are poised to enhance the application of deep learning techniques in solving solutions and modeling of higher-order NLPDEs.

Introduction

Nonlinear partial differential equations (NLPDEs) constitute an important branch of modern mathematics. Many significant problems in natural sciences and engineering can be formulated as the study of nonlinear partial differential equations, both in theoretical research and practical applications. NLPDEs play a crucial role in fields such as mechanics, control processes, ecosystems, economics and finance, chemical cycle systems, and epidemiology. As research progresses, scientists have discovered that nonlinear effects must also be taken into account for some problems previously treated with linear differential equations.

The study of NLPDEs can generally be categorized into three major types: quantitative research, qualitative research, and numerical solution research. Quantitative research aims to find exact analytic solutions of equations with certain scientific significance. Due to the complexity caused by nonlinearity and other factors, there is no universally effective method for the exact analytic solution of NLPDEs. Common methods currently used include inverse scattering transform, Bäcklund transformation, Darboux transformation, Hirota bilinear method, Painlevé finite expansion method, Lie group method, and so on^1,2,3,4,5,6. In recent years, there have been many new and valuable achievements in the field of analytical solutions of NLPDEs^7,8,9,10,11. Qualitative research analyzes the existence, uniqueness, periodic branching, chaos, and other characteristics of the models without obtaining analytic solutions. Numerical solution research, on the other hand, verifies the correctness of theoretical analysis through numerical solutions when no analytical solution is available, making it another important research branch of NLPDEs. Commonly used methods include finite difference methods¹², finite element methods¹³, and spectral methods^14, etc.

In the mid-1980s, the back-propagation algorithm and its development caused the second wave of research in the field of artificial neural networks(ANN)¹⁵. ANN was applied in many fields and showed their powerful capabilities in the last half century^{16,17,18,19,20}. In 1981, a paper published by Rall proposed the automatic differential method²¹, which can use the chain rule to accurately calculate the derivative and can differentiate the entire neural network model according to the input coordinates and network parameters of the neural network, thus replacing the complex gradient calculation in the partial differential equation, and laying the foundation for the solution of the partial differential equation based on artificial neural network. Since the 1990s, scholars began to study the mathematical theories and methods of solving partial differential equations using neural networks and achieved a series of valuable results^{22,23,24,25,26}. The data-driven artificial neural network solving algorithm relies on data labels, leading to some problems such as poor generalization ability. Scholars have begun to explore network frameworks that combine data-driven approaches with the structured prior information implicit in partial differential equations, known as the method of physics-informed constraints. The deep Galerkin method proposed by Sirignamo et al.²⁷ is the first attempt in this direction, and they provide the theorem for neural network approximation under physical constraints. Raissi et al.²⁸ introduced the physics informed neural network (PINN) under physical constraints, combining data-driven and physical constraint methods to address the weak generalization ability of data-driven approaches and proposing a new approach for modeling and solving partial differential equations.

The PINN algorithm has attracted wide attention from researchers since it was proposed^29,30,31. For example, Chen’s team focuses on the local wave phenomenon in nonlinear integrable systems, and they successfully obtained data-driven solutions for local waves using the PINN algorithm^32,33,34. Yan’s team uses the PINN algorithm to study several variants of the nonlinear Schrödinger equation (NLS), including the Hirota equation, and explored the data-driven solutions of these equations and the associated inverse problems^35,36,37. Mishra et al. gave data-driven solutions for some higher-order nonlinear dispersion equations using the PINN algorithm and provided a theoretical analysis of the error estimates of the equations³⁸. Some research on the improvement of the PINN algorithm has also received attention³⁹.

The Korteweg-de Vries (KdV) family of equations is an important NLPDE. The original equation was derived by Korteweg and de Vries in 1895 to describe shallow water waves with long wavelengths and small amplitudes⁴⁰. The KdV equation simulates various important finite amplitude dispersion wave phenomena in nonlinear evolution equations. It is also used to describe some important physical phenomena, such as acoustic waves in harmonic crystals and ion-acoustic waves in plasmas. As research progresses, a batch of new KdV equations has been obtained by modifying and extending the third-order original KdV equation. Additionally, higher-order KdV equations of order 5 and above have appeared in scientific applications and practical problems. These models have been favored by scholars, and researchers in the field of mathematics and physics have carried out in-depth research on these models and obtained a large number of valuable results^{41,42,43,44,45,46,47}.

The main work in this paper is to obtain predictive solutions and predictive parameters of several higher-order KdV equations by constructing a suitable PINN framework and obtaining a reliable network through data training. Previous studies have found that using the sine function as the activation function can solve some problems that exist in PINN with the traditional tanh function, for example, the asymptotic flattening output, and can also improve the convergence speed to a certain extent⁴⁸. Inspired by this, an improvement strategy is proposed to evaluate the performance of the standard PINN, i.e., replacing tanh with sine as activation function in the PINN algorithm. A family of KdV equations, including 5 equations, is studied on two PINN frameworks with sine and tanh activation functions, respectively. Seven distinguishing solutions and six parameters are obtained successfully on the two proposed PINN frameworks, and the experimental results are mainly presented in the form of graphs and tables. Furthermore, we explore the effect of PINN on fitting the solutions and the unknown parameters of NLPDEs based on these experiment results. These results indicate that the sine activation function really has better performance in both predictive solutions and parameter estimation problems. We also analyze the influence of the complexity of equations and solutions on the data-driven problem by the experimental results.

The structure of this paper is as follows: In “Main ideas of the methods” section, we present a detailed description of the PINN algorithm, discussing its application in solving forward and inverse problems of NLPDEs. We also analyze and discuss three different activation functions and account for the details of the computational platform. In “Data-driven solution” section, by comparing the standard PINN algorithm and the PINN algorithm using sine function as activation function, we conduct a comprehensive study on five high-order Korteweg-de Vries (KdV) equations: a three-order KdV equation, a K(2, 2) equation, a mKdV equation, a five-order KdV equation (CDG) and a seven-order KdV equation (Lax’s). In “Data-driven parameter estimation of NLPDEs” section, the PINN algorithm with sine activation function shows its obvious advantage in the inverse problem of the NLPDEs. We also analyzed the possible cause of the special case. Finally, in “Discussion and Conclusion” section, we provide a summary of the work in this paper and give future research directions.

Main ideas of the methods

We discuss the following general form of $(n+1)$ dimensional partial differential equation

$$\begin{aligned} f:=u(x,t)_{t}+\mathscr {N}[u(x,t)],\quad x \in \Omega , \quad t \in [t_0, T], \end{aligned}$$

(1)

together with the initial and boundary conditions

$$\begin{aligned} \mathscr {B}(t_0,u)=u_0, \quad \mathscr {I}(x_1,u)=a, \quad \mathscr {I}(x_2,u)=b, \end{aligned}$$

(2)

where u(x, t) represents the undetermined solution, $\mathscr {N}[\cdot ]$ is a nonlinear differential operator, and $\Omega$ is a subset of $\mathbb {R}^{d}$.

PINN for solving forward and inverse problems of NLPDEs

PINN is a type of neural network whose central idea is to encode a model, such as a PDE, as a component of the neural network itself. A L layers feed-forward neural network consisting of an input layer, L-1 hidden layers, and an output layer is considered, where the lth layer (l= 1,2,... L − 1) has $N_{l}$ neurons. The connection between the two layers is established by a linear transformation $\mathscr {F}_{l }$ and nonlinear activation function $\sigma (\cdot )$, then the input of layer L can be shown as:

$$\begin{aligned} {\alpha }^{[l]}= \sigma ^{[l]}\mathscr {F}_{l }=\sigma ^{[l]}(\textbf{W}^{[l]}{\alpha }^{[l-1]} + \textbf{b}^{[l]}), \quad l=1,2,...,L-1, \end{aligned}$$

(3)

where the input data ${\alpha }^{[0]}= \textbf{x}_0$ is the transpose of the vector $(x_0, t_0)$, ${\alpha }^{[l]}, l=2,3,...L-1$ represents the output of layer l, $\mathscr {F}_{l }=\textbf{W}^{[l]}{\alpha }^{[l-1]} + \textbf{b}^{[l]}$ represents the input of layer l, and the weight matrix $\textbf{W}^{[l]}\in \mathbb {R}^{\textbf{N}_{l }\times \textbf{N}_{l -1}}$ and bias vector $\textbf{b}^{[l]}\in \mathbb {R}^{\textbf{N}_{l }}$ are trainable parameters. Let $\varvec{\theta } = \{\textbf{W}, \textbf{b}\}^{L}_{l=1}$ represents the set of parameters to be learned in all the weight matrices and bias vectors of the network. Therefore, the connection relationship between input $\textbf{x}_0$ and output $u(\textbf{x}_0;\varvec{\theta })$ is

$$\begin{aligned} u(\textbf{x}_0;\varvec{\theta })= \mathscr {F}_{L } \circ \sigma \circ \mathscr {F}_{L -1} \circ \cdot \cdot \cdot \circ \sigma \circ \mathscr {F}_{1}(\textbf{x}_0), \end{aligned}$$

(4)

In “Data-driven solution” section, the standard PINN method and the improved method are used to compare the accuracy and efficiency in solving five KdV equations. The two methods use the hyperbolic tangent ($\tanh$) function and sine function as activation function respectively. The weight matrix and bias vector are initialized by Xavier⁴⁹. The automatic differentiation²¹ is used to find the derivative of u(x, t) with respect to time t and space x. The Adam algorithm⁵⁰ or the L-BFGS-B algorithm⁵¹ is mainly used to update the parameters, and minimize the loss function of the mean square error ($MSE_{pinn-forward}$)

$$\begin{aligned} MSE_{pinn-forward}=MSE_{u}+MSE_{f}, \end{aligned}$$

(5)

where

$$\begin{aligned} MSE_{u}= \frac{1}{N_{u}}\sum _{i=1}^{N_{u}} \left| u(x_{u}^{i}, t_{u}^{i}) - u^{i} \right| ^{2}, \end{aligned}$$

(6)

and

$$\begin{aligned} MSE_{f}= \frac{1}{N_{f}}\sum _{i=1}^{N_{f}} \left| f(x_{f}^{i}, t_{f}^{i}) \right| ^{2}. \end{aligned}$$

(7)

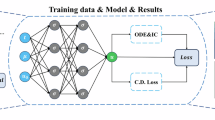
The loss $MSE_{u}$ corresponds to the initial and boundary data while $MSE_{f}$ enforces the structure imposed by Eq. (1) at a finite set of collocation points. $\{x_{u}^{i},t_{u}^{i},u^{i}\}_{i=1}^{N_{u}}$ denote the initial and boundary training data on u(x, t) and $\{x_{f}^{i},t_{f}^{i}\}_{i=1}^{N_{f}}$ specify the collocations points for f(x, t), which are usually obtained by the Latin hypercube sampling⁵² and automatic differentiation techniques, respectively. To clarify the whole procedure of PINN, we state the main steps of PINN in Table 1 and depict the schematic diagram in Fig. 1.

Table 1 PINN algorithm.

On the other hand, for the inverse problem, the parameterized NLPDEs is presented as the general form

$$\begin{aligned} f:=u(x,t)_{t}+\mathscr {N}[u(x,t);\lambda ],x \in \Omega , t \in [0,T], \end{aligned}$$

(8)

where u(x, t) represents the undetermined (or latent) solution, $\mathscr {N}[ \cdot ;\lambda ]$ is a nonlinear operator with unknown parameter $\lambda$ ($\lambda$ is a parameter or a vector consisting of several parameters), and $\Omega$ is a subset of $\mathbb {R}^{d}$. The loss function for the inverse problem of NLPDEs is given by

$$\begin{aligned} MSE_{pinn-inverse}=MSE_{u}+MSE_{f}, \end{aligned}$$

(9)

where

$$\begin{aligned} MSE_{u} = \frac{1}{N}\sum _{i=1}^{N} \left| u(x_{u}^{i}, t_{u}^{i}) - u^{i} \right| ^{2}, \end{aligned}$$

(10)

and

$$\begin{aligned} MSE_{f}= \frac{1}{N}\sum _{i=1}^{N} \left| f(x_{u}^{i}, t_{u}^{i}) \right| ^{2}. \end{aligned}$$

(11)

Here, $\{x_{u}^{i},t_{u}^{i},u^{i}\}_{i=1}^{N}$ is the dataset generated by u(x, t) using the LHS technique in the specified region and used as the training dataset for $MSE_{u}$ and $MSE_{f}$ .The network structure and approaches of every calculation step is same as forward problem.

Fig. 1

Flowchart of PINN.

Activation function

The activation function introduces a nonlinear mapping to the neural network, which enables the neural network to learn and represent more complex functional relationships. In the absence of an activation function, the combination of multiple linear layers still produce only linear transformations, which limits the expressive power of neural networks. Common activation functions include the Sigmoid function, the ReLu function, the Tanh function, etc⁵³. Depending on the specific task and the requirements of the network structure, selecting a suitable activation function can have a significant impact on the performance and effectiveness of the neural network. This section discusses the distinction among the three common activation functions: the Sigmoid function, the Tanh function, and the Sine function.

Sigmoid(x)

The sigmoid function, also known as the Logistic function, is one of the most commonly used activation functions. It is often used in binary classification tasks and non-mutually exclusive multi-category prediction. The sigmoid function has the nice property of mapping the input from negative infinity to positive infinity to a range between 0 and 1. Since the probability values lie exactly between 0 and 1, the sigmoid function is often used in tasks that require the output of probability values. The specific mathematical expression for the function is given in Eq. (12)

$$\begin{aligned} Sigmoid(x) = \frac{1}{1+e^{-x}}, \end{aligned}$$

(12)

from this expression and the image of the function shown in Fig. 2, it is clear that the sigmoid function (abbreviated as S(x)) is continuously smooth and derivable. Its derivative can easily be expressed directly using the function itself without additional calculations,i.e., $S(x)^{'} = S(x)(1-S(x))$. However, as can be seen from the image and the mathematical expression of the derivative, when the function value is close to 0 or 1, the derivative value is close to 0, which leads to the problem of “vanishing gradient.” In deep networks, since the chain rule is essentially a multiplication of derivatives (gradients), when there are one or more small values in the multiplication, the gradient of the entire network approaches 0. This results in the network not being able to learn new knowledge efficiently or learning very slowly.

Tanh(x)

The tanh function and the sigmoid function have similar S-shaped curves, which means that the tanh function may also suffer from the “vanishing gradient” problem when used as an activation function. The mathematical expression of the tanh function is:

$$\begin{aligned} \tanh (x)= \frac{{e^x - e^{-x}}}{{e^x + e^{-x}}}=2Sigmoid(2x)-1. \end{aligned}$$

(13)

It can be observed that the tanh function is a linear transformation and scaling of the sigmoid function. Unlike the sigmoid function, which has a range of (0, 1), the tanh function has a range of $(-1, 1)$. The graph of this function is shown in Fig. 2.

Compared to the sigmoid function, the gradients produced by the tanh function are steeper. According to the chain rule, the derivative of the tanh function is four times the derivative of the sigmoid function. Therefore, when a larger gradient is needed to optimize the model or when there are restrictions on the output range, the tanh function can be chosen as the activation function.

Sin(x)

In standard PINN algorithms, using the tanh activation function and the Xavier initialization strategy can lead to asymptotic flattening of the solution outputs. This flattening of the solution outputs often limits the model’s performance as it tends to get trapped in trivial local minima in many practical scenarios. The sine function ($\sin (x)$) is chosen as the activation function to overcome this problem, for the sine function offers the following advantages:

Overcoming asymptotic flattening output problem: Sigmoid and tanh functions saturate at extreme input values, leading to the vanishing gradient problem and causing the network’s output to flatten. In contrast, using the sine function can maintain relatively smooth outputs throughout the input space and is less prone to saturation. Therefore, using the sine function can effectively overcome the asymptotic flattening output problem and enhance the network’s expressive power.

Symmetry: The sine function is symmetrical at the origin, i.e., $\sin (-x) = -\sin (x)$. This symmetry enhances the stability and symmetry of the neural network model. It helps the model respond similarly to positive and negative input values, reducing model asymmetry and further improving the model’s expressive power.

Improved optimization and convergence speed: The sine function is a continuously differentiable function with smooth properties. This allows the sine activation function to better propagate gradients during the training process, facilitating information flow and optimization convergence. Compared to some discontinuous or non-differentiable activation functions, the smoothness of the sine function makes the network easier to learn and adjust parameters, accelerating the optimization process and improving the model’s training efficiency and performance.

Increased nonlinear fitting capability: The sine function is a nonlinear function, introducing the sine activation function adds richer nonlinear features and increases the neural network’s representation capacity. This is important for solving problems with complex nonlinear relationships, such as image, audio, or time-series data analysis. The periodic nature of the sine function allows it to better capture periodic patterns or variations in the data, further enhancing the model’s fitting capability.

Fig. 2

The images of three activation functions and their derivatives.

In conclusion, using the sine function as the activation function offers advantages such as overcoming asymptotic flattening output, periodicity, symmetry, and increased nonlinear fitting capability. These characteristics enable the sine activation function to improve the performance of models in solving real-world problems and avoid getting stuck in trivial local minima.

Error reduction rate

When examining the differences in prediction accuracy between the PINN with the sine function and the standard PINN, a metric noted as ’the Error Reduction Rate (ERR)’⁵⁴ is adopted. The ERR is designed to quantify the improvement in prediction precision that a method offers over another method. ERR is a dimensionless quantity that indicates the percentage reduction in relative error when using a method compared to another method. Specifically, the formula for calculating the ERR is as follows:

$$\begin{aligned} {ERR:=\frac{Re_{1}-Re_{2}}{Re_{1}}}. \end{aligned}$$

(14)

In this paper, $Re_{1}$ represents the relative error of the results obtained by the standard PINN, and $Re_{2}$ represents the relative error of the results obtained by the PINN with the sine function. A positive ERR value indicates that the sine function has improved the prediction accuracy, with higher values signifying greater improvements. With this measure, the effectiveness of the ’Sine’ activation function in enhancing PINN’s predictive power can be evaluated more accurately.

Details of the computational platform

In order to ensure the reliability and comparability of experimental results, all experiments were conducted in one experimental environment. We give the specific information of the computing platform to provide a reference for readers to do related research or reproduce the experiments in this paper. All the experiments in this article were completed on a Lenovo computer with an Intel(R) Core(TM) i5-8250U CPU @ 1.60GHz 1.80 GHz processor and 8.00 memory. The environment in which the codes are written and run is based on Python 3.6 and TensorFlow 1.14.

Data-driven solution

In this paper, we consider the following $(1+1)$-dimensional NLPDE:

$$\begin{aligned} u_{t}+\mathscr {N}(u, u_x,u_{xx},u_{xxx},... )=0, \end{aligned}$$

(15)

where the subscripts denote the partial derivatives, e.g., $u_t = \frac{\partial u}{\partial t}$, $\partial _x = \frac{\partial }{\partial x}$, $\partial _{xx} = \frac{\partial ^2}{\partial x^{2}}$. $\mathscr {N}(u, u_x , u_{xx}, u_{xxx}, . . .)$ is some nonlinear function of related variables such that Eq. (15) contains many famous nonlinear dispersion equations. In this paper, we focus on the following five equations:

• (1) The third-order dispersion KdV equation^55,56

  $$\begin{aligned} u_{t}+ auu_x +bu_{xxx}=0, \end{aligned}$$

  (16)

  where a denotes the strength of the nonlinear term or the magnitude of the interaction force. In nonlinear fluctuations, the term describes wave interactions and nonlinear correction effects. b denotes the strength of the dispersion term.

• (2) The mKdV equation^57,58

  $$\begin{aligned} u_{t}+a u^2 u_x + u_{xxx}=0, \end{aligned}$$

  (17)

  where a is the free parameter. Eq. (17) can be used as an isolated sub-model for describing the multiplicity of plasma and phonon interactions in a non-tonal lattice, and is generally referred to by researchers as the modified KdV equation.

• (3) The general K(2, 2) equation⁵⁹

  $$\begin{aligned} u_{t}+a (u^2)_x + (u^2)_{xxx}=0, \end{aligned}$$

  (18)

  where a is a parameter indicating the strength or force of the nonlinear term. Eq. (18) is also known as the two-dimensional KdV equation of the second kind.

• (4) The fifth-order Caudrey-Dodd-Gibbon (CDG) equation⁶⁰

  $$\begin{aligned} u_{t}+ au^2 u_x + bu_x u_{xx} + cu u_{xxx} + u_{xxxxx}=0, \end{aligned}$$

  (19)

  where a, b, c are arbitrary non-zero constants and $u_{xxx},u_{xxxxx}$ denote dispersion terms. Eq. (19) is a generalized fifth order dispersion KdV studied primordially by Caudrey et al^61,62.

• (5) The seventh-order KdV equation(Lax’s equation)⁶³

  $$\begin{aligned} u_{t}+ (35u^4+70(u^2u_{xx}+uu^2_{x})+7(2uu_{xxxx}+3u^2_{xx}+4u_xu_{xxx})+u_{xxxxxx})_x =0. \end{aligned}$$

  (20)

  It was introduced by Pomeau et al., in order to discuss the stability of the structure of KdV equations in cases of abnormal disorder⁶⁴.

In this section, we use the PINN algorithm to learn the solutions of the higher-order KdV equations described above. A 5-layer feed-forward neural network (4 hidden layers of 20 neurons each) is constructed, using tanh and sine functions as the activation functions for comparison. The L-BFGS-B algorithm is adopted to optimize the loss function and use the relative $\mathbb {L}_{2}$ norm to measure the norm error in the solution predictions. In addition, each equation has the same number of randomly selected points $N_{u}$ at the initial boundaries and the same number of randomly selected configuration points $N_{f}$ in the space-time domain.

The KdV equation

The general expression for the KdV equation is shown in Eq. (16). In this paper we consider only the parameters are $a = -6$, $b=1$^55,56, then the equation is

$$\begin{aligned} u_{t}-6uu_x + u_{xxx}=0. \end{aligned}$$

(21)

The single soliton and double soliton solutions are discussed separately in this subsection.

Case 1

In⁵⁵, the authors used the sine-cosine method to obtain a single soliton solution of Eq. (21), and the expression was given as follows:

$$\begin{aligned} u(x,t)=-2sech^2(x-4t). \end{aligned}$$

(22)

The initial value and boundary value conditions are considered as

$$\begin{aligned} {\begin{matrix} u(x,-2)=-2sech^2(x+8), \quad x\in [-2,2],\\ u(-2,t)=-2sech^2(-2-4t), \quad t\in [-2,2],\\ u(2,t)=-2sech^2(2-4t), \quad t\in [-2,2]. \end{matrix}} \end{aligned}$$

(23)

The residual term of Eq. (21) is:

$$\begin{aligned} f:=u_{t}-6uu_x + u_{xxx}. \end{aligned}$$

(24)

To obtain the training dataset, we divide the spatial region $x\in [-2,2]$ and the temporal region $t\in [-2,2]$ into $N_{x}=512$ and $N_{t}=512$ discrete equidistant points, respectively. Thus, the training dataset is the discrete 262,144 points in the given spatio-temporal domain [− 2,2]$\times$[− 2,2]. The training data used for the loss function(MSE) consists of $N_{u}=120$ points randomly selected from the initial boundary data and $N_{f}=10000$ points randomly selected from the spatio-temporal domain(The following positive problem generates training data in the same way as here and will not be redefined). The experiment results are illustrated in Figs. 3, 4, 5 and 6.

The top panel of Fig. 3 shows the heat map predicted by the PINN algorithm with sine function. The left of the bottom of Fig. 3 shows the more specific comparison between the exact solution and the prediction solution at four different times t = − 0.5, − 0.25, 0.25, and 0.5, and the spatiotemporal dynamics behavior of the prediction single soliton solution of the Eq. (21) is shown on the right. The spatiotemporal dynamics of the exact single soliton solution of the Eq. (21) is shown in Fig. 4 for comparison.

Figure 5 shows the error dynamics between the exact soliton solution and the predictive solution learned by the PINN algorithm with the sine function. Figure 6 illustrates the loss curve in the process of solving the single soliton solution.

Fig. 3

The dynamical evolution of the predictive single soliton solution of the Eq. (21).

Fig. 4

The exact single soliton solution of the Eq. (21).

Fig. 5

Error dynamics.

Fig. 6

Loss curve.

As shown in Table 2, the PINN method with the sine activation function can improve the accuracy of the prediction solution. The relative $\mathbb {L}_{2}$ error of size $1.62\times 10^{-4}$ is reached when the model runs for about 73 seconds.

Table 2 KdV equation: $\mathbb {L}_{2}$ relative error and time cost of PINN(tanh) and PINN(sine).

Case 2

In this subsection, we focus on the double soliton solution of Eq. (21). The expression is as follows⁵⁶

$$\begin{aligned} u(x,t)=-12\frac{3+4\cosh 2(x-4t)+\cosh 4(x-16t)}{[3\cosh (x-28t)+\cosh 3(x-12t)]^2}. \end{aligned}$$

(25)

The initial value and boundary value conditions are considered as

$$\begin{aligned} u(x, - 2) & = - 12\frac{{3 + 4\cosh 2(x + 8) + \cosh 4(x + 32)}}{{[3\cosh (x + 56) + \cosh 3(x + 24)]^{2} }},\quad x \in [ - 2,2], \\ u( - 2,t) & = - 12\frac{{3 + 4\cosh 2( - 2 - 4t) + \cosh 4( - 2 - 16t)}}{{[3\cosh ( - 2 - 28t) + \cosh 3( - 2 - 12t)]^{2} }},\quad t \in [ - 2,2], \\ u(2,t) & = - 12\frac{{3 + 4\cosh 2(2 - 4t) + \cosh 4(2 - 16t)}}{{[3\cosh (2 - 28t) + \cosh 3(2 - 12t)]^{2} }},\quad t \in [ - 2,2]. \\ \end{aligned}$$

(26)

The residual term is same as Case 1, we omit it.

The experiment results are illustrated in Figs. 7, 8, 9 and 10.

Fig. 7

The dynamical evolution of the predictive double soliton solution of the Eq. (21).

Fig. 8

The exact double soliton solution of the Eq. (21).

The top panel of Fig. 7 shows the heat map predicted by the PINN algorithm with the sine function. The left of the bottom of Fig. 7 shows the more specific comparison between the exact solution and the prediction solution at four different times $t=-0.25, -0.05, 0.05, 0.25$, and the spatiotemporal dynamics behavior of the prediction double soliton solution of the Eq. (21) is shown on the right. The spatiotemporal dynamics of the exact double soliton solution of the Eq. (21) is shown in Fig. 8 for comparison.

Figure 9 shows the error dynamics between the exact soliton solution and the predictive solution learned by the PINN algorithm with the sine function. Figure 10 illustrates the loss curve in the process of solving the prediction double soliton solution.

Fig. 9

Error dynamics.

Fig. 10

Loss curve.

As shown in Table 3, the PINN method with the sine activation function can improve the accuracy of the prediction solution. The relative $\mathbb {L}_{2}$ error of size $9.65\times 10^{-3}$ is reached when the model runs for about 679 seconds.

Table 3 KdV equation: $\mathbb {L}_{2}$ relative error and time cost of PINN(tanh) and PINN(sine).

mKdV equation

We investigate the mKdV equation Eq. (17) in this subsection.

Case 1

When $a=6$, Eq. (17) is

$$\begin{aligned} u_{t}+6 u^2 u_x + u_{xxx}=0. \end{aligned}$$

(27)

An solitary wave solution of the Eq. (27) is obtained in⁵⁷:

$$\begin{aligned} u(x,t)=sech(x-t), \end{aligned}$$

(28)

and the initial value and boundary value conditions are

$$\begin{aligned} {\begin{matrix} u\left( x,-4\right) =sech(x+4), \quad x\in \left[ -4,4\right] ,\\ u\left( -4,t\right) =sech(-4-t), \quad t\in \left[ -4,4\right] ,\\ u\left( 4,t\right) =sech(4-t), \quad t\in \left[ -4,4\right] . \end{matrix}} \end{aligned}$$

(29)

The residual term can be obtained by Eq. (27), we omit it. The experiment results are illustrated in Figs. 11, 12, 13 and 14:

Fig. 11

The dynamical evolution of the predictive solitary wave solution of the Eq. (27).

Fig. 12

The exact solitary wave solution of the Eq. (27).

Fig. 13

Error dynamics.

Fig. 14

Loss Curve.

The top panel of Fig. 11 shows the heat map predicted by the PINN algorithm with the sine function. The left of the bottom of Fig. 11 shows the more specific comparison between the exact solution and the prediction solution at four different times $t=-2, -1, 1, 2$, and the spatiotemporal dynamics behavior of the prediction solitary wave solution of the Eq. (27) is shown on the right. The spatiotemporal dynamics of the exact solitary wave solution of the Eq. (27) is shown in Fig. 12 for comparison.

Figure 13 shows the error dynamics between the exact soliton solution and the predictive solution learned by the PINN algorithm with the sine function. Figure 14 illustrates the loss curve in the process of solving the solitary wave solution.

As shown in Table 4, the PINN method with the sine activation function can improve the accuracy of the prediction solution. The relative $\mathbb {L}_{2}$ error of size $9.44\times 10^{-4}$ is reached when the model runs for about 11 seconds.

Table 4 MKdV equation: $\mathbb {L}_{2}$ relative error and time cost of PINN(tanh) and PINN(sine).

Case 2

When $a=-6$, Eq. (17) is

$$\begin{aligned} u_{t}-6 u^2 u_x + u_{xxx}=0. \end{aligned}$$

(30)

A kink solution of the Eq. (30) is obtained in⁵⁸:

$$\begin{aligned} u(x,t)=\tanh (x+2t), \end{aligned}$$

(31)

and the initial value and boundary value conditions is

$$\begin{aligned} {\begin{matrix} u\left( x,-4\right) =\tanh (x-8), \quad x\in \left[ -4,4\right] ,\\ u\left( -4,t\right) =\tanh (-4+2t), \quad t\in \left[ -4,4\right] ,\\ u\left( 4,t\right) =\tanh (4+2t), \quad t\in \left[ -4,4\right] . \end{matrix}} \end{aligned}$$

(32)

The residual term can be obtained by Eq. (30). The experiment results are illustrated in Figs. 15, 16, 17 and 18:

Fig. 15

The dynamical evolution of the predictive kink solution of the Eq. (30).

Fig. 16

The exact kink solution of the Eq. (30).

Fig. 17

Error dynamics.

Fig. 18

Loss Curve.

The top panel of Fig. 15 shows the heat map predicted by the PINN algorithm with the sine function. The left of the bottom of Fig. 15 shows the more specific comparison between the exact solution and the prediction solution at four different times $t=-2, -1, 1, 2$, and the spatiotemporal dynamics behavior of the prediction kink solution of the Eq. (30) is shown on the right. The spatiotemporal dynamics of the exact kink solution of the Eq. (30) is shown in Fig. 16 for comparison.

Figure 17 shows the error dynamics between the exact kink solution and the prediction solution learned by the PINN algorithm with the sine function. Figure 18 illustrates the loss curve in the process of solving the kink solution.

As shown in Table 5, the PINN method with the sine activation function can improve the accuracy of the prediction solution. The relative $\mathbb {L}_{2}$ error of size $1.33\times 10^{-4}$ is reached when the model runs for about 7 seconds.

Table 5 MKdV equation: $\mathbb {L}_{2}$ relative error and time cost of PINN(tanh) and PINN(sine).

The K(2, 2) equation

We consider the following specific form of the K(2, 2) equation when $a=1$:

$$\begin{aligned} u_{t}+(u^2)_x + (u^2)_{xxx}=0{.} \end{aligned}$$

(33)

In this section, we focus on the period travelling wave solution of Eq. (33). Through the travelling wave transformation method, the period travelling wave solution of the Eq. (33) is obtained in⁵⁹:

$$\begin{aligned} u(x,t)= \frac{2c}{3a}+\frac{\sqrt{4c^2+18ag}}{3a}\sin \frac{\sqrt{a}(x-ct-c_1)}{2}, \end{aligned}$$

(34)

where c is wave velocity, g and c1 are integral constants. In⁵⁹, the parameters are selected as $c = 2, c_1=1, g=3$, then the initial value and boundary value conditions for the Eq. (33) are

$$\begin{aligned} u\left( {x, - 20} \right) & = \frac{4}{3} + \frac{{\sqrt {70} }}{3}\sin \frac{{x + 39}}{2},\quad x \in \left[ { - 4,4} \right], \\ u\left( { - 4,t} \right) & = \frac{4}{3} + \frac{{\sqrt {70} }}{3}\sin \frac{{ - 2t - 5}}{2},\quad t \in \left[ { - 20,20} \right], \\ u\left( {4,t} \right) & = \frac{4}{3} + \frac{{\sqrt {70} }}{3}\sin \frac{{3 - 2t}}{2},\quad t \in \left[ { - 20,20} \right]. \\ \end{aligned}$$

(35)

The residual term can be obtained by Eq. (33), we omit it. The experiment results are illustrated in Figs. 19, 20, 21 and 22:

Fig. 19

The dynamical evolution of the predictive periodic travelling solution of the Eq. (33).

Fig. 20

The exact periodic travelling wave solution of the Eq. (33).

The top panel of Fig. 19 shows the heat map predicted by the PINN algorithm with the sine function. The left bottom of Fig. 19 shows the more specific comparison between the exact solution and the prediction solution at four different spaces $x=-2, -1, 1, 2$, and the spatiotemporal dynamics behavior of the prediction periodic traveling wave solution of the Eq. (33) is shown on the right. The spatiotemporal dynamics of the exact periodic traveling wave solution of the Eq. (33) is shown in Fig. 20 for comparison.

Figure 21 shows the error dynamics between the exact solution and the predictive solution learned by the PINN algorithm with the sine function. Figure 22 illustrates the loss curve in the process of solving the periodic traveling wave solution.

Fig. 21

Error dynamics.

Fig. 22

Loss curve.

As shown in Table 6, the PINN method with the sine activation function can improve the accuracy of the prediction solution. The relative $\mathbb {L}_{2}$ error of size $5.83\times 10^{-4}$ is reached when the model runs for about 93 seconds.

Table 6 K(2, 2) equation: $\mathbb {L}_{2}$ relative error and time cost of PINN(tanh) and PINN(sine).

The CDG equation

When $a=180$, $b=30$, $c=30$, the CDG equation⁶⁰ is

$$\begin{aligned} u_{t}+180 u^2 u_x + 30 u_x u_{xx} + 30 u u_{xxx} + u_{xxxxx}=0. \end{aligned}$$

(36)

Zhou et al obtained the solitary wave solution of the Eq. (36) by using the Sine-Cosine expansion method⁶⁰ as follows:

$$\begin{aligned} u(x,t)=\frac{1}{4}sech^2[\frac{1}{2}(x-t)], \end{aligned}$$

(37)

and the initial value and boundary value conditions is

$$\begin{aligned} u\left( {x, - 2} \right) & = \frac{1}{4}sech^{2} \left[\frac{1}{2}(x + 2)\right],\quad x \in \left[ { - 10,10} \right], \\ u\left( { - 10,t} \right) & = \frac{1}{4}sech^{2} \left[\frac{1}{2}( - 10 - t)\right],\quad t \in \left[ { - 2,2} \right], \\ u\left( {10,t} \right) & = \frac{1}{4}sech^{2} \left[\frac{1}{2}(10 - t)\right],\quad t \in \left[ { - 2,2} \right]. \\ \end{aligned}$$

(38)

The residual term can be obtained by Eq. (36), we omit it. The experiment results are illustrated in Figs. 23, 24, 25 and 26:

Fig. 23

The dynamical evolution of the predictive solitary wave solution of the Eq. (36).

Fig. 24

The exact solitary wave solution of the Eq. (36).

Fig. 25

Error dynamics.

Fig. 26

Loss curve.

The top panel of Fig. 23 shows the heat map predicted by the PINN algorithm with the sine function. The left of the bottom of Fig. 23 shows the more specific comparison between the exact solution and the prediction solution at four different times $t=-1, -0.5, 0.5, 1$, and the spatiotemporal dynamics behavior of the prediction solitary wave solution of the Eq. (36) is shown on the right. The spatiotemporal dynamics of the exact solitary wave solution of the Eq. (36) is shown in Fig. 24 for comparison.

Figure 25 shows the error dynamics between the exact solution and the predictive solution learned by the PINN algorithm with the sine function. Figure 26 illustrates the loss curve in the process of solving the solitary wave solution.

As shown in Table 7, the PINN method with the sine activation function can improve the accuracy of the prediction solution. The relative $\mathbb {L}_{2}$ error of size $1.25\times 10^{-2}$ is reached when the model runs for about 312 seconds.

Table 7 CDG equation: $\mathbb {L}_{2}$ relative error and time cost of PINN(tanh) and PINN(sine).

The Lax’s equation

We discuss the following solitary wave solution⁶³ to Eq. (20)

$$\begin{aligned} u(x,t)=\frac{1}{2}sech^2[\frac{1}{2}(x-t)]. \end{aligned}$$

(39)

The initial value and boundary value conditions for the Eq. (20) is

$$\begin{aligned} u\left( {x, - 4} \right) & = \frac{1}{2}sech^{2} \left[ {\frac{1}{2}(x + 4)} \right],\quad x \in [ - 5,5] \\ u\left( { - 10,t} \right) & = \frac{1}{4}sech^{2} \left[ {\frac{1}{2}( - 10 - t)} \right],\quad t \in \left[ { - 2,2} \right], \\ u\left( {10,t} \right) & = \frac{1}{4}sech^{2} \left[ {\frac{1}{2}(10 - t)} \right],\quad t \in \left[ { - 2,2} \right]. \\ \end{aligned}$$

(40)

The residual term can be obtained by Eq. (20), we omit it. The experiment results are illustrated in Figure 27, 28, 29 and 30:

Fig. 27

The dynamical evolution of the predictive solitary wave solution of the Lax’s equation.

Fig. 28

The exact solitary wave solution of the Lax’s equation.

Fig. 29

Error dynamics.

Fig. 30

Loss curve.

The top panel of Fig. 27 shows the heat map predicted by the PINN algorithm with the sine function. The left of the bottom of Fig. 27 shows the more specific comparison between the exact solution and the prediction solution at four different times $t=-2, -1, 1, 2$, and the spatiotemporal dynamics behavior of the prediction solitary wave solution of Eq. (20) is shown on the right. The spatiotemporal dynamics of the exact solitary wave solution (39) is shown in Fig. 28 for comparison.

Figure 29 shows the error dynamics between the exact solution and the predictive solution learned by the PINN algorithm with the sine function. Figure 30 illustrates the loss curve in the process of solving the solitary wave solution.

As shown in Table 8, the PINN method with the sine activation function can improve the accuracy of the prediction solution. The relative $\mathbb {L}_{2}$ error of size $1.10\times 10^{-3}$ is reached when the model runs for about 3961 seconds.

Table 8 Lax equation: $\mathbb {L}_{2}$ relative error and time cost of PINN (tanh) and PINN(sine).

Under a fixed framework (4 hidden layers and 20 neurons each), 7 different solutions of 5 equations are learned successfully by the PINN method. Tanh and sine as activation functions are used in the PINN method, respectively, aiming to explore the influence of different activation functions on the accuracy and efficiency of learning results. Experiments show that in the problem of learning the solution of the KdV equation family, the sine function can improve the accuracy, but the degree of improvement is not very obvious; especially in the case of simple solution forms (kink solution, single soliton solution), the original PINN (tanh) can obtain an acceptable learning effect. When the form of the solution is more complex (double soliton solution, periodic solution), the PINN framework using sine as the activation function can improve the accuracy by 1 order of magnitude.

The experiment also shows that the more complex the form of the differential equation, such as higher order differential terms, more nonlinear terms, are obvious factors that affect the learning accuracy and efficiency. We can see that both the five-order and seven-order equations are less accurate than the third-order equations, and the time required increases sharply with the complexity of the equations.

Data-driven parameter estimation of NLPDEs

In this section, the PINN method with tanh and sine as activation functions, respectively, is used to study the inverse problem of nonlinear partial differential equations: that is, to learn the unknown parameters of the above five KdV equations. In order to obtain the estimated parameters and investigate the effects of the activation functions, all examples in this section continue to use the same structural framework: 3 hidden layers with 20 neurons each. The L-BFGS-B algorithm is used to optimize the loss function, the relative $\mathbb {L}_{2}$ norm is used to measure the error between the predicted and actual, and the Latin hypercubic sampling method is used to get the training dataset N.

Data-driven parameter estimation in the KdV equation

We consider the following three-order KdV equation with an unknown real-valued parameter $\alpha$:

$$\begin{aligned} u_{t}-6 uu_{x}+\alpha u_{xxx}=0, \end{aligned}$$

(41)

then the residual term is

$$\begin{aligned} f_{KdV}:=u_{t}-6uu_{x}+\alpha u_{xxx}. \end{aligned}$$

(42)

The PINN algorithm learns u(x, t) and the parameter $\alpha$ by minimizing the mean square error loss

$$\begin{aligned} MSE=\frac{1}{N}\sum _{i=1}^{N} \left| u(x_{u}^{i}, t_{u}^{i}) - u^{i} \right| ^{2} + \frac{1}{N}\sum _{i=1}^{N} \left| f_{KdV}(x_{u}^{i}, t_{u}^{i}) \right| ^{2}, \end{aligned}$$

(43)

where $\{x_{u}^{i},t_{u}^{i},u^{i}\}_{i=1}^{N}$ represents the training data come from the exact double soliton solution of Eq. (41) with $\alpha =1$ and $(x,t)\in [-2,2]\times [-2,2]$:

$$\begin{aligned} u(x,t)= -12\frac{3+4\cosh 2(x-4t)+\cosh 4(x-16t)}{[3\cosh (x-28t)+\cosh 3(x-12t)]^2}. \end{aligned}$$

The spatial region $x\in [-2,2]$ and the temporal region $t\in [-2,2]$ are divided into $N_{x}=512$ and $N_{t}=512$ discrete equidistant points, respectively. Thus, the dataset is a discrete set of 262144 points in the given time-space region [-2,2]$\times$[-2,2]. We use Latin hypercubic sampling to select $N=40000$ points out of the 262144 points in $(x, t)\in [-2, 2]\times [-2, 2]$ as the training dataset. (The training data used in the following four subsections are generated in the same way as here and are omitted.)

Table 9 shows the performance comparison between the PINN algorithm with the sine function and the standard PINN algorithm to solve the double soliton solution and the parameter $\alpha$ of the Eq. (41). It can be easily found from Table 9 that the performance of the PINN algorithm with the sine function is better than the standard PINN algorithm in both the accuracy of learning solutions and the accuracy of identifying unknown parameter $\alpha$.

Table 9 Performance comparison of the predictive solution and predictive parameter of Eq. (41).

Data-driven parameter estimation in the mKdV equation

We consider the following three-order mKdV equation with an unknown real-valued parameter $\alpha$:

$$\begin{aligned} u_{t}-6 u^2 u_x + \alpha u_{xxx}=0, \end{aligned}$$

(44)

then the residual term is

$$\begin{aligned} f_{mKdV}:=u_{t}-6 u^2 u_x + \alpha u_{xxx}. \end{aligned}$$

(45)

The PINN algorithm learns u(x, t) and the parameter $\alpha$ by minimizing the mean square error loss

$$\begin{aligned} MSE=\frac{1}{N}\sum _{i=1}^{N} \left| u(x_{u}^{i}, t_{u}^{i}) - u^{i} \right| ^{2} + \frac{1}{N}\sum _{i=1}^{N} \left| f_{mKdV}(x_{u}^{i}, t_{u}^{i}) \right| ^{2}, \end{aligned}$$

(46)

where $\{x_{u}^{i},t_{u}^{i},u^{i}\}_{i=1}^{N}$ represents the training data on the exact kink solution of Eq. (44) with $\alpha =1$, and $(x,t)\in [-4,4]\times [-4,4]$:

$$\begin{aligned} u(x,t)=\tanh (x+2t). \end{aligned}$$

Table 10 shows the performance comparison between the PINN algorithm with the sine function and the standard PINN algorithm to learn the parameter $\alpha$ of the Eq. (44). It is obvious that the performance of the PINN algorithm with the sine activation function is better than the standard PINN algorithm in the accuracy of the learning solution. However, the accuracies of the values of unknown parameter $\alpha$ obtained by the two methods is very high, and there are no obvious difference.

Table 10 Performance comparison of the predictive solution and predictive parameter of Eq. (44).

Data-driven parameter estimation in the K(2, 2) equation

We consider the following K(2, 2) equation with two unknown real-valued parameter $\alpha$ and $\beta$:

$$\begin{aligned} u_{t}+\alpha (u^2)_x + \beta (u^2)_{xxx}=0, \end{aligned}$$

(47)

then the residual term is

$$\begin{aligned} f_{K(2,2)}:=u_{t}+\alpha (u^2)_x + \beta (u^2)_{xxx}. \end{aligned}$$

(48)

The PINN algorithm learns u(x, t) and the parameter $\alpha$ and $\beta$ by minimizing the mean square error loss

$$\begin{aligned} MSE=\frac{1}{N}\sum _{i=1}^{N} \left| u(x_{u}^{i}, t_{u}^{i}) - u^{i} \right| ^{2} + \frac{1}{N}\sum _{i=1}^{N} \left| f_{K(2,2)}(x_{u}^{i}, t_{u}^{i}) \right| ^{2}, \end{aligned}$$

(49)

where $\{x_{u}^{i},t_{u}^{i},u^{i}\}_{i=1}^{N}$ represents the training data which comes from the exact double soliton solution of Eq. (47) with $\alpha =1$ and $\beta =1$, in $(x,t)\in [-4,4]\times [-20,20]$:

$$\begin{aligned} u(x,t)= \frac{4}{3}+\frac{\sqrt{70}}{3}\sin \frac{\left( x-2t-1\right) }{2}. \end{aligned}$$

Table 11 shows the performance comparison between the PINN algorithm with the sine function and the standard PINN algorithm to solve the unknown parameters $\alpha$ and $\beta$ of the K(2,2) equation. It can be easily found from Table 11 that the performance of the PINN algorithm with the sine function is better in both the accuracy of learning solutions and the accuracy of identifying unknown parameters $\alpha$ and $\beta$.

Table 11 Performance comparison of the predictive solution and predictive parameter of Eq. (47).

Data-driven parameter estimation in the CDG equation

In this section, we consider the CDG equation with an unknown parameter $\alpha$:

$$\begin{aligned} u_{t}+180 u^2 u_x + 30 u_x u_{xx} + \alpha u u_{xxx} + u_{xxxxx}=0, \end{aligned}$$

(50)

then the residual term is

$$\begin{aligned} f_{CDG}:=u_{t}+180 u^2 u_x + 30 u_x u_{xx} + \alpha u u_{xxx} + u_{xxxxx}. \end{aligned}$$

(51)

The PINN algorithm learns u(x, t) and the parameter $\alpha$ by minimizing the mean square error loss

$$\begin{aligned} MSE=\frac{1}{N}\sum _{i=1}^{N} \left| u(x_{u}^{i}, t_{u}^{i}) - u^{i} \right| ^{2} + \frac{1}{N}\sum _{i=1}^{N} \left| f_{CDG}(x_{u}^{i}, t_{u}^{i}) \right| ^{2}, \end{aligned}$$

(52)

where $\{x_{u}^{i},t_{u}^{i},u^{i}\}_{i=1}^{N}$ represents the training data on the exact solitary wave solution of Eq. (50) with $\alpha =30$,in $(x,t)\in [-10,10]\times [-2,2]$:

$$u(x,t)=\frac{1}{4}sech^2\left( \frac{1}{2}(x-t)\right) .$$

Table 12 shows the performance comparison between the PINN algorithm with the sine function and the standard PINN algorithm to learn the unknown parameter $\alpha$ of the CDG equation. It can be seen from Table 12, that the value of the loss function is small, and the precisions of the solution and the unknown parameter are acceptable. The learning effects of the two activation functions are not much different.

Table 12 Performance comparison of the predictive solution and predictive parameter of Eq. (50).

Data-driven parameter estimation in the Lax’s equation

In this section, we consider the Lax’s equation with coefficient $\alpha$:

$$\begin{aligned} u_t+140u^{3}u_{x}+70u^{3}_{x}+280uu_{x}u_{xx}+70u^{2}u_{xxx}+70u_{xx}u_{xxx}+42u_{x}u_{xxxx}+14uu_{xxxxx}+\alpha u_{xxxxxxx}=0, \end{aligned}$$

(53)

Then the residual term is

$$\begin{aligned} f_{Lax^{prime}s}:=u_t + 140u^{3}u_{x} +70u^{3}_{x}+280uu_{x}u_{xx}+70u^{2}u_{xxx}+70u_{xx}u_{xxx}+42u_{x}u_{xxxx}+14uu_{xxxxx}+\alpha u_{xxxxxxx}. \end{aligned}$$

(54)

The PINN algorithm learns u(x, t) and the parameter $\alpha$ by minimizing the mean square error loss

$$\begin{aligned} MSE=\frac{1}{N}\sum _{i=1}^{N} \left| u(x_{u}^{i}, t_{u}^{i}) - u^{i} \right| ^{2} + \frac{1}{N}\sum _{i=1}^{N} \left| f_{Lax}(x_{u}^{i}, t_{u}^{i}) \right| ^{2}, \end{aligned}$$

(55)

where $\{x_{u}^{i},t_{u}^{i},u^{i}\}_{i=1}^{N}$ represents the training data on the exact solitary solution of Eq. (53) with $\alpha =1$ and $(x,t)\in [-4,4]\times [-4,4]$:

$$\begin{aligned} u(x,t)= \frac{1}{2}sech^2\left[ \frac{1}{2}(x-t)\right] . \end{aligned}$$

Table 13 shows the performance comparison between the PINN algorithm with the sine function and the standard PINN algorithm to learn the unknown parameter $\alpha$ of the CDG equation. It can be seen from Table 13, that the value of the loss function is small, and the precisions of the solution and the unknown parameter are acceptable. The learning effect of PINN with the tanh activation function is better than the other.

Table 13 Performance comparison of the predictive solution and predictive parameter of Eq. (53).

In this section, we learn the solutions and unknown parameters of 5 equations using two different activation functions on the same PINN framework. Experiments show that PINN can learn the values of unknown parameters very well. In addition to the 7-order Lax’s equation, the PINN method using the sine function as the activation function can obtain relatively higher precision.

Discussion and conclusion

Through the tireless research of mathematical researchers, a number of effective methods have been obtained in both exact analytical solutions and numerical solutions. However, for various NLPDEs, there are still a lot of problems to be solved. The excellent performance of artificial neural networks in many research fields provides a new way for studying nonlinear partial differential equations. The PINN framework imparts the model structure of PDE into the learning iterative process of the artificial neural network, which guarantees the reliability of the method theoretically and has been validated effectively in practice. However, can the robustness of PINN be maintained for NLPDEs with complex structures, such as high-order partial derivatives and nonlinear terms of various forms? Even for equations with simple structures, it still has special solutions with complex forms such as multi-soliton solutions, periodic solutions, etc.. Can PINN learn solutions with high precision based on the data-driven principle? These are many questions worth investigating.

In this paper, a series of high-order NLPDEs are studied to get predicted solutions and parameters and explore the effects of different activation functions on learning accuracy and efficiency. At the same time, we hope to analyze the influence of the structure of the model on the reliability of the PINN method through the experimental results. The PINN algorithm with the sine activation function and the standard PINN algorithm(with the tanh activation function) are applied to solving the forward problem and inverse problem of a family of higher order dispersive KdV equations. The results show that both algorithms can learn data-driven single soliton solutions, double soliton solutions, period traveling wave solutions, and kink solutions. Experiments show that PINN with sine activation function can obtain better accuracy than the standard PINN in the problem. For the parameter estimation of these higher-order NLPDEs, the same is true in most cases, and the PNN algorithm using the sine activation function can obtain higher accuracy.

The experiment also shows that when the form of the solution is relatively simple, the PINN algorithm can learn the solution with high precision in a short time, while when the form of the solution is more complex, the PINN algorithm needs more time to get the solution with acceptable precision. For the solution of the same form, the more complex the structure of the equation, the more learning time is required, which is consistent with the structure of the loss function. These results show that it is necessary to improve the PINN algorithm for complex equations or complex solutions.

In order to make a comparison, this paper uses one framework to learn the solutions of different equations for the forward problem and another framework to learn the solutions and unknown parameters for the inverse problem. In practice, the number of PINN layers and the number of neurons in each layer can be adjusted to fit different equations. A typical example is the 7th-order Lax’s equation, in the learning of the positive problem, using the PINN method with 5 hidden layers, the accuracy of the learned solution obtained by the two activation functions can only reach $10^{-3}$. In the inverse problem, four hidden layers are used, and the learning accuracy of the standard PINN can be improved by an order of magnitude, and the performance of the standard PINN exceeds that of the PINN using the sine activation function.

It should be emphasized that the research in this paper is not limited to various KdV equations. We also performed experiments on other types of higher order partial differential equations (not included in this paper). A large number of experimental results show that for problems with rich physical backgrounds, it is effective to use the PINN framework and known information to train models to solve or estimate model parameters(modeling). When the complexity of the problem increases (high derivative or complex nonlinearity, etc.), it is necessary to improve the PINN, such as the selection of activation function, the correction of the loss function and the improvement of optimization measures. The results of these experiments also show that the PINN algorithm still has the potential to explore depth. Most of the NLPDEs can be used to describe the complex phenomena in the real world, which contains rich physical information and mechanisms. Therefore, the research in this paper provides a research idea for exploring deep learning in the aspects of physical problems (optics, electromagnetism, microwave, quantum, etc.) or problems based on the intrinsic mechanism of physics (econophysics, biophysics). Future research will continue to focus on the PINN algorithm, exploring algorithm improvements and applications in more areas.