Dynamical evolution of a five-level atom interacting with an intensity-dependent coupling regime influenced by a nonlinear Kerr-like medium

Abstract

We present an analytical solution for a quantum system characterized by a double $\Lambda$ five-level atom interacting with an intensity-dependent coupling regime, influenced by a nonlinear Kerr-like medium. We also derive the constants of motion through Heisenberg’s equations. Furthermore, the dynamical evolution of the entanglement and quantum coherence between the atom and the field is discussed using linear entropy and $l_{1}$-norm of coherence. Through a comprehensive examination of the quantum system, it is observed that both the detuning and the Kerr-like parameters exert a significant impact on the degree of entanglement and coherence. However, the impacts of detuning and the Kerr effect become less pronounced when the photon multiplicity is high. In addition, we conduct a comparison between the five-level atomic system and a four-level system, revealing that the number of energy levels has a profound impact on the behavior of entanglement and coherence. These findings highlight the importance of atomic structure and photon multiplicity in controlling and optimizing quantum processes, particularly in applications involving quantum communication and information processing.

Introduction

In recent years, the study of atom-field interaction has gained great importance in quantum computation^1,2,3,4, quantum teleportation^5,6, and quantum cryptography^7,8. The quantum mechanical perspective of atom-field interaction reveals novel features that underscore the inherently quantum nature of both the field and the atom. The Jaynes-Cummings (JC) model⁹ is a fundamental theoretical model in quantum optics that describes the interaction between a two-level quantum system and a single mode of a quantized electromagnetic field. The JC model has been extended and generalized in various ways^10,11,12 to accommodate more complex scenarios in quantum optics. These extensions play a crucial role in advancing our understanding of quantum coherence and collective phenomena in complex quantum optical setups beyond the original JC model. The intensity-dependent JC model proposed in Refs.^13,14 has found applications in the study of quantum optics and cavity quantum electrodynamics (QED) under strong coupling regimes¹⁵. Fang et al. studied the properties of the entropy and phase of the field in the two-photon JC model with an added Kerr medium¹⁶. Besides, Abdel-Aty investigated the entanglement degree of a three-level atom interacting with pair-coherent states¹⁷. A three-level atom with $\Lambda$, V, and $\Xi$ configurations interacting with a single mode cavity field has been discussed in¹⁸. Recently, Rizk et al.¹⁹ presented an analytical solution for $\Xi$-type 3-level atom interacting nonlinearly with a cavity field through a Kerr-like medium under intrinsic noise. Notice, the models that explain how four-level ladder-type^20,21, N-type^22,23 and W-type²⁴ atomic systems interact with the electromagnetic cavity field have been studied.

A $\Lambda$ five-level atom holds high significance in the realm of quantum optics and quantum information processing due to its intricate energy level structure and rich quantum dynamics^25,26,27,28. Moreover, the optical switching in a five-level atom in a novel configuration of electromagnetically induced transparency has been investigated in Ref.²⁹. A detailed theoretical study of the electromagnetically induced transparency in a $\Lambda$ type five-level atom along with some applications has been conducted in Ref.³⁰. Interestingly, the dual $\Lambda$ configurations, each comprising three ground-state sub-levels and two excited-state levels, introduce a higher degree of complexity compared to a single-$\Lambda$ system³¹. Thus, understanding the dynamics of a double $\Lambda$ five-level atom is crucial for exploring advanced quantum coherence phenomena, such as multilevel quantum interference³² and enhanced quantum information processing capabilities³³. Specifically, Salah et al.³³ investigated the dynamics of a five-level $\Lambda$-configuration atom interacting with a two-mode quantized field, incorporating the effects of damping and nonlinearity³⁴. The interaction was analyzed using the generalized nonlinear JC model and the Schrödinger equation’s analytical solution. They explored the wave function of the system under specific conditions and examined several physical aspects of the atom-field interaction, focusing on entanglement and non-classical statistical features. The mentioned study demonstrated that the choice of physical parameters in the interaction process-such as the strength of the Kerr medium, the level of detuning, and the nature of the intensity-dependent coupling-plays a crucial role in determining the system’s behavior. Notable applications of such systems have been extended to quantum communication³⁵, where the intricate level structure allows for the creation of entangled states and the implementation of novel quantum protocols.

On one hand, Abdel-Aty³⁶ explored the evolution of field quantum entropy and the entanglement dynamics between the atom and the field in a three-level atom system, incorporating an additional Kerr-like medium for one mode. On the other hand, the authors of Ref.³¹ delved into investigating a double $\Lambda$ five-level atom’s interaction with a single-mode electromagnetic cavity field, specifically in the non-resonant case. Motivated by this, we extend the model in another direction.

In this paper, we present an analytical solution for the quantum system involving a double $\Lambda$ five-level atom interacting within an intensity-dependent coupling regime, while considering the influence of a nonlinear Kerr-like medium. Note that a nonlinear Kerr-like medium is a type of optical medium where the refractive index changes in response to the intensity of light passing through it and follows a behavior similar to the Kerr effect but with possible deviations^37,38. This property is fundamental to many nonlinear optical phenomena and applications. We observe that both the detuning parameters and the Kerr-like parameter exert a detrimental influence on the degree of entanglement and coherence in the system. Entanglement and coherence are fundamental concepts in quantum information theory that reflect the non-classical correlations in quantum systems^{39,40,41,42,43,44}. Entanglement measures quantify the degree of entanglement between subsystems and play a key role in quantum computing and communication. Coherence measures^45,46, on the other hand, assess the superposition of quantum states, which is essential for understanding quantum resources. Both measures are pivotal for evaluating the potential of quantum systems in various applications, such as quantum error correction and cryptography. Understanding and accurately measuring entanglement and coherence are critical to the advancement of quantum technologies. Notice that entanglement is a strict subset of quantum coherence^40,44. Indeed, coherence can occur within a single system or between subsystems, while entanglement is a special type of coherence that involves correlations across multiple quantum systems. Thus, while entanglement represents a more constrained form of coherence, the broader concept of coherence can describe a wider range of quantum phenomena. For this reason, we explore the dynamical evolution of the entanglement and coherence between the atom and the field by examining the linear entropy and $l_1$-norm of quantum coherence.

The organization of this work is as follows. In “Description of the theoretical model”, we introduce the model and formulate the expressions for the Hamiltonian governing the dynamics of the system. In “Analytical solution of the model”, we elucidate the dynamical evolution and present the wavefunction describing the proposed quantum system. The “Entanglement and quantum coherence” delves into the discussion of entanglement and coherence among the various components of the system. The main results of the paper are discussed in “Numerical results”. Finally, conclusions are presented in “Conclusion”.

Description of the theoretical model

In alignment with the insights gleaned from the Ref.³¹, our focus is on the dynamics of a double $\Lambda$ five-level atom interacting with a coherent cavity field via k-photon process (intensity-dependent coupling regime) and the Kerr medium. Hence, adopting the rotating wave approximation (RWA), the Hamiltonian can be expressed as (setting $\hbar =1$)

$$\begin{aligned} \hat{H}=\sum _{j=1}^{5}\omega _j\hat{\sigma }_{jj}+\Omega \hat{a}^\dagger \hat{a}+\hat{H}_{af}. \end{aligned}$$

(1)

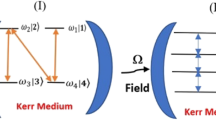
Here, $\omega _j$ denotes the energies associated with the $|j\rangle$ levels of the atom, where $j=1,2,\ldots ,5$. The atomic operators, represented by $\hat{\sigma }_{ij}=|i\rangle \langle j|$ with $i,j=1,2,\ldots ,5$, adhere to the relation $\left[ \hat{\sigma }_{ij},\hat{\sigma }_{kl}\right] =\hat{\sigma }_{il}\delta _{jk}-\hat{\sigma }_{kj}\delta _{li}$, where $\delta _{ij}$ is the Kronecker delta. The operators $\hat{a}^{\dagger }$ and $\hat{a}$ pertain to the creation and annihilation, respectively, of the quantized field characterized by frequency $\Omega$. The Hamiltonian $\hat{H}_{af}$ represents the interaction between the $\Lambda$-type five-level atom and the field, expressed by (see Fig. 1)

$$\begin{aligned} \hat{H}_{af}=\chi n(n-1)+\hat{R}\left( \lambda _1 \hat{\sigma }_{12}+\lambda _2 \hat{\sigma }_{13}+\lambda _3 \hat{\sigma }_{15}+\lambda _4 \hat{\sigma }_{34}\right) +h.c., \end{aligned}$$

(2)

where $\chi$ represents the nonlinear Kerr parameter, $\hat{R}=\hat{a}^k F(\hat{n})$ is the deformed annihilation operator with the nonlinear function $F(\hat{n})$ which is based on the intensity of the light (number of photons $\hat{n}=\hat{a}^\dagger \hat{a}$), k (a positive integer) takes into account the multiplicity of photons, and $\lambda _i$ are the coupling constants between atom and the field. It is crucial to note that our considered model encompasses many other models. In the case where $\chi =0$, $F(\hat{n})=\hat{I}$, and $k=1$, the system corresponds to the one described in Ref.³¹. Consequently, the intensity-coupling regime accurately reflects the conditions outlined in the selected references^13,14. The model successfully captures multiple configurations of the three-level atom interacting with a single-mode cavity field. Specifically, we get $\Lambda$ and $\Xi$ configurations elucidated in Refs.^47,48 when $\lambda _3=\lambda _4=0$ and $\lambda _1=\lambda _3=0$, respectively. Moreover, the four-level atomic system discussed in Refs.^49,50,51 can also be explained with our model when $\lambda _3=0$.

Fig. 1

A schematic representation of a $\Lambda$-type five-level atom within a single-mode cavity field, filled with a Kerr medium, is illustrated in the diagram. Here is a diagram representing a five-level atomic system with all five atomic energy levels labeled by $|1\rangle$, $|2\rangle$, $|3\rangle$, $|4\rangle$, and $|5\rangle$. The green arrows indicate possible transitions between these levels.

One approach to propose the dynamical operators is solving the Heisenberg equations of motion $\left( i\frac{d\hat{O}}{dt}=[\hat{O},\hat{H}]\right)$ for $\hat{n}=\hat{a}^\dagger \hat{a}$ and $\hat{\sigma }_{jj}$ operators as follows

$$\begin{aligned} \begin{aligned} i\frac{d\hat{n}}{dt}=&-k\hat{R}\left( \lambda _1 \hat{\sigma }_{12}+\lambda _2 \hat{\sigma }_{13}+\lambda _3 \hat{\sigma }_{15}+\lambda _4 \hat{\sigma }_{34}\right) +k\hat{R}^{\dagger }\left( \lambda _1 \hat{\sigma }_{21}+\lambda _2 \hat{\sigma }_{31}+\lambda _3 \hat{\sigma }_{51}+\lambda _4 \hat{\sigma }_{43}\right) ,\\ i\frac{d\hat{\sigma }_{11}}{dt}=&\hat{R}\left( \lambda _1 \hat{\sigma }_{12}+\lambda _2 \hat{\sigma }_{13}+\lambda _3 \hat{\sigma }_{15}\right) -\hat{R}^{\dagger }\left( \lambda _1 \hat{\sigma }_{21}+\lambda _2 \hat{\sigma }_{31}+\lambda _3 \hat{\sigma }_{51}\right) ,\\ i\frac{d\hat{\sigma }_{22}}{dt}=&-\lambda _1\left( \hat{R}\hat{\sigma }_{12}-\hat{R}^{\dagger }\hat{\sigma }_{21}\right) ,\\ i\frac{d\hat{\sigma }_{33}}{dt}=&-\lambda _2\left( \hat{R}\hat{\sigma }_{13}-\hat{R}^{\dagger }\hat{\sigma }_{31}\right) +\lambda _4\left( \hat{R}\hat{\sigma }_{34}-\hat{R}^{\dagger }\hat{\sigma }_{43}\right) ,\\ i\frac{d\hat{\sigma }_{44}}{dt}=&-\lambda _4\left( \hat{R}\hat{\sigma }_{34}-\hat{R}^{\dagger }\hat{\sigma }_{43}\right) ,\\ i\frac{d\hat{\sigma }_{55}}{dt}=&-\lambda _3\left( \hat{R}\hat{\sigma }_{15}-\hat{R}^{\dagger }\hat{\sigma }_{51}\right) . \end{aligned} \end{aligned}$$

(3)

Thus, the constants of motion are

$$\begin{aligned} \hat{a}^\dagger \hat{a}-k(\hat{\sigma }_{22}-\hat{\sigma }_{33}-2\hat{\sigma }_{44}-\hat{\sigma }_{55})=\hat{N}, \end{aligned}$$

(4)

where $\hat{N}$ is the constant operator of motion. Utilizing this conserved quantity, we can represent the total Hamiltonian $\hat{H}$ in the following form

$$\begin{aligned} \begin{aligned} \hat{H}=&\Omega \hat{N}+\omega _1\hat{I}+\sum _{j=1}^{4}\Delta _j \hat{\sigma }_{j+1~j+1} +\hat{H}_{af}, \end{aligned} \end{aligned}$$

(5)

where $\Delta _j$ are the detuning parameters

$$\begin{aligned} \Delta _1=\omega _{21}+k\Omega ,\quad \Delta _2=\omega _{31}-k\Omega , \quad \Delta _3=\omega _{41}-2k\Omega , \quad \Delta _4=\omega _{51}-k\Omega , \end{aligned}$$

with $\omega _{ij}=\omega _i-\omega _j$ and $\hat{I}=\sum _{j=1}^{5}\hat{\sigma }_{jj}$.

Henceforth, we neglect the first two terms since they are constants, and the remaining terms represent the interaction between the atom and the field. Consequently, the interaction Hamiltonian can be expressed in the following form

$$\begin{aligned} \begin{aligned} \hat{H}&=\chi n(n-1)+\sum _{j=1}^{4}\Delta _j \hat{\sigma }_{j+1~j+1} +\hat{a}^k F(\hat{n})\left( \lambda _1 \hat{\sigma }_{12}+\lambda _2 \hat{\sigma }_{13}+\lambda _3 \hat{\sigma }_{15}+\lambda _4 \hat{\sigma }_{34}\right) +F(\hat{n})(\hat{a}^{k})^\dagger \left( \lambda _1 \hat{\sigma }_{21}+\lambda _2 \hat{\sigma }_{31}+\lambda _3 \hat{\sigma }_{51}+\lambda _4 \hat{\sigma }_{43}\right) . \end{aligned} \end{aligned}$$

(6)

Subsequently, our focus will be on deriving the exact solution for this model, particularly the wavefunction. Let us consider the scenario where the atom is initially in its excited state, and the field is in a coherent state. The initial state is then defined as

$$\begin{aligned} |\Psi (0)\rangle =\sum _{n=0}^{\infty }q_n |1\rangle \otimes |n\rangle , \end{aligned}$$

(7)

where $q_n=\frac{\alpha _0^n}{\sqrt{n!}}\exp [-|\alpha _0|^2/2]$ represents the amplitude of the state $|n\rangle$, which corresponds to the Fock states of the mode field and $\alpha _0$ is the initial mean photon number.

Analytical solution of the model

In our proposed quantum system, the $\Lambda$-atom absorbs and emits k photons in the cavity field and the basis for the wavefunction consists of the states $|1,n \rangle , |2,n+k \rangle , |3,n+k\rangle$, $|4,n+2k \rangle$, and $|5,n+k\rangle$. So, the wavefunction for the proposed quantum system at any time can be expressed as

$$\begin{aligned} \begin{aligned} |\Psi (t) \rangle =&\sum _{n}q_n\bigg [X_1(n,t)|1,n \rangle +X_2(n+k,t)|2,n+k\rangle +X_3(n+k,t)|3,n+k\rangle +X_4(n+2k,t)|4,n+2k\rangle +X_5(n+k,t) |5,n+k\rangle \bigg ], \end{aligned} \end{aligned}$$

(8)

where $X_j(n,t)$ denotes the probability amplitude that describes the probability of finding the atom in the state $|j\rangle$. In order to deduce the dynamical evolution of the considered model, it is imperative to determine the coefficients $X_j$ (where $j=1,2,\ldots ,5$) by solving the interaction picture of the time-dependent Schrödinger equation. Thus, employing the Schrödinger equation, we can articulate the coupled system of differential equations for the probability amplitudes arising from the actions of the atomic and field operators as follows

$$\begin{aligned} \begin{aligned} i \frac{d}{dt} \left( \begin{array}{ccccc} X_1 \\ X_2 \\ X_3 \\ X_4\\ X_5\\ \end{array} \right)&= \left( \begin{array}{ccccc} \varUpsilon _1 & f_1 & f_2 & 0 & f_3 \\ f_1 & \varUpsilon _2 & 0 & 0 & 0 \\ f_2 & 0 & \varUpsilon _3 & f_4 & 0\\ 0 & 0 & f_4 & \varUpsilon _4 & 0 \\ f_3 & 0 & 0 & 0 & \varUpsilon _5 \\ \end{array} \right) \left( \begin{array}{ccccc} X_1 \\ X_2 \\ X_3 \\ X_4\\ X_5\\ \end{array} \right) , \end{aligned} \end{aligned}$$

(9)

where

$$\begin{aligned} \begin{aligned} \varUpsilon _1=&\chi n(n-1), \quad \varUpsilon _2=\Delta _1+\chi (n+k)(n+k-1), \quad \varUpsilon _3=\Delta _2+\chi (n+k)(n+k-1), \\ \varUpsilon _4=&\Delta _3+\chi (n+2k)(n+2k-1),\quad \varUpsilon _5=\Delta _4+\chi (n+k)(n+k-1), \\ f_1=&\lambda _1 \gamma _+F(n+k), \quad f_2=\lambda _2 \gamma _+F(n+k),\quad f_3=\lambda _3 \gamma _+F(n+k), \quad f_4=\lambda _4 \gamma _-F(n+2k), \end{aligned} \end{aligned}$$

(10)

with

$$\begin{aligned} \gamma _+=\sqrt{\frac{(n+k)!}{n!}} \quad \textrm{and} \quad \gamma _-=\sqrt{\frac{(n+2k)!}{(n+k)!}}. \end{aligned}$$

(11)

The analytical solution of the Eq. (9) can be deduced by applying the method employed in Ref.⁵². Thus, we obtain

$$\begin{aligned} \begin{aligned} \left( \begin{array}{ccccc} X_1(n,t) \\ X_2(n+k,t) \\ X_3 (n+k,t) \\ X_4(n+2k,t)\\ X_5(n+k,t)\\ \end{array} \right)&= \left( \begin{array}{ccccc} \eta _{11} & \eta _{12} & \eta _{13} & \eta _{14} & \eta _{15}\\ \eta _{21} & \eta _{22} & \eta _{23} & \eta _{24} & \eta _{25} \\ \eta _{31} & \eta _{32} & \eta _{33} & \eta _{34} & \eta _{35}\\ \eta _{41} & \eta _{42} & \eta _{43} & \eta _{44} & \eta _{45} \\ \eta _{51} & \eta _{52} & \eta _{53} & \eta _{54} & \eta _{55} \\ \end{array} \right) \left( \begin{array}{ccccc} e^{i\mu _1 t} \\ e^{i\mu _2 t} \\ e^{i\mu _3 t} \\ e^{i\mu _4 t} \\ e^{i\mu _5 t} \\ \end{array} \right) , \end{aligned} \end{aligned}$$

(12)

where

$$\begin{aligned} \begin{aligned} \left( \begin{array}{ccccc} \eta _{1a} \\ \eta _{2a} \\ \eta _{3a} \\ \eta _{4a}\\ \eta _{5a}\\ \end{array} \right)&= \frac{1}{\mu _{ab}\mu _{ac}\mu _{ad}\mu _{af}}\left( \begin{array}{ccccc} \alpha _1 & \beta _1 & \gamma _1 & \delta _1 & \epsilon _1 \\ \alpha _2 & \beta _2 & \gamma _2 & \delta _2 & \epsilon _2 \\ \alpha _3 & \beta _3 & \gamma _3 & \delta _3 & \epsilon _3 \\ \alpha _4 & \beta _4 & \gamma _4 & \delta _4 & \epsilon _4 \\ \alpha _5 & \beta _5 & \gamma _5 & \delta _5 & \epsilon _5 \\ \end{array} \right) \times \left( \begin{array}{ccccc} 1 \\ \mu _b+\mu _c+\mu _d\\ \mu _b\mu _c+\mu _b\mu _d+\mu _b\mu _f+\mu _c\mu _d+\mu _c\mu _f+\mu _d\mu _f\\ \mu _b\mu _c\mu _d+\mu _b\mu _c\mu _f+\mu _c\mu _d\mu _f\\ \mu _b\mu _c\mu _d\mu _f\\ \end{array} \right) , \end{aligned} \end{aligned}$$

with $\mu _{ab}=\mu _a-\mu _b$ where $a\ne b \ne c\ne d\ne f$, and

$$ \begin{aligned}\left( \begin{array}{ccccc} \alpha _1 \\ \alpha _2 \\ \alpha _3 \\ \alpha _4\\ \alpha _5 \\ \end{array} \right) & =\left( \begin{array}{ccccc} \Gamma _1^2+f_1^2\varUpsilon _{12}^2+f_2^2\varUpsilon _{13}^2+f_3\varUpsilon _{15}^2+f_2^2f_4^2\\ f_1\left[ \Gamma _2\varUpsilon _{12}+f_2^2\varUpsilon _{13}+f_3^2\varUpsilon _{15}\right] \\ f_2\left[ \Gamma _3\varUpsilon _{13}+f_1^2\varUpsilon _{12}+f_3^2\varUpsilon _{15}+f_4^2\varUpsilon _3\right] \\ f_2f_4\left[ \Gamma _1+f_4^2+\varUpsilon _4^2+\varUpsilon _{13}a_{34}\right] \\ f_3\left[ \Gamma _4\varUpsilon _{15}+f_1^2\varUpsilon _{12}+f_2^2\varUpsilon _{13}\right] \end{array} \right) ,\qquad \left( \begin{array}{ccccc} \gamma _1 \\ \gamma _2 \\ \gamma _3 \\ \gamma _4\\ \gamma _5\\ \end{array} \right)=\left( \begin{array}{ccccc} \Gamma _1 \\ f_1\varUpsilon _{12} \\ f_2\varUpsilon _{13}\\ f_2f_4\\ f_3\varUpsilon _{15}\\ \end{array} \right) , \\ \left( \begin{array}{ccccc} \beta _1 \\ \beta _2 \\ \beta _3 \\ \beta _4\\ \beta _5\\ \end{array} \right)&=\left( \begin{array}{ccccc} \Gamma _1\varUpsilon _1+f_1^2\varUpsilon _{12}+f_2^2\varUpsilon _{13}+f_3^2\varUpsilon _{15} \\ f_1\Gamma _1+f_1\varUpsilon _2\varUpsilon _{12} \\ f_2\Gamma _1+f_4^2+f_2\varUpsilon _3\varUpsilon _{13}\\ f_2f_4\varUpsilon _4+f_2f_4\varUpsilon _{13}\\ f_3\Gamma _1+f_3\varUpsilon _5\varUpsilon _{15}\\ \end{array} \right) ,\qquad \left( \begin{array}{ccccc} \delta _1 \\ \delta _2 \\ \delta _3 \\ \delta _4\\ \delta _5 \\ \end{array} \right)=\left( \begin{array}{ccccc} \varUpsilon _1 \\ f_1 \\ f_2\\ 0\\ f_3\\ \end{array} \right) , \quad \left( \begin{array}{ccccc} \epsilon _1 \\ \epsilon _2 \\ \epsilon _3 \\ \epsilon _4\\ \epsilon _5 \\ \end{array} \right) =\left( \begin{array}{ccccc} 1 \\ 0 \\ 0\\ 0\\ 0\\ \end{array} \right) , \end{aligned} $$

in which

$$\begin{aligned} \begin{aligned} \Gamma _1=&f_1^2+f_2^2+f_3^2+\varUpsilon _1^2, \quad \Gamma _2=\Gamma _1+f_1^2+\varUpsilon _2^2, \quad \Gamma _3=\Gamma _1+f_2^2+f_4^2+\varUpsilon _3^2, \quad \Gamma _4=\Gamma _1+f_3^2+\varUpsilon _5^2, \end{aligned} \end{aligned}$$

with

$$\begin{aligned} \varUpsilon _{1j}=\varUpsilon _1+\varUpsilon _j, \quad (j=2,3,5). \end{aligned}$$

The roots $\mu _j$ satisfy the fourth-order equation

$$\begin{aligned} \mu ^4+x_1\mu ^3+x_2\mu ^2+x_3\mu +x_4=0, \end{aligned}$$

(13)

where

$$\begin{aligned} \begin{aligned} x_1=&\sum _{k=1}^5\varUpsilon _k,\\ x_2=&\sum _{i<j}\varUpsilon _i\varUpsilon _j-\sum _{i} f_i^2,\\ x_3=&\sum _{i<j<k}\varUpsilon _i\varUpsilon _j\varUpsilon _k-f_4^2\varUpsilon _1-\varUpsilon _2(f_2^2+f_3^2+f_4^2)-\varUpsilon _3(f_1^2+f_3^2) -\varUpsilon _4(f_1^2+f_2^2+f_3^2)-\varUpsilon _5(f_1^2+f_2^2+f_5^2),\\ x_4=&\sum _{i<j<k<l}\varUpsilon _i\varUpsilon _j\varUpsilon _k\varUpsilon _l+(f_1^2+f_3^2)f_4^2-(f_2^2+f_3^2)\varUpsilon _2\varUpsilon _4-(f_1^2+f_3^2)\varUpsilon _3\varUpsilon _4-(f_2^2+f_4^2)\varUpsilon _2\varUpsilon _5\\&-(f_1^2+f_2^2)\varUpsilon _4\varUpsilon _5-f_4^2\varUpsilon _1\varUpsilon _2-f_3^2\varUpsilon _2\varUpsilon _3-f_4^2\varUpsilon _1\varUpsilon _5-f_1^2\varUpsilon _3\varUpsilon _5,\\ x_5=&\varUpsilon _1\varUpsilon _2\varUpsilon _3\varUpsilon _4\varUpsilon _5+f_1^2f_4^2\varUpsilon _5+f_3^2f_4^2\varUpsilon _2-f_1^2\varUpsilon _3\varUpsilon _4\varUpsilon _5-f_2^2\varUpsilon _2\varUpsilon _4\varUpsilon _5-f_3^2\varUpsilon _2\varUpsilon _3\varUpsilon _4-f_4^2\varUpsilon _1\varUpsilon _2\varUpsilon _5. \end{aligned} \end{aligned}$$

We can determine the values of $\mu _j$ by solving Eq. (13). On the other hand, as a physical manifestation of our proposition in this study, the nonlinear function $F(\hat{n})$ can be formulated as follows⁵³

$$\begin{aligned} F(\hat{n})=\frac{L_n^1(\eta ^2)}{(n+1)L_n^0(\eta ^2)}. \end{aligned}$$

(14)

This expression represents the nonlinear function for the center of mass of a trapped ion, commonly referred to as the Lamb-Dicke parameter ($\eta <1$). Here, $L_n^1$ and $L_n^0$ denote the associated Laguerre polynomials. In what follows, we consider the vector form of the probability amplitudes as

$$\begin{aligned} \begin{aligned} |X_1\rangle=&\sum_{n=0}^{\infty} q_n X_1(n,t)|n \rangle, \\ |X_2\rangle=&\sum_{n=0}^{\infty} q_{n+k} X_2(n+k,t)|n+k \rangle,\\ |X_3\rangle=&\sum_{n=0}^{\infty} q_{n+k} X_3(n+k,t)|n+k \rangle, \\ |X_4\rangle=&\sum_{n=0}^{\infty} q_{n+2k} X_4(n+2k,t)|n+2k \rangle,\\ |X_5\rangle=&\sum_{n=0}^{\infty} q_{n+k} X_5(n+k,t)|n+k \rangle.\\ \end{aligned} \end{aligned}$$

(15)

Subsequently, the reduced atomic density matrix that is derived from the state vector of Eq. (8) can be expressed as

$$\begin{aligned} \begin{aligned} \hat{\rho }_{\textrm{atom}}=&\left( \begin{array}{ccccc} \rho _{11} & \rho _{12} & \rho _{13} & \rho _{14} & \rho _{15}\\ \rho _{21} & \rho _{22} & \rho _{23} & \rho _{24} & \rho _{25}\\ \rho _{31} & \rho _{32} & \rho _{33} & \rho _{34} & \rho _{35}\\ \rho _{41} & \rho _{42} & \rho _{43} & \rho _{44} & \rho _{45}\\ \rho _{51} & \rho _{52} & \rho _{53} & \rho _{54} & \rho _{55}\\ \end{array} \right) . \end{aligned} \end{aligned}$$

(16)

Here

$$\begin{aligned} \begin{aligned} \rho_{jj}=&\langle X_j|X_j \rangle=\sum_{n=0}^{\infty}P_n |X_j(n,t)|^2,\\ \rho_{12}=&\rho_{21}^*=\langle X_1|X_2 \rangle=\sum_{n=0}^{\infty}q_n q_{n+k}^* X_1(n,t) X_2^{*}(n+k,t),\\ \rho_{13}=&\rho_{31}^*=\langle X_1|X_3 \rangle=\sum_{n=0}^{\infty}q_n q_{n+k}^* X_1(n,t) X_3^{*}(n+k,t),\\ \rho_{14}=&\rho_{41}^*=\langle X_1|X_4 \rangle=\sum_{n=0}^{\infty}q_n q_{n+2k}^* X_1(n,t) X_4^{*}(n+2k,t),\\ \rho_{15}=&\rho_{51}^*=\langle X_1|X_5 \rangle=\sum_{n=0}^{\infty}q_n q_{n+k}^* X_1(n,t) X_5^{*}(n+k,t),\\ \rho_{23}=&\rho_{32}^*=\langle X_2|X_3 \rangle=\sum_{n=0}^{\infty}q_{n+k} q_{n+k}^* X_2(n+k,t) X_3^{*}(n+k,t),\\ \rho_{24}=&\rho_{42}^*=\langle X_2|X_4 \rangle=\sum_{n=0}^{\infty}q_{n+k} q_{n+2k}^* X_2(n+k,t) X_4^{*}(n+2k,t),\\ \rho_{25}=&\rho_{52}^*=\langle X_2|X_5 \rangle=\sum_{n=0}^{\infty}q_{n+k} q_{n+k}^* X_2(n+k,t) X_5^{*}(n+k,t),\\ \rho_{34}=&\rho_{43}^*=\langle X_3|X_4 \rangle=\sum_{n=0}^{\infty}q_{n+k} q_{n+2k}^* X_3(n+k,t) X_4^{*}(n+2k,t),\\ \rho_{35}=&\rho_{53}^*=\langle X_3|X_5 \rangle=\sum_{n=0}^{\infty}q_{n+k} q_{n+k}^* X_3(n+k,t) X_5^{*}(n+k,t),\\ \end{aligned} \end{aligned}$$

(17)

with $P_n=|q_n|^2$, and the star $*$ represents the complex conjugate.

Equipped with the wavefunction and density matrix, we can now delve into the fascinating time-dependent characteristics of the atomic system. The following sections will explore this topic in detail.

Entanglement and quantum coherence

Linear entropy

Quantum entanglement, a fundamental phenomenon in quantum mechanics, plays a crucial role in the manipulation and creation of quantum states^{54,55,56,57,58}. It stands as a cornerstone in the resources of quantum information, contributing significantly to applications such as quantum teleportation⁵⁹, quantum cryptography⁶⁰, quantum computations⁶¹, and quantum tomography^62,63. There are various measures of entanglement^64,65, including entanglement of formation⁶⁶, negativity⁶⁷, concurrence^68,69, and entropy⁷⁰. In our study, we employ linear entropy as the quantifier to assess the entanglement of our system.

The degree of entanglement among various components of a system can be assessed by examining the linear entropy of the electromagnetic field. Higher linear entropies correspond to greater degrees of entanglement, while lower entropies indicate smaller levels of entanglement. The linear entropy can be formulated using the following equation⁷¹

$$\begin{aligned} S_L(\hat{\rho })=1-\textrm{tr} [\hat{\rho }^2], \end{aligned}$$

(18)

where $\hat{\rho }$ is the reduced density matrix of the atoms.

In general, linear entropy satisfies the following inequality

$$\begin{aligned} 0\le S_L\le 1-\frac{1}{n}. \end{aligned}$$

(19)

Here, n is the dimension of the Hilbert space, and in the case of a $\Lambda$ five-level atom, we have $n=5$. Thus, the linear entropy $S_L$ satisfies the inequality $0 \le S_L \le \frac{4}{5}$ for our considered case. The system is identified as being in a pure state when the linear entropy of the electromagnetic field equals zero, signifying that the cavity field is not influencing the atom. Conversely, reaching the upper limit of system entanglement indicates that the entanglement between the atoms and the field is at its maximum level. From Eq. (16), we get

$$\begin{aligned} S_L=1-\sum _{j=1}^{5}\left( \sum _{n=0}^{\infty } |X_j|^2\right) ^2-2 \sum _{i<j}|\sum _{n=0}^{\infty } X_i X_j^*|^2. \end{aligned}$$

(20)

The primary objective of this study is to investigate entanglement within an atom-field bipartite system. This goal is pursued by implementing an optimal configuration and carefully selecting appropriate parameter values.

$l_1$-norm of quantum coherence

The $l_1$-norm of quantum coherence is a widely employed measure that quantifies the amount of coherence in a quantum state by summing the absolute values of all off-diagonal elements in the density matrix $\hat{\rho }$, mathematically given by^45,46

$$\begin{aligned} C_{l_1}(\hat{\rho }) = \sum _{i\ne j} |\langle i|\hat{\rho }|j\rangle |. \end{aligned}$$

(21)

This measure is straightforward to compute and clearly indicates how much a quantum state deviates from being classical. It captures the superposition properties of the state and is useful in various quantum information processing tasks.

Numerical results

Let us explore the impact of detuning parameters ($\Delta$) and the nonlinearity parameter ($\chi$) on the time evolution of the linear entropy with two fixed values of k, i.e. $k=1$ and $k=2$. Throughout all figures, we set $|\alpha _0|^2 =\bar{n}=10,$$\lambda _s=\lambda$, and $\Delta _s=\Delta$ for $s=1$ to 4.

In Figs. 2 and 3, we explore the entanglement dynamics between a $\Lambda$ five-level (and four-level) atom and an intensity-dependent coupling regime by examining the temporal evolution of the linear entropy $S_L$ for two fixed values of $k=1$ and $k=2$. As mentioned, a four-level atomic system can be obtained by our model when $\lambda _3=0$ in Eq. (2). We optimize the values of $\Delta$ and $\chi$ to deduce an optimal dynamical behavior that generates maximal entanglement between the atom and the field. These figures reveal that the linear entropy is initially zero, indicating that the system starts in a disentangled state, as expected from the initial separable state shown in Eq. (7). Subsequently, there is a rapid increase in the curves, fluctuating between maximum and minimum values as time progresses.

Fig. 2

The plots illustrate the influence of detuning parameters ($\Delta$) and the nonlinearity parameter ($\chi$) on the time evolution (scaled time $\lambda t$) of the five-level atom and four-level atom captured by linear entropy with the fixed value of $k=1$. Plot (a) depicts the linear entropy when $\Delta = \chi = 0$, while plot (b) illustrates the scenario when $\Delta = 5$ and $\chi = 0$. Additionally, plots (c) and (d) showcase the linear entropy for the cases where $\Delta = 0$, $\chi = 0.5$ and $\Delta = 5$, $\chi = 0.5$ respectively.

Fig. 3

Same as Fig. 2 but for $k=2$.

In Figs. 2a and 3a, the detuning parameters and the nonlinear Kerr parameter are both set to zero $(\Delta =\chi =0)$ with $k=1$ and $k=2$. The physical interpretation centers around how the detuning parameter $\Delta$ and the nonlinear Kerr parameter $\chi$ influence the dynamics of a quantum system, particularly in the context of its entanglement behavior as measured by the linear entropy function. The linear entropy function quantifies the degree of mixedness or loss of coherence in the quantum system. The rapid generation of linear entropy suggests that the system quickly moves away from a pure state to a more mixed one. This could indicate fast entanglement dynamics or interaction between different parts of the system, even in the absence of nonlinear or detuning influences. Since both $\Delta = 0$ and $\chi = 0$, the system is operating in an idealized regime without any detuning effects or nonlinear Kerr interactions. In this scenario, we observe a rapid generation of the linear entropy function. Additionally, the curves exhibit some fluctuations over time. For $k=1$, we observe a decrease in the amplitude of oscillations while the maximum value remains constant. However, for $k=2$, we see more fluctuations than the previous case ($k=1$). When $k = 1$, the system exhibits oscillations in the linear entropy function, indicating periodic changes in the entanglement or coherence. The amplitude of these oscillations decreases over time, suggesting a gradual stabilization of the system, though the maximum value remains constant. This stabilization might point to the system settling into a particular entangled state. When $k = 2,$ the system experiences more fluctuations in the linear entropy compared to $k = 1$, implying more complex or dynamic entanglement behavior. These additional fluctuations could be due to higher energy states or more degrees of freedom available in the system, leading to more intricate quantum interactions.

Furthermore, a clear difference between the entanglement values in five-level and four-level atomic systems is visible. The obvious difference in entanglement values between the five-level and four-level systems suggests that the number of atomic energy levels plays a significant role in the entanglement dynamics. The five-level system likely provides more pathways for interaction and entanglement, leading to more complex and possibly higher degrees of entanglement compared to the four-level system.

In Figs. 2b and 3b, the detuning parameters are increased (i.e., $\Delta =5$), while the nonlinear Kerr parameter parameter is kept at zero ($\chi =0$). Surprisingly, the rate of fluctuations slows down, which is evident in the decreasing amplitudes of the oscillations over time. When the detuning parameter $\Delta$ is increased, the system’s response becomes less resonant, causing the fluctuations in the system to slow down. This suggests that the system becomes less responsive to external perturbations, leading to more stable or “damped” behavior over time. The decreasing amplitude of oscillations could indicate energy dissipation or reduced entanglement in the system’s evolution.

Furthermore, due to the increased detuning parameters, we observe that the curves for both cases $k=1$ and $k=2$ shift downward, suggesting that the system can be adversely affected by highly detuning parameters. Increasing the detuning means that the system is being driven further away from its natural resonant frequency. Physically, this could reduce the system’s ability to interact efficiently with the driving field, leading to altered dynamic behavior.

We examine the effect of the Kerr medium ($\chi =0.5$) on the entanglement between the atom and the field in the absence of detuning parameters for two fixed values of k in Figs. 2c and 3c. Under the influence of the Kerr medium, the linear entropy function experiences a rapid increase to a certain value for a brief period, followed by significant suppression. This leads to a state of purity, with the linear entropy approaching zero for $k=1$, signifying a condition where no information transfer occurs between the field and the atom. However, when the multiplicity of photons k increases ($k=2$), the impact of Kerr effect is reduced. Over time, for $k=1$, one can observe that the curve moves periodically and consistently, with an increase in the number of oscillations and their amplitudes. This is more evident for $k=2$. It is noteworthy that the linear entropy demonstrates a more pronounced and strong negative effect compared to the scenario where detuning parameters are increased, as depicted in Figs. 2b and 3b.

In Figs. 2d and 3d, when considering the non-zero values for both detuning parameters and nonlinear Kerr parameter ($\Delta =5, \chi =0.5$), it becomes evident that entanglement can be destroyed over time for both five-level and four-level atomic systems. Nevertheless, the effects of detuning and the Kerr effect are reduced when the multiplicity of photons k increases. This attenuation occurs because the system’s response to these nonlinear interactions becomes less sensitive as the photon number grows⁷². Therefore, by carefully adjusting the value of k, we can effectively mitigate these negative impacts and enhance the system’s performance. Overall, this description emphasizes how the system’s entanglement behavior varies depending on the value of k and the structure of the atomic system (five-level or four-level), even when detuning and nonlinear effects are absent.

To comprehensively compare the impact of both detuning and nonlinear Kerr parameters on quantum coherence, we plot the $l_1$-norm of quantum coherence $C_{l_1}$ against the scaled time $\lambda t$ for five-level and four-level atomic systems with $k=1$ and $k=2$. Figures 4 and 5 capture the dynamical behavior of quantum coherence over $\lambda t$, as measured by the $l_1$-norm of coherence $C_{l_1}$. A higher value of $C_{l_1}$ indicates greater quantum coherence, meaning that the quantum state has a more significant superposition of basis states.

Fig. 4

Same as Fig. 2 but for $l_1$-norm of quantum coherence.

Fig. 5

Same as Fig. 3 but for $l_1$-norm of quantum coherence.

In Figs. 4a and 5a, the detuning and nonlinear Kerr parameters are set to zero, meaning no external influences are affecting the system’s dynamics. The focus is on how the quantum coherence of the system evolves, as measured by the $l_1$-norm of coherence, which tracks how much the system remains in a coherent superposition state. The system quickly develops a high level of coherence, suggesting fast internal dynamics even without external detuning or nonlinear effects. For $k = 1$, we see periodic changes in coherence with decreasing oscillation amplitude over time, indicating the system is stabilizing but still retaining a constant maximum level of coherence. This stabilization could mean the system is finding a coherent state where it tends to settle. For $k = 2$, the system shows more complex behavior, with more fluctuations, likely due to the availability of more energy levels or degrees of freedom. This points to a more dynamic and intricate quantum coherence evolution. Lastly, the difference in coherence between five-level and four-level atomic systems highlights the impact of atomic structure on coherence dynamics. The five-level system, having more interaction possibilities, demonstrates more complex and higher degrees of coherence compared to the four-level system. This underscores the importance of the number of energy levels in determining how quantum coherence evolves in atomic systems.

Increasing the detuning parameter ($\Delta =5$) while keeping the nonlinear Kerr effect at zero causes the system’s coherence to fluctuate more slowly over time, as illustrated in Figs. 4b and 5b. This reduction in fluctuation rate implies that the system is less responsive to external influences, stabilizing the quantum coherence. The diminishing oscillation amplitude may reflect a loss of energy or coherence, as the system becomes less interactive with its environment.

Regarding Figs. 4c and 5c, we analyze how the Kerr medium influences the quantum coherence between an atom and the field, rather than focusing on entanglement. Initially, the coherence rapidly rises and then falls sharply for $k=1$. This suggests that there is little coherent interaction between the atom and the field at this point. When the photon number k increases to 2, we see a different pattern for coherence suppression. For $k=1,$ periodic oscillations of coherence occur with increasing intensity over time. This effect is more pronounced for higher photon numbers, indicating that increasing photon multiplicity changes how coherence evolves in the presence of the Kerr medium.

From Figs. 4d and 5d, we see that the quantum coherence of the atomic systems can degrade over time due to the influence of detuning and nonlinear Kerr interactions. However, as the number of photons (k) in the system increases, the sensitivity of the quantum coherence to these disturbances decreases. In other words, when there are more photons, the destructive effects on coherence caused by detuning and Kerr nonlinearity become less pronounced. By tuning the photon multiplicity, we can minimize the disruption to coherence and maintain the system’s quantum properties, leading to better overall performance. This suggests that photon multiplicity acts as a control parameter to optimize the resilience of the system against coherence loss.

Conclusion

In conclusion, this study has provided an analytical solution for a quantum system featuring a double $\Lambda$ five-level atom interacting with an intensity-dependent coupling regime, influenced by a nonlinear Kerr-like medium. The constants of motion were derived through the application of Heisenberg’s equations. The discussion on the dynamical evolution of entanglement and quantum coherence, respectively measured by linear entropy and $l_1$-norm of coherence, sheds light on the intricate relationship between the atom and the field. Upon a comprehensive examination of the quantum system, it became evident that both the detuning and nonlinear Kerr parameters contribute negatively to the degree of entanglement and coherence. However, the influence of detuning and the Kerr effect diminishes remarkably when the photon multiplicity k is elevated. Therefore, these detrimental effects can be substantially mitigated by carefully controlling the value of k. Additionally, a noticeable distinction in entanglement and coherence values between the five-level and four-level atomic systems was observed. This clear difference indicates that the number of atomic energy levels significantly influences the dynamics of entanglement and coherence. The five-level system likely offers more interaction pathways, resulting in more complex and potentially higher degrees of entanglement and coherence compared to the four-level system. In summary, these results highlight how the system’s entanglement and coherence behavior changes based on the value of k and the configuration of the atomic system (whether five-level or four-level), even in the absence of detuning and nonlinear effects.