Introduction

The glomerular filtration rate (GFR) quantifies the functioning of kidneys and is used to diagnose chronic kidney disease (CKD). GFR is also employed to indicate the severity of kidney damage, for example patients whose GFR values are lower than 15 mL/min/1.73m2 may require dialysis or even transplantation. Thus, accurately measuring and/or estimating GFR is essential for managing kidney health.

In clinical practice, GFR is commonly estimated using equations, such as the Chronic Kidney Disease Epidemiology (CKD-EPI)1 and European Kidney Function Consortium (EKFC)2 equations, which are based on age, sex, serum creatinine (SCr), and/or cystatin C (CysC)3. Both equations are recognized as valid by the recent Kidney Disease Improving Global Outcomes (KDIGO) guidelines4. EKFC, the most recently proposed equation, relies on rescaling SCr or CysC with the so-called Q-value, the median SCr or CysC of healthy people and is applicable across the full age spectrum (2–100 years), and adaptable to any population, making it the most general equation. Using two separate equations CKiD (Chronic Kidney Disease in children)5 and CKD-EPI (for adults)1 presents shortcomings, such as an implausible rise in estimated GFR (eGFR) in patients who are transitioning from adolescence to adulthood, despite no change in SCr6. Finally, EKFC does not show overestimation in young adults (18–25 years), as is the case for CKD-EPI7,8.

Despite many advantages, the EKFC-equation, like all other eGFR-equations, still presents deficiencies7,9. For instance, its imprecision remains rather large, which limits its clinical applicability, namely most eGFR equations are only able to predict the GFR in about 80–85% of patients within 30% of measured GFR (P30 = 80–85%). The performance increases up to P30 = 90–95% when both SCr and cystatin C are included. However, when P10, the performance of patients with an estimated GFR within 10% of measured GFR, is evaluated, the performance of equations does not surpass 50% in most of the cases1,2,3. Improving precision of GFR estimations is an important clinical need in the diagnosis of individual patients.

In this context, ML methods have been investigated to improve GFR estimations. Nonetheless, recent studies using this methodology often present limitations. For instance, several studies are specifically designed for a population, namely, older people (above 65 years), adults only, ICU patients or they just present a limited sample size10,11,12,13,14 .

The aim of the current study is to explore to what extent established ML methods can improve GFR estimation compared with EKFC (both for children and adults), representing the state-of-the-art among currently available equations.

Methods

Design overview

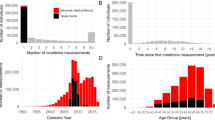
The ML models have been obtained using the datasets used for developing and validating the SCr-based EKFC equation2 and in case cystatin C was available, for the combined SCr/CysC-based EKFC-equation. We have limited the analysis to white patients since we are using the same cohorts as in2. More details about participants centers, measurement methods and patient characteristics are available in the Supplementary Material Tables S1–S4. Briefly, we have data from 19,629 patients from 13 cohorts for development, internal and external validation. These cohorts were divided into development-internal validation or external validation datasets according to their age, exogenous marker used to measure GFR (mGFR) and mGFR levels, as described in Tables S1–S3 (Supplementary material). For the models based on the single biomarker SCr, we used 13 cohorts, 7 for the development and internal validation, which were further randomly split into development (n = 8473; 25%) and internal validation (n = 2778; 25%) dataset, and the remaining 6 cohorts (n = 8378) were used for external validation, which are described in Table 1 and S4. For the models based on both SCr and cystatin C, we selected the patients from the same cohorts where both biomarkers were available (Table 2 and S4), leading to the following subsets: development (n = 4849; 41%), internal validation (n = 1603; 13.5%) and external validation (n = 5389, 45.5%).

Table 1 Basic participant characteristics with only serum creatinine available in the development, internal and external validation datasets.
Full size table
Table 2 Basic participant characteristics with both serum creatinine and cystatin C available in the development, internal and external validation datasets.
Full size table

All data were anonymized and the original study was approved by the Ethical Board at Lund University (Sweden) with amendment approved by the Swedish Ethical Review Agency.

We used the single biomarker SCr-based EKFC equation and the mean of the SCr-based EKFC and cystatin C based EKFC as benchmark for the current comparison. As cystatin C is not always available in clinical practice, we focused on the single biomarker SCr-based EKFC-equation in a first part of the analysis, but, as the combined equation has the highest accuracy and precision, in a second analysis, we also evaluated the difference between the combined SCr/CysC-based EKFC and the ML models.

Covariates

ML models were allowed to use age, sex, SCr (and CysC), height, weight and BMI, as these data were also available for most of the participants. SCr was measured using assays traceable to the gold standard isotope dilution mass spectrometry method (results from the CRIC study were recalibrated) as described in2. Cystatin C assays were standardized to the international reference material (ERM-DA471/IFCC)3.

Outcomes

Measured GFR was obtained using two methods: plasma clearance and urinary clearance. As previously described2, GFR was measured with different markers, but they all are recognized as reference methods15,16,17. For more details see Supplementary Material Tables S1–S3.

Machine learning models

Several different ML models were evaluated: multi-layer perceptron (neural network), support vector machines, k nearest neighbors, linear regression, Random Forest regression, and XGBoost regression. We selected the best performing ML models regarding their performance on the internal validation set: linear regression, XGBoost and random forest.

  • Linear regression: A linear regression model with L1 (lasso regression) and L2 (ridge regression) regularization. Lasso is an acronym for least absolute shrinkage and selection operator. Lasso regression adds the ‘absolute value of magnitude’ of the coefficient as a penalty term to the loss function, so the cost of outliers increases linearly. Ridge regression adds the ‘squared magnitude’ of the coefficient as the penalty term to the loss function, so the cost of outliers increases exponentially. This method has been added as a baseline comparison.

  • Random forest regression: Random forest is an ensemble supervised ML algorithm made up of decision trees, which is used for both classification and regression problems. A random forest model with 100 trees was used. The model is constructed using bootstrapping, i.e., by constructing multiple datasets of the same size as the original dataset, created using resampling with replacement. Furthermore, candidate variables at each split are randomly selected to maximize diversity among the decision trees18,19.

  • XGBoost for regression: XGBoost is another powerful approach for building supervised regression models. An XGBoost model with 100 trees which employs mean squared error as its loss function was used. Boosting is a popular ensemble method, that sequentially builds models, in this case decision trees, where each model learns from the errors of the previous one20.

Random Forest creates decision trees independently and combines their outputs, whereas XGBoost builds trees sequentially to correct errors. As their base models, the random forests used predictive clustering trees19, a variant of decision trees which employ variance reduction as their heuristic. Furthermore, these trees can naturally handle missing covariate values. The library scikit-learn (version 1.4.2) was used for the linear regression and the random forest, whereas XGBoost was implemented using the homonymous library XGBoost (version 2.0).

Statistical analysis

The following usual metrics were used to compare the performance of ML methods with the EKFC equations2,3.

The median bias is the difference between the estimated GFR and the measured GFR. Values close to 0 are desired for this measure, but an absolute bias less than 5 mL/min/1.73m2 may be considered clinically acceptable.

The Interquartile Range (IQR) is the range of values between the 25th percentile and the 75th percentile of the difference between the estimated GFR and the measured GFR and represents the precision expressed in mL/min/1.73m2. Smaller values are associated with better precision.

The percentage of patients whose GFR was estimated within 10 or 30% of the measured GFR is the accuracy within 10 or 30% (P10 and P30). The goal for P30 is 100%, but P30 > 75% has been considered as “sufficient for good clinical decision making” by the Kidney Disease Outcomes Quality Initiative (K/DOQI), although their goal was to reach a P30 > 90%21. The Mean-square error (MSE) is the average of the squared differences between estimated and measured GFR. Smaller values are associated with better precision.

Median quantiles for bias across the age spectrum were graphically presented using fractional polynomials (linear, square and logarithmic). Likewise, accuracy P30 (%) was graphically presented across the age spectrum using cubic splines with two free knots and using 3rd degree polynomials. Bland–Altman plots (difference versus average) were also used to comprehend the differences in performance between ML models and EKFC.

Median bias, P10 and P30 are reported with 95% CIs. To test if an equation is different from another equation in the same population, we did not use statistical tests to avoid numerous p-value calculations, but the reader may consider an equation as different when the 95% CI between equations was not overlapping (which is a more conservative criterion). We made sub-analyses according to age (younger than 6, 6 to 12, 12 to 18, 18 to 40, 40 to 65 and > 65 years), body mass index (BMI) (< 20, 20 to 25, 25 to 30, 30 to 35 and > 35 kg/m2), measured GFR (mGFR) (< 30, 30 to 60, 60 to 90, 90 to 120, > 120 mL/min/1.73m2), and sex. SHAP (Shapley additive explanations) values were used to better understand the variable importance in the ML models22. SHAP values were generated using the homonymous library SHAP, version (0.43.0).

Results

In the external validation dataset, participants had a mean ± SD age of 50.9 ± 22.3 years (range [2–97]), mGFR was 78.9 ± 32.2 (range [3–354]) mL/min/1.73m2, SCr/Q was 1.37 ± 0.97 (range [0.08–12.8] and 47.2% were male. During the learning phase, we had 2056 children aged 2–18, with 1031 aged 2–12 years (see Table S4 (development cohort)).

Among all ML models, the best model was systematically the random forest regression model (RF). In the main manuscript, we only report the overall results for the SCr-based (Table 3) and SCr/CysC based (Table 4) eGFR models on the external validation set. More detailed results (according to subgroups) on the internal and external datasets obtained using EKFC, the random forest model, linear regression and XGBoost models are available in the Supplementary Material Tables S5–S24. First, we present results considering the patients with only SCr available (Table 3 and S5–S14), followed by the results for the patients with both SCr and cystatin C (Table 4 and S15–S24).

Table 3 Performance statistics of the different machine learning models, and EKFCcrea-equation, in the external validation dataset using only serum creatinine as biomarker.
Full size table
Table 4 Performance statistics of the different machine learning models, and EKFCcrea+cys-equation, in the external validaton dataset.
Full size table

Serum creatinine-based results

Overall, regarding cohorts with SCr available, random forest (RF) and EKFC are competitive with each other. Table 3 shows the overall performance results of the EKFC-equation and the three best performing ML models, in the external validation dataset. More specifically, RF reached a P10 and P30 of 0.41 (95% CI 0.40;0.42) and 0.85 (95% CI 0.85;0.86), whereas EKFC yielded 0.43 (95% CI 0.42; 0.44) and 0.87 (95% CI 0.86; 0.87), respectively.

In Figs. 1 and 2, we plotted bias and P10/P30 against age for EKFC and the best ML model (Random Forest). Figure 3 shows the Bland–Altman plots to evaluate the bias according to GFR-level.

Fig. 1
figure 1

Bias versus age for the SCr-based (left panel) and SCr/CysC-based (right panel) EKFC and RF models.

Full size image
Fig. 2
figure 2

P10/P30 accuracy versus age for the SCr-based (left panel) and SCr/CysC-based (right panel) EKFC and RF models.

Full size image
Fig. 3
figure 3

Bland–Altman plots for the SCr-based EKFC (left panel) and RF model (right panel).

Full size image

The subgroup analyses according to age, mGFR, BMI and sex are shown in Supplement Tables S11–S14. The results based on age-subgrouping (Table S11, Figs. 1 and 2) show very comparable results between the RF model and EKFC. For subjects younger than 6–12 years, the two models are both less performant. According to Fig. 1 (and Table S11), there is a trend for a poorer bias for the EKFC model in young children, while RF stays within the clinically acceptable range. In all other subgroups, the results were very similar between the EKFC and the RF models. The Bland–Altman (Fig. 3) plots show that both methods (EKFC and RF) are overall unbiased and have similar imprecision (the 95% limits of agreement are nearly equal).

Serum creatinine and cystatin C based results

When considering both SCr and cystatin C as biomarkers, presented in Table 4, Supplement Tables S15–S24 and Figs. 1, 2 and 4, a very similar pattern is observed. That is, RF provided respectively P10 and P30 values of 0.45 (95% CI 0.44;0.46) and 0.89 (95% CI 0.88;0.90), whereas EKFC yielded 0.44 (95% CI 0.43; 0.44) and 0.89 (95% CI 0.88; 0.90). However, occasional small differences were observed in specific subgroups regarding median bias, as RF tends to perform better in patients younger than 12 years (Table S21 and Fig. 1) and patients with mGFR > 120 (Table S23).

Fig. 4
figure 4

Bland–Altman plots for the SCr/CysC-based EKFC (left panel) and RF models (right panel).

Full size image

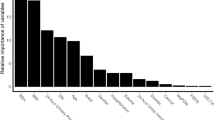
Shapley values or SHAP plots help interpret prediction models as they show the contribution and the importance of each feature on the predictions. We present the SHAP diagram for the RF model using both creatinine and cystatin C in Fig. 5. As can be seen, the biomarkers are the most relevant features (with higher values associated with a lower GFR prediction), followed by age, weight (Wt), sex, height (Ht) and BMI.

Fig. 5
figure 5

SHAP plot to show feature importance for the RF model. That is, serum creatinine and BMI are the most and the least relevant features, respectively. Feature values (e.g., higher or lower serum creatinine values) are represented using the colors blue and red, where blue values are associated with lower values and red with higher ones. The placement of the dots is related to their impact on the output. Dots to the left side of (x = 0) reduce the output and dots to the right increase the output.

Full size image

Discussion

In this work, we have compared several ML algorithms, using age, sex, SCr (and CysC), height, weight and BMI as features, with the EKFC equation. According to the results, RF, the best performing ML method, managed to be competitive with EKFC in most of the cases. The only noticeable difference was observed in patients younger than 12 years where RF including both SCr and CysC slightly outperformed EKFC. We also performed experiments where height, weight and BMI were not included as features. In this case, all ML models performed systematically worse than their counterparts which could use all features.

It has been suggested that ML methods could be superior to equations resulting from traditional statistical methods in estimating glomerular filtration rate23. Moreover, most ML methods are classification models to predict chronic kidney disease outcomes (risk of end-stage renal disease)10,12,13, rather than regression models to predict glomerular filtration rate23. In case GFR was the outcome of interest, the ML models were limited to specific populations (e.g. intensive care unit patients14, US population23) or were intended to choose the most optimal estimating GFR equation11. However, these ML methods were trained and validated on other datasets, making them difficult to compare with the performance of the ML models we obtained. In the current study, we used exactly the same data to develop and validate (internally and externally) an ML prediction model for estimating GFR as the data we used to develop and validate the SCr-based EKFC equation2. Many different models were evaluated (multi-layer perceptron (neural network), support vector machines, k nearest neighbors, linear regression, Random Forest regression, XGBoost regression) to come up with the best performing ML model as possible, with measured GFR as the outcome, and age, sex, SCr (and CysC), height, weight and BMI as features. As the EKFC equation is a full age range equation, we included data of both children and adults in this study.

The best performing model was the RF model, based on the overall performance in terms of bias, IQR, MSE and P10/P30 accuracy. This was the case both for the SCr-based RF model and SCr/CysC-based RF model. However, the results of our analysis (bias vs age, P10/P30 vs age, and Bland–Altman plots) and sub analysis (according to age, mGFR, sex and BMI subgroups) show that these RF models were not superior to the SCr-based and SCr/CysC-based EKFC-equations, respectively, in the external validation dataset. Furthermore, we noticed that using weight and height as features for the ML did not improve the results. The conclusion of our analysis is that ML models could not consistently outperform EKFC. EKFC and the random forest model slightly outperform each other in some subsets of patients, but not systematically. Accordingly, the RF model was slightly less biased in patients younger than 12 years and when mGFR was exceeding 120 mL/min/1.73m2. However, especially in the latter subgroup, the performance of all equations was relatively poor, and the best recommendation would probably be to measure GFR.

One advantage of the EKFC-equation over the RF model is the ease with which you can implement it in the software of a clinical laboratory, which is not straightforward for a ML model. The EKFC-equation can also be explained in an intuitive manner: a person with a normal SCr-value (i.e. a SCr/Q value close to ‘1’) will have an estimated GFR close to 107.3 for people younger than 40 years and an eGFR equal to 107.3 × 0.990(Age−40) for people older than 40 years, as renal decline naturally begins around the age of 40 years. Such interpretation is not as intuitively made from a ML model that only gives a prediction from a black box algorithm. However, random forests may use post-hoc methods, such as SHAP (Fig. 5), which can help to provide a clear explanation of the importance of the variables responsible for the prediction.

Limitations

Limitations of this study include the presence of only white patients. Further studies should investigate the performance of ML methods in cohorts with a mixture of ethnicities cohorts. Also, to make them directly comparable, ML methods were allowed to use the same features as the EKFC-equation, which might have limited their performance. Using more covariates, whenever applicable, such as albuminuria, diabetes status, blood pressure as input to the ML models, could theoretically lead to superior results for ML models, even when these features are not available, as missing features can be handled without imputation. One of the important advantages of ML models is that introducing new variables in the model is much easier than in the development of classical statistical equations like EKFC, as ML methods can directly incorporate new features, whereas the equations would require a functional form of the new features.

Conclusions

Given that ML models are able to model non-linearity and were allowed to use all available covariates (including age, sex, height, weight, BMI, SCr and CysC), but could not outperform the EKFC-equation (which only uses age, sex, SCr and/or CysC), we may assume that we are reaching the limits of accuracy and precision in estimating GFR, with the current features available. It also shows that the proposed two-spline EKFC-equation is a very realistic model, optimally matching measured GFR within the current limitations of accuracy and precision.