Analyzing boron oxide networks through Shannon entropy and Pearson correlation coefficient

Abstract

In the current age of chemical science, chemical graph theory has significantly advanced our understanding of the characteristics of chemical compounds. To simulate the mathematical, chemical, and physical aspects of networks, a topological index, a numerical measure obtained from the graph of a chemical network, employed. Recent work has explored the topological properties of boron oxide using chemical graph theory. In this work, we conduct a Pearson correlation analysis of boron oxide to assess the correlations between the Van and S indices and entropy metrics. We analyze the Pearson correlation coefficients between the entropy values and the calculated indices using a heatmap. In this article, a significant positive correlation between the Van, and S indices, and entropy values, which is represented by the heatmap of the strong linear correlations. To avoid duplication, a dimensionality reduction technique should be used for highly connected variables. Additionally, this study gives a detailed explanation of the link between the indices and entropy, which will form the basis of further statistical investigations.

Introduction

A topic from mathematical chemistry’s branch of topology is employed in chemical graph theory, which is topological. For this reason, when supporters of graph theory pointed out that it could be applied to mathematical modeling, for instance, chemical characteristics, it became extremely popular¹. It is crucial in many fields of chemistry, biology, and materials science and offers a foundation for understanding molecular structures, characteristics, and reactions. Using chemical graph theory, it enables us to anticipate chemical structures based on their connections. It is possible to characterize the molecular graph’s chemical and physical characteristics using the topological indices, or TIs for short. Accompanying this concept with our intrinsic functioning of nanochemistry and obtaining these numerical descriptors for nanostructures will make more sense and be more beneficial².

It will make more sense and be more beneficial if we connect this concept to how nanochemistry naturally functions. These indices find applications in the quantitative structure-activity relationship (QSAR) and chemical graph theory, which establish a connection between molecule structure and physical, chemical, or biological characteristics. The molecule structure can be explained considerably more effectively by topological indices, which are also faster to compare and forecast molecular attributes for. Numerous degree- and distance-based topological indices have been proposed in the literature; however, some are better since they are applied to attributes of chemicals including stability, high boiling point, and strain energy.

For representing and comprehending intricate systems and interactions, graph theory provides a solid framework. With several practical applications, it offers methods and tools for solving issues with connectivity, structure, and optimisation in graphs. Molecular structure influences molecular properties, which supports the relationship between topological indices and a molecule’s physical-chemical properties³. Ediz et al.⁴ discussed the topological properties of the Sierpinski triangle networks using Van, R, and S indices. Ediz⁵ analyzed the graphene structure by using novel topological characteristics. Ciubotariu et al.⁶ describe how chemical structures are transformed into mathematical molecular descriptors for QSPR and QSAR analyses, which are essential for comprehending the physical, chemical, and biological aspects of objects. Also, they emphasize the significance of topological indices (TIs), which are primarily focused on shape and size variables and are generated from the topological distance matrix D, in assessing structural information in molecular graphs. The bibliometric analysis based on the first author’s work on Van, S topological indices is shown in Fig. 1.

Fig. 1

First author-based bibliography.

Let $G(\mathcal {V}, \mathcal {E})\cong B_{2}O_{3}$ be a molecular graph, with $\mathcal {V}$ representing an atom (vertex) and $\mathcal {E}$ representing a covalent bond (edge). The total number of bonds incident to a vertex u is called the degree of the vertex and is shown as $d_{u}$. The collection of the vertex that is neighboring u is denoted by $N_{u}$. The sum of all the degrees of vertices that are neighbouring to one another in v is called the degree sum of vertex v and is shown as $\mathcal {S}_{v}$. $\mathcal {M}$ stands for the multiplication of all the degrees of the vertex’s nearby vertices. The following are the definitions of degrees, such as $van(u)=\Omega _u=\frac{\mathcal {S}_{u}}{\mathcal {M}_{u}}$ and $s_{u}=|\mathcal {M}_{u}-\mathcal {S}_{u}|$. Reverse degrees, like $Van=\Omega$ and Sum (S), are defined as follows: $r\Omega _{u}=\frac{\mathcal {M}_{u}}{\mathcal {S}_{u}}$, and $rs_{u}=\frac{1}{|\mathcal {M}_{u}-\mathcal {S}_{u}|+1}$. Similar to $\Omega _{u}$ and $s_{u}$, the topological indices are defined as follows: The first Van index $\Lambda ^{1}$ of a molecular graph $(B_{2}O_{3})$ is.

$$\begin{aligned} \Lambda ^{1}(B_{2}O_{3})=\sum _{u\in \mathcal {V}(B_{2}O_{3})}(\Omega _{u})^{2} \end{aligned}$$

(1)

The second Van index $\Lambda ^{2}$ of a molecular graph $(B_{2}O_{3})$ is.

$$\begin{aligned} \Lambda ^{2}(B_{2}O_{3})=\sum _{uv\in \mathcal {E}(B_{2}O_{3})}(\Omega _{u}\times \Omega _{v}) \end{aligned}$$

(2)

The third Van index $\Lambda ^{3}$ of a molecular graph $(B_{2}O_{3})$ is.

$$\begin{aligned} \Lambda ^{3}(B_{2}O_{3})=\sum _{uv\in \mathcal {E}(B_{2}O_{3})}(\Omega _{u}+\Omega _{v}) \end{aligned}$$

(3)

The first reverse Van index $\Lambda ^{1r}$ of a molecular graph $(B_{2}O_{3})$ is.

$$\begin{aligned} \Lambda ^{1r}(B_{2}O_{3})=\sum _{v\in \mathcal {V}(B_{2}O_{3})}(r\Omega _{v})^{2} \end{aligned}$$

(4)

The second reverse Van index $\Lambda ^{2r}$ of a molecular graph $(B_{2}O_{3})$ is.

$$\begin{aligned} \Lambda ^{2r}(B_{2}O_{3})=\sum _{uv\in \mathcal {E}(B_{2}O_{3})}(r\Omega _{u}\times r\Omega _{v}) \end{aligned}$$

(5)

The third reverse Van index $\Lambda ^{3r}$ of a molecular graph $(B_{2}O_{3})$ is.

$$\begin{aligned} \Lambda ^{3r}(B_{2}O_{3})=\sum _{uv\in \mathcal {E}(B_{2}O_{3})}(r\Omega _{u}+r\Omega _{v}) \end{aligned}$$

(6)

The first S index $S^{1}$ of a molecular graph $(B_{2}O_{3})$ is.

$$\begin{aligned} S^{1}(B_{2}O_{3})=\sum _{v\in \mathcal {V}(B_{2}O_{3})}(s_{v})^{2} \end{aligned}$$

(7)

The second S index $S^{2}$ of a molecular graph $(B_{2}O_{3})$ is.

$$\begin{aligned} S^{2}(B_{2}O_{3})=\sum _{uv\in \mathcal {E}(B_{2}O_{3})}(s_{u}\times s_{v}) \end{aligned}$$

(8)

The third S index $S^{3}$ of a molecular graph $(B_{2}O_{3})$ is.

$$\begin{aligned} S^{3}(B_{2}O_{3})=\sum _{uv\in \mathcal {E}(B_{2}O_{3})}(s_{u}+s_{v}) \end{aligned}$$

(9)

The first reverse S index $S^{1r}$ of a molecular graph $(B_{2}O_{3})$ is.

$$\begin{aligned} S^{1r}(B_{2}O_{3})=\sum _{v\in \mathcal {V}(B_{2}O_{3})}(rs_{v})^{2} \end{aligned}$$

(10)

The second reverse S index $S^{2r}$ of a molecular graph $(B_{2}O_{3})$ is.

$$\begin{aligned} S^{2r}(B_{2}O_{3})=\sum _{uv\in \mathcal {E}(B_{2}O_{3})}(rs_{u}\times rs_{v}) \end{aligned}$$

(11)

The third reverse S index $S^{3r}$ of a molecular graph $(B_{2}O_{3})$ is.

$$\begin{aligned} S^{3r}(B_{2}O_{3})=\sum _{uv\in \mathcal {E}(B_{2}O_{3})}(rs_{u}+rs_{v}) \end{aligned}$$

(12)

Manzoor et al.⁷ examine graph entropies using a unique information function, taking into consideration the number of vertices with varying degrees and the connections that link them. In addition to a range of topological indices for these networks, Nandini et al.⁸ addressed the analytic formula for the thermodynamic entropies of pandemic trees based on the reproduction number (R0) and spread level. Using topological indices, Shanmukha et al.⁹ calculated the entropy of graphenylene. Using topological indices, Arockiaraj et al.¹⁰ examined the benzenoid medications and talked about their uses. Zhou et al.¹¹ discussed the On iron (II) chloride via graph entropy measures and statistical models. Koam et al.¹² analyzed structural properties of gamma-sheet of boron clusters. As per the topological index TI based definition of Shannon’s entropy for 2D networks, which is as follows:

$$\begin{aligned} Entropy_{(TI)}(B_{2}O_{3})=ENT_{(TI)}(B_{2}O_{3})=\log {(TI)}-\frac{1}{(TI)}\sum _{uv\in \mathcal {E}(B_{2}O_{3})}P(uv)\log (P(uv)) \end{aligned}$$

(13)

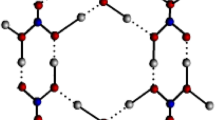
where P(uv) is the structural-functional identifier of the topological index. Three oxygen atoms are spaced 1.37 A apart from the boron atoms to form a triangle shape. Two boron atoms are bound to each oxygen atom, which adds to the material’s overall structure¹³. Because measured pair function regions displaying neutral atoms reveal that the bonding in vitreous $B_{2}O_{3}$ is mostly covalent. The work offered vital information for comprehending boron oxidation at the molecular level by shedding light on the stability and architecture of boron oxide clusters. Borosilicate glasses, which have a low thermal expansion coefficient and good thermal shock resistance, may be made using boron oxide. Because of its high melting point and hardness, it is used in the creation of specialized ceramics such as boron carbide and boron nitride¹⁴. In the semiconductor industry, boron oxide is used for doping, which modifies the electrical characteristics of materials. Figure 2 shows the molecular structure of boron oxide $(B_{2}O_{3})$.

Fig. 2

Boron oxide($B_{2}O_{3}$) structure.

Table 1 Vertex partition based on sum and multiplication.

By using the definitions of sum and multiplicative degree, we have obtained Table 1 showing the vertex partition based on sum and multiplication, and Table 2 showing the edge partition based on degree sum and multiplication, as well as reverse degree sum and multiplication.

Table 2 Edge partition of boron oxide.

Main results

In this section, we calculate the entropy, Van, and S indices. Extensive tables and pictorial representations are integrated to facilitate in-depth discussions and an exhaustive examination of the outcomes. To properly understand the effects of entropy measurements and generated indices, several visual elements are necessary. We gain a better grasp of the fundamental characteristics of the system we are researching by employing this tiered method. Basic measures like the computed Van and S indices aid in our understanding of the molecular structures and facilitate further research that follows.

Using Table 1 into Eq. 1, the first Van index is as follows:

$$\begin{aligned} \Lambda ^{1}(B_{2}O_{3})= & \sum _{i=1}^{7}\sum _{u\in \mathcal {V}_{i}(B_{2}O_{3})}(\Omega _{u})^{2}\\= & (1)^{2}(4mn)+\left(\frac{6}{9}\right)^{2}(10m+16n+8mn-12)+\left(\frac{7}{12}\right)^{2}(2m+4)+\left(\frac{8}{9}\right)^{2}(2mn)\\ & \quad +\left(\frac{9}{24}\right)^{2}(12m+8n+4mn-8)+\left(\frac{11}{48}\right)^{2}(16mn-8m)+\left(\frac{12}{81}\right)^{2}(10m+10n+4mn-12)\\ \Lambda ^{1}(B_{2}O_{3})= & 10.62637174mn + 6.611839849m + 8.455589849n - 5.360596708. \end{aligned}$$

Using Table 2 into Eq. 2, the second Van index is as follows:

$$\begin{aligned} \Lambda ^{2}(B_{2}O_{3})= & \sum _{i=1}^{11}\sum _{uv\in \mathcal {E}_{i}(B_{2}O_{3})}(\Omega _{u}\times \Omega _{v})\\= & \left(1\times \frac{8}{9}\right)(4mn)+\left(\frac{6}{9}\times \frac{7}{12}\right)(4mn+8)+\left(\frac{6}{9}\times \frac{9}{24}\right)(12m+8n-4m-8)+\left(\frac{7}{12}\times \frac{9}{24}\right)(2m+4)\\ & \quad +\left(\frac{8}{9}\times \frac{9}{24}\right)(2m)+\left(\frac{8}{9}\times \frac{11}{48}\right)(8mn-4n+6m+4)+\left(\frac{9}{24}\times \frac{9}{24}\right)(6m-4)\\ & \quad +\frac{9}{24}\times \frac{11}{48})(2m+8n-4mn+4)\\ & \quad +(\left(\frac{9}{24}\times \frac{12}{81}\right)(10m+8n-4mn+8)+\left(\frac{11}{48}\times \frac{11}{48}\right)(12mn-6m+8n+4)\\ & \quad +\left(\frac{11}{48}\times \frac{12}{81}\right)(36mn+38m-16n+48)\\ \Lambda ^{2}(B_{2}O_{3})= & 8.027199074mn + 4.866319444 + 6.872588735m + 2.194058642n. \end{aligned}$$

Using Table 2 into Eq. 3, the third Van index is as follows:

$$\begin{aligned} \Lambda ^{3}(B_{2}O_{3})= & \sum _{i=1}^{11}\sum _{uv\in \mathcal {E}_{i}\left(B_{2}O_{3}\right)}\left(\Omega _{u}+\Omega _{v}\right)\\= & \left(1+\frac{8}{9}\right)\left(4mn\right)+\left(\frac{6}{9}+\frac{7}{12}\right)\left(4mn+8\right)+\left(\frac{6}{9}+\frac{9}{24}\right)\left(12m+8n-4m-8\right)+\left(\frac{7}{12}+\frac{9}{24}\right)\left(2m+4\right)\\ & \quad +\left(\frac{8}{9}+\frac{9}{24}\right)\left(2m\right)+\left(\frac{8}{9}+\frac{11}{48}\right)\left(8mn-4n+6m+4\right)+\left(\frac{9}{24}+\frac{9}{24}\right)\left(6m-4\right)\\ & \quad +\left(\frac{9}{24}+\frac{11}{48}\right)\left(2m+8n-4mn+4\right)\\ & \quad +\left(\frac{9}{24}+\frac{12}{81}\right)\left(10m+8n-4mn+8\right)+\left(\frac{11}{48}+\frac{11}{48}\right)\left(12mn-6m+8n+4\right)\\ & \quad +\left(\frac{11}{48}+\frac{12}{81}\right)\left(36mn+38m-16n+48\right)\\ \Lambda ^{3}\left(B_{2}O_{3}\right)= & 36.07407407mn + 33.51851852 + 42.01388889m + 10.50925926n. \end{aligned}$$

Using Table 1 into Eq. 4, the first reverse Van index is as follows:

$$\begin{aligned} \Lambda ^{1r}\left(B_{2}O_{3}\right)= & \sum _{i=1}^{7}\sum _{u\in \mathcal {V}_{i}\left(B_{2}O_{3}\right)}\left(r\Omega _{u}\right)^{2}\\= & \left(1\right)^{2}\left(4mn\right)+\left(\frac{9}{6}\right)^{2}\left(10m+16n+8mn-12\right)+\left(\frac{12}{7}\right)^{2}\left(2m+4\right)+\left(\frac{9}{8}\right)^{2}\left(2mn\right)\\ & \quad +\left(\frac{24}{9}\right)^{2}\left(12m+8n+4mn-8\right)+\left(\frac{48}{11}\right)^{2}\left(16mn-8m\right)+\left(\frac{81}{12}\right)^{2}\left(10m+10n+4mn-12\right)\\= & 539.8868515mn + 417.0053058m + 548.5138889n - 618.883786. \end{aligned}$$

Using Table 2 into Eq. 5, the second reverse Van index is as follows:

$$\begin{aligned} \Lambda ^{2r}\left(B_{2}O_{3}\right)= & \sum _{i=1}^{11}\sum _{uv\in \mathcal {E}_{i}\left(B_{2}O_{3}\right)}\left(\Omega _{u}\times \Omega _{v}\right)\\= & \left(1\times \frac{9}{8}\right)\left(4mn\right)+\left(\frac{9}{6}\times \frac{12}{7}\right)\left(4mn+8\right)+\left(\frac{9}{6}\times \frac{24}{9}\right)\left(12m+8n-4m-8\right)+\left(\frac{12}{7}\times \frac{24}{9}\right)\left(2m+4\right)\\ & \quad +\left(\frac{9}{8}\times \frac{24}{9}\right)\left(2m\right)+\left(\frac{9}{8}\times \frac{48}{11}\right)\left(8mn-4n+6m+4\right)+\left(\frac{24}{9}\times \frac{24}{9}\right)\left(6m-4\right)\\ & \quad +\left(\frac{24}{9}\times \frac{48}{11}\right)\left(2m+8n-4mn+4\right)\\ & \quad +\left(\frac{24}{9}\times \frac{81}{12}\right)\left(10m+8n-4mn+8\right)+\left(\frac{48}{11}\times \frac{48}{11}\right)\left(12mn-6m+8n+4\right)\\ & \quad +\left(\frac{48}{11}\times \frac{81}{12}\right)\left(36mn+38m-16n+48\right)\\= & 1224.372491mn + 1678.577988 + 1327.561590m - 69.48760331n. \end{aligned}$$

Using Table 2 into Eq. 6, the third reverse Van index is as follows:

$$\begin{aligned} \Lambda ^{3r}\left(B_{2}O_{3}\right)= & \sum _{i=1}^{11}\sum _{uv\in \mathcal {E}_{i}\left(B_{2}O_{3}\right)}\left(\Omega _{u}+ \Omega _{v}\right)\\= & \left(1+ \frac{9}{8}\right)\left(4mn\right)+\left(\frac{9}{6}+ \frac{12}{7}\right)\left(4mn+8\right)+\left(\frac{9}{6}+ \frac{24}{9}\right)\left(12m+8n-4m-8\right)+\left(\frac{12}{7}+ \frac{24}{9}\right)\left(2m+4\right)\\ & \quad +\left(\frac{9}{8}+ \frac{24}{9}\right)\left(2m\right)+\left(\frac{9}{8}+ \frac{48}{11}\right)\left(8mn-4n+6m+4\right)+\left(\frac{24}{9}+ \frac{24}{9}\right)\left(6m-4\right)\\ & \quad +\left(\frac{24}{9}+ \frac{48}{11}\right)\left(2m+8n-4mn+4\right)\\ & \quad +\left(\frac{24}{9}+ \frac{81}{12}\right)\left(10m+8n-4mn+8\right)+\left(\frac{48}{11}+ \frac{48}{11}\right)\left(12mn-6m+8n+4\right)\\ & \quad +\left(\frac{48}{11}+ \frac{81}{12}\right)\left(36mn+38m-16n+48\right)\\= & \frac{221105}{462}mn - \frac{91087}{154} + \frac{21395}{42}m - \frac{2303}{22}n. \end{aligned}$$

Using Table 1 into Eq. 7, the first S index is as follows:

$$\begin{aligned} S^{1}\left(B_{2}O_{3}\right)= & \sum _{i=1}^{7}\sum _{v\in \mathcal {V}_{i}\left(B_{2}O_{3}\right)}\left(s_{v}\right)^{2}\\= & \left(0\right)^{2}\left(4mn\right)+\left(3\right)^{2}\left(10m+16n+8mn-12\right)+\left(5\right)^{2}\left(2m+4\right)+\left(1\right)^{2}\left(2mn\right)\\ & \quad +\left(15\right)^{2}\left(12m+8n+4mn-8\right)+\left(37\right)^{2}\left(16mn-8m\right)+\left(69\right)^{2}\left(10m+10n+4mn-12\right)\\= & 41922mn + 39498m + 49554n - 58940. \end{aligned}$$

Using Table 2 into Eq. 8, the second S index is as follows:

$$\begin{aligned} S^{2}\left(B_{2}O_{3}\right)= & \sum _{i=1}^{11}\sum _{uv\in \mathcal {E}_{i}\left(B_{2}O_{3}\right)}\left(s_{u}\times s_{v}\right)\\= & \left(0\times 1\right)\left(4mn\right)+\left(3\times 5\right)\left(4mn+8\right)+\left(3\times 15\right)\left(12m+8n-4m-8\right)+\left(5\times 15\right)\left(2m+4\right)\\ & \quad +\left(1\times 15\right)\left(2m\right)+\left(1\times 37\right)\left(8mn-4n+6m+4\right)+\left(15\times 15\right)\left(6m-4\right)\\ & \quad +\left(15\times 37\right)\left(2m+8n-4mn+4\right)\\ & \quad +\left(15\times 69\right)\left(10m+8n-4mn+8\right)+\left(37\times 37\right)\left(12mn-6m+8n+4\right)\\ & \quad +\left(37\times 69\right)\left(36mn+38m-16n+48\right)\\= & 102332mn + 102372m - 16964n + 137828. \end{aligned}$$

Using Table 2 into Eq. 9, the third S index is as follows:

$$\begin{aligned} S^{3}\left(B_{2}O_{3}\right)= & \sum _{i=1}^{11}\sum _{uv\in \mathcal {E}_{i}\left(B_{2}O_{3}\right)}\left(s_{u}+ s_{v}\right)\\= & \left(0+1\right)\left(4mn\right)+\left(3+5\right)\left(4mn+8\right)+\left(3+15\right)\left(12m+8n-4m-8\right)+\left(5+15\right)\left(2m+4\right)\\ & \quad +\left(1+15\right)\left(2m\right)+\left(1+37\right)\left(8mn-4n+6m+4\right)+\left(15+15\right)\left(6m-4\right)\\ & \quad +\left(15+37\right)\left(2m+8n-4mn+4\right)\\ & \quad +\left(15+69\right)\left(10m+8n-4mn+8\right)+\left(37+37\right)\left(12mn-6m+8n+4\right)\\ & \quad +\left(37+69\right)\left(36mn+38m-16n+48\right)\\= & 4500mn + 5152m - 24n + 6296. \end{aligned}$$

Using Table 1 into Eq. 10, the first reverse S index is as follows:

$$\begin{aligned} S^{1r}\left(B_{2}O_{3}\right)= & \sum _{i=1}^{7}\sum _{v\in \mathcal {V}_{i}\left(B_{2}O_{3}\right)}\left(rs_{v}\right)^{2}\\= & \left(1\right)^{2}\left(4mn\right)+\left(\frac{1}{4}\right)^{2}\left(10m+16n+8mn-12\right)+\left(\frac{1}{6}\right)^{2}\left(2m+4\right)+\left(\frac{1}{2}\right)^{2}\left(2mn\right)\\ & \quad +\left(\frac{1}{16}\right)^{2}\left(12m+8n+4mn-8\right)+\left(\frac{1}{38}\right)^{2}\left(16mn-8m\right)+\left(\frac{1}{70}\right)^{2}\left(10m+10n+4mn-12\right)\\= & 5.027521659mn + 0.7239312057m + 1.033290816n - 0.6725878685. \end{aligned}$$

Using Table 2 into Eq. 11, the second reverse S index is as follows:

$$\begin{aligned} S^{2r}\left(B_{2}O_{3}\right)= & \sum _{i=1}^{11}\sum _{uv\in \mathcal {E}_{i}\left(B_{2}O_{3}\right)}\left(rs_{u}\times rs_{v}\right)\\= & \left(1\times \frac{1}{2}\right)\left(4mn\right)+\left(\frac{1}{4}\times \frac{1}{6}\right)\left(4mn+8\right)+\left(\frac{1}{4}\times \frac{1}{16}\right)\left(12m+8n-4m-8\right)\\ & \quad +\left(\frac{1}{6}\times \frac{1}{16}\right)\left(2m+4\right)\\ & \quad +\left(\frac{1}{2}\times \frac{1}{16}\right)\left(2m\right)+\left(\frac{1}{2}\times \frac{1}{38}\right)\left(8mn-4n+6m+4\right)+\left(\frac{1}{16}\times \frac{1}{16}\right)\left(6m-4\right)\\ & \quad +\left(\frac{1}{16}\times \frac{1}{38}\right)\left(2m+8n-4mn+4\right)\\ & \quad +\left(\frac{1}{16}\times \frac{1}{70}\right)\left(10m+8n-4mn+8\right)+\left(\frac{1}{38}\times \frac{1}{38}\right)\left(12mn-6m+8n+4\right)\\ & \quad +\left(\frac{1}{38}\times \frac{1}{70}\right)\left(36mn+38m-16n+48\right)\\= & 2.283623533mn + 0.3215435793 + 0.1751720997m + 0.1974574594n. \end{aligned}$$

Using Table 2 into Eq. 12, the third reverse S index is as follows:

$$\begin{aligned} S^{3r}\left(B_{2}O_{3}\right)= & \sum _{i=1}^{11}\sum _{uv\in \mathcal {E}_{i}\left(B_{2}O_{3}\right)}\left(rs_{u}+ rs_{v}\right)\\= & \left(1+\frac{1}{2}\right)\left(4mn\right)+\left(\frac{1}{4}+\frac{1}{6}\right)\left(4mn+8\right)+\left(\frac{1}{4}+\frac{1}{16}\right)\left(12m+8n-4m-8\right)\\ & \quad +\left(\frac{1}{6}+\frac{1}{16}\right)\left(2m+4\right)\\ & \quad +\left(\frac{1}{2}+\frac{1}{16}\right)\left(2m\right)+\left(\frac{1}{2}+\frac{1}{38}\right)\left(8mn-4n+6m+4\right)+\left(\frac{1}{16}+\frac{1}{16}\right)\left(6m-4\right)\\ & \quad +\left(\frac{1}{16}+\frac{1}{38}\right)\left(2m+8n-4mn+4\right)\\ & \quad +\left(\frac{1}{16}+\frac{1}{70}\right)\left(10m+8n-4mn+8\right)+\left(\frac{1}{38}+\frac{1}{38}\right)\left(12mn-6m+8n+4\right)\\ & \quad +\left(\frac{1}{38}+\frac{1}{70}\right)\left(36mn+38m-16n+48\right)\\= & 13.30802005mn + 6.484210526 + 10.16378446m + 1.490977444n. \end{aligned}$$

Table 3 displays a numerical comparison of the indices. We see that the indices’ values rise quickly along with the values of m and n. To illustrate the graphical behaviour of the indices, we create 3D plots, as seen in Fig. 3.

Table 3 Comparative analysis of many indices numerically.

Fig. 3

Graphical behaviour of the indices.

We calculate various entropy values using the previously calculated indices. The entropy estimates provide important details on the level of disorder or uncertainty in the system under study.

The entropy linked to the first Van index is the first Van entropy, obtained using Table 1 in Eq. 13 as follows:

$$\begin{aligned} ENT_{{\Lambda ^{1} }} \left( {B_{2} O_{3} } \right) & = \log \left( {10.62637174mn + 6.611839849m + 8.455589849n - 5.360596708} \right) \\ & \quad - \left( {\frac{1}{{(10.62637174mn + 6.611839849m + 8.455589849n - 5.360596708)}}} \right)((4mn)(1)\log (1) \\ & \quad + \left( {10m + 16n + 8mn - 12} \right)\left( {\frac{4}{9}} \right)\log \left( {\frac{4}{9}} \right) + \left( {2m + 4} \right)\left( {\frac{{49}}{{144}}} \right)\log \left( {\frac{{49}}{{144}}} \right) + \left( {2mn} \right)\left( {\frac{{64}}{{81}}} \right)\log \left( {\frac{{64}}{{81}}} \right) \\ & \quad + \left( {12m + 8n + 4mn - 8} \right)\left( {\frac{9}{{64}}} \right)\log \left( {\frac{9}{{64}}} \right) + \left( {16mn - 8m} \right)\left( {\frac{{121}}{{2304}}} \right)\log \left( {\frac{{121}}{{2304}}} \right) \\ & \left. {\quad + \left( {10m + 10n + 4mn - 12} \right)\left( {\frac{{16}}{{729}}} \right)\log \left( {\frac{{16}}{{729}}} \right)} \right) \\ \end{aligned}$$

The entropy linked to the second Van index is second Van entropy, obtained using Table 2 in Eq. 13 as follows:

$$\begin{aligned} ENT_{{\Lambda ^{2} }} \left( {B_{2} O_{3} } \right) & = \log \left( {8.027199074mn + 4.866319444 + 6.872588735m + 2.194058642n} \right) \\ & \quad - \left( {\frac{1}{{(8.027199074mn + 4.866319444 + 6.872588735m + 2.194058642n)}}} \right) + ((4mn)\left( {\frac{8}{9}} \right)\log \left( {\frac{8}{9}} \right) \\ & \quad + (4mn + 8)\left( {\frac{7}{{18}}} \right)\log \left( {\frac{7}{{18}}} \right) + (12m + 8n - 4m - 8)\left( {\frac{1}{4}} \right)\log \left( {\frac{1}{4}} \right) + (2m + 4)\left( {\frac{7}{{32}}} \right)\log \left( {\frac{7}{{32}}} \right) \\ & \quad + (2m)\left( {\frac{1}{3}} \right)\log \left( {\frac{1}{3}} \right) + 8mn - 4n + 6m + 4)\left( {\frac{{11}}{{54}}} \right)\log \left( {\frac{{11}}{{54}}} \right) + (6m - 4)\left( {\frac{9}{{64}}} \right)\log \left( {\frac{9}{{64}}} \right) \\ & \quad + (2m + 8n - 4mn + 4)\left( {\frac{{11}}{{128}}} \right)\log \left( {\frac{{11}}{{128}}} \right) + (10m + 8n - 4mn + 8)\left( {\frac{1}{{18}}} \right)\log \left( {\frac{1}{{18}}} \right) \\ & \quad + (12mn - 6m + 8n + 4)\left( {\frac{{121}}{{2304}}} \right)\log \left( {\frac{{121}}{{2304}}} \right) + (36mn + 38m - 16n + 48)\left( {\frac{{11}}{{324}}} \right)\left. {\log \left( {\frac{{11}}{{324}}} \right)} \right) \\ \end{aligned}$$

The entropy linked to the third Van index is the third Van entropy, obtained using Table 2 in Eq. 13 as follows:

$$\begin{aligned} ENT_{{\Lambda ^{3} }} \left( {B_{2} O_{3} } \right) & = \log \left( {36.07407407mn + 33.51851852 + 42.01388889m + 10.50925926n} \right) \\ & \quad - \left( {\frac{1}{{(36.07407407mn + 33.51851852 + 42.01388889m + 10.50925926n)}}} \right) + ((4mn)\left( {\frac{{17}}{9}} \right)\log \left( {\frac{{17}}{9}} \right) \\ & \quad + (4mn + 8)\left( {\frac{5}{4}} \right)\log \left( {\frac{5}{4}} \right) + (12m + 8n - 4m - 8)\left( {\frac{{25}}{{24}}} \right)\log \left( {\frac{{25}}{{24}}} \right) + (2m + 4)\left( {\frac{{23}}{{24}}} \right)\log \left( {\frac{{23}}{{24}}} \right) \\ & \quad + (2m)\left( {\frac{{91}}{{72}}} \right)\log \left( {\frac{{91}}{{72}}} \right) + 8mn - 4n + 6m + 4)\left( {\frac{{161}}{{144}}} \right)\log \left( {\frac{{161}}{{144}}} \right) + (6m - 4)\left( {\frac{3}{4}} \right)\log \left( {\frac{3}{4}} \right) \\ & \quad + (2m + 8n - 4mn + 4)\left( {\frac{{29}}{{48}}} \right)\log \left( {\frac{{29}}{{48}}} \right) + (10m + 8n - 4mn + 8)\left( {\frac{{113}}{{216}}} \right)\log \left( {\frac{{113}}{{216}}} \right) \\ & \quad + (12mn - 6m + 8n + 4)\left( {\frac{{11}}{{44}}} \right)\log \left( {\frac{{11}}{{44}}} \right) + (36mn + 38m - 16n + 48)\left( {\frac{{163}}{{432}}} \right)\left. {\log \left( {\frac{{163}}{{432}}} \right)} \right) \\ \end{aligned}$$

When the first reverse Van index and Table 1 are put in Eq. 13 , the third Van entropy, which is associated with the first reverse Van index, is derived as follows:

$$\begin{aligned} ENT_{{\Lambda ^{{1r}} }} \left( {B_{2} O_{3} } \right) & \quad = \log \left( {539.8868515mn + 417.0053058m + 548.5138889n - 618.883786} \right) \\ & \quad - \left( {\frac{1}{{(539.8868515mn + 417.0053058m + 548.5138889n - 618.883786)}}} \right)((4mn)(1)\log (1) \\ & \quad + (10m + 16n + 8mn - 12)\left( {\frac{9}{4}} \right)\log \left( {\frac{9}{4}} \right) + (2m + 4)\left( {\frac{{144}}{{49}}} \right)\log \left( {\frac{{144}}{{49}}} \right) + (2mn)\left( {\frac{{81}}{{64}}} \right)\log \left( {\frac{{81}}{{64}}} \right) \\ & \quad + (12m + 8n + 4mn - 8)\left( {\frac{{64}}{9}} \right)\log \left( {\frac{{64}}{9}} \right) + (16mn - 8m)\left( {\frac{{2304}}{{121}}} \right)\log \left( {\frac{{2304}}{{121}}} \right) \\ & \quad + (10m + 10n + 4mn - 12)\left( {\frac{{729}}{{16}}} \right)\left. {\log \left( {\frac{{729}}{{16}}} \right)} \right) \\ \end{aligned}$$

When the second reverse Van index and Table 2 are put in Eq. 13 , the third Van entropy, which is associated with the second reverse Van index, is derived as follows:

$$\begin{aligned} ENT_{{\Lambda ^{{2r}} }} \left( {B_{2} O_{3} } \right) & = \log \left( {1224.372491mn + 1678.577988 + 1327.561590m - 69.48760331n} \right) \\ & \quad - \left( {\frac{1}{{(1224.372491mn + 1678.577988 + 1327.561590m - 69.48760331n)}}} \right) + ((4mn)\left( {\frac{9}{8}} \right)\log \left( {\frac{9}{8}} \right) \\ & \quad + (4mn + 8)\left( {\frac{{18}}{7}} \right)\log \left( {\frac{{18}}{7}} \right) + (12m + 8n - 4m - 8)(4)\log (4) + (2m + 4)\left( {\frac{{32}}{7}} \right)\log \left( {\frac{{32}}{7}} \right) \\ & \quad + (2m)(3)\log (3) + 8mn - 4n + 6m + 4)\left( {\frac{{54}}{{11}}} \right)\log \left( {\frac{{54}}{{11}}} \right) + (6m - 4)\left( {\frac{{64}}{9}} \right)\log \left( {\frac{{64}}{9}} \right) \\ & \quad + (2m + 8n - 4mn + 4)\left( {\frac{{128}}{{11}}} \right)\log \left( {\frac{{128}}{{11}}} \right) + (10m + 8n - 4mn + 8)(18)\log (18) \\ & \quad + (12mn - 6m + 8n + 4)\left( {\frac{{2304}}{{121}}} \right)\log \left( {\frac{{2304}}{{121}}} \right) + (36mn + 38m - 16n + 48)\left( {\frac{{324}}{{11}}} \right)\left. {\log \left( {\frac{{324}}{{11}}} \right)} \right) \\ \end{aligned}$$

When the third reverse Van index and Table 2 are put in Eq. 13 , the third Van entropy, which is associated with the third reverse Van index, is derived as follows:

$$\begin{aligned} ENT_{{\Lambda ^{{3r}} }} \left( {B_{2} O_{3} } \right) & = \log \left( {504.2965368mn + 682.3441558 + 592.7922078m + 34.95454545n} \right) \\ & \quad - \left( {\frac{1}{{(504.2965368mn + 682.3441558 + 592.7922078m + 34.95454545n)}}} \right)((4mn)\left( {\frac{{17}}{8}} \right)\log \left( {\frac{{17}}{8}} \right) \\ & \quad + (4mn + 8)\left( {\frac{{45}}{{14}}} \right)\log \left( {\frac{{45}}{{14}}} \right) + (12m + 8n - 4m - 8)\left( {\frac{{25}}{6}} \right)\log \left( {\frac{{25}}{6}} \right) + (2m + 4)\left( {\frac{{92}}{{21}}} \right)\log \left( {\frac{{92}}{{21}}} \right) \\ & \quad + (2m)\left( {\frac{{91}}{{24}}} \right)\log \left( {\frac{{91}}{{24}}} \right) + 8mn - 4n + 6m + 4)\left( {\frac{{483}}{{88}}} \right)\log \left( {\frac{{483}}{{88}}} \right) + (6m - 4)\left( {\frac{{16}}{3}} \right)\log \left( {\frac{{16}}{3}} \right) \\ & \quad + (2m + 8n - 4mn + 4)\left( {\frac{{232}}{{33}}} \right)\log \left( {\frac{{232}}{{33}}} \right) + (10m + 8n - 4mn + 8)\left( {\frac{{113}}{{12}}} \right)\log \left( {\frac{{113}}{{12}}} \right) \\ & \quad + (12mn - 6m + 8n + 4)\left( {\frac{{96}}{{11}}} \right)\log \left( {\frac{{96}}{{11}}} \right) + (36mn + 38m - 16n + 48)\left( {\frac{{489}}{{44}}} \right)\left. {\log \left( {\frac{{489}}{{44}}} \right)} \right) \\ \end{aligned}$$

When the first S index and Table 2 are put in Eq. 13 , the third Van entropy, which is associated with the S index, is derived as follows:

$$\begin{aligned} ENT_{{S^{1} }} \left( {B_{2} O_{3} } \right) & = \log \left( {41922mn + 39498m + 49554n - 58940} \right) \\ & \quad - \left( {\frac{1}{{(41922mn + 39498m + 49554n - 58940)}}} \right)((10m + 16n + 8mn - 12)(9)\log (9) \\ & \quad + (2m + 4)(25)\log (25) + (2mn)(1)\log (1) + (12m + 8n + 4mn - 8)(225)\log (225) \\ & \quad + (16mn - 8m)(1369)\log (1369) + (10m + 10n + 4mn - 12)(4761)\log (4761)) \\ \end{aligned}$$

The entropy linked to the second S index is the second S entropy, which is obtained as follows when $m.n\ge {2}$, Table 2, and then the second S index are put in Eq. 13:

$$\begin{aligned} ENT_{{S^{2} }} \left( {B_{2} O_{3} } \right) & = \log \left( {102332mn + 102372m - 16964n + 137828} \right) \\ & \quad - \left( {\frac{1}{{(102332mn + 102372m - 16964n + 137828)}}} \right) + (4mn + 8)(15)\log (15) \\ & \quad + (12m + 8n - 4m - 8)(45)\log (45) + (2m + 4)(75)\log (75) \\ & \quad + (2m)(15)\log (15) + 8mn - 4n + 6m + 4)(37)\log (37) + (6m - 4)(225)\log (225) \\ & \quad + (2m + 8n - 4mn + 4)(555)\log (555) + (10m + 8n - 4mn + 8)(1035)\log (1035) \\ & \quad + (12mn - 6m + 8n + 4)(1369)\log (1369) + (36mn + 38m - 16n + 48)(2553)\log (2553)) \\ \end{aligned}$$

The entropy linked to the third S index is the third S entropy obtained as follows, where Table 2 and the third S index are put in Eq. 13:

$$\begin{aligned} ENT_{{S^{3} }} \left( {B_{2} O_{3} } \right) & = \log (4500mn + 5152m - 24n + 6296) \\ & \quad - \left( {\frac{1}{{(4500mn + 5152m - 24n + 6296)}}} \right)((4mn)(1)\log (1) \\ & \quad + (4mn + 8)(8)\log (8) + (12m + 8n - 4m - 8)(18)\log (18) \\ & \quad + (2m + 4)(20)\log (20) + (2m)(16)\log (16) + 8mn - 4n + 6m + 4)(38)\log (38) \\ & \quad + (6m - 4)(30)\log (30) + (2m + 8n - 4mn + 4)(52)\log (52) \\ & \quad + (10m + 8n - 4mn + 8)(84)\log (84) + (12mn - 6m + 8n + 4)(74)\log (74) \\ & \quad + (36mn + 38m - 16n + 48)(106)\log (106)) \\ \end{aligned}$$

The entropy associated with the first reverse S index is the first reverse S entropy determined as follows, where Table 1 and the first reverse S index are put in Eq. 13.

$$\begin{aligned} ENT_{{S^{{1r}} }} \left( {B_{2} O_{3} } \right) & = \log \left( {5.027521659mn + 0.7239312057m + 1.033290816n - 0.6725878685} \right) \\ & \quad - \left( {\frac{1}{{(5.027521659mn + 0.7239312057m + 1.033290816n - 0.6725878685)}}} \right)((4mn)(1)^{2} \log (1)^{2} \\ & \quad + (10m + 16n + 8mn - 12)\left( {\frac{1}{{16}}} \right)\log \left( {\frac{1}{{16}}} \right) + (2m + 4)\left( {\frac{1}{{36}}} \right)\log \left( {\frac{1}{{36}}} \right) + (2mn)\left( {\frac{1}{4}} \right)\log \left( {\frac{1}{4}} \right) \\ & \quad + (12m + 8n + 4mn - 8)\left( {\frac{1}{{256}}} \right)\log \left( {\frac{1}{{256}}} \right) + (16mn - 8m)\left( {\frac{1}{{1444}}} \right)\log \left( {\frac{1}{{1444}}} \right) \\ & \quad + (10m + 10n + 4mn - 12)\left( {\frac{1}{{4900}}} \right)\left. {\log \left( {\frac{1}{{4900}}} \right)} \right) \\ \end{aligned}$$

The entropy linked to the second reverse S index is the second reverse S entropy obtained as follows, where Table 2 and the second reverse S index are put in Eq. 13:

$$\begin{aligned} ENT_{{S^{{2r}} }} \left( {B_{2} O_{3} } \right) & = \log (2.283623533mn + 0.3215435793 + 0.1751720997m + 0.1974574594n) \\ & \quad - \left( {\frac{1}{{(2.283623533mn + 0.3215435793 + 0.1751720997m + 0.1974574594n)}}} \right) + ((4mn)\left( {\frac{1}{2}} \right)\log \left( {\frac{1}{2}} \right) \\ & \quad + (4mn + 8)\left( {\frac{1}{{24}}} \right)\log \left( {\frac{1}{{24}}} \right) + (12m + 8n - 4m - 8)\left( {\frac{1}{{64}}} \right)\log \left( {\frac{1}{{64}}} \right) + (2m + 4)\left( {\frac{1}{{96}}} \right)\log \left( {\frac{1}{{96}}} \right) \\ & \quad + (2m)\left( {\frac{1}{{32}}} \right)\log \left( {\frac{1}{{32}}} \right) + 8mn - 4n + 6m + 4)\left( {\frac{1}{{76}}} \right)\log \left( {\frac{1}{{76}}} \right) + (6m - 4)\left( {\frac{1}{{256}}} \right)\log \left( {\frac{1}{{256}}} \right) \\ & \quad + (2m + 8n - 4mn + 4)\left( {\frac{1}{{608}}} \right)\log \left( {\frac{1}{{608}}} \right) + (10m + 8n - 4mn + 8)\left( {\frac{1}{{1120}}} \right)\log \left( {\frac{1}{{1120}}} \right) \\ & \quad + (12mn - 6m + 8n + 4)\left( {\frac{1}{{1444}}} \right)\log \left( {\frac{1}{{1444}}} \right) + (36mn + 38m - 16n + 48)\left( {\frac{1}{{2660}}} \right)\left. {\log \left( {\frac{1}{{2660}}} \right)} \right) \\ \end{aligned}$$

The entropy linked to the third reverse S index is the third reverse S entropy that is obtained as follows when Table 2 and the third reverse S index are put in Eq. 13:

$$\begin{aligned} ENT_{{S^{{3r}} }} \left( {B_{2} O_{3} } \right) & = \log \left( {13.30802005mn + 6.484210526 + 10.16378446m + 1.490977444nn} \right) \\ & \quad - \left( {\frac{1}{{(13.30802005mn + 6.484210526 + 10.16378446m + 1.490977444nn)}}} \right)((4mn)\left( {\frac{3}{2}} \right)\log \left( {\frac{3}{2}} \right) \\ & \quad + (4mn + 8)\left( {\frac{5}{{12}}} \right)\log \left( {\frac{5}{{12}}} \right) + (12m + 8n - 4m - 8)\left( {\frac{5}{{16}}} \right)\log \left( {\frac{5}{{16}}} \right) + (2m + 4)\left( {\frac{{11}}{{48}}} \right)\log \left( {\frac{{11}}{{48}}} \right) \\ & \quad + (2m)\left( {\frac{9}{{16}}} \right)\log \left( {\frac{9}{{16}}} \right) + 8mn - 4n + 6m + 4)\left( {\frac{{10}}{{19}}} \right)\log \left( {\frac{{10}}{{19}}} \right) + (6m - 4)\left( {\frac{1}{8}} \right)\log \left( {\frac{1}{8}} \right) \\ & \quad + (2m + 8n - 4mn + 4)\left( {\frac{{27}}{{304}}} \right)\log \left( {\frac{{27}}{{304}}} \right) + (10m + 8n - 4mn + 8)\left( {\frac{{43}}{{560}}} \right)\log \left( {\frac{{43}}{{560}}} \right) \\ & \quad + (12mn - 6m + 8n + 4)\left( {\frac{1}{{19}}} \right)\log \left( {\frac{1}{{19}}} \right) + (36mn + 38m - 16n + 48)\left( {\frac{{27}}{{665}}} \right)\left. {\log \left( {\frac{{27}}{{665}}} \right)} \right) \\ \end{aligned}$$

The numerical comparison between entropies is shown in Table 4. We observe that when we increase the values of m and n the value of the entropies also increases rapidly. We draw 3D plots as shown in Fig. 4 to see the graphical behaviour of the entropies.

Table 4 Comparative analysis of many entropies numerically.

Fig. 4

Graphical behaviour of the entropies.

Pearson correlation coefficient

A statistical tool used to quantify the strength of a linear relationship between two variables is the Pearson correlation. A perfect positive linear relationship is represented by a value of 1, a perfect negative linear relationship by a value of -1, and no linear relationship by a value of 0. The notation of first, second, and third van indices, and the reverse of first, second, and third van indices and entropies are shown as V1, V2, V3, VR1, VR2, VR3, EV1, EV2, EV3, EVR1, EVR2, EVR3, respectively. The notation of first, second, and third S indices, and the reverse of first, second, and third S indices and entropies are shown as S1, S2, S3, SR1, SR2, SR3, ES1, ES2, ES3, ESR1, ESR2, ESR3, respectively The Pearson correlation coefficient, which calculates the linear correlation between entropy and indices, is shown in Fig. 5.

The Pearson correlation coefficient (r) is calculated as follows:

$$r = \frac{{\sum {( {{\mathcal{X}}_{i} - \overline{{\mathcal{X}}} } } ( {{\mathcal{Y}}_{i} - \overline{{\mathcal{Y}}} } }}{{\sqrt {\sum {( {{\mathcal{X}}_{i} - \overline{{\mathcal{X}}} } ^{2} } ( {{\mathcal{Y}}_{i} - \overline{{\mathcal{Y}}} } ^{2} } }}$$

The summations in this instance are applied to all data points, the means of the related variables are $\mathcal {X}$ and $\mathcal {Y}$, and the individual data points are represented by $\mathcal {X}_{i}$ and $\mathcal {Y}_{i}$. Using the formula’s numerator and denominator, one can determine the covariance between the two variables (the numerator and denominator). Next, a number between $-1$ and 1 is obtained by normalizing the numerator using the denominator, which is the total of their standard deviations.

The Pearson correlation coefficient, a statistical measure that indicates the degree and direction of a linear relationship, helps assess the relationship between variables. As seen in Fig. 5, the heatmap displays the correlation coefficients between entropy and indices, indicating either positive or negative correlations between them.

Figure 6a depicts an intriguing situation in which the Pearson correlation coefficient between all indices is precisely 1. A heat map of this scenario demonstrates that there is a perfect and very strong positive linear connection between every possible pair of indices. This occurs when all of the variables or indices in the dataset move in perfect sync with each other. To be clear, all the other indices rise or decrease concurrently with the rise of any one indicator, and vice versa. This level of connectedness is often observed in intentionally generated or highly controlled datasets where variables are selected with the intention of proving exact correlations specific to a given analytical goal.

As Figure 6b illustrates, the correlation coefficients are often between 0.84 and 1 for most of the entropies that are taken into account. When the correlation is 1, these entropies increase simultaneously, indicating a perfect positive linear connection. There is one notable exception to the generality of correlations. Compared to the other correlations, the correlation with the entropies is lower than 1, ranging from 0.84 to 1.

Fig. 5

Pearson correlation heat map between entropy and several indices.

Figure 5 illustrates the linear Pearson correlation coefficient correlations between various indices and entropy levels using a heatmap visualisation. Values on the diagonal, as expected 1.0, represent the perfect self-correlation. Only Van, S, and entropy measures are highly positively correlated with each other, and all the other variables have weak correlations with the other variables in the same group. This indicates that those variables probably measure to some extend the same underlying phenomenon, and thus their relation should be driven by the same factors. Some moderate to high positive correlations ($0.8< r < 0.9$) between the Van/S indices and entropy variables further support the importance of linear associations but not perfect ones. It seems as if negative correlations are relatively rare, but sometimes specific Van indices and entropy measures have inverse relationships. This suggests that within each group there is high consistency, or perhaps redundancy.

Fig. 6

(a) Pearson correlation for indices. (b) Pearson correlation for entropy.

Conclusion

Our analysis, in which we calculated Van and S indices and entropy-based measures, followed by Pearson correlations, shows total significant linear relationships between the variables. The heatmap indicates very high positive correlations between the Van, S indices and entropies, so the latter 3 groups probably map to similar latent factors. The high internal consistency of the results indicates that many of the indicators used might be redundant, prompting further refactoring of the dataset using dimensionality reduction methods and helping to streamline the dataset without loss of information to a large extent. Furthermore, there was evidence of robust linear associations with moderate-to-strong positive correlations of the Van, S indices with the entropy variables. Negative correlations are a more occasional occurrence and tend to suggest particular inverse relationships that deserve a closer look.