Enhancement of groundwater resources quality prediction by machine learning models on the basis of an improved DRASTIC method

Abstract

Determining situation of groundwater vulnerability plays a crucial role in studying the groundwater resource management. Generally, the preparation of reliable groundwater vulnerability maps provides targeted and practical scientific measures for the protection and management of groundwater resources. In this study, in order to evaluate the groundwater vulnerability of Kerman–Baghin plain aquifer, two developed indicators including composite DRASTIC index (CD) and nitrate vulnerability index (NVI) based on DRASTIC index were considered. Soft computing methods, including Gene Expression Programming (GEP), Evolutionary Polynomial Regression (EPR), Multivariate Adaptive Regression Spline (MARS), and M5 Model Tree (MTM5) have been used to provide formulations for prediction of NVI. Soft computing techniques were fed nine input parameters: depth to water level, net recharge, aquifer environment, soil environment, topography, effect of unsaturated area, hydraulic conductivity, land use, and potential risk related to land use. After calculating the vulnerability by soft computing methods, the results showed that the EPR model with Correlation Coefficient (R) of 0.9999 and Root Mean Square Error (RMSE) = 0.2105 has the best performance in the testing stage in comparison with MARS (R = 0.9966 and RMSE = 2.408), M5MT (R = 0.9956 and RMSE = 2.988), and GEP (R = 0.9920 and RMSE = 3.491). Although the EPR and GEP models have more complex mathematical computations than other soft computing models, the MARS and MT model that have quadratic polynomial and multivariable linear structures respectively, can be considered as the best alternative. According to the MARS model, the vulnerability of the region is divided into two categories: very low vulnerability (73.06%) and low vulnerability (26.94%). Overall, the statistical results of soft computing techniques were indicative of effective formulations for evaluating the DRASTIC index.

Introduction

As the main concern, water scarcity is accelerating due to the destruction of available water resources and an increase in environmental contamination in dry and semi-dry areas. Due to the negative impacts on human health and ecosystem services, groundwater pollution is a global problem. As a complex and long-term process, pollution of groundwater resources is irrecoverable and costly to treat due to the large volume of the reservoir, long time, and lack of physical access to the reservoir. Therefore, the prevention of aquifer pollution is a necessity for the stability and protection of groundwater resources (e.g.^{1,2,3,4,5,6,7,8,9,10,11}).

Since protecting groundwater from pollution is much simpler and more logical than removing it, so identifying pollution-prone-aquifer is the first step to preventing groundwater pollution. This identification allows the area to be subdivided into sub-areas in terms of the severity of the vulnerability and relevant measures to be taken to prevent contamination of vulnerable areas. Therefore, groundwater vulnerability and risk maps are the prime cause in the management and safeguarding of groundwater resources (e.g.^12,13). Due to the expensive and time-intensive nature of groundwater sampling and quality monitoring, therefore, there is an essential need for groundwater vulnerability modeling as a fast and reliable tool to investigate groundwater aquifer vulnerability³. It is accompanied by understanding the possible events of pollution and determining the extent of pollutants and describing them (e.g.^14,15,16,17). Models for groundwater vulnerability take into account a range of factors to evaluate the likelihood of groundwater pollution. These factors typically fall into different categories: hydrogeological elements (i.e., hydraulic conductivity, porosity, depth to water table), geological factors (i.e., nature of subsurface materials and structural features), Land Use and Land Cover (i.e., type of land use and presence of impervious surfaces), source of pollution (i.e., proximity to potential contaminant sources and depth of the contaminant source), hydraulic factors (i.e., groundwater flow velocity and direction of groundwater flow), climate and hydrological conditions (precipitation patterns and temperature), depth and construction of wells, soil type and properties, soil permeability, and unsaturated zone properties (e.g.^18,19,20).

Integrating these elements into a groundwater vulnerability model aids in pinpointing districts that are at a higher risk of contamination, aiding in the improvements of methods for groundwater protection and management. While groundwater vulnerability models employ comparable influential factors, they adopt distinct methods for integrating and analyzing data. In general, three categories of methods exist for evaluating vulnerability, namely Point Count System Models (PCSM) (or ranking and weighting methods), statistical methods, and process methods (e.g.^18,21,22). Index and overlap methods consider the combination of different regional maps with the assignment of a numerical index¹⁹. Among these methods, DRASTIC, SINTACS, and Susceptibility Index (SI) are introduced as the most widely used techniques due to their simplicity, the need for minimal data, and the provision of a clear description of groundwater vulnerability. DRASTIC is a numerical model first proposed by the US Environmental Protection Agency (USEPA) in order to appraise the potential for aquifer contamination while considering hydrogeological data²³.

There are a plenty of research works in which circumstances of groundwater vulnerability have been investigated for diverse parts of the world (e.g.^{24,25,26,27,28,29}). Since the main problem of this model is to apply expert opinions to rank and weight the effective factors used in it, therefore the need to apply Artificial Intelligence (AI) models so as to improve rankings and optimize weights, that have been applied in DRASTIC evaluation, is of utmost importance for enhancement of the accuracy of susceptibility results (e.g.^{24,30,31,32,33,34,35}). Table 1 summarized the explored literature review of AI models applications into vulnerability indices of groundwater resources.

Table 1 List of related research works.

When evaluating the prediction of the DRASTIC index for groundwater resource quality, it is important to consider the drawbacks of other AI models such as Support Vector Machines (SVM), Random Forests (RF), and Deep Learning models. SVMs, while effective in handling high-dimensional data and finding complex decision boundaries, can be challenging to tune. Their performance is highly dependent on the choice of kernel and parameters, which may require extensive cross-validation. Additionally, SVMs can struggle with large datasets, as their computational complexity increases significantly with the number of samples, leading to longer training times and potentially less interpretable results. Random Forests are known for their robustness and ability to handle nonlinear relationships. However, they can produce models that are difficult to interpret, as the ensemble approach obscures individual feature contributions. While they generally perform well in many scenarios, they may not always capture subtle interactions effectively, particularly in cases where relationships among variables are not purely additive. Moreover, Deep Learning models, particularly neural networks, have gained popularity due to their ability to model complex patterns in large datasets. However, they require large amounts of training data to generalize well, which may not be available in many environmental contexts. Additionally, deep learning models often act as "black boxes," making it difficult to extract interpretable insights, which is a significant drawback in environmental assessments where understanding the relationship between variables is crucial.

In contrast, Gene-Expression Programming (GEP), Evolutionary Polynomial Regression (EPR), Multivariate Adaptive Regression Spline (MARS), and Model Tree (MT) offer several advantages in the evaluation of groundwater quality. GEP is capable of generating interpretable models that represent relationships in a tree-like structure, making it easier to understand how inputs affect predictions. It combines the adaptability of genetic programming with a focus on evolving mathematical expressions, which can capture complex interactions effectively. EPR stands out for its ability to evolve polynomial equations that fit the data without requiring a predefined model structure. This flexibility allows for a tailored approach to modeling complex relationships, making it suitable for capturing the intricacies of groundwater pollution dynamics. MARS is particularly adept at identifying and modeling nonlinearities and interactions between variables. Its piecewise linear approach allows it to fit models that can adapt to changes in the data, enhancing predictive performance while maintaining a degree of interpretability. MTM5, as a variant of Model Trees, combines decision tree structures with linear regression, enabling it to capture both local patterns and overall trends. This dual approach enhances its interpretability and provides insights into how different factors influence the DRASTIC index.

Overall, the use of GEP, EPR, MARS, and MT in predicting the DRASTIC index offers a balanced approach that combines flexibility, interpretability, and robustness. These models are particularly well-suited for environmental applications, where understanding the underlying relationships is as important as achieving accurate predictions. In predicting the DRASTIC index for groundwater resource quality using nine input parameters—depth to water level, net recharge, aquifer environment, soil environment, topography, effect of unsaturated area, hydraulic conductivity, land use, and potential risk related to land use—it’s important to evaluate the limitations of certain AI models like SVM, RF, and Deep Learning models. As a major drawbacks of other AI models, SVMs are effective for classification tasks but can face challenges with the high dimensionality of groundwater data. Tuning SVM requires careful selection of hyperparameters, and the model can become sensitive to noise in the data. Additionally, the interpretability of SVM is limited; understanding how input parameters influence the DRASTIC index can be difficult. RF, while robust and capable of handling nonlinear relationships, tend to produce complex ensemble models that lack transparency. It can be hard to ascertain the importance of individual parameters, which is critical for understanding groundwater pollution dynamics. Moreover, RF may not effectively model interactions unless they are explicitly captured in the trees. Deep Learning models excel at handling large datasets and capturing intricate patterns. However, they require significant amounts of training data, which may not be available in groundwater studies. Their “black box” nature makes it challenging to extract interpretable insights about parameter influences, reducing their utility for environmental management.

Overall, the selection of GEP, EPR, MARS, and MTM5 provides a robust framework for modeling the DRASTIC index. These models not only capture complex relationships among the input parameters but also offer greater transparency and interpretability, which are vital for effective groundwater resource management.

The novelty of the present paper lies in several key contributions that differentiate it from previously published works. Firstly, the integration of diverse machine learning methodologies—including classification, regression splines, and evolutionary computing—provides a comprehensive framework for enhancing DRASTIC index predictions. While prior studies may have focused on individual techniques, this paper offers a comparative analysis that highlights the strengths and weaknesses of each approach in the context of groundwater quality assessment. Secondly, the paper addresses specific limitations observed in the existing literature, particularly concerning the interpretability and robustness of predictions. By utilizing models like GEP, EPR, MARS, and MT, the present AI models not only improves predictive accuracy but also provides clear insights into the relationships among input parameters. This dual focus on performance and interpretability is a significant advancement over many existing models that prioritize accuracy at the expense of transparency. Moreover, the paper contributes to the field by incorporating a comprehensive set of nine input parameters that reflect the multifaceted nature of groundwater quality assessment. This nuanced approach contrasts with previous studies that may have simplified their analyses by using fewer parameters, thus potentially overlooking critical interactions. The literature review within the paper serves as a critical foundation, highlighting gaps in previous research and justifying the need for this novel approach. By systematically comparing their results with those from established studies, the authors demonstrate the superiority of their model in terms of predictive capability and practical applicability. Overall, this paper presents a significant advancement in the modeling of groundwater resource quality, bridging the gap between sophisticated machine learning techniques and practical environmental applications. Its contributions not only enhance the understanding of groundwater dynamics but also provide valuable tools for policymakers and resource managers striving for sustainable water management.

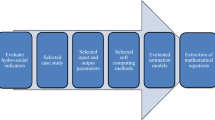
In this study, the standard DRASTIC framework is modified by land use and nitrate pollution effects. After that, four AI models (i.e., MARS, EPR, GEP, and MT) are applied to evaluate the situation of vulnerability of nitrate pollutions in the arid regions of Kerman plain, southwestern Iran. This research integrates the results with the land use map in order to foster precision degree in preparing the spatial distribution map of aquifer vulnerability risk.

Overview of case study

Descriptions of under study plain

The study area of Kerman–Baghin plain, located on the edge of Lut Desert in the southeast of Iran, lies between 56.18° and 57.35° east longitude, and 29.46° and 30.32° north latitude, as seen in Fig. 1. The plain is located in the southern area of the Daranjir-Saghand basin, Kerman Province. in this basin, the cities of Kerman, Mahan, and Joupar are considered important population centers. The Kerman–Baghin plain spans an area of 5420 kilometers, of which 3200 square kilometers are alluvial surfaces and 2220 square kilometers are mountainous and foothill areas. The plain aquifer has an area of 2023.4 square kilometers. Additionally, the highest elevation is situated at 4200 m above sea level in the southern part of the plain whereas the lowest elevation in the central region of the Kerman–Baghin plain, reaching 1700 m above sea level.

The recharge of the plain is primary driven by rainfall. Running water flows through the riverbeds and existing channels in the region, including Seyedi River, Tigran Sekonj River, and Chari River. The annual average rainfall between 2015 and 2018 ranged from 120-140mm, while in recent drought events, it has decreased to 90–100 mm. Data obtained from the nearest rain gauge station in the Sirch County show that the maximum and minimum values of temperatures during the summer are 39.5 ^oC and 14 ^oC, respectively. . In addition, the maximum temperature in winter is 27 ^oC while the minimum temperature reaches − 10 °C. The average temperature in winter is 2.9 °C. The amount of humidity is 40% and the amount of annual evaporation is 2690.4 million mm per year and the amount of relative humidity is 28%.

Limitations and uncertainty sources

Various sources of limitation and uncertainties can affect the measurements of key parameters used in the computation of the DRASTIC index, which assesses groundwater vulnerability. Uncertainties can arise from the accuracy of well measurements, the timing of measurements (seasonal variations), and the spatial variability of the water table. Inconsistent monitoring techniques and equipment can also contribute to inaccuracies. In this study, due to the availability of field data limitations, the incomplete database within relevant organizations has resulted in some wells being excluded from calculations due to missing information. This gap underscores the need for comprehensive data collection practices to ensure that all relevant wells are accounted for in analyses. Additionally, conducting new pumping tests with appropriate spatial distribution is crucial for accurately understanding the hydraulic properties of the aquifer and for calculating hydraulic conductivity more precisely. Moreover, the situation is exacerbated by the fact that several piezometric wells (19 in total) have either dried up or have restricted access, highlighting the necessity for drilling new wells to monitor groundwater levels and other quality parameters. The insufficiency of exploratory wells further complicates the accurate recording of the aquifer’s hydraulic characteristics. Estimating net recharge involves complexities such as variations in precipitation, evaporation, land use, and soil characteristics. Uncertainty in hydrological models used to calculate recharge, as well as limited long-term data, can further complicate accurate assessments. The geological complexity of aquifers can lead to uncertainties in characterizing their properties. Variability in rock types, fractures, and other geological features can affect how groundwater flows and is stored, complicating assessments of vulnerability. Furthermore, the limited number of drilling logs, coupled with inadequate spatial distribution relative to the area of interest, hampers the ability to assess the aquifer comprehensively. Moreover, soil properties, including texture, structure, and moisture retention capacity, can vary significantly across small distances. Inaccurate soil sampling and the use of generalized data can lead to uncertainties in determining how effectively soil can filter contaminants. On the other hand, the complexities of unsaturated zone dynamics can introduce uncertainty, particularly in estimating the thickness and properties of this zone. Variability in soil moisture content and saturation can complicate assessments of how pollutants may migrate toward the water table. Measuring hydraulic conductivity can be challenging due to spatial variability in subsurface materials. Inadequate sampling techniques or reliance on a limited number of measurements can lead to significant uncertainties in understanding how easily water and contaminants can move through the soil and aquifer. Furthermore, changes in land use practices can happen rapidly, and existing datasets may be outdated. Variability in agricultural practices, urban development, and natural land cover can all impact groundwater quality, but capturing these changes accurately in assessments can be difficult. There is also a significant lack of monthly monitoring of nitrate levels in the groundwater of the Kerman–Baghin plain, which is essential for assessing contamination risks and managing water quality effectively. Evaluating potential risks associated with land use involves uncertainty in identifying pollution sources, their proximity to groundwater, and the potential for contamination. Variability in land management practices and unforeseen events (like spills) can further complicate this assessment. In summary, the measurement of parameters integral to the DRASTIC index is fraught with uncertainties arising from spatial variability, temporal changes, limitations in data collection methods, and the inherent complexities of groundwater systems. Addressing these uncertainties through comprehensive monitoring and advanced modeling techniques is crucial for improving the reliability of DRASTIC index assessments.

Data utilized

The data used in this study include precipitation, depth to groundwater level, well logs, digital elevation model, hydraulic conductivity, soil texture, land use, and nitrate pollution. Monthly rainfall data for the years 2015 to 2018 were recorded from four rain gauge stations, while depth to groundwater level was recorded on a monthly basis from 38 piezometer wells during the same period. drilling logs of piezometer wells, digital elevation model, and hydraulic conductivity were provided by Kerman Regional Water Company (KRWC). Soil texture was used for 117 samples prepared by Kerman Agricultural Research and Training Center. The land use map was prepared by the Forests, Rangelands and Watershed Management Organization.

Fig. 1

Location of study area.

DRASTIC index

Composite DRASTIC index

The CD index is a modified version of the DRASTIC index, introducing a parameter (L) to specifically assess the potential risk related to the land use. The goal of this methodology is to assess the potential impact of widespread land use on aquifer quality, arising from changes in the soil matrix and unsaturated zone media over a period of time. The DRASTIC Index considers seven parameters related to hydrogeological conditions, namely Depth to water table (D), net Recharge (R), Aquifer media (A), Soil media (S), Topography (T), Impact of the vadose zone (I), and hydraulic Conductivity (C). Based on the impact of parameters on potential vulnerability, each parameter is attributed a relative numerical weight varying from 1 to 5, where 1 and 5 indicate the least and most influential, respectively. Moreover, these seven effective parameters are categorized into ranges and attributed a numerical value from 1 to 10 based on their influences on the susceptibility. Ultimately, following the collection and digitalization of hydrogeological data using GIS, the information is overlaid and integrated to generate vulnerability maps. The outcome is a new layer referred to as the DRASTIC index (Eq. 1). This index is expressed as follows,

$${\text{DRASTIC}} {\text{index}} = D_{r} \cdot D_{w} + R_{r} \cdot R_{w} + A_{r} \cdot A_{w} + S_{r} \cdot S_{w} + T_{r} \cdot T_{w} + I_{r} \cdot I_{w} + C_{r} \cdot C_{w}$$

(1)

where subscripts “r” and “w” note the corresponding ratings and weights, respectively; that are summarized in Table S1, Supplementary Information (e.g.^30,38,50,51). To compute the Composite DRASTIC index, an extra parameter, namely land use, is incorporated into the DRASTIC index. Consequently, the CD index is determined as,

$${\text{DC}} {\text{index}} = D_{r} \cdot D_{w} + R_{r} \cdot R_{w} + A_{r} \cdot A_{w} + S_{r} \cdot S_{w} + T_{r} \cdot T_{w} + I_{r} \cdot I_{w} + C_{r} \cdot C_{w} + L_{r} \cdot L_{w}$$

(2)

In this context, L_r signifies the assigned rating for the potential risk linked with land use, L_w indicates the relative weight attributed to the potential susceptibility related to land use (as outlined in Table S2), and the remaining effective parameters are in accordance with Eq. (1). The ultimate results range from 28 to 280 and are categorized based on the classifications outlined in Table S3.

Nitrate vulnerability index

The NVI, as a modification of the DRASTIC index, designed to enhance precision in estimating the particular susceptibility to nitrate pollution. The NVI relies on the actual influence of each land use. This model aims to consolidate the risks of nitrate pollution in groundwater by taking into account land use as an expected nitrogen source. The framework considers both potential negative and positive impacts of land uses that do not contribute significantly to nitrate levels and do not lead to increased leaching over time, such as safeguarded natural zones. It relies on a framework based on multiplication that introduces a new parameter named the "potential risk associated with land use" (LU). This parameter is computed as³⁰,

$${\text{NVI}} = (D_{r} \cdot D_{w} + R_{r} \cdot R_{w} + A_{r} \cdot A_{w} + S_{r} \cdot S_{w} + T_{r} \cdot T_{w} + I_{r} \cdot I_{w} + C_{r} \cdot C_{w} ) \cdot LU$$

(3)

In this equation, LU represents the potential risk linked with land use (as specified in Table S4), while the remaining parameters remain consistent with Eq. (1). The ultimate results are categorized according to the classifications outlined in Table S3.

Preparation of vulnerability zone

Depth to water table (D)

The D parameters, as a pivotal factor in the DRASTIC framework, significantly affects the thickness of the unsaturated zone through which potential pollutants need to pass prior reaching the aquifer (e.g.^48,52). It imperatively represents the distance a contaminant would have to traverse to reach the water surface. This depth serves as an indicative factor for potential aquifer protection, with deeper water levels leading to longer travel times for pollutants. Generating the depth pixel map entailed interpolating existing data through the utilization of the Inverse Distance Weighting (IDW) technique, which is a spatial analysis tool in ArcGIS 10.8. The employment of this interpolation technique enabled the development of a seamless map depicting the depth to the water table throughout the research area. Following this, D values underwent reclassification, with rankings assigned on a scale from 1 to 10 (see Table S1). These rankings are essential for the subsequent assessment and computation of the NVI. It is the distance from the ground surface to the water table. In order to provide D layer, the latest information on water level of 38 pizometric wells has been applied. The locations of these wells were also presented in Fig. 1. The methodology based interpolation conception has been employed to change the mentioned point data into raster map of water level. Ultimately, this layer has been generated and then classified by the provided ranges in Table S1. Spatial variations of D values was presented in Fig. 2a. Over 90% of Kerman–Baghin plain area had D > 30.5 m.

Fig. 2

Input maps for the various DRASTIC and NVI models: (a) depth to water table, (b) recharge, (c) aquifer media, (d) soil media, (e) topography, (f) impact of vadose zone, (g) hydraulic conductivity, (h) land use, and (i) spatial variation of nitrate pollution.

Net recharge (R)

The net recharge parameter indicates the quantity of water that annually infiltrates from the Earth’s surface to reach the saturated zone, which is particularly pertinent for understanding the various types of contaminations movements (convection and diffusion) from the unsaturated zone to the saturated zone (e.g.^48,53). In order to evaluate this parameter, the precipitation layer has been formed with aid of interpolation process on average values of the annual rainfall. The spatial variation of R map was then produced using the spatial analysis tool in ArcGIS 10.8, incorporating additional information on evaporation and runoff. The resultant map offers information regarding the average values of annual R across the entire study area. These values underwent reclassification and were assigned rankings within the range of 6–9, as illustrated in Fig. 2b and detailed in Table S1. In general, a higher R value indicates an elevated potential for contaminants to reach the water surface, given that larger volumes of infiltrating water create more pathways for the transport of pollutants. This study employs Piscopo’s method⁵¹ to generate the R layer for the Kerman–Baghin Plain using Table S1 and the Eq. (4) provided below:

$${\text{Net}}\,{\text{Recharge}}\,{\text{index}} = Soil\,permeability + Rainfall + Slope\left( \% \right)$$

(4)

In Eq. (4), the slope percentage was obtained from a Digital Elevation Model (DEM) created using the topographic map of the Kerman–Baghin Plain. Soil map, logarithmic observations, and exploration wells have been utilized in order to measure soil permeability. As seen in Fig. 2b, the map resulting from the spatial distribution shows that 53.2% of the plain area falls within the Class 3 range with a recharge level of 5 to 7. This class is uniformly scattered across the plain’s surface.

Aquifer media (A)

The A parameter describes the characteristics of materials within the aquifer that impact the processes of pollutant attenuation, as detailed by reliable literature (e.g.^36,37,48). The aquifer formations, recognized using lithology and hydrogeology maps, consist of fine silt and silty sand, sand, conglomerate, and shale. According to Table S1, the spatial variations of A map has been categorized into six groups and then ranged from 1 to 9, as illustrated in Fig. 2c. In this study, information from 35 well-log profiles (Lithological wells) of the alluvial aquifer prepared in 1964 from KRWC has been employed in order to generate the A layer. A superior rank was attributed to conglomerate, indicating a highly coarse porous medium with outstanding capabilities in drainage and transmission. The spatial distribution map of the aquifer (Fig. 2c) illustrates that the aquifer environment covers the majority of the plain’s surface (61.8%), particularly in its eastern region, comprising Gravel, Sand, Silt, and Clay. In the western half of the plain (37%), it mainly includes Gravel and Sand.

Soil media (S)

The S parameter plays a critical role in characterizing the influx of nutrients and pollutants into the aquifer, influencing the purification processes, as emphasized by diverse investigations (e.g.^1,3,4,5). Additionally, soil characteristics impact the removal of pollutants. The data has been obtained from the disciplines of environmental and geological science. Rankings and weights have been designated according to the hydrological characteristics (porosity and permeability) of the soil. Table S1 present the rankings and weights related to various classes of S values and additionally Fig. 2d illustrates spatial variation map of soil media. Sandy loam soils, possessing favorable drainage that facilitates substantial water flow, were assigned a heightened ranking in terms of contaminant transmission. Conversely, clay soils hinder water flow and are less prone to groundwater contamination, leading to a lower rating. Soil data were obtained from the Kerman Institute of Agricultural Science (KIAS). Spatial variations of soil texture has been mapped by using the soil information derived from log of observation and exploration wells. The soil environment map in Fig. 2d illustrates that the majority of the plain’s surface (41.2%) is characterized by loamy soil texture, and this soil exhibits dispersion throughout all parts of the plain. Sandy soil (0.3%) with Class 9 is allocated the smallest area.

Topography (T)

This parameter signifies the incline of the terrain in the studied districts and then affects the quantity of water on the capability of soil infiltration without any intermediary. A gentler slope encourages increased infiltration, leading to an increased likelihood of pollutants migrating into the aquifer (e.g.^20,54). To create the T layer, a digital elevation model (DEM) has been employed, and the slope function in ArcGIS 10.8 has been utilized to categorize it into five ranges. Steeper slopes are less likely to experience contamination because of the heightened potential for surface runoff. Figure 2e and Table S5 indicates the map and rankings/weights assigned to the T parameter, respectively. DEM with spatial resolution (30 m) has been utilized in order to calculate T values in ArcGIS 10.8 software. The T layer was created using the same methodology applied in generating the R layer and subsequently underwent classification. As illustrated in Fig. 2e, the slope domain map indicates that the majority of the plain’s surface (60%) has slopes less than 2%, falling into Class 10. Slopes in the ranges of 12–18% and greater than 18% constitute the smallest area (0.1%).

Impact of vadose zone (I)

The I layer is created by considering characterizations derived from hydrogeology information. The spatial variations on geological properties of the studied plain has been grouped into three ranges: Conglomerate, Marl, and calcareous shale with intercalations of limestone, and Marl, shale, sandstone, and limestone. Each category signifies unique geological units situated above the groundwater level. The vadose zone parameter map delineates the diverse geological units above the water level, as discussed by Karimzadeh-Motlagh et al.⁴⁸. The vadose zone includes the area between the Earth’s surface and the aquifer, specifically referring to the unsaturated material above the water table. The dimensions and depth of the unsaturated zone have considerable importance in the computation process of DRASTIC framework. The properties of the vadose zone media have a profound impact on both water flow and the migration of pollutants. Each geological unit has been attributed to a score between 3 and 9, with permeable media such as gravel and conglomerate receiving a score of 9, while shale has been attributed to a lower rank of 3 (refer to Table S1). This research utilized lithologic data obtained from observation and exploration wells to construct the vadose zone media of the Kerman–Baghin plain. Subsequently, utilizing this information in conjunction with Table S1, we formulated the raster map for the Kerman–Baghin plain (see Fig. 2f). The unsaturated zone map on the plain’s surface (Fig. 2f) indicates that the eastern half of the plain (45.7%) is characterized by Silt and Clay textures. The central to western part of the plain contains Sand, Silt, and Clay textures (44.6%), while the westernmost layer of the plain consists of Gravel and Sand (9.7%).

Hydraulic conductivity (C)

The C parameter serves as an indicator of the porous medium’s ability within an aquifer to transport water, as noted by Baghapour et al.³⁰, Wang et al.⁵⁵, and Karimzadeh-Motlagh et al.⁴⁸, and it is considered as contributory factor of assessing the movement of contaminants. Elevated C values indicate a faster transportation of pollutants. Hydraulic conductivity denotes the ability of soil or rock to facilitate the movement of water, a feature affected by factors such as the proportion of pore spaces, interconnections, voids, grain size, and sorting. The C values underwent categorization, and a rating between 1 and 7 was allocated to each aquifer media type with consideration of hydraulic conductivity characterizations (refer to Table S1). We utilized data from 22 pumping tests conducted by KRWC to create the hydraulic conductivity layer. The spatial variation of C values is illustrated in Fig. 2g and additionally demonstrated that the majority of the plain’s surface (67.1%) in the eastern half and central parts has hydraulic conductivity ranging from 1.12 to 1.4 m per day. The smallest area (1.7%) corresponds to hydraulic conductivity levels of 12.2–28.5 m per day, scattered in small patches in the eastern and central regions of the plain.

Land use

A land use map is a visual representation of how the land in a specific geographic area is utilized or occupied by different human activities. It illustrates the various types of land uses, such as residential, commercial, industrial, agricultural, recreational, or natural areas. Land use maps provide a comprehensive overview of the spatial distribution and patterns of human activities on the Earth’s surface. The map shows the spatial distribution of land uses, indicating where specific activities or land cover types are located within the study area. In urban planning, land use maps often align with zoning regulations. Zoning boundaries define areas with specific land-use designations, such as residential, commercial, or industrial zones. Land use maps help assess the influence of human activities on the natural surroundings and ecological systems. They are valuable for conservation efforts and natural resource management. This layer is essential as it is needed for both CD and NV indices. This layer was obtained from Landsat images in 2018 and then Tables S2–S4 were utilized to assign ratings for the creation of the land use map and its corresponding risk assessment. As seen in Fig. 2h, the vast area of the Kerman–Baghin plain is red with low density pasture. The land use map of the watershed (Fig. 2h) indicates that the majority of the watershed area (49.9%) is characterized by low-density grasslands, and urban land use class constitutes the smallest area (6%).

Field measurement of nitrate concentration

Groundwater sampling was conducted at selected well locations during the summer of 2022 (from August 6 to August 10), as part of field operations. It is important to highlight that the investigation into the groundwater quality in the investigated region, characterized by an arid climate, took place during the dry season. This method aimed to evaluate the water quality over the long-term, alleviating the influence of short-term variations induced by aquifer recharge and fluctuations in water quality typically observed during the humid season, especially after severe precipitation. Dark glass containers with a volume of 250 ml were utilized for sampling, pre-washed with distilled water before collection. Each sample bottle has been marked with details including location, sampling time (date and time), sampling depth (varying from 22 to 146 m), and water temperature. Following collection, the water samples have been stored at a temperature below 4 °C and transferred to the central laboratory of the Graduate University of Advanced Technology within 6 h. Nitrate content analysis was promptly conducted using a Varian Cary 50 spectrophotometer⁵⁶. Subsequently, geostatistical analysis of the nitrate data was carried out to generate a zonation map using ArcGIS 10.4.1 and GS + software packages. It is important to mention that the geostatistical technique, particularly the Kriging estimator, has been extensively used to assess the spatial and temporal variations of groundwater. The spatial variations of nitrate concentrations (mg/l) for Kerman–Baghin plain was illustrated in Fig. 2i. The major fraction of the plain had 2.2–14 mg/l Nitrate concentration whereas the 70–100.4 nitrate concentration had minimum coverage.

Dataset overview

From Fig. 3, Table 2 indicates fractional areas of effective DRASTIC parameters for the case study area. In this research, DRASTIC index which has been effected by NV and LU indices, is predicted by AI models. To begin with, normal effective parameters (i.e., D, R, A, S, T, I, and C) were employed to provide map of DRASTIC index and then effects of LU and nitrate pollutions were considered to provide the spatial zoning map of nitrate pollution. To develop AI models for estimating Nitrate pollution, 9 input parameters were considered: D_r, R_r, A_r, S_r, T_r, I_r, C_r, L_r, and LU. In this way, a dataset containing 100 data series were used for this purpose in which 75 and 25% of dataset have been selected to carry out the training and testing stages of the AI models, respectively. Statistical descriptions of input–output parameters were presented in Table 3

Fig. 3

Spatial variations of (a) DRASTIC, (b) DRASTIC-LU, and (c) NVI models.

Table 2 Fractional areas for effective DRASTIC parameters.

Table 3 Statistical descriptions of input–output parameters obtained in the Baghin Plain.

Artificial intelligence models

Multivariate adaptive regression spline

The MARS model utilizes the concepts of piecewise linear regression to formulate a linear regression expression, identifying overall patterns within the input–output system^57,58. The MARS method estimates the function by employing a sequence of piecewise linear regressions, accomplished through an adaptive process referred to as Basis Functions (BFs). The curve-fitting component of MARS is essentially built by a collection of Basis BFs in both the forward and backward stages. Each BF comprises a single variable (x) and a knot (K), resulting in two potential pairs: (z − K)₊ and (K − z)₊, where (z − K)₊ equals (z − K) if z > K, and 0 otherwise; and (K − z)₊ equals (K − z) if z < K, and 0 otherwise. The final result from the MARS model is determined through a curve-fitting equation, as described by Friedman⁵⁸.

$${\text{NVI}} = \omega_{0} + \mathop \sum \limits_{i = 1}^{s} \omega_{i} \cdot BF_{i} \left( {D_{r} ,R_{r} ,A_{r} ,S_{r} ,T_{r} ,I_{r} ,C_{r} ,LU,L_{r} } \right)$$

(5)

in which ${BF}_{i}$ notes the basis function including input variables with the second-order polynomial pattern. Additionally, ${\omega }_{0}$, ${\omega }_{i}$, and s note the bias term, the constant coefficient related to the typical basic functions, and the number of basis functions in the MARS model, respectively.

The MARS approach implemented using MATLAB2008a whose programming codes are freely available. In the present research, MARS produces 18 BFs using a second-order polynomial (or linear model) in order to approximate NVI values. The mathematical formulations for the BFs and their associated constant coefficients employed in NVI modeling are outlined in Table 3. Furthermore, the subsequent mathematical model establishes a correlation between NVI and nine influential parameters.

$$\begin{aligned} NVI = & 73.03 + 44.331 \times BF_{1} - 95.044 \times BF_{2} \\ & \quad + 8.0589 \times BF_{3} + 5.4617 \times BF_{4} - 5.1886 \times BF_{5} \\ & \quad - 7.5732 \times BF_{6} + 7.121 \times BF + 3.024 \times BF_{8} \\ & \quad - 3.8399 \times BF_{9} + 4.0564 \times BF_{{10}} - 6.0339 \times BF_{{11}} \\ & \quad - 1.418 \times BF_{{12}} + 25.861 \times BF_{{13}} + 0.81522 \times BF_{{14}} - 1.4806 \times BF_{{15}} \\ & \quad - 3.1012 \times BF_{{16}} + 4.7424 \times BF_{{17}} + 1.8296 \times BF_{{18}} \\ \end{aligned}$$

(6)

In the present study, the k-fold value was specified as 10, indicating that the MARS procedure was repeated 10 times to mitigate the risk of overfitting. Both forward and backward stages were executed for each k-fold setting. Furthermore, the determination of the final MARS model involved establishing the number of basis functions and identifying the count of effective parameters. The optimal model derived from the MARS approach for assessing NVI is expressed by Eq. 6, with BF₁ to BF₁₈ detailed in Table 4. The basis functions in Eq. 6 are established using input parameters LU, C_r, I_r, S_r, A_r, R_r, and D_r, while T_r and L_r are omitted. Table 5 provides insights into the features observed in 10 iterations of the MARS model, presenting outcomes across both forward and backward stages. All coefficients in Eq. 6 were determined through the Particle Swarm Optimization (PSO) algorithm, resulting in an MSE (Mean Squared Error) of 0.35661 as the optimal outcome. In Fig. 4, within the aquifer’s total area of 4202.3 square kilometers, around 3147.8 square kilometers (approximately 74.73%) in the region characterized by very low vulnerability exhibit an NVI value below 70. The remaining 1,545 square kilometers (25.26% of the total area) fall within the NVI range of 70–110, indicating low vulnerability.

Table 4 List of BF developed in MARS model.

Table 5 Characterization of MARS model within forward and backward passes.

Fig. 4

Spatial variation of Nitrate vulnerability pollution by MARS.

Model tree

Quinlan⁵⁹ introduced the MT as a powerfull data-mining model rooted in classification principles. A more sophisticated extension of MT, known as the M5 model, was subsequently proposed by Wang and Witten⁶⁰. The M5 Model Tree (M5MT) is capable of breaking down a complex problem into manageable domains or subspaces, with the final output being a linear summation of the input variables throughout all realms of inputs⁵⁷. The M5MT technique employs recursive methods in order to divide the search space of datasets into one or more subspaces. This involves using if–then rules to categorize input variables into one or more domains, specifying input variables to subdomains. Consequently, a set of multilinear relationships is generated within each sub-domain.

In the current study, the M5MT approach has been implemented using Weka 3.9 software. Initially, the decision tree is formed during the training phase, and subsequently, nine influential parameters (i.e., LU, C_r, I_r, S_r, A_r, R_r, D_r, T_r and L_r) were employed to acquire the multilinear regression model for classification. In order to approximate NVI, Eq. (7) is expressed as

$$NVI = \left\{ \begin{gathered} \begin{array}{*{20}c} {{ - 9}{.6162 + 1}{.3959 }R_{r} { + 0}{.1561 }S_{r} { + 0}{.7123 }I_{r} { + 86}{.5834 }LU} & {L_{r} \le { 7}} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {{ - 11}{.6632 + 4}{.9336 }R_{r} { + 4}{.9111 }I_{r} { + 54}{.8834 }LU} & {L_{r} {> 7}} \\ \end{array} \hfill \\ \end{gathered} \right.$$

(7)

In Eq. (7), the M5 tree model utilizes the input parameter L_r as a criterion to partition the input space, and the parameters LU, I_r, S_r, and R_r are incorporated into the mathematical expression. However, the input parameters C_r, T_r, A_r, and D_r are not considered. In Fig. 5, within the total area of 4,202.3 square kilometers of the aquifer, an area of approximately 3,141.5 square kilometers (approximately 94.69%) in the region characterized by very low vulnerability has an NVI value below 70. The remaining 608 square kilometers (around 5.30% of the total area) fall within the NVI range of 70 to 110, signifying a low vulnerability zone.

Fig. 5

Spatial variation of Nitrate vulnerability pollution by M5MT.

Gene-expression programming

The GEP approach is essentially built upon the principles of Genetic Algorithm (GA), a technique capable of simplifying relationships within sophisticated systems into simpler equations. GEP integrates inherent features of GA, encompassing fixed-length and linear configurations linked to chromosomes. Moreover, GEP utilizes Expression Trees (ETs) with sub-elements of diverse sizes and shapes, including aspects such as tree depth, mathematical expressions and algebraic symbols. The GEP model is constructed through five distinct phases. In the initial stage, a fitness function (FF) is employed in order to appraise an individual program^61,55,63. In this investigation, the Mean Squared Error (MSE) is assigned as the fitness function,

$$FF = \frac{1}{1 + MSE} \times 1000$$

(8)

The second phase commences with the specification of terminals and mathematical functions so as to provide the chromosomes. During the third stage, the overall attributes of chromosomes, such as size and shape, are configured. Following that, the fourth stage utilizes a well-established algebraic operator to construct a mathematical expression from a set of genes. Lastly, various genetic operators (as delineated in Table 6) are applied to obtain the optimal relationship. The GEP model, implemented using GeneXproTools 5 software, produced the most efficient correlation for predicting the influential parameters of NVI. In this research, the number of generations was extended to 244 until the optimal fitness function value reached 214.665 during the training phase.

$$\begin{aligned} NVI = & \max \left( {LU - \left( { - 8.70967} \right),A_{r} } \right) + \left[ {\left( {\left( {LU + LU} \right) \times L_{r} } \right) \times \left( {\frac{{A_{r} + R_{r} }}{2}} \right)} \right] \\ & \quad + 1 - \left[ {\min \left( {\left( {\frac{{L_{r} }}{{LU \times I_{r} }}} \right),\left( {A_{r} + 0.034084} \right)} \right) - \left( {\frac{{T_{r} + A_{r} }}{{L_{r} + LU}}} \right)} \right] \\ & \quad + \frac{{\exp \left( {\frac{{(S_{r} - ( - 5.2031)) + \exp ( - 9.3446)}}{2} + ( - 5.2031)} \right) + (0.891546 - R_{r} )}}{2} \\ \end{aligned}$$

(9)

Table 6 Setting parameters of GEP model.

In the GEP model, Eq. (9) incorporates input parameters LU, L_r, I_r, T_r, S_r, A_r, and R_r, while excluding the input parameters D_r and C_r. In Fig. 6, within the total area of 4,202.3 square kilometers of the aquifer, approximately 1,461 square kilometers (around 34.72%) in the area characterized by very low vulnerability exhibit an NVI value below 70. The remaining 562 square kilometers (approximately 65.27% of the total area) fall within the NVI range of 70 to 110, indicating low vulnerability.

Fig. 6

Spatial variation of Nitrate vulnerability pollution by GEP.

Evolutionary polynomial regression

EPR, grounded in a global search technique, is capable of constructing a symbolic regression equation linking input–output vectors (or variables) so as to make systems straightforward. Conceptually, EPR generates a regression equation comprising numerous algebraic terms^{64,58,59,60,68}:

$$NVI = \theta _{0} + \sum\limits_{{g = 1}}^{T} {\theta _{g} \cdot \left( D \right)^{{EX(g,1)}} \cdot \left( R \right)^{{EX(g,2)}} \cdot \left( A \right)^{{EX(g,3)}} \ldots \left( {LU_{g} } \right)^{{EX(g,T)}} \cdot INF\left( {D_{1} ^{{EX(g,G + 1)}} \cdot \left( R \right)^{{EX(g,G + 2)}} \cdot \left( A \right)^{{EX(g,G + 3)}} \ldots LU_{g} ^{{EX(t,2G)}} } \right)}$$

(10)

in which U, L₀, L_u, INF, and EX note the customizable symbolic terms, an optional bias term, a group of invariable coefficients, the customizable inner function (e.g., natural logarithm, tangent hyperbolic), and customizable exponents input vectors applied in Eq. (7), respectively^69,70. During the development stage, a matrix is created that encompasses effective DRASTIC parameters. Following this, initial population values associated with the exponent vectors are provided. In the subsequent step, exponent vectors associated with influential DRASTIC parameters are specified; then, invariable coefficients (L_u), presented in Eq. (10), are adjusted by the least square technique. After fixing the L values and ES vectors, the values of NVI are estimated in the training phase. Subsequently, the quality provided by the EPR performance is evaluated. In this study, a logarithmic inner function (INF) is employed to deliver the most accurate estimation of the NVI, as opposed to other types of INFs such as tangent and secant hyperbolic functions and exponential function^64,58,66.

In this research, the EPR model was implemented using the EPR MOGA-XL software, which is programmed within the Excel environment. The execution of the EPR model involved the utilization of the multi-objective genetic algorithm (MOGA). The software settings were configured with an inner function (natural logarithm) defined, a power range for input variables spanning from − 2 to 2 with increments of 0.5, and a total of 19,440 generations. Additionally, a maximum of six mathematical terms (U = 6) was specified. Through this software, six models were generated for the evaluation of NVI, as presented in Table 7. Model#6, exhibiting the lowest mean squared error (MSE = 0.066) during training, outperforms the other models and is selected as the most accurate model for NVI evaluation. In Model#6 (as presented in Table 7), input parameters LU, C_r, I_r, T_r, A_r, R_r, and D_r were used for modeling nitrate pollution, while S_r and L_r were excluded. In Fig. 7, out of a total area of 4,202.3 square kilometers of the aquifer, an area of approximately 1,521 square kilometers (about 2.75%) in the region with very low vulnerability has an NVI value less than 70. A total of 501 square kilometers (about 79.27% of the total area) falls within the NVI range of 70 to 110 in the low vulnerability zone. These models perform a refinement in the final model by considering the impact of each input parameter on vulnerability assessment through NVI, resulting in some input parameters participating in the mathematical expression, while others are excluded.

Table 7 Mathematical expressions given by EPR.

Fig. 7

Spatial variation of Nitrate vulnerability pollution by EPR.

Results and discussions

Statistical performance of AI models

According to reliable relevant research works, various statistical tests have been applied in order to appraise the performance of AI models in the groundwater evaluation in terms of quality and quantity literature (e.g.^{1,24,30,31,39,63,71,65,66,67,68,69,70,76,78}). Through this method, statistical indicators such as the Correlation Coefficient (R), Root Mean Square Error (RMSE), Mean Absolute Error (MAE), and Scatter Index (SI) were employed to evaluate the effectiveness of the performance of soft computing models in two development stages (i.e., training and testing stages) related to the assessment of NVI. These statistical metrics are defined as follows:

$$R = \frac{{\sum\nolimits_{{i = 1}}^{N} {\left( {NVI_{p}^{i} - \overline{{NVI_{P} }} } \right)} \left( {NVI_{o}^{i} - \overline{{NVI_{o} }} } \right)}}{{\sqrt {\sum\nolimits_{{i = 1}}^{N} {\left( {NVI_{o}^{i} - \overline{{NVI_{o} }} } \right)^{2} \left( {NVI_{p}^{i} - \overline{{NVI_{P} }} } \right)^{2} } } }}$$

(11)

$$RMSE = \sqrt {\frac{{\sum\nolimits_{{i = 1}}^{N} {\left( {NVI_{p}^{i} - NVI_{o}^{i} } \right)^{2} } }}{N}}$$

(12)

$$MAE = \frac{{\sum\nolimits_{{i = 1}}^{N} {\left| {NVI_{p}^{i} - NVI_{o}^{i} } \right|} }}{N}$$

(13)

$$SI = \frac{{\sqrt {\frac{1}{N}\sum\nolimits_{{i = 1}}^{N} {\left[ {\left( {NVI_{p}^{i} - \overline{{NVI_{P} }} } \right) - \left( {NVI_{o}^{i} - \overline{{NVI_{o} }} } \right)} \right]^{2} } } }}{{\overline{{NVI_{o} }} }}$$

(14)

In these equations, N is the number of data points, the $NVI_{o}^{i}$ ith value represents the observed value, the $NVI_{p}^{i}$ ith is the predicted value by the soft computing models, and the $\overline{{NVI_{o} }}$ averages refer to the mean of observed values and $\overline{{NVI_{p} }}$ is the mean of predicted values by the soft computing models.

The value of R is in the range [+ 1, −1] and expresses a linear (direct or inverse) relationship between parameters. When R approaches + 1, it indicates a direct correlation, and when it approaches − 1, it signifies an inverse correlation between parameters. When there is weak correlation between parameters, R approaches zero; moreover, R is dimensionless. RMSE has a value between 0 and + ∞, reflecting the spread of predictions of each model relative to observed values. The closer it is to zero, the more accurate the model is, and it has dimensions similar to the evaluated parameters (here, dimensionless). Changes in MAE range between 0 and + ∞, indicating the difference between observed and predicted values by the model. The closer it is to zero, the more accurate the model, with dimensions similar to the evaluated parameters (here, dimensionless). SI provides an indication of the relative spread of model predictions compared to the average of the observed values. A lower SI suggests that the model predictions are relatively concentrated and close to the mean of the observed values, indicating better model performance. The reliable range of SI is as same as RMSE and MAE.

Moreover, the assessment of AI model performance in both training and testing phases involves the use of receiver-operating characteristic (ROC) curves. To construct the ROC curve, it is essential to comprehend the concepts of sensitivity and specificity, which are directly employed to evaluate AI model effectiveness. Subsequently, the computation of the area under the curve (AUC) is required⁷⁷. The literature provides comprehensive explanations of ROC curves. Broadly speaking, the diverse AUC ranges are capable of characterizing AI models efficacy as follows: 0.5–0.6 (low precision), 0.6–0.7 (moderate precision), 0.7–0.8 (high accuracy), 0.8–0.9 (remarkably high precision), and 0.9–1 (excellent precision).

The comparison presented in Table 8 clearly indicates that the EPR soft computing model performs the best among the soft computing models during the training phase, achieving an R of 0.9999, RMSE of 0.246, MAE of 0.191, and SI of 0.0064. Following this, in descending order of performance, are the MARS model (R = 0.9998, RMSE = 0.597, MAE = 0.443, and SI = 0.0156), M5MT model (R = 0.9984, RMSE = 0.679, MAE = 0.189, and SI = 0.0439), and GEP model, which is the least effective with an R of 0.9958, RMSE of 0.766, MAE of 0.721, and SI of 0.0724. In Table 8, a similar comparison among the soft computing models is conducted during the testing phase, and once again, the EPR model exhibits the best performance with an R of 0.9999, RMSE of 0.2105, MAE of 0.1712, and SI of 0.0040. Subsequently, in decreasing order of performance, are the MARS model (R = 0.9966, RMSE = 0.408, MAE = 0.342, SI = 0.0530), M5MT model (R = 0.9956, RMSE = 0.988, MAE = 0.996, SI = 0.0580), and the GEP model, which performs the least effectively with an R of 0.9920, RMSE of 0.491, MAE of 0.673, and SI of 0.0781.

Table 8 Evaluation of Statistical analysis of AI models performance in the NVI prediction.

Another way to investigate the correlation between the predicted values by soft computing models and the observed values is through scatter plots. In fact, Fig. 8a and b illustrate the qualitative performance of the soft computing models in both training and testing phases. Considering Fig. 8a, all data points during the training phase are concentrated within the ± 10% acceptable error range. For NVI in the range (30, 10), the predicted values of the M5MT model are mostly higher than the observed values, and the predicted values of the GEP model are lower. The GEP model predicts NVI values less than the observed values for the range (70, 60), higher for the range (80, 70), less for the range (90, 80), and higher for the range (110, 90). The M5MT model generally predicts higher NVI values in the range (100, 60). Throughout the plot, the predictions of the EPR and MARS models are nearly equal to the observed values. Similarly, in Fig. 8b, as in the previous figure, all data points during the testing phase fall within the acceptable error range. The predicted values of the M5MT model are higher than the observed values throughout the plot. The GEP model overestimates the predicted values in the range (80, 70) but underestimates them in the range (90, 80). In contrast to the training phase where the predictions by the MARS model align almost perfectly on the y = x line, in the testing phase, it predicts higher NVI values for the range (70, 50). The predicted values by the EPR model, like the training phase, are in line with the observed values. Regarding the complexity of the model structures, the mathematical expressions of the GEP model (Eq. 9) and the EPR model (Model#6 in Table 7) are more intricate compared to the MARS and M5MT models. The EPR model, due to the presence of six algebraic expressions, a natural logarithm internal function, and the utilization of eight input parameters, has a higher degree of mathematical complexity compared to the GEP model, which consists of three internal functions (Min, Max, Exp), four algebraic expressions, and the use of seven input parameters. Additionally, the Eq. (6) provided by the MARS model includes 18 sets of second-degree polynomials with 7 input parameters along with 10 forward and backward steps, representing more complex expressions than those generated by the M5MT (Eq. 7). As mentioned earlier, the EPR model demonstrates favorable performance compared to other soft computing models. The MARS model is well-positioned as an alternative to the EPR model among the three other models.

Fig. 8

Performance of AI models for both (a) training and (b) testing stages

To draw the ROC curve and calculate the AUC, GraphPad Prism 8 software was utilized. According to Fig. 9, the GEP model (AUC = 94.50%) performed excellently, followed by the MARS and M5MT models (AUC = 94.38%), and finally, the EPR model (AUC = 94.37%).

Fig. 9

ROC curve of AI models for predicting NVI.

Comparisons of present research with relevant literature

These artificial intelligence models, based on regression and providing relationships, have found extensive application in the realm of groundwater pollution control. The mentioned AI methods can automatically identify input variables and select those with higher importance for modeling. In this study, the EPR model, using a multi-objective genetic algorithm in its structure, optimizes the number of algebraic expressions and input variables. Additionally, models such as MT and MARS, by incorporating characteristics of data mining methods like adaptive regression, the concept of standard deviation error in the structure of tree and regression models, and the inclusion of forward stages for initial regression model building and backward stages for removing algebraic expressions leading to overfitting, reduce the computational load in estimating the DRASTIC index. Moreover, the GEP model, similar to the EPR model, can easily represent the complexities in modeling the DRASTIC index (parameter uncertainties and groundwater system complexity) by simultaneously using mathematical operators. The mentioned features of the AI models in this study contribute to computational efficiency reduction. On the other hand, some AI models like ANN, ANFIS, and SVM use all input variables. The results of the AI models, based on their formulas, can be easily interpreted, and with only the values of DRASTIC input parameters (considering land use effects and nitrate pollution), the status of groundwater contamination can be examined.

In Fijani et al.’s²⁴ research, SCMAI was used based on Sugeno Fuzzy Logic (SFL), Mamdani Fuzzy Logic (MLF), ANN, and ANFIS models in order to assess groundwater vulnerability via DRASTIC index while considering Nitrate–N concentration for Maragheh–Bonab plain aquifer, Iran. In terms of accuracy levels, all AI models (R = 0.61, 0.82, 0.76, 0.84, 0.98 for MFL, SFL, ANN, SCMAI, respectively) used in their study have stood at the lower precision stages compared with the present research (see Table 8). In addition, Fijani et al.²⁴ did not consider LU effects on the DRASTIC index whereas we took it into consideration for evaluation of pollution assessment of Kerman–Baghin Plain.

A notable limitation of Fijani et al.’s²⁴ study was their omission of land use (LU) effects on the DRASTIC index. This aspect is critical in understanding groundwater vulnerability, as land use changes significantly influence the dynamics of groundwater contamination. In contrast, the current research specifically considered land use effects, which allows for a more nuanced evaluation of pollution impacts in the Kerman–Baghin Plain. By integrating land use data into the analysis, the present study provides a more accurate and holistic assessment of groundwater vulnerability, reflecting the real-world complexities of how human activities interact with natural systems. Overall, the incorporation of land use considerations and the employment of more precise AI modeling techniques not only enhance the accuracy of groundwater vulnerability assessments but also address gaps identified in previous studies, such as that of Fijani et al.²⁴. This approach underscores the importance of continuously improving methodologies to ensure effective management of groundwater resources and to protect them from contamination.

In the study conducted by Barzegar et al.¹ in the Tabriz Plain aquifer, the ANN model (constructed by three hidden layers and 12 neurons with R = 0.847) and ANFIS models (constructed by Mamdani with a correlation of 0.784 and Sugeno with a correlation of 0.784) demonstrated high accuracy in evaluating the DRASTIC index. However, the AI models ANN and ANFIS exhibited lower accuracy compared to the results of the present study (e.g., R = 0.9920, 0.9999, 0.9966, and 0.9956 for GEP, EPR, MARS, and M5MT, respectively). Additionally, in terms of structure, the artificial intelligence models such as ANN and ANFIS act like black boxes, making the interpretation of DRASTIC data somewhat more challenging compared to the simpler AI models employed in the present research, such as M5MT and MARS, which have simpler structures represented by Eqs. (6 and 7). The developed SCMAI model, due to its simultaneous use of the inherent characteristics of ANNs and fuzzy models (Mamdani and Sugeno), achieved a correlation coefficient of 99.0%. This performance is comparable to the results of the present study, which used GEP (R = 9920), EPR (R = 0.9999), MARS (R = 9966), and M5MT (R = 9956). It is worth mentioning that the SCMAI model, due to its use of multiple artificial intelligence methods, has greater complexity compared to EPR and GEP models. Therefore, it can be concluded that these AI models, considering land use effects and nitrate pollutant concentrations, provides a cost-effective relationship.

Baghapour et al.³⁰ utilized an ANN model to enhance the DRASTIC method in an unrestricted aquifer in the Shiraz Plain. The outcomes indicated that the ANN was more influential in improving the DRASTIC framework when compared to the CD and NV indices. This is deduced through three plausible ways: (1) ANN, as a black-box framework, is capable of more persuasive explaining the non-linear behavior of aquifers, which are complex systems. (2) Unlike NV and CD methods, the supervised learning approach adopted by ANN has modified vulnerability, making it more suitable for training. (3) The ANN model optimizes the model’s fitness using the LM optimization methodology in order to obtain a persuasive DRASTIC framework. The ANN model showed R of 0.890, which compared to the models used in the present study, exhibited a slightly lower correlation coefficient.

Barzegar et al.³¹ employed four separate machine learning models (ELM, MARS, SVR, and M5 Tree) for mapping the risk of groundwater pollution in the Marand Plain, northwest Iran. The SVR model (R = 0.8673) demonstrated the best performance, followed by ELM (R = 0.8556), M5 Tree (R = 0.8452), and MARS (R = 0.8045). Both ELM and SVR models exhibited the highest R values; thus, they outperformed MARS and M5 Tree models in assessing groundwater pollution risk. However, according to the present study, all GEP (R = 0.992), EPR (R = 0.999), MARS (R = 0.996), and M5MT (R = 0.9956) models showed better performance compared to the separate machine learning models (ELM, MARS, SVR, and M5 Tree). Additionally, the ELM model, due to its black-box nature, posed challenges in interpreting DRASTIC data compared to the simpler models MARS and M5MT. The SVR model, using the Gaussian expression as the kernel function, exhibited higher complexity than the models used in this study.

Since the constrained target-oriented genetic algorithm plays an effective role in determining the structural form of GEP (R = 0.992) and EPR (R = 0.999) models, it leads to the creation of complex equations (Eq. 9) and the sixth model in Table 7. However, the performance level of these models is higher compared to the study conducted by Bordbar et al.³², who used the Grey Wolf Optimizer (GWO) algorithm to determine the weights of the GALDIT method in the coastal aquifer of the Gorgan River in northern Iran (R = 0.64). It is worth mentioning that they considered TDS pollution in their study.

Bordbar et al.⁴², in another study, employed frequency ratio (FR) methods and a genetic algorithm to enhance the rate and weight of the GALDIT model in the coastal aquifer of the Gorgan River. The correlation (R) between the combined models GALDIT-FR and GALDIT-GA was obtained as 0.69 and 0.61, respectively. However, this correlation increased to 0.76 after combining the adjusted rates using the statistical FR method and the optimized weights of the genetic algorithm. In any case, the correlation established between the GALDIT model and the combined models is lower than the GEP (R = 0.992), EPR (R = 0.999), MARS (R = 0.996), and M5MT (R = 0.995) models. Barzegar et al.⁷¹ used two resampling methods [e.g., Bootstrap Aggregating (BA) and Disjoint Aggregating (DA)] in order to improve performance of ML models (i.e., XGBoost [R = 0.613], Light Gradient Boosting Machine [LGBM], AdaBoost, Categorical Boosting [CatBoost], and RF) for prediction of the GALDIT groundwater vulnerability in the Shabestar Plain aquifer, Iran. From their study, although ML models used were fast-to-learn with lower number of setting parameters, the efficacy of the all coupled ML models was not efficient in the evaluation of groundwater vulnerability (BA-XGBoost [R = 0.6598], BA-LGBM [0.525], BA-AdaBoost [R = 0.591], BA-RF [R = 0.591], BA-CatBoost [R = 0.584], DA-XGBoost [R = 0.562], DA-LGBM [0.571], DA-AdaBoost [R = 0.587], DA-RF [R = 0.616], DA-CatBoost [R = 0.571]) than those yielded in the present study. Furthermore, Norouzi et al.⁴⁴ utilized the Random Forest (RF) method to optimize the DRASTIC framework in the unconfined aquifer of the Miyandouab Plain, northwest Iran. The raster layer data of 7 parameters and the output of the DRASTIC model were used as input and the target variable for the RF model, respectively. According to the ROC-AUC performance criterion, the RF method has a high AUC (AUC = 0.977), and the weight of the DRASTIC model has been optimized with greater reliability. In the present study, the GEP model (AUC = 0.9450) performed first, followed by the MARS and M5MT (AUC = 0.9438), and finally, the EPR model (AUC = 0.9437), all demonstrating excellent performance compared to the BDF-RF method with less reliable optimization.

Elzain et al.⁴⁵ used successfully RFR (R = 0.96 and AUC = 0.97) so as to ascertain the most precise performance during the assessment of adjusted vulnerability index (AVI) related to DRACTIC index, LU parameter, and nitrate values for Miryang City (located South Korea) when compared with SVR (R = 0.866 and AUC = 0.89) and RBNN (R = 0.781 and AUC = 0.76). From their study, the performance of RFR model was the best accurate as well as the results given by this research: EPR (R = 0.9999 and AUC = 0.9437), M5MT (R = 0.9956 and AUC = 0.9438), GEP (R = 0.9920 and AUC = 0.9450), and MARS (R = 0.9966 and AUC = 0.9438). However, the general structure of RFR with 100 trees and SVM with four polynomial kernel functions are more complex than M5MT and MARS developed by two rules and 18 BFs, respectively.

Later, Elzain et al.⁴⁹ concluded that the performance of combination of KNN, BA, and ERT models in order to evaluate DRASTIC index by considering Nitrate pollution and LU parameters, demonstrated the most accurate predictions (R = 0.974) as well as the present investigation. In this regards, ERT model developed by Elzain et al.’s⁴⁹ research, has potential disadvantages of pollution vulnerability predictions when compared to M5MT and MARS given by the present investigation: (i) Interpretability: Extra Trees (ERT) tend to be less interpretable compared to M5MT and MARS models. The randomness in feature selection and splitting decisions may make it harder to understand the specific relationships between features and the target variable. (ii) Overfitting: while ERT are designed to be more robust to overfitting than conventional RFs, they can still be prone to overfitting, especially when dealing with noisy datasets or datasets with a small number of samples. (iii) Less control over splitting: the randomness in feature selection and threshold determination in ERT model means less control over how splits are made. In some cases, this lack of control may result in suboptimal splits, particularly when dealing with certain types of pollution data patterns. Recent investigations, carried out by Karimzadeh-Motlagh et al.⁴⁸, concluded that RF (AUC = 0.987) had the best performance in the approximation of DRASTIC index than GLM (AUC = 0.788) and SVM (0.78) for Najafabad Plain, Iran. Additionally, RF model was classified DRASTIC index as well as AI models in the present investigation (e.g., AUC = 0.9450, 0.9438, and 0.9437 for GEP, MARS, and EPR, respectively).

According to the above-mentioned comparisons, the advantages of MT, EPR, MARS, and GEP in assessing the DRASTIC index for groundwater quality can be particularly pronounced when compared to boosting learning models such as AdaBoost, XGBoost, LightGBM, and CatBoost. One key advantage of the aforementioned models lies in their structural complexity. Model Trees, for instance, combine the interpretability of decision trees with regression capabilities, allowing for a clear visualization of how input variables influence the output. This is crucial when assessing factors (ecological and geochemical factors) that affect groundwater vulnerability, as stakeholders can easily comprehend the relationships and impacts of various parameters like land use and nitrate concentrations. Similarly, MARS employs piecewise linear splines, which allow for flexibility in modeling non-linear relationships while maintaining interpretability. This stands in contrast to boosting models, which often function as black boxes, making it challenging to discern how specific features contribute to predictions. EPR offers a unique approach by evolving polynomial expressions that can capture complex relationships among variables while still being interpretable. This is especially beneficial for groundwater studies where multiple interacting factors must be considered. GEP also presents a clear advantage through its genetic programming framework, allowing the discovery of mathematical models that succinctly represent relationships in the data, facilitating easier understanding and communication of results. When it comes to handling uncertainty in parameter settings, MT, EPR, MARS, and GEP provide greater robustness and flexibility. The present AI models are generally less sensitive to hyperparameter tuning compared to boosting algorithms, which often require meticulous adjustment to achieve optimal performance. For example, boosting models can be quite susceptible to overfitting if parameters like learning rate and tree depth are not carefully calibrated. In contrast, the other models tend to perform well across a wider range of parameter settings, reducing the burden on researchers to fine-tune models extensively. Furthermore, the simplicity in the application of these models allows researchers and practitioners to focus more on understanding the implications of their findings rather than getting lost in complex tuning processes. This is particularly advantageous in the context of groundwater management, where clear communication of results to non-expert stakeholders is crucial for effective decision-making. Additionally, the ability of these models to incorporate domain knowledge into their structures enhances their applicability in environmental studies. For instance, the polynomial expressions generated by EPR can directly reflect scientific understanding of hydrological processes, while MARS can effectively model interactions between multiple environmental factors. This incorporation of expert knowledge helps in developing models that are not only accurate but also relevant to real-world scenarios. In summary, the structural advantages and robustness of MT, EPR, MAR S, and GEP models present compelling benefits over boosting learning models. Their interpretability, flexibility in handling uncertainties, and ability to incorporate domain knowledge make them particularly suitable for assessing the DRASTIC index in groundwater quality studies. This ultimately leads to more reliable and understandable assessments, facilitating better groundwater management practices.

Conclusion

This research aimed to investigate susceptibility state of groundwater resources by the DRASTIC framework. Subsequently, two indices, CD and NVI, based on the same DRASTIC model, were employed to evaluate vulnerability. Due to uncertainties in hydrogeological parameters and complexities of the groundwater system, AI methods such as GEP, EPR, MARS, and MTM5 were applied for the susceptibility evaluation. In this way, the ranges of DRASTIC index values were classified into three categories: no vulnerability (35.7%), very low vulnerability (60.2%), and low vulnerability (4.1%). The CD index indicated that the lowest classification of vulnerability was associated with very low vulnerability (17.4%), while the highest was related to low vulnerability (82.6%). In contrast to the other two indices, the NVI index showed that 75.52% of the study area falls into the category of very low vulnerability, and 24.48% falls into the category of low vulnerability. All soft computing methods used in both the testing and training phases have high correlation coefficients. However, the EPR model ranked first, followed by the MARS, MTM5, and GEP models. The order of these AI models in terms of precision levels and expected error is consistent. According to the ROC-AUC method, all models demonstrated excellent performance. The EPR model has a higher level of complexity when compared to other AI models, so the MARS model can be a suitable alternative. Vulnerability classification through the MARS model reveals that approximately 73.06% of the studied plain is in the very low vulnerability zone, while 26.94% is in the low vulnerability zone, covering an area of about 1478.3 square kilometers and 545.1 square kilometers, respectively, in the Kerman–Baghin aquifer. Furthermore, the outcomes of the present investigation were absolutely comparable with those reported in reliable literature. This means that the AI models used in this study had superiority in the prediction of DRASTIC index, influenced by nitrate pollution and land use factors, over similar investigations.

The practical implications for groundwater management using the DRASTIC index for agricultural purposes are significant and multifaceted. First, by identifying areas of varying vulnerability to contamination, farmers and agricultural planners can implement targeted practices to protect groundwater quality. For instance, regions classified with high vulnerability can benefit from best management practices (BMPs) that minimize the use of fertilizers and pesticides, thus reducing nitrate leaching into groundwater. Additionally, the DRASTIC index provides a framework for assessing the potential impacts of different land use practices on groundwater quality. Agricultural managers can use this information to make informed decisions about crop selection, irrigation methods, and land management strategies that align with the vulnerability classifications. For example, crops that require less water or are less nutrient-intensive could be favored in more vulnerable areas to mitigate contamination risks. The research also emphasizes the need for regular monitoring and assessment of groundwater quality in agricultural regions. Implementing a monitoring program that tracks changes in the DRASTIC index over time can help identify emerging risks and facilitate timely interventions. This ongoing assessment can guide adaptive management strategies that respond to changing environmental conditions and agricultural practices. Moreover, collaboration with local communities and stakeholders is crucial. Educating farmers about the implications of groundwater vulnerability and encouraging sustainable practices can foster a collective effort to protect these vital resources. Initiatives that promote community engagement in groundwater management can enhance compliance with protective measures and contribute to better overall water quality. Finally, the findings can support policy development aimed at regulating agricultural practices in sensitive areas. Policymakers can use the DRASTIC index to prioritize regions for conservation efforts, funding, and technical assistance, ensuring that resources are allocated efficiently to safeguard groundwater quality. In summary, leveraging the DRASTIC index for agricultural purposes can lead to improved groundwater management through targeted practices, informed decision-making, regular monitoring, community engagement, and effective policy development, ultimately promoting sustainable agricultural practices and protecting vital water resources.

The research on groundwater resource susceptibility using the DRASTIC framework reveals several current challenges that warrant attention. One significant challenge is the inherent uncertainty in hydrogeological parameters, which complicates the accurate assessment of groundwater vulnerability. These uncertainties arise from variations in data quality, availability, and the complexity of the groundwater systems themselves. Additionally, the interaction of multiple environmental factors, such as land use changes and climate impacts, adds another layer of complexity, making it difficult to develop universally applicable models. Another challenge is the interpretability of AI models. While the EPR model demonstrated high predictive accuracy, its complexity can make it difficult for stakeholders and policymakers to understand the underlying relationships between input parameters and the DRASTIC index. This lack of clarity can hinder effective decision-making and limit the practical application of the results in groundwater management.

In light of these challenges, several future recommendations can enhance the robustness of groundwater vulnerability assessments. Firstly, there is a need for the integration of diverse data sources, including remote sensing and advanced geospatial analytics, to provide a more comprehensive understanding of hydrogeological conditions. This integration could improve the accuracy and reliability of the models used in vulnerability assessments. Furthermore, future research should focus on refining AI models to balance complexity and interpretability. Exploring ensemble approaches that combine the strengths of various models may yield more robust predictions while maintaining clarity in the results. Conducting longitudinal studies to monitor changes in groundwater quality over time will also provide valuable insights into how dynamic environmental factors influence vulnerability. Strengthening community engagement and raising public awareness about groundwater conservation is crucial for effective resource management. Educating local stakeholders about the implications of land use and pollution on groundwater quality can foster greater involvement in protection efforts. Lastly, addressing the challenges of data availability and quality remains vital. Ensuring access to reliable hydrogeological data will enhance the accuracy of assessments and facilitate ongoing research in the field. By focusing on these future directions and overcoming current challenges, the research can contribute significantly to the sustainable management of groundwater resources.