Abstract
Extreme short-duration rainfall is intensifying with climate warming, and growing evidence suggests that subhourly rainfall extremes are increasing faster than more widely studied durations at hourly and daily timescales. In this case study, we used 55 years (1968–2022) of 5-min precipitation data from Mahantango Creek, a long-term experimental agricultural watershed in east-central Pennsylvania, United States, to examine annual and seasonal changes in subhourly (15-min), hourly, and daily rainfall extremes. Specifically, we evaluated temporal trends in the magnitude and frequency of subhourly, hourly, and daily rainfall extremes. We then estimated apparent scaling rates between rainfall extremes and dew point temperature (Td) and compared these rates to the Clausius-Clapeyron (CC) rate (∼ 7% per °C). We also determined the coincidence of extreme rainfall trends with indicators of atmospheric instability and convective-type precipitation. Overall, we found the most significant changes in rainfall extremes at 15-min durations during the spring, with magnitudes of these subhourly extremes increasing by 0.6 to 0.9% per year, and frequencies rising by 3.4% per year. Apparent scaling rates in the spring showed that 15-min rainfall extremes transitioned from sub-CC scaling to greater than 2CC scaling when Td reached 11° C, implying a possible shift from stratiform rains to more intense convective rains above this Td threshold. Notably, trends in maximum hourly convective available potential energy (CAPE) increased during spring, as did the ratio of 15-min rainfall extremes to their corresponding daily rainfall totals. Findings indicate that convective-type precipitation may be playing an increasing role in the intensification of springtime 15-min rainfall extremes in Mahantango Creek.
Similar content being viewed by others
Introduction
Extreme precipitation poses considerable challenges to society and the environment. For instance, short-duration (< 1 d) rainfall extremes represent a key ingredient in flash flooding1, and areas susceptible to flash flooding are likely to expand as these rainfall extremes intensify with climate change2,3,4. Agriculture is also adversely affected by extreme precipitation, as crop yields are reduced5,6and nutrient losses in agricultural runoff are enhanced7.
There is strong evidence that rainfall extremes are intensifying worldwide. Many studies document that daily precipitation extremes are rising at global8,9,10and continental11,12scales. Studies in the United States (U.S.) also indicate that the magnitude and frequency of daily rainfall extremes are increasing13,14,15. Such observations have supported theoretical expectations that increases in the frequency and magnitude of precipitation extremes are largely attributable to anthropogenic climate warming11,16,17.
Climate warming is expected to intensify extreme precipitation because a warmer atmosphere can hold more moisture. This understanding is formalized by the Clausius-Clapeyron (CC) relationship18,19, which states that atmospheric moisture increases by about 7% per °C of warming assuming constant relative humidity. Provided that weather circulation patterns remain mostly unchanged, the CC relationship suggests that the amount of moisture available to rainstorms would follow the expected CC rate20. Given this theoretical knowledge, many researchers have used observational records to relate rainfall extremes with short-term changes in air temperature or dew point temperature – termed “apparent scaling”21. Assuming other atmospheric properties exhibit similar covariance over short and long-term climatic periods, apparent scaling relationships might then provide clues to the possible response of extreme rainfall to climate change – termed “climate scaling”22.
Using the apparent scaling approach, a number of global-scale studies suggest that extreme daily rainfall scales with temperature at roughly the CC rate or less23. For instance, Westra et al10. showed the median intensity of maximum daily precipitation increased with global temperature at rates of roughly 6–8% per °C in line with CC scaling theory. Recent studies have confirmed this finding, showing that daily rainfall extremes generally scale at the CC rate24,25. However, other studies of CC scaling at finer spatiotemporal scales have revealed a wide range of apparent scaling rates with temperature, dew point temperature, or a combination thereof22.
In particular, short-duration (< 1d) rainfall extremes have deviated appreciably from the CC relation, frequently intensifying at rates less than (sub-CC) or greater than (super-CC) theoretical expectations22,26. For example, in Australia, apparent scaling of hourly rainfall extremes followed sub-CC scaling in the northwestern and central regions, but CC and super-CC scaling in the southeastern regions27. Elsewhere, regional studies have shown super-CC scaling of hourly extremes in Europe28, the U.S.29,30 , and Asia31, even noting apparent scaling rates of up to three times the CC rate (3CC) in Australia32. Studies of subhourly rainfalls have shown apparent scaling rates of nearly double the CC rate (2CC) in the Netherlands33and Austria34.
A variety of factors may contribute to the shift from sub-CC to super-CC behavior for short-duration extremes. Such factors include changes in atmospheric circulation, moisture availability, and the relative contribution of two major precipitation types – stratiform and convective – to total rainfall35. Stratiform rains are generally characterized by cyclonic, large-scale frontal systems that are sustained by forced lifting of airmasses, while convective storms are driven by uplift processes and atmospheric instability that operate over smaller spatial scales36. At lower temperatures, stratiform rains of low to medium intensity generally prevail, producing sub-CC to CC scaling. Convective rainfall is typically more responsive to temperature increases than stratiform rainfall35. Thus, more intense convective storms regularly dominate at higher temperatures, generating CC to super-CC scaling35. In general, the expectation is that short-duration rainfall extremes will intensify faster with warming than daily extremes, as hourly and subhourly rainfall extremes commonly exhibit higher scaling rates with temperature (cf25).
Recent studies have confirmed that subhourly rainfall extremes are increasing faster than hourly and daily extremes37,38,39. These studies affirm earlier modeling by Kendon et al40. suggesting that changes in 10-min and hourly rainfall extremes would arise before changes in daily extreme precipitation. While a growing number of studies have compared trends in subhourly rainfall extremes to hourly and daily extremes22,26, few studies of this nature have been undertaken in the U.S. As such, there is a need for research that evaluates changes in subhourly rainfall extremes relative to more widely reported rainfall durations, with emphases on long-term trends in the magnitude and frequency of extremes41, as well as their relationships with temperature. There is also a need to understand the influence of convection on subhourly rainfall extremes, as recent studies in Eurasia have shown that contributions of convective precipitation to total precipitation have risen42, especially in the shoulder seasons, which have become more summerlike36.
In this case study, we examined annual and seasonal trends in subhourly, hourly, and daily rainfall extremes using 55 years of 5-min precipitation observations from a USDA Agricultural Research Service (ARS) experimental watershed in east-central Pennsylvania, U.S. The 5-min precipitation records analyzed herein are among the longest running records at this temporal resolution in the U.S., making them ideal for studying changes to extreme rainfalls at varying durations, including subhourly durations, which have been relatively understudied in this region. Specifically, we aimed to: (1) characterize the climatology of subhourly, hourly, and daily rainfall extremes, (2) quantify changes in the magnitude and frequency of subhourly rainfall extremes relative to hourly and daily extremes, (3) estimate apparent scaling rates between rainfall extremes and dew point temperature and compare these scaling rates to the Clausius-Clapeyron (CC) rate (∼ 7% per °C), and (4) determine the extent to which significant trends in extreme rainfall are coincident with trends in indicators of atmospheric instability and convective-type precipitation. Findings from this case study have important implications for studies of short-duration rainfall extremes, as well as for agroecosystem management in a changing climate in the central Appalachian region of the eastern U.S.
Study area
The case study was carried out in the 7.3-km2 WE-38 experimental watershed, an intensively monitored upland basin in the Ridge and Valley region of east-central Pennsylvania, U.S. (Fig. 1). The WE-38 watershed (outlet: 40°42’16” N, 76°35’16” W) – a headwater basin that is situated in the northcentral region of the 420-km2 Mahantango Creek watershed – has a long record of high-quality hydrometeorological observations43that support the study of short-duration rainfall extremes. The watershed has been managed by ARS as a long-term observatory since the late 1960s when ARS’s National Experimental Watershed Network44,45was formally authorized by Congress46. Since the inception of continuous monitoring in 1968, accumulated precipitation has been recorded every 5 min in the WE-38 watershed43,47. Such high-frequency monitoring of precipitation – a hallmark of long-term ARS watershed research (see section S2 in the Supplemental Information) – has produced some of the longest running 5-min precipitation records in the nation. Currently, the WE-38 watershed is one of 23 benchmark experimental watersheds and ranges maintained by ARS across the U.S48. The watershed is also part of several national research networks, including the Conservation Effects Assessment Project49and the Long-Term Agroecosystem Research (LTAR) network50,51.
Site map of ARS’s WE-38 experimental watershed in east-central Pennsylvania, U.S. The top panel shows the location of the 420-km2 Mahantango Creek watershed within the contiguous U.S. (CONUS), as well as a zoomed-in map depicting the location of the 7.3-km2 WE-38 watershed in the northcentral region of Mahantango Creek. The lower left-hand panel shows the locations of the three permanent rain gauges in WE-38 (1 = RB-37 rain gauge; 2 = MD-38 rain gauge, which is collocated with a climate station; and 3 = RE-37 rain gauge). Also mapped are the Chesapeake Bay Program’s 1-m land use / land cover data52, showing mostly cropland and pasture in the valleys, with intact forests confined to the ridges. Maps were created using ArcGIS Pro software (version 3.2.2; ESRI; Redlands, California, U.S.).
Data
Precipitation measurements
The case study uses continuous 5-min precipitation records from three long-term rain gauging stations in the WE-38 watershed (Fig. 1). Two stations (RB-37 and RE-37) have been operating since 1968, while the third station (MD-38) came online in 1979 (Table 1). From 1968 to 1996/97, all three gauging stations were instrumented with unshielded Fischer and Porter digital punch paper tape weighing rain gauges (a.k.a. Fischer-Porter rain gauges53,54,55). In 1996/97, ARS technicians upgraded the Fischer-Porter rain gauges with load cell datalogging systems, which replaced the digital punch paper systems and weighing mechanisms on the original Fischer-Porter gauges47. These upgrades increased the measurement resolution from 2.54 mm under the legacy Fischer-Porter system to 0.254 mm under the newer load cell system. Buda et al47. offer more details on rain gauge maintenance and calibration, data processing, and routine quality-control (QC) procedures.
Record homogenization
Analyses of long-term changes in subdaily precipitation have to account for shifts in instrumentation that affect measurement resolution, as such shifts produce inhomogeneities in the data that cloud the interpretation of trends and event-based statistics56. Given the tenfold improvement in measurement resolution that occurred in the WE-38 watershed in 1996/97 (Table 1), it was essential to homogenize the 5-min precipitation time series of each gauge to reflect a common measurement resolution for the entire period of record. To do this, we employed the algorithm of Groisman et al57. to convert the finer-resolution measurement period (post 1996/97) to a uniform precision of 2.54 mm for the entire 55-year record (see section S4 and Fig. S4 in the Supplemental Information). This same method has been used to harmonize hourly precipitation data from the National Climatic Data Center’s Hourly Precipitation Data network25,58,59, which saw a similar change in precision during its tenure57.
Data aggregation and additional QC procedures
We used RB-37, the longest running and most complete rain gauge record, to generate a nearly serially-complete (i.e., virtually gap free, with missing data < 0.1%) time series of homogenized 5-min precipitation data (see section S3 in the Supplemental Information for more details). We then aggregated the 5-min data to 15-min (subhourly), hourly, and daily intervals. We summarized the data using fixed intervals (e.g., 00:00–00:15, 00:15–00:30 for 15-min data; 00:00–01:00, 01:00–02:00 for hourly data; and 00:00–24:00, 24:00–48:00 for daily data). Data were also separated by meteorological seasons: winter (December-January-February), spring (March-April-May), summer (June-July-August), and fall (September-October-November). Lastly, as an added check on data quality, we subjected the 15-min and hourly time series to additional QC checks using open-source QC algorithms for subhourly (“SubHourlyQC” package60) and hourly (“intense-qc” package61) rainfall data. These algorithms, implemented in the Python programming environment, automate a series of QC procedures recommended by the World Meteorological Organization (WMO), including constraint, consistency, spike, rapid change, flat line (streak), and domain tests60,61.
Atmospheric reanalysis data
We used two gridded data products from the fifth generation of European ReAnalysis (ERA5) to provide atmospheric data in support of our study. We retrieved daily mean temperature (Ta, °C) and daily mean dewpoint temperature (Td, °C) from the ERA5-Land dataset62, as continuous temperature data were not available in WE-38 prior to 199763(see section S6 the Supplemental Information for comparisons between observations and ERA5-Land data). ERA5-Land data are provided at a horizontal resolution of 9 km. In addition, we retrieved hourly data on convective available potential energy (CAPE; J kg-1) from the ERA5 global reanalysis64, as ERA5 offers some of the most reliable reanalyses of convective parameters65. ERA5 data are provided at a horizontal resolution of 31 km. We selected the corresponding grid boxes for ERA5-Land and ERA5 to obtain data for the local region that included the WE-38 watershed. All data were downloaded from the Copernicus Climate Change Service66.
Methods
Assessing the magnitude of rainfall extremes with block maxima
We used a block maxima approach to assess changes in the magnitude of rainfall extremes41. To implement the block maxima approach, we divided the observational periods for 15-min, hourly, and daily rainfall time series into non-overlapping blocks of years and seasons and extracted the largest 15-min (Rx15min), hourly (Rx1h), or daily (Rx1d) rainfall value within each block. The resultant datasets could then be used to evaluate general climatological patterns in rainfall extremes and to estimate trends using nonparametric trend tests like the Mann-Kendall test41and extreme value theory67.
Quantifying trends in annual and seasonal rainfall maxima
The block maxima approach enabled us to use two compatible methods for quantifying trends in annual and seasonal rainfall extremes (e.g., Westra et al10.). The first method is the nonparametric Mann-Kendall test68,69, which has been widely used to evaluate the significance of monotonic trends in hydrometeorological time series70,71. A key advantage of the Mann-Kendall test is that it makes no assumptions about the distribution of the data, making it robust to outliers. The second method, which is derived from extreme value theory67, fits the nonstationary generalized extreme value (GEV) distribution to annual and seasonal maxima of rainfall extremes, and determines if one (or more) of the three parameters is changing as a function of time or another covariate of interest72.
Briefly, we used the R package “modifiedmk”73 to execute the Mann-Kendall test and evaluate the significance of monotonic trends in annual and seasonal Rx15min, Rx1h, and Rx1d. The magnitude of the trends was estimated with Sen’s slope estimator74. Trends with p values less than 0.05 were considered significant.
To conduct nonstationary GEV modeling, we used the R package “extRemes”75. The GEV distribution is estimated with three parameters76: (1) location (µ), which defines the center of the distribution, (2) scale (σ), which measures the size of the deviations around the location parameter, and (3) shape (ξ), which controls the tail behavior of the distribution. Following the approach of Konstali and Sorteberg77, we introduced time as a covariate to the location parameter, while holding the scale and shape parameters constant. We employed the method of maximum likelihood to estimate the GEV parameters. We then used the likelihood ratio test to assess the significance of the time-varying location parameter relative to a stationary model with no covariates. Significant trends in annual and seasonal Rx15min, Rx1h, and Rx1d were inferred when likelihood ratio tests yielded p values less than 0.05.
Quantifying trends in the 99th percentile of rainfall extremes
As noted by Villarini et al78., Mann-Kendall tests offer insight into monotonic trends in the center of the data distribution. Using a time-varying location parameter in nonstationary GEV models also focuses on temporal changes in the center of the distribution. To provide a more complete picture of changing rainfall extremes, it is also meaningful to examine changes in other parts of the rainfall distribution using methods like quantile regression79,80. Indeed, several recent studies have used quantile regression to assess trends in extreme precipitation39,77,78,81,82.
Herein, we used the R package “quantreg”83 to assess linear trends in the 99th percentile of annual and seasonal 15-min (P9915min), hourly (P991h), and daily (P991d) rainfalls. Unlike the block maxima approach, which utilizes only a small portion of the rainfall data (e.g., the single largest value in a year or season), quantile regression uses the entire rainfall time series. We fitted quantile regression models using a modified version of the Barrodale and Roberts84algorithm85. Quantile regressions were deemed significant when p values were less than 0.05.
Assessing changes in the frequency of rainfall extremes
There exists a close association between the magnitude and frequency of rainfall extremes, as increases in magnitude are often accompanied by increases in frequency41. To test for changes in the frequency of rainfall extremes, we adopted a peaks-over-threshold (POT) approach14. To generate annual and seasonal POT time series, we used the 30-year reference period (e.g., Dunn and Morice86) from 1971 to 2000 to estimate 99th percentile rainfall thresholds for 15-min, hourly, and daily durations. We included both wet and dry time intervals in the analysis in order to avoid known biases with changes in wet periods87. To ensure event independence, we declustered the time series as follows: we retained the maximum 15-min and hourly rainfall amount for each calendar day32,88, while a 1-d separation rule was applied to the daily rainfall extremes. Using the declustered time series, we then counted the number of time intervals in the 15-min, hourly, and daily time series that exceeded their respective 99th percentile thresholds.
We used Poisson regression in the R software environment (R Core Team, 2023; version 2.4.3) to evaluate trends in the frequency of rainfall extremes. As noted by Villarini et al78. and Mallakpour and Villarini89, Poisson regression is a class of generalized linear model (GLM) that is used to model count data90, such as the number of extreme rainfall events per year exceeding a high threshold (e.g., Ivancic and Shaw91). Poisson regression models were judged significant when p values were less than 0.05.
Scaling of rainfall extremes with dew point temperature
The relationship between extreme rainfall and temperature (a.k.a. “apparent scaling”, or scaling) is essential to understanding how a warming climate influences rainfall extremes22. In this study, we used the binning method28to analyze apparent scaling relationships between rainfall extremes and Td. We selected Td as a scaling variable over Ta because it is a more reliable indicator of the actual humidity of the air92, which has a large effect on scaling26. The Glossary of Meteorology93defines Td as the temperature a given parcel of air needs to be cooled to at constant pressure to attain a relative humidity of 100%. Thus, a 1 °C rise in Td can be considered roughly equivalent to a ~ 7% rise in atmospheric moisture content94. The binning method has been widely applied in the literature (see review by Westra et al26.) to analyze the apparent scaling between extreme rainfall and Td (e.g., Ali et al24.). Herein, we implemented the binning method using local data on Td from the ERA5-Land model.
To execute the binning method, we compiled separate time series of 15-min, hourly, and daily precipitation using wet intervals only (i.e., intervals with precipitation ≥ 2.54 mm). For each of the time series, we paired each wet interval with its corresponding daily value for Td. Time series of precipitation-Td pairs were constructed for all observations, as well as for seasons. We then arranged the annual and seasonal time series into 20 bins of equal size and sorted the bins from lowest to highest Td. For each bin, we estimated the 99th percentile precipitation amount and the mean Td. We then regressed the logarithm of the 99th percentile precipitation amount onto mean Td. The regression coefficient (β) represented the precipitation-Td scaling rate. Using the conversion (eβ– 1) × 100%, we expressed the scaling rate as a % change per °C warming95.
Examining the role of convection in extreme rainfall trends
Extreme rainfall events often arise from convective storm systems, especially thunderstorms96. These storms are driven by atmospheric instability and moisture availability, which can be formally expressed in terms of CAPE. As such, CAPE provides insight into the potential for convection to influence rainfall extremes97,98. Several recent studies have also derived a useful indicator of convection-driven storms that involves estimating a metric called Rx1hP, which is defined as the fractional contribution of Rx1h to its corresponding daily rainfall total59,99,100. A similar calculation can be made for 15-min rainfall extremes, which we denote as Rx15minP (see section S7 in the Supplemental Information for more details on the calculations of Rx15minP and Rx1hP). As Blenkinsop et al99. note, values of Rx1hP approaching 1 indicate rainfall concentrated in a small part of the day, as would be expected from convective precipitation, while Rx1hP values closer to 0 suggest a more even distribution of rainfall throughout the day, as would be expected from stratiform precipitation.
To assess the role of convection in hourly and subhourly rainfall extremes, we assessed whether trends in the annual and seasonal maxima of CAPE were coincident with trends in annual and seasonal Rx1hP and Rx15minP. We used the Mann-Kendall test and Sen’s slope estimator to evaluate monotonic trends in convective parameters from ERA5. To estimate trends in Rx1hP and Rx15minP, we employed one-inflated beta regression101, which is used to describe rates and proportions that assume values greater than 0 and up to and including 1; beta regression was recently used by Lavers and Villarini102to estimate trends in the fractional contribution of atmospheric rivers to total precipitation. One-inflated beta regression models were executed in the R package “gamlss”103.
Results and discussion
What are the climatological attributes of subhourly, hourly, and daily rainfall extremes?
Prior to conducting trend analyses, we sought to characterize the general climatology of annual and seasonal Rx15min, Rx1h, and Rx1d in the WE-38 watershed. With the exception of summer, seasonal rainfall maxima in WE-38 were generally lower than annual rainfall maxima based on long-term climatological averages (1968–2022) of Rx15min, Rx1h, and Rx1d (Fig. 2). On a seasonal basis, the highest median values of Rx15min and Rx1h occurred in the summer due to the strong influence of convective precipitation on short-duration rainfall extremes. The highest median values of Rx1d occurred in the fall owing to the effects of larger scale, longer duration precipitation events (e.g., stratiform precipitation), including tropical cyclones, which have increased in frequency in the Northeast104. The winter months experienced the lowest median values of Rx15min, Rx1h, and Rx1d in the WE-38 watershed.
Here in the U.S., the climatological features of annual Rx1d have received considerably more attention than hourly and subhourly rainfall maxima. Therefore, we compared our Rx1d results with other studies that have examined Rx1d climatologies for the region that included WE-38. In a recent study, Hoerling et al105. examined the spatial patterns of Rx1d across the U.S. using observations and climate models, with long-term (1948–2018) climatological averages of Rx1d ranging from 60 to 70 mm in eastern Pennsylvania. Elsewhere, a global study by Bador et al106. also showed that Rx1d averaged 60–70 mm in the eastern U.S., albeit with a much shorter period of station-based observations (2001–2013). In the WE-38 watershed, we found that annual Rx1d attained a median value of 61.0 mm (IQR = 35.6 mm) over the 55-year study period, which is in line with these national and global scale studies. Unlike Rx1d, which is well-studied nationally and globally, long-term data on subdaily rainfall climatologies are currently limited in the U.S. Thus, it was difficult to place our findings for Rx15min and Rx1h in broader context. That said, this situation is likely to change with the recent advent of global subdaily rainfall datasets61,107, which enable the estimation of indices to study these short-duration rainfall extremes100,108.
Box plots showing the distribution of annual and seasonal maxima of 15-min (Rx15min; top panel), hourly (Rx1h; middle panel), and daily (Rx1d; lower panel) rainfall in the WE-38 watershed; long-term climatological averages are based on 55 years of data from 1968–2022. For each plot, the box indicates the interquartile range, the whiskers show the extreme values (1.5 times the interquartile range), the asterisks designate potential outliers (values greater or less than three times the interquartile range), the solid line depicts the median, and the “x” indicates the mean. Different letters above each box plot indicate significant differences in the medians based on a Kruskal–Wallis analysis followed by Dunn’s post hoc test (p < 0.05). For a comparison of fixed-window vs. moving window results, see Fig. S5 in Supplemental Information.
Is the magnitude of subhourly, hourly, and daily rainfall extremes increasing?
We used the nonparametric Mann-Kendall test and nonstationary GEV models to estimate annual and seasonal trends in Rx15min, Rx1h, and Rx1d. While these tests leveraged fixed-interval data, we also examined moving windows with lengths of 15 min, 1 h, and 24 h, as such aggregation methods can overcome event truncation issues when time steps are fixed25. Notably, the results of these tests were mostly consistent for fixed interval and moving window aggregations, therefore, we focused on the fixed window aggregations herein (Figs. 3 and 4) and provided moving window results in supplemental information (Figs. S6 and S7).
Annual and seasonal trends in the magnitude of Rx15min, Rx1h, and Rx1d based on Sen’s slope. Slopes are normalized over the mean value of each variable and expressed as a percent change per year. Statistically significant trends are determined with the Mann-Kendall test. Significant trends are underlined and bolded, with asterisks indicating the level of significance: * p ≤ 0.05; ** p ≤ 0.01; *** p ≤ 0.001.
Several lines of evidence demonstrate that the most consequential trends in extreme precipitation occurred at subhourly timescales in the spring. For instance, Mann-Kendall tests revealed that spring Rx15min increased at a rate of 0.9% per year, which was statistically significant (Fig. 3). Notably, nonstationary GEV models on spring Rx15min also showed that the increases in spring Rx15min were statistically significant, although the yearly rates of increase (~ 0.6% per year) were slightly lower than those derived from Mann-Kendall tests (Fig. 4).
Annual and seasonal trends in the magnitude of Rx15min, Rx1h, and Rx1d using nonstationary GEV models with a time-varying location parameter. Slopes are normalized over the mean value of each variable and expressed as a percent change per year. Statistically significant trends are determined with the likelihood ratio test. Significant trends are underlined and bolded, with asterisks indicating the level of significance: * p ≤ 0.05; ** p ≤ 0.01; *** p ≤ 0.001.
To offer a better sense of changing rainfall extremes in the WE-38 watershed, we also tested for trends in the 99th percentile of the 15-min (P9915min), hourly (P991h), and daily (P991d) rainfall time series using quantile regression (Fig. 5). Notably, quantile regression suggested a greater proportion of positive trends relative to the Mann-Kendall tests and nonstationary GEV models (Figs. 3 and 4). Even so, we found noteworthy agreement in terms of which trends were most consequential, as quantile regression models also indicated a statistically significant upward trend in spring 15-min rainfall extremes, with P9915min increasing at a rate of 0.7% per year. In addition, quantile regression models also detected statistically significant rising trends in annual and summer P9915min (Fig. 5), albeit at slightly lower rates of 0.3% per year. In concordance with the Mann-Kendall tests, quantile regression models found no statistical evidence for changes in hourly or daily rainfall extremes at annual and seasonal timescales.
Annual and seasonal trends in the magnitude of P9915min, P991h, and P991d based on quantile regression. Regression slopes are normalized over the mean value of each variable and expressed as a percent change per year. Significant trends are underlined and bolded, with asterisks indicating the level of significance: * p ≤ 0.05; ** p ≤ 0.01; *** p ≤ 0.001.
Our results support the hypothesis that the intensification of subhourly and hourly rainfall extremes might be detected earlier than daily extremes. Indeed, Kendon et al40. applied a 1.5-km convection-permitting model to demonstrate that 10-min and hourly rainfall extremes would likely emerge before changes to daily extreme precipitation in the southern U.K. Several observational studies have recently corroborated this assertion. For instance, Ayat et al37. employed rain-gauge observations and ground-based radars in the vicinity of Sydney, Australia to show that extreme (99th percentile) and very extreme (99.9th percentile) rainfalls had increased faster at the 10-min resolution than at hourly or daily resolutions. Similarly, Treppiedi et al39. determined that 99th percentile 10-min rainfall amounts intensified faster than 99th percentile hourly or daily rainfalls in Sicily, Italy. Most recently, Jayaweera et al38. evaluated annual rainfall maxima across a range of storm durations (6 min to 7 d), and showed that the magnitude of short-duration (< 1 h) rainfalls increased faster than longer duration events (> 1 h) for the continent of Australia. Notably, the results of Ayat et al37., which were reported for the annual timescale, suggested that extreme and very extreme 10-min rainfalls increased by 0.5 to 2% per year during their 20-year analysis, while Jayaweera et al38. reported that the annual intensity of 6- to 18-min rainfalls had increased at rates of roughly 0.4 to 0.6% per year over the course of 55 years. In our 55-year study in the WE-38 watershed, we found equally strong evidence that 15-min rainfall extremes had increased by upwards of 0.9% per year, although the largest increases occurred in the spring season rather than annually as noted by Ayat et al37. and Jayaweera et al38..
Are subhourly, hourly, and daily rainfall extremes happening more frequently?
A related objective of our study was to determine if changes in extreme rainfall magnitudes were accompanied by changes in the frequency of rainfall extremes. As such, we adopted a POT modeling approach to ascertain the frequency with which 15-min, hourly, and daily rainfall extremes exceeded their respective 99th percentile thresholds (Table 2).
Using Poisson regression, we found that the spring exhibited a statistically significant upward trend in the frequency of 15-min rainfall extremes (Fig. 6). These extreme events, which increased by 3.4% per year (0.03 events per year), accompanied the increases in extreme 15-min rainfall amounts that were also observed in the spring (Figs. 3, 4 and 5). Notably, the spring experienced an attendant rising trend in the frequency of hourly rainfall extremes, which increased by 3.7% per year (0.03 events per year). Aside from the increasing frequencies of 15-min and hourly rainfall extremes in the spring, we found no additional evidence that the frequency of 15-min, hourly, or daily rainfall extremes was changing at other times of year.
Annual and seasonal trends in the number of events exceeding P9915min, P991h, and P991d intensity thresholds using Poisson regression. Regression slopes are normalized over the mean value of each variable and expressed as a percent change per year. Significant trends are underlined and bolded, with asterisks indicating the level of significance: * p ≤ 0.05; ** p ≤ 0.01; *** p ≤ 0.001.
To date, studies that have examined changing frequencies of subhourly and hourly rainfall extremes have been limited relative to those that have assessed daily rainfall extremes. Indeed, there is an extensive literature showing increases in the frequency of daily rainfall extremes at regional109, national14,78,91, and global110,111scales. Recently, however, several studies have indicated that the frequency of hourly rainfall extremes is increasing faster than daily extremes. For instance, Yu et al112. used the North American Land Data Assimilation System forcing data to illustrate that increases in the frequency of hourly rainfall extremes outpaced changes in daily extremes, especially in the eastern U.S. More recently, a global study using gridded ERA5 reanalysis data revealed that the frequency of hourly rainfall extremes was increasing nearly two times faster than daily extremes, with some of the largest changes in eastern North America113. Our study in the WE-38 experimental watershed lends support to these national and global scale studies of hourly and daily rainfall extremes, showing that increases in the frequency of subhourly and hourly rainfall extremes have emerged well ahead of daily extremes, particularly in the spring. Moreover, the increasing frequency of springtime 15-min rainfall extremes has been accompanied by an attendant increase in the magnitude of these subhourly extremes.
How does dew point temperature affect subhourly, hourly, and daily rainfall extremes?
Increasing temperatures along with changes in atmospheric moisture availability are key factors governing the intensity of extreme rainfall26. Such changes are best captured by Td, as it represents the combined effects of temperature and humidity on rainfall intensification processes22. Herein, we used the binning method to establish apparent scaling relations between 15-min, hourly, and daily rainfall extremes and daily Td in the WE-38 watershed. While we were generally interested in the overall scaling patterns between 15-min, hourly, and daily rainfall extremes (Fig. 7), we were specifically interested in examining potential shifts in seasonal scaling relations (Fig. 8), as these shifts could offer further insight into the role of precipitation types (e.g., stratiform vs. convective precipitation) on extreme subhourly rainfall trends, especially those that were noted during the spring season.
Apparent scaling of annual and seasonal 15-min, hourly (1-h), and daily (1-d) rainfall extremes with dew point temperature (Td, °C). Scaling rates are expressed as a % change per °C of warming. Significant regression relationships between the logarithm of the 99th percentile precipitation amount and mean Td are underlined and bolded. Asterisks indicate the level of significance: * p ≤ 0.05; ** p ≤ 0.01; *** p ≤ 0.001.
In terms of overall scaling relations, we found that scaling rates between extreme rainfall and Td generally declined with increasing rainfall duration in the WE-38 watershed (Fig. 7). On an annual basis, 15-min rainfall extremes exhibited super-CC scaling (> ∼7% per °C), with hourly extremes closer to CC rates (∼7% per °C), and daily extremes displaying sub-CC rates (< ∼7% per °C). These findings were generally in line with a study by Schroeer and Kirchengast34, who showed that 10-min rainfall extremes in southeastern Austria displayed super-CC scaling, while hourly rates scaled closer to the CC rate, and sub-CC rates prevailed for daily extremes. In the Netherlands, Loriaux et al33. also reported that 10-min rainfall extremes attained higher scaling rates with Td than hourly and daily extremes, with nearly 2CC scaling (∼14% per °C) for 10-min rainfalls. We also found that hourly scaling rates generally exceeded daily rates in WE-38, which is consistent with studies that have compared scaling rates among these two durations114,115. It is important to note that other studies have reported more similar scaling rates between daily and hourly rainfall extremes using different estimation procedures for apparent scaling (e.g., Bayesian quantile regression, as in Najibi et al95.). Even so, super-CC scaling of 15-min rainfall extremes, as was found herein, is in agreement with previous work finding that the intensification of short-duration rainfall extremes generally exceeds thermodynamic expectations of CC scaling (see review by Fowler et al22.).
We then evaluated the seasonal scaling patterns in greater detail to assess potential non-linearities in apparent scaling relations that could shed further light on the extreme rainfall trends we observed in WE-38. As Blenkinsop et al116. observed, seasonal scaling relationships between extreme hourly rainfalls and temperature are not always linear, and such nonlinearities can offer clues into the types of precipitation that drive rainfall extremes at different times of year. For instance, during summertime in the WE-38 watershed, we found that 15-min and hourly rainfall extremes exceeded 2CC scaling rates (∼ 15 to 19% per °C) up to a Td of ∼ 18 °C, and then leveled off above this threshold (Fig. 8). Such high scaling rates were clearly masked by the overall linear scaling rates indicated in Fig. 7. Convective processes (e.g., thunderstorms) are the prevailing rainfall generating mechanism in the summer, especially for temperatures ranging between 10° and 20 °C35,94. As such, the greater than 2CC scaling rates observed for 15-min and hourly rainfall extremes in summer clearly point to convective storms as generators of these extreme rainfalls.
In the spring months, we observed significant increases in the magnitude and frequency of 15-min rainfall extremes (Figs. 4, 5, 6 and 7). More importantly, along with winter, spring was the only other season that exhibited a statistically significant increasing trend in Td (Table S4). In the spring, Td increased 0.02 °C per year, which was generally in line with earlier studies on long-term Td trends in the U.S117,118. Given the importance of Td to rainfall intensification processes, we were keenly interested in exploring the extent to which scaling relations in the spring shifted as a function of Td.
Dependency of 15-min, hourly (1-h), and daily (1-d) rainfall extremes (top to bottom) on dew point temperature (Td, °C) for spring, summer, fall, and winter (left to right). Gray dashed lines indicate the Clausius-Clapeyron (CC) rate of ∼7% per °C, while pink dashed lines demarcate apparent scaling at twice the CC rate (2CC) of ∼14% per °C. Note that the Y-axis for daily scaling plots (bottom row) differs from the Y-axes of 15-min and hourly scaling plots (top and middle rows, respectively).
Nonlinear apparent scaling relations were clearly evident in spring, as 15-min and hourly rainfall extremes exhibited sub-CC scaling (∼ 5 to 6% per °C) up to Td values of ∼ 11° to 12 °C, and then shifted to greater than 2CC scaling rates (∼ 17 to 18% per °C) above this threshold (Fig. 8). As with the summer, springtime shifts in apparent scaling were concealed by the linear scaling across all values of Td (Fig. 8). A recent study by Blenkinsop et al116. in the U.K. also found that hourly rainfall extremes in the spring displayed a threshold-like scaling relation, shifting from sub-CC scaling to super-CC scaling when air temperatures reached 10 °C. According to Haerter and Berg119and Berg et al35., shifts from sub-CC to super-CC scaling may simply reflect a statistical change in the type of precipitation causing extreme rainfalls from large-scale frontal storms with stratiform precipitation at lower temperatures to smaller scale convective storms at higher temperatures. In an apparent scaling study of hourly rainfall extremes in the U.S., Ivancic and Shaw29 suggested that the transition between frontal and convective rains partly explained the super-CC rates they observed in the northeastern U.S. As such, we sought to determine if convection could be playing an increasingly important role in generating springtime rainfall extremes in the WE-38 watershed.
What is the role of convection in subhourly and hourly rainfall extremes?
We hypothesized that a warming and moistening spring season, as evidenced by the increasing trends in Td (Table S4), might be giving rise to increasingly favorable environments for convection that could be contributing to the intensification of 15-min rainfall extremes in the WE-38 watershed. Indeed, convection plays an important role in the generation of extreme rainfall events120,121,122, and emerging evidence indicates that the length of the thunderstorm season is increasing in the spring and fall due to warming-induced instability123. Moreover, recent research also suggests that the frequency and intensity of mesoscale convective systems (organized groupings of thunderstorms) has also risen across central and eastern portions of the U.S124. To shed light on this possibility, we used ERA5 hourly CAPE measurements64 to assess trends in seasonal maxima of hourly CAPE, as well as the number of hours per year in each season with favorable thunderstorm environments (Fig. 9). Consistent with Taszarek et al125., we defined favorable thunderstorm environments as any hour with CAPE exceeding 150 J kg-1.
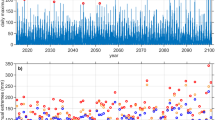
Trends in seasonal maxima of hourly CAPE (top row) and the number of hours per year with favorable thunderstorm environments (bottom row) for spring, summer, fall, and winter (left to right). Best fit regression lines are plotted using Theil-Sen regression. Statistically significant trends are determined with the Mann-Kendall test. Sen’s slope is reported for significant trends, along with the p-value.
As shown in Fig. 9, spring was the only season with a statistically significant upward trend in CAPE. According to the Mann-Kendall test, maximum hourly CAPE increased by 14 J kg-1yr-1in the spring, while other seasons showed no noteworthy changes in CAPE. We also found that the number of hours with favorable thunderstorm environments increased by 0.67 h-1yr-1 in the spring, although the trend was only significant at the α = 0.10 level. Taken together, these trends suggest that the environment for convective storms has become more favorable in the spring, which may partly explain increases in the magnitude and frequency of 15-min rainfall extremes during this time frame. We note here that increasingly favorable convective environments should not be equated with increases in the frequency or severity of thunderstorms, as CAPE is but one of several ingredients needed for thunderstorm development125.
Considering the potential for increasingly favorable convective environments in the spring, we next explored whether the spring displayed any coincident changes in indicators of convective precipitation (Fig. 10). In accordance with previous studies59,99,100, we used Rx15minP and Rx1hP as indicators of convectively-triggered storms, as these indicators quantify the fractional contributions of Rx15min and Rx1h to their corresponding daily rainfall totals.
Trends in seasonal Rx15minP (top row) and Rx1hP (bottom row) for spring, summer, fall, and winter (left to right). Consistent with Barbero et al59., we define Rx15minP and Rx1hP as the fractional contributions of Rx15min and Rx1h to their corresponding daily rainfall totals. Best fit regression lines are plotted using one-inflated beta regression101. Regression slopes are reported for statistically significant trends, along with the p-value. Note that the slopes of beta regression models indicate the change in the log odds of Rx15minP or Rx1hP being 1 given a unit increase in year.
As shown in Fig. 10, spring experienced by far the largest increases in Rx15minP and Rx1hP, while other seasons showed smaller increases (e.g., Rx15minP in summer) and even decreases (e.g., Rx15minP and Rx1hP in fall). In the spring, the probability of Rx15minP being 1 increased from roughly 0.36 in 1968 to 0.55 in 2022, while the probability of Rx1hP being 1 rose from nearly 0.44 in 1968 to 0.63 in 2022. Collectively, these trends indicated that 15-min and hourly rainfall extremes in the spring were becoming increasingly concentrated in smaller parts of the day, as would be anticipated if convective precipitation was emerging as the primary driver of these short-duration rainfall extremes. Put another way, 15-min and hourly rainfall extremes in the spring have apparently shifted from contributing less than half of the daily rainfall total in the late 1960s to contributing more than half to nearly two-thirds of the daily rainfall total in the present day. Such evidence suggests an increasingly important role for convection as a trigger for springtime subhourly and hourly rainfall extremes in the WE-38 watershed. These findings are in line with recent studies in Eurasia showing rising contributions of convective precipitation to total precipitation42, especially in the shoulder seasons like spring, which have become demonstrably more summerlike with climate warming36.
Limitations and future research needs
Our case study provides important insight into the changing nature of subhourly rainfall extremes in an intensively-monitored agricultural watershed in east-central Pennsylvania, U.S. Indeed, several of the watersheds that are part of ARS’s National Experimental Watershed Network, including the WE-38 watershed, possess some of the longest running 5-min precipitation records in the U.S. These high-quality records enabled the subhourly rainfall trends reported herein using methods that have commonly been applied in the study of hydroclimatic extremes41. Even so, we grant that there is ongoing discussion in the literature about the limitations of nonstationary methods of trend testing126,127, and that the conclusions we draw from these analyses are strictly germane to the 55-year record we characterized in this study. Moreover, we note that the site-specific nature of the study limited our ability to make definitive statements about the regional significance of these trends128,129,130. While a regionalized analysis was beyond the scope of our case study, future studies should seek to analyze trends across wider geographic areas using larger networks of rain gauges with long-term data on subdaily (or subhourly) rainfall. Regional analyses of subhourly rainfall trends would also offer needed data to test whether subhourly rainfall extremes are systematically intensifying in the spring season, as observed herein, or whether these trends are more locally relevant (e.g., Libertino et al131.).
We also recognize that there are alternate approaches to estimating how rainfall extremes scale with Ta and Td58. In addition to the binning method used herein28, other scaling studies have successfully used quantile regression132and the Zhang method for dealing with seasonality133. We acknowledge that there is considerable debate in the literature about the most appropriate scaling methods134,135,136, as well as the most informative scaling variables26. Moreover, we realize that the apparent scaling estimates obtained in this case study do not necessarily translate to climate scaling estimates. Climate scaling can inform how rainfall extremes might evolve with future climate change22, but such estimates are best obtained through broad-scale (regional to global) studies that account for important variations in the atmospheric environment. In our case study, we mainly used the binning approach to obtain useful information about the processes that might have affected apparent scaling relations between subhourly, hourly, and daily rainfall extremes and Td (e.g., Lenderink et al136.). Future studies on the apparent scaling of subhourly rainfall extremes with Td would clearly benefit from multimethod (e.g., binning scaling, quantile regression, etc.) regional- to national-scale analyses, such as those used by Ali et al58..
Finally, using indicators of convective environments (CAPE) and precipitation triggering mechanisms (Rx15minP and Rx1hP) represented an indirect way of inferring the role of convective storms in the intensification of subhourly rainfall extremes. Convective storms, or thunderstorms, are rarely monitored directly over long periods of time137, and therefore environmental proxies for instability and moisture availability (CAPE) alongside measures of initiation mechanisms like lift are routinely used to assess the ingredients necessary for convection. Other approaches such as radar systems35and lightning detection networks29,138can be used to obtain information on thunderstorm occurrences, but these data were unavailable for use in this study. Similarly, local observations like storm reports and cloud observations35,42 can help to classify rain events as stratiform or convective in nature, but such data were not collected as part of the routine monitoring efforts in the WE-38 watershed. Consequently, leveraging additional sources of data on convective storms (beyond CAPE and proxy variables like Rx15minP and Rx1hP) would serve to enhance our interpretations regarding the influence of convection on springtime subhourly rainfall extremes.
Conclusions and implications
In this study, we leveraged 55 years of 5-min precipitation observations in the WE-38 experimental watershed to shed light on annual and seasonal trends in subhourly, hourly, and daily rainfall extremes. We drew the following conclusions from our analyses:
-
1.
Climatology of extremes: On average, the highest Rx15min and Rx1h rainfall amounts occurred in summer due to the preponderance of convective storms in the warm season, while Rx1d amounts were highest in the fall, as large scale, stratiform rainfalls typically prevail over convective rainfall types during this time of year. These patterns generally agreed with expectations for daily and subdaily rainfall extremes in the eastern U.S.
-
2.
Magnitude and frequency: Over the 55-year study period, the magnitude of 15-min rainfall extremes increased by 0.6 to 0.9% per year in the spring, while the frequency of these springtime extremes also rose by 3.4% per year. The rates at which 15-min rainfalls intensified in the WE-38 watershed were consistent with other studies that have recently examined long-term trends in subhourly rainfall extremes in Europe and Australia. Moreover, the emergence of subhourly rainfall extremes ahead of hourly and daily extremes aligned with recent experimental findings from convection-permitting models.
-
3.
Effect of Td: Subhourly, hourly, and daily rainfall extremes scaled strongly with Td. Apparent scaling rates with Td generally declined with increasing rainfall duration, with super-CC scaling for 15-min extremes, CC-scaling for hourly extremes, and sub-CC scaling for daily extremes. Notably, scaling relations in the spring shifted from sub-CC scaling at Td values below 11° C, to greater than 2CC scaling above this Td threshold. This nonlinear pattern indicated a possible statistical shift in the relative importance of stratiform versus convective rains in generating springtime subhourly rainfall extremes.
-
4.
Role of convection: The spring season saw upward trends in maximum hourly CAPE and the number of hours per year with CAPE > 150 J kg−1, suggesting that the springtime environment had become increasing favorable for convection during the study period. These trends coincided with increasing trends in Rx15minP and Rx1hP, indicating that 15-min and hourly rainfall extremes were becoming progressively concentrated in smaller parts of the day. Such patterns would be expected if convective precipitation was contributing more to springtime subhourly rainfall extremes than it had in the past.
The implications of our research have relevance to the study of subhourly rainfall extremes, as our investigation adds to the growing number of studies examining extreme subhourly rainfalls in the context of global warming. To date, such studies have been limited due to issues with the quality, accessibility, and coverage (spatial and temporal) of rain gauges with subhourly data139. This is especially true in the U.S., where few studies have evaluated trends in subhourly rainfall extremes. While our study offered a local perspective on changes to subhourly rainfall extremes in a long-term experimental watershed, there are opportunities to regionalize and nationalize these findings by leveraging other subhourly rainfall datasets, including those from USDA’s networks of benchmark agricultural watersheds50and experimental forests and ranges140, as well as the U.S. Climate Reference Network141and NOAA’s COOP network142. Such studies, along with efforts to collate global subdaily rainfall datasets143, will lead to important advances in our knowledge of short-duration rainfall extremes.
From a practical standpoint, findings from this study also have important implications for agricultural interests in the Upper Chesapeake Bay region of the northeastern U.S. A key result of our research was that subhourly rainfall extremes were intensifying faster than hourly and daily extremes in the spring. From an agricultural perspective, spring is an important season for field work, planting, and fertilization, and these activities are often planned around expected precipitation patterns144. Increases in the magnitude and frequency of subhourly rainfall extremes, as observed in the WE-38 agricultural watershed, will likely impose challenges to agricultural management. Indeed, extreme rainfalls early in the spring season create a heightened risk for soil erosion, especially if fields are not covered by crops. Extreme rainfalls later in the spring, shortly after crops have been planted, can increase the odds of crop damage5,6. Thus, there is an urgent need for additional research on the changing character of subhourly rainfall extremes, as such information will be essential to helping farmers cope with fluctuating weather extremes in a rapidly changing climate.
Data availability
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
References
Fowler, H. J., Wasko, C. & Prein, A. F. Intensification of short-duration rainfall extremes and implications for flood risk: current state of the art and future directions. Philos. Trans. Math. phys. eng. sci. 379, 20190541. https://doi.org/10.1098/rsta.2019.0541 (2021).
Li, Z. et al. The conterminous United States are projected to become more prone to flash floods in a high-end emissions scenario. Commun. Earth Environ. 3, 86. https://doi.org/10.1038/s43247-022-00409-6 (2022).
Swain, D. L. et al. Increased Flood exposure due to Climate Change and Population Growth in the United States. Earth’s Future. 8 https://doi.org/10.1029/2020EF001778 (2020). e2020EF001778.
Tabari, H. Climate change impact on flood and extreme precipitation increases with water availability. Sci. Rep. 10, 13768. https://doi.org/10.1038/s41598-020-70816-2 (2020).
Li, Y., Guan, K., Schnitkey, G. D., DeLucia, E. & Peng, B. Excessive rainfall leads to maize yield loss of a comparable magnitude to extreme drought in the United States. Global Change Biol. 25, 2325–2337. https://doi.org/10.1111/gcb.14628 (2019).
Rosenzweig, C., Tubiello, F. N., Goldberg, R., Mills, E. & Bloomfield, J. Increased crop damage in the US from excess precipitation under climate change. Global Environ. Change. 12, 197–202. https://doi.org/10.1016/S0959-3780(02)00008-0 (2002).
Costa, D. et al. Impact of climate change on catchment nutrient dynamics: insights from around the world. Environ. Rev. 31, 4–25. https://doi.org/10.1139/er-2021-0109 (2023).
Donat, M. G., Angélil, O. & Ukkola, A. M. Intensification of precipitation extremes in the world’s humid and water-limited regions. Environ. Res. Lett. 14, 065003. https://doi.org/10.1088/1748-9326/ab1c8e (2019).
Sun, Q. et al. Continental, and Regional Analysis of changes in Extreme Precipitation. J. Clim. 34, 243–258. https://doi.org/10.1175/jcli-d-19-0892.1 (2021).
Westra, S., Alexander, L. V. & Zwiers, F. W. Global increasing trends in Annual Maximum Daily Precipitation. J. Clim. 26, 3904–3918. https://doi.org/10.1175/jcli-d-12-00502.1 (2013).
Kirchmeier-Young, M. C. & Zhang, X. Human influence has intensified extreme precipitation in North America. PNAS. 117, 13308–13313. https://doi.org/10.1073/pnas.1921628117 (2020).
Zeder, J. & Fischer, E. M. Observed extreme precipitation trends and scaling in Central Europe. Weather Clim. Extrem. 29, 100266. https://doi.org/10.1016/j.wace.2020.100266 (2020).
Li, M. et al. Non-uniform changes in different daily precipitation events in the contiguous United States. Weather Clim. Extrem. 35, 100417. https://doi.org/10.1016/j.wace.2022.100417 (2022).
Mallakpour, I. & Villarini, G. Analysis of changes in the magnitude, frequency, and seasonality of heavy precipitation over the contiguous USA. Theor. Appl. Climatol. 130, 345–363. https://doi.org/10.1007/s00704-016-1881-z (2017).
Sun, X. & Lall, U. Spatially coherent trends of annual maximum daily precipitation in the United States. Geophys. Res. Lett. 42, 9781–9789. https://doi.org/10.1002/2015GL066483 (2015).
Fischer, E. M. & Knutti, R. Observed heavy precipitation increase confirms theory and early models. Nat. Clim. Change. 6, 986–991. https://doi.org/10.1038/nclimate3110 (2016).
Min, S. K., Zhang, X., Zwiers, F. W. & Hegerl, G. C. Human contribution to more-intense precipitation extremes. Nature. 470, 378–381. https://doi.org/10.1038/nature09763 (2011).
Clapeyron, E. Mémoire sur la puissance motrice de la chaleur. Bachelier. (1834).
Clausius, R. Ueber die bewegende Kraft Der Wärme Und die Gesetze, Welche Sich Daraus für die Wärmelehre selbst ableiten lassen. Ann. Phys. 155, 368–397. https://doi.org/10.1002/andp.18501550306 (1850).
Pall, P., Allen, M. R. & Stone, D. A. Testing the Clausius–Clapeyron constraint on changes in extreme precipitation under CO2 warming. Clim. Dyn. 28, 351–363. https://doi.org/10.1007/s00382-006-0180-2 (2007).
Bao, J., Sherwood, S. C., Alexander, L. V. & Evans, J. P. Future increases in extreme precipitation exceed observed scaling rates. Nat. Clim. Change. 7, 128–132. https://doi.org/10.1038/nclimate3201 (2017).
Fowler, H. J. et al. Anthropogenic intensification of short-duration rainfall extremes. Nat. Rev. Earth Environ. https://doi.org/10.1038/s43017-020-00128-6 (2021).
Fowler, H. J. et al. Towards advancing scientific knowledge of climate change impacts on short-duration rainfall extremes. Philos. Trans. Math. phys. eng. sci. 379, 20190542. https://doi.org/10.1098/rsta.2019.0542 (2021).
Ali, H., Fowler, H. J. & Mishra, V. Global observational evidence of strong linkage between Dew Point temperature and precipitation extremes. Geophys. Res. Lett. 45 https://doi.org/10.1029/2018GL080557 (2018). 12,320 – 312,330.
Barbero, R., Fowler, H. J., Lenderink, G. & Blenkinsop, S. Is the intensification of precipitation extremes with global warming better detected at hourly than daily resolutions? Geophys. Res. Lett. 44, 974–983. https://doi.org/10.1002/2016gl071917 (2017).
Westra, S. et al. Future changes to the intensity and frequency of short-duration extreme rainfall. Rev. Geophys. 52, 522–555. https://doi.org/10.1002/2014RG000464 (2014).
Hardwick Jones, R., Westra, S. & Sharma, A. Observed relationships between extreme sub-daily precipitation, surface temperature, and relative humidity. Geophys. Res. Lett. 37 https://doi.org/10.1029/2010GL045081 (2010).
Lenderink, G. & van Meijgaard, E. Increase in hourly precipitation extremes beyond expectations from temperature changes. Nat. Geosci. 1, 511–514. https://doi.org/10.1038/ngeo262 (2008).
Ivancic, T. J. & Shaw, S. B. A U.S.-based analysis of the ability of the Clausius-Clapeyron relationship to explain changes in extreme rainfall with changing temperature. J. Geophys. Res. Atmos. 121, 2015JD024288. https://doi.org/10.1002/2015JD024288 (2016).
Mishra, V., Wallace, J. M. & Lettenmaier, D. P. Relationship between hourly extreme precipitation and local air temperature in the United States. Geophys. Res. Lett. 39 https://doi.org/10.1029/2012GL052790 (2012).
Utsumi, N., Seto, S., Kanae, S., Maeda, E. E. & Oki, T. Does higher surface temperature intensify extreme precipitation? Geophys. Res. Lett. 38 https://doi.org/10.1029/2011GL048426 (2011).
Guerreiro, S. B. et al. Detection of continental-scale intensification of hourly rainfall extremes. Nat. Clim. Change. 8, 803–807. https://doi.org/10.1038/s41558-018-0245-3 (2018).
Loriaux, J. M., Lenderink, G., De Roode, S. R. & Siebesma, A. P. Understanding Convective Extreme Precipitation Scaling using observations and an Entraining Plume Model. J. Atmos. Sci. 70, 3641–3655. https://doi.org/10.1175/JAS-D-12-0317.1 (2013).
Schroeer, K. & Kirchengast, G. Sensitivity of extreme precipitation to temperature: the variability of scaling factors from a regional to local perspective. Clim. Dyn. 50, 3981–3994. https://doi.org/10.1007/s00382-017-3857-9 (2018).
Berg, P., Moseley, C. & Haerter, J. O. Strong increase in convective precipitation in response to higher temperatures. Nat. Geosci. 6, 181–185. https://doi.org/10.1038/ngeo1731 (2013).
Ye, H., Fetzer, E. J., Wong, S. & Lambrigtsen, B. H. Rapid decadal convective precipitation increase over Eurasia during the last three decades of the 20th century. Sci. Adv. 3, e1600944. https://doi.org/10.1126/sciadv.1600944 (2017).
Ayat, H., Evans, J. P., Sherwood, S. C. & Soderholm, J. Intensification of subhourly heavy rainfall. Science. 378, 655–659. https://doi.org/10.1126/science.abn8657 (2022).
Jayaweera, L., Wasko, C., Nathan, R. & Johnson, F. Non-stationarity in extreme rainfalls across Australia. J. Hydrol. 624, 129872. https://doi.org/10.1016/j.jhydrol.2023.129872 (2023).
Treppiedi, D., Cipolla, G., Francipane, A. & Noto, L. V. Detecting precipitation trend using a multiscale approach based on quantile regression over a Mediterranean area. Int. J. Climatol. 41, 5938–5955. https://doi.org/10.1002/joc.7161 (2021).
Kendon, E. J., Blenkinsop, S. & Fowler, H. J. When will we detect changes in short-duration precipitation extremes? J. Clim. 31, 2945–2964. https://doi.org/10.1175/JCLI-D-17-0435.1 (2018).
Slater, L. J. et al. Nonstationary weather and water extremes: a review of methods for their detection, attribution, and management. Hydrol. Earth Syst. Sci. 25, 3897–3935. https://doi.org/10.5194/hess-25-3897-2021 (2021).
Chernokulsky, A. et al. Observed changes in convective and stratiform precipitation in Northern Eurasia over the last five decades. Environ. Res. Lett. 14, 045001. https://doi.org/10.1088/1748-9326/aafb82 (2019).
Bryant, R. B. et al. US Department of Agriculture Agricultural Research Service Mahantango Creek Watershed, Pennsylvania, United States: Physiography and history. Water Resour. Res. 47 https://doi.org/10.1029/2010wr010056 (2011).
Goodrich, D. C., Starks, P. J., Schnabel, R. R. & Bosch, D. D. Effective use of USDA-ARS experimental watersheds. In: Richardson, C.W., Rango, A., Owens, L.B., Lane, L.J. (Eds.), Agricultural Research Service Conference on Hydrology. U.S. Department of Agriculture, Denver, Colorado, 35–46 (1994).
Slaughter, C., Richardson, C. & W. & Long-term Watershed Research in USDA-Agricultural Research Service. Water Resour. Impact. 2, 28–32 (2000).
86th Congress. Senate Document 59 (Facility Needs – Soil and Water Conservation Research, 1959).
Buda, A. R. et al. US Department of Agriculture Agricultural Research Service Mahantango Creek Watershed, Pennsylvania, United States: long-term precipitation database. Water Resour. Res. 47 https://doi.org/10.1029/2010wr010058 (2011).
Walbridge, M. R. & Shafer, S. R. A long-term agro-ecosystem research (LTAR) network for agriculture, The Fourth Interagency Conference on Research in the Watersheds, Fairbanks, AK, 1–7. (2011).
Duriancik, L. F. et al. The first five years of the Conservation effects Assessment Project. J. Soil. Water Conserv. 63 https://doi.org/10.2489/jswc.63.6.185A (2008). 185A-197A.
Goodrich, D. C. et al. The USDA-ARS Experimental Watershed Network: evolution, lessons learned, Societal benefits, and moving Forward. Water Resour. Res. 57 https://doi.org/10.1029/2019WR026473 (2021). e2019WR026473.
C Goodrich, D. et al. Long term agroecosystem research experimental watershed network. Hydrol. Proc. 36, e14534. https://doi.org/10.1002/hyp.14534 (2022).
Chesapeake Bay Program Office (CBPO). One-meter Resolution Land Use/Land Cover Dataset for the Chesapeake Bay Watershed, 2017/18. Dev. by, Conservancy, C., Geological, U. S., Survey & University of Vermont Spatial Analysis Lab. and. (access on 07 September 2023). https://www.chesapeakeconservancy.org/conservation-innovation-center/high-resolution-data/lulc-data-project-2022/ (2022).
Carr, J. C. Rain gage network reports, in Klingerstown, Pennsylvania: Agricultural Research Service Precipitation Facilities and Related Studies, USDA-ARS 41–176, edited by D.M. Hershfield, Chap. 11, 83–87. (1971).
Carr, J. C. A system for collection, preparation, translation, and computer reduction of digital hydrologic data. Report No. ARS-NE-18, 58. Beltsville, MD (1973).
Hamon, W. R. et al. In Field Manual for Research in Agricultural Hydrology, Agriculture Handbook No. 2241–74 (U.S. Department of Agriculture, 1979).
Wasko, C., Visser, J. B., Nathan, R., Ho, M. & Sharma, A. Automating rainfall recording: ensuring homogeneity when instruments change. J. Hydrol. 609, 127758. https://doi.org/10.1016/j.jhydrol.2022.127758 (2022).
Groisman, P. Y., Knight, R. W. & Karl, T. R. Changes in intense precipitation over the Central United States. J. Hydrometeorol. 13, 47–66. https://doi.org/10.1175/jhm-d-11-039.1 (2012).
Ali, H. et al. Towards Quantifying the Uncertainty in Estimating Observed Scaling Rates. Geophys. Res. Lett. 49, eGL099138 (2022). (2022). https://doi.org/10.1029/2022GL099138
Barbero, R. et al. A synthesis of hourly and daily precipitation extremes in different climatic regions. Weather Clim. Extrem. 26, 100219. https://doi.org/10.1016/j.wace.2019.100219 (2019).
Villalobos-Herrera, R., Blenkinsop, S., Guerreiro, S. B., O’Hara, T. & Fowler, H. J. Sub-hourly resolution quality control of rain-gauge data significantly improves regional sub-daily return level estimates. Q. J. R Meteorol. Soc. 148, 3252–3271. https://doi.org/10.1002/qj.4357 (2022).
Lewis, E. et al. Quality control of a global hourly rainfall dataset. Environ. Model. Softw. 144, 105169. https://doi.org/10.1016/j.envsoft.2021.105169 (2021).
Muñoz-Sabater, J. et al. ERA5-Land: a state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data. 13, 4349–4383. https://doi.org/10.5194/essd-13-4349-2021 (2021).
Lu, H. et al. Long-term trends in climate and hydrology in an agricultural, headwater watershed of central Pennsylvania, USA. J. Hydrol. Reg. Stud. 4, 713–731. https://doi.org/10.1016/j.ejrh.2015.10.004 (2015).
Hersbach, H. et al. The ERA5 global reanalysis. Q. J. R Meteorol. Soc. 146, 1999–2049. https://doi.org/10.1002/qj.3803 (2020).
Taszarek, M. et al. Comparison of convective parameters derived from ERA5 and MERRA-2 with Rawinsonde Data over Europe and North America. J. Clim. 34, 3211–3237. https://doi.org/10.1175/JCLI-D-20-0484.1 (2021).
Copernicus Climate Change Service (C3S). ERA5: fifth generation of ECMWF atmospheric reanalyses of the global climate. Copernicus Climate Change Service Climate Data Store (CDS). [https://cds.climate.copernicus.eu/cdsapp#!/home], (2023). (access on 10 July 2023).
Coles, S. An Introduction to Statistical Modeling of Extreme ValuesSpringer London,. (2013).
Kendall, M. G. Rank correlation methods. 4th, 2d impression ednCharles Griffin, (1975).
Mann, H. B. Nonparametric tests against Trend. Econometrica. 13, 245–259. https://doi.org/10.2307/1907187 (1945).
Helsel, D. R., Hirsch, R. M., Ryberg, K. R., Archfield, S. A. & Gilroy, E. J. Statistical methods in water resources. Report No. 4-A3, 484Reston, VA, (2020).
Yue, S., Pilon, P. & Cavadias, G. Power of the Mann–Kendall and Spearman’s rho tests for detecting monotonic trends in hydrological series. J. Hydrol. 259, 254–271. https://doi.org/10.1016/S0022-1694(01)00594-7 (2002).
Katz, R. W., Parlange, M. B. & Naveau, P. Statistics of extremes in hydrology. Adv. Water Resour. 25, 1287–1304. https://doi.org/10.1016/S0309-1708(02)00056-8 (2002).
Patakamuri, S. K. & O’Brien, N. Modified version of the Mann Kendall and Spearman’s Rho trends tests (modifiedmk). R package version 1.6. (2021).
Sen, P. K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 63, 1379–1389. https://doi.org/10.1080/01621459.1968.10480934 (1968).
Gilleland, E. & Katz, R. W. extRemes 2.0: an extreme value analysis package in R. J. Stat. Softw. 72, 1–39 (2016).
Katz, R. W. Statistics of extremes in climate change. Clim. Change. 100, 71–76. https://doi.org/10.1007/s10584-010-9834-5 (2010).
Konstali, K. & Sorteberg, A. Why has Precipitation Increased in the Last 120 Years in Norway? J. Geophys. Res. Atmos. 127, eJD036234 (2022). (2021). https://doi.org/10.1029/2021JD036234
Villarini, G. et al. On the frequency of heavy rainfall for the Midwest of the United States. J. Hydrol. 400, 103–120. https://doi.org/10.1016/j.jhydrol.2011.01.027 (2011). https://doi.org/https://doi.org/
Koenker, R. Quantile Regression (Cambridge University Press, 2005).
Koenker, R. & Bassett, G. Jr Regres. Quantiles Econometrica 46, 33 (1978).
Bohlinger, P. & Sorteberg, A. A comprehensive view on trends in extreme precipitation in Nepal and their spatial distribution. Int. J. Climatol. 38, 1833–1845. https://doi.org/10.1002/joc.5299 (2018).
Fan, L. & Chen, D. Trends in extreme precipitation indices across China detected using quantile regression. Atmos. Sci. Lett. 17, 400–406. https://doi.org/10.1002/asl.671 (2016).
Quantreg Quantile Regression v. R Package Version 5.97 (2023).
Barrodale, I. & D. K. Roberts, F. Algorithm 478: solution of an overdetermined system of equations in the l1 norm [F4]. Commun. ACM. 17, 319–320. https://doi.org/10.1145/355616.361024 (1974).
Koenker, R. W. D’Orey, V. Computing Regression quantiles. J. Roy Stat. Soc. Ser. C (Appl Stat). 36, 383–393. https://doi.org/10.2307/2347802 (1987).
Dunn, R. J. H. & Morice, C. P. On the effect of reference periods on trends in percentile-based extreme temperature indices. Environ. Res. Lett. 17, 034026. https://doi.org/10.1088/1748-9326/ac52c8 (2022).
Schär, C. et al. Percentile indices for assessing changes in heavy precipitation events. Clim. Change. 137, 201–216. https://doi.org/10.1007/s10584-016-1669-2 (2016).
Li, Y. et al. Strong Intensification of Hourly Rainfall Extremes by Urbanization. Geophys. Res. Lett. 47, eGL088758 (2020). (2020). https://doi.org/10.1029/2020GL088758
Mallakpour, I. & Villarini, G. Investigating the relationship between the frequency of flooding over the central United States and large-scale climate. Adv. Water Resour. 92, 159–171. https://doi.org/10.1016/j.advwatres.2016.04.008 (2016).
Dobson, A. J. & Barnett, A. G. An Introduction to Generalized Linear Models (CRC, 2018).
Ivancic, T. J. & Shaw, S. B. Examining why trends in very heavy precipitation should not be mistaken for trends in very high river discharge. Clim. Change. 133, 681–693. https://doi.org/10.1007/s10584-015-1476-1 (2015).
Lenderink, G. et al. Scaling and responses of extreme hourly precipitation in three climate experiments with a convection-permitting model. Philos. Trans. Math. phys. eng. sci. 379, 20190544. https://doi.org/10.1098/rsta.2019.0544 (2021).
American Meteorological Society. dewpoint. Glossary of Meteorology, (2023). https://glossary.ametsoc.org/wiki/Dewpoint
Lenderink, G. & van Meijgaard, E. Linking increases in hourly precipitation extremes to atmospheric temperature and moisture changes. Environ. Res. Lett. 5, 025208. https://doi.org/10.1088/1748-9326/5/2/025208 (2010).
Najibi, N., Mukhopadhyay, S. & Steinschneider, S. Precipitation scaling with temperature in the Northeast US: variations by Weather Regime, season, and Precipitation Intensity. Geophys. Res. Lett. 49, e2021GL097100. https://doi.org/10.1029/2021GL097100 (2022).
Ng, C. P., Zhang, Q., Li, W. & Zhou, Z. Contribution of thunderstorms to changes in hourly Extreme Precipitation over China from 1980 to 2011. J. Clim. 35, 4485–4498. https://doi.org/10.1175/JCLI-D-21-0701.1 (2022).
Lepore, C., Veneziano, D. & Molini, A. Temperature and CAPE dependence of rainfall extremes in the eastern United States. Geophys. Res. Lett. 42, 74–83. https://doi.org/10.1002/2014GL062247 (2015).
Lepore, C., Allen, J. T. & Tippett, M. K. Relationships between Hourly Rainfall Intensity and Atmospheric Variables over the Contiguous United States. J. Clim. 29, 3181–3197. https://doi.org/10.1175/JCLI-D-15-0331.1 (2016).
Blenkinsop, S., Lewis, E., Chan, S. C. & Fowler, H. J. Quality-control of an hourly rainfall dataset and climatology of extremes for the UK. Int. J. Climatol. 37, 722–740. https://doi.org/10.1002/joc.4735 (2017).
Pritchard, D. et al. An Observation-based dataset of global Sub-daily Precipitation Indices (GSDR-I). Sci. Data. 10, 393. https://doi.org/10.1038/s41597-023-02238-4 (2023).
Ospina, R. & Ferrari, S. L. P. A general class of zero-or-one inflated beta regression models. Comput. Stat. Data Anal. 56, 1609–1623. https://doi.org/10.1016/j.csda.2011.10.005 (2012).
Lavers, D. A. & Villarini, G. The contribution of atmospheric rivers to precipitation in Europe and the United States. J. Hydrol. 522, 382–390. https://doi.org/10.1016/j.jhydrol.2014.12.010 (2015).
Stasinopoulos, D. M. & Rigby, R. A. Generalized additive models for location scale and shape (GAMLSS) in R. J. Stat. Softw. 23, 1–46. https://doi.org/10.18637/jss.v023.i07 (2007).
Huang, H. P., Winter, J. M. & Osterberg, E. C. Mechanisms of Abrupt Extreme Precipitation Change over the Northeastern United States. J. Geophys. Res. Atmos. 123, 7179–7192. https://doi.org/10.1029/2017jd028136 (2018).
Hoerling, M. et al. Explaining the spatial pattern of U.S. Extreme Daily Precipitation Change. J. Clim. 34, 2759–2775. https://doi.org/10.1175/jcli-d-20-0666.1 (2021).
Bador, M., Alexander, L. V., Contractor, S. & Roca, R. Diverse estimates of annual maxima daily precipitation in 22 state-of-the-art quasi-global land observation datasets. Environ. Res. Lett. 15, 035005. https://doi.org/10.1088/1748-9326/ab6a22 (2020).
Lewis, E. et al. A Global Sub-daily Rainfall dataset. J. Clim. 32, 4715–4729 (2019). https://doi.org/https://doi.org/10.1175/JCLI-D-18-0143.1
Alexander, L. V. et al. On the use of indices to study extreme precipitation on sub-daily and daily timescales. Environ. Res. Lett. 14, 125008. https://doi.org/10.1088/1748-9326/ab51b6 (2019).
Olafsdottir, H. K., Rootzén, H. & Bolin, D. Extreme Rainfall events in the Northeastern United States become more frequent with rising temperatures, but their intensity distribution remains stable. J. Clim. 34, 8863–8877. https://doi.org/10.1175/jcli-d-20-0938.1 (2021).
Myhre, G. et al. Frequency of extreme precipitation increases extensively with event rareness under global warming. Sci. Rep. 9, 16063. https://doi.org/10.1038/s41598-019-52277-4 (2019).
Papalexiou, S. M. & Montanari, A. Global and Regional increase of precipitation extremes under global warming. Water Resour. Res. 55, 4901–4914. https://doi.org/10.1029/2018WR024067 (2019).
Yu, L., Zhong, S., Pei, L., Bian, X. & Heilman, W. E. Contribution of large-scale circulation anomalies to changes in extreme precipitation frequency in the United States. Environ. Res. Lett. 11, 044003. https://doi.org/10.1088/1748-9326/11/4/044003 (2016).
Chinita, M. J., Richardson, M., Teixeira, J. & Miranda, P. M. A. Global mean frequency increases of daily and sub-daily heavy precipitation in ERA5. Environ. Res. Lett. 16, 074035. https://doi.org/10.1088/1748-9326/ac0caa (2021).
Ali, H., Fowler, H. J., Lenderink, G., Lewis, E. & Pritchard, D. Consistent Large-Scale Response of Hourly Extreme Precipitation to Temperature Variation Over Land. Geophys. Res. Lett. 48, e2020GL090317 (2021). https://doi.org/10.1029/2020GL090317
Lenderink, G., Mok, H. Y., Lee, T. C. & van Oldenborgh, G. J. Scaling and trends of hourly precipitation extremes in two different climate zones – Hong Kong and the Netherlands. Hydrol. Earth Syst. Sci. 15, 3033–3041. https://doi.org/10.5194/hess-15-3033-2011 (2011).
Blenkinsop, S., Chan, S. C., Kendon, E. J., Roberts, N. M. & Fowler, H. J. Temperature influences on intense UK hourly precipitation and dependency on large-scale circulation. Environ. Res. Lett. 10, 054021. https://doi.org/10.1088/1748-9326/10/5/054021 (2015).
Brown, P. J. & DeGaetano, A. T. Trends in U.S. Surface Humidity, 1930–2010. J. Appl. Meteorol. Clim. 52, 147–163. https://doi.org/10.1175/JAMC-D-12-035.1 (2013).
Robinson, P. J. Temporal trends in United States dew point temperatures. Int. J. Climatol. 20, 985–1002. https://doi.org/10.1002/1097-0088(200007)20:9%3c985::AID-JOC513%3e3.0.CO;2-W.(2000).
Haerter, J. O. & Berg, P. Unexpected rise in extreme precipitation caused by a shift in rain type? Nat. Geosci. 2, 372–373. https://doi.org/10.1038/ngeo523 (2009).
Schumacher, R. S. Heavy rainfall and flash flooding. Oxford Research Encyclopedia of Natural Hazard Science. (Oxford University Press, https://doi.org/10.1093/acrefore/9780199389407.013.132 (2017).
Schumacher, R. S. & Johnson, R. H. Organization and Environmental properties of Extreme-rain-producing Mesoscale Convective systems. Mon Weather Rev. 133, 961–976. https://doi.org/10.1175/MWR2899.1 (2005).
Schumacher, R. S. & Johnson, R. H. Characteristics of U.S. Extreme rain events during 1999–2003. Weather Forecast. 21, 69–85. https://doi.org/10.1175/WAF900.1 (2006).
Allen, J. T. Climate Change and Severe Thunderstorms. Oxford Research Encyclopedia of Climate Science (Oxford University Press, 2018). https://doi.org/10.1093/acrefore/9780190228620.013.62
Schumacher, R. S. & Rasmussen, K. L. The formation, character and changing nature of mesoscale convective systems. Nat. Rev. Earth Environ. 1, 300–314. https://doi.org/10.1038/s43017-020-0057-7 (2020).
Taszarek, M., Allen, J. T., Brooks, H. E., Pilguj, N. & Czernecki, B. Differing trends in United States and European severe thunderstorm environments in a warming climate. Bull. Am. Meteorol. Soc. 102, E296–E322. https://doi.org/10.1175/BAMS-D-20-0004.1 (2021).
Serinaldi, F., Kilsby, C. G. & Lombardo, F. Untenable nonstationarity: an assessment of the fitness for purpose of trend tests in hydrology. Adv. Water Resour. 111, 132–155. https://doi.org/10.1016/j.advwatres.2017.10.015 (2018).
Serinaldi, F. Scientific logic and spatio-temporal dependence in analyzing extreme-precipitation frequency: negligible or neglected? Hydrol. Earth Syst. Sci. 28, 3191–3218. https://doi.org/10.5194/hess-28-3191-2024 (2024).
Renard, B. et al. Regional methods for trend detection: assessing field significance and regional consistency. Water Resour. Res. 44 https://doi.org/10.1029/2007WR006268 (2008).
Wilks, D. S. On field significance and the false Discovery Rate. J. Clim. Appl. Meteorol. 45, 1181–1189. https://doi.org/10.1175/JAM2404.1 (2006).
Wilks, D. S. The stippling shows statistically significant Grid points: how Research results are routinely overstated and overinterpreted, and what to do about it. Bull. Am. Meteorol. Soc. 97, 2263–2273. https://doi.org/10.1175/BAMS-D-15-00267.1 (2016).
Libertino, A., Ganora, D. & Claps, P. Evidence for increasing rainfall extremes remains elusive at large spatial scales: the case of Italy. Geophys. Res. Lett. 46, 7437–7446. https://doi.org/10.1029/2019GL083371 (2019).
Wasko, C. & Sharma, A. Quantile regression for investigating scaling of extreme precipitation with temperature. Water Resour. Res. 50, 3608–3614. https://doi.org/10.1002/2013WR015194 (2014).
Zhang, X., Zwiers, F. W., Li, G., Wan, H. & Cannon, A. J. Complexity in estimating past and future extreme short-duration rainfall. Nat. Geosci. 10, 255–259. https://doi.org/10.1038/ngeo2911 (2017).
Bao, J., Sherwood, S. C., Alexander, L. V. & Evans, J. P. Comments on temperature-extreme precipitation scaling: a two-way causality? Int. J. Climatol. 38, 4661–4663. https://doi.org/10.1002/joc.5665 (2018).
Barbero, R., Westra, S., Lenderink, G. & Fowler, H. J. Temperature-extreme precipitation scaling: a two-way causality? Int. J. Climatol. 38, e1274–e1279. https://doi.org/10.1002/joc.5370 (2018).
Lenderink, G., Barbero, R., Westra, S. & Fowler, H. J. Reply to comments on temperature-extreme precipitation scaling: a two-way causality? Int. J. Climatol. 38, 4664–4666. https://doi.org/10.1002/joc.5799 (2018).
Taszarek, M. et al. A climatology of thunderstorms across Europe from a synthesis of multiple data sources. J. Clim. 32, 1813–1837. https://doi.org/10.1175/JCLI-D-18-0372.1 (2019). https://doi.org/https://doi.org/
Molnar, P., Fatichi, S., Gaál, L., Szolgay, J. & Burlando, P. Storm type effects on super Clausius–Clapeyron scaling of intense rainstorm properties with air temperature. Hydrol. Earth Syst. Sci. 19, 1753–1766. https://doi.org/10.5194/hess-19-1753-2015 (2015).
Fowler, H. J. & Ali, H. Chapter 11 - Analysis of extreme rainfall events under the climatic change. In: Morbidelli, R. (Ed.), Rainfall. 307–326. (Elsevier, 2022). https://doi.org/10.1016/B978-0-12-822544-8.00017-2
Mukherjee, S. et al. Comparison of on-site versus NOAA’s extreme precipitation intensity-duration-frequency estimates for six forest headwater catchments across the continental United States. Stoch. Environ. Res. Risk Assess. https://doi.org/10.1007/s00477-023-02495-0 (2023).
Diamond, H. J. et al. U.S. Climate Reference Network after one decade of operations: Status and Assessment. Bull. Am. Meteorol. Soc. 94, 485–498. https://doi.org/10.1175/BAMS-D-12-00170.1 (2013).
Lawrimore, J. H. et al. Quality Control and Processing of Cooperative Observer Program Hourly Precipitation Data. J. Hydrometeorol. 21, 1811–1825. https://doi.org/10.1175/JHM-D-19-0300.1 (2020). https://doi.org/https://doi.org/
Blenkinsop, S. et al. The INTENSE project: using observations and models to understand the past, present and future of sub-daily rainfall extremes. Adv. Sci. Res. 15, 117–126. https://doi.org/10.5194/asr-15-117-2018 (2018).
Walsh, M. K. et al. Ziska, L. Climate Indicators for Agriculture. USDA Technical Bulletin 1953. U.S. Department of Agriculture. Washington, D.C. https://doi.org/10.25675/10217/210930 (2020).
Acknowledgements
This research was a contribution from two national networks operated by the U.S. Department of Agriculture (USDA): (1) the Natural Resources Conservation Service’s Conservation Effects Assessment Project (CEAP) and (2) the Agricultural Research Service’s Long-Term Agroecosystem Research (LTAR) network. Additional funding was provided by USDA-ARS’s Pasture Systems and Watershed Management Research Unit in University Park, Pennsylvania. The existence, accuracy, and consistency of the Mahantango Creek watershed data are a testament to the dedication of numerous past and present USDA-ARS employees. USDA is an equal opportunity provider and employer.
Author information
Authors and Affiliations
Contributions
Anthony R. Buda (ARB) conceived and designed the study. ARB and David J. Millar (DJM) compiled, analyzed, and interpreted the data; Casey D. Kennedy (CDK), Adrian R.H. Wiegman (ARHW), and Molly K. Welsh (MKW) further contributed with hydrometeorological and environmental interpretations of the results. ARB drafted the first manuscript. All the authors discussed the results, revised, and contributed to the final manuscript. All the authors approved the final version of the manuscript to be published.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Buda, A.R., Millar, D.J., Kennedy, C.D. et al. Trends in extreme rainfall over the past 55 years suggest springtime subhourly rainfall extremes have intensified in Mahantango Creek, Pennsylvania. Sci Rep 14, 27837 (2024). https://doi.org/10.1038/s41598-024-79196-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-024-79196-3