Introduction

Underwater micro-bubble image detection plays a significant role in marine environmental monitoring, ocean engineering, and biological research1. This technology not only aids in accurately locating underwater pipeline leaks, providing scientific evidence for repair plans, but also monitors potential marine pollution and observes ecological activities in specific areas to assess the impact of resource development on ecosystems2,3. However, due to the small size and uneven distribution of bubbles, as well as the limited depth of field in underwater imaging, the clarity of both bubbles and background information is often insufficient, making accurate identification and analysis challenging4. This decline in image quality may affect the precise evaluation of bubble distribution, thereby impacting the accuracy of ocean engineering, environmental monitoring, and ecological research. When confronted with such a situation, the first solution that springs to mind is the use of multiple cameras to capture images, which would yield images of various focal regions5. However, there are scenarios where the need arises to incorporate information from two focal regions within a single image6,7. The use of multiple cameras alone cannot satisfy this requirement. Consequently, employing a method of multi-focus image fusion becomes essential to resolve this issue8. Multi-focus image fusion technology allows for the inclusion of more bubble information in a single image, significantly increasing the probability of bubble detection, which aids in subsequent analysis and research.

Fig. 1
figure 1

Example of multi-focus image fusion of underwater micro bubbles. Source A and Source B are images with different focal points, while Fuse is the image obtained after multi-focus image fusion.

Full size image

Multi-focus image fusion is a technique designed to create a single, globally focused image from multiple images that are each focused in different regions9. This technique effectively overcomes the limitation of a shallow depth of field. The algorithms for multi-focus image fusion are broadly categorized into traditional and deep learning-based approaches4. Traditional methods are further divided into those utilizing the transform domain and those operating in the spatial domain10. Deep learning methods are typically categorized as either decision map-based or end-to-end architectures4. Notably, Li et al. have introduced the innovative concept of treating image fusion as an image generation task, yielding impressive outcomes11. Despite the promising results of existing methods in multi-focus image fusion, to the best of our knowledge, these state-of-the-art (SOTA) techniques have not yet been evaluated for their effectiveness in fusing underwater micro-bubble scenes.

Figure 1 illustrates an example of multi-focus image fusion in an underwater micro-bubble scene. In underwater micro-bubble environments, existing image fusion methods often encounter difficulties in effectively extracting target features due to the minute scale of the targets. This challenge leads to inferior fusion performance compared to that in standard imaging scenarios. Additionally, underwater imaging is significantly affected by water quality, with captured images potentially containing substantial impurities that further impact fusion performance12. Moreover, the diversity of current underwater micro-bubble image datasets is limited, which poses substantial challenges to the models’ ability to generalize. Finally, existing evaluation metrics are not optimized for scenarios characterized by “large backgrounds with small targets.” This can impede the ability to accurately assess the quality of fusion outcomes through data analysis alone.

This paper presents a multi-focus image fusion model, RCFusion, specifically designed for underwater micro-bubble scenarios. To address the issue of limited data in such scenarios, a lightweight and efficient data augmentation module named RCBlock was developed, and a dataset was constructed in a laboratory environment. Experimental results demonstrate that RCFusion outperforms existing methods in underwater micro-bubble scenarios.

The main contributions of this paper are as follows:

  1. 1.

    This paper introduces a multi-focus image fusion model named RCFusion for underwater micro-bubble scenarios, filling a gap in the academic research on multi-focus image fusion for such scenes. It makes a significant contribution by advancing the application of multi-focus image fusion technology in this domain.

  2. 2.

    We developed a dedicated dataset for multi-focus image fusion in underwater micro-bubble scenarios. This dataset was meticulously constructed in a controlled indoor environment using a synchronized imaging system, ensuring both consistency and relevance to our research. As the first large-scale dataset for this scenario, it provides unprecedented resources for the field and establishes a solid foundation for future research.

  3. 3.

    By analyzing the characteristics of the captured images, we have carefully designed a novel evaluation metric to assess the fusion performance of the model. Our experiments provide evidence that our model achieves superior performance compared to existing state-of-the-art (SOTA) methods.

The rest of this work is organized as follow. Section “Related Work” briefly introduces traditional methods and deep learning-based approaches for multi-focus image fusion, and commonly used evaluation metrics for multi-focus image fusion. The specific details of the proposed method and evaluation metrics proposed in this paper are presented in the “Methods” Section. In the “Experiments” Section, we provide a brief overview of the dataset construction and training details, and compare the performance of the proposed method with existing methods on the dataset. Finally, the “Conclusions” Section provides a comprehensive summary of the proposed method, highlighting its key aspects and emphasizing the significance of the findings.

Related work

Multi-focus image fusion

Traditional multi-focus image fusion techniques encompass methods based on both spatial and transform domains13. The typical workflow for transform domain-based methods includes three main steps: First, the source image is decomposed into sub-images representing various frequency bands through a transformation process. Second, these sub-images are merged using selected fusion rules. Finally, the merged sub-images are inverse-transformed back into the spatial domain4. A quintessential example of such methods is the Laplacian pyramid transformation14, with derivative approaches including the gradient pyramid15, contrast pyramid16, and morphological pyramid17. On the other hand, spatial domain-based methods approach multi-focus image fusion by refining the clarity discrimination task at a more granular processing level10. They are typically categorized into three types: block-based18, region-based19, and pixel-based fusion20. Despite yielding acceptable fusion outcomes, traditional methods are constrained by their reliance on manually designed activity levels and fusion rules, which hinders their scalability and can result in inadequate robustness4.

The recent advancements in hardware have fueled the rapid growth of deep learning, prompting its application into multi-focus image fusion by numerous researchers21. Deep learning techniques in this field are primarily categorized into two types: decision map-based and end-to-end approaches4. Decision map-based methods initiate the fusion process by creating decision maps, which guide the subsequent image combination. These methods bear conceptual similarities to traditional spatial domain-based techniques. In contrast, end-to-end methods process images directly, leveraging the sophisticated feature extraction capabilities of convolutional neural networks or transformers. This allows for a direct derivation of the fused image, bypassing the need for image preprocessing4. While end-to-end methods simplify the workflow by removing the preprocessing step, they necessitate careful network architecture design to ensure effective feature extraction and image reconstruction11.

Metrics

A variety of quantitative assessment methods for multi-focus image fusion have been proposed to date22. Due to the difficulty in obtaining Ground Truth, these metrics are typically classified based on their reliance on source images: source image-based metrics and fused image-based metrics. The common evaluation metrics for multi-focus image fusion are presented in Table 1.

Table 1 Common evaluation metrics for multifocal image fusion. It can be categorized as source image-based and fused image-based metrics.
Full size table

While these evaluation metrics have been validated through extensive experiments for assessing image fusion performance, they face significant limitations when applied to underwater micro-target scenarios. The main issue is their uniform treatment of pixels, which overlooks the fact that in such scenarios, the majority of the image is background, with the target occupies a minor portion of the frame. Consequently, these metrics may not well represent the fusion quality of the target in the final assessment.

Methods

RCFusion

Expanding on previous work, this paper presents RCFusion, a novel multi-focus image fusion model tailored for underwater micro-bubble environments. RCFusion incorporates a simple yet robust data augmentation module, which includes a random crop operation on the input images. This random crop not only enhances the model’s generalization capabilities but also improves its fusion performance under adverse conditions. The random crop is a core step in the data augmentation module and is also the origin of the name RCFusion, as it adeptly addresses two central challenges in underwater image fusion: suboptimal imaging conditions and limited data availability.

DDPM is a type of deep generative model designed to simulate and generate complex high-dimensional data distributions36. In the diffusion process, Gaussian noise is added to the clear image at each time step, and after T iterations, a pure noise image following a Gaussian distribution is obtained. During the denoising process, Gaussian pure noise image is inputted. By predicting the noise added at t step, obtaining the image at the previous time step. Repeating this process results in the initial original image. RCFusion concurrently processes both source images, using them to inform the prediction of noise, ultimately yielding a single image that is in focus across the entire scene. Figure 2 demonstrates the generate principle of RCFusion.

Fig. 2
figure 2

The denoising principle demonstration of RCFusion.

Full size image

The denoising process of RCFusion can be expressed as follows:

$$\begin{aligned} F_{t-1} = \frac{1}{\root \of {\alpha _t} } \left( F_t-\frac{1-\alpha _t}{\root \of {1-\bar{\alpha }_t } } \varepsilon _{\theta }\left( S_1,S_2,F_t,t\right) \right) \end{aligned}$$
(1)

Where \(S_1\) and \(S_2\) are two source images respectively, \(F_t\) represents the latent variable, \(\alpha\) is hyper-parameter and \(\varepsilon _\theta\) is predicted noise. Through Eq. (1), it can generate \(F_{t-1}\) that is slightly clearer than \(F_t\). Multi-focus image fusion is a relatively deterministic process. Therefore, Eq. (1) does not incorporate random noise. The exclusion of random noise facilitates the generation of higher quality fused images11. The loss function of FusionDiff can be updated as:

$$\begin{aligned} L_t=E\left( \left\| \varepsilon _t -\varepsilon _\theta \left( S_1,S_2,F_t,t\right) \right\| ^2\right) \end{aligned}$$
(2)

Where \(\varepsilon _t\) denotes the actual noise.

Fig. 3
figure 3

The demonstration of noise prediction process and its constituent components in RCFusion. The core structure of the predictor is an U-Net network.

Full size image

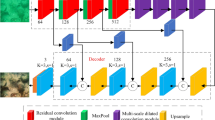
Figure 3 illustrates a schematic of the RCFusion model’s workflow and its core components. The backbone of the predictor adopts the U-Net network37. Initially, the two source images and the image at time step t are combined along the channel axis, followed by random cropping via the RCBlock. The images then undergo a preliminary channel expansion through the InBlock prior to being input into the U-Net. The U-Net structure comprises down-sampling, middle-sampling, and up-sampling modules. The down-sampling module includes four down-sample stages, each preceded by two ResBlocks that incorporate Time encoding which. This Time encoding is akin to the positional encoding used in Transformers. The up-sampling module mirrors the down-sampling process, with the addition of concatenation with the output from the corresponding down-sampling layer. The noise predictor outputs the noise \(\varepsilon _{\theta }\) that the model predicts to be added to the source image at time step t. The model training is facilitated by leveraging the noise forecasted by our noise predictor, the actual noise introduced into the input, and the principles outlined in Eq. 2.

RCBlock

Fig. 4
figure 4

The schematic representation of the random cropping process in RCBlock.

Full size image

Enhancing the model’s generalization capability is pivotally achieved through the RCBlock. Simply cropping the three images independently does not guarantee aligned cropping regions among them. To address this, we concatenate the images along the channel dimension before executing a unified cropping operation. Post-cropping, the images are resized to their original dimensions prior to model input. Figure 4 illustrates the RCBlock schematic, highlighting that bubbles in the input images predominantly appear in the central frame area. The randomness of the cropping regions and sizes means that, in theory, bubbles could be positioned anywhere within the image boundaries. This technique is a cost-effective method to substantially boost the model’s ability to generalize across various conditions.

Defects of metrics

As depicted in Fig. 1, the captured bubbles images reveal that the bubbles targets occupy a relatively minor portion of the overall image, while the majority comprises background. Traditional image fusion evaluation metrics allocate uniform significance to each pixel, potentially diluting the distinction of bubbles targets within the evaluation results.

For instance, when considering the classic source-image-based evaluation metrics, such as cross-entropy, the calculation formula for cross-entropy as follow:

$$\begin{aligned} CE_{X,F} = \sum _{i=0}^{255}h_X(i)log_2 \frac{h_X(i)}{h_F(i)} \end{aligned}$$
(3)

where X is source image A or B, h(i) is the normalized histogram of the image. Through Eq. (3), we observe that cross-entropy (CE) treats each pixel with equal weight, which dilutes the representation of the target fusion effect.

The same situation is reflected in fused-image-based evaluation metrics as well. For instance, the standard deviation (SD):

$$\begin{aligned} SD = \sqrt{\sum _{i=1}^{M} \sum _{j=1}^{N} (F(i,j) - \mu )^2} \end{aligned}$$
(4)

where \(\mu\) represents the mean value of the fused image.

Actually, all evaluation metrics take into account every pixel thoroughly, but in the context of this paper’s scenario, such comprehensive consideration of each pixel is not appropriate.

Fig. 5
figure 5

Examples of captured image pairs.

Full size image
Table 2 The evaluation results of nine evaluation metrics for example fused image.
Full size table

Figure 5 presents the comparative results of fifteen common multi-focus image fusion methods, including both traditional methods and those grounded in deep learning. Figure 5 highlights several issues present in the fused images, primarily including the emergence of artifacts, brightness deviations, target loss, detail loss, and the introduction of noise.In detail, the fusion images from SESF and DT-CWT introduced artifacts, with SESF experiencing the most severe manifestation. The DeepFuse images exhibited an overall increase in brightness. SwinFusion and MUFusion showed varying degrees of brightness deviation in targets, whereas MWG and CVT primarily displayed background brightness discrepancies. CNN missed a minor target, IMF resulted in the loss of a substantial number of targets, and ZMFF failed to capture the largest target. Furthermore, LP and GF did not excel in detail preservation and notably introduced noise, especially in the cases of LP. Upon comprehensive evaluation of various image fusion techniques, RCFusion, FusionDiff, and MWG demonstrated the best fusion performance, followed by LP, CVT, DT-CWT, and GF methods, while the fusion outcomes of the remaining approaches were relatively suboptimal.

Simultaneously, nine common evaluation metrics are employed to assess the fusion performance of the methods, including Entropy (EN), Mutual Information (MI), Normalized Mutual Information (NMI), Peak Signal-to-Noise Ratio (PSNR), Average Gradient (AG), Quality Assessment of Blur and Fringes \(\left( {Q^{{AB/F}} } \right),\) Standard Deviation (SD), Entropy Index (EI), and Structural Similarity Index (SSIM). Table 2 presents the evaluation results, where the highest and second highest scores are highlighted in bold and italic, respectively. From the results in the table, it is evident that although RCFusion exhibits superior fusion effects in subjective evaluations, it scores the highest in only one of the nine metrics. Other methods, despite their relatively better performance, have not achieved significant scores in these evaluative metrics. This suggests that existing evaluation metrics are not effective in reflecting image fusion performance in scenarios with small targets.

AGMSE

Given that the captured images feature bubble targets concentrated in small areas, with each bubble occupying only a few pixels and lacking sufficient structural texture information, this paper introduces the adaptive grayscale mean squared error (AGMSE), based on MSE, to better evaluate image fusion performance in such scenarios. The basic idea is that most of the captured images have a black background with only a small portion of the white target. Utilizing the characteristics of the grayscale image, a threshold is set to classify pixels as background if they are below the threshold and as targets if they are above. The MSE is then assessed solely for the target pixels.

In the specific implementation, the threshold is calculated as follows:

$$\begin{aligned} \theta _X = \frac{\lambda }{HW} \sum _{i=1}^{H} \sum _{j=1}^{W} gray(i,j) \end{aligned}$$
(5)

where \(\theta _X\) is specific to the threshold, denoted by X which may be either A or B, and the hyperparameter \(\lambda\) is set accordingly, H and W denote the image’s height and width, respectively, and gray(i, j) refers to the grayscale value at the pixel located at coordinates (i, j).

Subsequently, the pixels with grayscale values above the threshold form a set \({\textbf {X}}\). The MSE for the coordinates in set \({\textbf {X}}\) can be calculated using the following formula:

$$\begin{aligned} MSE_X=\frac{1}{\left| {\textbf {X}} \right| } \sum (X_{(i,j)}-F_{(i,j)})^2,(i,j)\in {\textbf {X}} \end{aligned}$$
(6)

Where \(\left| {\textbf {X}} \right|\) denotes the number of coordinates in set \({\textbf {X}}\), \(X_{(i,j)}\) and \(F_{(i,j)}\) represent the grayscale values of the source image and fused images, respectively, at coordinates (i, j).

Finally, the mean value of the obtained MSE is the final AGMSE:

$$\begin{aligned} AGMSE = \frac{MSE_A + MSE_B}{2} \end{aligned}$$
(7)

In Eq. 5, the hyperparameter \(\lambda\) is crucial for distinguishing background from target pixels, especially when the target bubbles are sparse and occupy only a few pixels. When the grayscale values of the target and background are similar, we use a lower \(\lambda\) to avoid filtering out target pixels. Conversely, when the target and background are more distinct, a higher \(\lambda\) helps isolate the target regions more effectively. This approach ensures that AGMSE focuses on the target areas rather than the background under different imaging conditions.

AGMSE is an evaluation metric based on MSE, thus a smaller value indicates better performance. AGMSE is designed to filter out the black background, focusing solely on the bubble targets. This targeted approach ensures that AGMSE ignores background pixels, concentrating on the pixel intensity differences within the bubble targets. This design enhances the assessment’s accuracy and relevance by zeroing in on the bubble targets’ fusion effect rather than the entire image’s pixel differences.

Experiment

Dataset

Fig. 6
figure 6

The schematic diagram of the experimental setup.

Full size image

The experiment was conducted in an indoor water tank with dimensions of 18 m in length, 2 m in width, and 3 m in height. A pulsed laser illuminator, set at a wavelength of 532 nm, an energy output of 10 mJ, and a frequency of 3 kHz, was vertically aligned with synchronized cameras. The underwater images were captured through an optical window, creating an underwater optical imaging system. Two ceramic micro-bubble pumps were situated 2.6 m and 3.1 m away from the optical window, generating bubbles approximately 300 \(\upmu\)m in diameter. The synchronized cameras had an exposure time of 1 \(\upmu\)s and were focused at the respective distances of 2.6 m and 3.1 m. Figure 6 presents a schematic of the experimental setup.

A total of 22,000 image pairs were captured, each with a resolution of 360 by 240 pixels, as depicted in the Fig. 7. The vertical beam depicted in the image represent the laser paths. The laser is positioned approximately 20 cm below the camera, so when the laser illuminates the bubbles, the camera captures the bubble images from above. Bubbles at 2.6 m, being relatively closer, appear in the lower part of the image, while those at 3.1 m, being farther away, appear in the upper part. According to the principle of perspective projection48, the downward angle of the camera causes closer objects to be projected in the lower part of the image, while distant objects are projected in the upper part. However, it is important to note that the distance between the two camera lenses is less than 3 cm, and the small bubbles are at least 2.6 m away. Based on the parallel projection approximation theory49, the images of different focal regions can be considered as captured from the same location.

Fig. 7
figure 7

Examples of captured image pairs.

Full size image

Train details

Since RCFusion operates as a few-shot model, we selected 100 image pairs from the total capture for training. Training lasted for 100,000 epochs at an initial learning rate of 0.0002, with a 0.99 decay every 1,000 epochs. The noise predictor had 64 channels, and Eq. 2 defined our loss function. To avoid tiny loss values halting network updates, we multiplied the loss by 128. Images were resized to 256 × 256 pixels. The RCBlock, essential for improving generalization, cropped images to between 0.08 and 0.5 of their original size before resizing to 256x256. We used the PyTorch framework for training, and experiments were performed on systems with Intel i9-12900KF CPU and NVIDIA GeForce RTX 3090Ti GPU.

Comparison with SOTA methods

In this subsection we compare RCFusion with existing SOTA methods, as detailed in Table 3. The evaluation metric used in this study is the AGMSE, as proposed herein, to assess the quality of the fused images.

Table 3 The SOTA methods selected for comparative experiments.
Full size table

We employed the AGMSE metric, introduced in this paper,for a comprehensive evaluation of image fusion performance. The images’ predominant black background and the minimal pixel occupation by bubble targets, which lack substantial structural texture, make AGMSE a precise and pertinent evaluation tool for this scenario. For our experimental images, a higher \(\lambda\) is more suitable, as it better separates the target regions from the background, which is the primary focus of our evaluation. However, we deliberately selected different \(\lambda\) values to explore how various methods perform under different conditions, providing a comprehensive comparison.

Table 4 The average AGMSE\(\downarrow\) of all algorithms in test dataset.
Full size table

Table 4 displays the mean AGMSE for each method, demonstrating that RCFusion surpasses other SOTA methods. These results suggest that RCFusion provides superior fusion outcomes in the context of underwater micro-bubble multi-focus image fusion. Concurrently, these evaluative outcomes align with the subjective analysis depicted in Fig. 5, further confirming that AGMSE is a more appropriate evaluative metric in this scenario.

Conclusion

This paper introduces RCFusion, a novel multi-focus image fusion model tailored for underwater micro-bubble imaging and grounded in the Denoising Diffusion Probabilistic Model (DDPM). This approach uses locally focused images to inform the generation of a globally focused image from Gaussian noise. The incorporation of the RCBlock, featuring random image cropping, bolsters the model’s ability to generalize. It adeptly tackles the dual challenges of suboptimal underwater optical conditions and data scarcity, which are commonly implicated in generalization deficiencies. The principal contributions of this study are outlined below:

  1. 1.

    We introduce a multi-focus image fusion model specifically designed for underwater micro-target environments, marking what is, to our knowledge, the inaugural application of such technology to underwater micro-bubble scenes.

  2. 2.

    We develope an optical imaging system within an indoor environment to construct a dataset for multi-focus image fusion of underwater micro-bubbles.

  3. 3.

    We have developed a novel image fusion evaluation metric, specifically tailored for assessing the performance of models in underwater micro-bubble scenarios.