Introduction

Heavy-duty vehicles have the characteristics of large mass and high center of mass. The centrifugal force and roll moment generated during steering are larger than other models, and rollover accidents are more likely to occur. Vehicle rollover is an extreme condition of vehicle transient instability. In all vehicle traffic accidents, the rollover risk is the highest and the mortality rate is the highest. According to NHTSA rollover accident statistics, from 1982 to 2021, the average fatality rate of heavy truck rollover in the United States is as high as 44.1%1. As an important hardware execution part of vehicle active safety control, vehicle braking system plays a decisive role in vehicle anti-rollover control. In order to meet the development goals of vehicle environmental protection and intelligence, in the braking system of electric vehicles, Electro-Mechanical-Brake (EMB) gradually replaces the traditional hydraulic braking system. The EMB system completely cancels the traditional hydraulic pipeline and replaces it with an electric drive component. Although its structure is compact and the response speed is fast, it can achieve independent and accurate control of each wheel, the EMB cancels the hydraulic backup of the traditional vehicle and increases the failure risk of its braking failure2. Therefore, considering the fault tolerance of EMB braking failure, anti-rollover control of vehicles is one of the urgent problems to be solved in the driving safety of electric vehicles, which is of great value to reduce the accident risk of rollover vehicles under extreme conditions with braking failure.

Aiming at the problem that whether the cause of vehicle rollover is caused by road excitation, scholars have established vehicle non-tripped and tripped rollover models. For the non-tripped vehicle model, scholars mainly analyze the degree of freedom of the vehicle’s own motion, while ignoring the pitch degree of freedom during the vehicle ‘s driving. For example, Doumiati3 designed a LPV controller based on a two-degree-of-freedom model to simplify the vehicle into a linear vehicle to maintain good stability. In order to realize the rollover prediction of heavy vehicles, Ye4 established a three-degree-of-freedom model and calculated the critical frequency of rollover. In order to improve the lateral stability of the vehicle during rapid steering, Huang5 established a multi-model control system based on a seven-degree-of-freedom vehicle model. Aiming at the problem of vehicle rollover caused by road excitation, scholars have established the corresponding tripped rollover model. For example, in order to improve the anti-rollover ability of vehicles on uneven roads, Jin Zhilin6 established an eight-degree-of-freedom rollover model considering the characteristics of independent rotation of wheels, and proposed a hierarchical controller including roll angle sliding mode control. Shi7 established an eight-degree-of-freedom vehicle model to verify the effect of the controller. In order to improve the spatial stability of the vehicle, Zhang Lipeng et al.8 established a 14-degree-of-freedom spatial vehicle model and proposed a spatial stability cooperative control method including four-wheel differential drive and front wheel active steering. Some scholars model vehicles through neural network methods. In order to improve the prediction accuracy of vehicle lateral stability, Chen9 established a hybrid model combining physical and dual-attention neural networks to simulate the lateral dynamics of vehicles. In order to explore the driving stability of vehicles, Zhou10 used neural networks to embed data-driven models into physical models to achieve accurate and interpretable modeling. Luo11 used neural network identification to construct unknown nonlinear system dynamics and solve the optimal control problem. Although scholars have established the rollover model of tripped vehicles based on road excitation, most of them are aimed at two-axle passenger vehicles, and there are few tripped models for three-axle heavy vehicles. Therefore, according to the characteristics of high center of mass of heavy vehicles and easy to be affected by road excitation, the rollover dynamic model of tripped three-axis heavy vehicles can be established, and the rollover problem of three-axis heavy vehicles can be studied based on this model.

In the active anti-rollover control of automobiles, scholars use active steering and differential braking to control the transient instability of vehicles12. Zhang proposed a new rear wheel pulse steering system to improve the roll stability of the vehicle. By designing the hydraulic-mechanical pulse steering system, a model reflecting the characteristics of the pulse steering system is given13. Ono uses a four-wheel distributed steering and braking system to improve the handling stability of the vehicle14. Although active steering can balance the yaw moment during body rollover, when the angle correction of the system output is too large, it will affect the driver’s steering intention and increase the risk of secondary collision in the process of obstacle avoidance, which is not conducive to the trafficability of the car. Both the active suspension and the active stabilizer bar achieve the purpose of anti-rollover by adjusting the equivalent roll stiffness and damping of the body. Active suspension can realize the dynamic adjustment of vehicle handling stability and ride comfort by adjusting the vertical stiffness and damping of the suspension15. Chu designed an active suspension anti-rollover control strategy based on smooth sliding mode control for heavy vehicles16; the active lateral stabilizer bar is also effective in the field of anti-rollover. Vu proposed an active lateral stabilizer bar composed of four electronic servo valve hydraulic actuators, and modeled and integrated it into the rollover model of heavy vehicles. The linear quadratic regulator (LQR) controls the output of the actuator to achieve active anti-rollover17. Muniandy developed an active stabilizer bar based on a self-tuning PI-PD controller and applied it to a bus to improve its driving stability18. Although the active lateral stabilizer bar has a certain anti-roll ability, it mainly acts on the sprung mass of the car, and the control effect on the roll of the unsprung mass is not obvious. In order to solve the problem of insufficient control effect, many scholars have used other methods to carry out anti-rollover control research. In order to ensure the lateral stability of the three-axis vehicle, Liu et al.19 designed an integrated chassis control strategy including differential braking. In order to reduce the oscillation of vehicle lateral response parameters under extreme conditions, Soltani20 proposed a comprehensive control method based on differential braking. The particle swarm optimization algorithm proposed by Shi21 can explore the influence of road texture on vehicle rollover. The optimal predictive repetitive control proposed by Lan22 can offset the shock problem caused by the vehicle due to the road. Based on differential braking, a vehicle anti-rollover control system was developed by Dong23. In order to improve vehicle handling and safety, Termous24 proposed a coordinated control strategy including differential braking. In order to improve the roll stability of distributed drive tram, Chang25 designed a control strategy based on differential braking. Zang26 carried out differential braking control on the vehicle under extreme conditions, and effectively controlled the lateral stability of the vehicle. Wang27 proposed a differential braking control based on the tire force distribution rule. The vehicle rollover control process is accompanied by the problem of signal mutation and multi-signal fusion stability. Xu28 designed two low-gain controllers to solve the global stability problem when the input is saturated, which provides a basis for improving the control stability when the vehicle signal suddenly changes. Yao29 proposed an iterative algorithm to solve the problem of mutual interference between vehicle radar and communication systems in the same frequency band. The neural network algorithm designed by Liu30 can realize the rapid distribution of braking torque during real vehicle driving. Therefore, the differential braking control can reduce the influence of unsprung mass on roll without changing the driver ‘s intention, and has certain reliability in the anti-rollover control of three-axle heavy vehicles.

Aiming at the braking failure problem of EMB system automobiles, scholars mostly overcome the yaw moment caused by asymmetric braking by correcting the yaw moment. Hirkoka et al.31 confirmed the idea that the stability of the vehicle can be controlled by the coordination of steering and braking according to the failure of different actuators of the vehicle. Intelligent fault detection can detect braking failure during vehicle driving32. During the continuous braking process, the working pressure of the crankshaft becomes larger, accompanied by high temperature and vibration33. Lubrication based on nanofluids34 and micro-lubrication35 can reduce the generation of high temperature during vehicle driving. At the same time, sustainable lubrication helps to prolong the service life of the brake and reduce the occurrence of faults36. Aiming at the problem of vibration, Deng et al.37 proposed a multi-type flutter detection method using multi-channel internal and external signals, which can detect the vibration effect during vehicle control. The sliding mode controller proposed by Tan38 can reduce the vibration of the actuator and provide ideas for reducing the vibration phenomenon caused by vehicle control. The neutral number proposed by Mondal39 can detect the uncertainty of vibration caused by the control process, which provides a basis for optimizing the control effect. In order to ensure the effectiveness and real-time performance of vehicle braking in extreme weather, Peng40 proposed a task offloading scheme called dynamic pricing-driven double-wide reinforcement learning. Wang et al.41 proposed a fault-tolerant control structure for cooperative front wheel steering and braking for the special conditions of single wheel tire burst. When selecting the controller, although the improved fuzzy control can have advantages in the case of uncertain parameters, it still cannot achieve ideal control when its empirical standard is not accurate42. The time-varying actuator fault and its braking response under dynamic conditions have a certain delay43 and the braking fault aggravates the vehicle instability44, so the sliding mode controller can be used in the vehicle control process. Ji et al.45 designed a sliding mode controller to redistribute the braking force for the problem of single-wheel braking failure. Straky et al.46 conducted a simulation experiment on the actuator failure control of the traditional braking system, and controlled the yaw angle by controlling the steering system. This method is also applicable to distributed drive vehicles. During the HIL test, the braking control effect may be inaccurate due to the delay of the execution signal. Xu47 proposed a method based on partial differential equation observer to deal with distributed infinite output delay, which can solve the problem of signal delay. For multi-input and multi-output nonlinear systems with uncertain input delay, Wang48 proposed an adaptive PI event-triggered control method. The convergence speed of the control algorithm also affects the control effect, especially for the sudden situation of braking failure fault, real-time performance is particularly important. The adaptive memory trigger scheme proposed by Ding49 can quickly process the abrupt signal and provide guarantee for the real-time performance of the algorithm. Sugisaka et al.50 used fuzzy PI and PD to adjust the braking force of the vehicle to ensure the stability of the vehicle when the braking fails. Aiming at the problem of braking failure, although the coordinated control of steering and braking systems can maintain the stability of the vehicle during straight-line braking, the active steering system may increase the risk of vehicle rollover during emergency steering. Differential braking control alone can also correct yaw moment and maintain vehicle stability. Therefore, in the process of single wheel braking failure and emergency steering, it is reasonable to use differential braking control as its anti-rollover control.

In order to improve the EMB braking fault tolerance and anti-rollover control of heavy-duty vehicles, the structure of this paper is as follows: In the second part, the spatial dynamic model of single-wheel braking failure of three-axle heavy-duty vehicles is established, and the rollover evaluation index is improved. The third part describes the overall structure of the anti-rollover control strategy based on improved LTR. Based on the normalized tire road adhesion coefficient identification system, the braking model of anti-lock braking system based on sliding mode variable structure is established. The control logic of differential braking is expounded, and the braking torque is redistributed. In the fourth part, the single-wheel braking failure heavy vehicle is tested by Trucksim/simulink co-simulation, and the control effect of the anti-rollover control algorithm based on improved LTR in the case of single-wheel braking failure is verified. In the fifth part, the hardware-in-the-loop test of the anti-rollover algorithm under the two conditions of hook and angle step is carried out, and the test results are analyzed. The sixth part summarizes the above content.

The establishment of heavy-duty vehicle dynamics model

Vehicle dynamics model

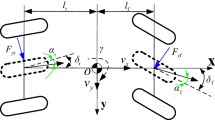
According to the research content of this paper, this paper takes the braking failure of the right middle wheel of the heavy vehicle as an example to establish the dynamic model of the right middle failure heavy vehicle. The model includes the longitudinal, lateral and vertical motion of the body, pitch, roll, yaw, wheel rotation and wheel vertical motion. The 18-degree-of-freedom spatial dynamics model is shown in Fig. 1.

Fig. 1
figure 1

Vehicle model diagram.

Full size image

In Fig. 1, \(v_{x}\) and \(v_{{\text{y}}}\) are the longitudinal and lateral speed of the vehicle; \(\theta_{b},\) \(\varphi\) and \(\omega _{r}\) are body pitch angle, roll angle and yaw rate; \(m_{b}\) and \(z_{b}\) are the sprung mass and the vertical displacement of the body, respectively; \(l_{1},\) \(l_{2},\) \(l_{3}\) respectively represent the distance from the center of mass to the front axis, the middle axis and the rear axis; \(b_{1}\) and \(b_{2}\) are the distance from the left and right sides of the vehicle to the central axis respectively; \({m_{ti}},\) \({F_{xi}}\) and \({F_{yi}}\) are the tire mass and the longitudinal force and lateral force of the tire, respectively. The subscript \(i=1\sim 6\) represents the left front, right front, left middle, right middle, left rear and right rear, respectively. \({z_{si}},\) \({q_{i}}\) and \(\alpha _{i}\) are the input of suspension displacement, road roughness and tire sideslip angle, respectively. \({c_{i}},\) \({k_{i}}\) and \({f_{ai}}\) are suspension stiffness, damping and active suspension force, respectively. \(\delta\) is the front wheel angle; his the centroid height. The meanings of the above symbols are applicable in the full text.

The displacement relationship between the suspension and the vehicle contact part is shown in Eq. (1)

$$\left\{ {\begin{array}{*{20}l} {z_{s1} = z_{b} - \theta_{b} l_{1} + \varphi b_{1} } \hfill \\ {z_{s2} = z_{b} - \theta_{b} l_{1} - \varphi b_{2} } \hfill \\ {z_{s3} = z_{b} + \theta_{b} l_{2} + \varphi b_{1} } \hfill \\ {z_{s4} = z_{b} + \theta_{b} l_{2} - \varphi b_{2} } \hfill \\ {z_{s5} = z_{b} + \theta_{b} l_{3} + \varphi b_{1} } \hfill \\ {z_{s6} = z_{b} + \theta_{b} l_{3} - \varphi b_{2} } \hfill \\ \end{array} } \right.$$
(1)

The suspension force is expressed as Eq. (2)

$$f_{si} = k_{i} (z_{si} - z_{ti} ) + c_{i} (\dot{z}_{si} - \dot{z}_{ti} )$$
(2)

In formula (2), \({f_{si}}\) is the suspension force.

When the right middle wheel brake fails, the wheel braking force is 0, that is, \({F_{x4}}=0\). According to D ‘Alembert ‘s principle, the whole kinetic equation can be established as shown in Eq. (3).

$$\left\{ {\begin{array}{*{20}l} {m_{z} \left( {\dot{v}_{y} + v_{x} \omega_{r} } \right) - m_{b} \dot{z}_{b} \dot{\varphi } - m_{b} h\ddot{\varphi } = \sum\limits_{i = 1}^{2} {\left( {F_{yi} \cos \delta + F_{xi} \sin \delta } \right)} + \sum\limits_{i = 3}^{6} {F_{yi} } } \hfill \\ {m_{z} \left( {\dot{v}_{x} - v_{y} \omega_{r} } \right) + m_{b} \dot{z}_{b} \dot{\theta }_{b} = \sum\limits_{i = 1}^{2} {\left( {F_{xi} \cos \delta + F_{yi} \sin \delta } \right)} + F_{x3} + \sum\limits_{i = 5}^{6} {F_{xi} } } \hfill \\ {m_{b} \left( {\ddot{z}_{b} - v_{x} \dot{\theta }_{b} + v_{y} \dot{\varphi }} \right) = - \sum\limits_{i = 1}^{6} {f_{i} } } \hfill \\ {I_{y} \ddot{\theta }_{b} = l_{1} \sum\limits_{i = 1}^{2} {f_{i} - l_{2} } \sum\limits_{i = 3}^{4} {f_{i} - l_{3} } \sum\limits_{i = 5}^{6} {f_{i} } } \hfill \\ {I_{z} \dot{\omega }_{r} + I_{xz} \ddot{\varphi } = l_{1} \sum\limits_{i = 1}^{2} {\left( {F_{yi} \cos \delta + F_{xi} \sin \delta } \right) - l_{2} \sum\limits_{i = 3}^{4} {F_{yi} - l_{3} } \sum\limits_{i = 5}^{6} {F_{yi} + } } } \hfill \\ {B/2\left[ {\left( {F_{x2} - F_{x1} } \right)\cos \delta + \left( {F_{y2} - F_{y1} } \right)\sin \delta + F_{x3} - F_{x4} + F_{x5} - F_{x6} } \right]} \hfill \\ {\left( {I_{x} + m_{b} h^{2} } \right)\ddot{\varphi } - m_{b} ha_{y} = - b_{1} \left( {f_{s1} + f_{s3} + f_{s5} } \right) + b_{2} \left( {f_{s2} + f_{s4} + f_{s6} } \right) + M_{T} } \hfill \\ {I_{i} \dot{\omega }_{i} = F_{xi} R_{i} - T_{bi} (i \ne 4)} \hfill \\ \end{array} } \right.$$
(3)

In formula (3), \({I_{x}}\), \({I_{y}}\), \({I_{z}}\) and \({I_{xz}}\) are the moment of inertia around x, y, z axis and \(xz\) plane respectively; \({m_{z}}\) is the vehicle mass; \({k_{ti}}\) is the tire stiffness; B is the body width; \({F_{xi}}\) and \({F_{yi}}\) are the longitudinal force and lateral force of the tire, respectively; \({I_{i}}\) is the moment of inertia of the wheel; \({\omega _{i}}\) is the wheel speed; \({R_{i}}\) is the radius of the wheel; \({T_{bi}}\) is the braking torque; \({M_{T}}\) is the roll moment.

The vertical dynamic equation of unsprung mass is shown in Eq. (4).

$$m_{ti} \ddot{z}_{ti} = f_{si} - k_{ti} \left( {z_{ti} - q_{i} } \right)$$
(4)

The vertical dynamic load of the wheel is composed of the static load and the dynamic load of the tire. The vertical force of each wheel is expressed as (5)

$$\left\{ {\begin{array}{*{20}l} {F_{z1} = m_{b} g\frac{B/2 - h\sin \varphi }{B} - \frac{{m_{b} a_{y} h\cos \varphi }}{B} - m_{b} a_{x} h\cos \varphi \frac{B/2 + h\sin \varphi }{B} + k_{t1} \left( {z_{t1} - q_{1} } \right)} \hfill \\ {F_{z2} = m_{b} g\frac{B/2 + h\sin \varphi }{B} + \frac{{m_{b} a_{y} h\cos \varphi }}{B} - m_{b} a_{x} h\cos \varphi \frac{B/2 + h\sin \varphi }{B} + k_{t2} \left( {z_{t2} - q_{2} } \right)} \hfill \\ {F_{z3} = m_{b} g\frac{B/2 - h\sin \varphi }{B} - \frac{{m_{b} a_{y} h\cos \varphi }}{B} + m_{b} a_{x} h\cos \varphi \frac{B/2 + h\sin \varphi }{B} + k_{t3} \left( {z_{t3} - q_{3} } \right)} \hfill \\ {F_{z4} = m_{b} g\frac{B/2 + h\sin \varphi }{B} + \frac{{m_{b} a_{y} h\cos \varphi }}{B} + m_{b} a_{x} h\cos \varphi \frac{B/2 + h\sin \varphi }{B} + k_{t4} \left( {z_{t4} - q_{4} } \right)} \hfill \\ {F_{z5} = m_{b} g\frac{B/2 - h\sin \varphi }{B} - \frac{{m_{b} a_{y} h\cos \varphi }}{B} + m_{b} a_{x} h\cos \varphi \frac{B/2 + h\sin \varphi }{B} + k_{t5} \left( {z_{t5} - q_{5} } \right)} \hfill \\ {F_{z6} = m_{b} g\frac{B/2 + h\sin \varphi }{B} + \frac{{m_{b} a_{y} h\cos \varphi }}{B} + m_{b} a_{x} h\cos \varphi \frac{B/2 + h\sin \varphi }{B} + k_{t6} \left( {z_{t6} - q_{6} } \right)} \hfill \\ \end{array} } \right.$$
(5)

In formula (5), \({a_{x}}\) and \({a_{y}}\) are the longitudinal and lateral acceleration of the vehicle respectively; \({F_{zi}}\) is the vertical dynamic load of each wheel.

Tire model

The tire adopts the ‘magic formula’ tire model, and the longitudinal force and lateral force of the tire are shown in Formula (6)51.

$$F(x) = D\sin (C\arctan [Bx - E(Bx - \arctan Bx)])$$
(6)

In the formula (6), \(F(x)\) is the longitudinal force or lateral force on the tire, x is the tire slip rate or sideslip angle, and B, C, D and E are the fitting parameters.

The tire cornering angle is expressed as Eq. (7) :

$$\left\{ {\begin{array}{*{20}l} {\alpha_{1} = \alpha_{2} = \arctan \left[ {\left( {v_{y} + l_{1} \omega_{r} } \right)/v_{x} } \right] - \delta } \hfill \\ {\alpha_{3} = \alpha_{4} = \arctan \left[ {\left( {v_{y} - l_{2} \omega_{r} } \right)/v_{x} } \right]} \hfill \\ {\alpha_{5} = \alpha_{6} = \arctan \left[ {\left( {v_{y} - l_{3} \omega_{r} } \right)/v_{x} } \right]} \hfill \\ \end{array} } \right.$$
(7)

Rollover evaluation index based on improved LTR

The rollover evaluation index is a key part of formulating the anti-rollover control strategy. In this paper, the feasibility and applicability of the NLTR control strategy in the single-wheel braking failure rollover condition are illustrated by comparing the control under the standard LTR and the RI2 (Traditional LTR) index proposed by the research group. The following part is the introduction of each rollover index.

The standard vehicle rollover evaluation index is defined as the ratio of the difference between the vertical forces of the left and right wheels of the vehicle to the sum of the vertical forces of the left and right sides. When its absolute value is 1, it indicates vehicle rollover. The definition of rollover index is shown in (8)7.

$$LTR = \left( {F_{zr} - F_{zl} } \right)/\left( {F_{zr} + F_{zl} } \right)$$
(8)

In the formula (8), \({F_{zl}}\) and \({F_{zr}}\) are the vertical forces on the left and right sides of the wheel respectively.

Since the vertical force of the wheel in the standard rollover index of formula (8) is not easy to measure directly, the traditional rollover evaluation index is based on the three-degree-of-freedom vehicle model combined with LTR to derive the RI2 index, as shown in formula (9)52.

$$RI_{2} = 2\left( {m_{s} hg\varphi_{s} - I_{x} \ddot{\varphi }_{s} + m_{s} ha_{y} } \right)/Bmg$$
(9)

The NLTR index is derived by combining the vehicle dynamics model of formula (1) ~ formula (7) with the rollover index definition formula (8), and the detailed derivation process of the index and the accuracy of the classic rollover condition have been demonstrated in the literature54. The NLTR is shown in formula (10).

$$NLTR = \frac{{2\left[ {\left( {3g\varphi + 2a_{y} } \right)m_{b} h + \left( {I_{x} + m_{b} h^{2} } \right)\ddot{\varphi }} \right] + B\left( {m_{tl} \ddot{z}_{tl} - m_{tr} \ddot{z}_{tr} } \right)}}{{B\left[ {m_{b} \left( {3g + a_{x} h - \ddot{z}_{b} + v_{x} \dot{\theta }_{b} - v_{y} \dot{\varphi }} \right) - \left( {m_{tl} \ddot{z}_{tl} + m_{tr} \ddot{z}_{tr} } \right)} \right] + 2m_{b} a_{x} \varphi h^{2} }}$$
(10)

It can be seen from the above description that the parameters in the rollover evaluation index can be calculated or measured, so the parameters in the verification and control strategy can be directly output by TruckSim and used as known parameters for subsequent calculation. Although NLTR requires many dynamic parameters, it requires high reliability of signal sources54, the NLTR index includes the unsprung mass vertical and vehicle pitch motion signals. When the wheel brake fails and the road surface information changes, the response is more sensitive. In theory, NLTR is more suitable than the traditional RI2 index for vehicle rollover conditions when the brake fails.

In order to verify the accuracy of the index in braking failure, the standard LTR, traditional RI2 and NLTR indexes are compared under extreme conditions. The simulation results are shown in Fig. 2.

Fig. 2
figure 2

Comparison of simulation results of braking failure index.

Full size image

Under the limit conditions of J-turn and Fish-Hook, the simulation shows that NLTR reaches the rollover threshold 0.3 s earlier than RI2, and the maximum value is about 0.2 larger than RI2 and LTR, and the response is more sensitive under braking failure conditions.

Based on NLTR single-wheel braking failure heavy-duty vehicle anti-rollover hierarchical control strategy

The hierarchical control strategy can pass the rollover index value and decide whether to open the controller. The controller calculates the braking torque required to maintain the lateral stability of the vehicle in real time, and applies the braking torque to a single wheel or multiple wheels through the differential braking distribution strategy, and realizes the vehicle anti-rollover control through the chassis braking. At the same time, the complex suspension, steering and braking systems in the vehicle chassis control system are divided into upper control and lower control. The control algorithm calculates the braking torque in real time. When the rollover index reaches the threshold, the actuator preferentially brakes the wheel according to the results received by the braking system, and the braking torque resists the roll torque, thereby achieving anti-rollover. The anti-rollover control strategy logic based on NLTR index is shown in Fig. 3.

Fig. 3
figure 3

Anti-rollover control strategy of right middle wheel braking failure.

Full size image

Anti-rollover upper control of right middle wheel braking failure heavy vehicle

Identification based on normalized tire-road adhesion coefficient

According to the normalized tire model, the tire force can be expressed as the form (11).

$$\left\{ {\begin{array}{*{20}l} {F_{xi} = u_{R\max g} F_{xi}^{0} } \hfill \\ {F_{yi} = u_{R\max g} F_{yi}^{0} } \hfill \\ \end{array} } \right.$$
(11)

In Formula (11), \(F_{{xi}}^{0}\) and \(F_{{yi}}^{0}\) are longitudinal and lateral normalized tire forces, which are the road adhesion coefficients to be identified. The normalized tire force is shown in Eq. (12).

$$\left\{ {\begin{array}{*{20}l} {F_{x}^{0} = \frac{{\left| {\sigma_{x} } \right|}}{{\sigma u_{Rmaxh} }}\left\{ {D\sin \left( {C\arctan \left[ {B\lambda - E\left( {B\lambda - \arctan B\lambda } \right)} \right]} \right)} \right\}} \hfill \\ {F_{y}^{0} = \frac{{\left| {\sigma_{y} } \right|}}{{\sigma u_{Rmaxh} }}\left\{ {D\sin \left( {C\arctan \left[ {B\alpha_{y} - E\left( {B\alpha_{y} - \arctan B\alpha_{y} } \right)} \right]} \right)} \right\}} \hfill \\ \end{array} } \right.$$
(12)

In Eq. (12), \(u_{R\max h}\) is the adhesion coefficient of adjacent pavement, \(\lambda\) is the slip rate, \({\alpha _{y}}\) is the sideslip angle.

The Kalman filter (UKF) is integrated to identify the road adhesion coefficient. The UKF measures the noise covariance \(0.05 \times {I_{3 \times 3}}\), the process noise covariance is \(0.019 \times {I_{6 \times 6}}\), and the initial error covariance is \(0.01 \times {I_{3 \times 3}}\).

According to the formula (12), the state Eq. (13) and the measurement Eq. (14) of pavement recognition are established respectively.

$$\left[ \begin{gathered} u_{1} (n + 1) \hfill \\ u_{2} (n + 1) \hfill \\ u_{3} (n + 1) \hfill \\ u_{4} (n + 1) \hfill \\ u_{5} (n + 1) \hfill \\ u_{6} (n + 1) \hfill \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}l} 1 \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill \\ {} \hfill & 1 \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill \\ {} \hfill & {} \hfill & 1 \hfill & {} \hfill & {} \hfill & {} \hfill \\ {} \hfill & {} \hfill & {} \hfill & 1 \hfill & {} \hfill & {} \hfill \\ {} \hfill & {} \hfill & {} \hfill & {} \hfill & 1 \hfill & {} \hfill \\ {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & 1 \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {u_{1} (n)} \hfill \\ {u_{2} (n)} \hfill \\ {u_{3} (n)} \hfill \\ {u_{4} (n)} \hfill \\ {u_{5} (n)} \hfill \\ {u_{6} (n)} \hfill \\ \end{array} } \right] + w(t)$$
(13)
$$\left[ {\begin{array}{*{20}c} {\dot{v}_{x} - v_{y} \omega_{r} + \frac{{m_{b} }}{{m_{z} }}\dot{z}_{b} \dot{\theta }_{b} } \\ {\dot{v}_{y} + v_{x} \omega_{r} - \frac{{m_{b} }}{{m_{z} }}\left( {\dot{z}_{b} \dot{\varphi } + h\ddot{\varphi }} \right)} \\ {\dot{\omega }_{r} + \frac{{I_{xz} }}{{I_{z} }}\ddot{\varphi }} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {A_{11} } \hfill & {A_{12} } \hfill & {A_{13} } \hfill & {A_{14} } \hfill & {A_{15} } \hfill & {A_{16} } \hfill \\ {A_{21} } \hfill & {A_{22} } \hfill & {A_{23} } \hfill & {A_{24} } \hfill & {A_{25} } \hfill & {A_{26} } \hfill \\ {A_{31} } \hfill & {A_{32} } \hfill & {A_{33} } \hfill & {A_{34} } \hfill & {A_{35} } \hfill & {A_{36} } \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {u_{1} } \hfill \\ {u_{2} } \hfill \\ {u_{3} } \hfill \\ {u_{4} } \hfill \\ {u_{5} } \hfill \\ {u_{6} } \hfill \\ \end{array} } \right] + v(t)$$
(14)

The unknown parameters in Eq. (14) are shown in Eqs. (15)~(17), where the random variables w(t) and v(t) are process noise and measurement noise, respectively.

$$\left\{ {\begin{array}{*{20}l} {A_{11} = \left( {F_{x1}^{0} \cos \delta - F_{y1}^{0} \sin \delta } \right)/m_{z} } \hfill \\ {A_{12} = \left( {F_{x2}^{0} \cos \delta - F_{y2}^{0} \sin \delta } \right)/m_{z} } \hfill \\ {\begin{array}{*{20}l} {A_{13} = F_{x3}^{0} /m_{z} } \hfill & {A_{14} = F_{x4}^{0} /m_{z} } \hfill \\ \end{array} } \hfill \\ {\begin{array}{*{20}l} {A_{15} = F_{x5}^{0} /m_{z} } \hfill & {A_{16} = F_{x6}^{0} /m_{z} } \hfill \\ \end{array} } \hfill \\ \end{array} } \right.$$
(15)
$$\left\{ {\begin{array}{*{20}l} {A_{21} = {{\left( {F_{y1}^{0} \cos \delta + F_{x1}^{0} \sin \delta } \right)} \mathord{\left/ {\vphantom {{\left( {F_{y1}^{0} \cos \delta + F_{x1}^{0} \sin \delta } \right)} {m_{z} }}} \right. \kern-0pt} {m_{z} }}} \hfill \\ {A_{22} = {{\left( {F_{y2}^{0} \cos \delta + F_{x2}^{0} \sin \delta } \right)} \mathord{\left/ {\vphantom {{\left( {F_{y2}^{0} \cos \delta + F_{x2}^{0} \sin \delta } \right)} {m_{z} }}} \right. \kern-0pt} {m_{z} }}} \hfill \\ {\begin{array}{*{20}l} {A_{23} = {{F_{y3}^{0} } \mathord{\left/ {\vphantom {{F_{y3}^{0} } {m_{z} }}} \right. \kern-0pt} {m_{z} }}} \hfill & {A_{24} = {{F_{y4}^{0} } \mathord{\left/ {\vphantom {{F_{y4}^{0} } {m_{z} }}} \right. \kern-0pt} {m_{z} }}} \hfill \\ \end{array} } \hfill \\ {\begin{array}{*{20}l} {A_{25} = {{F_{y5}^{0} } \mathord{\left/ {\vphantom {{F_{y5}^{0} } {m_{z} }}} \right. \kern-0pt} {m_{z} }}} \hfill & {A_{26} = {{F_{y6}^{0} } \mathord{\left/ {\vphantom {{F_{y6}^{0} } {m_{z} }}} \right. \kern-0pt} {m_{z} }}} \hfill \\ \end{array} } \hfill \\ \end{array} } \right.$$
(16)
$$\left\{ {\begin{array}{*{20}l} {A_{31} = {{\left[ {l_{1} \left( {F_{y1}^{0} \cos \delta + F_{x1}^{0} \sin \delta } \right) + \frac{B}{2}\left( {F_{y1}^{0} \sin \delta - F_{x1}^{0} \cos \delta } \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {l_{1} \left( {F_{y1}^{0} \cos \delta + F_{x1}^{0} \sin \delta } \right) + \frac{B}{2}\left( {F_{y1}^{0} \sin \delta - F_{x1}^{0} \cos \delta } \right)} \right]} {I_{z} }}} \right. \kern-0pt} {I_{z} }}} \hfill \\ {A_{32} = {{\left[ {l_{1} \left( {F_{y2}^{0} \cos \delta + F_{x2}^{0} \sin \delta } \right) + \frac{B}{2}\left( {F_{x2}^{0} \sin \delta - F_{y2}^{0} \cos \delta } \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {l_{1} \left( {F_{y2}^{0} \cos \delta + F_{x2}^{0} \sin \delta } \right) + \frac{B}{2}\left( {F_{x2}^{0} \sin \delta - F_{y2}^{0} \cos \delta } \right)} \right]} {I_{z} }}} \right. \kern-0pt} {I_{z} }}} \hfill \\ {\begin{array}{*{20}l} {A_{33} = {{\left( {\frac{B}{2}F_{x3}^{0} - l_{2} F_{y3}^{0} } \right)} \mathord{\left/ {\vphantom {{\left( {\frac{B}{2}F_{x3}^{0} - l_{2} F_{y3}^{0} } \right)} {I_{z} }}} \right. \kern-0pt} {I_{z} }}} \hfill & {A_{34} = {{\left( { - \frac{B}{2}F_{x4}^{0} - l_{2} F_{y4}^{0} } \right)} \mathord{\left/ {\vphantom {{\left( { - \frac{B}{2}F_{x4}^{0} - l_{2} F_{y4}^{0} } \right)} {I_{z} }}} \right. \kern-0pt} {I_{z} }}} \hfill \\ \end{array} } \hfill \\ {\begin{array}{*{20}l} {A_{35} = {{\left( {\frac{B}{2}F_{x5}^{0} - l_{3} F_{y5}^{0} } \right)} \mathord{\left/ {\vphantom {{\left( {\frac{B}{2}F_{x5}^{0} - l_{3} F_{y5}^{0} } \right)} {I_{z} }}} \right. \kern-0pt} {I_{z} }}} \hfill & {A_{36} = {{\left( { - \frac{B}{2}F_{x6}^{0} - l_{3} F_{y6}^{0} } \right)} \mathord{\left/ {\vphantom {{\left( { - \frac{B}{2}F_{x6}^{0} - l_{3} F_{y6}^{0} } \right)} {I_{z} }}} \right. \kern-0pt} {I_{z} }}} \hfill \\ \end{array} } \hfill \\ \end{array} } \right.$$
(17)

SM-ABS control

After estimating the tire adhesion coefficient from the “Identification based on normalized tire-road adhesion coefficient” section summary, the estimated road adhesion coefficient can be integrated into the vehicle ABS control, and then the braking torque required by each wheel during emergency braking can be calculated.

Theoretical basis for calculating braking torque

According to the principle of dynamic friction, the longitudinal force of the tire can be described as Eq. (18).

$$F_{xi} = \mu_{i} F_{zi}$$
(18)

From the formula (2), we can see that the braking torque is shown in formula (19).

$$T_{bi} = F_{xi} R_{i} - I\dot{\omega }_{i}$$
(19)

The slip ratio of each wheel is shown in Formula (20).

$$\lambda_{i} = \frac{{v_{i} - \omega_{i} R}}{{v_{i} }}$$
(20)
Design of sliding mode variable structure

The design of sliding mode control first needs to define the sliding surface. The sliding surface is shown in Formula (21) as follows.

$$s = \lambda - \lambda_{d}$$
(21)

Derivation of the sliding surface can be obtained:

$$\dot{s} = \dot{\lambda } - \dot{\lambda }_{d} = - K{\text{sgn}} (s)$$
(22)

In order to test the rationality of the sliding surface design, the Lyapunov function is designed as Eq. (23).

$$v = \frac{1}{2}s^{2}$$
(23)

The derivation of Eq. (23) is Eq. (24).

$$\dot{v} = s\dot{s} = - sK \cdot {\text{sgn}} (s) \le 0$$
(24)

From the formula (24), it can be seen that the calculation result is always less than or equal to 0, which meets the discriminant requirements, and the system can reach stability. Therefore, the designed sliding surface is reasonable.

Calculation of braking torque of each wheel

From formula (18) to formula (22), the braking torque of each wheel can be calculated as formula (25).

$$T_{bi} = \frac{{\mu_{i} R^{2} - I\left[ {(1 - \lambda )\dot{v} - \left( {\dot{\lambda }_{d} - K{\text{sgn}} (s)} \right)v} \right]}}{R}$$
(25)

Since the design of the sliding mode structure will cause a certain chattering of the system, it is necessary to reduce the chattering of the system after the design of the sliding mode control. In this paper, the boundary layer method is used to shake the controller.

The sign function \({\text{sat}} (\frac{S}{\Omega })\) in (23) is replaced by the saturation function \(sgn(s)\), where \(\Omega\) is the boundary thickness. The saturation function is the form (26).

$$sat\left( {\frac{S}{\Omega }} \right) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {\quad S \ge \Omega } \hfill \\ {\frac{S}{\Omega }} \hfill & {\quad \left| S \right| < \Omega } \hfill \\ { - 1} \hfill & {\quad S \le - \Omega } \hfill \\ \end{array} } \right.$$
(26)

According to the above description, the braking torque is calculated as formula (27).

$$T_{bi} = \frac{{\mu_{i} R^{2} - I\left[ {\left( {1 - \lambda_{i} } \right)\dot{v}_{i} - \left( {\dot{\lambda }_{d} - K{\text{s}} at} \right)v_{i} } \right]}}{R}$$
(27)

DBR control of heavy vehicle anti-rollover lower layer

The lower control receives dynamic information from the upper control, and uses NLTR to correct the decision-making scheme of the upper control. But to really apply this controller to the actual vehicle control, we must use the corresponding hardware implementation. Therefore, this section designs a differential braking redistribution control DBR (Differential-Braking-Redistribution). The differential braking control logic is shown in Fig. 4.

Fig. 4
figure 4

Lower differential braking control strategy.

Full size image

Differential braking distribution strategy can meet the braking requirements of normal vehicles, but it is not enough to meet the braking characteristics when the right middle wheel fails. Therefore, the above-mentioned distribution strategy can be used to redistribute the braking torque, that is, when the right middle wheel needs to be braked, the corresponding braking force is added to the right rear wheel to ensure that the braking effect will not fail. At this time, the braking torque redistribution diagram is shown in Fig. 5. After the braking torque is redistributed, the braking torque of the right rear wheel is shown in Formula (28).

Fig. 5
figure 5

Redistribution diagram of braking torque.

Full size image
$$T_{brak} = T_{b4} + T_{b6}$$
(28)

In the formula (28), \({T_{brak}}\) is the braking torque of the right middle wheel, \({T_{b4}}\) and \({T_{b6}}\) are the original calculation of the right middle and right rear braking torque respectively.

Simulation verification

In order to verify the effectiveness of hierarchical control under the condition of NLTR rollover index determination, two different working conditions of J-turn and Fish-Hook are set up in TruckSim. The road surface is flat, the adhesion coefficient is set to 0.8, the influence of lateral wind is not considered, the steering wheel transmission ratio is 1/25, and the engine with rated power of 300 kW is selected. The main parameters of the vehicle are shown in Table 1 and the steering wheel angle input is shown in Fig. 6.

Table 1 Simulation parameters.
Full size table
Fig. 6
figure 6

Steering wheel angle.

Full size image

J-turn condition simulation and analysis

The comparison results of yaw rate, sideslip angle, lateral acceleration and LTR under J-turn condition are shown in Fig. 7.

Fig. 7
figure 7

J-turn simulation results.

Full size image

It can be seen from Fig. 7 that the vehicle began to turn in the second seconds, and the lateral dynamic parameters increased rapidly. At 4.5 s, no control vehicle rollover occurred. The three control strategies control the yaw rate, sideslip angle, lateral acceleration and LTR around 16.3 deg/s, 0.76 deg, 0.35 g and 0.60, which can effectively prevent vehicle rollover. The comparison effects of the three controls are shown in Table 2.

Table 2 Control effect comparison.
Full size table

As shown in Table 2, under the condition of single wheel braking failure rollover, there is no control vehicle rollover. Taking LTR control as the standard, NTTR control improves the lateral stability control effect of the vehicle by 2.8% compared with the traditional TTR control, and the instantaneous instability time is delayed by 0.19s.

Fish-Hook condition simulation and analysis

The comparison results of Yaw rat, sideslip angle, lateral acceleration and LTR under Fish-Hook simulation conditions are shown in Fig. 8.

Fig. 8
figure 8

Fish-Hook simulation results.

Full size image

It can be seen from Fig. 8 that LTR control is not suitable for Fish-Hook condition with single wheel braking failure when no control and LTR control 8 vehicles roll over. The comparison effects of the two effective controls are shown in Table 3.

Table 3 Control effect comparison.
Full size table

It can be seen from Table 3 that under Fish-Hook simulation conditions, without control of vehicle rollover, LTR control does not work. The NLTR control effect increases the lateral stability of the vehicle by 9.1% compared with RI2, and the instantaneous instability time is delayed by 0.78 s.

In summary, the hardware parts of the signal acquisition, braking system and chassis control process are in an ideal state during the simulation process. The control strategy does not consider the characteristics of braking performance changing with heat. The brake may be unstable with the increase of temperature during continuous braking. The performance parameters of the brake will directly determine the braking effect. Therefore, the control strategy can be optimized by modeling the brake based on swarm intelligence55. The NLTR index improves the vehicle stability by only 9.1% compared with the traditional RI2 index control. However, the NLTR control has a maximum delay of 0.78 s compared with the lateral instantaneous instability time of the vehicle, which provides the driver with more time to control the vehicle in the actual process. However, there is a certain time lag in the actual driving of signal acquisition and braking system, and the traditional index also has hysteresis to the change of unsprung mass state, which makes the insensitivity of the traditional index amplified, and there is a risk of braking failure. Therefore, it is necessary to further simulate the actual vehicle driving process in the hardware-in-the-loop to verify the effectiveness of NLTR control.

Hardware-in-the-loop test verification

Because there is a certain danger in the real vehicle rollover test, the HIL test is used to simulate the driving condition of the vehicle under extreme conditions. Compared with the simulation test, the HIL test has higher accuracy. The HIL test bench uses PXI as a platform to co-simulate Trucksim with Labview. The core components can realize the HIL simulation of the steering system and the braking system in the real vehicle. The HIL test is based on the DFL1250A12 test bench of Dongfeng commercial vehicle. The test platform is divided into six parts: driving simulator, braking platform, wheel speed simulator, electric control cabinet console and bench. The HIL test simulates the real vehicle driving signal into the chassis, and the braking system brakes in real time. Compared with the real vehicle signal acquisition, it is more ideal and fast, and the braking response time is more accurate. However, with the development of the EMB system, the real vehicle signal reception is also more accurate, and the system response time will also increase. Therefore, although HIL cannot completely replace the real vehicle, it simulates the braking system of the real vehicle to explore the braking effect in the braking strategy and provide the basis for the EMB control strategy. The operation process of the three-axis heavy vehicle is shown in Fig. 9.

Fig. 9
figure 9

Hardware-in-the-loop test operation flow chart.

Full size image

J-turn condition test and analysis

In order to further verify the applicability and effectiveness of the control algorithm, hardware-in-the-loop test verification is carried out. Under the J-turn condition, the control effect of the test is shown in Fig. 10.

Fig. 10
figure 10

J-turn test results.

Full size image

From Fig. 10, it can be seen that no control and RI2 control vehicles have rollover, and RI2 control is not applicable to J-turn conditions. From Fig. 10b–d, it can be seen that LTR and NLTR control stabilize the yaw rate (deg) at 15.81 and 14.92, and the NLTR control is 5.6% higher than the LTR control effect; the sideslip angle of the center of mass (deg) is stable near 0.45 and 0.81, both within stable conditions; the maximum lateral acceleration is 0.42 g and 0.38 g, and the lateral acceleration effect of NLTR control is 9.5% higher than that of RI2 control.

Fish-Hook test and analysis

Under Fish-Hook condition, the test control effect is shown in Fig. 11.

Fig. 11
figure 11

Fish-Hook test comparison.

Full size image

From Fig. 11, it can be seen that the 12 ~ 20 s vehicle completes the first steering, the 22 ~ 35 s vehicle completes the second steering, and keeps the steering angle unchanged. From Fig. 11b–d, it can be seen that no rollover occurs in the first steering process of heavy vehicles, and no rollover occurs in the second steering process of uncontrolled vehicles. Vehicles with control strategies can effectively prevent vehicle rollover. The control comparison effect is shown in Table 4.

Table 4 Control effect comparison.
Full size table

It can be seen from Table 4 that in the hardware-in-the-loop test of single-wheel braking failure Fish-Hook rollover condition, without control of vehicle rollover, RI2 control can control each lateral dynamic parameter to the minimum and the effect is the best. However, with LTR control as the standard, NLTR control can improve the lateral stability control effect of vehicle by 68.18% compared with RI2 control.

In summary, the hardware-in-the-loop test shows that the traditional RI2 control does not consider the driving state of the unsprung mass, and its response is not sensitive enough for the braking failure vehicle, resulting in the controller missing the best opening time and increasing the risk of braking failure. Considering the hysteresis of the braking system in the hardware-in-the-loop test, the sensitivity advantage of the NLTR index is amplified, and the vehicle stability is increased by 68.18% compared with the RI2 control. The results show that for heavy vehicles equipped with EMB system, with the increase of braking system response time, it is safer to use NLTR index to control vehicles. At the same time, because NLTR is more sensitive, it can release braking signal more accurately, avoid over-control during driving, and reduce energy consumption during anti-rollover process.

Conclusion

In order to improve the EMB fault tolerance and anti-rollover problem of wire-controlled heavy vehicles, a hierarchical anti-rollover control method based on NLTR index is proposed, which has certain feasibility and practicability for improving the safety of vehicles when single-wheel braking fails.

  1. a.

    Aiming at the characteristics of large unsprung mass and susceptibility to road excitation of heavy vehicles, an 18-degree-of-freedom trip dynamics model is established and a single-wheel braking failure rollover index NLTR is proposed. Compared with the traditional RI2 index, the NLTR proposed in this paper considers the motion of unsprung mass, and the response of unsprung mass is more sensitive when the vibration changes caused by braking.

  2. b.

    The effectiveness of the control strategy is verified by simulation and hardware-in-the-loop test. Aiming at the problem of anti-rollover of brake failure of wire-controlled heavy-duty vehicles, a NLTR-based road adhesion coefficient identification, SM-ABS and DBR layered anti-rollover control strategy are proposed.

  3. c.

    Simulation and HIL test show that the traditional index does not consider the driving state of unsprung mass, and there is a risk of braking failure under the limit condition of braking failure. The NLTR index has a certain sensitivity compared with RI2. When the anti-rollover control considers the braking hysteresis, its sensitivity advantage is amplified, and the lateral stability of the vehicle is increased by 68.18%.