ANN-based chaotic PRNG in the novel jerk chaotic system and its application for the image encryption via 2-D Hilbert curve

Abstract

In this paper, we introduce a category of Novel Jerk Chaotic (NJC) oscillators featuring symmetrical attractors. The proposed jerk chaotic system has three equilibrium points. We show that these equilibrium points are saddle-foci points and unstable. We have used traditional methods such as bifurcation diagrams, phase portraits, and Lyapunov exponents to analyze the dynamic properties of the proposed novel jerk chaotic system. Moreover, simulation results using Multisim, based on an appropriate electronic implementation, align with the theoretical investigations. Additionally, the NJC system is solved numerically using the Dormand Prince algorithm. Subsequently, the Jerk Chaotic System is modeled using a multilayer Feed-Forward Neural Network (FFNN), leveraging its nonlinear mapping capability. This involved utilizing 20,000 values of x₁, x₂, and x₃ for training (70%), validation (15%), and testing (15%) processes, with the target values being their iterative values. Various network structures were experimented with, and the most suitable structure was identified. Lastly, a chaos-based image encryption algorithm is introduced, incorporating scrambling technique derived from a dynamic DNA coding and an improved Hilbert curve. Experimental simulations confirm the algorithm’s efficacy in enduring numerous attacks, guaranteeing strong resiliency and robustness.

Introduction

The exploration into chaotic systems has taken a turn and expanded beyond its traditional paradigms, leading to the discovery and investigation of novel feature chaotic systems^1,2,3. These systems, characterized by their distinctive dynamical behaviors and emergent properties, have garnered significant attention because of their potential applications in numerous areas including cryptography^4,5, secured communication⁶, and nonlinear control⁷. The Feature chaotic systems exhibit a rich spectrum of behaviors, ranging from irregular dynamics to complex attractors with intricate geometries. Unlike conventional chaotic systems, feature chaotic systems often possess unique characteristics, such as multiple coexisting attractors⁸, multi-spiral chaos⁹, Symmetric strange attractors¹⁰, extreme multistability¹¹, mega-stable behavior¹², multi-transient behavior¹³, intermittent transients¹⁴, high-dimensional chaos¹⁵, or specific synchronization phenomena¹⁶. These distinctive features challenge existing theoretical frameworks and computational methodologies, necessitating innovative approaches for their analysis and understanding.

Recently, machine learning has emerged as a prominent solution for addressing a multitude of challenges in chaotic systems, particularly in prediction and categorization tasks. For instance, Omidvar¹⁷ introduces an innovative algorithm aimed at determining the structure of RBF networks for dynamic modeling of chaotic time series. Meanwhile, Han et al.¹⁸ explore a novel methodology based on RPNN for modeling and predicting chaotic time series, outperforming Kalman filter and universal learning networks compared based on accuracy and RMSE. Additionally, Chang and Tsai¹⁹ present an advanced BPNN model specifically designed for analyzing signal deviation time series in the stock market, surpassing traditional approaches like ARMA and RBFNN, as evidenced by reduced MAD values. Using robust location estimates and neural networks, Chatzinakos and Tsouros²⁰ propose a novel algorithm for estimating chaotic dynamical systems’ dimension, while Wichard²¹ develops a machine learning technique hybridizing three models namely the artificial neural network, 1-year-cycle, and the nearest trajectory, for NN5 time series forecasting. Furthermore, He et al.²² introduce a novel CBP neural network procedure, leveraging the advantages of the Chebyshev map to mitigate premature convergence issues. Despite these advancements, accurately reproducing signals and diagrams remains challenging due to the highly complex and nonlinear dynamics involved. Thus, we leverage the capability of ANN to learn the intricate nonlinear dynamics of this system.

The advancement of chaotic encryption algorithms has witnessed significant theoretical strides, with researchers discovering relationship between the degree of randomness exhibited by chaotic orders to the efficacy of encryption algorithm. Based on coupled TSM and coupled LTM, Luo et al.²³ devised a fresh encryption framework incorporating permutation-EC-ElGamal encryption-diffusion, introducing a crossover permutation approach. Wang et al.²⁴ defined an innovative color image encryption system utilizing a hyper-chaotic scheme built upon a tri-valued memristor. The generation of initial key makes use of the plaintext image, by incorporating a permutation sequence structured with a Hash table. Murali and Sankaradass²⁵ proposed a straightforward and rapid image encryption method based on SFC, introducing a novel saw-tooth diffusion and square-wave confusion techniques for encrypting swift image. Shahna and Mohamed²⁶ proposed a fresh symmetric key encrypting method employing cyclic shift operation, scan method, chaotic map, utilizing Hilbert curve and Henon map. Moysis et al.²⁷ introduced a new B-spline encryption algorithm and analyzed mappings utilizing multiple remainder operators. Lai et al.²⁸ investigated a novel medical image encryption scheme that leverages compressive sensing techniques based on a newly designed memristive hyperchaotic system and introduces a new HNN that utilizes a memristor designed with hyperbolic tangent functions as a synapse, enabling the generation of multiscroll attractors²⁹. Acknowledging the challenges in fractal-based encryption methods, particularly regarding time consumption and encryption restrictions, we introduce a novel algorithm for image encryption utilizing Hilbert curve scrambling and dynamic DNA coding to enhance efficiency in encryption.

Many studies related to chaotic systems are applied using jerk systems such as Chen et al.³⁰ presented a novel four-dimensional chaotic jerk system characterized by coexisting and hidden attractors, with only one constant term. The system was implemented on FPGA to facilitate the discretization and simulation of chaotic behavior. Folifack Signing et al.³¹ proposed a cryptosystem for encrypting both text and images, leveraging the special randomness of a chaotic Jerk system with a hump structure and DNA coding. Vivekanandhan et al.³² investigated chaotic jerk oscillator with non-polynomial and piecewise linear terms to shape attractors and its application in the image encryption.

Based on the motivation above, we introduced and analyzed a new category of chaotic oscillators termed NJC oscillators, distinguished by their symmetrical attractors using dynamical analysis. Furthermore, we illustrate the NJC system’s capability to exhibit chaotic behavior, irregular and regular reverse period-doubling phenomena, periodic behavior, and coexisting attractors. Besides that, the NJC System is modeled using a multilayer FFNN, leveraging its nonlinear mapping capability and identifies the most suitable FFNN architecture for modeling the NJC system accurately. Finally, the paper presented an image encryption scheme that integrates the NJC system, incorporating dynamic DNA coding and improved Hilbert curve scrambling.

Mathematical model of the proposed NJC system

This work proposed a novel NJC system defined as the follows:

$$\left\{ \begin{gathered} {{\dot {x}}_1}={x_2} \hfill \\ {{\dot {x}}_2}=a{x_3} \hfill \\ {{\dot {x}}_3}={x_1} - b{x_2} - c{x_3} - |{x_1}|\sinh ({x_1}) \hfill \\ \end{gathered} \right.$$

(1)

We assume that X denotes the state $({x}_{1},{x}_{2},{x}_{3})$ and $a,b,c$ are positive constants.

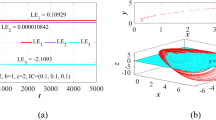
The NJC system (1) exhibits rotation symmetry centered around the ${x}_{3}$ coordinate axis. In this study, we showed that (1) is chaotic for $a=4, b=0.72$ and c = 0.48, with ${x}_{1}\left(0\right)=0.1,$${x}_{2}\left(0\right)=0.1$ and ${x}_{3}\left(0\right)=0.2$ as the initial conditions. The Lyapunov exponents (LE) of the NJC formula (1) for these initial and parameter values were computed via MATLAB with ${L}_{1}=0.1866,$${L}_{2}=0$ and ${L}_{3}$=$-0.6666.$ Thus, the NJC scheme (1) has dissipative motion with a chaotic attractor. The chaotic NJC system (1) has the Kaplan dimension given by

$${D_K}=2+\frac{{{L_1}+{L_2}}}{{|{L_3}|}}=2.2799.$$

(2)

Next, the rest points correspond to NJC system (1) are acquired in the chaotic case by arranging the values for $a=4, b=0.72$ and c = 0.48, and thus solving the equations below:

$${x}_{2}=0$$

(3a)

$$a{x}_{3}=0$$

(3b)

$${x}_{1}-b{x}_{2}-c{x}_{3}-\left|{x}_{1}\right|\text{sinh}\left({x}_{1}\right)=0$$

(3c)

Solving the equations (3a) and (3b), we get ${x}_{2}={x}_{3}=0.$ Then Eq. (3c) reduces to

$${x}_{1}-\left|{x}_{1}\right|\text{sinh}\left({x}_{1}\right)=0.$$

(4)

Solving (4) we get three roots as follows: ${x}_{1}=0$ or ${x}_{1}=\pm 0.8814.$

Thus, the proposed NJC system (1) has three rest points given by ${A}_{0}=\left(\text{0,0},0\right),$${A}_{1}=(\text{0.8874,0},0)$ and ${A}_{2}=\left(-\text{0.8874,0},0\right).$

The linearization matrix’s eigenvalues for NJC scheme (1) at ${A}_{0}$ in the chaotic case are given by $0.6705, -0.5753\pm 1.0773 i,$ demonstrating that ${A}_{0}$ unstable and a saddle-focus rest point.

Meanwhile, at ${A}_{1}$ and ${A}_{2}$, the linearization matrix’s the eigenvalues of (1) in the chaotic case are given by $-1.0104, 0.2652\pm 1.0888 i,$ demonstrating that ${A}_{1}$ and ${A}_{2}$are also saddle-foci rest points and unstable.

Since the rest points of the proposed NJC scheme (1) are unstable, in the chaotic case the system (1) is said to have a self-excited attractor.

MATLAB signal plots for the NJC system (1) is shown in Fig. 1 with values of the parameter defined as $a=4, b=0.72, c=0.48$ and the initial state ${x}_{3}\left(0\right)=0.2, {x}_{2}\left(0\right)=0.1,$ and ${x}_{1}\left(0\right)=0.1$.

Fig. 1

Phase plots for NJC system (1): (a) ${x_1} - {x_2}$ chaotic attractor, (b) ${x_1} - {x_3}$ chaotic attractor and (c) ${x_2} - {x_3}$ chaotic attractor

Dynamical analysis

Fix b = 0.78, c = 0.48, and vary a

To determine the sensitivity behavior of proposed NJC system (1) to changes in parameter a, the LEs spectrum and the bifurcation figure are depicted in Fig. 2 with a increases from 4 to 20. By studying these two diagrams, we noted that the NJC system (1) can display a variety of behaviors dependent on the value of a. When a increases, the system (1) can display chaos, no-regular reverse period-doubling, and periodic behavior.

Fig. 2

(a) Bifurcation plot and (b) Lyapunov exponents of proposed NJC scheme (1) for a$\in$^4,20, b = 0.72, and c = 0.48.

When a$\in$[4, 9.8], the new 3-D Jerk scheme (1) exhibits the ownership of one positive LE (refer to Fig. 2b). For this interval of parameter a, (1) exhibits chaotic behavior as demonstrated in Fig. 2a. In order to show an example of the chaotic attractors generated by NJC system (1) when a$\in$[4, 9.8], we select a value from this interval and set it to a as follow: a = 6. Then, the x₁-x₂ chaotic attractor of NJC system (1) is plotted for a = 6 as illustrated in Fig. 4a, the connecting LEs and D_KY are:

• LE₁ = 0.146, LE₂ = 0 and LE₃=-0.624.

• D_KY=2.234.

When a$\in$[9.8, 20], the NJC system (1) experience the well-known dynamical feature of reversal period doubling cascade (RPDC) exiting from chaos. As shown in Fig. 2(a), system (1) shows a no-regular period doubling route described as follow (chaos ◊ period-10 ◊ period-5 ◊ period-3 ◊ period-2 ◊ period-1). A detailed description is given as follows:

When a$\in$[4, 9.8], system (1) displays chaotic behavior as shown in Fig. 3(a). When a$\in$[9.80, 9.94], system (1) generates period-10 attractor as shown in Fig. 3(b) which is plotted for a = 9.84. When a$\in$[9.94, 10.45], system (1) generates period-5 attractor as shown in Fig. 3(c) which is plotted for a = 10.35. When a$\in$[10.45, 12.01], system (1) generates period-3 attractor as shown in Fig. 3(d) which is plotted for a = 11. When a$\in$[12.01, 15.1], system (1) generates period-2 attractor as shown in Fig. 3(e) which is plotted for a = 13. When a$\in$[15.1, 20], system (1) displays period-1 attractor as shown in Fig. 3(f) which is plotted for a = 17.

Fig. 3

Phase portraits of the NJC scheme (1) for various a. (a) x₁-x₂ chaotic attractor (a = 6), (b) x₁-x₂ period-10 attractor (a = 79.84), (c) x₁-x₂ period-5 attractor (a = 10.35), (d) x₁-x₂ period-3 attractor (a = 11), (e) x₁-x₂ period-2 attractor (a = 13), and (f) x₁-x₂ period-1 attractor (a = 17).

Fix a = 4, c = 0.48, and vary b

To explore the behavior of proposed NJC scheme (1) against changes in parameter values of b, the LEs spectrum and the bifurcation plot are illustrated in Fig. 4 with b increasing from 0.7 to 1.2. By analysing these diagrams, we noted that, the NJC system (1) can display chaos, no-regular reverse period-doubling, and periodic behavior depending on the value of b.

When b$\in$([0.700, 0.810], [0.817, 0.858], [0.905, 0.920], [0.944, 0.950]), the NJC system (1) exhibits the ownership of one positive LE (refer to Fig. 4(b)). For this set of intervals, (1) exhibits chaotic behavior as demonstrated in Fig. 4(a). As example, we take b = 0.75. Then, the x₁-x₃ chaotic attractors for (1) is plotted as in Fig. 5(a), the corresponding LEs and D_KY are:

Fig. 4

(a) Bifurcation graph, and (b) Lyapunov exponent of (1) for a = 4, b$\in$[0.7, 1.2], and c = 0.48.

Fig. 5

Phase portraits of (1) for different b. (a) x₁-x₃ chaotic attractor (b = 0.75), (b) x₁-x₃ period-10 attractor (b = 0.924), (c) x₁-x₃ period-5 attractor (b = 0.94), (d) x₁-x₃ period-3 attractor (b = 0.98), (e) x₁-x₃ period-2 attractor (b = 1.02), and (f) x₁-x₃ period-1 attractor (b = 1.14).

• LE₁ = 0.237, LE₂ = 0 and LE₃=-0.717.

• D_KY=2.331.

When b$\in$([0.810, 0.817], [0.858, 0.905], [0.920, 0.944], [0.950, 1.200]), the NJC system (1) exhibits no ownership of positive LE (refer to Fig. 3(b)). Hence, the system is said to behave periodically for these regions of parameter b. Moreover, the NJC system (1) experiences the well-known dynamical feature of RPDC exiting from chaos. As shown in Fig. 3(a), system (1) shows a no-regular period doubling route described as follow (chaos ◊ period-10 ◊ period-5 ◊ period-3 ◊ period-2 ◊ period-1). A detailed description is given as follows:

When b$\in$[0.92, 0.93], system (1) generates period-10 attractor as depicted by Fig. 5(b) which is plotted for b = 0.924. When b$\in$[0.93, 0.96], system (1) generates period-5 attractor as shown in Fig. 5(c) which is plotted for b = 0.94. When b$\in$[0.96, 0.99], system (1) generates period-3 attractor as shown in Fig. 5(d) which is plotted for b = 0.98. When b$\in$[0.99, 1.06], system (1) generates period-2 attractor as shown in Fig. 5(e) which is plotted for b = 1.02. When b$\in$[1.06, 1.2], system (1) displays period-1 attractor as shown in Fig. 5(f) which is plotted for b = 1.14.

Fix a = 4, b = 0.72, and vary c

The sensitivity behavior of the NJC system (1) to the changes in parameter c will be studied in this subsection. For that reason, the LEs spectrum and the bifurcation plot are illustrated in Fig. 6 with c increasing from 0.45 to 1.2. By examining these two diagrams, we deduced that the NJC system (1) can display chaos, regular RPDC exiting from chaos, and periodic behavior depending on the value of c.

Fig. 6

(a) Bifurcation plot and (b) Lyapunov exponent of the proposed scheme (1) with a = 4, b = 0.72, and c$\in$[0.45, 1.2].

When c$\in$([0.450, 0.535], [0.550, 0.690], [0.696, 0.720], [0.733, 0.955]), the NJC system (1) exhibits the ownership of one positive LE (refer to Fig. 6(b)). For these regions of parameter c, (1) exhibits chaotic behavior as demonstrated in Fig. 6(a).

We take c = 0.5. Then, the x₂-x₃ chaotic attractor of system (1) is plotted in Fig. 7(a), the corresponding LEs and D_KY are:

Fig. 7

Phase portraits of (1) for different values of c. (a) x₂-x₃ chaotic attractor (c = 0.5), (b) x₂-x₃ period-8 attractor (c = 0.958), (c) x₂-x₃ period-4 attractor (c = 0.965), (d) x₂-x₃ period-2 attractor (c = 1), and (e) x₂-x₃ period-1 attractor (c = 1.14).

• LE₁ = 0.202, LE₂ = 0 and LE₃ = - 0.701.

• D_KY=2.288.

When c$\in$([0.535, 0.550], [0.690, 0.696], [0.720, 0.733], [0.955, 1.200]), the NJC system (1) exhibits no ownership of positive LE (refer to Fig. 6(b)). Hence, it is said to behave periodically for this set of intervals. Moreover, system (1) experiences the well-known dynamical feature of RPDC exiting from chaos. As shown in Fig. 6(a), the proposed scheme (1) shows a regular period doubling route described as follow (chaos ◊ period-8 ◊ period-4 ◊ period-2 ◊ period-1). A detailed description is given as follows:

When c$\in$[0.955, 0.960], system (1) has period-8 attractor as shown in Fig. 7(b) which is plotted for c = 0.958. When c$\in$[0.96, 0.98], system (1) has period-4 attractor as shown in Fig. 7(c) which is plotted for c = 0.965. When c$\in$[0.98, 1.08], system (1) has period-2 attractor as shown in Fig. 7(d) which is plotted for c = 1. Finally, when c$\in$[1.08, 1.2], system (1) has period-1 attractor as shown in Fig. 7(e) which is plotted for c = 1.14.

Multistability and coexisting attractors

In nonlinear dynamics, the study on multistability has recently gained a lot of attention due to its importance. A multistable chaotic system can produce different coexisting attractors while maintaining constant values of parameters but varying initial conditions^33,34,35. Therefore, multistable chaotic systems provides a significant number of choices for the building chaos-based real-world applications. To show that our proposed Jerk system (1) experiences the phenomenon of multistability, we plotted the bifurcation graph of proposed scheme (1) against parameter c for two types of initial points.

For the new Jerk scheme (1), let’s define Y₀ and Z₀ as the two distinct initial points with their values given as:

$${{\text{Y}}_0}={\text{ }}\left( {0.{\text{1}},{\text{ }}0.{\text{1}},{\text{ }}0.{\text{2}}} \right) \quad \left( {{\text{Blue color}}} \right)$$

$${{\text{Z}}_0}={\text{ }}\left( {0.{\text{1}},{\text{ }}0.{\text{1}},{\text{ }} - 0.{\text{2}}} \right){\text{ }}\left( {{\text{Red color}}} \right)$$

The bifurcation plot of (1) for Y₀ and Z₀ is illustrated in Fig. 8 when c$\in$[0.45, 1.2]. The blue one is started from the initial point Y₀ and the red one is started from Z₀. From Fig. 8, we can observe that: when c$\in$[0.45, 0.75], the scheme (1) has almost the same chaotic attractor for both Y₀ and Z₀ as clearly shown in Fig. 9(a). When c$\in$[0.760, 0.955], (1) has coexistance of two distinct chaotic attractors instituting from Y₀ and Z₀ as clearly shown in Fig. 9(b). When c$\in$[0.955, 0.960], system (1) has coexistance of two period-8 attractors as shown in Fig. 9(c). When c$\in$[0.96, 0.98], system (1) has coexistance of two period-4 attractors as shown in Fig. 9(d). When c$\in$[0.98, 1.08], (1) has coexistance of two period-2 attractors as shown in Fig. 9(e). Finally, when c$\in$[1.08, 1.2], (1) has coexistance of two period-1 attractors as shown in Fig. 9(f).

Fig. 8

Bifurcation plot of (1) with a = 4, b = 0.78 and c$\in$ [0.45, 1.2] for Y₀ (Blue color) and Z₀ (Red color).

Fig. 9

Numerical phase plots of different coexisting attractors of scheme (1) in the x₁-x₂ plane: (a) chaotic attractors (c = 0.5), (b) two coexisting chaotic attractors (c = 0.85), (c) coexistance of two period-8 attractors (c = 0.958), (d) coexistance of two period-4 attractors (c = 0.965), (e) coexistance of two period-2 attractors (c = 1), (f) coexistance of two period-1 attractors (c = 1.14).

Circuit design

In this work, the system’s circuit is built utilizing Multisim 14.0, a circuit simulation software, to confirm the accuracy and viability of the scheme. Figure 10 displays the circuit schematic of proposed NJC scheme (1). The TL082CD operational amplifier is employed for circuit integration during simulation, while linear resistor and capacitor regulate system parameters. Additionally, the analog multiplier AD633JN, operating at a voltage range of ± 15 V, is utilized to introduce nonlinear terms. The equation of circuit for (1) can be derived from Kirchhoff’s circuit laws.

$$\left\{ \begin{gathered} {C_1}{{\dot {x}}_1}=\frac{1}{{{R_1}}}{x_2} \hfill \\ {C_2}{{\dot {x}}_2}=\frac{1}{{{R_2}}}{x_3} \hfill \\ {C_3}{{\dot {x}}_3}=\frac{1}{{{R_3}}}{x_1} - \frac{1}{{{R_4}}}{x_2} - \frac{1}{{{R_5}}}{x_3} - \frac{1}{{{R_6}}}|{x_1}|\sinh ({x_1}) \hfill \\ \end{gathered} \right.$$

(5)

Fig. 10

Circuit electronic of the novel Jerk system.

The electronic component depicted in Fig. 10 takes the following values: R1 = R3 = 400 kΩ, R4 = 555.56 kΩ, R5 = 833.33 kΩ, R6 = 40 kΩ, R17 = R16 = R15 = R14 = R13 = R12 = R11 = R10 = R9 = R8 = R7 = R2 = 100 kΩ, C1 = C2 = C3 = 1 nF. In Fig. 10, the circuit designed is the multi-wing chaotic circuit. The chaotic circuit evidently produces chaotic attractors (see Fig. 11), thereby confirming the preceding theoretical analysis and numerical simulation outcomes.

Fig. 11

Multisim output simulation: (a) ${x_1}-{x_2}$ chaotic attractor, (b) ${x_1}-{x_3}$ chaotic attractor and (c) ${x_2}-{x_3}$ chaotic attractor

ANN-based new jerk chaotic (NJC) PRNG on FPGA

The main important features of chaotic systems are that they exhibit non-periodic behavior, that they are sensitive to initial conditions, that they exhibit non-periodic behavior in the system state space, and that they are extremely sensitive to changes in system parameters³⁶. Chaotic signal generators, one of the most basic structures that should be used in chaotic systems, can be realized in two different ways: analog and digital. It is well-known that digital circuit-based chaotic generators are generally more advantageous than analog-structured chaotic generators. The best solution for these problems is to implement chaotic generators using digital hardware.

Digital circuit based chaotic generators can be implemented with different integrated structures in literature such as Digital Signal Processors (DSPs), Application Specific Integrated Circuits (ASICs) and Field Programmable Gate Arrays (FPGAs)³⁷. FPGA chips have a very flexible structure, as well as being able to perform parallel processing. In addition, the design and testing costs of FPGA chips are much lower than ASIC-based applications. Another important point is that FPGA-based chaotic systems and the applications using these systems are more flexible thanks to their digital base and reprogrammability. Chaotic circuit models are suitable for implementation in reprogrammable or reconfigurable systems. In this way, chaotic systems can produce signals in different forms according to parameter changes. For such reasons, FPGA-based modeling of chaotic systems provides significant advantages over analog-based or other digital processor-based chaotic generators^{37,38,39,40,41}.

Similar to the nonlinear structure of chaotic systems, an Artificial Intelligence (AI) scheme commonly referred to as Artificial Neural Network (ANN) has been known to be able to detect the nonlinearity properties in the formation of real-world problems, using its adaptive abilities and changing its own weights and biases according to the available data. Biologically inspired ANNs are distributed information processing systems and consist of massively parallel nonlinear computations. Therefore, we can exploit this sophistication for high-speed operations of real-time applications via the implementation of parallel hardware structure³⁶.

Since FPGA chips are inherently parallel devices, they are very suitable for hardware applications of ANN. FPGA-based ANN applications not only maintain the parallel structure of the network and enable working but also provide flexible, reconfigurable designs that are suitable for hardware implementation³⁷. At this point, ANNs are used in modeling systems thanks to their ability to map complex nonlinear relationships, error tolerance and handle noisy data.

Modeling chaotic systems with noise-like nonlinear properties using ANN has made it possible to use these modeled systems in cryptologic applications including secure communication, digital signature and embedded systems that today’s technology requires. In recent years, chaotic oscillator and chaotic-based random number generator designs using artificial neural networks (ANN) on FPGA have been published in the literature^38,39,40,41.

Random numbers are used for specific purposes in many different disciplines of engineering. The success of these applications relies upon the generated sequence randomness, and therefore the process of generating these numbers is of primary importance. Random numbers are defined as a series of independent numbers having a predefined distribution and a determined probability of falling on values within a particular range is referred to as random numbers³⁹. These generators are structures that have the capacity to generate output at a degree of unpredictability that is not predictable from historical data. Due to these features, many applications such that found in cryptography, equation solutions, numerical analysis, music and graphic composition, simulation, modeling and testing, digital signatures and secure communication making use of random number generators^42,43.

In this study, the New Jerk Chaotic (NJC) system has been computationally solved via Dormand Prince technique. Input and output values consist of 10,000 samples generated with the technique. Then, for the process of the modelling the New Jerk Chaotic (NJC) system, since Feed-Forward Neural Network (FFNN) provides a general prediction method and having one hidden layer is sufficient in many cases, this FFNN structure having one hidden layer has been chosen. The network structure and its parameters are presented in Fig. 12; Table 1, respectively.

Fig. 12

The network structure used in the modeling of the NJC system.

As can be observed from Fig. 12, the modeling of NJC system has been performed using 3 × 8 × 3 FFNN structure. In order to gain nonlinearity to model the New Jerk Chaotic system, 8 neurons, each containing a Log-Sigmoid activation function, were used in the hidden layer of the network structure and 3 neurons, each containing a linear activation function, were used for the output layer. In this step, 10,000 values of x₁, x₂ and x₃ have been applied to the input of the FFNN structure for the train (70%), validate (15%) and test (15%) processes. Therefore, there are 3 neurons in the input layer. The target for x₁, x₂ and x₃ values are the iterative values of x₁, x₂ and x₃. So, there are 3 neurons in the output layer.

Since the number of neurons in hidden layer depends on the system to be modeled, various structures with different numbers of hidden neurons were tried, and several trainings were performed. There is one hidden layer with 8 neurons and an output layer with 3 neurons. MSE value has been obtained as 7.28e-08; the sensitivity with this level is enough for the modeling of NJC system using FFNN structure and the implementation of this structure on FPGA. On the one hand, using more than 8 neurons in hidden layer is possible and this gives more accurate results. On the other hand, this creates more computational cost, more resource utilization needs for the FPGA implementation and increases the response time of the network. In other words, there is a tradeoff between the modeling performance and computational performance and this is a challenging problem to be handled for the FPGA implementation of FFNN structures.

Table 1 The resulting parameters obtained from the modeling of the NJC system.

The network has been trained several times using different initial weights and biases. After 200,000 iterations, the outputs of the network model have been converged to the target values, with the precision of 1.6e-09 as shown in Fig. 13. An important tool for evaluating the network performance is the scatter plot of network outputs versus targets. As can be observed from Fig. 13, the points in the scatter plot fell close to the 45° output = target line. For this reason, the fit is almost excellent.

Fig. 13

Scatter plot of FFNN model outputs vs. targets.

Figure 14 depicts the MSE against the number of iterations, with using the Levenberg-Marquardt training algorithm. MSE is an accepted measure of the performance index generally utilized in FFNN. The network has been trained for 200,000 iterations; at which time the performance changing has been very little as 7.28e-08. This value shows the network model can accurately map the input-output relationship.

Fig. 14

The performance plot of FFNN model.

As mentioned above, in the hidden layer, the size of neurons that has exponential activation function directly affects the chip utilization statistics of the implementation of FPGA. For this reason, not only to model the NJC system using FFNN but also to implement this model is an important trade-off that should be handled. Since the performance of the training network gives a satisfactory degree as 7.28e-08 using minimum number of neurons in hidden layer and the existence of 8 neurons in hidden layer does not create a problem related to the response time and resource utilization, as a result, implementation of FFNN structure on FPGA is continued with this selected structure.

After the successful results obtained from the training and testing stages in the process of developing the ANN-based chaotic model from the new 3-D Jerk system on FPGA, the real-time ANN-based NJC PRNG model stage on FPGA initiated. In this stage, to realize the PRNG design with the novel 3-D Jerk chaotic scheme on FPGA hardware, ANN-based NJC PRNG are modelled in VHDL via the high-precision floating point number standard (32-bit IEEE-754-1985). The top-level view of the proposed block diagram is given by Fig. 15. The module includes 1-bit input signals namely clk, start and reset, and 1-bit PRNG_out and Ready output signals.

Fig. 15

The top-level block design of ANN-based NJC PRNG design on FPGA.

Figure 16 illustrates the second top level block plot of the ANN-based NJC PRNG scheme implemented on FPGA. The design includes MUX, ANN_Based_Chaotic_Oscillator, Quantification, XOR_Unit and Ring_Osc units. The MUX unit is accounted for providing initial requirements needed by the chaotic oscillator. The chaotic oscillator takes the initial values as constant until it produces its first results. From the moment the oscillator starts to produce the first values, this value is sent to the MUX unit, and the MUX unit sends this value to the chaotic oscillator as an initial condition. ANN-based chaotic oscillator unit is designed for modeling chaotic system. The chaotic signals produced here are sent to the Quantification unit and discretized. In the design, a ring oscillator was used to increase the randomness quality of the ANN-based NJC PRNG system. Random values coming from Quantification and Ring oscillator are subjected to XOR operation in the XOR unit and transmit to the PRNG_out output. At this moment, the PRNG_Ready output is ‘1’.

Fig. 16

The second level block diagram of ANN-based NJC PRNG design on FPGA.

A testbench was designed in VHDL to test the ANN-based NJC PRNG unit on the designed FPGA. The designed system was tested by running it with ISIM which is one of the Xilinx ISE Design Tools. The graph of testbench results is displayed in Fig. 17.

Fig. 17

The simulation findings of ANN-based NJC PRNG design on FPGA.

To assess the quality of randomness for the Random Number Generators (RNG) produced bit sequences, NIST 800-22 Statistical Test Set is preferred over other test packages. Therefore, in order to prove the random numbers produced by the PRNG design presented in this study is suitable to be used in cryptographic applications, the obtained bit sequences must pass a list of tests specified in the international guidelines found in the NIST 800-22 Test Suite. This statistical suite comprises fifteen tests designed to evaluate the unpredictability of binary sequences produced by cryptographic random or PRNG that are based on hardware or software. These tests concentrate on diverse forms of non-randomness that could be present in a series, and certain tests can be divided into multiple smaller tests. Performing NIST Tests would require bitstreams of 1 Mbit length. Subsequently after succeeding with the PRNG employing ANN-based chaotic oscillator, VHDL codes was generated for testing the output sequence according to NIST Test cases.

Table 2 The NIST test results for ANN-based NJC PRNG design on FPGA.

Xilinx ISE design tool was responsible for compiling the code while the random bit sequences generated from the simulated FPGA-based design were stored in a .txt format. When testing with more than one subtest, the p value was evaluated as the arithmetic mean. The test results for the proposed ANN-based NJC PRNG are presented in Table 2. Based on the Random-Excursions Test, 18 results were produced for the x value in the PRNG modelled with the chaotic entropy seeds, and only one test result was given in the table, while another 17 met the test criteria. The results for the other 15 different tests from the NIST 800-22 Test Suite were recorded by focusing to the p values (probability values). The fact that the $p$ values $(p>0.01)$ from all tests proved that the generated bits sequence has shown excellent statistical properties.

The ANN-based NJC PRNG unit designed on Virtex-6 ML605 FPGA Evaluation Platform (device: XC6VLX240T, package: FF1156, speed: − 1) was synthesized with Xilinx ISE Design Tools. The chip resource utilization rates acquired after the Place & Route procedure are shown in Table 3. According to the results, the operating frequency maximum value of the proposed unit was found to be 114.903 MHz. In the design, since a random 1-bit value can be generated at each clock cycle, the designed systems’ bit generation rate was obtained as 114.9 Mbit/s.

Table 3 Resource utilization for ANN-based NJC PRNG design on FPGA.

Image encryption using 2-D Hilbert curve

This section deals with the implementation of the proposed 3D chaotic system to support image encryption. To verify the feasibility and effectiveness of this method, we selected five the standard grey-scale images (Moon surface, finger, hill, Boat, and Pepper) with a size of 256 × 256 from the image database http://sipi.usc.edu/database/. There are two categories of the encrypting algorithms: diffusion and permutation, and the image is encrypted according to the structure “permutation-diffusion-permutation-diffusion”. The design of the defined image encryption procedure is illustrated in Fig. 18.

Fig. 18

Architecture of image encryption.

The proposed image encryption algorithm

Key generation

The use of adaptive keys can significantly improve the security of encrypted images by increasing their resistance to attacks based on plaintext. The values for initial condition and other parameters of the chaos mapping are constructed from the hash value from the plaintext image.

A minor change in the plaintext image will tremendously change the hash value, and likewise significantly affecting the parameters and initial guesses of the chaotic scheme. The SHA-256 procedure is used to generate the 256 bits hash H by taking the plaintext image as an input. The 3D chaotic system transforms H into the initial values by byte-dividing into 32, denoted as h₁, h₂, …, h₃₂.

Initial guesses x₁(0), x₂(0), and x₃(0) needed by the 3D chaotic system need to be calculated upfront. We can use Eq. (6) to achieve this purpose.

$$\left\{\begin{array}{c}{x}_{1}\left(0\right)=\frac{1}{256*5*10}(\left({h}_{1}\oplus {h}_{2}\oplus {h}_{3}\oplus {h}_{4}\right)+{h}_{5}+{h}_{6}+{h}_{7}+{h}_{8})+{x}_{1}^{{\prime }}\left(0\right) \\ {x}_{2}\left(0\right)=\frac{1}{256*5*10}\left(\left({h}_{9}\oplus {h}_{10}\oplus {h}_{11}\oplus {h}_{12}\right)+{h}_{13}+{h}_{14}+{h}_{15}+{h}_{16}\right)+{x}_{2}^{{\prime }}\left(0\right)\\ {x}_{3}\left(0\right)=\frac{1}{256*5*10}\left(\left({h}_{17}\oplus {h}_{18}\oplus {h}_{19}\oplus {h}_{20}\right)+{h}_{21}+{h}_{22}+{h}_{23}+{h}_{24}\right)+{x}_{3}^{{\prime }}\left(0\right)\end{array} \right.$$

(6)

where ${x}_{1}^{{\prime }}$(0), ${x}_{2}^{{\prime }}\left(0\right)$, and ${x}_{3}^{{\prime }}\left(0\right)$ denotes the given values. The initial guesses produced by this technique have the benefits of randomness. Using these values, the 3D chaotic system can operate to generate three pseudo-random sequences, that are LX (Lx₁), LY(Lx₂), and LZ(Lx₃).

Image permutation

The permutation method of information encryption involves rearranging the image pixel matrix in order to break the image matrix’s correlation. In this process, image transmission in a safe manner can be accomplished. In this paper, we use a combination of global permutation and local permutation to achieve the purpose of permutation.

Global permutation

Given a pseudo-random sequence LX, we proceed by sorting the sequence into an ascending order to produce another new sequence X and a permuted index sequence Index, and use the index sequence index as a scrambled vector to permute the image.

Local permutation

In 1891, the German mathematician Hilbert gave the Hilbert curve to fill a square grid, using this continuous curve to traverse every node. Figure 19 demonstrate a route of a Hilbert curve through the grid. The basic idea of applying the two-dimensional Hilbert curve to image scrambling is to scan the pixels of an image matrix in turn according to the traversal rules of the two-dimensional Hilbert curve, store them in a one-dimensional sequence, and then rearrange them to generate the scrambled image.

Fig. 19

2-D Hilbert curve.

Pixel diffusion

Diffusion enhances the mutual influence between pixels, so that small changes in the plaintext can be diffused into the entire ciphertext, enhancing the algorithm’s ability to resist differential and statistical attacks. This paper uses the generated chaotic sequence and the previous pixel value to calculate according to the formula, and the calculated value is used as the current pixel value, which can effectively propagate the changes of a small amount of plaintext image to the entire encrypted image. According to Eq. (7), each element of the pseudo-random sequence LY and LZ sequence is preprocessed respectively.

$$\left\{\begin{array}{c}{ly}_{i}^{{\prime }}=mod\left(floor\left({10}^{14}\times {ly}_{i}\right),256\right)\\ {lz}_{i}^{{\prime }}=mod\left(floor\left({10}^{14}\times {lz}_{i}\right),256\right)\end{array}\right.$$

(7)

The image matrix is converted into a one-dimensional sequence S = {s₁, s₂, s₃ ,… s_M×N } of length M × N in row-first order, and the image matrix after forward diffusion is noted as C = {c₁, c₂, c₃ ,… c_M×N }, and the matrix after backward diffusion is noted as D = {d₁, d₂, d₃ ,… d_M×N }. The forward diffusion process is shown in Eq. (8).

$${{c}_{i}={s}_{i}\oplus {c}_{i-1}\oplus ly}_{i}^{{\prime }}$$

(8)

where the initial value c(0) = 127, and i = 1, 2, …, M*N. Meanwhile, the backward diffusion process is shown in Eq. (9).

$${{d}_{i}={c}_{i}\oplus {d}_{i+1}\oplus lz}_{i}^{{\prime }}$$

(9)

where the initial value d(M + N + 1) = 127, and i = M*N, …,2, 1.

The proposed algorithm

The steps of the encryption scheme proposed in this paper are as follows.

Step 1: Convert the grey-scale image matrix P into a two-dimensional matrix P₁of size M*N.

Step 2: Based on the given plaintext image, use the SHA-256 algorithm to obtain its hash value and calculate the initial values x₀, y₀, z₀.

Step 3: Iterate over the proposed 3D chaotic system, eliminate a designated number of iterations to minimize transient effects, and obtain the three sequences LX, LY, and LZ, each with length M*N.

Step 4: Reconstruct the image matrix P₁ into a one-dimensional sequence, sort in ascending order the sequence LX to produce the index sequence, which later be used to permute position-wise the pixel from the image sequence to obtain a scrambled image sequence P₂.

Step 5: Preprocess LY(Eq. (7)) and perform the forward diffusion operation on the image sequence P₂ (Eq. (8)), converting the diffused pixel sequence into an image matrix of M*N according to the length M as a row, which is the image matrix P₃.

Step 6: Local permutate of the image matrix P₃ using a Hilbert curve to produce a new image matrix P₄.

Step 7: Preprocess LZ(Eq. (7)), backward diffused the image (Eq. (9)), transform the diffused pixel sequence into an M*N image matrix according to the length M as a row, the image matrix is named P₅, correspond to cipher image.

Experimental results and analysis

To test our proposed image encryption algorithm, the standard grey-scale images Moon surface, finger, hill, Boat, and Pepper of size 256*256 are selected as plain images and the following initial values ${x}_{0}^{{\prime }}=0.1, {y}_{0}^{{\prime }}=0.1, {z}_{0}^{{\prime }}=0.2$ are chosen. Figure 20 shows the simulation results. It is clearly observable the capability of cipher image to hide the plaintext and render the information to unrecognizable. The decrypted image is identical to the plain image, which shows that the algorithm of this paper has good encryption and decryption effects. The effectiveness and security of the encryption algorithm are further demonstrated through histogram, information entropy, and correlation analyses.

Fig. 20

Source http://sipi.usc.edu/database/

Experimental result of encryption and decryption images. (a) Plain images, (b) cipher images, (c) decrypted images.

Keyspace analysis

The key space is the range in which the encryption key can be selected in size and is generally measured in bits. The encryption scheme proposed uses a 3D chaotic system having a large parameter space and therefore a large key space can be obtained. The algorithm is considered to be effective against exhaustive attacks whenever its size get larger than 2¹²⁸. This scheme makes use of the three initial parameters as the key, and the accuracy of the parameters and initial values of each system can reach 10^− 14, and its space reaches 10⁴², which is much larger than 2¹²⁸. Therefore, this algorithm can resist exhaustive attacks.

Histogram analysis

The histogram analysis shows how the pixel values are distributed across image. Based on some statistical properties of the plain image, an attacker may be able to break the encryption system if they count a certain amount of useful information. Therefore, the cipher images need to present as little useful information as possible to make the encryption system more secure. Figure 21 shows the histograms of the five sets of plain images and their corresponding cipher images, from which we can conclude that the histograms of the plain images are concentrated and follow a certain pattern, while the histograms of the cipher images are distributed evenly. This observation clearly evident the effectiveness of the proposed algorithm in hiding useful information in plain images while resisting statistical attacks.

Fig. 21

Histogram of five gray images before and after encryption: (a) moon surface image, (b) finger image, (c) hill image, (d) boat image, and (e) pepper image.

Correlation coefficient analysis

This analysis determines how related are the adjacent pixels within an image. A safe and effective encryption system needs to have the characteristics of low correlation between adjacent pixels. In this paper, the correlation coefficient is used to measure the relation among adjacent pixels within an image. The formula is given by Eq. (10):

$$\left\{\begin{array}{l}{r}_{x,y}=\frac{cov\left(x,y\right)}{\sqrt{D\left(x\right)D\left(y\right)}} \\ cov\left(x,y\right)=E\left(\left[x-E\left(x\right)\right]\left[y-E\left(y\right)\right]\right)\\ E\left(x\right)=\frac{1}{N}\sum _{i=1}^{N}{x}_{i} \\ D\left(x\right)=\frac{1}{N}\sum _{i=1}^{N}{\left[{x}_{i}-E\left(x\right)\right]}^{2} \end{array}\right.$$

(10)

where x and y are pairs of neighboring pixels in plain or cipher image, E(x) is the expectation of x, D(x) is the variance of x, and N is the total number of pixels available.

Calculations were made for adjacent pixel in three directions; horizontal, vertical, and diagonal directions. The results are shown in Fig. 22, we can see that there is a strong correlation among neighboring pixels in all three directions within the plain image, which shows approximately a linear distribution. For cipher image, we can see that the scatter plot is close to random distribution, indicating the low correlation between adjacent pixels.

Fig. 22

Correlation analysis from horizontal, vertical, and diagonal directions. (a) Boat plain image, (b) Boat cipher image.

Table 4 shows the values of correlation coefficient measured in all three directions, between two adjacent pixels. By comparing and analyzing the values from each plain images and their respective cipher images, we observed a significantly reduction in the correlation factor among neighboring pixels in the original image.

Table 4 Correlation coefficients of plain and cipher images for each direction.

Information entropy analysis

This type of analysis is commonly used for measuring the uncertainty within an image, and we use information entropy to measure the degree of chaos in a cryptographic system. The calculation is shown in Eq. (11).

$$H=-\sum _{x=1}^{N}p\left(x\right){log}_{2}p\left(x\right)$$

(11)

Here p(x) is the probability of a greyscale value of i, and N = 256.

The local information entropy can further analysis of the level of chaos in an image. By dividing the image into regions, the information entropy is then calculated for each region and fused into the complete image. The results of information entropy and local information entropy are shown in Table 5, where we can see that the information entropy value before encryption is relatively small, while that of cipher image is nearing to 8. The local information entropy is also close to the ideal value of 8. This number evidently shows the good performance and effectively of the proposed algorithm in hiding the information into an image.

Table 5 Information entropy and local information entropy.

Chi-square test

The result of the chi-square test is that the amount of useful information in the cipher image can be examined quantitatively by the pixel distribution. It is calculated as shown in Eq. (12).

$${x}^{2}=\sum _{i=0}^{255}\frac{{({v}_{i}-{v}_{0})}^{2}}{{v}_{0}},{v}_{0}=\frac{M\times N}{256}$$

(12)

In general, when conducting the chi-square test, we use a significance level of α = 0.05 and a theoretical value of 293.24783. Both plain imagen and cipher image have undergone the test and their results can be found in Table 6. We can see that the chi-square test results for the plain images are all greater than the theoretical value, while the chi-square test results for the cipher images are all lesser.

Table 6 Chi-square test.

Differential attack

A differential attack is used to break an encryption system by means of inducing a minor change to the plain image, and consequently begin an investigation based on the distinction between the altered cipher image against the normal encrypted cipher image. There are two parameters that are commonly used to determine the resistance of the proposed algorithm against differential attacks. The first one is called the number of pixels change rate (NPCR) calculated according to Eq. (13), while the second is the uniform average change intensity (UACI) calculated according to Eq. (14).

$$NPCR=\frac{{\sum }_{i,j}D(i,j)}{M*N}*100\%$$

(13)

$$UACI=\frac{1}{M*N}\frac{\sum ({C}_{1}\left(i,j\right)-{C}_{2}(i,j\left)\right)}{255}\times 100\%$$

(14)

where M and N represent the width and height of the two images, C₁ and C₂ represent the two different cipher images, one corresponds to before pixel changes and the other after pixel changes, on the plain image respectively. In a case of C₁(i, j) ≠ C₂(i, j), we obtain D(i, j) = 1, while for others D(i, j) = 0. In theory, for the best encryption effect scenario, the respective values for NPCR and UACI are 99.6093% and 33.4635%. In our simulation, the results are shown in Table 7. It is observable that the test results for different images all float around the theoretical values, indicating that this algorithm can effectively resist differential attacks.

Table 7 NPCR and UACI results of different attacks.

The proposed encryption method is evaluated against other schemes utilizing the Moon Surface image. The results, shown in Table 8, highlight the competitive advantages of the proposed approach.

Table 8 Performance comparison.

Conclusions

This paper introduces NJC oscillators with symmetrical attractors, employing traditional methods to analyze their dynamics. The system exhibits chaotic behavior and various attractor types, validated through simulations and numerical solving. Additionally, a multilayer FFNN models the system, and an image encryption algorithm integrating the NJC system is proposed, showing effectiveness against attacks. This work contributes to understanding chaotic systems, utilizing neural networks, and developing secure encryption techniques.

The current study on the NJC system demonstrates good potential, particularly in image encryption and chaotic PRNG development, but it faces several limitations and offers opportunities for future research. One limitation is the computational complexity associated with the ANN-based model on FPGA, which may impact performance and resource utilization. Additionally, the study primarily focuses on a single application—image encryption—leaving other potential applications like secure communication or financial modeling underexplored. Future studies could address these limitations by optimizing FPGA implementations, expanding the scope to real-time systems and diverse cryptographic techniques, and investigating more complex neural network architectures like RNNs to enhance prediction accuracy in chaotic systems.