Evaluation of modified fire hawk optimizer for new modification in double diode solar cell model

Abstract

The evaluation of photovoltaic (PV) model parameters has gained importance considering emerging new energy power systems. Because weather patterns are unpredictable, variations in PV output power are nonlinear and periodic. It is impractical to rely on a time series because traditional power forecast techniques are based on linearity. As a result, meta-heuristic algorithms have drawn significant attention for their exceptional performance in extracting characteristics from solar cell models. This study analyzes a new modification in the double-diode solar cell model (NMDDSCM) to evaluate its performance compared with the traditional double-diode solar cell model (TDDSCM). Modified Fire Hawk Optimizer (mFHO) is applied to identify the photovoltaic parameters (PV) of the TDDSCM and NMDDSCM models. The Modified Fire Hawks Optimizer (mFHO) algorithm, which incorporates two enhancement strategies to address the shortcomings of FHO. The experimental performance is evaluated by investigating the scores achieved by the method on the CEC-2022 standard test suite. The parameter extraction of the TDDSCM and NMDDSCM is an optimization problem treated with an objective function to minimize the root mean square error (RMSE) between the calculated and the measured data. Real data of the R.T.C France solar cell is used to verify the performance of NMDDSCM. The effectiveness of the mFHO algorithm is compared with other algorithms such as Teaching Learning-Based Optimization (TLBO), Grey Wolf Optimizer (GWO), Fire Hawk Optimizer (FHO), Moth Flame Optimization (MFO), Heap Based optimization (HBO), and Chimp Optimization Algorithm (ChOA). The best objective function for the TDDSCM equal to 0.000983634 and its value for NMDDSCM equal to 0.000982485 that is achieved by the mFHO algorithm. The obtained results have proved the NMDDSCM’s superiority over TDDSCM for all competitor techniques.

Introduction

Energy plays a crucial role in manufacturing, transportation, and other facets of life. Recently, there has been a rise in global energy demands^1,2,3,4. Human activity is releasing carbon dioxide and other greenhouse gases into our atmosphere. These gases allow heat to be trapped. The effect of global warming is both significant and varied, from more intense and regular hurricanes to drought, sea-level rise, and species extinction. Despite their heavy use for several decades, fossil fuels have faced a decline, meaning they are an unsustainable and intermittent energy source. Fossil fuels containing several carbon levels, such as coal, oil, and natural gas, significantly contribute to global warming, threatening life on Earth^5,6. This affects Earth as alternative energy sources, wind, waves, wood, and sunlight, are all sought as sustainable and renewable energy sources. In comparison, renewable energy sources create little or no global warming emissions. Even though “life cycle” emissions of renewable energy quote parameter^7,8.

Solar energy is an alternative source of energy. The second most common renewable source of energy is solar energy. After wind, it is one of the most promising sources of energy that has Stretched to include multiple applications such as solar water heating, solar heating of houses, solar distillation, solar pumping, solar furnaces, solar cooking, and solar electric power generation street heating, lighting, vehicles, solar farming, tourism, irrigation^9,10,11,12. Therefore, solar or photovoltaic (PV) is the most significant due to its broad applications among many renewable energy sources. It is abundant in energy, secure, without transport, and does not harm the environment. The idea of solar energy can revolutionize our society and bring us into an age of energy conservation. With the assistance of a building-based photovoltaic (PV) device, the solar cell block is used to transform the energy of light into electricity (Direct Present (DC), which is then transformed via an inverter to Alternating Contemporary (AC), and the reaction is generally referred to as a photovoltaic effect^13,14.

In addition, PV is a renewable distributed generation system that does not emit pollution. Directly use solar energy to fuel buildings and provide electricity for particular purposes¹⁵. Solar energy has several advantages over other types of energy. However, it has some possible drawbacks that serve new areas of study. The major shortcoming of solar energy is its high initial cost and lowest performance compared to fossil energy. Likewise, since PV modules are outside, their energy production is influenced by temperature. This also means that the cost of repair and replacement of components is very high¹⁶. The critical challenge is to optimize the PV device’s efficiency during service using an accurate model based on calculated voltage-current data. Different solar systems vary in design, technology, size, and location, resulting in a difference in energy generation and consumption. The effectiveness of the PV system construction and design depends on weather conditions¹⁷. Given the current and future research in this area, PV cells’ accurate design is crucial and challenging. There are two necessary steps for modeling PV cells. Firstly, the formulation of mathematical models. Secondly, evaluating the model predictions. The Current vs. Voltage (I-V) characteristics dominate the mathematical model’s SC behavior. Several mathematical approaches have been developed to describe the nonlinearity performance of PV systems¹⁸.

Therefore, three PV models have been produced, such as the Single Diode Model (SD)¹⁹, the Double Diode Model (DD)²⁰, the Modified Double Diode Model (MDD), the Triple Diode Model (TD)²¹. These models differ in the precision or the complexity of their equivalent circuits, with the most widely adopted models being the single-diode and double-diode models. The PV system’s accuracy generally relies on its model parameters, so it is crucial to define and estimate those parameters to improve its efficiency^{22,23,24,25,26}. The SD and MSD model has five unknown parameters that must be discovered, the DD and MDD model is expected to provide the answers for seven unknown parameters, and the TD and MTD model is expected to provide the answers for Nine or more unknown parameters²⁷. Regardless of the chosen model, the photo-generated current is calculated or defined, the diode saturation current is determined, the series resistance is determined, and the diode ideality factor is determined. These factors directly influence the efficiency of solar cells and solar panels. The main challenge is deciding the optimal values of parameters applied to the selected model and estimating the experimental data’s effects from the real PV²⁸.

Numerical computation methods, such as the Newton-Raphson (NRM) and Nelder-Mead simplex methods, usually use nonlinear algorithms²⁹. The fitness functions need continuity and differentiation conditions to apply the numerical methods. Many unknown parameters in the numerical methods complicate the extraction process. To estimate the DDM parameter of PV cells, a Newton-Raphson algorithm-based numerical approach was used in Ref.³⁰. In Ref.³¹ have suggested a simple and accurate method to define the design parameters of DDM.

Biology-based algorithms such as Genetic Algorithm (GA) and Differential Evolution (DE) are the first meta-heuristic algorithms used to model PV cells and parameter estimation (DE). In the same sense, improving the efficiency of traditional GA to test the parameters of PV cell models and extract two parameters in Ref.³². Adaptive GA (AGA) can also effectively increase computation efficiency for parameter estimation³³ relative to conventional GA methods. To increase convergence speed and global search efficiency, improved versions of DE^34,35, Artificial bee colony (ABC), and a hybrid strategy called teaching artificial bee colony (TLABC)³⁶, Whale optimization algorithm (WOA)³⁷, improved WOA (IWOA)³⁸. Chaotic WOA (CWOA)³⁹ are also recommended. In addition, modified Marine Predator Algorithm (MPA)⁴⁰, modified WOA (MWOA), Enhanced antlion optimizer (IAIO)⁴¹, and Biogeography-based optimization (BBO)⁴².

Several meta-heuristics are applied for several problems such as liver cancer algorithm⁴³, parrot optimizer⁴⁴, slime mould algorithm⁴⁵, moth search algorithm⁴⁶, hunger games search⁴⁷, Runge Kutta method^23,48, colony predation algorithm⁴⁹, Harris hawk’s optimization⁵⁰, rime optimization algorithm⁵¹, JAYA⁵², and differential evolution algorithm⁵³, beluga whale optimization algorithm⁵⁴.

The main contribution and objective of this work are summarized as follows:

• A new modification in the double diode solar cell model (NDDSCM) is analyzed.

• Evaluation of the NMDDSCM performance is compared with the traditional double diode solar cell model (TDDSCM).

• Estimation of variables for the NMDDSCM is nine parameters and seven for TDDSCM.

• Modified Fire Hawk Optimizer (mFHO) is used to identify the decision parameters for the NMDDSCM and TDDSCM based on minimizing the fitness function.

• The Modified Fire Hawks Optimizer (mFHO) algorithm, which incorporates two enhancement strategies to address the shortcomings of FHO.

• The experimental performance is evaluated by investigating the scores achieved by the method on the CEC-2022 standard test suite.

• Comparison between mFHO algorithm and another six algorithms such as Teaching Learning based optimization algorithm (TLBO), Grey wolf optimizer (GWO), Fire Hawk Optimizer (FHO), Moth Flame Optimization (MFO), Heap Based optimization (HBO), and Chimp optimization algorithm is performed for an R.T.C France cell data set.

• The characteristics curves of NMDDSCM were simulated based on the values of the estimated variables from the mFHO algorithm at the best objective function.

The structure of this paper is outlined as follows: The “Analysis of the PV Solar Cell Models” section introduces the modeling of the TDDSCM and NMDDSCM. The “Problem formulation” section elaborates on the problem formulation for identifying photovoltaic parameters of TDDSCM and NMDDSCM. The “Methodology” section comprehensively overviews the proposed method’s mathematical models and concepts. In the “Numerical experiment and analysis” section, the performance of mFHO on the CEC-2022 benchmark is evaluated. The “Results of TDDSCM and NMDDSCM” section discusses the results obtained for TDDSCM and NMDDSCM. Finally, the conclusion of this work is presented in the “Conclusion” section.

Analysis of the PV solar cell models

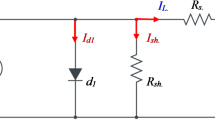
Identifying solar cell variables is one of the issues in the PV system. The mathematical formulation of Fig. 1, which analyzes TDDSCM equivalent circuit, is described as follows:

$$\begin{aligned} I=I_{ph}-I_{o1}\left[ exp\left( \frac{q{(V+IR_s)}}{n_1KT_c}\right) -1\right] \hspace{1em}-\hspace{0.16667em}I_{o2}\left[ exp\left( \frac{q{(V+IR_s)}}{n_2KT_c}\right) -1\right] \end{aligned}$$

(1)

The TDDSCM current output is I, the photo-current generated is $I_{ph}$, the current in the parallel resistor is $I_{sh}$, $I_{d1}$ is the current flows in diode, $R_{sh}$ is the parallel resistance, $R_s$ is the resistance connected in series, $n_1$ is the diode emission factor, K is the constant of Boltzmann, q is the electron charge, $T_c$ is the cell temperature.

Fig. 1

TDDSCM circuit.

where $I_{d2}$is the current flows in the second diode, $n_2$ is the second diode emission factor.

The NMDDSCM is performed by adding resistance in the diode branch for the two diodes to release the losses in its region. The mathematical formulation of Fig. 2, that analyzes NMDDSCM equivalent circuit is described as follow:

$$\begin{aligned} I=I_{ph}-I_{o1}\left[ exp\left( \frac{q{(V+IR_s-I_{d1}R_{s1})}}{n_1KT_c}\right) -1\right] \hspace{1em}-\hspace{0.16667em}I_{o2}\left[ exp\left( \frac{q{(V+IR_s-I_{d2}R_{s2})}}{n_2KT_c}\right) -1\right] \end{aligned}$$

(2)

where $R_{s1}$ is the adding resistance in the first diode, and $R_{s2}$ is the adding resistance in the second diode.

Fig. 2

NMDDSCM circuit.

The losses in the quasi-neutral region and The losses in the space charge region is expressed by adding the first series resistance and the second series resistance respectively.

Problem formulation

The main items in optimization algorithms are the objective function and the boundaries of variables. Table 1 illustrates the limits of decision variables.

Table 1 The limits of parameters.

The main objective function is minimizing the root means square error (RMSE). The formula that analyses RMSE is calculated as follows:

$$\begin{aligned} & J(V.I.X)=I-I{exp} \end{aligned}$$

(3)

$$\begin{aligned} & {RMSE=\sqrt{\frac{1}{N}\sum _{i=1}^{N}{(J(V.I.X))}^2}} \end{aligned}$$

(4)

where $I_{exp}$, is the measured current, N is the number of data reading and X is the extracted variables. The TDDSCM estimated variables are $X=\{(I_{ph}. I_{o1}. n. R_s. R_{sh}. I_{o2}. n_2. and R_s )\}$. The NMDDSCM estimated variables are $X=\{(I_{ph}. I_{o1}. n. R_s. R_{sh}. I_{o2}. n_2. R_s. R_{s1}.$ and $R_{s2})\}$.

Methodology

In this section, the “Theory of Fire Hawks Optimize” subsection reviews the mathematical model of the original FHO. Subsequently, the “Modified Fire Hawks Optimizer” subsection provides a brief overview of two modification operators designed to improve the optimization performance of FHO: the Phasor Operator and the Dimension Learning-Based Hunting (DLH) strategy.

Theory of fire hawks optimizer

Fire Hawk Optimizer (FHO) is a swarm-based meta-heuristic algorithm introduced by Azizi et al. in 2022⁵⁵. FHO draws inspiration from the foraging behaviors of certain birds, specifically whistling kites, black kites, and brown falcons, which attempt to spread fire by carrying flaming sticks in their beaks and claws—a rare but documented natural phenomenon. These birds use fire to flush out prey, such as rats and snakes, by scattering flaming sticks in unburned areas, creating small fires that frighten and displace the prey, making them easier to catch (see Fig. 3).

Fig. 3

Hawk during hunt [https://pixabay.com/fr/photos/faucon-chimango-des-stylos-à-chéri-7515684/ ; https://pixabay.com/fr/photos/le-vilain-marais-réserve-naturelle-433688].

The FHO algorithm mimics this behavior by simulating the process of starting and spreading fires and capturing prey. The algorithm begins with a set of possible solutions (X), representing the positions of fire hawks and prey in the search space. A random initialization mechanism is employed to determine the initial positions of these vectors, thus beginning the optimization process⁵⁵.

$$\begin{aligned} & X={\left[ \begin{array}{c}X_1\\ X_2\\ \vdots \\ X_i\\ \vdots \\ X_N\end{array}\right] }={\left[ \begin{array}{c}x_1^1x_1^2\cdots x_1^j\cdots x_1^D\\ x_2^1x_2^2\cdots x_2^j\cdots x_2^D\\ \vdots \vdots \vdots \ddots \vdots \\ x_i^1x_i^2\cdots x_i^j\cdots x_i^D\\ \vdots \vdots \vdots \ddots \vdots \\ x_N^1x_N^2\cdots x_N^j\cdots x_N^D\end{array}\right] },{\left\{ \begin{array}{c}i=1,2,...,N.\\ j=1,2,...,D.\end{array}\right. } \end{aligned}$$

(5)

$$\begin{aligned} & x_i^j{(0)}=x_{i,\min }^j+rand.{(x_{i,\max }^j-x_{i,\min }^j)},{\left\{ \begin{array}{c}i=1,2,...,N.\\ j=1,2,...,D.\end{array}\right. } \end{aligned}$$

(6)

where $X_i$ represents the i-th solution candidate in the search space, while $x_{i,\min }$ and $x_{i,\max }$ denote the minimum and maximum bounds of the j-th decision variable for this candidate, respectively. The variable rand is a uniformly distributed random number between 0 and 1. The term $x_i^j$ refers to the j-th decision variable of the i-th solution candidate, and $x_i^j{(0)}$ signifies the initial position of these candidates. The dimension of the problem is indicated by D, and N represents the total number of solution candidates in the search space.

Secondly, all solutions are evaluated using an objective function. The candidate solutions are then divided into two categories: fire hawks and prey. Solutions with higher objective function values fall into the fire hawks category, while those with lower objective function values are classified as prey, as illustrated in the equations below.

$$\begin{aligned} PR={\left[ \begin{array}{c}PR_1\\ PR_2\\ \vdots \\ PR_k\\ \vdots \\ PR_m\end{array}\right] },k=1,2,...,m,FH={\left[ \begin{array}{c}FH_1\\ FH_2\\ \vdots \\ FH_l\\ \vdots \\ FH_n\end{array}\right] },l=1,2,...,n \end{aligned}$$

(7)

where, $FH_l$ represents the l-th Fire Hawk in a search space containing n Fire Hawks, and $PR_k$ represents the k-th prey in a region with a total of m preys. The distance between the Fire Hawks and their prey is calculated in the next step of the algorithm, where $D_k^l$ is determined using the following equation⁵⁵:

$$\begin{aligned} D_k^l=\sqrt{{(x_2-x_1)}^2+{(y_2-y_1)}^2},{\left\{ \begin{array}{c}l=1,2,...,n.\\ k=1,2,...,m.\end{array}\right. } \end{aligned}$$

(8)

where ($x_1,y_1$) and ($x_2,y_2$) represent the coordinates of the Fire Hawks and prey in the search space. The variables m and n denote the number of prey and Fire Hawks in the search space.

In the subsequent step, each fire hawk gathers burning wood from the main fire to set its own territory ablaze, driving prey to flee. Furthermore, these hawks might also retrieve burning wood from the territories of other hawks to ignite their own areas. Reflecting these behaviors, the FHO updates the position of each hawk as follows⁵⁵:

$$\begin{aligned} FH_l^{new}=FH_l+{(r_1\times GB-r_2\times FH_{Near})},l=1,2,...,n. \end{aligned}$$

(9)

where $FH_l^{new}$ represents the new position vector of the lth Fire Hawk ($FH_l$), $FH_{Near}$ represents one of the Fire Hawks in the search space, GB indicates the global best solution in the search space, considered as the primary fire, and $r_1$ and $r_2$ are uniformly distributed random numbers in the range (0, 1) used to model the Fire Hawks’ movements towards the main fire and other Fire Hawks’ territories.

During the subsequent stage of the algorithm, the movement of prey within each Fire Hawk’s territory is regarded as a critical aspect of animal behavior for the position-updating process. When a prey sees the flaming stick dropped by a Fire Hawk, it may choose to hide, flee, or mistakenly run towards the Fire Hawk. The following equation incorporates these behaviors into the position-updating process⁵⁵:

$$\begin{aligned} PR_q^{new}=PR_q+{(r_3\times FH_1-r_4\times SP_1)},{\left\{ \begin{array}{c}l=1,2,...,n.\\ q=1,2,...,r.\end{array}\right. } \end{aligned}$$

(10)

where $PR_q^{new}$ represents the new position vector of the q-th prey ($PR_q$) within the territory of the l-th Fire Hawk ($FH_l$), and $r_3$ and $r_4$ are uniformly distributed random numbers in the range (0, 1). Additionally, $SP_1$ denotes a safe location within the territory of the l-th Fire Hawk, expressed as follows⁵⁵:

$$\begin{aligned} {\textrm{SP}}_{\mathrm l}=\frac{{\displaystyle \sum }_{\mathrm q=1}^{\mathrm r}{\textrm{PR}}_{\mathrm q}}{\mathrm r},\qquad {\{\begin{array}{c}\mathrm q=1,2,\dots ,\mathrm r.\\ \mathrm l=1,2,\dots ,\mathrm n.\end{array}} \end{aligned}$$

(11)

where $PR_q$ represents the q-th prey within the territory of the l-th Fire Hawk.

Furthermore, prey may also venture into the territories of other Fire Hawks. At the same time, there is a possibility that prey may approach Fire Hawks blocked by neighboring Fire Hawks, seeking refuge in a secure area beyond the Fire Hawk’s territory. Incorporating the following equation into the position updating process enables accounting for these behaviors⁵⁵:

$$\begin{aligned} PR_q^{new}=PR_q+{(r_5\times FH_{Alter}-r_6\times SP)},{\left\{ \begin{array}{c}l=1,2,...,n.\\ q=1,2,...,r.\end{array}\right. } \end{aligned}$$

(12)

where $PR_q^{new}$ represents the new position vector of the qth prey ($PR_q$) within the territory of the l-th Fire Hawk ($FH_l$); SP denotes a safe location outside the territory of the l-th Fire Hawk; $FH_{Alter}$ signifies one of the Fire Hawks in the search space; $r_5$ and $r_6$ are uniformly distributed random numbers in the range (0, 1) used to determine the movements of preys towards other Fire Hawks and the safe region outside the territory. Additionally, SP defines the safe location outside the territory of the l-th Fire Hawk, formulated as follows⁵⁵:

$$\begin{aligned} \textrm{SP}=\frac{{\displaystyle \sum }_{\mathrm k=1}^{\mathrm m}{\textrm{PR}}_{\mathrm k}}{\mathrm m},\qquad \mathrm {k=1,2,}\dots ,\textrm{m}. \end{aligned}$$

(13)

where $PR_k$ represents the k-th prey in the search space.

The solutions are updated until the stopping conditions are met, at which point the best solution is returned. The pseudo-code for the FHO algorithm is provided in Algorithm 1.

Algorithm 1

Pseudo-code of Fire Hawk optimizer (FHO).

Modified fire hawks optimizer

As a meta-heuristic algorithm, the FHO algorithm has demonstrated promising results in addressing optimization problems, thanks to its innovative imitation concept. However, the inherent limitations of biological behaviors in nature have led to challenges such as susceptibility to premature convergence and inadequate precision. This subsection introduces the Modified Fire Hawks Optimizer (mFHO) algorithm, which incorporates two enhancement strategies to address the shortcomings of FHO.

Phasor operator

Ghasemi et al.⁵⁶ proposed the Phasor Operator to enhance the Particle Swarm Optimization (PSO) performance and address its limitations. Derived from mathematical phasor theory, the Phasor Operator utilizes phase angles to transform the algorithm into a trigonometric nonparametric, self-adaptive, balanced algorithm. By integrating the Phasor Operator into the mFHO, the convergence speed of the original FHO is increased. This approach leverages periodic trigonometric functions, such as sine and cosine, which serve as control parameters through the phase angle $\theta$. These parameters transform into functions of $\theta$, providing various strategies. Consequently, Eq. (9) is updated using equation expressed as follows:

$$\begin{aligned} \begin{array}{c}FH_l^{new}\end{array}=\left\{ \begin{array}{cc}FH_l+p^{\left( \theta _i^t\right) }\times {(r_1\times GB-r_2\times FH_{Near})} \hspace{1em}& if\hspace{1em} rand\le coef\\ FH_l+g^{\left( \theta _i^t\right) }\times {(r_1\times GB-r_2\times FH_{Near})} \hspace{1em}& if\hspace{1em}rand>coef\end{array}\right. \end{aligned}$$

(14)

where rand is a random number between [0, 1], while $p^{\left( \theta _i^t\right) }$ and $g^{\left( \theta _i^t\right) }$ are mathematically expressed as follows:

$$\begin{aligned} & p^{\left( \theta _i^t\right) }={\left| sin\theta _i^t\right| }^{2\times cos\theta _i^t} \end{aligned}$$

(15)

$$\begin{aligned} & g^{\left( \theta _i^t\right) }={\left| cos\theta _i^t\right| }^{2\times sin\theta _i^t} \end{aligned}$$

(16)

Furthermore, coef is a control parameter which is expressed as bellow:

$$\begin{aligned} Q=exp(-t/T); \end{aligned}$$

(17)

where T denotes the maximum number of iterations and t represents the current iteration number.

Dimension learning-based hunting (DLH) strategy

In the standard FHO, individuals can readily become trapped in local optimal regions, leading to a lack of diversity. To address these challenges, an additional DLH strategy, proposed by Nadimi-Shahraki et al.⁵⁷, is incorporated into FHO. In this strategy, each agent is updated concerning its neighboring agents. The DLH strategy generates an alternative candidate, denoted as $X_{i-DLH}$, for the new position $X_{i-FHO}$ of Fire Hawks.

Initially, the radius $R_i$ is computed using the Euclidean distance between the current position $X_i$ and the candidate position $X_{i-FHO}$, as described by the following equation:

$$\begin{aligned} {\mathrm R}_{\mathrm i}=\left\| {\mathrm X}_{\mathrm i}-{\mathrm X}_{\mathrm i-\textrm{FHO}}\right\| \end{aligned}$$

(18)

where $X_{i-FHO}$ represents the candidate position obtained by the standard FHO.

Subsequently, Eq. (19) is employed to construct the neighborhood $N_i$ of $X_i$, where $D_i$ represents the Euclidean distance between $X_i$ and $X_j$, D is the dimension, and N is the population size.

$$\begin{aligned} N_i=\left\{ X_j{\vert }D_i\left( X_i,X_j\right) \leqslant R_i,X_j\in N\right\} \end{aligned}$$

(19)

The DLH search strategy generates another candidate, denoted as $X_{i-DLH,d}$, for the new position $X_i$ of Fire Hawks. Dimension-based learning is conducted using the following equation:

$$\begin{aligned} X_{i-DLH,d}=X_{i,d}+rand\times {(X_{n,d}-X_{r,d})} \end{aligned}$$

(20)

where $X_{i-DLH,d}$ is calculated by utilizing the d-dimension of the random individual $X_{r,d}$ from the initial population. and the randomly selected neighbor $X_{n,d}$ from $N_i$.

Algorithm 2 presents the pseudo-code of the mFHO algorithm.

Algorithm 2

Pseudo-code of modified Fire Hawk optimizer (mFHO).

Numerical experiment and analysis

This section empirically analyzes the efficiency of the mFHO algorithm. The experimental performance is evaluated by investigating the scores achieved by the method on the CEC-2022 standard test suite⁵⁸.

Benchmark description

This section discusses the efficiency testing of the proposed algorithm using the CEC-2022 standard test suite⁵⁸. This suite includes 12 challenging benchmark functions of varying difficulties, categorized as unimodal ($F_1$), multimodal ($F_2$-$F_4$), hybrid ($F_5$-$F_8$), and composite functions ($F_9$-$F_{12}$), as shown in Table 2. Unimodal problems, such as $F_1$, have a single global optimum with no local minima, evaluating the method’s exploitability and convergence rate. Functions $F_2$ through $F_4$ are multimodal, with multiple local optima within the test range, increasing the risk of stagnation and thus measuring the algorithm’s exploration capacity. Hybrid ($F_5$-$F_8$) and composite ($F_9$-$F_{12}$) problems test the algorithm’s ability to find the true solution and balance exploration and exploitation. Figure 4 illustrates some selected functions in three dimensions.

Table 2 Details of CEC-2022 benchmark functions.

Fig. 4

3D representation of same randomly selected CEC-2022 test functions.

Experimental setup

The proposed mFHO experimental results are documented and compared with several well-known recent algorithms across different problem sets. The experiments utilize 1,000 iterations and 30 search agents for the proposed mFHO method. To further demonstrate the effectiveness of mFHO, its performance is compared with the following algorithms: Moth Flame optimization (MFO)⁵⁹; Sine Cosine Algorithm (SCA)⁶⁰, Chimp Optimization Algorithm (ChOA)⁶¹; Coati Optimization Algorithm (COA)⁶²; Grey Wolf Optimizer (GWO)⁶³; and standard FHO⁵⁵. The parameters for these algorithms are provided in Table 3. To ensure fairness and obtain statistical results, each experiment is run 30 times to calculate average outcomes. The experiments were conducted in a Matlab R2023b environment on a 2.40 GHz Intel Core i7 system and 32 GB of RAM.

Table 3 Parameter settings for mFHO and its competitors.

Evaluation index

In this experiment, several performance metrics are utilized to evaluate the performance of each algorithm. These metrics include the standard deviation (Std), the mean value (Mean), the worst value (Worst), the optimum value (Best), the root mean square error (RMSE), the mean of the absolute errors (MAE), and the ranking (Rank). Specific descriptions are given below:

• Best: The smallest value the algorithm finds over all runs, indicating the best solution’s quality, which is expressed by the equation below:

  $$\begin{aligned} \begin{array}{c} Best =min\left\{ f_1\left( x\right) ,f_2\left( x\right) ,\cdots ,f_{ Runs }{(x)}\right\} \end{array} \end{aligned}$$

  (21)

• Worst: The largest value found by the algorithm over all runs, reflecting the worst-case scenario., which can be calculated by the equation below:

  $$\begin{aligned} \begin{array}{c} Worst =max\left\{ f_1\left( x\right) ,f_2\left( x\right) ,\cdots ,f_{ Runs }{(x)}\right\} \end{array} \end{aligned}$$

  (22)

• Mean: The average value of solutions obtained from all runs, providing an overall performance indicator which is expressed as follows:

  $$\begin{aligned} \begin{array}{c} Mean =\hspace{0.333333em}\frac{f_1\left( x\right) +\hspace{0.333333em}f_2\left( x\right) +\cdots +\hspace{0.333333em}f_{ Runs }{(x)}}{ Runs }\end{array} \end{aligned}$$

  (23)

• Std: The standard deviation of the solutions indicates the consistency and reliability of the algorithm.

  $$\begin{aligned} \begin{array}{c} Std =\sqrt{\frac{\sum _{i=1}^{ Runs }{(f_i\left( x\right) -Mean)}^2}{ Runs -1}}\end{array} \end{aligned}$$

  (24)

• RMSE: This metric measures the average error magnitude between the algorithm’s solutions and the actual optimum $f_{best}$.

  $$\begin{aligned} RMSE=\sqrt{\frac{1}{Runs}\sum _{i=1}^{Runs}{(f_i-f_{best})}^2} \end{aligned}$$

  (25)

• MAE: This metric indicates the average absolute difference between the solutions and the actual optimum $f_{best}$.

  $$\begin{aligned} MAE=\frac{1}{Runs}\sum _{i=1}^{Runs}{{\vert f}_i-f_{best}\vert } \end{aligned}$$

  (26)

• Rank: This metric effectively illustrates the method’s ranking. Researchers often regard above-average rankings as evidence of the method’s performance. If two algorithms have the same mean rank, they are further distinguished by their Std. A smaller mean rank indicates better performance of the corresponding algorithm. This approach ensures a comprehensive and fair assessment by considering both the average performance and the consistency of the algorithms.

Statistical results

In this section, the performance of mFHO in finding the optimal solution for the CEC-2022 benchmark functions, including unimodal, multimodal, hybrid, and composite functions, will be assessed. Table 4 presents the experimental results of mFHO compared with other test algorithms, including MFO, SCA, ChOA, COA, GWO, and FHO, with the optimal results displayed in bold. These test algorithms are selected for comparison because of their recognized effectiveness in solving global optimization problems.

From Table 4, it is evident that mFHO outperforms the original FHO across all benchmark functions. This improvement highlights the significant enhancement in the exploration and exploitation capabilities of the candidate solutions within the FHO population due to the embedded strategies in mFHO. The superior performance of mFHO suggests that these strategies effectively balance the trade-off between exploration and exploitation, enabling the algorithm to locate optimal solutions more efficiently and accurately.

When comparing mFHO to other optimization algorithms such as MFO, SCA, ChOA, COA, and GWO, it is evident that mFHO outperforms COA on nearly all problems. Specifically, the comparison with SCA and ChOA demonstrates mFHO’s superior search-ability on all multimodal, hybrid, and composite problems. However, in the unimodal problem (F1), SCA and ChOA yield better optimization results. Regarding the performance comparison between MFO and mFHO, MFO achieves better optimization results on $F_6$ and $F_8$, while mFHO provides superior results on the remaining problems. GWO delivers better results on $F_1$, $F_4$, $F_6$, and $F_7$ than mFHO, but mFHO surpasses GWO in the other problems. The lower Std, RMSE, and MAE values produced by mFHO in most problems indicate the reliability of its search procedure. Overall, the comparison indicates that mFHO enhances exploration and exploitation levels and successfully establishes an appropriate balance between them. Furthermore, as shown in the last row of Table 4, mFHO has a mean rank of 1.67, ranking first among all algorithms. It is followed closely by GWO and MFO, with mean ranks of 1.83 and 3.25, respectively

Table 4 CEC-2022 benchmark results of mFHO and other methods.

Table 5 p-values of mFHO versus other algorithms on Wilcoxon test.

Additionally, Fig. 5 displays the radar charts for the seven algorithms. The size of the radar chart area indicates the algorithm’s ranking: a larger area corresponds to a poorer solution provided by the algorithm, while a smaller area signifies better performance. As illustrated in the figure, the radar chart for mFHO has the smallest and most consistent radius, indicating that mFHO delivers high-precision solutions for each function. The GWO algorithm ranks closely behind mFHO. In contrast, the COA algorithm has the largest radar plot area, signifying that it produces relatively large errors in the accuracy of function solutions.

Fig. 5

Radar charts of the mFHO and its competitors on CEC-2022 functions.

On the other hand, this section analyzes the CEC-2022 test set using the Wilcoxon rank test to examine mFHO thoroughly. The p-value (p) from the Wilcoxon rank test statistically determines whether there is a significant difference between mFHO and other algorithms. The p-value serves as a threshold: if p is greater than 0.05, it suggests no significant difference between mFHO and the comparator; if p is less than 0.05, it indicates a significant difference. A p-value of 1 implies that multiple algorithms can achieve the same optimal values. The experimental results are detailed in Table 5, where the total in the last row indicates the number of instances with p-values less than 0.05. Table 5 demonstrates that mFHO shows significant differences from the compared algorithms—MFO, SCA, ChOA, COA, and FHO—in more than eight functions with p-values below 0.05. Furthermore, mFHO exhibits significant differences from GWO in six functions and achieves identical optimal values in $F_1$ and $F_6$. Therefore, it can be concluded that there are substantial distinctions between the mFHO algorithm and the other algorithms.

Boxplot behavior analysis

To assess the robustness and stability of the algorithms, box plots for each method on key functions were created, as illustrated in Fig. 6. These plots are linked to the previously discussed convergence curves. The box plots show that the data distribution for mFHO is generally more concentrated, indicating a robust and stable search function. This stability is due to its parameter adaptation mechanism, which continuously adjusts the search state and reduces the impact of complex problems. Moreover, while the data distributions for GWO and MFO are relatively stable, their higher box plot positions suggest they may not provide significant advantages.

Fig. 6

Boxplot of algorithms for different CEC-2022 functions.

Fig. 7

Convergence curves of algorithms for different CEC-2022 functions.

Convergence behavior analysis

Typically, search agents exhibit significant changes in the early iterations to explore promising areas of the search space as thoroughly as possible, followed by a period of exploitation and gradual convergence with increasing iterations. To analyze the convergence behavior of the algorithm in the search for the optimal solution, Fig. 7 plots the convergence curves of MFO, SCA, ChOA, COA, GWO, FHO, and mFHO on CEC-2022 benchmark functions throughout the iterations. As the figure shows, the proposed mFHO demonstrates superior and competitive convergence performance compared to other algorithms. Notably, mFHO shows excellent convergence in functions $F_3$, $F_8$, $F_9$, $F_{10}$, and $F_{11}$, quickly approaching the optimal value in the early iterations and maintaining this lead, with the convergence curve continuing to improve in the middle and later stages. Although mFHO’s early convergence advantage is less pronounced on functions $F_2$, $F_5$, $F_6$, and $F_{12}$, the algorithm sustains its convergence behavior over 1000 iterations, ultimately achieving better final results than the other algorithms, indicating strong spatial search capability and local optimization. However, mFHO encounters challenges with inadequate convergence accuracy and a propensity to get trapped in local optima on functions $F_1$, $F_4$, and $F_7$.

In summary, the above results demonstrate that integrating the Phasor operator significantly balances exploration and exploitation, enhancing the algorithm’s ability to identify the optimal solution. The DLH strategy improves convergence accuracy and accelerates convergence speed. Fusing multiple strategies greatly enhances the algorithm’s performance, enabling it to solve optimization problems accurately and quickly. Furthermore, mFHO exhibits stronger global search abilities and outperforms other algorithms regarding convergence accuracy and stability, representing a substantial improvement over the original FHO algorithm. This makes mFHO an algorithm with significant application potential.

Results of TDDSCM and NMDDSCM

The TDDSCM and NMDDSCM parameters are estimated in this section using the mFHO algorithm. The proposed mFHO algorithm is compared with other algorithms such as Teaching Learning based optimization algorithm (TLBO)⁶⁴, Grey wolf optimizer (GWO)⁶³, Moth Flame Optimization (MFO)⁵⁹, Heap Based optimization (HBO)⁶⁵, Chimp optimization algorithm (ChOA)⁶¹, Fire Hawk Optimizer (FHO)⁵⁵. Measured data from R.T.C France solar cells are used to measure the reliability and accuracy of all algorithms.

The results analysis for TDDSCM and NMDDSCM is distributed into four reports; the estimated variables at best RMSE from all algorithms are the first data. The second report is the I-V & P-V curves for the R.T.C solar cell, simulated based on the parameters identified from the mFHO algorithm at the best RMSE. The error for current and power is the third reported data. Finally, statistical analysis for the objective function is performed for all algorithms based on 30 independent runs for all algorithms.

Results for TDDSCM

The estimated variables at the best RMSE for TDDSCM are illustrated in Table 6. Based on this table, the best RMSE is achieved by the mFHO algorithm with a value of 0.000983634, then the TLBO algorithm achieves 0.000985419, then MFO, HBO, GWO, FHO, and ChOA, respectively. The extracted variables for each method over 30 runs are clarified in Tables 7, 8, 9, 10, 11, and 12 for mFHO, GWO, HBO, FHO, TLBO, and MFO, respectively. The difference between the simulated and experimental current or power data is the current error (IE) and power error (PE). Figure 8 explains the IE and PE for TDDSCM based on the recorded data in Table 6 for the mFHO algorithm. Based on the data in Fig. 8; the average IE is 0.000826057987880783 and the minimum IE is 0.000125189882881682. The average PE is 0.000338386400897011, and the minimum PE is 1.54003303454685E-06. The accuracy and quality of the proposed mFHO for TDDSCM are confirmed according to RMSE, IE, and PE results. Based on the results of the mFHO algorithm identified in Table 6, the I-V & P-V curves for TDDSCM are explained in Fig. 8. Based on Fig. 8, the mFHO algorithm achieves more efficient performance due to the high closeness between the experimental R.T.C solar cell data and the simulated data from the mFHO algorithm at the extracted data that achieves the best RMSE.

Table 6 The variable estimated for TDDSCM at the best RMSE.

Fig. 8

I-V and P-V curves and errors for TDDSCM based on mFHO extracted parameters.

Table 7 Decision variables based on mFHO method for TDDSCM over 30 independent runs.

Table 8 Decision variables based on GWO method for TDDSCM over 30 independent runs.

Table 9 Decision variables based on HBO method for TDDSCM over 30 independent runs.

Table 10 Decision variables based on FHO method for TDDSCM over 30 independent runs.

Table 11 Decision variables based on TLBO method for TDDSCM over 30 independent runs.

Table 12 Decision variables based on MFO method for TDDSCM over 30 independent runs.

Results for NMDDSCM

The estimated variables at the best RMSE for NMDDSCM are illustrated in Table 13. Based on this table, the best RMSE is achieved by the mFHO algorithm with a value of 0.000983634, then the TLBO algorithm achieves 0.000985419, then MFO, HBO, GWO, ChOA, GWO, and FHO, respectively. The extracted variables for each method over 30 runs are clarified in Tables 14, 15, 16, 17, 18, and 19 for mFHO, GWO, HBO, FHO, TLBO, and MFO, respectively. The difference between the simulated and experimental current or power data is the current error (IE) and power error (PE). Figure 4 explains the IE and PE for TDDSCM based on the recorded data in Table 13 for the mFHO algorithm. Based on the data in 9; the average IE is 0.000818260124697911 and the minimum IE is 0.0000165347134314375. The average PE is 0.000337560913082263, and the minimum PE is 1.85878030101432E-06. The accuracy and quality of the proposed mFHO for TDDSCM are confirmed according to RMSE, IE, and PE results. Based on the results of the mFHO algorithm identified in Table 13, the I-V & P-V curves for TDDSCM are explained in Fig. 9. Based on Fig. 9, the mFHO algorithm achieves more efficient performance due to the high closeness between the experimental R.T.C solar cell data and the simulated data from the mFHO algorithm at the extracted data that achieves the best RMSE.

Fig. 9

I-V and P-V curves and errors for NMDDSCM based on mFHO extracted parameters.

Table 13 The variable estimated for NMDDSCM at the best RMSE.

Table 14 Decision variables based on mFHO method for NMDDSCM over 30 independent runs.

Table 15 Decision variables based on GWO method for NMDDSCM over 30 independent runs.

Table 16 Decision variables based on HBO method for NMDDSCM over 30 independent runs.

Table 17 Decision variables based on FHO method for NMDDSCM over 30 independent runs.

Table 18 Decision variables based on TLBO method for NMDDSCM over 30 independent runs.

Table 19 Decision variables based on MFO method for NMDDSCM over 30 independent runs.

Statistical analysis

While a more detailed analysis could further strengthen validation, we also recorded comprehensive statistical results. Specifically, we computed the minimum (Min), mean (Mean), maximum (Max), standard deviation (Std), and ranking of the RMSE over 30 independent runs for each algorithm. By comparing the Min, Mean, Max, and Std values of the RMSE, we assessed accuracy, average performance, and robustness. To evaluate the significance of differences between mFHO and its competitors, we applied the Wilcoxon signed rank test at a 0.05 significance level. The symbols “+” and “-” indicate whether mFHO’s performance is significantly superior or inferior, respectively, while “=” denotes similar performance. Tables 20 and 21 present the statistical results of the seven algorithms for the TDDDSCM and NMDDSCM models, respectively.

The results in Table 20 highlight the superiority of the mFHO algorithm over the compared algorithms in most statistical metrics for the TDDDSCM model. mFHO achieved the lowest RMSE (0.000983634), outperforming GWO, ChOA, HHO, FHO, TLBO, and MFO, indicating superior accuracy. Additionally, the lower mean and standard deviation of mFHO suggest greater robustness and consistency. In terms of ranking, mFHO consistently outperformed the other algorithms, with TLBO and HBO following. The significance column further confirms that mFHO’s performance is significantly better than most competitors, particularly the original FHO, validating the effectiveness of the modifications made to the original FHO for parameter extraction optimization in the TDDDSCM model.

Table 20 The statistical data for TDDSCM.

For the NMMDDSCM model, the results in Table 21 show similar performance to those observed in the TDDSCM model. mFHO once again achieves the lowest RMSE value (0.000982485), demonstrating its superior accuracy. Additionally, its mean value (0.000994651) and standard deviation (1.47E-05) are the lowest among all the algorithms, reflecting accuracy and robustness across multiple runs. In terms of ranking, mFHO secures the top position, outperforming GWO, ChOA, HHO, FHO, TLBO, and MFO. The Wilcoxon signed-rank test further confirms that mFHO’s performance is significantly better than several other algorithms, particularly mFHO.

Table 21 The statistical data for NMDDSCM.

The RMS values for the 30 runs of the R.T.C. France TDDSCM are shown in Fig. 10. Since all of the obtained RMSE values based on mFHO are the lowest values when compared to the other approaches, this figure illustrates the substantial resilience feature of the proposed mFHO. The RMS values for the 30 runs of the R.T.C. France NMDDSCM are shown in Fig. 11. Since all of the obtained RMSE values based on mFHO are the lowest values when compared to the other approaches, this figure illustrates the substantial resilience feature of the proposed mFHO.

Fig. 10

TDDSCM robustness curve.

Fig. 11

NMDDSCM robustness curve.

Conclusion

One of the most widely used renewable energy technologies for producing electricity is photovoltaic systems. Creating a precise PV model that replicates the system’s behavior in many environmental scenarios is crucial. The PV model’s discovered parameters are mostly determined by the objective function of different optimization approaches. The NMDDESCM creates a decision parameter equal to nine variables. In addition to that, seven variables are estimated for TDDSCM. Measured data of R.T.C France SC is used in this study based on minimizing the RMSE of this data and the data simulated from all algorithms. A recently modified optimization algorithm called the Modified Fire Hawk Optimizer (mFHO) is applied to estimate the parameters of the two models. The NMDDSCM achieved the best value of RMSE for all algorithms used in this study compared with TDDSCM. The best RMSE values of NMDDSCM are 0.000982485, 0.000984576, 0.000986183, 0.000994794, 0.009283792, 0.001171073, and 0.002251074 for mFHO, TLBO, MFO, HBO, ChOA, GWO and FHO respectively. The superiority of the mFHO algorithm over the compared algorithms in most statistical metrics for the TDDDSCM and NMDDSCM models. The mFHO achieved the lowest RMSE , outperforming GWO, ChOA, HHO, FHO, TLBO, and MFO, indicating superior accuracy. Additionally, the lower mean and standard deviation of mFHO suggest greater robustness and consistency. The best value of RMSE for TDDSCM is 0.000983634, which is achieved by the mFHO method. So, the new modification in double-diode solar cells achieves higher performance than the traditional double-diode solar cell model. Also, the proposed mFHO can produce more reliable and accurate results, have a higher success rate, and faster convergence compared to all competitor algorithms used in this work. Our future research will focus on three main areas: First, we plan to integrate various optimization strategies into advanced intelligent algorithms to develop competitive solutions for real-world challenges. Second, we will enhance its exploitation capabilities to better utilize potential solutions by addressing the mFHO suboptimal performance on unimodal problems, which is attributed to excessive search space exploration. Lastly, we aim to extend the application of mFHO to tackle more complex engineering problems with additional constraints, thereby expanding our approach to address a broader range of challenging engineering scenarios.