Abstract
Structural health monitoring based on vibration signal analysis has been extensively employed for damage identification. Mainstream machine learning techniques, such as convolutional neural networks (CNN), often rely on single-domain inputs, which may provide limited information for accurate damage identification. To overcome this limitation, this study proposes a novel approach that combines an inner product matrix (IPM) with a parallel CNN (IPM-PCNN) to extract multidimensional features for detecting structural damage in a steel frame structure. The proposed IPM-PCNN framework consists of a one-dimensional (1D) CNN branch for processing time series data, a two-dimensional (2D) CNN branch for handling structural modal data, and several fully connected layers. This unique combination leverages the strengths of both 1D and 2D CNNs to capture temporal and modal features of the signal effectively. To validate the effectiveness and superiority of the proposed method, a five-story steel frame model is used as the research object, and five comparative methods are evaluated under the same experimental conditions. The results demonstrate that the IPM-PCNN model can automatically extract relevant features from the signals to accurately identify structural damage, achieving an accuracy of 96.60% on the test set, outperforming machine learning methods in performance. Furthermore, the internal inference processes of these methods are explored and visualized to provide insights into their decision-making mechanisms.
Similar content being viewed by others
Introduction
Frame structure, serving as a crucial support system, finds extensive application in civil engineering, industrial engineering, automotive engineering, and other fields1,2. During their lifetime, due to corrosion, temperature changes, heavy loads, and other reasons, frame structures may be damaged or even collapsed, resulting in unquantifiable economic damages and significant incidents involving personnel3. Therefore, it has become one of the critical challenges facing structural engineering to effectively maintain the durability and safety of the frame structure, extend its service life, and improve its disaster prevention and mitigation ability and structural toughness. For frame structures, typical fault diagnosis methods and structural health monitoring (SHM) evaluate the structural condition through the analysis of vibration signals. These signals are acquired using acceleration sensors installed in critical locations within the frame structures. Early fault diagnosis and SHM methods mainly rely on vibration signals, encompassing wavelet analysis, Hilbert-Huang transform, and singular spectrum analysis. As science and technology advance, researchers have incorporated advanced methods into the realms of fault diagnosis and SHM, such as random forest4,5, support vector machines6,7, gradient boosting8,9, and decision trees10,11. These methods have been widely applied in fault diagnosis and SHM, delivering commendable results. However, due to complex fault types, massive monitoring data, and different signal characteristics, these methods present severe challenges in big data. Thus, it is imperative to introduce innovative approaches in fault diagnosis and SHM.
The development of computer hardware has led to the swift evolution of deep learning, heralding the advent of a new era in artificial intelligence advancement. Deep learning (DL) algorithms play a pivotal role in vibration-based damage detection by gradually extracting hierarchical damage-sensitive features from vibration data. They have significantly addressed various problems in artificial intelligence, such as image processing12,13, speech and audio recognition14,15, natural language processing16,17, and SHM18,19. Among them, convolutional neural networks (CNNs), an advanced deep learning neural network crafted specifically for analyzing structured arrays of data, such as images or time series data, boasts three notable advantages: local connection, weight sharing, and translational invariance. These characteristics play a crucial role in diminishing the number of network parameters and expediting calculations. Thus, CNNs have been commonly used in SHM20,21. From the view of convolutional dimensions, CNNs include one-dimensional (1DCNN), two-dimensional CNN (2DCNN), and others.
Many researchers have conducted more significant studies on fault diagnosis and SHM based on 1DCNN. For example, Chen et al.22 introduced a deep learning model that integrates a 1DCNN and a bidirectional long short-term memory network (BiLSTM). This model autonomously extracts spatio-temporal features from structural vibration signals, enhancing precise identification of local structural changes in concrete beams. Notably, it exhibits improved noise immunity and robustness in managing missing data. Fathnejat et al.23 introduced a novel model, combining a 1DCNN and recurrent neural network (RNN) with an attention mechanism. This approach, evaluated using IASC-ASCE phase II and Qatar University benchmarks, excels in accuracy, training time, and model size compared to other deep learning architectures. The model’s strength lies in processing raw acceleration time-history data, showcasing its robustness under environmental variations for improved structural damage identification. Thang et al.24 introduced a deep learning approach that integrates a 1DCNN, long short-term memory network (LSTM), and residual network for the purpose of detecting structural damage. This method effectively extracts features from time-series data, identifies long-term dependencies, and mitigates the issue of gradient vanishing during network training. Consequently, it substantially enhances the accuracy and efficiency of structural damage detection using time-series data. Dang et al.25 introduced a building health monitoring framework that employs a hybrid deep learning architecture. This approach incorporates 1DCN to obtain low-dimensional representation vectors, preserving structural dynamics features. Additionally, LSTM captures temporal relationships, while graph attention networks aggregate inter-sensor information, resulting in latent representations that imply spatio-temporal features. Existing studies show that 1DCNN demonstrates a robust capability in identifying structural damage from vibration time series, but their limitation lies in handling high-dimensional vectors constructed from diverse sensor types. In contrast, 2DCNN are designed to operate on high-dimensional data, allowing them to effectively analyze horizontal and vertical relationships simultaneously. This is beneficial for recognizing complex spatial features in structural damage, which can aid in the accurate detection of damages and anomalies.
Researchers have conducted numerous studies for fault diagnosis and SHM utilizing 2DCNN methods. For instance, He et al.26 proposed a novel damage detection model by combining echo state networks (ESN) and multi-scale convolutional neural networks (MSCNN). This model extracts structural information effectively from both time and frequency domains, achieving superior performance in damage detection tasks. Yessoufou et al.27 presented an innovative two-stage CNN and LSTM framework for bridge damage identification, accounting for the impact of temperature. This model demonstrates exceptional performance in multiclass detection, localization, and severity prediction tasks, outperforming both regular CNNs and conventional machine learning methods in bridge damage assessment. Bilotta et al.28 advocate the utilization of 2DCNN for detecting damage in the connections of steel–concrete composite beams. Their approach involves training the CNN using grayscale images generated from transmissibility functions. The evaluation process focuses on determining the identified damage’s position and intensity. Existing studies indicate that 2DCNN demands input data in tensor form, necessitating preprocessing the SHM system’s collected data. This conversion process poses a potential risk of distorting or even losing some of the valuable data information, which can negatively impact the accuracy of damage detection. Thus, it is crucial to select a suitable data conversion process as an input feature for 2DCNN, reducing the loss of valuable information.
This study selects the inner product matrix (IPM) as the input of 2DCNN. The main reason is that general environmental excitation spectra can be regarded as a combination spectrum of bandpass white noise in various frequency band ranges29,30,31. According to the superposition principle of linear systems, it is known that under environmental excitation, the inner product vector remains a weighted sum of the modal shapes of the structure at all orders. Simultaneously, the weighted coefficients of each modal order are also related to the modal parameters of the structure. Furthermore, variations in structural physical parameters (such as local stiffness reduction due to structural damage) are reflected in abrupt changes in the corresponding modal shapes. Therefore, the inner product vector undergoes mutations due to local structural damage, making it possible to utilize the inner product matrix as an indicator of structural damage in structural health monitoring. Thus, the modal feature can be gained from vibration data through the inner product vector, and then, it can be used as the input of 2DCNN.
Although 1DCNN or 2DCNN can identify structural damage based on the vibration data in the SHM system, the collected data inevitably contains environmental and electromagnetic noises in addition to the structural damage information. This vibration data with noise poses a significant challenge, leading to low accuracy in damage detection using 1DCNN or 2DCNN methods. To solve the above problem, the information fusion technique demonstrates exceptional proficiency in feature extraction, outperforming deeper networks in structural damage detection32,33,34. Inspired by its influence. The study proposed a novel approach that combines an inner product matrix (IPM) with a parallel CNN, namely (IPM-PCNN), that can fuse the features in the time domain and the modal feature from the vibration data, improving the robustness and anti-noise ability in structural damage identification. Even if noisy vibration data leads to difficulty in feature extraction using 1DCNN methods, as long as the same features may be discernible in an alternative dimension, which can improve the accuracy of parallel CNN in identifying structural damage.
The proposed IPM-PCNN method mainly includes a 1DCNN branch, a 2DCNN branch, and a fully connected layer, which fuses different features from the vibration data. For the 1DCNN branch, vibration data is directly selected as 1DCNN input, extracting the temporal feature. For the 2DCNN branch, vibration data is first converted to two-dimensional tensors through the inner product process. Then, two-dimensional tensors are input 2DCNN to extract the modal feature. Subsequently, all these combined features, including time series and modal features, are input into the fully connected layer. Because vibration data can be characterized comprehensively from temporal and modal features, it can get high accuracy in damage identification. The rest of the paper is arranged as follows. “Damage identifications by an IPM-PCNN embedded framework” section describes the damage identification method based on the proposed IPM-PCNN model. “Implementation of the IPM-PCNN framework” section presents the experimental datasets and model parameters. “Results and discussion” section describes the experimental results and discussion. “Conclusions” section finally summarizes the conclusions and future work.
Damage identifications by an IPM-PCNN embedded framework
The general framework using the IPM-PCNN model
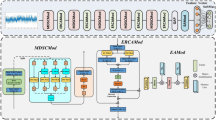
The proposed IPM-PCNN framework comprises three layers in Fig. 1: the data conversion layer, the parallel branch layer, and the fully connected layer. The data conversion layer converts the original time series to appropriate data dimensions as the input of the parallel branch layer. For the parallel branch layer, the raw time-domain signal undergoes parallel analysis using 1DCNN and 2DCNN branches. First, the original time series is segmented into non-overlapping training slices. For the 1DCNN branch, it processes these slices directly, one by one, through a time-domain CNN. The other branch gains two-dimensional tensors with modal information using an inner product process, followed by extracting modal features in a separate 2DCNN. Finally, the time and modal features are merged and fed to the fully connected layer, culminating in the generation of the classification output.
Data conversion layer
In the IPM-PCNN model, 1DCNN and 2DCNN branches have different input data. For the 1DCNN branch, original time series \({\mathbf{Y}}\) are selected as its input data to extract the time feature, \({\mathbf{Y}}\) is represented as follows:
where \({\mathbf{Y}}\) is the time series data containing all sensors. \(Y_{k} (t)\) A denote time series of the k-th sensor.
For the 2DCNN branch, original time series are converted to IPM data as its input to extract the modal feature. To be specific, given a finite-dimensional inner product space, the inner product matrix is a matrix representation of the inner product defined on that space. Assuming the original time series \({\mathbf{Y}} = [Y_{1} (t),Y_{2} (t), \cdots ,Y_{m} (t)]^{{\text{T}}}\), are available for m measurement points, with the response at measurement point k taken as the reference response, the inner product vector is defined as:
where \(h_{jk} (0)\) denotes the value of cross-correlation function between the response \(Y_{j} (t)\)(\(j = 1,2,...,m\)) and \(Y_{k} (t)\) at a time delay t = 0. According to the definition of the cross-correlation function, \(h_{jk} (0)\) can be represented as follows:
where \(< , >\) denotes inner product operator. The superposition principle in linear systems reveals that the inner product vector, influenced by environmental excitation, is a weighted sum of structure modal shapes across all orders35,36,37. Weighted coefficients correlate with modal parameters. Structural damage, like local stiffness reduction, causes abrupt changes in modal shapes, leading to mutations in the inner product vector. This mutation allows using the inner product vector as a structural damage indicator in health monitoring.
For a single measurement point, the inner product vector utilizes the response of a specific point k as the reference response, performing inner product operations with the responses of other measurement points. Considering the deployment of multiple measurement points in the structure, it is possible to efficiently perform all inner product calculation data from the time-domain responses of each measurement point. This allows the expansion of the inner product vector into an inner product matrix, denoted as \(k = 1,2,...,m\). Consequently, the IPM data can be obtained as follows:
From the definition of the inner product matrix, it can be observed that the IPM is essentially a matrix formed by arranging multiple inner product vectors, each calculated with a reference response point set to different measurement points. When structural physical parameters change, particularly involving local stiffness reduction due to structural damage, modal shapes can exhibit significant modifications. IPM effectively captures changes in modal shapes, which serve as valuable structural feature parameters for fault diagnosis and SHM.
Parallel branch layer
The parallel branch layer consists of 1DCNN and 2DCNN, which adopt a parallel mechanism and are used to accept different input data, respectively. 1DCNN is used to accept one-dimensional time series data. 2DCNN is used to accept two-dimensional IPM data. To be specific, 1DCNN branch is mainly used to extract the time features of matrix \({\mathbf{Y}}\). One-dimensional input time series is input into 1DCNN, which is as follows:
where \(Y_{i}^{l}\) are the \(ith\) output of the l layer. \(Y_{j}^{l - 1}\) are the \(jth\) output of the l-1 layer. * and \(f\) are a convolution symbol and activation function, respectively. \(\omega_{ij}^{l}\) denotes the convolution kernel, whose width matches that of \(Y_{i}^{l}\). \(b_{j}^{l}\) denotes the \(lth\) layer bias.
After the 1D convolutional layer, the max-pooling layers and the global max-pooling layer are selected to reduce the dimensionality and retain the information of the feature maps. To be specific, max-pooling can divide the feature map into a grid of non-overlapping regions and take the maximum value from each region. The formula for max-pooling is given by:
where \(P_{i}^{l}\) is the \(i^{th}\) output of the \(lth\) layer. \(Y_{i}^{l}\) is the \(ith\) output of the \(lth\) layer.
Unlike traditional max-pooling operating on local regions, global max-pooling takes the maximum value across the entire feature map. This helps capture the most significant features present in the entire input. The formula for global max-pooling is given by:
where \(Y_{i}^{l}\) and \(G_{i}^{l}\) are the \(ith\) output of the l layer.
For the 2DCNN branch, it is used to extract the modal features of structural IPM. Two-dimensional IPM data is input into 2DCNN, which is as follows:
where \(\otimes\) denotes the convolution operation. The \({\mathbf{W}}_{c} \in {\mathbf{R}}^{j \times m}\) is a weight matrix with a size of \(j\). The bias of the layer is \({\mathbf{b}}_{c}\) and the ReLU activation function accelerates model convergence. The convolution kernel feature map result is \({\mathbf{o}}_{c}\).
After the 2D convolutional process, max-pooling layers and the global max-pooling layer are employed, as described in the preceding content.
Fully connected layer
After processing by convolution and pooling layers, the outputs from the 1DCNN and 2DCNN branches are merged and then passed to a fully connected layer. A fully connected layer is a neural network layer that maps the input data into an output. The output of the fully connected layer is the final classification result. The specific formula is as follows:
where \(G_{1}\), \(G_{2}\) are extracted time features and modal features through 1DCNN and 2DCNN branches. Then, \(concatenate(.)\) fuse the extracted features. \({\mathbf{W}}_{{\text{o}}}\) is the weight matrix of the output layer. Bias is represented by \({\mathbf{b}}_{{\text{o}}}\). Softmax denotes the activation function.
Data augmentation and preprocessing
To verify the effectiveness of the proposed IPM-CNN approach, an extensive analysis is conducted using the five-story steel frame. Given the clarity and straight analysis in the time domain, this study focused on the acceleration data. Specifically, acceleration data is chosen as the primary variable of interest, as it provides damage features for monitoring diverse frame structure states. This selection allows for the effective identification of structural abnormalities and damage assessments, contributing to the steel frame structure’s overall reliability and safety.
The performance of the IPM-PCNN model for vibration signal analysis is contingent upon the number of training samples and the depth of the network architecture. While deeper networks enhance feature extraction capabilities, they concomitantly necessitate larger datasets for effective training. However, practical engineering constraints often limit the feasibility of extensive data collection. To address this challenge, data augmentation techniques, such as sliding window repeated sampling, are employed to amplify the available vibration data. By creating a sliding window of length l and employing sliding step s, this method generates multiple data samples from the original signal, augmenting the dataset without compromising its integrity in Fig. 2.
where N denotes the sample number, and L is the length of the original vibration data. l and s is the step length of a sliding window. The extent of the input data samples of the neural network can be manipulated by altering the value of l, while the number of samples can be adjusted by altering the value of s.
Data preprocessing is a crucial step in signal analysis, aiming to transform input information into a consistent and comparable format. This facilitates feature extraction and improves the effectiveness of the IPM-PCNN model. Two commonly used normalization methods are the gray image method and the ratio method, which scale data to a suitable range. The gray image method is widely applied in color image normalization, whereas the ratio method, particularly min–max normalization, is more suitable for vibration data normalization, addressing the limitation of the gray image method in handling negative values. Min–max normalization transformed the acceleration data obtained from each sensor into a decimal value ranging from 0 to 1. The mathematical representation of min–max normalization is expressed as follows:
where \(X\) and \(X_{norm}\) indicate the origin vibration data and the normalized vibration data from each sensor, respectively. This normalization process effectively scales the data to a common range, allowing for meaningful comparisons and analysis across different sensors and measurements. By constraining the data within a uniform scale, min–max normalization enhances the interpretability and comparability of the results, facilitating the identification of patterns and trends in the data.
The proposed framework for damage identification
Figure 3 presents the proposed framework for identifying frame structure damage utilizing the IPM-PCNN model. The framework collects experimental datasets from a frame structure under various structural scenarios. Subsequently, data augmentation is employed to significantly increase the number of available samples. Following augmentation, the data undergoes preprocessing to transform it into suitable 1D time-series data. Next, the inner product process is applied to each sample, generating 2D modal data. This 1D temporal series and 2D modal data are used to establish a dataset for the subsequent analysis. To facilitate the training and testing, data slicing is performed on each vibration signal, dividing the data from the frame structure into training and testing sets, maintaining an 8:2 ratio. Then, the classification-based IPM-PCNN model is trained on both undamaged and damaged frame structure data within the training set. The training process aims to minimize the prediction error loss, thereby establishing a robust model for structural condition assessment. Finally, the trained IPM-PCNN model is evaluated on the testing set to perform multi-class damage detection, effectively predicting the frame structure into various damage states (e.g., undamaged, damaged level 1, …, damaged level n).
Evaluation metrics
For fault diagnosis and SHM, evaluating the performance of a damage degree of structure is crucial. Precision, Recall, Accuracy, and F1-score38,39,40 are widely used metrics for assessing the effectiveness of a model. Precision measures the proportion of correctly classified positive instances among all instances classified as positive. Recall, also known as True Positive Rate (TPR), indicates the proportion of correctly classified positive instances among all actual positive instances. Accuracy represents the overall correctness of the model in classifying instances, including both positive and negative cases. F1 score, a harmonic mean of Precision and Recall, provides a balanced measure of model performance by considering both Precision and Recall. These metrics can evaluate the model’s ability to identify damage accurately. These evaluation metrics are defined as follows:
where TP is the number of correctly predicted positive instances. FP denotes the number of incorrectly predicted positive instances. FN is the number of incorrectly predicted negative instances. TN represents the number of correctly predicted negative instances.
Implementation of the IPM-PCNN framework
Geometric details of the steel frame and damage scenarios
The frame structure is a five-story steel frame built in the Indian Institute of Technology Mandi41. The experimental setup consists of a modular three-dimensional frame model. This design allows for simple assembly and disassembly of its components without excessive complexity. The structure comprises a total of forty joints, twenty 8 mm × 8 mm column elements, and twenty 6 mm × 6 mm beam elements in Fig. 4. The elements come together to form a three-dimensional configuration. The beam and column ends connect using C-shaped joints, providing convenient reconfigurability. This elegant design enables effortless reconfiguration of the frame model, facilitating a wide range of experimental investigations. An impact hammer furnished with a piezoelectric tip is employed to generate excitation in a frame structure. Several uni-axial accelerometers, totaling twelve, are strategically placed on various points of the structure. These accelerometers, along with three strain sensors, are connected to a data acquisition system, which samples their signals at a constant frequency of 500 Hz. For each scenario, whether damaged or undamaged, three distinct sets of time-series data are recorded. Each set consists of three consecutive hammer strikes imparted within a narrow time window of approximately 30 s, aiming for equidistant intervals between the strikes.
This experimental investigation delves into the assessment of structural damage conditions in the frame structure by simulating varying degrees of damage through the replacement of an intact beam with a damaged one (Type 1, Type 2, and Type 3) in the third story of the frame in Fig. 5a,c. Figure 5b shows four Beam-column connections of a five-story steel frame. The damaged and healthy frame structure is then subjected to an impact force using an impact hammer while acceleration sensors strategically placed at various locations on the structure capture vibration data. By meticulously comparing the vibration responses obtained from both the damaged and healthy conditions, the damaged condition of the frame structure can be evaluated.
In this study, four scenarios are established, including the healthy and three damaged conditions. The original data points for conditions D1, D2, D3, and D4 are 137,500, 120,250, 139,500, and 109,500, respectively. The sample point number of four Cases is basic maintenance balance, which contributes to the generalization ability of the neural network. The sliding window length of 50 is used to cut the original times series of four cases. Table 1 shows the data augmentation result of four damage cases. After data enhancement processing, 10,135 data samples are obtained from the times series data collected by sensors. Subsequently, all sample data is divided into training and test sets at an 8:2 ratio. Thus, the number of data samples in the training dataset is 8108, and the number of data samples in the test dataset is 2027.
Figure 6 illustrates the original partial time signals obtained from all 12 sensors under four different structural conditions. Each sub-figure in Fig. 6 displays the acceleration data in the y-direction, which reflects the vertical vibration of the structure. The x-direction represents the sample points collected at a sampling rate of 500 Hz by each sensor, which corresponds to the duration of the measurement. It is noteworthy that the recorded data from the same sensor exhibit distinguishable patterns across various damage scenarios, as shown by the different shapes and amplitudes of the signals. This indicates that the sensors are sensitive and reliable in detecting the damage of the structure and that the acceleration data can be used as a useful feature for damage identification.
Data augmentation and preprocessing techniques are employed on original time signals to gain 1D time series data, serving as the input of 1DCNN. Then, the 1D time series data undergoes transformation utilizing the inner product process, converting it into 2D modal features reflecting the damaged features of a frame structure, as depicted in Fig. 7. Figure 8 presents the modal data of the frame structure under four different scenarios. The modal data vary when the frame structure suffers damage at different stories. In this study, the proposed IPM-PCNN model can extract features from two aspects, namely temporal and modal features, thereby enhancing the accuracy of structural damage identification.
Model parameter design
In this study, the IPM-SVM, IPM-DTC, IPM-KNN, 1DCNN, 2DCNN, and IPM-PCNN models are established utilizing the Python Science Suite and Tensorflow framework. The high-performance workstation used for the experimental analysis had the following specifications: Intel Core i9-10900K processor, for the CPU, NVIDIA RTX 3080 GPU with 10 GB, and 64 GB of memory. In terms of the operating environment, the workstation runs on the latest software stack, including Tensorflow 2.2.0, Keras 2.3.1, and Python 3.9, employed for data processing and model training.
For the IPM-SVM, IPM-DTC, and IPM-KNN comparative models, parameter settings are presented in Table 2. Leveraging the given parameter ranges, an optimization process is conducted utilizing the grid search algorithm to identify the optimal parameters for each model. For the IPM-SVM model, the parameters are set as follows: C is set to 100, gamma is set to 1, and the kernel is set to ‘rbf’. For the IPM-DTC model, the parameter max depth is set to 10. Lastly, for the IPM-KNN model, the parameter n neighbors are set to 4.
For the comparative analysis of the 1DCNN, 2DCNN, and IPM-PCNN models, the training process adopts the Adam optimizer42 with an initial learning rate and batch size set at 0.0005 and 128, respectively. The training procedure consists of 200 epochs. To address potential overfitting, dropout regularization with a rate of 50% and L2 regularization are employed. Model evaluation is conducted using the cross-entropy loss metric.
Table 3 presents the parameters of two CNN models, 1DCNN and 2DCNN. Both architectures consist of 7 layers in depth. The number of neurons in each layer for 1DCNN and 2DCNN is [4,20,32,32]. However, the convolutional kernel sizes differ between the two architectures. 1DCNN employs a convolutional kernel size of 3, whereas 2DCNN utilizes two different kernel sizes, namely 5 × 5 and 3 × 3. Additionally, the pooling operations also vary between the two architectures. The pooling window size for 1DCNN is 2, whereas 2DCNN uses a 2 × 2 window size, indicating that a 2 × 2 pooling window is applied along each dimension of the feature maps.
Table 4 presents the architecture and configuration details of the IPM-PCNN model, which includes 1D, 2D branches, and fully connected layers. The input data consists of time series with dimensions of 8108 × 600 for the 1D branch and IPM features with dimensions of 8108 × 12 × 12 for the 2D branch. Feature extraction is performed separately for each branch, utilizing different layers and convolutional kernel sizes. In the 1D branch, convolutional kernels of sizes 7 and 5 are employed, with a maximum pooling size of 5, resulting in a dimensionality reduction to an 8108 × 128 feature vector through global max-pooling. Similarly, in the 2D branch, convolutional kernels of sizes 5 × 5 and 3 × 3 are utilized, with a 3 × 3 max-pooling size of 2 × 2, resulting in an 8108 × 128 feature vector through global max-pooling. Feature fusion is achieved by concatenating the feature vectors from both branches and passing them through fully connected layers with 256, 150, and 100 neurons, respectively. Dropout with a dropout rate of 0.5 is applied before the final fully connected layer, which consists of 4 neurons and utilizes a softmax activation function for classification.
Results and discussion
Comparisons of model performance
In order to assess the damage identification capability of the proposed IPM-PCNN model, the steel frame structure is tested on different methods, including IPM-PCNN, 1DCNN, 2DCNN, IPM-SVM, IPM-DTC, and IPM-KNN. The results, as depicted in Fig. 9, reveal that these models exhibit an accuracy greater than 90% and a smooth loss curve, which suggests their exceptional fitting ability. However, among these models, the proposed IPM-PCNN model stands out for its robust learning and fitting capabilities. It demonstrates a faster convergence speed and achieves the highest accuracy of 96%. Compared with 1DCNN and 2DCNN, the proposed IPM-PCNN model achieves at least a 2% improvement in accuracy. This significant enhancement highlights the effectiveness and superiority of the method in damage identification tasks. The enhanced performance of the IPM-PCNN model can be attributed to its robust temporal and modal feature extraction capabilities from the data. Furthermore, the IPM-PCNN model’s ability to achieve high accuracy and rapid convergence suggests its potential for real-time damage identification in practical applications. This is particularly valuable in structural health monitoring, where timely and accurate detection of damage is crucial for ensuring the safety and reliability of structures.
To analyze the classification ability of every scenario, Fig. 10 shows the confusion matrix of six compared models. For the 1DCNN confusion matrix, it achieved relatively high accuracy across all classes. The diagonal values are noticeably higher than off-diagonal ones, indicating a strong capability in correctly classifying instances. However, some confusion is evident, particularly between classes 1 and 4, as well as 2 and 1, as seen in the off-diagonal elements. This suggests that the algorithm may struggle with distinguishing these pairs of classes. Similar to the 1DCNN results, the 2DCNN confusion matrix showcases a commendable performance overall. The diagonal values are predominant, indicating correct classifications. However, there are still some instances of confusion, particularly between classes 1 and 2. This implies that despite the algorithm’s overall accuracy, there are specific class pairs where it faces challenges in differentiation. The IPM-SVM, IPM-DTC, and IPM-KNN models exhibited limitations in effectively discriminating between different classes. For particularly classes 2 and 4, they exhibited considerably higher error rates, suggesting potential shortcomings in traditional machine learning approaches regarding feature extraction. Overall, the IPM-PCNN illustrates a robust performance across all classes, with predominantly high diagonal values, demonstrating a high level of accuracy in the classification task.
Figure 11 and Table I1 show the classification results of different models in every scenario. Firstly, focusing on Precision, IPM-PCNN consistently exhibits superior precision rates across all datasets. Specifically, in D1, IPM-PCNN achieves a Precision of 0.9569, followed by 0.9624 in D2, 0.9801 in D3, and 0.9635 in D4. This indicates the model’s exceptional ability to correctly classify positive instances with minimal false positives. Secondly, examining Recall, IPM-PCNN also demonstrates commendable performance, showcasing the highest Recall rates in most datasets. Notably, the model achieves Recall scores of 0.9691 in D1, 0.9584 in D2, 0.9713 in D3, and 0.9635 in D4. These values suggest the model’s effectiveness in capturing a significant proportion of true positive instances while minimizing false negatives. Furthermore, considering the F1-Score, which harmonizes Precision and Recall, IPM-PCNN consistently outperforms other models across all datasets. With an F1-Score ranging from 0.9604 to 0.9757, IPM-PCNN demonstrates a robust balance between Precision and Recall, indicating its ability to achieve high classification accuracy while maintaining strong sensitivity to positive instances.
Among the compared models, 1DCNN and 2DCNN models both exhibit remarkable performance across all datasets, showcasing consistent Precision, Recall, and F1-Score. Specifically, 1DCNN achieves Precision values ranging from 0.8947 to 0.9532, Recall from 0.8836 to 0.9618, and F1-Score from 0.8891 to 0.9497. Similarly, 2DCNN demonstrates Precision ranging from 0.9124 to 0.9669, recall from 0.8919 to 0.9655, and F1-Score from 0.9060 to 0.9537. These models exhibit robust and balanced performance across all metrics, indicating their efficacy in accurate classification tasks. IPM-SVM showcases a decent performance across various datasets, with Precision ranging from 0.6184 to 0.9778, Recall from 0.6027 to 0.9231, and F1-Score from 0.7458 to 0.8561. However, its F1-Score suggests a notable trade-off between Precision and Recall, indicating potential challenges in achieving a balanced classification. Similarly, IPM-DTC demonstrates strong Precision and Recall values, particularly notable in D3 with a Precision of 0.9092 and Recall of 0.9337, but its F1-Score shows some variability across datasets. While IPM-KNN exhibits high Recall rates across all datasets, with values ranging from 0.7785 to 0.9873, its precision values vary, indicating potential challenges in minimizing false positives.
Consequently, the comprehensive analysis of Precision, Recall, and F1-Score suggests that IPM-PCNN is a top-performing model across all evaluated datasets. It demonstrates that IPM-PCNNs perform well in classification tasks and can be an effective choice for damage identification.
Table 5 shows the overall accuracy of different models on the steel frame structure. The experimental result demonstrates that the proposed IPM-PCNN model outperforms 1DCNN, 2DCNN, IPM-SVM, IPM-DTC, and IPM-KNN by achieving a significantly higher accuracy of 96.60%, achieving an improvement of at least 3%. Since it can capture the temporal and modal features from the vibration signals, the IPM-PCNN model outperforms the single time-feature methods (i.e., 1DCNN model) or the single modal features methods (i.e., 2DCNN model).
Figure 12 and Table 7 show overall evaluated results of damaged identification based on the Precision, Recall, and F1-score metric. Among these models, IPM-PCNN stands out with the highest scores across all metrics, achieving an Accuracy of 0.9660, Precision of 0.9660, Recall of 0.9660, and F1-score of 0.9660. This indicates its consistent and reliable performance across various evaluation criteria. Following closely, both 2DCNN and 1DCNN demonstrate competitive performance, with 2DCNN achieving an Accuracy of 0.9369 and a Precision of 0.9270, and 1DCNN achieving an Accuracy of 0.9270 and a Precision of 0.9270. These results suggest that 1D and 2D with a single feature extraction have some limation in damaged identification. IPM-SVM lags significantly behind the CNN models in terms of Accuracy, Precision, Recall, and F1-score, with values of 0.8027, 0.8467, 0.8027, and 0.8048 respectively. Meanwhile, IPM-DTC and IPM-KNN exhibit low performance, with Accuracy values of 0.8633 and 0.8900, and Precision values of 0.8621 and 0.8934 respectively. It indicates the IPM-SVM, IPM-DTC, and IPM-KNN models have low Accuracy and F1-score, and have a large gap between Precision and Recall. This means that they are either too strict or too lenient in making positive predictions, and have a high rate of false positives or false negatives.
Visualization of the extracted features
To further investigate the capability of structural damage identification, analysis is carried out from the perspective of feature extraction visualization using the T-distributed stochastic neighbor embedding method (T-SNE). To be specific, for 1DCNN, 2DCNN, and IPM-PCNN models, the most abstract and high-level features are stored in the last fully connected (FC) layer after undergoing a sequence of convolutional and pooling operations. Then, the final extracted features of the last fully connected block are converted into a 2-dimensional feature for visualization using T-SNE method. For IPM-SVM IPM-DTC and IPM-KNN, the extracted feature is directly fed into T-SNE method, because these algorithms don’t network back-propagation.
Figure 13 shows the visualization results of the feature extraction on four case scenarios and compares the performance among IPM-SVM, IPM-DTC, IPM-KNN, 1DCNN, 2DCNN, and IPM-PCNN. A total of 2,027 data points are used for each scenario, distinguished by unique colors. Ideally, data points originating from the same damage scenario should cluster closely together, indicating similar characteristics. Conversely, data points belonging to different scenarios should be distinctively separated by clear boundaries formed by the different colored clusters. This visual representation facilitates the identification of inherent patterns within the data and potential relationships between damage scenarios. Specifically, for IPM-SVM, IPM-DTC, and IPM-KNN, the data points from this method cannot form clusters under the same scenario. Instead, they are located in different positions in the space. This indicates that machine learning algorithms cannot effectively extract structural damage features and identify structural damage when facing acceleration data. For 1DCNN, 2DCNN, and PCNN models, the results showed that four colored clusters are observed in the feature space of each model, corresponding to four different damage scenarios. However, the IPM-PCNN model performed the best among the three models, as it achieved a clear separation of the colored groups with no overlaps. On the other hand, the 1DCNN and 2DCNN models showed some overlaps among the points from different damage scenarios, indicating that they are less effective in distinguishing the damage features and identifying the structural damage.
Conclusions
This study presents a novel IPM-PCNN framework for structural damage identification, which extracting both time-domain and modal features from vibration data from the input signal. The proposed model has been validated through experimental tests on a steel frame structure. The main findings of this study can be summarized as follows:
-
(1)
The IPM-PCNN model outperforms mainstream damage detection methods, such as IPM-SVM, IPM-DTC, IPM-KNN, 1DCNN, and 2DCNN, by extracting features from vibration-based data in both temporal domain and modal features. The IPM-PCNN model demonstrated superior performance, achieving a high accuracy rate of 96.60% in structural damage detection.
-
(2)
Compared to single input feature models, such as 1DCNN and 2DCNN, the IPM-PCNN model demonstrated superior performance. It achieves an accuracy improvement of at least 3% for the steel frame structure. This result highlights the model’s robustness and reliability in real-world applications.
-
(3)
Visualization of feature extraction using the T-SNE method further confirms the effectiveness of the IPM-PCNN model. The model consistently achieved distinct separations between different damage states, with no overlap, outperforming all other evaluated models (IPM-SVM, IPM-DTC, IPM-KNN, 1DCNN, 2DCNN) in terms of feature differentiation.
Data availability
The datasets generated during the analysis are available from the corresponding author.
Code availability
The datasets generated during the analysis are available from the corresponding author.
References
Sun, B., Zhang, Y., Dai, D., Wang, L. & Ou, J. Seismic fragility analysis of a large-scale frame structure with local nonlinearities using an efficient reduced-order Newton–Raphson method. Soil Dyn. Earthq. Eng. 164, 107559 (2023).
Jung, J.-S., Lee, B.-G. & Lee, K.-S. Seismic capacity evaluation of existing reinforced concrete buildings strengthened with a novel prestressing steel frame system for increasing lateral strength. J. Build. Eng. 79, 107856 (2023).
Kiakojouri, F., De Biagi, V., Chiaia, B. & Sheidaii, M. R. Progressive collapse of framed building structures: Current knowledge and future prospects. Eng. Struct. 206, 110061 (2020).
Yang, J., Zhuang, H., Zhang, G., Tang, B. & Xu, C. Seismic performance and fragility of two-story and three-span underground structures using a random forest model and a new damage description method. Tunn. Undergr. Space Technol. 135, 104980 (2023).
Lin, J., Lu, S., He, X. & Wang, F. Analyzing the impact of three-dimensional building structure on CO2 emissions based on random forest regression. Energy 236, 121502 (2021).
Farfani, H. A., Behnamfar, F. & Fathollahi, A. Dynamic analysis of soil-structure interaction using the neural networks and the support vector machines. Expert Syst. Appl. 42, 8971–8981 (2015).
Zhou, C., Chase, J. G. & Rodgers, G. W. Support vector machines for automated modelling of nonlinear structures using health monitoring results. Mech. Syst. Signal Process. 149, 107201 (2021).
Chen, S.-Z., Feng, D.-C., Wang, W.-J. & Taciroglu, E. Probabilistic machine-learning methods for performance prediction of structure and infrastructures through natural gradient boosting. J. Struct. Eng. 148, 04022096 (2022).
Nguyen, H. D., Dao, N. D. & Shin, M. Prediction of seismic drift responses of planar steel moment frames using artificial neural network and extreme gradient boosting. Eng. Struct. 242, 112518 (2021).
Salkhordeh, M., Mirtaheri, M. & Soroushian, S. A decision-tree-based algorithm for identifying the extent of structural damage in braced-frame buildings. Struct. Control Health Monit. 28, e2825 (2021).
Karbassi, A., Mohebi, B., Rezaee, S. & Lestuzzi, P. Damage prediction for regular reinforced concrete buildings using the decision tree algorithm. Comput. Struct. 130, 46–56 (2014).
Zeng, Y., Guo, Y. & Li, J. Recognition and extraction of high-resolution satellite remote sensing image buildings based on deep learning. Neural Comput. Appl. 34, 2691–2706 (2022).
Yu, B., Yang, A., Chen, F., Wang, N. & Wang, L. SNNFD, spiking neural segmentation network in frequency domain using high spatial resolution images for building extraction. Int. J. Appl. Earth Observ. Geoinf. 112, 102930 (2022).
Kong, Q. et al. PANNs: Large-scale pretrained audio neural networks for audio pattern recognition. IEEE/ACM Trans. Audio Speech Lang. Process. 28, 2880–2894 (2020).
Maccagno A. et al. A CNN approach for audio classification in construction sites. In Progresses in Artificial Intelligence and Neural Systems (eds. Esposito A., Faundez-Zanuy M., Morabito F. C. & Pasero E.) Vol. 184 371–381 (Springer Singapore, 2021).
Olivetti, E. A. et al. Data-driven materials research enabled by natural language processing and information extraction. Appl. Phys. Rev. 7, 041317 (2020).
Min, B. et al. Recent advances in natural language processing via large pre-trained language models: A survey. ACM Comput. Surv. 56, 1–40 (2024).
Jia, J. & Li, Y. Deep learning for structural health monitoring: Data, algorithms, applications, challenges, and trends. Sensors 23, 8824 (2023).
Torzoni, M., Rosafalco, L., Manzoni, A., Mariani, S. & Corigliano, A. SHM under varying environmental conditions: An approach based on model order reduction and deep learning. Comput. Struct. 266, 106790 (2022).
Hou, X., Zeng, Y. & Xue, J. Detecting structural components of building engineering based on deep-learning method. J. Constr. Eng. Manag. 146, 04019097 (2020).
Oh, B. K., Park, Y. & Park, H. S. Seismic response prediction method for building structures using convolutional neural network. Struct. Control Health Monit. 27, e2519 (2020).
Chen, X., Jia, J., Yang, J., Bai, Y. & Du, X. A vibration-based 1DCNN-BiLSTM model for structural state recognition of RC beams. Mech. Syst. Signal Process. 203, 110715 (2023).
Fathnejat, H., Ahmadi-Nedushan, B., Hosseininejad, S., Noori, M. & Altabey, W. A. A data-driven structural damage identification approach using deep convolutional-attention-recurrent neural architecture under temperature variations. Eng. Struct. 276, 115311 (2023).
Le-Xuan, T., Bui-Tien, T. & Tran-Ngoc, H. A novel approach model design for signal data using 1DCNN combing with LSTM and ResNet for damaged detection problem. Structures 59, 105784 (2024).
Dang, V.-H. & Pham, H.-A. Vibration-based building health monitoring using spatio-temporal learning model. Eng. Appl. Artif. Intell. 126, 106858 (2023).
He, Y., Zhang, L., Chen, Z. & Li, C. Y. A framework of structural damage detection for civil structures using a combined multi-scale convolutional neural network and echo state network. Eng. Comput. 39, 1771–1789 (2023).
Yessoufou, F. & Zhu, J. Classification and regression-based convolutional neural network and long short-term memory configuration for bridge damage identification using long-term monitoring vibration data. Struct. Health Monit. 22, 4027–4054 (2023).
Bilotta, A., Morassi, A. & Turco, E. Damage identification for steel-concrete composite beams through convolutional neural networks. J. Vib. Control 30, 876–889 (2024).
Yang, S., Wan, M. P., Chen, W., Ng, B. F. & Dubey, S. Model predictive control with adaptive machine-learning-based model for building energy efficiency and comfort optimization. Appl. Energy 271, 115147 (2020).
Faqih, F., Zayed, T. & Soliman, E. Factors and defects analysis of physical and environmental condition of buildings. J. Build. Rehabil. 5, 19 (2020).
Jeong, S. Y., Kang, T.H.-K., Yoon, J. K. & Klemencic, R. Seismic performance evaluation of a tall building: Practical modeling of surrounding basement structures. J. Build. Eng. 31, 101420 (2020).
Gao, J., Li, P., Chen, Z. & Zhang, J. A survey on deep learning for multimodal data fusion. Neural Comput. 32, 829–864 (2020).
Meng, T., Jing, X., Yan, Z. & Pedrycz, W. A survey on machine learning for data fusion. Inf. Fusion 57, 115–129 (2020).
Zhang, C., Yang, Z., He, X. & Deng, L. Multimodal intelligence: Representation learning, information fusion, and applications. IEEE J. Sel. Top. Signal Process. 14, 478–493 (2020).
Martini, A., Tronci, E. M., Feng, M. Q. & Leung, R. Y. A computer vision-based method for bridge model updating using displacement influence lines. Eng. Struct. 259, 114129 (2022).
Ciambella, J. & Vestroni, F. The use of modal curvatures for damage localization in beam-type structures. J. Sound Vib. 340, 126–137 (2015).
Gordan, M. et al. State-of-the-art review on advancements of data mining in structural health monitoring. Measurement 193, 110939 (2022).
Sony, S., Gamage, S., Sadhu, A. & Samarabandu, J. Multiclass damage identification in a full-scale bridge using optimally tuned one-dimensional convolutional neural network. J. Comput. Civ. Eng. 36, 04021035 (2022).
Sony, S., Gamage, S., Sadhu, A. & Samarabandu, J. Vibration-based multiclass damage detection and localization using long short-term memory networks. Structures 35, 436–451 (2022).
Zhang, L. & Pan, Y. Information fusion for automated post-disaster building damage evaluation using deep neural network. Sustain. Cities Soc. 77, 103574 (2022).
Hoda, M. A., Kuncham, E. & Sen, S. Response and input time history dataset and numerical models for a miniaturized 3D shear frame under damaged and undamaged conditions. Data Brief 45, 108692 (2022).
Modarres, C., Astorga, N., Droguett, E. L. & Meruane, V. Convolutional neural networks for automated damage recognition and damage type identification. Struct. Control Health Monit. 25, e2230 (2018).
Acknowledgements
We would like to express our heartfelt gratitude to the esteemed reviewers for their invaluable contributions to the refinement of this scientific manuscript.
Funding
The work described in this paper is supported by the Science and Technology Research Program of Chongqing Municipal Education Commission (Grant No. KJQN202301801, KJQN202201805, KJZD-M202201801), the Humanities and Social Sciences Research Program of Chongqing Municipal Education Commission (Grant No. 22SKGH493, 24SKGH346), Natural Science Foundation of Chongqing Municipality (Grant No. CSTB2024NSCQ-MSX1067), the Science and Technology Research Program of Chongqing College of Humanities, Science & Technology (Grant No. CRKZK2023007, JSJGC202201).
Author information
Authors and Affiliations
Contributions
The authors confirm their contribution to the paper as follows: draft manuscript preparation: Y.H.; data collection: J.F. and J.J.; analysis and interpretation of results: B.S.; methodology: F.W. and L.Z.; funding acquisition: Y.H.. All authors reviewed the results and approved the final version of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no conflict of interest.
Consent to participate
Informed consent was obtained from all individual participants included in the study.
Consent for publication
Publication consent was obtained from all individual participants included in the study.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
He, Y., Feng, J., Sun, B. et al. Damage identification based on the inner product matrix and parallel convolution neural network for frame structure. Sci Rep 14, 30548 (2024). https://doi.org/10.1038/s41598-024-82058-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-024-82058-7