Introduction

One approach to improving heat transmission in heat exchangers is by incorporating materials with efficient thermal conductivity into the base fluid. For many years, researchers have invested significant time and effort in investigating the potential for improving heat transmission by using an integration of nanometer-scale solid particles suspended in fluids. Nevertheless, these fluids encountered several problems such as sedimentation, contaminants, corrosion, and heightened loss of pressure, among other factors. Before 1881, when Maxwell initially suggested the use of nanoparticles, there had been no notable advancement in the study of heat transmission in fluids. However, there was a significant and abrupt transformation that occurred after the year 1881. He introduced an innovative viewpoint on the behavior of mixtures of solids and fluids including nanoparticles. In their study, Masuda et al.1 introduced nanofluid (NF) to refer to a fluid that consists of particles that are suspended inside it, and later Choi2 further developed this concept. Nanofluid (NF) is a colloidal dispersion consisting of extremely small solid particles, that are 1 to 100 nm in size. Nanoparticles (NPs) have greater stability compared to larger particles such as microparticles, and they also possess the fluid region having a larger surface area in contact. NF is known for its exceptional stability and thermal conductivity. Base fluids are commonly used in industries for heat exchange, with water and ethylene glycol, and similar fluids. On the other hand, NPs are generally composed of metals like copper, aluminum, and iron, as well as carbon nanotubes (CNTs) and including their oxides. The small size of the particles reduces the potential for corrosion and pressure loss, while also enhancing the fluids’ ability to resist sedimentation. Over the past decade, several studies have been explored on the NFs3,4,5.

Typically, nanofluids provide advantages in improving the thermal stability of traditional fluids. In 1991, Iijima6 was the first to discover carbon nanotubes (CNTs). CNTs are graphene sheets having tubular structures that are rolled into long cylinders. The diameter of these cylinders can range from 0.7 to 50 nm. CNTs are divided into two types based on the number of graphene layers they contain SWCNTs and MWCNTs. CNTs are anticipated to be the optimal nano-materials of the twenty-first century because of their distinctive form, groundbreaking physicochemical properties, and exceptional thermal, electrical, and mechanical traits. Choi et al.7 examined the enhancement of heat conductance in CNTs dispersed in oil. The researchers discovered that the nanofluid containing carbon nanotubes (CNTs) had a higher thermal conductivity than typical fluids. Nadeem et al.8 highlighted the significance of MWCNTs in enhancing the flow of hybrid nanofluids in a wavy rectangular duct. They employed the eigenvalue expansion approach to increase the thermal conductivity. When comparing the liquid flow models, the pressure gradient exhibits a rapid increase in the hybrid NF model. In their study, Ibrahim and Khan9 examined the combined convection flow of SWCNT and MWCNT with water across a stretchy permeable sheet. The NF populated a porous media. Darcy’s law is employed to describe porous media. Haq et al.10 utilize the Xue model to examine the flow of nanofluids containing CNTs. In this case, a notable increase in the Nusselt number was noticed when higher concentrations of carbon nanotubes (CNT) were used in the engine oil. Hayat et al.11 considered both the single-wall and multi-wall properties of CNTs in a mixed convective flow. The results illustrate that an increment in the quantity of carbon nanotubes leads to a reduction in heat transfer. Khan et al.12 elucidated the structural aspects of the flow of MWCNTs and SWCNTs in conjunction with quartic chemical processes and induced flux. The results demonstrate that the surface drag coefficient and the velocity ratio parameter are inversely proportional. A multitude of studies13,14,15,16 have elucidated numerous properties of nanofluids and carbon nanotubes (CNTs).

Magnetohydrodynamic (MHD) fluxes are essential for preserving the flow characteristics and enhancing the thermal efficiency of different fluids. The physical characteristics of a fluid are susceptible to a significant transformation when it interacts with a magnetic field. Researchers have shown particular interest in this pursuance due to the vast array of uses of MHD. Shahid et al.17 used computer simulations to demonstrate how a magnetic field alter the flow characteristics of a viscous, in-compressible fluid approaching a stagnation point in a non-Darcian permeable medium. The physical phenomenon between electrically conducting fluids and magnetic fields has a significant impact on several industrial instruments, including bearings, MHD generators, and MHD pumps. The entropy generation analysis for a power-law fluid flow occurs in the presence of heat radiation and magnetic field conducted by Hayat et al.18. The flow and heat transmission are regulated using a linked system of partial differential equations which turned into a dimensionless form by using appropriate parameters and numerical computations conducted using the finite difference (FD) technique. Abdulaziz and Alkuhayli19 studied the characteristics of the magnetohydrodynamic flow of NF containing copper nanoparticles of nano-size in a rigid circular disc. Shahid et al.20 studied the in-compressible continuous flow of magnetohydrodynamic NF with temperature-dependent viscosity across a vertically extended porous sheet. The impacts of activation energy, magnetohydrodynamics and Joule heating, on the flow of third-grade nanofluid induced by a spinning stretchable disk investigated by Salman et al.21. Jakeer et al.22 found the combined impacts of chemical reactions and magnetic fields on convective radiated cross-NF flow using an artificial neural network. Using finite difference scheme Salman et al.23,24 scrutinized viscous fluid flow caused by a stretchy spinning disk applying magnetic field considering Joule heating effect and the implications of the magnetic field impact in the vertical orientation relative to the plates. References25,26,27,28,29 reported the recent research conducted on magnetic fields.

The Darcy–Forchheimer (DF) model is the predominant method for modifying Darcian flow to report the impacts of analogous inertia. Forchheimer’s extension incorporates the influence of inertia in the momentum equation by including a factor of velocity squared. Ramonu et al.30 investigated the natural convection flow and heat transportation of an NF via a porous plate in a DF flow. In their study, Vishnu et al.31 explored the flow of hydromagnetic NF across a stretched sheet in a thermally stratified porous environment, considering the ohmic dissipation effect and the DF flow. Hayat et al.32 studied the convective stagnation point flow of nanofluids using the Darcy–Forchheimer relation. Falana and Alao33 found the solution for the heat and mass transfer flow of NF along a porous sheet in a DF flow. Ibrahim34 explored the time-dependent flow of a viscous fluid caused by a revolving stretchable disk. Fluid infiltrating a porous media and Darcy’s law is employed to characterize porous media. Khan and Nadeem35 developed a model for the steady flow of Maxwell fluid across a vertically stretched sheet, considering the double stratified DF effect. Gbadeyan et al.36 studied non-Darcian porous media’s impact on the flow of Casson NF with magnetohydrodynamics across a vertical flat plate. The effects of a DF medium on the flow of a Cross fluid model across a stretched surface studied by Hayat et al.37. Shahid et al.38 explored the effect of activation energy on steady NF flow across an elastic stretched surface. They employed the Reynolds exponential model for mathematical modeling since the viscosity of fluid changes with temperature and solved non linear differential equation by applying the spectral local linearization method. Awais et al.39 examined the properties of the radiated DF flow with the Dufour and Soret effects of the Eyring–Powell fluid. Upreti et al.40 examined the behavior of CNTs submerged in water-based dielectric fluid flow.

An artificial neural network (ANN) refers to a machine learning technique that is designed to mimic the structure and functionality of the human brain. The system consists of several linked processing units known as neurons, which are arranged in layers. The input layer gets data from the external environment and transmits it to the hidden levels. The hidden layers do intricate calculations on the incoming data and transmit the outcomes to the output layer. The output layer generates the final result of the network. Artificial neural networks are used for a range of applications, such as, pattern identification, time-series analysis, language processing, image and audio recognition. They can undergo training utilizing supervised, unsupervised, and reinforcement learning methodologies. ANNs have demonstrated effectiveness in several applications, however they do possess certain limitations. In order to achieve optimal performance, these models need substantial quantities of data for training and may incur significant computing costs. Artificial neural networks have been used to study various mathematical models, such as astrophysics studied by Ahmad et al.41, studies related to plasma physics conducted by Raja et al.42, nanofluid modelling43, Thomas–Ferri models44,45, ferrofluid modelling46, corneal shape model and systems of the Flanker Skan47, prediction of COVID-19 disease in Pakistan via artificial neural networks48, wire coating problem49, and numerical treatment of computer virus model50. The evidence mentioned above indicates that stochastic techniques based on ANNs have a strong potential for tackling problem related fluid models.

Neural networks featuring recurrent connections are termed as recurrent neural networks (RNNs). RNNs can accurately depict sequential input, allowing them to execute tasks such as recognizing and predicting sequences. Recurrent neural networks are machine learning algorithm characterized by artificial neurons that comprises artificial neurons with one or more feedback cycles. Feedback cycles are iterative processes that occur again over a specific duration or sequence. In order to train a RNN using supervised learning, it is necessary to have a training data set that includes input-target pairs organized in cell form. The main objective is to minimize the discrepancy between the output and target pairs through the optimization of the network’s weights. As stated in the literature above, there have been no applications of recurrent neural network (RNN)-based computational methods to address the Darcy–Forchheimer flow of propylene glycol with carbon nanotubes (DFPG-CNTs) model under magnetic influence and activation energy across a stretched cylinder. The authors are motivated to develop a novel algorithm based on RNN by the widespread use of the technique and its well-established efficacy across numerous applications. The authors present a new intelligent computing approach to study the DFPG-CNTs model by implementing recurrent Bayesian regularization based neural networks RNNs-BRO. The following aspects highlight the novel contributions of the proposed scheme:

  • An application of recurrent neural networks with Bayesian regularization optimizer is implemented to investigate numerically the DFPG-CNTs model across a stretched cylinder.

  • The reference data-set for the model is generated through state of the art Adam’s numerical method for different scenarios by the variation of curvature parameter (\(\gamma\)), inertia coefficient (\({F}_{r}\)), porosity parameter (\({K}_{p}\)), Eckert number (\(Ec\)), Prandtl number (\(Pr\)), radiation parameter (\(Rd\)), Hartmann number (\(M\)), activation energy variable (\({E}_{1}\)), Schmidt number (Sc) and reaction rate parameter (\(\beta\)).

  • The refinement of each data-set is processed through RNNs-BRO for attestation of the proposed scheme.

  • Regression analysis, histogram analyses, mean squared error, transition state analysis, and auto-correlation are utilized to examine the effectiveness of numerical computing approach.

  • In addition, the impact of significant parameters on the profiles of fluid velocity, temperature and mass concentration is analyzed, and their implications for various physical scenarios are discussed in detail.

The study is arranged in the following way: After doing a literature assessment, “Modelling of the problem” section illustrates a model formulation for the DFPG-CNTs model. “Proposed methodology” section presents the proposed methodology used, “Results and discussion” section and “Impact of parameters on velocity, temperature and concentration profiles” section presents the numerical results obtained. Finally, “Conclusions” section is structured to get the findings from the entire evaluation.

Modelling of the problem

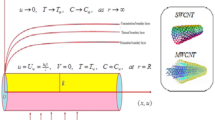
This study examines the flow of a nanofluid that contains MWCNT and SWCNT immersed as nanoparticles in propylene glycol (\({\text{C}}_{3}{\text{H}}_{8}{\text{O}}_{2}\)). In order to investigate the flow properties, a stretched cylinder with porous walls is considered. Various factors, including DF, thermal radiation, and intermolecular friction force, are taken into account. Moreover, a chemical process involving Arrhenius kinetics takes place at the cylinder’s surface. The cylinder is stretched along the x-direction with a velocity of \(u_{1w} = \frac{{u_{{1_{0} }} x}}{l}\). \({T}_{w}\) and \({T}_{\infty }\) represent the surface and ambient temperatures of the fluid, respectively. The flow is influenced by a uniform magnetic field oriented perpendicularly. Figure 1 is a representation of the flow diagram in its schematic form. The mathematical model governing the steady flow across a stretched cylinder with porous walls, considering Darcy–Forchheimer effects and thermal radiation under the boundary layer approximation is expressed as follows51,52:

$$\frac{{\partial u_{1} }}{\partial x} + \frac{{\partial u_{2} }}{\partial r} + \frac{{u_{2} }}{r} = 0,$$
(1)
$$u_{1} \frac{{\partial u_{1} }}{\partial x} + u_{2} \frac{{\partial u_{1} }}{\partial r} = \nu_{nf} \left( {\frac{{\partial^{2} u_{1} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial u_{1} }}{\partial r} - \frac{{u_{1} }}{{K_{1} }}} \right) - \frac{{\sigma_{nf} B_{0}^{2} u_{1} }}{{\rho_{nf} }} - F_{e} u_{1}^{2} ,$$
(2)
$$u_{1} \frac{\partial T}{{\partial x}} + u_{2} \frac{\partial T}{{\partial r}} = \alpha_{nf} \left( {\frac{{\partial^{2} T}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial T}{{\partial r}}} \right) + \frac{1}{{(\rho C_{p} )_{nf} }}\left( {\frac{{16\sigma^{ * } T_{\infty }^{3} }}{{3k^{ * } }}\frac{{\partial^{2} T}}{{\partial r^{2} }} + \sigma_{nf} B_{0}^{2} u_{1}^{2} + \mu_{nf} \left( {\frac{{\partial u_{1} }}{\partial r}} \right)^{2} } \right),$$
(3)
$$u_{1} \frac{\partial C}{{\partial x}} + u_{2} \frac{\partial C}{{\partial r}} = D\left( {\frac{{\partial^{2} C}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial C}{{\partial r}}} \right) - \left( {\frac{T}{{T_{\infty } }}} \right)^{n} Kr^{2} (C - C_{\infty } )e^{{{\raise0.7ex\hbox{${ - Ea}$} \!\mathord{\left/ {\vphantom {{ - Ea} {kT}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${kT}$}}}} ,$$
(4)

with boundary conditions as follows51,52:

$$\left. {\begin{array}{*{20}c} {u_{1} = u_{{1_{w} }} = u_{{1_{o} }} x/l,\,\,u_{2} = 0,\,T = T_{w} ,\,\,C = C_{w} ,\,\,{\text{at }}r = R} \\ {u_{1} \to 0,\,\,T \to T_{\infty } ,\,\,C \to C_{\infty } ,{\text{ as }}r \to \infty} \\ \end{array}. } \right\}$$
(5)
Fig. 1
figure 1

Geometry of DFPG-CNTs model.

Full size image

The term \(\left( { - \frac{{u_{1} }}{{K_{1} }} - F_{e} u_{1}^{2} } \right)\) in the momentum equation stands for the Darcy–Forchheimer drag, which takes into consideration the resistance effects exerted by the porous medium. The Darcy term \(\left( { - \frac{{u_{1} }}{{K_{1} }}} \right)\) reflects the viscous resistance resulting from the porous medium’s permeability, while the Forchheimer term (\(- F_{e} u_{1}^{2}\)) denotes the inertial drag induced by the flow velocity. The incorporation of the Darcy–Forchheimer term assures that the governing equations accurately represent the physical behavior of the NF within a porous medium.

The properties of nanofluids with mathematical modeling are defined51,52 as:

$$\left. \begin{gathered} \mu_{nf} = \frac{{\mu_{f} }}{{(1 - \varphi )^{2.5} }}, \, \alpha_{nf} = \frac{{k_{nf} }}{{(\rho C_{p} )_{nf} }}, \, \rho_{nf} = \rho_{f} (1 - \varphi ) + \rho_{CNT} \varphi ,{\text{ (C}}_{p} \rho )_{nf} = {\text{(C}}_{p} \rho )_{f} (1 - \varphi ) + \varphi {\text{(C}}_{p} \rho )_{CNT} ,\, \hfill \\ k_{nf} { = }k_{f} \left( {\frac{{2\varphi \left( {\frac{{k_{CNT} }}{{k_{CNT} - k_{f} }}} \right)ln\left( {\frac{{k_{f} + k_{CNT} }}{{2k_{f} }}} \right) + (1 - \varphi )}}{{2\varphi \left( {\frac{{k_{f} }}{{k_{CNT} - k_{f} }}} \right)\ln \left( {\frac{{k_{f} + k_{CNT} }}{{2k_{f} }}} \right) + (1 - \varphi )}}} \right). \hfill \\ \end{gathered} \right\}$$
(6)

Taking following conversions from reported studies51,52:

$$\left. \begin{gathered} \eta = \frac{{r^{2} - R^{2} }}{2R}\sqrt {\frac{{u_{{1_{o} }} }}{{lv_{f} }}} , \, u_{1} = \frac{{u_{{1_{o} }} x}}{l}f^{\prime}(\eta ), \, u_{2} = - \frac{R}{r}\sqrt {\frac{{u_{{1_{o} }} v_{f} }}{l}} f(\eta ),\, \hfill \\ \theta (\eta ) = \frac{{T - T_{\infty } }}{{T_{w} - T_{\infty } }}, \, \phi (\eta ) = \frac{{C - C_{\infty } }}{{C_{w} - C_{\infty } }}. \hfill \\ \end{gathered} \right\}$$
(7)

Utilizing Eq. (7), in Eqs. (2), (3) and (4) we get:

$$\frac{1}{{A_{1} \left( {1 - \varphi } \right)^{2.5} }}\left[ {\left( {1 + 2\eta \gamma } \right)f^{\prime\prime\prime} + 2\gamma f^{\prime\prime} - K_{p} f^{\prime}} \right] + ff^{\prime\prime} - Mf^{\prime} - (1 + F_{r} )f^{^{\prime}2} = 0,$$
(8)
$$\begin{aligned} Prf\theta^{\prime} &+ \frac{{k_{nf} /k_{f} }}{{A_{2} }}\left[ {\left( {1 + 2\eta \gamma } \right)\theta^{\prime\prime} + 2\gamma \theta^{\prime}} \right] + \frac{4}{{3A_{2} }}Rd\left[ {\left( {1 + 2\eta \gamma } \right)\theta^{\prime\prime} + \gamma \theta^{\prime}} \right] \hfill \\ &+\frac{1}{{\left( {1 - \varphi } \right)^{2.5} A_{2} }}\Pr Ecf^{\prime\prime}\left( {1 + 2\eta \gamma } \right)f^{^{\prime\prime}2} + \frac{1}{{A_{1} }}\Pr EcMf^{^{\prime}2} = 0, \hfill \\ \end{aligned}$$
(9)
$$Scf\phi^{\prime} + \left( {1 + 2\eta \gamma } \right)\phi^{\prime\prime} + 2\gamma \phi^{\prime} - \beta Sc(1 + \theta \delta )^{n} \phi e^{{\frac{{ - E_{1} }}{1 + \theta \delta }}} = 0,$$
(10)

where dimensionless parameters defined as:

$$\begin{gathered} \gamma = \sqrt {\frac{{l\nu_{f} }}{{u_{{1_{0} }} R^{2} }}} ,\,\,K_{p} = \frac{{l\nu_{f} }}{{u_{{1_{0} }} K_{1} }},\,\,M = \sqrt {\frac{{B_{0}^{2} l\sigma_{nf} }}{{u_{{1_{0} }} \rho_{f} }}} ,\,\,F_{r} = \frac{{C_{b} }}{{\sqrt {k^{ * } } }},\,\,A_{1} = 1 + \varphi \frac{{\rho_{CNT} }}{{\rho_{f} }} - \varphi ,\,\,Sc = \frac{{\nu_{f} }}{D},\, \hfill \\ A_{2} = 1 - \left( {1 - \frac{{\left( {\rho C_{p} } \right)_{CNT} }}{{\left( {\rho C_{p} } \right)_{f} }}} \right)\varphi ,\,\,Pr = \frac{{(\mu C_{p} )_{f} }}{{k_{f} }},\,\,Ec = \frac{{u_{{1_{w} }}^{2} }}{{(T_{w} - T_{\infty } )C_{p} }},\,\,E_{1} = \frac{Ea}{{T_{\infty } k^{ * } }},\,\,\beta = \frac{{lKr^{2} }}{{u_{{1_{0} }} }}, \hfill \\ Rd = \frac{{4T_{\infty }^{3} \sigma^{ * } }}{{k_{f} k^{ * } }},\,\,\delta = \frac{{T_{w} - T_{\infty } }}{{T_{\infty } }}, \hfill \\ \end{gathered}$$
(11)

along boundary conditions given as51,52:

$$\begin{gathered} f(0) = 0,\,\,\theta (0) = 1,\,\,f^{\prime}(0) = 1,\,\,\phi (0) = {\text{1 at }}r = R, \hfill \\ f^{\prime}(\eta ) = 0,\,\,\theta (\eta ) = 0,\,\,\phi (\eta ) = {\text{0 as }}\eta \to \infty . \hfill \\ \end{gathered}$$
(12)

Proposed methodology

This section of study consists of the three steps for solving the DFPG-CNTs model using the recurrent neural network based on Bayesian regularization optimizer (RNNs-BRO). The datasets of the created scenarios of the DFPG-CNTs are generated through the ND solve technique using Adam’s numerical method in the initial step. The second step involves implementing the RNNs-BRO algorithm and is executed in the neural networks’ environment in MATLAB software R2020a available at https://www.mathworks.com by way of the ‘layrecnet’ tool to train the datasets, while the third step presents the trained results. The procedure for solving the DFPG-CNTs model using purposed RNNs-BRO technique is visually depicted in Fig. 2.

Fig. 2
figure 2

Graphical abstract of DFPG-CNTs model.

Full size image

Prior to executing the outlined procedures, thirteen scenarios of the proposed model are established. Each scenario consists of four cases, with the aim of generating datasets for the DFPG-CNTs model. The datasets are generated by altering the values of certain parameters, such as the curvature parameter (\(\gamma\)), inertia coefficient (\({F}_{r}\)), porosity parameter (\({K}_{p}\)), Eckert number (\(Ec\)), Prandtl number (\(Pr\)), radiation parameter (\(Rd\)), Hartmann number (\(M\)), activation energy variable (\({E}_{1}\)), Schmidt number (Sc) and reaction rate parameter (\(\beta\)). All other parameters are kept constant throughout this process. All the parameters of the DFPG-CNTs model, along with their numerical values obtained from the published study52, are presented in Table 1. After creating the scenarios of the proposed model, Adam’s numerical method is used in the “NDSolve” command of Mathematica software to create the datasets of multiple scenarios for the velocity profile denoted as fʹ(η), the temperature profile denoted by θ(η) as well as the concentration field ϕ(η). The provided datasets are subjected to processing using a hidden layer consisting of 10 neurons in order to obtain the training results in the output layer. The datasets were divided into three subsets: 70% of the data was used for training, 20% for testing, and 10% for validating the presented RNNs-BRO algorithm.

Table 1 Alterations of parameters of DFPG-CNTs model.
Full size table

We implemented Bayesian regularization with RNN in this investigation, which altered the cost function by introducing a regularization term that integrates previous information about the network weights. The goal is to reduce the regularized cost function, which is a means of balancing the model’s complexity and its fit to the data. In mathematical form cost function is given as:

$$E = \alpha E_{d} + \beta E_{w} .$$
(13)

Here \(\alpha\) and \(\beta\) are hyper-parameters that regulate the balance between the accuracy of data fitting and the regularization. The entire cost denoted as E, and \(E_{d}\) data error term which can be computed by using following expression

$$E_{d} = \frac{1}{2}\sum\limits_{j = 1}^{n} {(y_{j} - \tilde{y}_{j} )^{2} } ,$$
(14)

where \(y_{j}\) and \(\tilde{y}_{j}\) represent actual and predicted output respectively, and regularization term reducing large weights is defined as:

$$E_{w} = \frac{1}{2}\sum\limits_{i = 1}^{m} {w_{i}^{2} } .$$
(15)

Here \(w_{i}\) are the network weights. The architecture of the RNN utilized in this study is depicted in Fig. 3.

Fig. 3
figure 3

Recurrent neural network architecture for DFPG-CNTs model.

Full size image

Results and discussion

This section presents the implementation of the RNNs-BRO algorithm, which is based on recurrent neural networks for addresses the solution of the DFPG-CNTs model employing the MATLAB recurrent neural networks toolbox’s ‘layrecnet’ built-in command in the Matlab software R2020a available at https://www.mathworks.com. The objective of this implementation is to train the datasets of each case of all scenarios, with 70% training, 10% validation, and 20% testing in the input layer. The provided datasets are subjected to processing using a hidden layer consisting of 10 neurons in order to obtain the training results in the output layer. The study formulates thirteen distinct scenarios of the DFPG-CNTs model by altering the curvature parameter (\(\gamma\)), inertia coefficient (\({F}_{r}\)), porosity parameter (\({K}_{p}\)), Eckert number (\(Ec\)), Prandtl number (\(Pr\)), radiation parameter (\(Rd\)), Hartmann number (\(M\)), activation energy variable (\({E}_{1}\)), Schmidt number (Sc) and reaction rate parameter (\(\beta\)), for the fluid velocity, temperature and mass concentration profiles of the DFPG-CNTs model as displayed in Table 1. Thermophysical properties of Propylene glycol and carbon nanotube are displayed in Table 2.

Table 2 Thermophysical properties of propylene glycol and carbon nanotubes51,52.
Full size table

Figures 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 and 15 depict the RNNs-BRO solutions for each of the six scenarios comprising different cases, as determined by the performance, training state analysis, regression, histogram graphs, auto-correlation, and fitness function. Additionally, Table 3 describe the convergence through mean squared error (MSE) for training, the optimal performance index, Mu, effective parameters, gradient, epochs, sum squared parameters, and time required for each scenario of DFPG-CNTs model.

Fig. 4
figure 4

Performance analysis of MSE to express the efficiency of RNN-BRO for SWCNTs.

Full size image
Fig. 5
figure 5

Performance analysis of MSE to express the efficiency of RNN-BRO for MWCNTs.

Full size image
Fig. 6
figure 6

Training-state analysis of designed RNN-BRO for SWCNTs.

Full size image
Fig. 7
figure 7

Training-state analysis of designed RNN-BRO for MWCNTs.

Full size image
Fig. 8
figure 8

Regression graphs of developed RNN-BRO for SWCNTs.

Full size image
Fig. 9
figure 9

Regression graphs of developed RNN-BRO for MWCNTs.

Full size image
Fig. 10
figure 10

Plots of error-histograms of designed technique RNN-BRO for SWCNTs.

Full size image
Fig. 11
figure 11

Plots of error-histograms of designed technique RNN-BRO for MWCNTs.

Full size image
Fig. 12
figure 12

Error-auto correlation plots to define the accuracy of RNN-BRO for SWCNTs.

Full size image
Fig. 13
figure 13

Error-auto correlation plots to define the accuracy of RNN-BRO for MWCNTs.

Full size image
Fig. 14
figure 14

Plots of trained data analysis on the fitness curve through RNN-BRO for SWCNTs.

Full size image
Fig. 15
figure 15

Plots of trained data analysis on the fitness curve through RNN-BRO for MWCNTs.

Full size image
Table 3 Outcomes of RNN-BRO for variants of DFPG-CNTs model.
Full size table

The process of evaluating the outcomes of generated scenarios in artificial intelligence is referred to as performance analysis. In this study, we analyze the performance of the proposed model by using generated datasets to find out the reliability of the applied algorithm RNN-BRO. The analysis was conducted by the training algorithm, which utilized the train parameters to execute the performance function specified as “net.trainFcn”. The results of case-4 of six scenarios of the DFPG-CNTs model are provided in Figs. 4 and 5, along with the corresponding mean-square error (MSE) values for both SWCNTs and MWCNTs, respectively. For SWCNTs, these values are 1.3048E−13, 3.2434E−12, 1.412E−12, 2.3905E−13, 2.1578E−13, and 5.452E−14 at the epochs 267, 87, 68, 228, 66, and 434 respectively, as depicted in Fig. 4. In addition, Fig. 4f demonstrates the highest convergence rate of the RNN-BRO algorithm, corresponding to the value of 5.452E−14 during the 434th epoch compared to Fig. 4a-e. The convergence on mean squared error (MSE) values for MWCNTs are 1.3011E−13, 2.4598E−12, 2.5139E−13, 3.9212E−13, 2.0845E−13, and 4.5801E−12 at the epochs 251, 39, 86, 323, 669 and 139 respectively, as depicted in Fig. 5. The highest achieved mean squared error (MSE) training performance was observed during 323th epoch which is 3.9212E−13 as illustrated in Fig. 5d. Table 3 displays the MSE values for training in all scenarios, with a focus on values closer to zero.

The analysis of the training state involves evaluating various parameters in neural networks to determine the rate of convergence of the solution. These parameters include the gradient level, numeric values, mu, sum squared parameter, and validation checks at different epochs. The results of the training are visually displayed in Figs. 6 and 7 for both SWCNTs and MWCNTs respectively, to assess the effectiveness of the algorithm. The Figs. 6a–f and 7a–f illustrate the changes in the gradient, numeric parameters, mu, and sum squared parameter over the course of the epochs, for both SWCNTs and MWCNTs, respectively. The gradient values at different epochs such as 2.1848E−08, 8.0446E−08, 4.1827E−08, 5.7607E−08, 6.7929E−09, and 9.9509E−08 for SWCNTS depicted in the Fig. 6a–f and the values of gradient for MWCNTs are 2.3241E−08, 2.92166E−08, 7.6304E−08, 9.7676E−08, 4.7182E−08 and 9.2871E−08 depicted in the Fig. 7a–f for all the scenarios respectively, indicate a significant slope of the tangent at those points where a high rate of change is observed. The accuracy of the discussed RNN-BRO algorithm is determined by the value of mu at different epochs. Furthermore, Table 3 presents the values of the mu, gradient, numeric parameter, epoch, sum squares parameter, and time utilized for all scenarios.

Regression analysis is a key concept in mathematics that helps establish correlations between predicted values and obtained results. This analysis presents the correlations, perfect fitness, trained network data, and best fitness using the correlation coefficient (R). The regression analysis is conducted in this study for both SWCNTs and MWCNTs using the RNN-BRO.

The regression plots in Figs. 8a–f and 9a–f demonstrate the similarity between the generated datasets and the trained results for SWCNTs and MWCNTs, respectively for all scenarios. These plots demonstrate a significant correlation between the generated datasets and the computationally trained results, as evidenced by the regression level of R = 1. The Figs. 8a–f and 9a–f illustrate the ideal fitness, enhanced network outcomes, and optimal fit.

All the plots demonstrate the validity and reliability of the designed algorithm RNN-BRO. The error histogram plots in recurrent neural networks provide valuable illustrations for depicting the representation of errors resulting from discrepancies between generated datasets and trained results. The representation of errors using error bars and values that approach zero demonstrates the effectiveness and higher performance of the algorithm employed. In addition, the minimum error values indicate that the trained results closely match the generated datasets. This study includes a thorough analysis of errors using histograms to examine the accuracy, efficiency, and convergence of the algorithm employed, which relies on recurrent neural networks. Figures 10a–f and 11a–f displayed error histograms for SWCNTS and MWCNTs for all the scenarios, respectively, indicating minimal discrepancies between the generated datasets and trained results, as the errors’ values are extremely close to zero.

The auto-correlation plots are graphical representations of the correlations between errors, based on the specified range of lags. These plots are illustrated in Fig. 12a–f for SWCNTs and in Figs. 13a–f for MWCNTs to highlight the correlations, zero correlation and confidence limit for all scenarios. It is evident that a correlation value R close to one signifies a high level of accuracy in the training and testing process, hence confirming the validity of the suggested RNN-BRO for the DFPG-CNTs model.

Time series theory explains how measurements of observations occur in a regular way across time. It is utilized to forecast future outcomes based on the observed values of the system. The plots in Figs. 14 and 15 depict the discrepancy or difference between the desired time-series and the actual output time-series for both SWCNTs and MWCNTs respectively, in the same direction. In addition, Figs. 14 and 15 illustrates the training targets, training outputs, testing targets, testing outputs, errors, and time involved in the design and testing of data. Therefore, by displaying the desired fitness of the computed data on the curve, all of the Figs. 14a–f and 15a–f define the effectiveness, dependability, and correctness of the applied Bayesian-regularization algorithm based on recurrent neural-networks RNNs-BRO.

Impact of parameters on velocity, temperature and concentration profiles

This section is compiled to analyse the effects of various parameters on fʹ(η), θ(η) and ϕ(η) profiles of DFPG-CNTs model through the developed RNN-BRO algorithm. These parameters include the curvature parameter (\(\gamma\)), inertia coefficient (\({F}_{r}\)), Hartmann number (\(M\)), porosity parameter (\({K}_{p}\)), Eckert number (\(Ec\)), Prandtl number (\(Pr\)), radiation parameter (\(Rd\)), activation energy variable (\({E}_{1}\)), Schmidt number (\(Sc\)) and reaction rate parameter (\(\beta\)). The outputs of the ANN-BR method were examined and have been displayed in Figs. 16a, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40 and 41a, and the absolute errors were depicted in Figs. 16b, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40 and 41b. Figures 16a and 17a illustrate the effect of the \(\gamma\) on the fʹ(η). It is evident that the derivative fʹ(η) exhibits a rising trend as \(\gamma\) increases for SWCNT and MWCNT. Increased \(\gamma\) leads to a decrease in the contact area between the fluid and the surface. This is because there is an inverse relationship between \(\gamma\) and the radius of the cylinder, resulting in a decrease in fʹ(η), while the absolute error (AE) is determined within the range of 10−05 to 10−10 for SWCNTs and 10−05 to 10−11 for MWCNTs, as portrayed in Figs. 16b and 17b respectively, which confirms the correctness and reliability of the discussed RNN-BRO algorithm.

Fig. 16
figure 16

Solution plots of designed RNN-BRO for fʹ(η) of DFPG-CNTs model for SWCNT.

Full size image
Fig. 17
figure 17

Solution plots of designed RNN-BRO for fʹ(η) of DFPG-CNTs model for MWCNT.

Full size image
Fig. 18
figure 18

Solution plots of designed RNN-BRO for fʹ(η) of DFPG-CNTs model for SWCNT.

Full size image
Fig. 19
figure 19

Solution plots of designed RNN-BRO for fʹ(η) of DFPG-CNTs model for MWCNT.

Full size image
Fig. 20
figure 20

Solution plots of designed RNN-BRO for fʹ(η) of DFPG-CNTs model for SWCNT.

Full size image
Fig. 21
figure 21

Solution plots of designed RNN-BRO for fʹ(η) of DFPG-CNTs model for MWCNT.

Full size image
Fig. 22
figure 22

Solution plots of designed RNN-BRO for fʹ(η) of DFPG-CNTs model for SWCNT.

Full size image
Fig. 23
figure 23

Solution plots of designed RNN-BRO for fʹ(η) of DFPG-CNTs model for MWCNT.

Full size image
Fig. 24
figure 24

Solution plots of designed RNN-BRO for θ(η) of DFPG-CNTs model for SWCNT.

Full size image
Fig. 25
figure 25

Solution plots of designed RNN-BRO for θ(η) of DFPG-CNTs model for MWCNT.

Full size image
Fig. 26
figure 26

Solution plots of designed RNN-BRO for θ(η) of DFPG-CNTs model for SWCNT.

Full size image
Fig. 27
figure 27

Solution plots of designed RNN-BRO for θ(η) of DFPG-CNTs model for MWCNT.

Full size image
Fig. 28
figure 28

Solution plots of designed RNN-BRO for θ(η) of DFPG-CNTs model for SWCNT.

Full size image
Fig. 29
figure 29

Solution plots of designed RNN-BRO for θ(η) of DFPG-CNTs model for MWCNT.

Full size image
Fig. 30
figure 30

Solution plots of designed RNN-BRO for θ(η) of DFPG-CNTs model for SWCNT.

Full size image
Fig. 31
figure 31

Solution plots of designed RNN-BRO for θ(η) of DFPG-CNTs model for MWCNT.

Full size image
Fig. 32
figure 32

Solution plots of designed RNN-BRO for θ(η) of DFPG-CNTs model for SWCNT.

Full size image
Fig. 33
figure 33

Solution plots of designed RNN-BRO for θ(η) of DFPG-CNTs model for MWCNT.

Full size image
Fig. 34
figure 34

Solution plots of designed RNN-BRO for ϕ(η) of DFPG-CNTs model for SWCNT.

Full size image
Fig. 35
figure 35

Solution plots of designed RNN-BRO for ϕ(η) of DFPG-CNTs model for MWCNT.

Full size image
Fig. 36
figure 36

Solution plots of designed RNN-BRO for ϕ(η) of DFPG-CNTs model for SWCNT.

Full size image
Fig. 37
figure 37

Solution plots of designed RNN-BRO for ϕ(η) of DFPG-CNTs model for MWCNT.

Full size image
Fig. 38
figure 38

Solution plots of designed RNN-BRO for θ(η) of DFPG-CNTs model for SWCNT.

Full size image
Fig. 39
figure 39

Solution plots of designed RNN-BRO for ϕ(η) of DFPG-CNTs model for MWCNT.

Full size image
Fig. 40
figure 40

Solution plots of designed RNN-BRO for ϕ(η) of DFPG-CNTs model for SWCNT.

Full size image
Fig. 41
figure 41

Solution plots of designed RNN-BRO for ϕ(η) of DFPG-CNTs model for MWCNT.

Full size image

Figures 18a and 19a demonstrate the \({F}_{r}\) impact on the fʹ(η) as \({F}_{r}\) value increases, the fʹ(η) decreases for both CNTs. In terms of physicality, inertial forces cause acceleration through an increase in \({F}_{r}\), which in turn counteracts fluid flow and slows down the velocity of nanofluid for SWCNT/MWCNT, while the AE is found within the range of 10−04 to 10−10 for SWCNTs and MWCNTs as portrayed in Figs. 18b and 19b respectively, which confirms the efficacy of the discussed RNN-BRO algorithm. The impact of \(M\) on fʹ(η) is demonstrated in Figs. 20a and 21a for SWCNTs and MWCNTs, respectively. Higher values of \(M\) correlate to a greater Lorentz force, which causes to decrease the fʹ(η) curves for SWCNT/MWCNT. The absolute error (AE) is determined within the range 10−05 → 10−10, which confirms the correctness of the suggested approach, as illustrated in Figs. 20b and 21b for SWCNTs and MWCNTs, respectively. Figures 22a and 23a display the fluctuation in fʹ(η) for larger estimates of the porosity parameter (\({K}_{p}\)). The velocity profile decreases for larger concentrations of (\({K}_{p}\)) in both SWCNT and MWCNT. As the size of pores on a permeable surface evolves, the resistance between the surface and fluid also rises, resulting in a drop in velocity. The absolute error (AE) is found within the range of 10−04 to 10−12 for SWCNTs and 10−05 to 10−10 for MWCNTs, as portrayed in Figs. 22b and 23b respectively, which confirms the efficacy of the discussed RNN-BRO algorithm.

The temperature profiles in Figs. 24a and 25a demonstrate the impact of the \(\gamma\) on its behaviour for SWCNTs and MWCNTs, respectively. An increase in thermal field is observed when \(\gamma\) increases. Decreasing the value of \(\gamma\) decreases the contact area between the cylinder and fluid, resulting in a smaller amount of heat being transferred from the surface to the fluid showed the decline in the thermal field. The AE is found within the range of 10−05 to 10−11 for SWCNTs and 10−04 to 10−12 for MWCNTs, as portrayed in Figs. 24b and 25b, respectively. Figures 26a and 27a illustrate the effect of \(Ec\) on θ(η). An increase in θ(η) has been noticed in order to increase \(Ec\).

The increment in \(Ec\) results in a greater drag force between fluid molecules. Consequently, an increase in the generation of heat occurs, leading to an enhancement in θ(η). The absolute error (AE) is determined within the range 10−05 → 10−11 and 10−04 → 10−12 as illustrated in Figs. 26b and 27b for SWCNTs and MWCNTs, respectively.

The impact of \(M\) on θ(η) is demonstrated in Figs. 28a and 29a for SWCNTs and MWCNTs, respectively. The curves in Figs. 28a and 29a demonstrate that θ(η) decreased as the \(M\) became larger. Increasing the value of \(M\) results in an increase in the Lorentz resistive force, which leads to the addition of more heat to the system. As a result, the thermal field θ(η) is enhanced, while the absolute error (AE) is determined within the range of 10−04 to 10−12 for SWCNTs and 10−05 to 10−11 for MWCNTs, as portrayed in Figs. 28b and 29b respectively. The impact of Pr on θ(η) is depicted in Figs. 30a and 31a for SWCNTs and MWCNTs, respectively. As Pr increases, the thermal diffusivity decreases, leading to a decrease in θ(η) of the NF. The AE is found within the range of 10−04 → 10−12 for SWCNTs and 10−05 → 10−11 for MWCNTs, as illustrated in Figs. 30b and 31b respectively. Figures 32a and 33a is designed to analyze the efficiency of θ(η) with increasing radiation parameter (\(Rd\)). It is evident that \(Rd\) has a direct correlation with θ(η) in this scenario. Higher \(Rd\) values contribute additional heat to the system, resulting in an enhancement of thermal field θ(η) curves through greater \(Rd\) estimations. The AE is found within the range of 10−05 to 10−11 for SWCNTs and MWCNTs as portrayed in Figs. 32b and 33b respectively, which confirms the efficacy of the discussed RNN-BRO algorithm.

The relationship between ϕ(η) of DFPG-CNTs model and various factors is analyzed in Figs. 34, 35, 36, 37, 38, 39, 40 and 41. The effect of increased \({E}_{1}\) on ϕ(η) is displayed in Figs. 34a and 35a for SWCNTs and MWCNTs, respectively. Here, the magnitude of ϕ(η) increases as \({E}_{1}\) increases. The modified Arrhenius function experiences a rise in magnitude when the value of (\({E}_{1}\)) increases, resulting in an increase in the value of ϕ(η) for SWCNT/MWCNT. The absolute error (AE) is determined within the range 10−05 → 10−10 which confirms the correctness of the developed RNN-BRO technique, as illustrated in Figs. 34b and 35b for SWCNTs and MWCNTs, respectively..

Figures 36a and 37a provide the graphical representations of the concentration ϕ(η) profile solutions for the impact of \(\gamma\) on the function ϕ(η) for SWCNTs and MWCNTs, respectively. respectively. Here, ϕ(η) experiences enhancement at the ambient, whereas a opposite impact is noticed at the surface of the stretched cylinder.

The AE is found within the range of 10−05 to 10−11 for SWCNTs and 10−04 to 10−10 for MWCNTs, as portrayed in Figs. 36b and 37b, respectively. The effects of \(Sc\) on ϕ(η) are presented in Figs. 38a and 39a and it is observed that increased \(Sc\) values restrict the ϕ(η) for both types of CNTs. By increasing \(Sc\) lowers the diffusion of molecular mass within the fluid for SWCNT and MWCNT. As a result, the value of ϕ(η) decreased, while AE is determined within the range 10−06 → 10−10 and 10−05 → 10−10 as illustrated in Figs. 38b and 39b for SWCNTs and MWCNTs, respectively. Figures 40a and 41a is designed to analyze the efficiency of ϕ(η) with an increasing value of \(\beta\). It is evident that increasing the accuracy of \(\beta\) variables leads to a decrease in ϕ(η). The reactive substances evaporate more quickly as \(\beta\) increases, causing ϕ(η) to decrease for both SWCNT and MWCNT. The AE is found within the range of 10−05 to 10−11 and 10−04 to 10−10 for SWCNTs and MWCNTs, as portrayed in Figs. 40b and 41b respectively, which confirms the efficacy of the developed RNN-BRO algorithm.

Conclusions

This study is the application of a recurrent neural networks with Bayesian regularization optimizer (RNNs-BRO) to analyze the effect of various physical parameters on fluid velocity, temperature, and mass concentration profiles in the Darcy–Forchheimer flow of propylene glycol mixed with carbon nanotubes across a stretched cylinder. The main objective is to investigate the influence of range of physical parameters, including the dimensionless curvature parameter (\(\gamma\)), inertia coefficient (\({F}_{r}\)), porosity parameter (\({K}_{p}\)), Eckert number (\(Ec\)), Prandtl number (\(Pr\)), radiation parameter (\(Rd\)), Hartmann number (\(M\)), activation energy variable (\({E}_{1}\)), Schmidt number (\(Sc\)) and reaction rate parameter (\(\beta\)) on fʹ(η), θ(η) and ϕ(η) profiles through RNNs-BRO intelligent computing technique. The RNNs-BRO employed a random selection of data 70% for training, 20% for testing, and 10% for validity. This approach aimed to get approximation solutions for the DFPG-CNTs model for different scenarios. This study has yielded the following significant findings:

  • The increment of curvature parameter (\(\gamma\)) results in the acceleration of the velocity profile, while an opposite behavior is noticed for higher values of inertia coefficient (\({F}_{r}\)), Hartmann number (\(M\)), porosity parameter (\({K}_{p}\)) for SWCNTs as well as MWCNTs.

  • The temperature of fluid increases for both SWCNTs and MWCNTs as the curvature parameter (\(\gamma\)), radiation parameter (\(Rd\)), Eckert number (\(Ec\)), and Hartmann number (\(M\)) are increased. However, an opposite trend is noticed for Prandtl number (\(Pr\)).

  • The concentration profile is enhanced for higher values of activation energy variable (\({E}_{1}\)) and curvature parameter (\(\gamma\)) for both SWCNTs and MWCNTs, whereas opposite trend is observed for reaction rate parameter (\(\beta\)), and Schmidt number (\(Sc\)).

  • The obtained results demonstrate the model’s validity, exhibiting an accuracy ranging from 10−12 to 10−04 consistently across all the scenarios of the DFPG-CNTs model.

  • The suggested RNN-BRO algorithm’s dependability, stability, and convergence were assessed using a fitness measure based on mean squares errors, histogram drawings, auto-correlation, and regression analysis for each scenario of the DFPG-CNTs model.

Recurrent neural networks are considered to be a powerful and versatile approach in the emulation of complex data interrelation. The adoption of RNNs to solve fluidic problems has emerged to be a revolutionary approach in engineering as well as the study of fluid dynamics. RNNs have provided innovative solutions for modeling fluidic systems and are a rather powerful alternative for computer-based modeling. RNNs with Bayesian regularization computing approach is applicable in areas ranging from aerodynamics, flow control, variants and fluid control systems due to their effectiveness in solving complex non linear computations fluidic systems. RNNs utility in the fluid dynamics is favorable for the future as innovative prospects can be opened in aerospace, civil engineering, and numerous industrial areas.