Fault detection for Li-ion batteries of electric vehicles with segmented regression method

Abstract

Electric vehicles are increasingly popular for their environmental benefits and cost savings, but the reliability and safety of their lithium-ion batteries are critical concerns. Current regression methods for battery fault detection often analyze charging and discharging as a single continuous process, missing important phase differences. This paper proposes segmented regression to better capture these distinct characteristics for accurate fault detection. The focus is on detecting voltage deviations caused by internal short circuits, external short circuits, and capacity degradation, which are primary indicators of battery faults. Firstly, data from real electric vehicles, operating under normal and faulty conditions, is collected over a period of 18 months. Secondly, the segmented regression method is utilized to segment the data based on the charging and discharging cycles and capture potential dependencies in battery behavior within each cycle. Thirdly, an optimized gated recurrent unit network is developed and integrated with the segmented regression to enable accurate cell voltage estimation. Lastly, an adaptive threshold algorithm is proposed to integrate driving behavior and environmental factors into a Gaussian process regression model. The integrated model dynamically estimates the normal fluctuation range of battery cell voltages for fault detection. The effectiveness of the proposed method is validated on a comprehensive dataset, achieving superior accuracy with values of 99.803% and 99.507% during the charging and discharging phases, respectively.

Introduction

Electric vehicles (EVs) are transforming the automotive industry with sustainable lithium-ion (Li-ion) batteries, known for their high energy density and longer lifespan¹. The increased EV demand is the result of growing carbon emissions and a shift towards renewable energy sources². In 2023, approximately 14 million EVs were sold globally, marking a 35% increase year-on-year³. However, EV battery faults, particularly voltage deviations, pose significant safety risks, leading to issues like thermal runaway⁴, capacity degradation⁵, and short circuits⁶. These interconnected faults emphasize the critical need for accurate fault detection⁷, which is essential for implementing timely corrective measures and maintaining battery health, thus ensuring the safe and efficient operation of EVs.

Voltage deviations are a primary indicator of battery faults and can arise from various causes, including internal short circuits, external short circuits, and capacity degradation⁸. These deviations are critical for timely fault detection and prevention, thus ensuring the reliability and safety of EV batteries. Temperature variations do influence battery performance, but their impact on fault detection is less pronounced compared to voltage deviations⁹. Additionally, voltage sensors are more commonly integrated into battery management systems, providing continuous and detailed monitoring of cell behavior. The larger number of voltage sensors compared to temperature sensors makes voltage readings more comprehensive, enhancing the robustness and effectiveness of voltage-based detection methods for early and accurate fault identification in EV batteries.

Current research on battery fault detection can be categorized into three types: model-based, signal processing-based, and data-driven methods¹⁰. Model-based methods use mathematical models to predict battery behavior¹¹. However, they can be computationally intensive and struggle with complex real-world scenarios¹². Signal processing-based methods analyze voltage signals for abnormalities¹³. Nonetheless, they are limited by their sensitivity to noise and parameter variations¹⁴. The emphasis has shifted towards data-driven methods, which employ machine learning algorithms to recognize patterns associated with voltage faults, continuously adapting and improving over time. Among these, deep learning advancements, including innovative architectures and attention mechanisms, have significantly enhanced the effectiveness of predictive modeling across domains¹⁵.

Data-driven methods are commonly classified into three main types: regression, classification, and clustering approaches¹⁶. Regression methods aim to capture continuous patterns and detect deviations from expected values, making them effective for identifying fault trends in real-time¹⁷. Classification methods, on the other hand, categorize battery states into discrete fault classes, enabling rapid identification of fault types without requiring detailed knowledge of underlying system complexities¹⁸. Clustering methods, often used in unsupervised learning, detect anomalies by grouping similar data points and identifying deviations from normal patterns¹⁹. Among these methods, regression methods are widely used in fault detection due to their capability to continuously monitor and detect early signs of faults, offering a reliable approach for various battery applications.

Existing regression-based methods for fault detection offer valuable solutions to the challenges in battery systems. These approaches, leveraging machine learning, can effectively filter noise and provide accurate fault detection even in the presence of environmental and operational variability²⁰. Advanced regression-based models, such as the transformer-based approach by Zhao et al.²¹, have demonstrated significant effectiveness in predicting battery faults across varied operating environments. Similarly, Khaleghi et al.²² introduced an RNN-based regression model that reliably detects battery faults, demonstrating the potential of deep learning in handling complex temporal data. Furthermore, unsupervised learning methods that integrate regression techniques allow for post-model fault detection using normal samples, as highlighted by Li et al.²³, enhancing battery system safety and reliability.

Building on the capabilities of standard regression methods, segmented regression introduces a more refined approach by modeling data that exhibits structural shifts or distinct phases. This technique segments data into different intervals, fitting separate regression lines to each segment, allowing for a more accurate representation of non-linear trends and variable behaviors. Segmented regression has been widely applied in fields like epidemiology, where it models changes in health trends before and after an intervention²⁴. In healthcare, it helps monitor patient outcomes following treatment changes, analyze trends in disease incidence, and evaluate the effects of healthcare policies or interventions over time²⁵. Environmental science also benefits from segmented regression, where it is used to analyze the response of ecosystems to environmental stressors, such as pollution or temperature changes, identifying critical thresholds that indicate potential ecological impacts²⁶. These applications highlight the versatility of segmented regression in capturing complex, phased patterns, which can be essential for areas requiring precise monitoring and intervention across a wide range of disciplines.

These studies highlight the potential of segmented regression for real-time battery fault detection. But, it is not a straightforward task. While segmented regression captures non-linearity within cycles, it fails to consider temporal dependencies between charging and discharging cycles, leading to inaccuracies during transitions. Existing methods also suffer from limited real-world data²⁷, computational intensity²⁸, and a lack of adaptability to dynamic environments²⁹. They typically analyze entire datasets, overlooking individual charge and discharge cycles and cell-specific issues that are not apparent at the pack level³⁰. Additionally, the computational intensity of these methods can make them unsuitable for real-time applications, limiting their practical use in dynamic operational conditions³¹.

To address these limitations, a cell voltage fault detection method for EVs is proposed in this paper. Firstly, data from real EVs, one operating normally and the other with a fault occurrence, is collected over a period of 18 months under dynamic working conditions. Secondly, the segmented regression method is utilized to segment the data based on the charging and discharging cycles and capture the potential dependencies in battery behavior within each cycle. This pre-processing step reduced the computational load significantly. Thirdly, a gated recurrent unit network is optimized with the AdaGrad and adjustable momentum to enhance the training performance. The optimized method is integrated with the segmented regression method to allow accurate and efficient cell voltage estimation. Lastly, an adaptive threshold algorithm is proposed, which integrates driving behavior and environmental factors into the Gaussian process regression (GPR) model and dynamically estimates the normal fluctuation range of cell voltage to adjust the fault threshold, achieving an accurate cell fault detection. The following are the key contributions of this paper:

• 1. A significant contribution is the use of segmented regression for data pre-processing to capture dependencies in battery behavior within charging and discharging cycles, reducing computational load. This method, combined with an optimized GRU network enhances cell voltage estimation.

• 2. An innovative adaptive threshold algorithm is proposed. This algorithm dynamically estimates the normal fluctuation range of battery cell voltages, enabling a more accurate and adaptable fault detection method.

• 3. The effectiveness of the proposed method is validated using real EV data. The experimental results demonstrate that the proposed approach outperformed the current fixed threshold-based techniques. Furthermore, the method demonstrates enhanced computational efficiency when compared to the established baseline methods.

Dataset description and motivation

Dataset description

In this paper, the data collected from real EVs is utilized, operating with normal and faulty batteries. The data collection period spanned from July 31, 2021, to January 23, 2023. Each vehicle was outfitted with a Li-ion battery pack comprising 96 Li-ion cells connected in series, organized into 8 modules. Each module consists of 12 cells and is monitored by a total of 96 voltage sensors and 24 temperature sensors.

Fig. 1

Correlation matrix among variables of the normal battery (a) Correlation matrix (Charging Mode) (b) Correlation matrix (Discharging Mode).

Fig. 2

Correlation matrix among variables of the faulty battery (a) Correlation matrix (Charging Mode) (b) Correlation matrix (Discharging Mode).

The dataset includes various battery pack states, including pack current, pack voltage, and SoC. Additionally, the dataset tracks the charging state, indicating whether the battery is charging or discharging. It also includes individual voltage and temperature measurements for each cell. This comprehensive approach provides a more detailed understanding of how the battery pack behaves under various conditions. By capturing the states of each cell, underlying battery faults can be detected.

Fig. 3

Individual cell voltages of the battery packs (a) Battery with normal operation (b) Battery with fault occurrence.

Data analysis and processing

Figures 1 and 2 illustrates the correlation matrices for each variable within the normal and faulty battery packs respectively. In general, variables are deemed strongly correlated if their correlation coefficient exceeds 0.6 or falls below − 0.6. As shown in the figures, the correlation between the battery pack and variables of individual cell voltages is strong, whereas the correlation with individual cell temperature is notably weak.

In this study, the primary focus is directed toward individual cell voltages within the battery pack of the vehicle. This is due to several key reasons. Firstly, individual cell voltage is an important factor in fault detection due to its highest correlation with pack voltage. Secondly, the correlation between pack voltage and cell temperature is notably weak.

The weak correlation between pack voltage and cell temperature can be attributed to various reasons. First is the inconsistency in the number of sensors monitoring voltage and temperature. The temperature sensors are fewer as compared to voltage sensors, leading to incomplete data and potentially uneven correlations. Additionally, external influences, further degrade the relationship between voltage and cell temperature.

To provide a visual representation of the analysis, Fig. 3a and b illustrate the individual cell voltages for normal and faulty vehicles respectively. The data for each vehicle is organized to display all 96 cells. This visualization presents the voltages of all individual cells, providing a detailed view of battery performance over time. By plotting all cells together, the analysis facilitates the identification of patterns and trends in cell voltages, enabling a comprehensive evaluation of the behavior of the battery pack.

It is essential to note that the large size of the data set posed a significant challenge in terms of analysis. To address this challenge, a downsampling technique was employed with a factor of 2500. This downsampling process effectively reduced the dataset to a more manageable size and ensured that computational resources were utilized efficiently, enabling a more streamlined and focused analysis without compromising the accuracy or validity of the results.

Upon analyzing the individual cell voltages within the faulty vehicle, a notable deviation in the voltage of Cell 49 was discovered. A sudden and significant drop in voltage was observed, indicating a potential fault within the battery system. Such deviations from the normal voltage range are indicative of underlying issues, requiring further investigation and corrective action. The observed drop in voltage suggests the presence of an underlying fault within the battery. Voltage deviations can severely impact the performance and safety of the battery, leading to diminished efficiency, reduced capacity, battery degradation, and potential safety hazards.

Motivation

The accurate estimation of cell voltage and detection of faults in batteries is crucial for ensuring the safety, reliability, and longevity of EVs. Existing methods primarily rely on regression techniques to estimate voltage and diagnose faults within the battery pack³². However, these methods often treat the charging and discharging cycles of the battery as a continuous process, applying a single regression line to model the entire dataset. This approach fails to account for the inherent complexities and distinct properties of different charging and discharging cycles, which can vary significantly in real-world scenarios.

Fig. 4

Voltage fluctuations observed in EV battery charging and discharging cycles. The figure highlights the significant variations across cycles.

In real-world, EV batteries undergo numerous charging and discharging cycles, each influenced by factors such as driving behavior, environmental conditions, and the state of health. These cycles show unique voltage variations and temporal dependencies that a single regression model cannot adequately capture. As illustrated in Fig. 4, charging and discharging cycles display significant voltage fluctuations across each cycle. Current continuous regression methods overlook these variations, resulting in inaccurate voltage estimations.

One of the major problems with current methods is the oversimplification of battery behaviors. Batteries do not follow a single, smooth, continuous pattern during their operation. Instead, they exhibit distinct phases of charge and discharge, each with its own characteristics. This variability is compounded by external factors such as temperature fluctuations, varying load demands, and the aging process of the battery itself. Ignoring these factors leads to models that are not only inaccurate but also unreliable for real-time applications. For instance, during rapid charging or discharging, voltage changes can be abrupt and non-linear, something a single regression line fails to represent.

Moreover, these models lack the detail needed to detect small but important voltage changes that signal early faults or degradation. This is especially problematic for EVs, where early fault detection is crucial to prevent failures and ensure safety. Inaccurate modeling of these changes reduces the effectiveness of battery management systems, leading to poor performance and safety risks.

Segmented regression offers a promising solution by allowing the data to be divided into distinct segments corresponding to individual charging and discharging cycles. This segmentation enables the model to capture the specific dependencies and variations within each cycle, providing a more accurate and detailed representation of the battery’s performance. By applying segmented regression, it becomes possible to reduce computational load significantly while enhancing the precision of voltage estimations and fault diagnoses.

The motivation for this research arises from the limitations of current continuous regression models in accurately estimating voltages and diagnosing faults in EV batteries. By adopting a segmented regression approach, this study aims to address these shortcomings, providing a more reliable and effective method for maintaining the health and safety of EV batteries in real-world applications. This approach not only improves the accuracy of voltage estimations but also enhances the overall fault detection process, thereby contributing to the advancement of EV technology and its sustainable future.

Fig. 5

The scheme of the proposed fault detection method.

The proposed fault detection framework

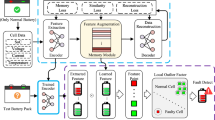
In this section, we introduce the scheme of the proposed fault detection system for Li-ion battery of EVs, which consists of two main modules, integrated segmented regression and GRU neural network-based prediction module and a threshold-based fault detection module. The scheme of the proposed fault detection system is shown in Fig. 5.

The methodology of the proposed approach is detailed as follows. Initially, the segmented regression model is employed to process input features, which include pack voltage, maximum voltage, and charging state. This model operates on the principle of segmented regression, adjusting its analysis based on the charging and discharging cycles of the battery. The outcome of this segmented regression is the computation of the mean voltage. Subsequently, the mean voltage, together with the pack voltage, maximum voltage, and charging state, is fed into a GRU network. The GRU network leverages its internal gating mechanisms to capture temporal dependencies within the data, which is crucial for accurate voltage estimation, especially in the context of battery systems that exhibit complex temporal dynamics. The GRU network then generates the estimated voltage as its output, which is a prediction of the battery voltage at the subsequent moment in time. This integration of segmented regression for initial feature analysis and GRU for temporal pattern recognition is designed to enhance the accuracy and reliability of the voltage estimation process in BMS.

To ensure the data was in optimal condition for analysis, several pre-processing steps were undertaken. Outliers were identified and removed using a Z-score threshold of 1.88 to eliminate extreme deviations that could distort the results. Missing values were handled through linear interpolation, maintaining continuity in the time-series data. Additionally, all input features were normalized to a range of [0, 1], ensuring consistent scaling across variables and improving the performance of both the segmented regression model and the GRU network. These pre-processing steps were critical in enhancing the robustness and accuracy of the fault detection framework.

Then, an adaptive threshold algorithm is proposed that takes into account environmental conditions and driving patterns, formulated using a Gaussian process regression model. Given the consistent voltage behavior across a battery pack, it is assumed that the voltage at any moment follows a Gaussian distribution, with its mean and standard deviation matching those of the overall pack voltage. However, the battery state in EVs varies due to different driving behaviors and complex environmental factors, which leads to shifts in the voltage fluctuation range within the battery pack. To address this variability, parameters that reflect driving behavior, such as gear position, vehicle speed, and motor metrics, are used to define the operational profile. Additionally, temperature data is included to account for environmental impacts. These parameters, along with historical battery voltage readings, serve as key features for the Gaussian process regression model. The objective of this model is to predict the standard deviation of the battery voltage for the next time interval, enabling a more advanced and adaptive BMS.

Additionally, the proposed algorithm integrates the $3\sigma$ criterion to define the normal operating range for battery voltage fluctuations, with three times the estimated standard deviation marking the threshold. This ensures that 99.9% of normal voltage readings fall within this stable range. To capture the input feature data in real-time, forward expansion techniques are applied, allowing for the dynamic acquisition of relevant battery parameters. The covariance matrix of these parameters is continuously refined using a modified radial basis kernel function, which, combined with Bayesian inference, enables the Gaussian process regression model to adapt to shifts in environmental conditions and driving behaviors. This adaptive approach ensures accurate predictions of voltage fluctuations under dynamic conditions. It calculates the residual between the actual and estimated voltages, and if this residual exceeds the adaptive threshold, it indicates a possible cell voltage fault. This systematic method provides an effective and early warning system for detecting faults in Li-ion batteries.

Battery voltage estimation

Segmented regression

Standard regression methods assume a single linear relationship between the independent and dependent variables³³. However, battery cell voltage exhibits distinct behaviors during charging and discharging cycles due to the underlying electrochemical processes. A different modeling approach is required to capture voltage changes during various charging cycles in both the charging and discharging phases.

Segmented regression is a statistical technique used to model relationships between variables that indicate nonlinear behavior across different segments or intervals³⁴. Unlike traditional regression analysis, which assumes a single continuous relationship between the independent and dependent variables, segmented regression acknowledges that the relationship may change at certain breakpoints or thresholds.

In this study, the inputs for the segmented regression model are $V_{\text {pack}}$, which is the pack voltage; $V_{\max }$, which is the maximum single cell voltage; and i, the charging state indicator, where $i = 1$ represents discharging and $i = 2$ represents charging. The output is the mean voltage, denoted as $V_{\text {mean}, i}$ for each segment i.

To enhance the reliability of the segmented regression model, outlier detection was employed. Outliers are data points that deviate significantly from other observations and can adversely affect the accuracy of the model. Z-scores were used to identify outliers, which measure the number of standard deviations a data point is from the mean. The Z-score for each data point is calculated as:

$$\begin{aligned} Z_{i j}=\frac{X_{i j}-\mu _j}{\sigma _j} \end{aligned}$$

(1)

where $X_{i j}$ is the i-th observation of the j-th variable, $\mu _j$ is the mean of the j-th variable, and $\sigma _j$ is the standard deviation of the j-th variable. A threshold of 3 was used to filter out outliers, ensuring that extreme values did not distort the regression model.

In segmented regression, the data is divided into distinct segments based on the charging state indicator, i. Each segment is characterized by its own regression equation. These segments are defined by breakpoints, $\tau _i$, where the relationship between the variables shifts. To explicitly address all cases, the segmented regression model is expressed as:

$$\begin{aligned} V_{\text {mean}, i}= {\left\{ \begin{array}{ll} \beta _{0,1}+\beta _{1,1} V_{\text {pack}}+\beta _{2,1} V_{\max }+\varepsilon _1 & \text {if } i< \tau _1 \\ \beta _{0,2}+\beta _{1,2} V_{\text {pack}}+\beta _{2,2} V_{\max }+\varepsilon _2 & \text {if } \tau _1 \le i< \tau _2 \\ \beta _{0,n-1}+\beta _{1,n-1} V_{\text {pack}}+\beta _{2,n-1} V_{\max }+\varepsilon _{n-1} & \text {if } \tau _{n-2} \le i < \tau _{n-1} \\ \beta _{0,n}+\beta _{1,n} V_{\text {pack}}+\beta _{2,n} V_{\max }+\varepsilon _n & \text {if } i \ge \tau _{n-1} \end{array}\right. } \end{aligned}$$

(2)

where $V_{\text {mean}, i}$ is the dependent variable (mean voltage) for segment i, $V_{\text {pack}}$ and $V_{\max }$ are the independent variables, $\beta _{0,i}, \beta _{1,i}, \beta _{2,i}$ are the intercept and slope parameters for segment i, $\tau _i$ are the breakpoints, and $\varepsilon _i$ is the error term for segment i. This explicit notation avoids ambiguity and improves uniformity.

To determine the breakpoints $\tau _i$, changes in the charging state indicator i were identified. The segmented regression model can also be represented in matrix form as:

$$\begin{aligned} \textbf{y}_i = \textbf{X}_i \varvec{\beta }_i + \varvec{\varepsilon }_i \end{aligned}$$

(3)

where $\textbf{y}_i$ is the vector of observed mean voltages for segment i, $\textbf{X}_i$ is the matrix of independent variables $V_{\text {pack}}$ and $V_{\max }$, $\varvec{\beta }_i$ is the vector of parameters for segment i, and $\varvec{\varepsilon }_i$ is the vector of error terms for segment i.

To ensure the reliability and accuracy of the model, segments with an $R^2$ score of more than 0.90 were considered. The $R^2$ score is calculated as:

$$\begin{aligned} R^2=1-\frac{\sum _{i=1}^n\left( V_{\text {mean}, i}-\hat{V}_{\text{ mean }, i}\right) ^2}{\sum _{i=1}^n\left( V_{\text {mean}, i}-\bar{V}_{\text {mean}}\right) ^2} \end{aligned}$$

(4)

where $V_{\text {mean}, i}$ is the observed value, $\hat{V}_{\text{ mean }, i}$ is the predicted value, $\bar{V}_{\text {mean}}$ is the mean of the observed values, and n is the number of observations. Segments with an $R^2$ score below 0.90 were excluded to maintain the robustness of the analysis.

Fig. 6

3D scatter plot of battery cell voltage data. The plot visualizes the segmented regression applied to battery cell voltage data, with colors representing different segments.

600 charging/discharging cycles with an $R^2$ score above 0.90 were selected for analysis. Figure 6 illustrates the segmented regression lines and the corresponding data points for different segments. The x-axis represents the pack voltage, and the y-axis represents the maximum cell voltage, both used as inputs to the model. The z-axis represents the mean cell voltage, which is the output. Different colors denote distinct segments, each corresponding to different phases of the charging and discharging cycles. The clustering of colors along the diagonal provides insights into the segmentation based on voltage characteristics. This highlights the model’s ability to capture the non-linear behavior of battery cell voltage during various phases of operation. The segmented regression approach provides a more accurate representation of battery behavior compared to a single continuous model.

Estimation model development

While segmented regression captures the non-linearity within each cycle, it does not consider the temporal dependencies between voltage measurements across charging and discharging cycles. This limitation could lead to inaccuracies, especially when predicting voltage during transitions between charging and discharging or vice versa. For instance, segmented regression might not accurately capture the gradual voltage rise at the beginning of charging or the voltage drop just before discharge ends.

In contrast, GRU offers a promising solution to this challenge. GRU networks are specifically designed to handle sequential data by effectively capturing temporal dependencies between consecutive observations. Unlike traditional regression models, which treat each data point independently, GRU networks maintain an internal state that evolves over time, allowing them to retain information from previous time steps and incorporate it into predictions for future time steps³⁵.

This ability of GRU networks to learn sequential information makes them particularly well-suited for modeling the temporal relationships between voltage measurements and charging state changes within the battery cell. By analyzing the sequence of voltage measurements alongside corresponding changes in charging states, the GRU network can determine patterns and trends that are indicative of the dynamic behavior of the battery.

Fig. 7

The architecture of the GRU network.

The architecture of the GRU network is illustrated in Fig. 7. It comprises of input layer, GRU layers, and a dense output layer. The detailed explanation is as follows.

• 1. Input layer: The input layer in the GRU network receives two separate inputs.

  • a. Voltage feature $\left( v_t\right)$: This represents the actual voltage measurement (total voltage and maximum voltage) and the output of the segmented regression model i.e. mean voltage at the current time step $\left( t\right)$. It is typically a vector containing multiple features related to voltage.

  • b. Charging state encoding $\left( e_s\right)$: This encodes the charging state information (1 for discharging, 2 for charging) using an embedding layer. The embedding layer transforms the categorical charging state into a continuous vector representation.

• 2. GRU Layers with Update and Reset Gates: These layers process the sequential voltage features and charging state information. The update and reset gates within each GRU unit control the flow of information, allowing the network to learn longterm dependencies. The core operation within each GRU layer involves the update gate $\left( z_t\right)$, reset gate $\left( r_t\right)$, candidate hidden state $\left( h^{\prime } _t\right)$, and new hidden state $\left( h_{\textrm{t}}\right)$. These gates control the flow of information through the network and determine how much past information to retain for voltage prediction at each time step.

  • a. Update gate $\left( \textrm{z}_{\textrm{t}}\right)$:

    $$\begin{aligned} z_t=\sigma \left( W_z \cdot I_t+U_z \cdot h_{t-1}+b_z\right) \end{aligned}$$

    (5)

    where, $\sigma$ denotes the sigmoid activation function, $W_z$ represents the weight matrix associated with the input $I_t, U_z$ denotes the weight matrix associated with the previous hidden state $h_{t-1}$, and $b_z$ represents the bias term.

  • b. Reset gate $\left( r_t\right)$:

    $$\begin{aligned} r_t=\sigma \left( W_r \cdot I_t+U_r \cdot h_{t-1}+b_r\right) \end{aligned}$$

    (6)

    where, $\sigma$ denotes the sigmoid activation function, $W_r$ represents the weight matrix associated with the input $I_t, U_r$ denotes the weight matrix associated with the previous hidden state $h_{t-1}$, and $b_z$ represents the bias term.

  • c. Candidate hidden state $\left( h^{\prime }\right)$:

    $$\begin{aligned} h^{\prime } _t=\tanh \left( W_h \cdot I_t+\left( U_h \cdot \left( r_t \cdot h_{t-1}\right) \right) +b_r\right. \end{aligned}$$

    (7)

    where $\tanh$ denotes the hyperbolic tangent activation function, $W_h$ represents the weight matrix for the candidate hidden state, and $U_h$ denotes the weight matrix associated with the reset gate $r_t$, which is multiplied by the previous hidden state $h_{t-1}$ in the candidate state.

  • d. New hidden state $\left( h_t\right)$:

    $$\begin{aligned} h_t=\left( 1-z_t\right) \cdot h_{t-1}+z_t \cdot h_t^{\prime } \end{aligned}$$

    (8)

    The new hidden state $h_t$ incorporates information from both the previous hidden state $\left( h_{t-1}\right)$ and the candidate hidden state $\left( h_t^{\prime }\right)$, weighted by the update gate $\left( z_t\right)$. This equation combines “how much to forget” from the past (controlled by the reset gate) with “how much to update” based on the current input (determined by the update gate).

  Multiple GRU layers are stacked to create a deeper network. Each GRU layer takes the output of the previous layer as its input. By stacking more layers, the network is able to learn more complex relationships within the sequential voltage data and charging state information. In each GRU layer, the update gate, reset gate, candidate hidden state, and new hidden state equations remain consistent. However, these calculations are conducted iteratively across each layer. Initially, in the first GRU layer, these equations are applied using the combined input vector along with the initial hidden state, typically initialized with zeros. The resultant hidden state obtained from this layer serves as the input for the subsequent GRU layer. Subsequently, in subsequent GRU layers, the equations are applied again for each layer. However, this time, the hidden state from the previous layer is utilized as input. This iterative process allows the network to capture increasingly complex temporal dependencies within the sequential data.

• 3. Output dense layer: This layer is placed after the final GRU layer. It receives the hidden state $\left( h_t\right)$ obtained from the last GRU layer (representing the information after processing the entire sequence). It is represented as

  $$\begin{aligned} \hat{y}_t=\sigma \left( W_o \cdot h_t+b_o\right) \end{aligned}$$

  (9)

  where, $\hat{y}_t$ represents the the predicted output, $W_o$ represents the weight factor for the output layer, $b_o$ is the bias term for the output layer, $\sigma$ is the activation function. The dense layer has a single output unit with the activation function. This activation function avoids introducing non-linear scaling or modifications to the output. The final layer performs a weighted linear combination of the elements in the hidden state, which results in a prediction for the cell voltage based on the learned representation.

Similar to classical RNNs and LSTMs, the GRU typically employs the stochastic gradient descent (SGD) algorithm with momentum to adjust its weights and biases by minimizing the mean squared error (MSE) between the actual and predicted outputs. This is expressed as

$$\begin{aligned} E= & \sum _{t=1}^T \frac{(y_t - \hat{y}_t)^2}{2T} \end{aligned}$$

(10)

$$\begin{aligned} \theta _{q+1}= & \theta _q - \eta \cdot \frac{\partial E}{\partial \theta _q} + \beta \cdot (\theta _q - \theta _{q-1}) \end{aligned}$$

(11)

where $E$ represents the MSE function, while $\theta _q$ denotes the parameter set at the $q$th iteration, comprising various weights and biases as defined in Eqs. 5–9. Here, $y_t$ is the actual output, $T$ is the total number of training samples, and $\eta$ is the learning rate. This framework enables effective training of the GRU by ensuring that the model learns to minimize the prediction error iteratively.

In the basic training algorithm, the learning rate and momentum remain constant throughout the training process, which is insufficient for effectively adjusting all the weights and biases of the GRU-RNN. Although the AdaGrad strategy significantly improves training performance by adjusting the learning rate in real-time, the constant momentum can lead to slow convergence and overfitting³⁶.

To address the limitations of AdaGrad and improve training performance, a modified algorithm is developed that combines AdaGrad with adjustable momentum. This approach allows for an adaptive learning rate and momentum at varying gradients throughout the training process. The adaptive learning principle is expressed as

$$\begin{aligned} \theta _{q+1}= & \theta _q - \eta _q \cdot \frac{\partial E_q}{\partial \theta _q} + \beta _q \cdot (\theta _q - u_b \theta _{q-1}) \end{aligned}$$

(12)

$$\begin{aligned} \eta _q= & \frac{\eta _0}{\sqrt{\sum _{i=1}^q g_i^2 + \lambda }} \end{aligned}$$

(13)

$$\begin{aligned} g_q= & \frac{\partial E_q}{\partial \theta _q} \end{aligned}$$

(14)

$$\begin{aligned} \beta _q= & e^{-\kappa - \Vert g_q\Vert } \end{aligned}$$

(15)

where $\theta _{q+1}$ represents the updated parameters at iteration $q+1$. The term $E_q$ denotes the MSE at the current iteration, while $\eta _q$ is the adaptive learning rate defined in Eq. 13, which adjusts based on the accumulated gradients. The gradient $g_q$ is the derivative of the error with respect to the parameters $\theta _q$. The momentum factor $\beta _q$ is calculated using an exponential decay function influenced by the norm of the gradient $g_q$ and a coefficient $\kappa$, which serves as the initial parameter for the momentum term.

Additionally, $\lambda$ is a small positive constant (default value $1 \times 10^{-8}$) that prevents division by zero. The initial learning rate is denoted as $\eta _0$. This modified algorithm enables adaptive adjustments to both the learning rate and momentum, optimizing the training process for better convergence and reduced overfitting

Adaptive threshold algorithm

Battery states must remain consistent within a certain range over their lifetime under similar operating conditions. Fluctuations in these states, often following a Gaussian distribution, can indicate abnormal behavior. The $3\sigma$ criterion, based on the standard deviation, is commonly used to determine if the measured values fall within the expected range. However, traditional approaches using fixed thresholds may be inadequate in capturing variations due to different driving behaviors and environmental conditions. Therefore, an adaptive threshold algorithm is proposed, integrating driving behavior and environmental factors into a GPR model to dynamically estimate the normal fluctuation range of battery voltage.

A Gaussian Process is a collection of random variables, any finite number of which have a joint Gaussian distribution. In the context of regression, GPR is a powerful Bayesian non-parametric approach that models the distribution over functions directly³⁷. It provides a flexible framework for regression tasks where predictions are made based on a distribution over functions rather than point estimates. By employing GPR iteratively with a sliding window, the proposed method continuously adapts to new data, accounting for temporal changes and improving fault detection accuracy. This iterative use of GPR ensures that the model remains responsive to varying operational conditions, capturing indistinct changes in battery behavior that fixed thresholds can overlook.

This approach is inspired by relevant research, such as the framework presented by Meng et al.³⁸, which combines GPR and Kalman filters for battery end-of-life prediction without relying on degradation empirical models. Their work demonstrated the effectiveness of using GPR for dynamic prediction and adaptation in battery management systems, providing a robust foundation for our adaptive threshold algorithm. By integrating environmental and operational factors, the proposed method enhances the precision and reliability of fault detection, ultimately contributing to safer and more efficient battery management.

Consider a set of input-output pairs $\left\{ \left( x_i, y_i\right) \right\} _{i=1}^n$, where $x_i \in \mathbb {R}^d$ denotes the input feature vector and $y_i$ represents the corresponding output (target) value. Let $f=$ $\left( f\left( x_1\right) , f\left( x_2\right) , \ldots , f\left( x_n\right) \right) ^T$ be the vector of function values at the observed inputs, and K be the kernel matrix such that $K_{i j}=k\left( x_i, x_j\right)$, where $k(\cdot , \cdot )$ is a positive definite kernel function.

The Gaussian Process Regression model is defined as

$$\begin{aligned} f(x) \sim \operatorname {GP}\left( \mu (x), k\left( x_i, x_j\right) \right) \end{aligned}$$

(16)

where $\mu (x)$ represents the mean function, which is often assumed to be zero for simplicity, and $k\left( x_i, x_j\right)$ is the covariance function (kernel) between the input vectors $x_i$ and $x_j$, capturing the similarity between data points.

The choice of kernel function is crucial as it determines the smoothness and properties of the resulting functions. Commonly used kernel functions include the Radial Basis Function (RBF) kernel, Matérn kernel, and Linear kernel.

Algorithm 1

Adaptive threshold algorithm

The RBF kernel is particularly popular and is defined as

$$\begin{aligned} k\left( \left( x_i, x_j\right) \right) =\exp \left( -\frac{1}{2 \ell ^2}\left\| x_i-x_j\right\| ^2\right) \end{aligned}$$

(17)

where $\left\| x_i-x_j\right\| ^2$ is the squared Euclidean distance between two points $x_i$ and $x_j$, and $\ell$ is the length scale parameter of the kernel.

A kernel function is positive definite if and only if the Gram matrix is positive definite for any finite set of points. This property ensures that the resulting Gaussian Process is well-defined and valid.

The adaptive threshold is a dynamic threshold used for anomaly detection in battery voltage. The adaptive threshold $h_{\textrm{th}}$ is computed using a smoothing factor $\alpha$ and the standard deviation of the difference between the observed battery voltage and the predicted mean

$$\begin{aligned} h_{\textrm{th}} = \alpha \cdot \operatorname {std}(y - \mu (x)) \end{aligned}$$

(18)

where $\operatorname {std}(y - \mu (x))$ represents the standard deviation of the residuals.

Sliding window and forward extension techniques were used to dynamically update the Gaussian process regression model in real time. This method allows the model to adapt to variations in environmental conditions and driving behavior, ensuring accurate estimation of the normal range of battery voltage fluctuations. The sliding window size is set to 1000, and the initial adaptive threshold is established at 0.08. The detailed algorithm is outlined in Algorithm 1.

Experimental results and discussion

Experimental setup

In this section, the hardware and software configurations for implementing the proposed method for battery cell fault detection are discussed. The hardware setup includes a 12th Gen Intel^® Core™ i7-12700H processor (20 CPUs at 2.30 GHz), 32 GB memory, and an NVIDIA GeForce RTX 4070 GPU with 8 GB memory, running on a 64-bit Microsoft Windows 10 OS with a 2 TB SSD. For software, we utilized Windows 10 Pro, Python 3.12.0, and PyCharm Professional 2023.3 for development and implementation.

In addition to hardware and software configurations, the parameter settings for the key components of the proposed methods were carefully chosen to optimize performance. Table 1 summarizes the parameter settings for segmented regression, GRU network, GPR, and the adaptive threshold algorithm.

Table 1 Parameter settings for the proposed methods.

Fig. 8

Prediction results of the battery cell voltages in the charging mode (a) Cell 16 (b) Cell 32 (c) Cell 48 (d) Cell 64 (e) Cell 80 (f) Cell 96.

Fig. 9

Prediction results of the battery cell voltages in the discharging mode (a) Cell 16 (b) Cell 32 (c) Cell 48 (d) Cell 64 (e) Cell 80 (f) Cell 96.

Experimental results

Figure 8 showcases the effectiveness of the proposed method in predicting battery cell voltages during charging for faulty vehicles. The Li-ion battery system under study consists of 8 modules, each containing 12 cells. This intricate design requires a model capable of capturing distinct behavior across all components.

The plot highlights representative cells (16, 32, 48, 64, 80, and 96) from different modules, offering a detailed perspective on prediction accuracy across the entire battery pack. As depicted, the predicted and measured cell voltages shows a notable similarity, emphasizing the robustness of the proposed method in accurately forecasting cell voltages during the charging process, even in the presence of a faulty battery pack. Moreover, the consistency observed across multiple cells underscores the reliability and precision of the proposed method.

Figure 9 demonstrates the effectiveness of the proposed method in precisely predicting battery cell voltages during the discharging phase of the vehicle, despite its faulty battery pack. The Li-ion battery system consists of 8 modules, each containing 12 cells, requiring a model capable of capturing distinct behaviors across all components.

Fig. 10

Results of fault detection based on adaptive threshold (a) Cell 16 (Charging) (b) Cell 49 (Charging) (c) Cell 32 (Discharging) (d) Cell 49 (Discharging).

The plot showcases representative cells (16, 32, 48, 64, 80, and 96) from different modules, providing a detailed insight into prediction accuracy across the entire battery pack. As depicted, there is a notable similarity between the predicted and measured cell voltages, highlighting the robustness of the proposed method in accurately forecasting cell voltages during the discharging process, even with a faulty battery pack. Furthermore, the consistency observed across multiple cells and modules emphasizes the reliability and precision of the proposed model, confirming its ability to perform consistently and accurately throughout the entire battery system, despite potential module-to-module variations or specific cell locations.

Figure 10 illustrates the results of the fault detection conducted using the adaptive threshold method. The plotted graphs depict the comparison between the residual values, which represent the differences between the measured and predicted voltages, and the adaptive thresholds.

Upon examination, it becomes evident that the battery exhibits abnormal battery behavior, particularly in cell 49. In both scenarios, cell 49 experiences a sudden and significant drop in voltage. This abnormal behavior in cell 49 is highlighted by the fact that the residual differences between the predicted and measured voltages consistently exceed the threshold range established for normal values.

In contrast, cells 16 and 32 show no indications of faults or abnormalities, as the residual values remain within the acceptable threshold range throughout the charging and discharging processes. The effectiveness of the proposed fault detection method is underscored by its ability to accurately detect abnormalities in cell 49 while correctly identifying the normal operation of cells 16 and 32. By consistently identifying deviations from expected voltage profiles and exceeding the threshold range multiple times, the method provides valuable insights for prioritizing maintenance actions and ensuring the overall reliability and performance of the EV battery system.

Fig. 11

Results of fault detection (Discharging Mode) (a) Cell 16 proposed method (Adaptive Threshold) (b) Cell 16 proposed method (Fixed Threshold) (c) Cell 49 without segmentation (Adaptive Threshold) (d) Cell 49 without segmentation (Fixed Threshold).

Figure 11 presents the results of fault detection for Cell 16 (Normal Cell) under discharging mode, showcasing different methods and their effectiveness in identifying faults. In Fig. 11a, the adaptive threshold method effectively distinguishes normal behavior from the absence of faults in Cell 16. By dynamically adjusting the threshold based on the data characteristics, the method accurately identifies the absence of faults without producing a false detection. This reliability ensures a dependable fault detection process, crucial for maintaining the integrity of the system. Figure 11b illustrates the proposed fault detection method utilizing a fixed threshold. Unlike the adaptive threshold method, which adjusts to the data, the fixed threshold remains constant regardless of the data characteristics.

Consequently, the fixed threshold method may exhibit reduced accuracy in fault detection due to its inability to adapt to varying conditions. Figure 11c demonstrates the fault detection method without segmentation but still utilizing adaptive threshold. The absence of proper segmentation in the fault detection method leads to inaccurate prediction results. This inaccuracy has resulted in a false detection, clearly demonstrating the critical role of segmentation in refining fault detection accuracy. Figure 11d depicts the fault detection method without segmentation, utilizing a fixed threshold instead. Without segmentation, the analysis lacks the ability to isolate relevant data segments, which is essential for accurate fault detection. By employing a fixed threshold, the method did not adapt to varying conditions, leading to false detection or missed detection.

Fig. 12

The distribution of absolute errors in estimating the cell voltage during the charging phase (a) Proposed method (b) Transformer-based method (c) LSTM-based method (d) BPNN-based method.

Fig. 13

The distribution of absolute errors in estimating the cell voltage during the discharging phase (a) Proposed method (b) Transformer-based method (c) LSTM-based method (d) BPNN-based method.

Performance evaluation

Figures 12 and 13 demonstrate the superior performance of the proposed method in estimating the voltage of cell 16 during both the charging and discharging phases. The boxplots highlight significantly reduced absolute errors compared to estimations derived from other models in literature like Transformer, LSTM, and BPNN based models. In addition to showcasing enhanced accuracy in voltage prediction, the method shows robustness across varying operational phases, contributing to its reliability in real-world applications. This indicates the effectiveness of the Segmented Regression-based approach in accurately capturing the complex voltage patterns, thereby underscoring the potential of the proposed method.

Table 2 Comparison of absolute error statistics for different methods during the charging process.

Table 3 Comparison of absolute error statistics for different methods during the discharging process.

Table 4 Comparison of estimation results for different methods during the charging process.

Table 5 Comparison of estimation results for different methods during the discharging process.

Tables 2 and 3 further explain the absolute error statistics for different methods during the charging and discharging processes, respectively. These tables provide detailed metrics such as the mean, standard deviation, minimum, 25th percentile, median, 75th percentile, and maximum errors. The proposed method consistently achieves lower mean and median absolute errors compared to the other methods, underscoring its superior performance and accuracy in voltage estimation across different operating conditions.

Tables 4 and 5 provide a detailed comparison of the estimation results using various metrics such as Mean Squared Error (MSE), Root Mean Squared Error (RMSE), and Mean Absolute Error (MAE) during the charging and discharging processes, respectively.

Table 4 presents the regression metrics for the charging phase. The proposed method achieves the highest accuracy of 99.803%, indicating superior performance in accurately estimating the cell voltage compared to the other methods. The Transformer model, while better than the LSTM and BPNN models, still lags behind with an accuracy of 98.245%. The LSTM and BPNN models show significantly lower accuracy values of 95.450 and 92.208%, respectively, highlighting the effectiveness of the proposed method in this phase.

Table 5 showcases the regression metrics for the discharging phase. Similar to the charging phase, the proposed method outperforms the other models with an accuracy of 99.507%. The Transformer again ranks second, though with slightly lower accuracy compared to the charging phase, recording an accuracy of 97.864%. The LSTM and BPNN models continue to show lower accuracy metrics of 93.472 and 91.662%, respectively, emphasizing the robustness and accuracy of the proposed method in various operational phases.

Overall, the results from both figures and tables confirm the superior performance of the proposed method in accurately estimating cell voltages during both the charging and discharging phases. The ability to maintain low error rates across different conditions makes it a promising tool for effective battery management and fault detection in EVs. The ability of the proposed method to maintain such low error rates across both charging and discharging phases highlights its robustness and effectiveness in various operational scenarios. This consistency in performance is crucial for real-world applications, where accurate and reliable voltage estimation is essential.

Conclusion

This paper presents a novel cell voltage fault detection method for electric vehicles, integrating segmented regression, GRU networks, and the GPR model. Using data from real electric vehicles for over 18 months, the method captures dependencies within charging and discharging cycles. The optimized GRU network, enhanced with Adagrad and adjustable momentum, improves cell voltage estimation accuracy.

A key innovation is the adaptive threshold algorithm, which dynamically integrates driving behavior and environmental factors into the GPR model for precise fault detection. Validation on comprehensive datasets demonstrated the method’s superior performance, achieving accuracy values of 99.803% during the charging phase and 99.507% during the discharging phase. These accuracy metrics are higher than those of other models, such as Transformer, LSTM, and BPNN-based approaches, highlighting the effectiveness of the proposed method in accurate fault detection across different operational phases.

The robustness of the proposed method across varying conditions highlights its potential for effective battery management and fault detection in electric vehicles, ensuring better health monitoring and predictive maintenance. This contributes to extending battery lifespan and enhancing overall vehicle performance.

In conclusion, the proposed method enables advanced battery management systems, ensuring accurate and reliable fault detection. In future work, we plan to extend the scope of our methodology by integrating multi-feature models, allowing us to evaluate the combined impact of SOC, temperature, current, and other factors on fault detection. Additionally, we aim to explore other advanced machine learning techniques to enhance the accuracy and applicability of the system for detecting a broader range of battery faults.