Introduction

Composite lining is a permanent structure that ensures the long-term stable operation of tunnels, and cavity defects are the most common problem in composite lining. Cavity defects mainly occur in three locations within the lining: between the initial support and surrounding rock, between the initial support and secondary lining, and within the secondary lining. Among these locations, internal cavities in the lining concrete are widely present and often lead to other problem such as cracking, frost heaving, water leakage, reinforcement corrosion, and insufficient thickness1. They are one of the key factors that cause accidents in tunnels, as shown in Fig. 1.

Fig. 1
figure 1

Secondary lining arch cavity.

Full size image

China’s transportation tunnels have reached an unprecedented scale. By the end of 2022, China had operated 24,850 highway tunnels with a total length of 26,784.3 km, 17,873 railway tunnels with a total length of 21,978 km, and 8008.17 km of operating subway lines2. Additionally, in tunnels constructed using drill and blast methods in China, over 80% of them have cavities behind the lining, which has been recognized as one of the inherent defects in tunnel engineering3. The key to preventing accidents in tunnels lies in how to quickly and accurately identify lining cavities, determine the danger status, and perform appropriate treatments.

Regarding concrete defect detection methods, they can be divided into two categories: destructive testing and non-destructive testing. Traditional concrete structure defect detection methods include visual inspection and hammer sounding. Visual inspection can only detect obvious defects, making it difficult to detect early-stage defects, and it relies on the professional skills of the inspectors. Hammer sounding involves tapping the surface of the lining and evaluating its quality and integrity based on the propagation and reflection characteristics of sound waves. However, this method has disadvantages such as subjectivity and limited information, and it can damage the surface of the lining and requires high environmental conditions. Due to the drawbacks of traditional testing methods, such as subjectivity, low efficiency, and poor accuracy, as well as the potential damage caused by destructive testing, non-destructive testing methods have taken the leading position in detection. These methods include rebound hammer, infrared thermography, ultrasonic testing, and ground-penetrating radar. Table 1 shows the conventional testing methods.

Table 1 Common methods for tunnel defect detection.
Full size table

Ultrasonic testing is a commonly used non-destructive testing technique that evaluates the quality and defects of concrete structures by utilizing the propagation characteristics of sound waves in materials. This method utilizes the velocity and reflection characteristics of ultrasonic waves during their propagation in materials to obtain internal structural information of concrete, such as cracks, cavities, voids, and reinforcement distribution. Ultrasonic testing does not damage the concrete structure and is suitable for on-site testing and long-term monitoring. The testing process is rapid, allowing for the evaluation of large-area structures within a short period. However, ultrasonic wave propagation is limited by the thickness of the concrete, and there may be limitations in the detection depth for thicker structures. When concrete structures have multiple layers or complex configurations, the propagation of ultrasonic waves may be affected, thereby impacting the accuracy of the test results.

Impact-echo testing is a non-destructive testing method that detects structural differences and subtle defects based on the variation in the propagation characteristics of sound waves inside the object being tested. The basic principle is as follows: an impact source excites transient resonances in the structure, and a sensor receives the dynamic signals of the structure. By analyzing the frequency domain peaks to identify the resonant frequency, the resonant frequencies at intact locations differ from those at defective locations, achieving the purpose of defect detection4. Applying this method to the detection of tunnel linings allows obtaining internal information about the lining through acoustic parameters, thereby detecting the thickness and cavity defects of the tunnel lining. Although the acoustic wave testing method has strong adaptability and has been widely used in concrete strength, uniformity, and internal defect detection, it is limited by being a point-by-point detection method, which restricts the detection speed. Moreover, the impact source (usually a handled steel ball) and the sensor (usually an accelerometer or microphone) placed near the impact location need direct contact with the surface of the component being tested to receive the structural response signal, which determines its inefficiency for large-scale detection applications5,6.

The infrared thermography method detects objects based on their infrared radiation characteristics. It analyzes the thermal images obtained by analyzing the temperature radiation information on the surface of the converted lining concrete to determine the distribution of tunnel lining defects and cavities. This method requires high working environment temperatures on-site and has low accuracy.

Ground-penetrating radar (GPR) is a non-destructive testing technique that analyzes the waveform, amplitude, width, and time characteristics of reflected electromagnetic waves to detect the construction quality of tunnel linings7. GPR has advantages such as high resolution, intuitive results, and fast scanning speed, making it the main method for detecting cavities and defects in tunnel linings8. GPR can effectively identify typical tunnel quality defects, such as cavities behind the lining and insufficient lining thickness, to determine the position and extent of the cavities9. However, GPR requires contact with the tunnel lining to obtain GPR data, usually by receiving reflected electromagnetic waves in a wideband manner. This approach inevitably receives other interference information, which can adversely affect data processing. Additionally, the accurate interpretation of GPR data is a key step in identifying and diagnosing tunnel safety conditions. Traditional methods of interpreting GPR data rely heavily on the engineering experience of professionals, resulting in subjectivity, low efficiency, and difficulty in providing key information about the geometric shape and dielectric constant of internal targets. Moreover, during data acquisition, the antenna needs to move forward along the measurement line at a constant speed and always be in close contact with the lining surface to ensure clear signal transmission and reception. However, in the case of narrow tunnel spaces, especially those already equipped with rail tracks and electromechanical equipment, the detection conditions are extremely challenging.

High-definition imaging technology uses cameras to capture images inside tunnels, and various data processing algorithms are used to analyze the collected images to detect various types of tunnel damage. Most digital cameras today use CCD cameras, and the core of this technology is how to use images for damage detection. Camera technology is mainly used for monitoring major tunnel problems such as cracks, water leakage, and deformation, and has achieved high resolution and accurate damage identification. However, digital photography technology requires high-quality photos, which places high demands on camera quality, tunnel lighting conditions, and tunnel surface cleanliness.

In summary, traditional detection methods face challenges such as high operational difficulty and the inability to achieve long-distance, non-contact non-destructive testing of internal damages in the lining. Finding more efficient and convenient non-destructive testing methods for detecting cavities and defects in tunnel linings has become a primary concern. Laser Doppler Vibrometry technology (hereinafter referred to as LDV technology) as a new non-contact and non-destructive testing technology, has been widely used in laboratories10,11. This technology has high sensitivity to weak vibration identification and high spatial resolution. It has been applied to non-contact vibration measurement and diagnosis of railway bridges12, detection of metal surface and shallow defects13,14, quality inspection of agricultural products15, and modal analysis of aerospace equipment16.

In the field of civil engineering, LDV can be utilized for detecting subsurface defects near the surface of concrete structures. Sugimoto et al.17 developed a non-contact acoustic inspection (NCAI) method using scanning LDV (SLDV) and Long Range Acoustic Devices (LRAD). Bending vibrations occur when there are internal defects near the concrete surface, and the resonance frequency can be measured remotely with high sensitivity using LDV or SLDV. Experimental results demonstrated that the proposed technique achieves detection accuracy nearly equivalent to that of impact testing. LDV can be applied to structural health monitoring of hydroelectric dams under non-stationary conditions. Klun M et al.18 describes the application of LDV under non-stationary conditions within hydroelectric power plants and introduces a method for using non-contact vibration monitoring for the health assessment of concrete dam structures. By eliminating inherent pseudo-vibrations and measurement noise under non-stationary conditions, substantial changes in characteristic frequencies over time can be observed, enabling the identification of fatigue levels in various structural elements of the power station. In a study by Jiang YJ et al.19, LDV technology was used to conduct fundamental tests for constant micro-motion detection of concrete structural samples under different conditions in a laboratory setting, analyzing changes in fundamental frequency before and after damage. It demonstrated that the fundamental frequency values based on constant micro-motion detection can quantitatively analyze variations in concrete strength grades and degrees of damage, further validating the efficacy of laser Doppler vibrometry in the non-destructive testing of concrete structures.

This paper focuses on conducting experimental research on remote detection using LDV technology on concrete slabs with different parameter cavities. The experiment measures the vibration parameters of the concrete slab surface in different-sized and different-depth cavities, with different types of filling materials inside the cavities and different detection distances. It analyzes the vibration velocity spectrum at various points in the scanning plane and uses spatial spectral entropy algorithms to analyze the differences in vibration signals between the defective and healthy parts, studying the vibration patterns at different frequencies.

Principle of detection

Principle of concrete void damage detection

According to the knowledge of structural dynamics, the free vibration solution for a damped system satisfying initial conditions20 is given by the following equation:

$$w(t) = e^{{ - \varsigma \omega_{n} t}} [w(0)\cos \omega_{{\text{D}}} t + (\frac{{\overline{w}(0) + \varsigma \omega_{{\text{n}}} w(0)}}{{\omega_{{\text{D}}} }})\sin \omega_{{\text{D}}} t]$$
(1)
$$\omega_{{\text{D}}} = \omega_{{\text{n}}} \sqrt {1 - \varsigma^{2} }$$
(2)

where \(w(t)\) represents the displacement as a function of time, ζ is the damping ratio,\(\omega_{{\text{D}}}\) is the natural frequency of the damped system,\(\omega_{{\text{n}}}\) is the natural frequency of the undamped system,\(w(0)\) is the initial deflection, and \(\overline{w}(0)\) is the initial velocity.

From the equation, it can be seen that the amplitude of free vibration depends on the damping ratio and the ratio of natural frequencies.

$$A = \sqrt {\left[ {w(0)} \right]^{2} + \left[ {\frac{{\overline{w}(0) + \varsigma \omega_{{\text{n}}} w(0)}}{{\omega_{{\text{D}}} }}} \right]^{2} }$$
(3)

The natural frequency of concrete with and without cavities can be calculated using the following structural dynamic formula21:

$$\omega_{{\text{n}}} = \sqrt{\frac{k}{m}}$$
(4)

where, k represents stiffness, and m represents mass.

In concrete structures, the presence of cavities changes the stiffness and mass values of the concrete surface. Equation (4) indicates that the resonant frequency changes at the location of the cavity. By substituting the resonant frequency of the cavity into Eq. (3), the change in the amplitude of free vibration at the location of the cavity can be determined. Therefore, structural damage that results in changes in stiffness and mass will cause corresponding changes in the resonant frequency of the structure, leading to variations in vibration amplitude. In practical engineering, when tunnel concrete linings and other structural elements suffer from damage without experiencing overall failure or complete instability, the vibration characteristics can be used to infer the extent of damage in concrete structures.

Measurement principle

LDV technology is based on the Doppler frequency shift of light. When light is reflected from a moving object, there is a frequency deviation between the reflected light and the incident light, which carries information about the vibration characteristics of the object22,23. With the light source and photodetector being stationary, and the positions of the light source, moving particles, and photodetector known, the velocity of the particles’ motion can be determined based on the principle of the Doppler frequency shift.

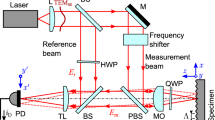
A laser Doppler vibrometer emits a laser beam with a wavelength of \(\lambda\), which illuminates the surface of a vibrating object. In the heterodyne interferometer, the laser beams are split into the target beam and the reference beam by beam splitter 1. The target beam interacts (interferes) with the reflected light from a specific point on the vibrating object and returns to beam splitter 2, where it mixes with the reference beam at beam splitter 3. The principle of LDV technology is shown in Fig. 224. If the object is in a state of vibration, this mixing process will result in fluctuations in the intensity of light. When the object has moved half a wavelength, the detector converts this signal into voltage fluctuation, which corresponds to the Doppler frequency shift. The sine wave of the Doppler frequency shift, with a period half of the wavelength, is proportional to the velocity of the object, and can be expressed by the following equation:

$$f_{D} = 2 \cdot v/\lambda$$
(5)
Fig. 2
figure 2

Laser Doppler vibration measurement principle.

Full size image

By measuring the Doppler frequency shift, the velocity of the object’s motion can be calculated. By decoding the output signal of the laser Doppler vibrometer using a controller and a decoder, information about the target’s vibrational frequency, amplitude, and other characteristics can be obtained.

The process of detecting concrete cavities through remote acoustic excitation is primarily based on the phenomenon of wave propagation since the core of detection and analysis lies in the propagation behavior of sound waves in the medium and their anomalous responses at defect sites. However, it also involves vibration phenomena. When the sound wave vibrations pass through the concrete surface and enter the interior, the presence of cavities may cause these areas to exhibit different vibration modes compared to the overall structure: the cavity areas may produce specific resonance frequencies due to their structural characteristics, forming local vibrating plate properties. Therefore, while LDV measures the surface vibration velocity, these vibration phenomena are actually a comprehensive manifestation based on the wave propagation phenomena.

Spatial spectral entropy principle

Optical noise due to euphotic leakage25 is detected as a vibration velocity waveform with an amplitude as high as that of external noise. This optical noise shows frequency characteristics similar to white noise. To quantify this characteristic, we introduce spectral entropy (HSE), which measures the whiteness of a signal. H represents spectral entropy, it is used to quantify the uncertainty or complexity of a signal in the frequency domain, reflecting the spectral characteristics of the signal.

HSE considers the signal spectrum as a probability distribution calculated from information entropy to reflect the white noise nature of the signal. It can be expressed by the following formula:

$$H_{{{\text{SE}}}} = - \sum\limits_{f} {P_{f} } \log_{2} P_{f}$$
(6)
$$P_{f} = \frac{{Q_{f} }}{{\sum\nolimits_{f} {Q_{f} } }}$$
(7)

where, Qf represents the amplitude of the signal at a particular frequency. Generally, the smaller the HSE value, the more concentrated the energy or the more pronounced the unevenness of the frequency spectrum. Signals with spectral characteristics similar to white noise or signals with a uniform frequency spectrum will have larger SE values.

Spatial spectral entropy extends the analysis of spectral entropy from individual signals to all measured signals on a two-dimensional scanning plane. It treats the amplitude sequence of the vibration velocity spectrum at each measurement point at the same frequency as a probability distribution. HSEE is defined as follows26:

$$H_{{{\text{SSE}}}} (f) = - \frac{{\sum\nolimits_{i = 1}^{{N_{all} }} {P_{i} (f)\log_{2} P_{i} (f)} }}{{\log_{2} (N_{all} )}}$$
(8)
$$P_{i} (f) = \frac{{K_{i} (f)}}{{\sum\nolimits_{i = 1}^{{N_{all} }} {K_{i} } (f)}}$$
(9)

where, Nall represents the number of measurement points within the scanning area, and Ki(f) represents the frequency amplitude of the vibration velocity spectrum at each measurement point.

When calculating the HSEE at a specific frequency f, the amplitude at that frequency is extracted from each measurement point, and then the SSE of that amplitude sequence is computed. The HSEE values for the remaining frequencies can be obtained through a similar process.

Experimental and testing

Experimental design and components

Experimental component were cast using C30 grade concrete with dimensions of 500 mm × 500 mm × 150 mm. Three concrete slab components were cast, each having different cavity sizes, depths, and filling materials. After casting, the components were placed in a standard curing environment for 28 days. The specific design scheme is shown in Fig. 3.

  1. 1.

    In component I, the cavities were simulated using four square foam polystyrene boards. The side lengths of the cavities were 50 mm, 100 mm, 150 mm, and 200 mm respectively, with a uniform thickness of 20 mm and a distance of 50 mm from the surface. The density of the boards was 26 kg/m3. They are represented as A1, A2, A3, and A4, as shown in Fig. 3a.

  2. 2.

    In component II, the cavities were also simulated using four square foam polystyrene boards. The side lengths of the cavities were all 100 mm, with a uniform thickness of 20 mm. The distances from the surface were 50 mm, 70 mm, 90 mm, and 110 mm respectively. They are represented as B1, B2, B3, and B4, as shown in Fig. 3b.

  3. 3.

    Component III contained four square cavities with a uniform thickness of 20 mm and a distance of 50 mm from the surface. They are represented as C1, C2, C3, and C4, as shown in Fig. 3c. Among them, C1 was filled with foam polystyrene boards with a density of 26 kg/m3 and a side length of 100 mm. C2 and C3 were filled with foam polystyrene boards with densities of 30 kg/m3 and side lengths of 100 mm and 150 mm respectively. C4 was an empty wooden box with a thickness of 5 mm and a side length of 100 mm.

Fig. 3
figure 3

Component physical and schematic diagrams.

Full size image

Laser Doppler vibration measurement test method

The experimental system consists of a PSV_500 laser vibrometer, a CDYX-500 long-distance directional acoustic wave transmitter, and an assembly platform, as shown in Fig. 5. The purpose of the CDYX-500 is for remote acoustic excitation of the concrete surface. The purpose of the input excitation is to induce bending vibrations in the cavities beneath the concrete. These cavities act as vibrating plates because of the defects such as cavities present in the shallow layers beneath the concrete surface. The regions with cavities exhibit bending vibrational resonance frequencies. The bending vibrations are excited by airborne sound waves containing the resonance frequency components. The excitation waveform used is a multitone burst wave with a frequency range of 50–6250 Hz (pulse width 2 ms, frequency interval 200 Hz, total waveform length 62 ms). This waveform is chosen because it includes the bending resonance frequencies of common internal defects in concrete structures. The characteristic of the multitone burst wave, where the frequency gradually increases while the amplitude remains constant, makes it more akin to a frequency-modulated signal. This type of signal can be classified as a steady-state wave because its amplitude is constant and only the frequency changes over time, but the entire waveform remains continuous and stable over a certain period.The core equipment of the laser Doppler vibrometer system is the PSV_500 laser vibrometer, which has the advantages of high measurement accuracy, high spatial resolution, fast dynamic response, and non-contact measurement. It has a measurement frequency range of 0.05 Hz to 25 kHz, making it suitable for vibration measurement in complex environments such as high temperature, high pressure, strong corrosiveness, and small spaces. The distance between the long-distance directional acoustic wave transmitter and the surface of the test component is 1.0 m. The PSV_500 laser vibrometer is controlled to be at distances of 3 m and 5 m from the surface of the test component for detection, as shown in Fig. 4.

Fig. 4
figure 4

Experimental equipment layout diagram.

Full size image

The experimental procedure mainly consists of the following three steps:

  1. (1)

    Place the CDYX-500 long-distance directional acoustic wave transmitter in front of the test component at a horizontal distance of 1.0 m. Place the PSV_500 laser vibrometer in front of the test component at a horizontal distance of 3.0 m. Connect the vibrometer to the acoustic wave transmitter and adjust the excitation sound wave frequency, ranging from 50 to 6250 Hz.

  2. (2)

    Rotate the laser head of the laser Doppler vibrometer and align the helium–neon laser beam with the test sample. Set the detection time in the Polytec laser vibrometer software. The total detection time for each test point is 4 s, with a sampling period of 80 microseconds, and a total of 50,000 time-domain waveform samples are collected. After performing a repeat check, the detection begins.

  3. (3)

    Under the excitation of the directional acoustic wave transmitter, the test component amplifies its own structural vibration. Divide the test component into a grid using the PSV_500 laser vibrometer, as shown in Fig. 5. The total number of measurement points for each component is 63 points (7 × 9), with a measurement spacing of 83 mm in the horizontal direction and 55 mm in the vertical direction.

  4. (4)

    Scan the test points one by one with the laser head to generate corresponding feature waveform sample signals.

  5. (5)

    After the detection is completed, the surface vibration of the cavities under different detection distance parameters is examined by moving the scanning head tripod to distances of 3 m and 5 m from the component to perform detection on specific points of Component III.

Fig. 5
figure 5

Component mesh division.

Full size image

Result analysis

Analysis of cavity position signal characteristics

Temporal signal characteristics

Figure 6 compares waveform samples in the time domain between the health part and the cavity part of the concrete slab. It can be observed that the waveforms of the health part exhibit relatively smooth time signals, while the cavity part shows more complex waveforms and anomalous amplitudes. In Fig. 6, Single-point measurements were performed at the positions of Point 17 and Point 32 on Component 2, which were selected to correspond to the cavity part and health part, respectively, to more clearly demonstrate the waveform characteristics under different conditions.

Fig. 6
figure 6

Time domain comparison of random samples.

Full size image

Spectral signal characteristics

Figure 7 depicts the linear amplitude spectra obtained by performing Fourier transform on the aforementioned signals. The spectra of various signals exhibit prominent peaks in the frequency range of 2–3.5 kHz. At a frequency of 3.33 kHz, the vibration peak of the void section is significantly higher than that of the healthy section. To amplify the low-amplitude components relative to the high-amplitude components for observing their periodic signals, Fig. 8 shows the logarithmic amplitude spectra obtained by Fourier transform, revealing that the vibrational amplitudes of the void section in the frequency range below 1 kHz and above 5kHz are generally higher than those of the healthy section. This indicates that the detected vibration waveform samples of the void section possess higher vibration peaks, more complex signals, and overall higher vibration amplitudes compared to the healthy section.

Fig. 7
figure 7

Linear amplitude spectrum of random samples.

Full size image
Fig. 8
figure 8

Logarithmic amplitude spectrum of random samples.

Full size image

Signal characteristics of cavities of different sizes

Figure 9 presents the spectrograms of different-sized voids on the surface of Component I at specific measurement points within the frequency range of 1000–5000 Hz. It can be observed that the amplitudes are higher in the frequency range of 1000–4000 Hz and significantly lower above 4000 Hz.

Fig. 9
figure 9

Vibration frequency spectrum of concrete surfaces with different sizes of cavities.

Full size image

By performing SSE (Spatial Spectral Entropy) feature extraction on the scanned measurement points of Component I, the vibration velocity amplitudes on the concrete surface are calculated at specific frequencies. The vibration velocity spectral amplitude sequences at each measurement point are treated as probability distributions, and the analysis results are shown in Fig. 10. It can be seen that the presence of voids leads to lower SSE values in the range of 1600–5000 Hz, indicating more complex signals. By calculating the first quartile (Q1), the third quartile (Q3), and the interquartile range (IQR) of the SSE values, we can identify outliers in the data. Typically, data points that fall below Q1 − 1.5 × IQR or above Q3 + 1.5 × IQR are considered outliers. The specific calculation shows that the value of Q1 − 1.5 × IQR is approximately 0.96. Therefore, we selected three frequencies with SSE values below 0.9627, three frequencies with SSE values lower than 0.96 are selected: 2019 Hz, 2222 Hz, 3371 Hz, 4230 Hz, 4394 Hz, and 4824 Hz.

Fig. 10
figure 10

Component I SSE analysis results diagram.

Full size image

Figure 11 depicts the vibration velocity fitting graphs on the surface of Component I at frequencies of 2019 Hz, 2222 Hz, 3371 Hz, 4230 Hz, 4394 Hz, and 4824 Hz for different-sized voids. Figure 12 shows the regression curve obtained from the regression analysis of the velocity amplitude with respect to the cavity size (edge length). Figure 13 illustrates the change factors between the cavity part and the health part at three different frequencies. The vertical axis represents the amplitude of the cavity part as a multiple of the amplitude of the health part. In other words, it shows how many times greater the amplitude in the cavity part is compared to the health part. For a void with a side length of 200 mm, the vibration velocity amplitudes on the void section’s surface changed by factors of 7.75, 10.68, 2.79, 2.5, 3.3, 4.56 and 7.51, respectively. Similarly, for voids with side lengths of 150 mm, the changes were 4.34, 6.7, 2.36, 1.75, 2.08, 2.45 and 4.35, and for voids with side lengths of 100 mm, the changes were 4.31, 6.3, 2.1, 1.12, 1.31, 1.44 and 2.68. For voids with a side length of 50 mm, the changes were 2.74, 1.9, 1.15, 1.04, 1.26, 1.42 and 1.39. It can be observed that as the size of the void increases, the vibration velocity amplitudes on the void section’s surface gradually increase compared to the healthy section.

Fig. 11
figure 11

Vibration velocity at different frequencies for Component I.

Full size image
Fig. 12
figure 12

Regression curve of vibration velocity for Component I.

Full size image
Fig. 13
figure 13

Velocity variation ratio diagram at different frequencies for Component I.

Full size image

Signal characteristics of cavities at different depths

Figure 14 displays the spectrograms of different-sized voids on the surface of Component II at specific measurement points within the frequency range of 1000–5000 Hz. It can be seen that the amplitudes are higher in the frequency range of 2000–4000 Hz and significantly lower above 4000 Hz.

Fig. 14
figure 14

Vibration frequency spectrum of concrete surfaces with cavities of different depths.

Full size image

By performing SSE feature extraction on the scanned points of Component II, the results shown in Fig. 15 indicate that the presence of voids leads to lower SSE values in the range of 2000–2200 Hz, indicating more complex signals. By calculating the value of Q1 − 1.5 × IQR, we find it to be approximately 0.96, three frequencies with SSE values lower than 0.96 are selected: 2003 Hz, 2074 Hz, and 2085 Hz.

Fig. 15
figure 15

Component II SSE analysis results diagram.

Full size image

Figure 16 presents the vibration velocity fitting graphs on the surface of Component II at frequencies of 2003 Hz, 2074 Hz, and 2085 Hz for voids with different depths. Figure 17 shows the regression curve obtained from the regression analysis of the velocity amplitude with respect to the cavity depth. Figure 18 illustrates the change factors between the void and healthy sections at the three frequencies. For a void with a depth of 50 mm, the vibration velocity amplitudes on the void section’s surface changed by factors of 2.11, 2.94, and 3.55, respectively. Similarly, for voids with depths of 70mm, the changes were 1.38, 1.44, and 3.41, and for voids with depths of 90mm, the changes were 1.36, 1.26, and 1.94. For voids with a depth of 110mm, the changes were 1.13, 1.09, and 1.32. It can be observed that as the depth of the void increases, the vibration velocity amplitudes on the void section’s surface also increase significantly compared to the healthy section.

Fig. 16
figure 16

Vibration velocity at different frequencies for Component II.

Full size image
Fig. 17
figure 17

Regression curve of vibration velocity for component II.

Full size image
Fig. 18
figure 18

Velocity variation ratio diagram at different frequencies for Component II.

Full size image

Signal characteristics of cavities filled with different materials

Figure 19 shows the frequency spectrum of the concrete surface with different types of filling materials for the specific measurement point of Component III in the frequency range of 1000–5000 Hz. It can be observed that there is a higher amplitude in the frequency range of 1000–4000 Hz, which decreases significantly below 4000 Hz.

Fig. 19
figure 19

Vibration frequency spectrum of concrete surfaces with cavities filled with different materials.

Full size image

By performing SSE analysis on the scanned measurement points of Component III, Fig. 20 displays the SSE analysis results. By calculating the value of Q1 − 1.5 × IQR, we find it to be approximately 0.96,six frequencies below 0.96 SSE value are selected, namely 1066 Hz, 1996 Hz, 2562 Hz, 4546 Hz, 4707 Hz, and 4812 Hz.

Fig. 20
figure 20

Component III SSE analysis results diagram.

Full size image

Figure 21 shows the fitted velocity curves of the concrete surface of Component III with different cavity filling materials at frequencies of 1066 Hz, 1996 Hz, 2562 Hz, 4546 Hz, 4707 Hz, and 4812 Hz. Figure 22 represents the fitted velocity curves when the surface velocity amplitude of the concrete is below 0.5 × 10−5 ms−1. Figure 23 illustrates the variation ratios between the cavity and intact sections of Component III at the six frequencies. The cavity filled with foam polystyrene board (density: 30 kg/m3) shows velocity amplitude changes of 0.72, 1.45, 1.36, 1.01, 1.17, and 1.51 times compared to the intact section. The cavity filled with foam polystyrene board (density: 26 kg/m3) exhibits changes of 0.90, 1.85, 1.89, 0.56, 1.48, and 1.33 times, while the cavity filled with a hollow wooden box shows changes of 0.72, 2.98, 2.60, 1.77, 4.01, and 2.56 times. It can be observed that, for the same size and depth, the cavity filled with foam polystyrene board (density: 26 kg/m3) has a higher surface velocity amplitude compared to the one filled with foam polystyrene board (density: 30 kg/m3). Additionally, the cavity filled with a hollow wooden box exhibits a higher surface velocity amplitude compared to the one filled with foam polystyrene board.

Fig. 21
figure 21

Vibration velocity at different frequencies for Component III.

Full size image
Fig. 22
figure 22

Vibration velocity at different frequencies for Component III.

Full size image
Fig. 23
figure 23

Velocity variation ratio diagram at different frequencies for Component III.

Full size image

Discussion

This study investigated the changes in vibration parameters on the concrete surface caused by cavity size, depth, and different types of fillers. In addition, we analyzed the vibration parameters of the concrete surface under different detection distances. Figure 24 shows the spectrum of surface vibrations of the cavity at randomly selected measurement points on Component III for different detection distances. Figure 25 displays the peak velocity values on the concrete surface at nine different randomly selected measurement points located at distances of 3 m and 5 m from the structure. It can be observed that when the laser head distance is 3 m, the surface velocity amplitude of the concrete is greater than that at 5 m, indicating that the peak surface velocity of the cavity decreases as the scanning distance increases. The peak velocity values in the spectrum are inversely proportional to the detection distance from the structure.

Fig. 24
figure 24

Fitting diagram of vibration velocity at different natural frequencies.

Full size image
Fig. 25
figure 25

Fitting diagram of vibration velocity at different natural frequencies for Component III.

Full size image

In tunnel inspection, high-precision and efficient detection is crucial for ensuring structural safety. Our study shows that shorter measurement distances (e.g., 3 m) can significantly enhance measurement accuracy. This improvement is primarily because shorter distances reduce signal attenuation and scattering effects, thereby enhancing signal quality. In the confined and complex environment of tunnels, ensuring high-precision vibration measurements is vital for accurately locating and assessing structural defects. Given that tunnel structures are often narrow and intricate, with limited space for operating instruments, it is particularly important to have equipment capable of long-distance, non-contact measurement with high accuracy, especially for areas like the tunnel vault. Such methods can accommodate different measurement needs and onsite conditions within the tunnel. By flexibly adjusting the equipment position, rapid deployment and efficient detection can be achieved, thereby improving the convenience and efficiency of field operations.

Future research can further explore the impact of laser head distance on measurement accuracy under varying environmental conditions. Additionally, integrating advanced algorithms for optimization and signal processing techniques can enhance the precision of long-distance measurements. Further investigation into the interaction of cavity size, depth, and other variables could also provide more comprehensive theoretical and practical support for the non-destructive testing of concrete structures.

Conclusions

The experimental research yields the following conclusions:

  1. (1)

    The SSE method is used to identify the vibration frequencies of the cavity surface. By detecting the surface velocity of the concrete under different cavity sizes, SSE analysis shows a decrease in SSE values within the frequency range of 1600–5000 Hz for the cavity section. The detection results indicate that three frequencies, 2019 Hz, 2222 Hz, 3371 Hz, 4230 Hz, 4394 Hz, and 4824 Hz, with SSE values below 0.96, correspond to a 200 mm cavity, resulting in surface velocity amplitude increases of 7.75, 10.68, 2.79, 2.5, 3.3, 4.56 and 7.51 times compared to the intact section. Moreover, the surface velocity amplitude shows an increasing trend with increasing cavity side length.

  2. (2)

    By detecting the surface velocity of the concrete under cavities of different depths, SSE analysis reveals decreased SSE values within the frequency range of 2000–2200 Hz for the cavity section. The detection results indicate three frequencies, 2003 Hz, 2074 Hz, and 2085 Hz, with SSE values below 0.96, corresponding to a 50 mm deep cavity. The surface velocity amplitude of the cavity increases by 2.11, 2.94, and 3.55 times compared to the intact section. The surface velocity amplitude decreases with increasing cavity depth.

  3. (3)

    Detection of surface vibration velocity of concrete voids under different types of filling materials. SSE analysis indicates a decrease in SSE values in the frequency range of 1000–5000 Hz for the voided portions. The detection results show that at a frequency of 4707 Hz, the surface vibration velocity amplitudes of voids filled with foam polystyrene boards of density 30 kg/m3, foam polystyrene boards of density 26 kg/m3, and hollow wooden boxes have increased by 1.51, 1.89, and 4.01 times, respectively, compared to the healthy portions. This indicates that voids filled with foam polystyrene boards of density 26 kg/m3 exhibit larger surface vibration velocity amplitudes than those filled with foam polystyrene boards of density 30 kg/m3, and voids filled with hollow wooden boxes exhibit even larger surface vibration velocity amplitudes than those filled with foam polystyrene boards.

  4. (4)

    Detection of surface vibration velocity of concrete voids at different detection distances for specific points on Component III. The results show that the surface vibration velocity amplitude of concrete at a distance of 3 m from the laser head is higher compared to 5 m, indicating that the overall peak surface vibration velocity decreases as the scanning distance increases. The peak spectral vibration velocity is inversely proportional to the detection distance from the tested component.

Doppler laser vibrometry has technological advantages such as intuitive measurement, high dynamic range, high accuracy, and high efficiency. It is suitable for modal analysis of surface vibration of objects and can be used for non-contact detection of shallow and deep voids beneath the surface of tunnel linings in complex tunnel environments. Compared to other methods for detecting voids in tunnel linings, it does not require direct contact with the tunnel lining to obtain surface vibration data, thereby improving detection efficiency. It can be effectively applied in tunnel lining inspections.