Abstract
The perturbed Korteweg-de Vries (PKdV) equation is essential for describing ion-acoustic waves in plasma physics, accounting for higher-order effects such as electron temperature variations and magnetic field influences, which impact their propagation and stability. This work looks at the generalized PKdV (gPKdV) equation with an M-fractional operator. It uses bifurcation theory to look at critical points and phase portraits, showing system changes such as shifts in stability and the start of chaos. Figures 1, 2 and 3 provide detailed analyses of static soliton formation through saddle-node bifurcation. We also use the modified simple equation (MSE) method to look for ion-acoustic wave solutions directly, without having to first define them. This lets us find shapes like hyperbolic, exponential, and trigonometric waves. These solutions reveal complex phenomena, including double periodic waves, periodic lump waves, bright bell-shaped waves, and singular soliton waves. Additionally, we analyze modulation instability in the gPKdV equation, which signifies chaotic transitions and is crucial for understanding nonlinear wave dynamics. Those methods demonstrate their value in generating precise soliton solutions relevant to nonlinear science and mathematical physics. This research illustrates how theoretical mathematics and physics can support solutions to practical world issues, especially in energy and technological advancement.

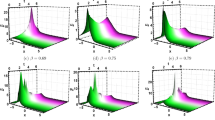
The phase portraits of the system (5) for \(2K{a}_{1}\left(\upepsilon -{a}_{3}K\right)>0\).

The two-dimensional phase portraits of the system (5) for \(2K{a}_{1}\left(\upepsilon -{a}_{3}K\right)<0\).

The two-dimensional phase portraits of the system (9) for \(\upepsilon ={a}_{3}K\).
Similar content being viewed by others
Introduction
Nonlinear evolution equations are pivotal in capturing the dynamics of complex systems across various scientific and engineering fields. Unlike linear equations, nonlinear ones can model phenomena where interactions lead to unpredictable and rich behaviors, such as turbulence in fluid dynamics1, chemical reaction pattern formation2, soliton of telecommunication systems3,4, quantum physics5,6, etc. These equations represent critical thresholds, bifurcations, and chaotic regimes, making them indispensable for understanding and predicting real-world phenomena. Their applications extend to physics, where they describe wave propagation and quantum mechanics, finance for modeling market fluctuations7, and ecology for ecosystem dynamics8. The study and solutions of nonlinear evolution equations deepen our theoretical understanding and drive advancements in technology and practical problem-solving across disciplines1,2,3,4,5,6,7,8,9,10. Numerous methods are continually being discovered to explore exact solutions of NLEEs such as multi exp-function technique11, Hirota bilinear process12,13, JEFE scheme14, variational technique15, enhanced MSE technique16, NK and improved F-expansion technique17, extended direct algebraic scheme18, MSSE technique19, new mapping scheme20, modified extended tanh and NMK techniques21, unified method22,23, exp-expansion and NMK schemes24, extended tanh expansion technique25, and so on26,27,28,29.
The generalized perturbed Korteweg-de Vries (gPKdV) equation is a mathematical model that describes the evolution of waves in a nonlinear and dispersive medium. The gPKdV equation30 can be written as follows:
where \(P\) is the wave function, \(t\) is the time variable, \(x\) is the spatial variable, and \({a}_{1}, {a}_{2}\), and \({a}_{3}\) are constants that characterize the nonlinear, dispersive, and perturbative effects, respectively. The term \({a}_{1}P{P}_{x}\) represents the nonlinear interaction in the wave. Nonlinearity often leads to wave steepening, which can cause the formation of shock waves or solitons. The constant \({a}_{1}\) determines the strength of this nonlinear effect. The term \({a}_{2}{P}_{xxx}\) accounts for the dispersion in the medium. Dispersion leads to the spreading of the wave packet over time and space. The constant \({a}_{2}\) controls the degree of dispersion, balancing the nonlinear steepening effect. The term \({a}_{3}{P}_{x}\) represents a perturbative effect, which could arise from various physical mechanisms such as damping, external forces, or higher-order corrections. The constant \({a}_{3}\) quantifies the magnitude of this perturbation. The coefficient of perturbation \({a}_{3}\) plays an acute role in articulating the influence of the Coriolis parameter in the horizontal module. The model in Eq. (1) is employed to illustrate particular events in theoretical physics associated with quantum mechanics. This model is applicable for representing phenomena such as the formation of shock waves, solitons, turbulence, boundary layer dynamics, and mass transport, particularly within the areas of fluid dynamics, aerodynamics, and continuum mechanics33,34,35.
In Eq. (1), the parameter \({a}_{3}\) represents the Coriolis effect, which is the deflection of moving objects like air and water caused by Earth’s rotation. Equation (1) provides a generalized version of both the geophysical and classical KdV equations. The geophysical KdV equation36,37,38 can be reconstructed by setting \({a}_{2}=\frac{3}{2}\), \({a}_{3}=\frac{1}{6}\) and \({a}_{1}={w}_{0}\). The perturbed-KdV model is commonly used in fields such as acoustics, aerodynamics, and medical engineering to explain sound propagation in fluids. Various significant characteristics and applications of the gPKdV equation have been thoroughly discussed in the literature30,31,32.
The primary objective of this work is to apply bifurcation theory to examine the critical points and phase portraits of the gPKdV model, where systems transition to new behaviors, such as changes in stability or the onset of chaos. To explore ion-acoustic wave solutions and the influence of fractional derivatives, we utilize a direct approach known as the modified simple equation technique on the M-fractional gPKdV model. Additionally, we illustrate some complex behaviors of the obtained solutions through three-dimensional, two-dimensional, and density diagrams, highlighting the impact of the fractional parameter in a two-dimensional diagram. Finally, we assess the modulation instability of the M-fractional gPKdV model.
The article is arranged as follows: Section two discusses the significance and features of the M-fractional derivative; Section three explores the working principles of the modified simple equation method; Section four applies bifurcation theory to Eq. (1) and presents the effect of parameters on equilibrium points and phase portraits. We execute orbits such as homoclinic, periodic, and heteroclinic, and obtain their corresponding phenomena, including periodic waves and kink waves. Section five implements the MSE technique to integrate the M-fractional gPKdV model. Section six discusses the numerical form of the obtained solutions with three-dimensional diagrams, density plots, and two-dimensional plots. Section seven presents the modulation instability of the M-fractional gPKdV model. Section eight provides the comparison, advantages, and limitations of this work and methodology. Finally, Section nine provides a summary of this work.
Fractional derivative
Fractional derivatives are crucial in the study of nonlinear evolution equations (NLEEs) due to their ability to model complex phenomena with greater accuracy than integer-order derivatives. They provide a more flexible framework for capturing the memory and hereditary properties inherent in many physical, biological, and engineering systems. By using fractional derivatives, NLEEs can describe unusual diffusion and wave propagation in various types of media. This lets us make more accurate predictions and find better solutions. This improved modeling capability is essential in fields such as viscoelasticity, fluid dynamics, and signal processing. Using fractional derivatives in NLEEs also makes it easier to come up with new numerical and analytical methods that help us understand and solve difficult nonlinear problems. The growing interest in fractional calculus underscores its significance in advancing theoretical and applied research across various scientific disciplines such as39,40,41,42.
Definition and some features of \({\varvec{M}}\)-fractional derivative
Definition:
The mapping \(\varphi :[0,\infty )\to \mathfrak{R}\) and an order χ, \(M\)-fractional operator is described as:
Here, \({\phi }_{\psi }(x)\) is Mittag–Leffler function in one parameter clear as41, and taking belong to \(\left(\text{0,1}\right):\)
Features. Let \(l,m\to \mathfrak{R}\), \(1\ge \chi >0\). Let \(R,H\) be functions. Then.
-
\({D}_{M,t}^{\chi ,\psi }\left(lR+mH\right)=l{D}_{M,t}^{\chi ,\psi }\left(R\right)+m{D}_{M,t}^{\chi ,\psi }\left(H\right).\)
-
\({D}_{M,t}^{\chi ,\psi }\left(RH\right)=R{D}_{M,t}^{\chi ,\psi }\left(H\right)+H{D}_{M,t}^{\chi ,\psi }\left(R\right).\)
-
\({D}_{M,t}^{\chi ,\psi }\left(\frac{R}{H}\right)=\frac{H{D}_{M,t}^{\chi ,\psi }\left(R\right)-R{D}_{M,t}^{\chi ,\psi }(H)}{{H}^{2}}\)
-
\({D}_{M,t}^{\chi ,\psi }\left({t}^{\varpi }\right)=\varpi {t}^{\varpi -\chi }\), \(\varpi \epsilon \mathfrak{R}\).
-
\({D}_{M,t}^{\chi ,\psi }\left(P\right)=0\), \(P\epsilon \mathfrak{R}\).
-
\({D}_{M,t}^{\chi ,\psi }\left(R\circ H\right)=R{\prime}(H){D}_{M,t}^{\chi ,\psi }H\left(t\right)\), for \(F\) is differentiable at \(G\).
-
\({D}_{M,t}^{\chi ,\psi }R\left(t\right)=\frac{{t}^{1-\chi }}{\Gamma (\psi +1)} \frac{dR}{dt}\), for \(F\) is differentiable.
Methodology of MSE technique
In this point, the working rule of the MSE technique43,44 is useful to solve any nonlinear PDEs problem. The main advantage of the MSE method is its ability to directly investigate traveling wave solutions for nonlinear partial differential equations (NLPDEs). This method does not use any auxiliary equation to find the solution such as an extended direct algebraic scheme18, MSSE technique19, new mapping scheme20, modified extended tanh and NMK techniques21, unified method22,23 and so on. For this purpose, we study nonlinear PDEs in the succeeding form:
Using the relation \(\zeta ={\Xi}-\Theta t;\text{G}\left(x,t\right)=G\left(\zeta \right)\) in Eq. (2) then we attain,
The proposed trial solution is:
Here, q is a balanced number that can be calculated using the following formula,
Now we use the proposed trial solution Eq. (4) in Eq. (3), then we get \(P\left(H\left(\zeta \right)\right)={C}_{0}+{C}_{1}{H\left(\zeta \right)}^{-1}+{C}_{2}{H\left(\zeta \right)}^{-2}+{C}_{3}{H\left(\zeta \right)}^{-3}+\dots +{C}_{n}{H\left(\zeta \right)}^{-n}\). If we set the coefficient \({C}_{k}=0;k=0, 1, 2, 3,\dots ,n\), then we get a system of equations. To get the values of \({p}_{q},\Xi\),\(H\left(\zeta \right),H{\prime}\left(\zeta \right),\Theta\), we solve the obtained system of equations. Substituting these parameters into Eq. (4) yields the required solutions.
Bifurcation analysis and phase portrait
In this section, we apply the bifurcation theory for analysis of the phase portrait of the time M-fractional generalized perturbed KdV (tMf-gPKdV) equation. To fully grasp the dynamics of nonlinear wave propagation, especially in the context of solitons and other wave phenomena, bifurcation analysis of the gPKdV equation is essential. The gPKdV equation models the evolution of shallow water waves and other physical systems with dispersive nonlinearity. Bifurcation analysis identifies critical parameter values at which the system undergoes qualitative changes, such as the creation or destruction of solitons. This analysis reveals how system behavior transitions between stable and unstable states, offering insights into wave stability and the formation of complex patterns. Phase portraits, which represent the state space of the system, provide a visual method for studying the stability and dynamics of solutions. By analyzing fixed points, limit cycles, and the system’s behavior near bifurcation points, one can predict the system’s long-term behavior. Fluid dynamics, optical fibers, and nonlinear media widely apply this approach for wave stability analysis and pattern formation.
The time M-fractional generalized perturbed KdV (tMf-gPKdV) equation is considered in the subsequent arrangement:
Using the relation \({\varphi }=\text{Kx}-\epsilon \frac{\Gamma \left(n+1\right){t}^{\sigma }}{\sigma };\text{ P}\left(x,t\right)=P\left({\varphi }\right)\) in Eq. (5) and we attain,
Integrating one time and setting integrating constant to zero.
From Eq. (7), we develop as,
According to the bifurcation theory, the Eq. (8) is as,
Here, \(L\) is the Hamiltonian constant.
The charge of \(L\), Eq. (10) generates a phase portrait of Eq. (9). When \(L\) varies, numerous types of orbits emerge in Eq. (10), resulting in diverse dynamical behaviors as explained for Eq. (10). According to bifurcation theory39, the periodic heteroclinic, and homoclinic orbit are identified by using phase portrait diagram. From Eq. (9), we attain the point of equilibrium as follows:
From the Eq. (11), we get the \({E}_{0}=\left(\text{0,0}\right)\) and \({E}_{1}=\left(\frac{2\left(\epsilon -{a}_{3}K\right)}{K{a}_{1}},0\right)\). The stability of equilibrium points is checked now. The Jacobian matrix of the linearized Eq. (9) is now shown to be:
According to the theory of planar, the observations are: if \(D(E) < 0\), then \(E\) is the saddle point. If \(D(E) > 0\) and \(T(E) = 0\), then the point \(E\) is the center point. If \(D(E) = 0\), then \(E\) is the cusp point.
Therefore, we get.
-
(a)
The point \({E}_{0}\) is saddle and \({E}_{1}\) is the center and when \(2K{a}_{1}\left(\epsilon -{a}_{3}K\right)>0\), and \(D({E}_{1}) > 0\), \(D({E}_{0}) <0 , T({E}_{1}) = 0.\)
-
(b)
The point \({E}_{1}\) is saddle and \({E}_{0}\) is the center and when \(2K{a}_{1}\left(\epsilon -{a}_{3}K\right)<0\), and \(D({E}_{1}) > 0\), \(D({E}_{0}) <0 , T({E}_{1}) = 0\).
According to the equilibrium point, the values of \(L\) are:
The behavior of Figure 1, 2, and 3 , as follows:
When \(2K{a}_{1}\left(\epsilon -{a}_{3}K\right)>0\), we obtain.
-
(i)
Eq. (1) has the bell-type solitary wave if \(L={L}_{0}\), and the orbit of the homoclinic is obtained.
-
(ii)
Eq. (1) has the periodic solitary wave if \(L<{L}_{0}\), and the orbit of the heteroclinic is obtained.
When \(2K{a}_{1}\left(\epsilon -{a}_{3}K\right)<0\), we obtain.
-
(i)
Eq. (1) has the bell-type solitary wave if \(L={L}_{0}\), and the orbit of the homoclinic is obtained.
-
(ii)
Eq. (1) has the periodic solitary wave if \(L<{L}_{0}\), and the orbit of the heteroclinic is obtained.
When \(\epsilon = {a}_{3}K.\)
If \(L=0\), then the Eq. (10) developed as:
When \(2K{a}_{1}\left(\epsilon -{a}_{3}K\right)>0\), the heteroclinic orbit is obtained in \(\left(P,H\right)\)–plane from Eq. (10). If we set the value of \(H\) into \(dP/d\xi = H\), then we attain,
Figure 4 for the values \(\epsilon =2, K=1, {a}_{1}=1.5, {a}_{2}=1, {a}_{3}=-0.2,n=1.5\), and Figure 5 for the values \(\epsilon =2, K=1, {a}_{1}=1.5, {a}_{2}=-1, {a}_{3}=-0.2,n=1.5\).
Visualization of the bright bell wave of the solution Eq. (12) for specific parametric values \(\epsilon =2, K=1, {a}_{1}=1.5, {a}_{2}=1, {a}_{3}=-0.2,n=1.5\).
Visualization of dark bell shape wave of the solution Eq. (12) for specific parametric values \(\epsilon =2, K=1, {a}_{1}=1.5, {a}_{2}=-1, {a}_{3}=-0.2,n=1.5\).
When \(2K{a}_{1}\left(\epsilon -{a}_{3}K\right)<0\), the heteroclinic orbit is obtained in \(\left(P,H\right)\)–plane from Eq. (10). Then similar to Eq. (12) we attain, The solitary periodic wave solution is shown in Fig. 6. for parametric values \(\epsilon =1 , K= 1, {a}_{1}=1.5, {a}_{2}= 1, {a}_{3}= 2,n= 1.5\)
Visualization of the periodic wave of the solution Eq. (13) for specific parametric values \(\epsilon =1, K=1, {a}_{1}=1.5, {a}_{2}=1, {a}_{3}=2,n=1.5\).
Application of modified simple equation technique
In this section, we solve the gPKdV model by using the MSE technique analytically. Under specific conditions on the free parameters, we expressed the obtained solution in terms of trigonometric and hyperbolic function forms. The main advantage of the proposed method is to solve all NLEEs directly. To solve the NLEEs, the MSE method doesn’t use any auxiliary equation or any predefined solutions like as tanh–coth method1, \((G{\prime}/G)\) -expansion technique2, Sardar sub-equation method3 and others4,5,6,7,8,9,10, it derives the exact solitary wave solution directly.
According to the MSE technique the balance number \(s=2\). So, the solution of the Eq. (7) is:
If we use the trial solution in Eq. (14) into Eq. (7), then the algebraic equations are obtained below:
Using the Maple software, we get the following solution sets.
Set 01: \(K=\sqrt{\frac{-{a}_{1}{\beta }_{2}}{12{a}_{2}}}\),\({\beta }_{0}=-\frac{2\left({a}_{3}\text{K}-\epsilon \right)}{\text{K}{a}_{1}}\),\(\epsilon =-\frac{1}{72{\beta }_{2}}\sqrt{\frac{-{3a}_{1}{\beta }_{2}}{{a}_{2}}}\left({a}_{1}{\beta }_{1}^{2}+2{a}_{3}{\beta }_{2}\right)\), \(\psi (\varphi )={h}_{1}+{h}_{2}{e}^{-\frac{{\beta }_{1}\varphi }{{\beta }_{2}}}.\)
Here, \(\theta =-\frac{{\beta }_{1}\varphi }{{\beta }_{2}}\), \({\varphi }=\sqrt{\frac{-{a}_{1}{\beta }_{2}}{12{a}_{2}}}x+\frac{1}{72{\beta }_{2}}\sqrt{\frac{-{3a}_{1}{\beta }_{2}}{{a}_{2}}}\left({a}_{1}{\beta }_{1}^{2}+2{a}_{3}{\beta }_{2}\right)\frac{\Gamma \left(n+1\right){t}^{\sigma }}{\sigma }\).
If \({a}_{1}{\beta }_{2}{a}_{2}>0\) then the following forms are derived.
If \({h}_{1}\ne {h}_{2}\), then Eq. (15) becomes,
If \({h}_{1}={h}_{2}\), then Eq. (15) becomes,
If \({h}_{1}=\pm i{h}_{2}\), then Eq. (15) becomes,
If \({a}_{1}^{2}{a}_{2}{a}_{3}{\beta }_{1}^{2}+36{\epsilon }^{2}{a}_{2}^{2}>0\) then the following forms are derived.
If \({h}_{1}\ne {h}_{2}\), then Eq. (15) becomes,
If \({h}_{1}={h}_{2}\), then Eq. (15) becomes,
If \({h}_{1}=\pm i{h}_{2}\), then Eq. (15) becomes,
Here, \(\theta =-\frac{{\beta }_{1}\varphi }{{\beta }_{2}}\), \({\varphi }=\sqrt{\frac{-{a}_{1}{\beta }_{2}}{12{a}_{2}}}x+\frac{1}{72{\beta }_{2}}\sqrt{\frac{-{3a}_{1}{\beta }_{2}}{{a}_{2}}}\left({a}_{1}{\beta }_{1}^{2}+2{a}_{3}{\beta }_{2}\right)\frac{\Gamma \left(n+1\right){t}^{\sigma }}{\sigma }\).
Set 02: \(K=\sqrt{\frac{-{a}_{1}{\beta }_{2}}{12{a}_{2}}}\),\({\beta }_{0}=0\),\(\epsilon =-\frac{1}{72{\beta }_{2}}\sqrt{\frac{-{3a}_{1}{\beta }_{2}}{{a}_{2}}}\left({a}_{1}{\beta }_{1}^{2}+2{a}_{3}{\beta }_{2}\right)\), \(\psi (\varphi )={h}_{1}+{h}_{2}{e}^{-\frac{{\beta }_{1}\varphi }{{\beta }_{2}}}.\)
Here, \({\varphi }=\sqrt{\frac{-{a}_{1}{\beta }_{2}}{12{a}_{2}}}x-\frac{1}{2}\sqrt{\frac{-{a}_{1}{\beta }_{2}}{12{a}_{2}}}\left({a}_{1}{\beta }_{0}+2{a}_{3}\right)\frac{\Gamma \left(n+1\right){t}^{\sigma }}{\sigma }.\)
If \({\beta }_{0}{\beta }_{2}>0\) and \({a}_{2}{a}_{1}{\beta }_{2}<0\) then the following forms are derived.
If \({h}_{1}\ne {h}_{2}\), then Eq. (22) becomes,
If \({h}_{1}={h}_{2}\), then Eq. (22) becomes,
If \({h}_{1}=\pm i{h}_{2}\), then Eq. (22) becomes,
If \({\beta }_{0}{\beta }_{2}<0\) or \({a}_{2}{a}_{1}{\beta }_{2}>0\) then the following forms are derived.
If \({h}_{1}\ne {h}_{2}\), then Eq. (22) becomes,
If \({h}_{1}={h}_{2}\), then Eq. (22) becomes,
If \({h}_{1}=\pm i{h}_{2}\), then Eq. (22) becomes,
Here \(\theta =\frac{{\beta }_{1}\varphi }{{\beta }_{2}}\), \({\varphi }=\sqrt{\frac{-{a}_{1}{\beta }_{2}}{12{a}_{2}}}\text{x}+\frac{1}{72{\beta }_{2}}\sqrt{\frac{-{3a}_{1}{\beta }_{2}}{{a}_{2}}}\left({a}_{1}{\beta }_{1}^{2}+2{a}_{3}{\beta }_{2}\right)\frac{\Gamma \left(n+1\right){t}^{\sigma }}{\sigma }\).
Set 03: \({\beta }_{0}=0,{\beta }_{2}=-\frac{12{K}^{2}{a}_{2}}{{a}_{1}}\), \({\beta }_{1}=\frac{12}{{a}_{1}}\sqrt{K\epsilon {a}_{2}-{K}^{2}{a}_{3}{a}_{2}}\), \(\psi (\varphi )={h}_{1}+{h}_{2}{e}^{\frac{\sqrt{K\epsilon {a}_{2}-{K}^{2}{a}_{3}{a}_{2}}}{{K}^{2}{a}_{2}}\varphi }\).
Here, \(\theta =\frac{\sqrt{K\epsilon {a}_{2}-{K}^{2}{a}_{3}{a}_{2}}}{{K}^{2}{a}_{2}}\varphi\), \({\varphi }=Kx-\epsilon \frac{\Gamma \left(n+1\right){t}^{\sigma }}{\sigma }\).
If \(K\epsilon {a}_{2}-{K}^{2}{a}_{3}{a}_{2}>0\) then the following forms are derived.
If \({h}_{1}\ne {h}_{2}\), Then Eq. (29) becomes,
If \({h}_{1}={h}_{2}\), then Eq. (29) becomes,
If \({h}_{1}=\pm i{h}_{2}\), then Eq. (29) becomes,
If \(K\epsilon {a}_{2}-{K}^{2}{a}_{3}{a}_{2}>0\) then the following forms are derived.
If \({h}_{1}\ne {h}_{2}\), then Eq. (29) becomes,
If \({h}_{1}={h}_{2}\), then Eq. (29) becomes,
If \({h}_{1}=\pm i{h}_{2}\), then Eq. (29) becomes,
Here, \(\theta =\frac{\sqrt{K\epsilon {a}_{2}-{K}^{2}{a}_{3}{a}_{2}}}{{K}^{2}{a}_{2}}\varphi\), \({\varphi }=Kx-\epsilon \frac{\Gamma \left(n+1\right){t}^{\sigma }}{\sigma }\).
Set 04: \({\beta }_{0}=-\frac{2\left(K{a}_{3}-\epsilon \right)}{K{a}_{1}}\), \({\beta }_{2}=-\frac{12{K}^{2}{a}_{2}}{{a}_{1}}\),\(K=\frac{144{a}_{2}\epsilon +24\sqrt{{a}_{1}^{2}{a}_{2}{a}_{3}{\beta }_{1}^{2}+36{\epsilon }^{2}{a}_{2}^{2}}}{288{a}_{2}{a}_{3}}\), \(\psi (\varphi )={h}_{1}+{h}_{2}{e}^{\theta }.\)
Here, \(\theta =\frac{6912{a}_{1}{\beta }_{1}{a}_{2}{a}_{3}^{2}}{{L}^{2}}\varphi\), \({\varphi }=\frac{144{a}_{2}\epsilon +24\sqrt{{a}_{1}^{2}{a}_{2}{a}_{3}{\beta }_{1}^{2}+36{\epsilon }^{2}{a}_{2}^{2}}}{288{a}_{2}{a}_{3}}x-\epsilon \frac{\Gamma \left(n+1\right){t}^{\sigma }}{\sigma }\).
If \({a}_{1}^{2}{a}_{2}{a}_{3}{\beta }_{1}^{2}+36{\epsilon }^{2}{a}_{2}^{2}>0\) then the following forms are derived.
If \({h}_{1}\ne {h}_{2}\), then Eq. (36) becomes,
If \({h}_{1}={h}_{2}\), then Eq. (36) becomes,
If \({h}_{1}=\pm i{h}_{2}\), then Eq. (36) becomes,
If \({a}_{1}^{2}{a}_{2}{a}_{3}{\beta }_{1}^{2}+36{\epsilon }^{2}{a}_{2}^{2}>0\) then the following forms are derived.
If \({h}_{1}\ne {h}_{2}\), then Eq. (36) becomes,
If \({h}_{1}={h}_{2}\), then Eq. (36) becomes,
If \({h}_{1}=\pm i{h}_{2}\), then Eq. (36) becomes,
Here, \(\theta =\frac{\sqrt{K\epsilon {a}_{2}-{K}^{2}{a}_{3}{a}_{2}}}{{K}^{2}{a}_{2}}\varphi\), \({\varphi }=Kx-\epsilon \frac{\Gamma \left(n+1\right){t}^{\sigma }}{\sigma }.\)
Set 05: \(K=\sqrt{\frac{-{a}_{1}{\beta }_{2}}{12{a}_{2}}}, \epsilon =\frac{1}{2}\sqrt{\frac{-{a}_{1}{\beta }_{2}}{12{a}_{2}}}\left({a}_{1}{\beta }_{0}+2{a}_{3}\right),{\beta }_{1}=\sqrt{6{\beta }_{0}{\beta }_{2}}, \psi (\varphi )={h}_{1}+{h}_{2}{e}^{-\frac{\sqrt{6{\beta }_{0}{\beta }_{2}}\varphi }{{\beta }_{2}}}.\)
Here, \({\varphi }=\sqrt{\frac{-{a}_{1}{\beta }_{2}}{12{a}_{2}}}x-\frac{1}{2}\sqrt{\frac{-{a}_{1}{\beta }_{2}}{12{a}_{2}}}\left({a}_{1}{\beta }_{0}+2{a}_{3}\right)\frac{\Gamma \left(n+1\right){t}^{\sigma }}{\sigma }.\)
If \({\beta }_{0}{\beta }_{2}>0\) and \({a}_{2}{a}_{1}{\beta }_{2}<0\) then the following forms are derived.
If \({h}_{1}\ne {h}_{2}\), then Eq. (43) becomes,
If \({h}_{1}={h}_{2}\), then Eq. (43) becomes,
If \({h}_{1}=\pm i{h}_{2}\), then Eq. (43) becomes,
If \({\beta }_{0}{\beta }_{2}<0\) or \({a}_{2}{a}_{1}{\beta }_{2}>0\) then the following forms are derived.
If \({h}_{1}\ne {h}_{2}\), then Eq. (43) becomes,
If \({h}_{1}={h}_{2}\), then Eq. (43) becomes,
If \({h}_{1}=\pm i{h}_{2}\), then Eq. (43) becomes,
Here, \(\theta =-\frac{\sqrt{6{\beta }_{0}{\beta }_{2}}\varphi }{{\beta }_{2}}\), \({\varphi }=\sqrt{\frac{-{a}_{1}{\beta }_{2}}{12{a}_{2}}}x-\frac{1}{2}\sqrt{\frac{-{a}_{1}{\beta }_{2}}{12{a}_{2}}}\left({a}_{1}{\beta }_{0}+2{a}_{3}\right)\frac{\Gamma \left(n+1\right){t}^{\sigma }}{\sigma }\).
Figure analysis
This section provides an in-depth examination of the graphical representation of solutions derived from the M-fractional generalized perturbed Korteweg–de Vries (gPKdV) equations, focusing on their waveforms and unique characteristics. The analysis highlights the importance of ion acoustic waves within the gPKdV framework due to their stability and persistence, making them essential for modeling nonlinear wave phenomena in environments like shallow water and plasma systems. The gPKdV equation integrates perturbation terms that account for real-world complexities, including higher-order dispersion and nonlinear effects, allowing it to model a wide range of wave behaviors. Solitary wave solutions arise from the balance between nonlinearity, which steepens the wave, and dispersion, which spreads it. This balance leads to stable, localized waveforms that travel without changing shape. Numerical simulations illustrate diverse wave patterns using 3D density plots and 2D representations. These include double periodic waves, interactions between kink and periodic lump waves, periodic rogue waves, bell-shaped bright and dark waves, singular soliton waves, and V-shaped periodic rogue waves. Different waveforms serve distinct purposes in modeling physical phenomena. Kink waves, which describe transitions between states, are crucial for systems with topological structures and phase interfaces. Bell waves, balancing nonlinearity and dispersion, are useful for studying localized energy transport in optical fibers and water waves. Periodic waves capture oscillatory behavior and pattern formation, aiding in the study of fluids and plasmas. Rogue waves, characterized by extreme amplitudes and sudden energy localization, are critical for understanding rare events in fields like oceanography and nonlinear optics.
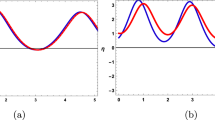
The gPKdV equation effectively models nonlinear wave phenomena across diverse systems, enhancing insights into wave stability, energy transport, and the emergence of complex patterns. This comprehensive approach reveals the equation’s versatility in capturing the intricate dynamics of nonlinear interactions. The effect of M-fractional parameters is shown in two-dimensional plots, here the red color is used for \(\sigma =0.1\); the red color is used for \(\sigma =0.5\); the red color is used for \(\sigma = 0.9\). Figure 7 represents the double periodic wave of Eq. (19) for specific parametric values \({a}_{1}=0.2, {a}_{2}=0.5, {a}_{3}=0.2, {h}_{1}=2, {h}_{2}=-0.2, {\beta }_{1}=3,{\beta }_{2}=1, n=1.5\). Figure 8 represents the periodic lump-type wave of the solution Eq. (20) for specific parametric values \({a}_{1}=0.2, {a}_{3}=0.2, {h}_{1}=2,{a}_{2}=0.5, {h}_{2}=-2, {\beta }_{1}=3,{\beta }_{2}=1, n=1.5\). The real portion of this solution provides an interaction of periodic lump wave and kink wave and the imaginary portion characterizes the episodic lump wave. Figure 9 represents the bell shape wave of Eq. (25) for specific parametric values \({h}_{1}=1, {a}_{3}=0.1,{\beta }_{2}=0.5, {a}_{1}=1, {h}_{2}=-i, {\beta }_{1}=0.5,{a}_{2}=-0.1, n=1.5\). The real portion characterizes a bright bell shape wave and the imaginary portion provides a singular soliton wave. Figure 10 visualizes the wave of the interaction of periodic wave and kink of Eq. (32) for specific parametric values \(\epsilon =1,{a}_{1}=1, {a}_{2}=-0.1, {a}_{3}=0.1, {h}_{1}=1, {h}_{2}=-i, K=0.5,{\beta }_{2}=0.5, n=1.5\). Figure 11, Visualizes the wave of double periodic wave periodic lump type wave interaction of periodic lump wave and kink wave episodic lump wave bright bell shape wave singular soliton wave interaction of periodic wave and kink wave of Eq. (33) for specific parametric values \(\epsilon =-1,{a}_{1}=1, {a}_{2}=3, {a}_{3}=0.5, {h}_{1}=0.5, {h}_{2}=1, K=0.5,{\beta }_{2}=0.5, n=1.5\). Figure 12, visualizes the diagram of the V-shape periodic rogue wave of Eq. (41) for specific parametric values \(\epsilon =3,{a}_{1}=3, {a}_{2}=0.5, {a}_{3}=-3, {h}_{1}=1, {h}_{2}=1,{\beta }_{1}=3, n=1.5\). Figure 13, visualizes the diagram of Eq. (47) for specific parametric values \({a}_{1}=1{h}_{1}=1, {a}_{2}=1, {\beta }_{0}=-0.5,{a}_{3}=2, {\beta }_{2}=0.5, n=1.5, {h}_{2}=-2\). The real portion provides a linked rogue wave with a dark bell shape and the imaginary part provides an episodic rogue wave. Figure 14, visualizes the diagram of Eq. (48) for the values \({a}_{1}=1, {a}_{2}=1, {a}_{3}=2, {h}_{1}=1, {h}_{2}=1, {\beta }_{0}=0.5,{\beta }_{2}=0.5, n=1.5\). The real portion provides the interaction of periodic wave and kink and the imaginary portion characterizes periodic lump wave.
Periodic wave of the solution Eq. (19).
Periodic wave of the solution Eq. (20).
Double bell waves the solution Eq. (25).
Kinky periodic of the solution Eq. (32).
Kinky periodic wave of the solution Eq. (33).
Linked periodic rogue wave of the solution Eq. (41).
Rogue wave of the solution Eq. (47).
Interaction of periodic wave and kink wave of the solution Eq. (48).
Modulation instability
Modulation instability (MI)45,46,47,48 refers to the exponential growth of small perturbations in a continuous wave or a uniform background, leading to the formation of localized structures or patterns. This phenomenon arises in nonlinear and dispersive media and plays a crucial role in various physical systems, including optical fibers, fluid dynamics, and plasma physics. The underlying mechanism of MI involves a balance between nonlinearity and dispersion (or diffraction), where a small initial disturbance can draw energy from the continuous background. This process amplifies specific frequencies, causing the system to evolve into localized wave packets or soliton-like structures. In this section, we investigate the modulation instability of traveling waves for \(M\)-fractional perturbed Korteweg-de Vries. Modulation instability in the gPKdV equations is significant because it describes the exponential growth of small perturbations in a wave train, leading to the formation of localized, high-amplitude structures. Nonlinear and dispersive effects drive this instability, which is crucial in generating rogue waves and other extreme events in fluids, plasmas, and optical systems. By analyzing modulation instability, researchers can better understand wave-breaking mechanisms, pattern formation, and the transition from regular wave patterns to chaotic states, enhancing the predictive power and real-world applicability of the gPKdV model in diverse nonlinear wave phenomena.
An MI analysis is performed by looking for perturbed solutions of the following form:
Inserting Eq. (51) into Eq. (50), then we get.
And linearizing in \(E\),
Let us consider the solution of Eq. (52) as:
Inserting Eq. (53) into Eq. (52) and divide the entire equation by \({e}^{\text{i}(\theta x+\epsilon \frac{\Gamma \left(n+1\right)}{\lambda }{t}^{\lambda })}\), then we get,
This equation defines the dispersion relation:
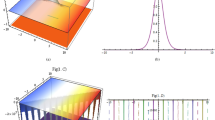
It is evident from Eq. (54) that the dispersion is stable and that, for negative values of \(\epsilon\), any superposition of the solutions will seem to decay. Figure 15 depicts the 3-D and 2-D diagram of the Eq. (54).
Comparison, advantages and limitations
In this section, we perform both analytical and graphical comparisons between our work and the published results42. Additionally, we highlight some advantages and limitations of our applied method.
Comparison with extended Tanh-method
In this subsection, we compare the solutions obtained in our study with those presented in32, which were derived using the extended tanh method and the generalized Kudryashov (GK) method. Using these methods, Sayed Saifullah et al.36 investigated the fractional gPKdV equation and identified eight analytical soliton solutions. Their work revealed known phenomena, including bright and dark solitons, singular solutions, hyperbolic traveling wave solutions, and singular periodic solutions under specific parameter conditions. In contrast, our research employed the modified simple equation method to address the fractional gPKdV equation, yielding thirty-four analytical soliton solutions. For selected parameter values, we uncovered phenomena such as double periodic waves, periodic lump-type waves, interactions between periodic lump and kink waves, bright bell-shaped waves, singular soliton waves, and V-shaped periodic rogue waves. Our approach proves effective and straightforward for identifying unique solitary wave solutions, introducing new phenomena for the M-fractional gPKdV equation.
Advantages and limitation of the MSE technique
The primary advantage of the MSE (Modified Simple Equation) technique lies in its ability to derive soliton solutions for nonlinear partial differential equations (NLPDEs) in various forms, including hyperbolic, trigonometric, or exponential functions. Unlike other methods, this technique does not require auxiliary differential equations or predefined solutions. In contrast, methods such as the NK and improved F-expansion technique17, the extended direct algebraic approach18, the MSSE method19, the new mapping approach20, the modified extended tanh and NMK methods21, the unified approach22,23, and the exp-expansion and NMK techniques24 rely on predefined auxiliary differential equations and predetermined solutions. Consequently, the MSE method uniquely allows for the direct resolution of NLPDEs. However, the scope of the MSE approach is limited; it cannot handle all types of NLPDEs, particularly when the balance number of an NLPDE exceeds two, making the solution process significantly more complex.
Conclusion
This work applies the modified simple equation (MSE) method to the gPKdV equation with an M-fractional derivative, elucidating key properties of the M-fractional operator. By using the MSE technique, we explored ion-acoustic wave solutions in hyperbolic, exponential, and trigonometric forms. These solutions manifested as double periodic waves, periodic lump-type waves, interactions between periodic lump and kink waves, bright bell-shaped waves, singular soliton waves, V-shaped periodic rogue waves, and more for specific constraint values. We further analyzed the system’s dynamic behavior through bifurcation and phase portrait studies. Additionally, we conducted a detailed modulation instability analysis, confirming the stability of the derived solutions in Fig. 15. To our knowledge, this approach to fractional nonlinear PDEs is novel. Consequently, our methods provide valuable tools for generating unique and precise soliton solutions, relevant for applications in nonlinear science and mathematical physics. In future work, we plan to investigate the chaotic dynamics and sensitivity analysis of the gPKdV equation and explore the efficacy of various fractional derivatives using a novel generalized approach.
The 3-D and 2-D diagram of the Eq. (54) (a) 3-D diagram for \({a}_{1}=1, {a}_{2}=0.1, {a}_{3}=1\). (b) \(red[{a}_{1}=1, {a}_{2}=0.1, {a}_{3}=1, g=0.5]\), \(blue[{a}_{1}=1.3, {a}_{2}=0.5, {a}_{3}=1.5, g=0.7]\), \(orage[{a}_{1}=1.5, {a}_{2}=0.9, {a}_{3}=2, g=0.9\), (c) \(red[{a}_{1}=1, {a}_{2}=0.1, {a}_{3}=1, \theta =0.5]\), \(blue[{a}_{1}=1.3, {a}_{2}=0.5, {a}_{3}=1.5, \theta =0.7]\), \(orage[{a}_{1}=1.5, {a}_{2}=0.9, {a}_{3}=2, \theta =0.9\).
Data availability
All data generated or analyzed during this study are included in this article.
References
Kaewkhiaw, P., Tiaple, P, Y., Dechaumphai, P. & Juntasaro, V. Application of nonlinear turbulence models for marine propulsors. J. Fluids Eng. 133(3) (2011).
Sadaf, M., Akram, G., Inc, M., Dawood, M., Rezazadeh, H., & Akgül, A. Exact special solutions of space–time fractional Cahn-Allen equation by beta and M-truncated derivatives. Int. J. Mod. Phys. B 24, 50118 (2023).
Roshid, M. M. & Rahman, M. M. Bifurcation analysis, modulation instability and optical soliton solutions and their wave propagation insights to the variable coefficient nonlinear Schrödinger equation with Kerr law nonlinearity. Nonlinear Dyn. 112(15), 163777 (2024).
Chakrabarty, A. K., Roshid, M. M., Rahaman, M. M., Abdeljawad, T. & Osman, M. S. Dynamical analysis of optical soliton solutions for CGL equation with Kerr law nonlinearity in classical, truncated M-fractional derivative, beta fractional derivative. Results Phys. 60, 107636 (2024).
Gasiorowicz, S., Gombás, P., Kisdi, D. & Litt, L. Quantum physics and wave mechanics and its applications. Phys. Today 28(2), 55–57 (1975).
Vichnevetsky, R. A quantum-like theory of wave propagation in periodic structures. Comput. Math. Appl. 19, 59–79 (1990).
Andreev, B., Sermpinis, G. & Stasinakis, C. Modelling financial markets during times of extreme volatility: Evidence from the gamestop short squeeze. Forecasting 4, 654–673 (2022).
Sinclair, A. R. E. & Byrom, A. E. Understanding ecosystem dynamics for conservation of biota. J. Anim. Ecol. 75(1), 64–79 (2016).
Osman, M. S., Rezazadeh, H. & Eslami, M. Traveling wave solutions for (3+1) dimensional conformable fractional Zakharov-Kuznetsov equation with power law nonlinearity. Nonlinear Eng. 8(1), 559–567 (2019).
Chakrabarty, A. K., Akter, S., Uddin, M., Roshid, M. M., Abdeljabbar, A., & Or-Roshid, H. Modulation instability analysis, and characterize time-dependent variable coefficient solutions in electromagnetic transmission and biological field. Partial Differ. Equ. Appl. Math. 11, 100765 (2024).
Ma, W. X., Huang, T. W. & Zhang, Y. A multiple exp-function method for nonlinear differential equations and its application. Phys. Scripta. 82, 065003 (2010).
Ma, W. X., Yi, Z., Yaning, T. & Tu, J. Hirota bilinear equations with linear subspaces of solutions. Appl. Math. Comput. 218, 7174–7183 (2012).
Juan, L. et al. Lax pair, Bäcklund transformation and N-soliton-like solution for a variable-coefficient Gardner equation from nonlinear lattice, plasma physics and ocean dynamics with symbolic computation. J. Math. Anal. Appl. 336, 1443–1455 (2007).
Farooq, A., Ma, W. X. & Khan, M. I. Exploring exact solitary wave solutions of Kuralay-II equation based on the truncated M-fractional derivative using the Jacobi Elliptic function expansion method. Opt. Quant. Electron. 56, 1105 (2024).
Seadawy, A. R. New exact solutions for the KdV equation with higher order nonlinearity by using the variational method. Comput. Math. Appl. 62(10), 3741–3755 (2011).
Hossain, M. M., Sheikh, M. A. N., Roshid, M. M., Roshid, H.-O. & Taher, M. A. New soliton solutions and modulation instability analysis of the regularized long-wave equation in the conformable sense. Partial Differ. Equ. Appl. Math. 9, 100615 (2024).
Ahmad, J., Akram, S., Rehman, S. U. & Ali, A. Analysis of new soliton type solutions to generalized extended (2 + 1)-dimensional Kadomtsev–Petviashvili equation via two techniques. Ain Shams Eng. J. 15(1), 102302 (2023).
Alizamini, S. M. M., Rezazadeh, H., Eslami, M., Mirzazadeh, M. & Korkmaz, A. New extended direct algebraic method for the Tzitzica type evolution equations arising in nonlinear optics. Comput. Methods Differ. Eqs. 8(1), 28–53 (2020).
Kamel, N. M., Ahmed, H. M. & Rabie, W. B. Retrieval of soliton solutions for 4th-order (2+1)-dimensional Schrödinger equation with higher-order odd and even terms by modified Sardar sub-equation method. Ain Shams Eng. J. 15(7), 102808 (2024).
Mahmood, A., Abbas, M., Nazir, T., Abdullah, F. A., Alzaidi, A. S., & Emadifar, H. Optical soliton solutions to the coupled Kaup-Newell equation in birefringent fibers. Ain Shams Eng. J. 15(7), 102757 (2024).
Roshid, M. M., Abdeljabbar, A., Begum, M. & Basher, H. Abundant dynamical solitary waves through Kelvin-Voigt fluid via the truncated M-fractional Oskolkov model. Results Phys. 55, 107128 (2023).
Roshid, M. M., Rahman, M. M., Roshid, H. O. & Bashar, M. H. A variety of soliton solutions of time M-fractional: Non-linear models via a unified technique. PLoS ONE 19(4), e0300321 (2024).
Roshid, M. M., Alam, M. N., İlhan, O. A., Rahim, M. A., Tuhin, M. M. H., & Rahman, M. M. Modulation instability and comparative observation of the effect of fractional parameters on new optical soliton solutions of the paraxial wave model. Opt. Quant. Electron. 56(6), 1010 (2024).
Roshid, M. M., Hossain, M. M., Hasan, M. S., Munshi, M. J. H. & Sajib, A. H. Dynamical structure of truncated M− fractional Klein-Gordon model via two integral schemes. Results Phys. 46, 106272 (2023).
Osman, M. S., Ali, K. K. & Gómez-Aguilar, J. F. A variety of new optical soliton solutions related to the nonlinear Schrödinger equation with time-dependent coefficients. Optik 222, 165389 (2020).
Younas, U., Ren, J., Akinyemi, L. & Rezazadeh, H. On the multiple explicit exact solutions to the double-chain DNA dynamical system. Math. Methods Appl. Sci. 46(6), 6309–6323 (2023).
Younas, U., Sulaiman, T. A. & Ren, J. Propagation of M-truncated optical pulses in nonlinear optics. Opt Quant Electron. 55, 102 (2023).
Younas, U., Sulaiman, T. A. & Ren, J. Diversity of optical soliton structures in the spinor Bose–Einstein condensate modeled by three-component Gross–Pitaevskii system. Int. J. Mod. Phys. B 37(1), 2350004 (2023).
Younas, U., Seadawy, A. R., Younis, M. & Rizvi, S. T. R. Construction of analytical wave solutions to the conformable fractional dynamical system of ion sound and Langmuir waves. Waves Random Complex Media 32(6), 2587–2605 (2020).
Alquran, M. & Alhami, R. Analysis of lumps, single-stripe, breather-wave, and two-wave solutions to the generalized perturbed-KdV equation by means of Hirota’s bilinear method. Nonlinear Dyn. 109, 1985–1992 (2022).
Saifullah, S., Ahmad, S., Alyami, M. A. & Inc, M. Analysis of interaction of lump solutions with kink-soliton solutions of the generalized perturbed KdV equation using Hirota-bilinear approach. Phys. Lett. A. 454, 128503 (2022).
Raut, S. R., Kairi, R., Chatterjee, P. & Roy, S. The non-autonomous generalized perturbed KdV equation: Its integrability, infinite conservation laws, multi soliton, high-order breather and hybrid solutions with mixed backgrounds, research square (2023).
Ozkan, E. M. & Ozkan, A. The soliton solutions for some nonlinear fractional differential equations with beta derivative. arXiv:2104.12388.
Gepreel, K. A. Explicit Jacobi elliptic exact solutions for nonlinear partial fractional differential equations. Adv. Differ. Equ. 286 (2014).
Saifullah, S., Fatima, N., Abdelmohsen, S. A., Alanazi, M. M., Ahmad, S., & Baleanu, D. Analysis of a conformable generalized geophysical KdV equation with Coriolis effect. Alex. Eng. J. 73, 651–663 (2023).
lharbi, A. R. & Almatrafi, M. B. Exact solitary wave and numerical solutions for geophysical KdV equation. J. King Saud Univ. Sci. 34(6), 102087 (2022).
Rizvi, S. T. R., Seadawy, A. R., Ashraf, F., Younis, M., Iqbal, H., & Baleanu, D. Lump and Interaction solutions of a geo-physical Korteweg-de Vries equation. Results Phys. 19, 103661 (2020).
Hosseini K., Akbulut A. R., Baleanu D. U., Salahshour S. O., Mirzazadeh M., & Akinyemi L. The geophysical KdV equation: its solitons, complexiton, and conservation laws. GEM Int. J. Geomath. 13(1), 12 (2022).
Vanterler da, J. & Capelas de Oliveira, S. E. A new truncated M-fractional derivative type unifying some fractional derivative types with classical properties. Int. J. Anal. Appl. 16(1), 83–96 (2018).
Ortigueiraa, M. D. & Machado, J. A. T. Fractional calculus applications in signals and systems. Signal Process 86, 2503–2504 (2006).
Roshid, M. M., Rahman, M. M., Bashar, M. H., Hossain, M. M., & Mannaf, M. A. Dynamical simulation of wave solutions for the M-fractional Lonngren-wave equation using two distinct methods. Alexandr. Eng J. 81, 460–468 (2023).
Roshid, M. M. & Rahman, M. M. Bifurcation analysis, modulation instability and optical soliton solutions and their wave propagation insights to the variable coefficient nonlinear Schrödinger equation with fractional derivative. Nonlinear Dyn. 112, 1–23 (2024).
Roshid, M. M., Rahman, M. M. & Roshid, H.O. Exact and explicit traveling wave solutions to two nonlinear evolution equations which describe incompressible viscoelastic Kelvin-Voigt fluid. Heliyon 4(8), e00756 (2018).
Roshid, M. M., Bairagi, T., Rahman, M. M. & Roshid, H. O. Lump, interaction of lump and kink and solitonic solution of nonlinear evolution equation which describe incompressible viscoelastic Kelvin-Voigt fluid. Partial Differ. Equ. Appl. Math. 5, 100354 (2022).
Talanov, V. I. Self-focusing of electromagnetic waves in nonlinear media. JETP Lett. 2(5), 218–220 (1965).
Zakharov, V. E. Stability of periodic waves of finite amplitude on the surface of a deep fluid. J. Appl. Mech. Tech. Phys. 9(2), 190–194 (1972).
Roshid, M. M., Rahman, M., Uddin, M. & Roshid, H. O. Modulation instability, analytical, and numerical studies for integrable time fractional nonlinear model through two explicit methods. Adv. Math. Phys. 2024, 6420467 (2024).
Jha, P., Kumar, P., Raj, G. & Upadhyaya, A. K. Modulation instability of laser pulse in magnetized plasma. Phys. Plasmas 12(12), 1399 (2005).
Acknowledgements
The authors extend their appreciation to the Deanship of Research and Graduate Studies at King Khalid University for funding this work through Large Research Project under grant number: RGP2/70/45.
Author information
Authors and Affiliations
Contributions
Mohammed Kbiri Alaoui: Configured the methodology and analyzed the figures. Md. Mamunur Roshid: Conceptualized this work, wrote and validated the codes, generated the figures, and wrote the main manuscript. Mahtab Uddin: Updated the result discussions and finalized the manuscript. Wen-Xiu Ma: Analyzed the findings and modified the manuscript. Harun-Or- Roshid: Reviewed the present works and wrote the initial manuscript. Mohammod Jahirul Haque Munshi: Investigated the work and wrote the initial manuscript. All authors have read and agreed to the published version of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Alaoui, M.K., Roshid, M.M., Uddin, M. et al. Modulation instability, bifurcation analysis, and ion-acoustic wave solutions of generalized perturbed KdV equation with M-fractional derivative. Sci Rep 15, 11923 (2025). https://doi.org/10.1038/s41598-024-84941-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-024-84941-9