Introduction

With the popularization of industrial intelligence, more and more "black light factories" and “unmanned factories” are reported in the news. In the unmanned industrial environment, robots play an indispensable role. The transportation of goods in the factory is mainly carried out by handling robots1,2,3, which sort, arrange and transport rough and finished parts etc. Handling robots are able to accurately and autonomously localize and navigate in industrial environments4,5,6, mainly relying on multi-sensor fusion technology7,8,9,10 and a variety of different algorithms to achieve environment sensing and map construction for localization and navigation and path planning, and so on.

Autonomous navigation technology is one of the core technologies of handling robots, which mainly relies on a variety of sensors to realize the environment perception in the unknown field. Currently, the main sensors are: lidar11, vision camera12, infrared thermal imager13, inertial measurement unit14, and wheeled odometer15. For the data information sensed by the sensor, we also need to process it using algorithms to improve its accuracy and robustness. The main algorithms are Monte Carlo algorithm16, Kalman filtering algorithm17 and so on.

There are two main approaches to localization, one is to utilize a single sensor for localization. Davison18 first used a monocular camera in SLAM, but there is still a big lack of perception of the environment and localization accuracy. Chen19 illustrated the limitations that exist in single sensors and provided an outlook on future directions. The second is to use multi-sensor fusion technology, using a variety of sensors to realize the perception and positioning of the environment. Xu20 summarized and prospected the development status of multi-sensor fusion technology based on lidar. Xie21 combined lidar with camera, which can be widely used in different indoor and outdoor scenes.

With the development of QR code technology, in recent years, people have begun to integrate QR codes into autonomous positioning and navigation. Bach22 applied QR codes in autonomous localization and navigation of mobile robots, which effectively solved the problem of localization error accumulation. Li23 used QR code technology in AGV to effectively solve the problem of multi-AGV route conflict. In order to improve the accuracy of positioning and navigation in industrial environment, electromagnetic guidance, magnetic stripe guidance or laser guidance are mainly used. Dai24 used the method of magnetic stripe positioning to guide the AGV car, but this method can only drive in a fixed route. Wang25 designed a high-precision positioning system for mobile robots in industrial environments by using laser recognition of artificial landmarks. However, the use cost and maintenance cost of artificial landmarks and magnetic stripes are large, and there are certain limitations. Therefore, it is not conducive to wide use.

In response to the above issues, this article proposes a positioning scheme for a handling robot based on improved AMCL fusion of multiple sensors and QR code assistance, achieving a low-cost and high-precision positioning scheme for handling robots in industrial environments. The main contributions of this article are:

  • 1. In order to achieve high-precision map construction, this article uses the Cartographer algorithm to fuse data from multiple sensors for mapping.

  • 2. In order to improve the global positioning accuracy, this paper proposes an improved AMCL algorithm. By incorporating improved optimal particle filters and intelligent particle filters, the success rate of pose tracking and global positioning can be improved. By incorporating an improved adaptive particle filter to handle global localization and increase the success rate in the event of robot hijacking, the accuracy of global localization can be improved.

  • 3. In order to improve the local positioning accuracy of homework points and reduce hardware and maintenance costs, this article uses QR codes for auxiliary positioning. Simultaneously using the YOLO Fastest algorithm based on DNN inference framework to improve the recognition efficiency of visual cameras for QR codes.

The structure of the remaining part of this article is as follows: Sect. 2 is the hardware introduction, mainly explaining the hardware architecture of the lower and upper systems of the handling robot. The third section is the autonomous positioning scheme, including map construction, multi-sensor fusion, and QR code assisted positioning scheme. The fourth section is the experimental part, mainly focusing on verifying the scheme and analyzing the results. The fifth section is a summary and outlook, mainly summarizing the usage plan of this article and providing prospects for the next steps of work.

Hardware introduction

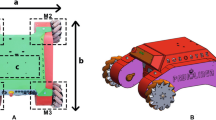
The hardware architecture of the handling robot is the basis for multi-sensor fusion positioning and navigation. The hardware architecture of the handling robot is mainly composed of two parts, the underlying system hardware architecture and the upper system hardware architecture. The hardware architecture of the underlying system includes auxiliary sensors and specific actuators, which control the actual motion of the robot. The hardware architecture of the upper system includes the main sensors, which are used to realize the mapping, positioning and navigation functions of the robot. The overall hardware architecture diagram, as shown in Fig. 1.

Fig. 1
figure 1

Total frame diagram.

Full size image

The underlying control system is one of the core architectures of the handling robot. During the operation of the robot, the system is responsible for actual execution, such as the start and stop of the motor in the servo mechanism, acceleration and deceleration, the start and stop of the hydraulic oil pump, and the on–off of the solenoid valve.

The upper control system of the handling robot is responsible for the positioning and navigation of the entire robot. This system includes a main controller, which is connected to multiple sensors and communicates with the main controller CX5130 of the lower system to achieve mapping, positioning, and navigation functions.

The underlying system of this plan is based on a PLC (Programmable Logic Controller) equipped with the Windows Embedded Standard 7P operating system, while the upper system is based on an industrial computer equipped with the Ubuntu operating system. Due to the fact that hardware devices and operating systems are not of the same type, we have adopted a special communication mechanism to combine the two, forming a physical link through Ethernet ports and network cables, and using ADS communication as data transmission to enable communication between the two systems.

Autonomous positioning scheme

Aiming at the positioning accuracy and cost of handling robots in industrial environments, we propose a high-precision positioning scheme under low-cost conditions. The scheme uses multi-sensor fusion technology for global positioning. When the robot reaches the vicinity of the moving target point, the QR code assisted positioning is started. The monocular camera is used to identify the QR code and track it, and the global cumulative error is corrected to improve the positioning accuracy. The localization scheme is shown in Fig. 2.

Fig. 2
figure 2

Localization scheme.

Full size image

Map construction

At present, the main methods of map construction are EKF-SLAM26, Fast-SLAM27, Gmapping28, Hector-SLAM29, Cartographer30 and so on. Through Table1, different mapping methods are compared and analyzed. Cartographer has high mapping accuracy and robustness, does not rely too much on odometers, and has a moderate amount of computation, which can well meet the industrial environment.

Table 1 LiDAR-Based SLAM Solution.
Full size table

The Cartographer algorithm was used for multi-sensor data fusion in mapping. As shown in Fig. 3, Scan refers to LiDAR data, Odometry refers to data from the wheeled odometer, and IMU refers to data from the inertial measurement unit.

Fig. 3
figure 3

The data flow for building map of cartographer.

Full size image

The three sensor’s data are fused by the Cartographer algorithm to obtain a two-dimensional map of the factory, as shown in Fig. 4.

Fig. 4
figure 4

Completed grid map.

Full size image

Multi-sensor fusion and algorithm optimization

Multi-sensor fusion scheme

In order to achieve high-precision positioning of handling robots in industrial environments, this paper adopts algorithms to fuse data from multiple sensors. Firstly, the unscented Kalman filtering algorithm is used to fuse the data of IMU and odometer, and then an improved adaptive Monte Carlo algorithm is used to further fuse the fused odometer data and LiDAR data, thereby achieving global high-precision autonomous positioning. In order to achieve high-precision positioning near the homework point, this article uses QR codes for auxiliary positioning. Firstly, a monocular camera is used to recognize the QR codes. In order to obtain depth information for the monocular camera, the point cloud information of the LiDAR is mapped onto the QR code image to achieve higher accuracy positioning. The entire multi-sensor fusion scheme is shown in Fig. 5.

fig. 5
figure 5

multi-sensor data fusion.

Full size image

Unscented Kalman filter algorithm

When selecting filtering algorithms for odometry fusion, the Extended Kalman Filter is the most commonly adopted approach by researchers. This method employs Taylor series expansion as a general technique for linearizing Gaussian transformations. Alternatively, other methods may also be considered to achieve improved results.

The Unscented Kalman Filter (UKF) represents an alternative linearization method, which achieves stochastic linearization through a weighted statistical linear regression process. While the asymptotic complexity of the UKF is equivalent to that of the Extended Kalman Filter (EKF), the UKF benefits from the advantages of linear unscented transformations. For linear systems, the estimates generated by the UKF are identical to those produced by the Kalman Filter, whereas for nonlinear systems, the UKF often yields results that are comparable to or surpass those of the EKF. Consequently, the UKF is selected in this study for odometry fusion, and the pseudocode for the UKF algorithm is provided in Table 2.

Table 2 UKF algorithm.
Full size table

Within a defined range, the wheeled odometer provides relatively accurate position data. Hence, the X-axis and Y-axis positional information from the odometer is used as input for the Unscented Kalman Filter (UKF) algorithm. Although the odometer also supplies heading angle data, it is not utilized due to its lower accuracy. Instead, the heading angle and angular velocity data from the IMU are employed, as they more accurately reflect variations in the heading angle. Once these inputs are appropriately configured, they are fed into the UKF algorithm node, which integrates the sensor data to generate new odometry, resulting in more precise outputs.

Improved AMCL algorithm

The most commonly used localization scheme in 2D LiDAR SLAM based on ROS system is AMCL (Adaptive Monte Carlo Localization). AMCL is a localization algorithm based on particle filtering algorithm, which uses Augmented MCL algorithm and combines KLD sampling filter to solve the problem of robot kidnapping that MCL (Monte Carlo Localization) cannot cope with, as well as the problem of low computational efficiency when the number of particles is too large. However, in large-scale scenarios such as factories, the global positioning accuracy of AMCL is poor. Therefore, this article proposes an improved AMCL algorithm that combines multiple filters into the algorithm to enhance the global localization ability of AMCL. Firstly, we incorporate an improved optimal particle filter and an improved intelligent particle filter to enhance the success rate of pose tracking and global positioning. Then an improved adaptive particle filter is added to handle global positioning and improve the success rate in the event of robot hijacking.

The optimal particle filter uses the rejection sampling method to calculate the particle attitude in the resampling phase. This method has no fixed running time. And in the case of positioning, its computational cost is high, because the measurement model needs to calculate each possible new attitude of the particles in ∆.

$$\Delta = \frac{{{\text{p(z}}_{t} |x_{t}^{[k]} )}}{{p\max (z_{t} |x_{t} )}}$$
(1)

The computational complexity of the refusing sampling method is equal to \(\text{O}({\text{T}}_{\text{L}}\cdot \text{R}\cdot \text{M})\), where \({\text{T}}_{\text{L}}\) denotes the calculation time of the measurement model under the new possible attitude of the particle. \(R\) denotes the number of attempts required for a particle to process a rejection sample. \(\text{M}\) represents the total number of particles.

In order to reduce the computational cost, an improved optimal particle filter is adopted, which relies on auxiliary particles and replaces the rejection sampling method with a time-fixed and low computational cost method. Equation (2) represents the attitude of the auxiliary particle \({\text{x}}_{\text{t}}^{[\text{m},\text{j}]}\), which gives the maximum measurement model value of the new attitude of the particle \({\text{x}}_{\text{t}}^{[\text{m}]}\).

$$x_{t}^{[m]} = x_{t}^{[m,j]} ;y \in \{ 1, \cdots ,B\} \wedge \arg max(z_{t} |x_{t}^{[m,y]} ) = \{ j\}$$
(2)

In Eq. (2), B is the number of auxiliary particles per particle.

In the intelligent particle filter, the effective particle number is usually used to measure the degree of degradation of the particle weight. However, the effective number of particles cannot be used for the localization problem. This is because the nature of the measurement model function determines the variance of the particle weight, especially the resampling stage imposes the same weight on all the drawn particles. In order to solve this problem, an improved intelligent particle filter is adopted, assuming a constant threshold weight, which is equal to the particle weight after the resampling stage:

$$W_{T} = W_{const} = \frac{1}{M}$$
(3)

In Eq. 3, M is the total number of particles, and Wcosnt is the particle whose weight is obtained by the measurement model. After standardization of the measurement model, the particles with increased weight are regarded as large weight particles, and the particles with decreased weight are regarded as small weight particles.

We take a third of the small-weight particles and cross and mutate them. The cross model modifies the attitude of small weight particles with the help of large weight particles, such as Eq. 4.

$$x_{ts}^{i} = \alpha x_{tL}^{i} + (1 - \alpha )x_{tH}^{i}$$
(4)

In Eq. 4, \(\alpha \in\)[0,1] is the crossover probability, \({x}_{tL}^{i}\) is the attitude of the i th particle from the small weight particle set \({X}_{tL}\), \({x}_{tH}^{i}\) is the attitude of the randomly selected particle from the large weight particle set \({X}_{tH}\), \({x}_{tS}^{i}\) is the new particle attitude after applying the crossover model.

In the implementation of the intelligent particle filter, the value of α is typically set within the range of 0.3 to 0.7, as this range effectively balances exploration diversity and convergence speed. In factory environments, which are relatively simple and stable, a smaller value of α can be chosen. Specifically, α is set to 0.4 in this study to facilitate faster map convergence.

The mutation model is to move the attitude of the small weight particles to a new unknown attitude, which is used to search for new results. This method can better solve the global positioning problem, such as Eq. 5.

$$x_{tM}^{i} = \left\{ {\begin{array}{*{20}c} {2x_{tH}^{i} - x_{tS}^{i} \left( {r \le pM} \right)} \\ {x_{tS}^{i} (r > pM)} \\ \end{array} } \right.$$
(5)

In Eq. 5, pM \(\in\)[0,1] represents the mutation probability, r \(\in\)[0,1] is a constant, and \({x}_{tM}^{i}\) is a new particle attitude after applying the mutation model.

In expansive yet relatively simple environments such as factories, the mutation probability pM should be set within the range of 0.1 to 0.3 to ensure that the algorithm effectively addresses the requirements of localization and path planning. In this study, pM is set to 0.2, as this value balances the stability of the particle swarm with adequate exploration capability, enabling particles to search for new solutions over a wide area.

The improved adaptive filter cancels the attenuation rate \(\alpha\) and defines a fixed number of global particles \({N}_{G}\). In the improved algorithm, the potential number of global particles is equal to the number of particles generated by the AMCL algorithm. Such as Eq. 6.

$$N_{G} \approx \max (0.0,1 - \omega_{fast} \div \omega_{slow} ) \times M$$
(6)

In Eq. 6, M is the total number of particles, \({\omega }_{fast}\) is the long-term likelihood average estimation, and \({\omega }_{slow}\) is the short-term likelihood average estimation.

After the filter is modified, they will be integrated with AMCL. Among them, the optimal particle filter and the intelligent particle filter are used to calculate the new attitude and weight of the particles, while the improved adaptive particle filter and the KLD sampling particle filter are used in the resampling stage. The pseudo code of the improved AMCL algorithm is shown in Table 3.

Table 3 Improved AMCL algorithm.
Full size table

QR code assisted positioning system

Using the improved AMCL algorithm, the handling robot can reach the target point smoothly. Limited by the resolution of the grid map and the accuracy of the sensor, the positioning error in the x coordinate system direction is positive and negative 12 cm, the positioning error in the y coordinate system direction is positive and negative 20 cm, and there is also an error in the heading angle. Although the positioning accuracy is improved compared with AMCL, the robot needs higher local positioning accuracy considering that target points require transportation operations. Therefore, this paper proposes a low-cost QR code assisted positioning scheme to achieve local high-precision positioning near the target point.

QR code is a target that is easy to identify, and the cost of laying and maintenance is low. The QR code identification with a size of 11 cm × 11 cm is attached to the target point. To successfully scan the QR code with the laser, its height must be aligned with the installation height of the LiDAR. The camera is utilized to determine the pose of the QR code within the map, with the depth information between the camera and the QR code obtained via Lidar. As the robot approaches the vicinity of the target point, the camera identifies and tracks the QR code to adjust the robot’s pose, thereby enhancing the precision of local positioning. The relationship between the QR code assisted positioning system and the improved AMCL positioning system is shown in Fig. 6.

Fig. 6
figure 6

Visual localization and improved AMCL localization diagram.

Full size image

Camera intrinsic parameter calibration

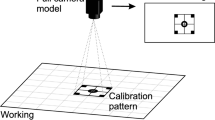
As the technology for camera intrinsic parameter calibration is well-established, this study employs the Zhang Zhengyou chessboard calibration method, which is widely acknowledged and representative in the field. The calibration chessboard features an 8 × 6 grid, with each square having a side length of 2.5 cm, as illustrated in Fig. 7.

Fig. 7
figure 7

Chessboard.

Full size image

The camera calibration was performed using the camera_calibration software, with the detailed procedure outlined in Fig. 8. After verifying the accuracy of the intrinsic parameters, the camera was securely mounted in the predetermined position. The calibration software was then initiated, and the chessboard was manually positioned in the camera’s field of view at various orientations. This approach ensured that the chessboard was captured from multiple angles, providing comprehensive calibration data. During the process, the software automatically selected several images from different perspectives as the foundation for subsequent calibration analysis.

Fig. 8
figure 8

Calibration process.

Full size image

Upon completion of the calibration, the software generates a YAML file named “camera,” where the “camera_matrix” entry represents the camera intrinsic parameters K, as illustrated in Fig. 9.

Fig. 9
figure 9

Context of calibration file.

Full size image

In this case, three decimal places were retained for the data, yielding the following results:

$$K = \left[ {\begin{array}{*{20}c} {722.517} & 0 & {291.229} \\ 0 & {725.301} & {295.809} \\ 0 & 0 & 1 \\ \end{array} } \right]$$
(7)

These represent the values of the camera intrinsic parameters K utilized in this system.

The calibration of the camera’s extrinsic parameters

To project points measured in the LiDAR coordinate system onto the camera image, the transformation between the LiDAR and camera coordinate systems must be calibrated. The camera determines the representation of the calibration board plane in its coordinate system by using the QR code or chessboard pattern on the board. Simultaneously, laser beams emitted by the LiDAR intersect with the calibration board plane. By combining the coordinates of the laser points in the LiDAR coordinate system with the plane equation in the camera coordinate system, constraints are established for points on the plane, enabling the computation of the extrinsic parameters.

To utilize this toolkit, the calibration configuration file must be properly set up. This file contains parameters such as the camera model, the name and save path of the rosbag file, the size and type of the calibration board, and other related details. Except for the rosbag file, all other data is already prepared. The next step involves recording the rosbag. During this process, the calibration board is systematically rotated and translated within a range of 0.3 to 1.5 m from the LiDAR and the camera. Concurrently, the rosbag captures both images of the calibration board and the corresponding LiDAR data.

Once all the data has been prepared, the alibr tool within the toolkit is executed to compute and save the pose between the camera and the calibration board as a txt file, which will be used in subsequent calibration steps. Following this, the LiDAR-camera extrinsic calibration tool, calibra_offline, is run to automatically detect the laser lines on the calibration board, perform the calibration, and store the results in a yaml file.

QR code recognition and positioning

This paper uses the YOLO-Fastest network model based on the DNN inference framework. This method improves the recognition speed and frame rate of the two-dimensional code image, and only consumes low CPU resources. The recognition result is shown in Fig. 10.

Fig. 10
figure 10

QR recognition result.

Full size image

Through the recognition of the QR code, the position information of the QR code relative to the camera can be obtained. Using the internal and external parameters obtained by the camera and lidar, the lidar point cloud can be projected onto the two-dimensional code image, as shown in Fig. 11.

Fig. 11
figure 11

Point cloud of laser projected to QR code.

Full size image

As shown in Fig. 11, a segment of the laser point cloud has been projected onto the QR code plane. To ensure the system’s accuracy and robustness, the points on the QR code plane must be fitted into a straight line and denoised. The detailed steps are outlined below:

(1) Define the equation of the straight line as:

$$y = kx + b$$
(8)

where x represents the distance of the laser point cloud along the x-axis direction;

y denotes the depth information of the laser point cloud;

k represents the slope of the straight line.

(2) the known point set is given as

$$(x_{1} ,y_{1} )...(x_{n} ,y_{n} )$$
(9)

(3) Ensure that the sum of squared residuals is minimized.

$$f = \sum\limits_{i = 1}^{n} {(y_{i} - kx_{i} - b)^{2} } \to 0$$
(10)

According to the extreme value theorem, the error equation reaches an extremum when its first derivative equals zero. Therefore, the derivatives with respect to k and b are computed, and k and b are solved to minimize the error function. Thus, the following equations are obtained:

$$\left\{ {\begin{array}{*{20}l} {\frac{\partial f}{{\partial k}} = \sum\limits_{i - 1}^{n} {[(y_{i} - kx_{i} - b)x_{i} ]} = 0} \hfill & {} \hfill \\ {\frac{\partial f}{{\partial b}} = \sum\limits_{i = 1}^{n} {(y_{i} - kx_{i} - b)} = 0} \hfill & {} \hfill \\ \end{array} } \right.$$
(11)
$$\left\{ {\begin{array}{*{20}l} {\sum\limits_{i = 1}^{n} {(x_{i} y_{i} )} - k\sum\limits_{i - 1}^{n} {(x_{i}^{2} )} - b\sum\limits_{i - 1}^{n} {(x_{i} )} = 0} \hfill & {} \hfill \\ {\sum\limits_{i = 1}^{n} {(y_{i} )} - k\sum\limits_{i - 1}^{n} {(x_{i} )} - nb = 0} \hfill & {} \hfill \\ \end{array} } \right.$$
(12)

Let \(A = \sum\limits_{i = 1}^{n} {(x_{i}^{2} )} ,B = \sum\limits_{i = 1}^{n} {(x_{i} )} ,C = \sum\limits_{i = 1}^{n} {(x_{i} y_{i} )} ,D = \sum\limits_{i = 1}^{n} {(y_{i} )}\), it follows that:

$$\left\{ {\begin{array}{*{20}l} {Ak + bB = C} \hfill & {} \hfill \\ {Bk + nb = D} \hfill & {} \hfill \\ \end{array} } \right.$$
(13)
$$\left\{ {\begin{array}{*{20}l} {k = \frac{Cn - BD}{{An - BB}}} \hfill & {} \hfill \\ {b = \frac{AD}{{An - BB}}} \hfill & {} \hfill \\ \end{array} } \right.$$
(14)

Next, the relative position of the QR code is determined. Based on the line Eq. (8), the formula for calculating the distance from the camera to the QR code plane is expressed as:

$$d = \frac{{\left| {kx - y + b} \right|}}{{\sqrt {k^{2} + 1} }}$$
(15)

Here, d denotes the distance.

Figure 12 illustrates the relative position of the QR code as determined by the laboratory’s QR code recognition and positioning algorithm. By referencing the predefined QR code target positions on the navigation map, the actual location of the robot can be determined. This location information is subsequently published to the ROS topic initial_pose to adjust the robot’s position on the navigation map. Finally, a target point is re-assigned on the navigation map, enabling the robot to follow the corrected target point and thereby refine its position at the designated location.

Fig. 12
figure 12

Relative position of QR code.

Full size image

Method for turning angle correction

Upon determining the relative position of the QR code target point, the robot must calculate the steering angle of the front wheel servo. Figure 13 presents the geometric relationship of the simplified mechanical model of the robot employed in this study. Typically, the linear velocity is controlled via the drive motor, while the steering is managed through the front wheel servo. Consequently, the calculation of the front wheel steering angle is required.

Fig. 13
figure 13

Geometric relationship of bicycle model.

Full size image

Where δ denotes the steering angle of the front wheel servo.

L denotes the wheelbase.

R denotes the radius of the circular arc traced by the rear axle center corresponding to a given steering angle.

It follows from the trigonometric relationship that:

$$\tan (\delta ) = \frac{L}{R}$$
(16)

In the formula, δ represents the steering angle to be determined, while R is the unknown variable.

The curvature k is inversely proportional to the radius R, and Eq. (16) can therefore be expressed as:

$$\delta = tan^{ - 1} (kL)$$
(17)

In this case, solving for δ is reduced to solving the expression on the right-hand side of the equation, where L is known, and the unknown variable is the curvature k. The following section provides the solution for k. The geometric relationship of the pure pursuit algorithm is illustrated in Fig. 14.

Fig. 14
figure 14

Geometric relationship of pure pursuit algorithm.

Full size image

As shown in the Fig. 14, (gx,gy) represents the target point g corresponding to the QR code.

ld denotes the look-ahead distance.

α represents the angle between the central plane of the vehicle and the look-ahead vector.

R represents the radius of the arc.

Then, based on the law of sines, we obtain:

$$\frac{{l_{d} }}{\sin (2\alpha )} = \frac{R}{{\sin (\frac{\pi }{2} - \alpha )}}$$
(18)
$$\frac{{l_{d} }}{\sin \alpha } = 2R$$
(19)
$$k = \frac{1}{R} = \frac{2\sin \alpha }{{l_{d} }}$$
(20)

k is determined, and taking time t into account, Eq. 17 can be rewritten as:

$$\delta (t) = \tan^{ - 1} (k(t)L) = \tan^{ - 1} (\frac{2L\sin (\alpha (t))}{{l_{d} }})$$
(21)

Finally, the problem of determining δ at each moment is converted into determining α at each moment.

The realization of QR code target point error correction algorithm

Since the handling robot uses a single steering wheel, the structure has a minimum turning radius, and it needs to leave a certain distance in the process of motion adjustment to facilitate the position correction during tracking. After obtaining the pose of the two-dimensional code target point, we need to judge whether the distance between the robot and the target point is greater than 1.3 m. Then, according to the current pose of the robot and the pose of the target point, the algorithm will continuously calculate the steering angle of the steering gear, publish the speed and angle control information, and let the robot move to the target point. Since other pure tracking algorithms only pay attention to the accuracy of the position at the target point, but do not pay attention to the adjustment of the heading angle, it will lead to a more deviated heading angle of the robot after reaching the target point. Therefore, after reaching the target point, this study also includes adjustments to the robot’s heading angle. The fundamental process of QR code target tracking is illustrated in Fig. 15.

Fig. 15
figure 15

Flow chart of QR code target point tracking.

Full size image

Experiments and analysis

In order to verify the actual performance of the crankshaft handling robot, the test was carried out in a real factory environment, and the obtained data were analyzed. Figure 16 illustrates the schematic layout of the transport robot’s working environment, where the working route is approximately 50 m in length and 6 m in width.

Fig. 16
figure 16

Actual environment of the factory.

Full size image

The testing experiment is divided into three parts, namely: 1 The algorithm testing experiment mainly compares the improved AMCL in this article with the traditional AMCL; 2. Emergency braking experiment, mainly to test the safety performance of the handling robot in the factory environment. 3. Method validation experiment, mainly comparing the proposed method with two-dimensional code assisted localization and traditional AMCL. The prototype of the handling robot for testing is shown in Fig. 17.

Fig. 17
figure 17

Transport robot prototype.

Full size image

Algorithm testing experiments

To validate the improved AMCL method proposed in this paper, an open area within the factory was selected and four target points, labeled A, B, C, and D, were designated. The crankshaft transportation robot was programmed to sequentially reach these four target points, and its path trajectory was analyzed. Starting from the origin (charging point), the transportation robot autonomously navigates through the designated target points in sequence. During navigation, the ROS rosbag tool is employed to record the mobile robot’s odometry, IMU, and other related data, resulting in the generation of a rosbag file. Additionally, the rviz visualization tool is utilized to inspect the robot’s planned navigation path. The detailed test steps are as follows:

Step 1: Control the robot to travel from the origin to the target point, record the key road point information needed for navigation, and make it into a path file;

Step 2: Control the robot to return to the origin, start the navigation-related ROS nodes, read the path file, and the robot starts autonomous navigation.

The robot navigation process is shown in Fig. 18.

Fig. 18
figure 18

Navigate to the first waypoint (a), Navigate to the second waypoint (b), Robot navigation process.

Full size image

Through experimental testing, the matplotlib tool on a PC was employed to extract data from files saved in the rosbag. The extracted data was used to generate coordinate systems and data plots, as shown in Fig. 19.

Fig. 19
figure 19

Path trajectory diagram.

Full size image

In Fig. 19, the blue dashed line denotes the theoretical path, the orange solid line represents the trajectory optimized using the traditional AMCL algorithm, and the green solid line corresponds to the trajectory optimized by the improved AMCL algorithm as proposed in this paper. It can be clearly seen from the Fig. that the path rules optimized by the improved AMCL algorithm proposed in this paper have better accuracy, which effectively proves the progressiveness and superiority of the algorithm in this paper. The experimental results show that the improved AMCL algorithm is used to fuse multiple sensors for positioning, effectively improving the global positioning accuracy.

Emergency braking test

During the robot navigation process, dynamic obstacles, such as workers and vehicles in motion, often appear in the factory. Due to the design of the transport robot, the LiDAR is installed at a height of 2.1 m, which prevents it from effectively detecting dynamic obstacles, thereby hindering obstacle avoidance. We experimentally tested emergency braking on the transport robot. For obstacle detection, data from the S30B safety laser scanner were used to determine whether obstacles were present in the driving direction. If an obstacle was detected, the robot decelerated and stopped, resuming navigation once the obstacle disappeared. This approach enables dynamic obstacle avoidance without requiring path re-planning. As shown in Fig. 20, the robot detects an obstacle and decelerates to a stop.

Fig. 20
figure 20

Robot deceleration and stop.

Full size image

Through the navigation test of the handling robot, we found that the robot can carry out safe handling operations in the vehicle channel and dynamic environment specified in the factory, which fully proves the reliability of the application of the path planning algorithm based on the waypoint in the real industrial environment.

Positioning scheme verification

To evaluate the accuracy of the positioning method proposed in this paper, a transportation point was selected as the testing target. First, the pose of the QR code at the target workstation was configured on the grid map. Subsequently, the robot’s positioning and navigation functions were activated, enabling it to autonomously navigate from a designated experimental location to the target point while recording the positioning data. The actual environment of the target point is depicted in Fig. 21.

Fig. 21
figure 21

Actual scene of target point.

Full size image

In order to facilitate comparative analysis, the test will be carried out in two groups. The first group uses the AMCL algorithm to locate, and the second group uses the improved· AMCL algorithm with the QR code to assist positioning. Two groups of tests use the position deviation between the robot’s own rotation center and the target point to investigate the positioning accuracy.

The test steps of each group are as follows:

Step 1: Control the robot to the specified experimental position, release the target point pose to the robot, and let it automatically go to the target point;

Step 2: When the robot reaches the target point and stops, manual measurement is performed to record the deviation between the robot 's rotation center and the target point, including the position deviation in the x coordinate system, the position deviation in the y coordinate system, and the heading angle deviation.

Using the method outlined in the algorithm testing experiment section, we measured the robot’s motion trajectory as it autonomously navigated from the specified experimental location to the target point, as depicted in Fig. 22.

Fig. 22
figure 22

Robot Motion Trajectory.

Full size image

In the figure above, the blue dashed line denotes the theoretical trajectory, the orange solid line represents the trajectory obtained using only the AMCL algorithm, and the green solid line corresponds to the trajectory obtained using the improved AMCL algorithm with QR code-assisted localization. Positional errors arise during the robot’s linear motion due to factors such as sensor limitations and mechanical manufacturing inaccuracies. Larger errors occur during turning, primarily caused by wheel slippage, which leads to abnormal odometry readings and positional deviations. The figure demonstrates that the improved AMCL achieves higher positioning accuracy compared to the standard AMCL, although significant positional errors remain. When the robot detects a QR code, it further corrects its trajectory, thereby achieving even more precise localization.

In order to prevent accidental errors, we repeated the test experiment 50 times. The measured position error results are shown in Fig. 23.

Fig. 23
figure 23

Distribution map of robot positioning error.

Full size image

In Fig. 23, the blue scatter is the AMCL test group, and the red scatter is the improved AMCL with QR code assisted positioning test group. It can be seen from the Figure that the red scattered points gather in the middle, and the blue scattered points disperse outward. The closer the point is to the middle, the smaller the positioning error is, indicating that the improved AMCL combined with visual-assisted positioning improves the positioning accuracy of the handling robot.

The heading angle error results of the two groups of tests are shown in Fig. 24.

Fig. 24
figure 24

Comparison diagram of robot heading angle error.

Full size image

In Fig. 24, the blue solid line is the AMCL test group, the yellow solid line is the improved AMCL combined with visual assisted positioning test group, and the blue dotted line is the reference horizontal line. It can be seen from the fluctuation range of the curve that the fluctuation range of the yellow solid line in the reference horizontal line is obviously smaller than that of the blue solid line. The improved AMCL combined with two-dimensional code assisted positioning improves the heading angle accuracy of the handling robot.

In order to have a more direct data comparison, the average data of the two sets of positioning results are calculated respectively, that is, the average positioning error of the x coordinate system, the y coordinate system and the heading angle. The results are shown in Table 4.

Table 4 Average error.
Full size table

It can be seen from Table 4 that the improved AMCL combined with the two-dimensional code assisted positioning test group has higher accuracy. Compared with the AMCL test group, it increased by about 64% in the x coordinate system, about 80% in the y coordinate system, and about 42% in the heading angle.

Conclusions and outlook

In response to the relationship between the positioning accuracy and cost of handling robots in industrial environments, this paper proposes a positioning scheme for handling robots based on improved AMCL fusion of multiple sensors and QR code assistance, achieving high-precision positioning of handling robots in industrial environments under low-cost conditions. Firstly, this article uses the Cartographer algorithm to fuse data from multiple sensors for mapping, achieving high-precision map construction. Then, an improved AMCL algorithm is designed to improve the global positioning accuracy. By adding an improved optimal particle filter and an improved intelligent particle filter, the success rate of pose tracking and global positioning is improved. By incorporating an improved adaptive particle filter to handle global localization and increase the success rate in the event of robot hijacking. Through the algorithm test experiment in the experimental part, we found that the path path of the crankshaft handling robot after using the improved AMCL algorithm proposed in this paper is significantly better than the path optimized by the traditional AMCL algorithm. The experimental results show that the improved AMCL algorithm proposed in this paper fuses multiple sensors for positioning, significantly improving the global positioning accuracy, effectively proving that the improved AMCL algorithm proposed in this paper has better advantages and progressiveness. At the same time, considering the safety issues of the handling robot in industrial environments, we also conducted experimental tests on its emergency braking performance and found that the handling robot has good emergency braking ability. Furthermore, in order to improve the local positioning accuracy of homework points while reducing hardware and maintenance costs, this paper uses QR codes for auxiliary positioning, and uses the YOLO Fastest algorithm based on DNN inference framework to improve the recognition efficiency of visual cameras for QR codes. Finally, we used the improved AMCL algorithm to fuse multiple sensors with a QR code assisted positioning method for actual testing in a factory environment, achieving a positioning error of ± 0.068 m in the x-direction, ± 0.069 m in the y-direction, and ± 0.107 rad in the heading angle at the workstation point. Compared with the traditional AMCL algorithm, it has improved by about 64% in the x coordinate system, about 80% in the y coordinate system, and about 42% in the heading angle, significantly improving the local positioning accuracy of the crankshaft handling robot at the work station. The experiment has proven that our method can achieve low-cost and high-precision positioning in industrial environments. Compared to methods such as magnetic stripe navigation and artificial landmarks, the method proposed in this article effectively reduces usage and maintenance costs, and is not affected by geographical environmental factors. For future research, we plan to further improve the recognition efficiency and accuracy of QR codes, and conduct multi machine collaborative experiments on multiple handling robots.