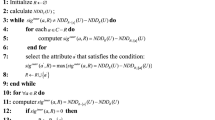Attribute reduction based on classes in incomplete ordered decision systems

Abstract

Dominance-based rough set approach (DRSA) has attracted much attention in multi-criteria decision-making problems for data with preference-ordered relations since its inception. However, in the real world, there is often the challenge of incomplete information. This paper addresses approaches to attribute reduction in an incomplete ordered decision system (IODS). Attribute evaluation is crucial in the attribute reduction process. Traditional evaluation functions primarily depend on the relationships between features, neglecting their impact on classification, and incur high computational costs when calculating lower and upper approximations. To address these issues, this paper proposes whole inter-class non-dominance as the criterion for attribute importance. First, we define the concepts of inter-class proximity and inter-class non-dominance in an IODS, with whole inter-class non-dominance serving as the evaluation index for attribute importance. Next, we propose a method for calculating inter-class non-dominance based on the expanded dominance matrix. Finally, combined with the heuristic search strategy, an attribute reduction algorithm based on inter-class non-dominance (HANDR) was designed, and experiments on various datasets from the University of California at Irvine (UCI) demonstrate that the proposed algorithm significantly improves running time and classification accuracy.

Introduction

Rough Set Theory (RST), introduced by Polish scholar Pawlak in 1982, to address uncertainty and inconsistencies in information systems¹. The core concept of RST is to is to treat objects with the same description as indistinguishable². To date, this theory has been widely applied in various fields including pattern recognition^3,4, data mining⁵, and decision analysis⁶. However, traditional RST has limitations in processing attribute domains and decision-making information with preference rankings, making it ineffective for handling ordered data such as student achievements and product quality^7,8. To address this issue, Greco et al.^9,10,11,12 proposed the dominance-based rough set approach (DRSA), which substitutes the equivalence relation in RST with a dominance relation. Currently, DRSA has been employed for multi-criteria classification and ordered attribute reduction, including risk assessment¹³, automobile evaluation¹⁴, and value analysis¹⁵.

In addition, RST assumes that each object within the universe of discourse is associated with specific information, characterized entirely by a set of attribute values without unknowns.However, practical applications frequently encounter missing data due to various uncertainties, such as fault detection^16,17, uncertainty measurement^18,19,20, and others^{21,22,23,24,25}. Such systems are termed incomplete information systems (IIS). There are two different semantic interpretations of an IIS. In the first interpretation, all unknown values are considered lost²⁶; in the second interpretation, all unknown values are irrelevant to the decision-making process, which we call the‘don’t care- condition²⁷. To address these issues, Greco et al. initially proposed using DRSA to handle IIS²⁸. However, this approach has a notable limitation: it does not provide a specific interpretation of unknown values. Subsequently, from the perspective of DRSA, Shao and Zhang considered the case where all unknown values are‘don’t care-and further proposed a method based on DRSA to deal with the reasoning problem of incompletely ordered information systems (IOIS) and proposed an extended dominance relation²⁹. Yang et al. defined incompletely ordered information systems (IOIS) and incompletely ordered decision systems (IODS) and proposed similarity dominance relations³⁰. Du et al. considered the coexistence of unknown values “lost”and“don’t care”and proposed a feature-based dominance relation². Based on the theory of Shao and Zhang, this paper mainly discusses the case where all unknown values in IODSs are“don’t care”and studies the attribute reduction of this type of information systems.

In recent years, research on incomplete information systems has demonstrated a multi-dimensional development trend. At the theoretical extension level, Li et al. integrated TOPSIS and regret theory through a three-branch decision model, achieving efficient classification and sorting of incomplete ordered information systems³¹. Khan et al. proposed a soft advantage multi-granularity rough set model, which combines preference relations with approximate precision analysis to effectively address the problem of incomplete multi-agent conflict analysis³². In terms of methodological innovation, Sahu et al. constructed a picture fuzzy set-rough set hybrid model, and effectively dealt with the inconsistency and ambiguity of occupational characteristics through lower and upper approximations and distance metrics³³. Irvanizam et al. proposed a hybrid decision support framework based on spherical fuzzy numbers (SFNs), which reduces subjectivity and data uncertainty in bank financial assistance decisions by employing objective weight allocation and sorting algorithms³⁴. Additionally, Sahu et al. combined linear regression, fuzzy sets, and game theory to dynamically optimize nurse resource allocation, thereby balancing the contradiction between medical supply and demand³⁵. Rudnik et al. utilized ordered fuzzy numbers (OFNs) to construct a dynamic supplier evaluation system, which simplified the knowledge base and enhanced decision-making transparency by integrating trend analysis with entropy values³⁶.

Attribute reduction is an important research topic in RST, referring to the deletion of redundant attributes while keeping the system classification unchanged. This process aims to form an effective rule base to assist decision-making. A key step in attribute reduction is the development of a reasonable and effective attribute evaluation function, as an efficient function enhances classification performance and reduces computational time. In other rough set models, the widely used attribute importance evaluation functions include: entropy^37,38,39, knowledge granularity^40,41,42, and dependency⁴³. However, the use of these evaluation functions is primarily based on indistinguishable or distinguishable relations⁴⁴. The influence of features on classification results is rarely considered. In response to the above problems, Hu et al. examined attribute subset separability in fuzzy decision systems, characterizing their classification capabilities⁴⁵. Jia et al. investigated intra-class and inter-class similarity in classical rough sets, proposing a similarity-based attribute reduction approach⁴⁶. Liang et al. integrated knowledge granularity theory into clustering models to propose a method that considers feature relevance and importance⁴⁷. In IODSs, Shao and Yang both calculated the attribute reduction by calculating the discernibility matrix^29,30. Later, Yang et al. proposed to calculate the simplification by using descriptors⁴⁸. Chen et al. studied the method of calculating the approximate set when the attribute value changes based on information granularity⁴⁹. Du et al. studied a reduction algorithm based on characteristic dominance relation and discernibility matrix². However, calculating reduction through the discriminability matrix is an NP-hard problem when determining the minimum disjunctive normal form. Moreover, the above studies have not considered the influence of conditional attributes on the classification results of decision attributes, thereby affecting the classification accuracy of the reduced subset. To resolve these issues, this paper first groups the decision classes, with one higher class and one lower class in each group. When performing the reduction calculation, it is necessary to ensure that lower-class objects are non-dominant over higher-class objects during reduction calculations. Therefore, for IODS with“don’t care” missing values, this paper proposes to use the overall inter-class non-dominance as an evaluation index of attribute importance, and proposes a heuristic attribute reduction algorithm (HANDR) based on the whole inter-class non-dominance. The primary contributions are threefold: (1) Definitions of inter-class proximity and inter-class non-dominance in IODS are provided, along with a set-based calculation method. (2) To enhance computational efficiency, a method for determining inter-class non-dominance using an extended dominance matrix is introduced, and based on this, a heuristic attribute reduction algorithm is proposed. (3) Experiments conducted on twelve UCI datasets illustrate the effectiveness and efficiency of the proposed algorithm.

The innovation points of this study are as follows:

• (1) A new attribute importance evaluation standard is proposed in IODS. Unlike traditional evaluation functions, this method does not require computing lower and upper approximations. Instead, it improves the simplification accuracy by grouping the decision classes and fully considering the influence of the features on the classification results.

• (2) At present, there are relatively few studies on the use of dominance matrix for attribute reduction in IODS. In the application of matrices, the difference matrix is usually used for calculation. This paper expands the concept of dominance matrix in OIS to IODS. By introducing the expanded dominance matrix, a new method for calculating inter-class non-dominance is proposed, thereby improving the efficiency of the algorithm.

• (3) The idea of local calculation is introduced in the attribute reduction process and combined with global calculation. The inter-class non-dominance between different decision class pairs is calculated first, and then the whole inter-class non-dominance is calculated, which improves the algorithm performance.

This paper is organized as follows. Section “Preliminaries” reviews the basic concepts and dominance relations of IODS, and proposes a set-based method for calculating whole inter-class non-dominance in IODS. Section “Computing reduction by matrix form” proposes and proves a method for calculating whole inter-class non-dominance based on an expanded dominance matrix, and proposes a heuristic attribute reduction algorithm. Section “Experimental analysis” provides experimental results on 12 datasets to validate the proposed algorithm’s efficiency and effectiveness. Section “Conclusion and future work” provides the conclusion of the paper and outlines future research directions.

Preliminaries

This section offers a concise overview of relevant concepts.

An information system can be denoted as a 4-tuple $S = (U, A, V, f)$, where $U = \{ x_1, x_2, \ldots , x_n \}$ represents a non-empty finite collection of objects, known as the universe. The attribute set $A$ is partitioned into condition attributes $C$ and decision attributes $D$, satisfying the condition $C \cap D = \emptyset$. The set $V$ represents the domain for all attributes. The information function $f: U \times A \rightarrow V$ defines that for any object $x$ in $U$ and attribute $a$ in $A$, the value $f(x,a)$ belongs to the domain of the attribute, $V_a$.

Ordered information system and dominance relation

Definition 1

² An attribute in an information system is classified as a criterion if its domain is organized according to a preference that is either increasing or decreasing. An information system is termed an ordered information system (OIS) if all its attributes are criteria, represented as $S \succcurlyeq = (U, A, V, f)$.

Definition 2

¹⁰ Consider an ordered information system $S \succcurlyeq = (U, A, V, f)$. For a non-empty finite set of attributes $P$ where $P \subseteq C$, if $x \succcurlyeq ay$ for all $a \in P$, we say that $x$ dominates $y$ with respect to the attribute set $P$, denoted as $x {D_P} y$. The relation ${D_P}$ establishes a dominance relation over the universe $U$ concerning the attribute set $P$.

$$\begin{aligned} {D_P} = \{ (x, y) \in U \times U : f(x,a) \geqslant f(y,a) \text { for all } a \in P \} \end{aligned}$$

(1)

Thus, we define two sets:

A set of objects that dominate, referred to as the $P$-dominating set,

$$\begin{aligned} D_P^ + (x) = \{ y \in U:y{D_P}x\}; \end{aligned}$$

(2)

And a set of objects that are dominated by, known as the $P$-dominated set,

$$\begin{aligned} D_P^ - (x) = \{ y \in U:x{D_P}y\}. \end{aligned}$$

(3)

Incomplete ordered information system and expanded dominance relation

If all attribute values within the decision system are present, it is classified as a completely ordered decision system. Conversely, when there is missing data, it is termed an Incomplete Ordered Decision System (IODS). In this paper, we specifically address scenarios where the values of ’condition attributes’ may be missing, while the values of ’decision attributes’ remain intact, missing values are represented by“*”.

Definition 3

(² Expanded Dominance Relation) Let $S \succcurlyeq = (U, A, V, f)$ be an IODS and $P \subseteq C$. The expanded dominance relation concerning $P$ is defined as follows:

$$\begin{aligned} D_P^* = \left\{ (x, y) \in U^2 \,\Bigg |\, \begin{aligned} f(x, a)&\geqslant f(y, a) \\ \text {or } f(x, a)&= * \\ \text {or } f(y, a)&= * ,\, \forall a \in P \end{aligned} \right\} \end{aligned}$$

(4)

The expanded dominance relation $D_P^*$ can be regarded as a combination of the tolerance relation found in incomplete information systems (IISs) and the dominance relation observed in ordered information systems (OISs). This relation is reflexive, yet it does not necessarily display anti-symmetry or transitivity. As a result, the $P$-dominating set and the $P$-dominated set concerning $x$ are defined as $D_{P}^{*+}(x) = \{ y \in U : y D_{P}^{*} x \}$ and $D_{P}^{*-}(x) = \{ y \in U : x D_{P}^{*} y \}$.

Example 1

Table 1 is an IODS, where $P = \{ a_1, a_2, a_3, a_4 \}$. According to Definition 3, we calculate the $P$-dominating set and the $P$-dominated set as follows:

$$\begin{aligned} & D_{P}^{*+}(x_1) = \{ x_1, x_2, x_4, x_5 \}, D_{P}^{*-}(x_1) = \{ x_3, x_6, x_7, x_8 \}; D_{P}^{*+}(x_2) = \{ x_2, x_4 \}, D_{P}^{*-}(x_2) = \{ x_1, x_3, x_6, x_7, x_8 \}; \\ & D_{P}^{*+}(x_3) = \{ x_1, x_2, x_3, x_4, x_5, x_6, x_7, x_8 \}, D_{P}^{*-}(x_3) = \emptyset ; D_{P}^{*+}(x_4) = \{ x_2, x_4 \}, D_{P}^{*-}(x_4) = \{ x_1, x_3, x_6, x_7, x_8 \}; \\ & D_{P}^{*+}(x_5) = \{ x_5 \}, D_{P}^{*-}(x_5) = \{ x_1, x_3, x_6, x_7, x_8 \}; D_{P}^{*+}(x_6) = \{ x_1, x_2, x_4, x_5, x_6, x_8 \}, D_{P}^{*-}(x_6) = \{ x_3, x_7 \}; \\ & D_{P}^{*+}(x_7) = \{ x_1, x_2, x_3, x_4, x_5, x_6, x_7, x_8 \}, D_{P}^{*-}(x_7) = \emptyset ; D_{P}^{*+}(x_8) = \{ x_1, x_2, x_4, x_5, x_6, x_8 \}, D_{P}^{*-}(x_8) = \{ x_3, x_7 \}. \end{aligned}$$

Table 1 An example of incomplete ordered decision system.

Definition 4

(¹⁰ Decision Classes) Let $S \succcurlyeq = (U, C \cup \{ d \}, V, f)$ be an Incomplete Ordered Decision System (IODS). Based on the decision attribute $d$, the universe $U$ can be partitioned into a collection of equivalence classes, denoted as $CL = \{ cl_n \mid n \in T \}$, where $T = \{ 1, 2, \ldots , | V_d | \}$. These decision classes are also organized in a preference order; specifically, for all $r, s \in T$, if $r > s$, then $cl_r \succ cl_s$.

Example 2

Table 1 is an IODS. $U = \{ {x_1},{x_2},{x_3},{x_4},{x_5},{x_6},{x_7},{x_8} \}$ is the universe, $C = \{ {a_1},{a_2},{a_3},{a_4} \}$ is the condition attribute set and d is the decision attribute. According to Definition 4, we have $CL = \{ c{l_1}, c{l_2}, c{l_3} \}$, $c{l_1} = \{ {x_3}, {x_7} \}$, $c{l_2} = \{ {x_1}, {x_6}, {x_8} \}$, $c{l_3} = \{ {x_2}, {x_4}, {x_5} \}$ and $c{l_1} \prec c{l_2} \prec c{l_3}$.

Attribute reduction based on inter-class non-dominance

In this subsection, we present fundamental concepts of inter-class proximity (IP), inter-class non-dominance (IND), and the attribute reduction method based on IND within IODSs.

In IODSs, decision attributes are organized according to ordinal relationships. Therefore, when calculating similarity and non-dominance inter-classes, it is crucial to consider the order of decision attributes to ensure that objects in lower classes do not dominate those in higher classes.

Definition 5

(Dominance inter-class) In an IODS the inter-class can be defined as

$$\begin{aligned} \text {Inter}\_cl = \{ (c{l_i},c{l_j})\left| {1 \leqslant i < j \leqslant T} \right. \} \end{aligned}$$

(5)

To ensure the dominance relationship between decision classes, the inter-class structure requires the selection of a lower class $c{l_i}$ and a higher class $c{l_j}$.

Example 3

In Table 1 we get $CL = \{ c{l_1}, c{l_2}, c{l_3} \}$, according to Definition 5, we can obtain three dominance inter-class groupings $\{ c{l_1},c{l_2}\}$,$\{ c{l_1},c{l_3}\}$,$\{ c{l_2},c{l_3}\}$.

Definition 6

(Inter-Class Proximity) For a pair of classes $c{l_i}, c{l_j} \in CL$, the inter-class proximity between $c{l_i}$ and $c{l_j}$ with respect to a subset of attributes $B \in C$ is defined as

$$\begin{aligned} I{P_B}(c{l_i},c{l_j}) = \frac{{\sum \limits _{k = 1}^{|c{l_i}|} {\left| {D{{_B^ * }^ + }(c{l_{ik}}) - \overline{(c{l_i},c{l_j})} } \right| } }}{{{{(|c{l_i}| + |c{l_j}|)}^2}}} + \frac{{\sum \limits _{k = 1}^{|c{l_j}|} {\left| {D{{_B^ * }^ + }(c{l_{jk}}) - \overline{(c{l_i},c{l_j})} } \right| } }}{{{{(|c{l_i}| + |c{l_j}|)}^2}}} \end{aligned}$$

(6)

where $c{l_{ik}}$ represents the k-th object in the decision class $c{l_{i}}$, $\left| \bullet \right|$ represents the basis of the set, and $\overline{(c{l_i},c{l_j})}$ represents the collection of elements that are not part of the inter-class $(c{l_i},c{l_j})$.

Example 4

Continuing from Example 3, according to Definition 6 we have $I{P_B}(c{l_1},c{l_2}) = 17/25$, $I{P_B}(c{l_1},c{l_3}) = 15/25$, $I{P_B}(c{l_2},c{l_3}) = 21/36$.

Definition 7

(Inter-Class Non-Dominance) Similarly, for the same classes $c{l_i}, c{l_j} \in CL$, the inter-class non-dominance between these classes with regard to attributes in $B$ is defined as

$$\begin{aligned} IN{D_B}(c{l_i},c{l_j}) = 1 - I{P_B}(c{l_i},c{l_j}) \end{aligned}$$

(7)

As the value of $IN{D_B}$ increases, the non-dominance between decision classes $c{l_i}$ and $c{l_j}$ strengthens, resulting in a significant reduction in the classification error of the decision classes under the current attribute subset B.

Example 5

Continuing from Example 4, according to Definition 7 the inter-class non-dominance of $c{l_i}$ and $c{l_j}$ are calculated as $IN{D_B}(c{l_1},c{l_2}) = 8/25$, $IN{D_B}(c{l_1},c{l_3}) = 10/25$ and $IN{D_B}(c{l_2},c{l_3}) = 15/36$.

Definition 8

(Whole Inter-Class Non-Dominance) For an IODS, $IN{D_B}(c{l_i},c{l_j})$ represents the inter-class non-dominance of $c{l_i}$ and $c{l_j}$ under the condition attribute subset B. Given n inter-class non-dominance values denoted as $N{D_1},N{D_2}, \ldots ,N{D_n}$. Then the whole inter-class non-dominance of the object set is defined as

$$\begin{aligned} WIN{D_U}(B,CL) = \frac{1}{n}\sum \limits _{i = 1}^n {N{D_i}} \end{aligned}$$

(8)

where $N{D_i}$ indicates the inter-class non-dominance value for the $i$-th class. A higher value among various different classes concerning the subset $B$ indicates a reduced classification error rate, suggesting that the conditional attribute set $B$ yields more precise ranking information for the object set, and conversely.

Example 6

Continuing from Example 5, according to Definition 8 the whole inter-class non-dominance are calculated as $WIN{D_U}(B, CL) = \frac{1}{3} \left( \frac{8}{25} + \frac{10}{25} + \frac{15}{36} \right) = 0.3789$.

Proposition 1

Let $S \succcurlyeq = (U,C \cup \{ d\} ,V,f)$, $\forall B \subseteq C$ and $B \ne \emptyset$, then $WIN{D_U}(C,CL) \geqslant$$WIN{D_U}(B,CL)$.

Proof

Let $S \succcurlyeq = (U, C \cup \{ d \}, V, f),\:\: C = \{ a_1, a_2, \ldots , a_n \}$. For all $B \subseteq C$ and $X \in U$, we have $D_C^{*+}(X) \subseteq D_B^{*+}(X)$, so $|D_C^{*+}(c{l_{ik}})| \le |D_B^{*+}(c{l_{ik}})|$. According to Definition 6, $I{P_B}(c{l_i}, c{l_j}) = \frac{{\sum _{k = 1}^{|c{l_i}|} \left| D_{B}^{*+}(c{l_{ik}}) - \overline{(c{l_i}, c{l_j})} \right| }}{{(|c{l_i}| + |c{l_j}|)^2}} + \frac{{\sum _{k = 1}^{|c{l_j}|} \left| D_{B}^{*+}(c{l_{jk}}) - \overline{(c{l_i}, c{l_j})} \right| }}{{(|c{l_i}| + |c{l_j}|)^2}}$ we can get $I{P_C}(c{l_i}, c{l_j}) \le$$I{P_B}(c{l_i}, c{l_j})$. Then, according to Definition 7, $IN{D_B}(c{l_i}, c{l_j}) = 1 - I{P_B}(c{l_i}, c{l_j})$, averaging over all class pairs, we obtain $WIN{D_U}(C, CL) \ge WIN{D_U}(B, CL)$. $\square$

Proposition 2

Compared with the traditional entropy-based attribute reduction method, WIND as an evaluation index of attribute importance has better globality.

Proof

In an ordered information system, conditional entropy (DCE) evaluates the importance of attributes by measuring the ranking consistency of conditional attribute A to decision attribute d. Its core formula is $DH_{d|A}^ \succcurlyeq (U) = - \frac{1}{{|U|}}\sum \limits _{i = 1}^n {\log \frac{{|D_{\{ d\} \cup A}^ + ({x_i})|}}{{|D_A^ + ({x_i})|}}}$. However, DCE only focuses on the local consistency of a single object and does not consider the inter-class relationships.

In an IODS, WIND constrains the classification boundary by maximizing the inter-class non-dominance. Its calculation formula is $WIN{D_U}(B,CL) = \frac{1}{n}\sum \limits _{i = 1}^n {N{D_i}}$. When calculating the reduction B, the inter-class non-dominance between each class pair must be satisfied $IN{D_B}(c{l_i},c{l_j}) = IN{D_C}(c{l_i},c{l_j})$, that is, the inter-class non-dominance of the complete attribute set C is completely preserved. In addition, according to Proposition 1, WIND is monotonic, and when calculating the reduction, the reduction set B must strictly inherit the inter-class non-dominance of the attribute set C. This property ensures the control ability of the reduced attribute subset on the global classification boundary, thereby minimizing the cross-class error. $\square$

During the attribute reduction procedure, informative attributes are identified using significance measures defined as follows.

Definition 9

(WIND-Based Inner Significance Measure) In an IODS, for every attribute set $B \in C$ and for each $a \in B$, the WIND-based inner significance measure of $a$ in $B$ is defined as follows:

$$\begin{aligned} sig_{inner}^{\succcurlyeq U}(a, B, d) = WIN{D_U}(B, CL) - WIN{D_U}(B - \{ a \}, CL) \end{aligned}$$

(9)

Based on the explanation of WIND, a greater value of $sig_{inner}^{\succcurlyeq U}(a, B, d)$ implies that the conditional attribute is more crucial. This measure helps to identify the necessary condition attributes within the entire set of condition attributes. Additionally, the core attribute set of the attribute set $B$ is defined as $Cor{e_B} = \{ a \in B \mid sig_{inner}^{\succcurlyeq U}(a, B, d) > 0 \}$.

Definition 10

(WIND-Based Outer Significance Measure) In an IODS, for any $P \in C$ and for each $a \in (C - P)$, the WIND-based outer significance measure of $a$ relative to $P$ is defined as:

$$\begin{aligned} sig_{outer}^{\succcurlyeq U}(a, P, d) = WIN{D_U}(P \cup \{ a \}, CL) - WIN{D_U}(P, CL) \end{aligned}$$

(10)

Much like the $sig_{inter}^{\succcurlyeq U}(a, P, d)$, the $sig_{outer}^{\succcurlyeq U}(a, P, d)$ can be used to identify necessary condition attributes that are distinct from those in the selected condition attribute set.

Definition 11

(Attribute Reduction) In an IODS, for any subset $P \in C$, the attribute subset $P$ is considered a reduct of $S \succcurlyeq$ if it meets the following criteria:

• (1) $WIN{D_U}(P, CL) = WIN{D_U}(C, CL)$ and

• (2) $\forall a \in P, WIN{D_U}(P - \{ a \}, CL) \ne WIN{D_U}(P, CL)$.

Condition (1) guarantees that the chosen attribute subset retains the same power as the complete attribute set, while condition (2) guarantees the indispensability of each attribute in the subset by excluding redundant attributes.

Computing reduction by matrix form

This section first defines the expanded dominance matrix of IODS. Next, we propose and prove a matrix-based method for computing inter-class non-dominance (MIND), and then introduce a heuristic attribute reduction algorithm based on MWIND.

Computation of IND based on matrix

Definition 12

(Expanded Dominance Relation Matrix) Let $S \succcurlyeq = (U,C \cup \{ d \},V,f)$ be an IODS. For any $B \subseteq C$, the expanded dominance relation under $B$ is denoted $D_B^*$. The expanded dominance matrix about $B$ is defined as $\mathbb {M}_U^{\succcurlyeq B} = [m_{(i,j)}^B]_{n \times n}$, where

$$\begin{aligned} m_{(i,j)}^B = \left\{ \begin{gathered} 1, {x_j}D_B^*{x_i}; \\ 0, otherwise. \\ \end{gathered} \right. \end{aligned}$$

(11)

Proposition 3

Let $S \succcurlyeq = (U,C \cup \{ d \},V,f)$ be an IODS, for $X \subseteq U$, $X = \{ {x_1},{x_2}, \ldots ,{x_m}\}$ $a,b \in X$, then $\mathbb {M}_X^{ \succcurlyeq B} = {[m_{(a,b)}^B]_{m \times m}}$, $\mathbb {M}_X^{ \succcurlyeq B} \subseteq \mathbb {M}_U^{ \succcurlyeq B}$.

Proof

Since $X \subseteq U$, it follows that $X \times X \subseteq U \times U$. This means that any pair (a, b) in $X \times X$ is also in $U \times U$. For any $a,b \in X$, there exists a corresponding element $m_{(a,b)}^B$ in $\mathbb {M}_U^{ \succcurlyeq B}$ because $(a,b) \in U \times U$. This proves that $\mathbb {M}_X^{ \succcurlyeq B}$ is a submatrix of $\mathbb {M}_U^{ \succcurlyeq B}$, containing all elements corresponding to $X \times X$. $\square$

Corollary 1

(MIP) Let $S \succcurlyeq = (U,C \cup \{ d \},V,f)$ be an IODS, for any $B \subseteq C$, $c{l_i},c{l_j} \in CL$, $X = \{ c{l_i},c{l_j}\}$ based on the expanded dominance relation matrix $\mathbb {M}_X^{ \succcurlyeq B}$, MIP of B is denoted as

$$\begin{aligned} MI{P_{(c{l_i},c{l_j})}} = \sum \limits _{a = 1}^m {\sum \limits _{b = 1}^m {\frac{{m_{ab}^B}}{{{m^2}}} = \frac{{Sum(\mathbb {M}_X^{ \succcurlyeq B})}}{{{m^2}}}} } \end{aligned}$$

(12)

where m represents the cardinality of the set $X$, and $Sum(\mathbb {M}_X^{\succcurlyeq B})$ represents the sum of all elements in the matrix $\mathbb {M}_X^{\succcurlyeq B}$.

Proof

According to Definition 6, we can get $I{P_B}(c{l_i},c{l_j})\! =$$\frac{{\sum \limits _{k = 1}^{|c{l_i}|} {\left| {D{{_B^ * }^ + }(c{l_{ik}}) \!- \!\overline{(c{l_i},c{l_j})} } \right| } }}{{{{(|c{l_i}|\! +\! |c{l_j}|)}^2}}} \!+$$\frac{{\sum \limits _{k = 1}^{|c{l_j}|} {\left| {D{{_B^ * }^ + }(c{l_{jk}}) - \overline{(c{l_i},c{l_j})} } \right| } }}{{{{(|c{l_i}| + |c{l_j}|)}^2}}}$. According to Definition 12 and Corollary 1, the expanded dominance relation matrix of $(c{l_i},c{l_j})$ is defined as: $\mathbb {M}_X^{ \succcurlyeq B} = {[m_{(a,b)}^B]_{m \times m}}$, and $MI{P_{(c{l_i},c{l_j})}} = \sum \limits _{a = 1}^m {\sum \limits _{b = 1}^m {\frac{{m_{ab}^B}}{{{m^2}}} = \frac{{Sum(\mathbb {M}_X^{ \succcurlyeq B})}}{{{m^2}}}} }$, where $m_{(a,b)}^B = \left\{ \begin{array}{l} 1, {x_b}D_B^*{x_a}; \\ 0, otherwise. \\ \end{array} \right.$, so $Sum(\mathbb {M}_X^{ \succcurlyeq B}) =$ $\sum \limits _{k = 1}^{|c{l_i}|} {\left| {D{{_B^ * }^ + }(c{l_{ik}}) - \overline{(c{l_i},c{l_j})} } \right| } +$ $\sum \limits _{k = 1}^{|c{l_j}|} {\left| {D{{_B^ * }^ + }(c{l_{jk}}) - \overline{(c{l_i},c{l_j})} } \right| }$. Thus, we can get $I{P_{(c{l_i},c{l_j})}} = MI{P_{(c{l_i},c{l_j})}}$. In summary, the results of calculating the Inter-Class Proximity based on matrix and non-matrix methods are consistent. $\square$

Corollary 2

(MIND) Let $S \succcurlyeq = (U,C \cup \{ d \},V,f)$ be an IODS, for any $B \subseteq C$, $c{l_i},c{l_j} \in CL$, $X = \{ c{l_i},c{l_j}\}$ based on the expanded dominance relation matrix $\mathbb {M}_X^{ \succcurlyeq B}$, MIND of B is denoted as

$$\begin{aligned} MIN{D_{(c{l_i},c{l_j})}} = 1 - MI{P_{(c{l_i},c{l_j})}} = 1 - \frac{{Sum(\mathbb {M}_X^{ \succcurlyeq B})}}{{{m^2}}} \end{aligned}$$

(13)

Proof

The proof here is the same as Proof 3.1. $\square$

Corollary 3

(MWIND) Let $S \succcurlyeq = (U,C \cup \{ d \},V,f)$ be an IODS, $MIN{D_B}(c{l_i},c{l_j})$ represents the inter-class non-dominance of $c{l_i}$ and $c{l_j}$ under the condition attribute subset B based on the expanded dominance relation matrix $\mathbb {M}_X^{ \succcurlyeq B}$. Given n inter-class non-dominance values denoted as $MN{D_1},MN{D_2}, \ldots ,MN{D_n}$. Then the whole inter-class non-dominance of the object set based on the expanded dominance relation matrix is defined as

$$\begin{aligned} MWIN{D_U}(B,CL) = \frac{1}{n}\sum \limits _{i = 1}^n {MIN{D_i}} \end{aligned}$$

(14)

The following example shows how to calculate whole inter-class non-dominance using the expanded dominance relation matrix.

Example 7

Table 1 is an IODS, $B = \{ a_1, a_2, a_3, a_4 \}$, $CL = \{ cl_1, cl_2, cl_3 \}$, $cl_1 = \{ x_3, x_7 \}$, $cl_2 = \{ x_1, x_6, x_8 \}$, $cl_3 = \{ x_2, x_4, x_5 \}$. According to Definition 5, we can obtain three dominance inter-class pairs $\{ cl_1, cl_2 \}$, $\{ cl_1, cl_3 \}$, and $\{ cl_2, cl_3 \}$. Let $X_1 = \{ cl_1, cl_2 \} = \{ x_1, x_3, x_6, x_7, x_8 \}$, $X_2 = \{ cl_1, cl_3 \} = \{ x_2, x_3, x_4, x_5, x_7 \}$, and $X_3 = \{ cl_2, cl_3 \} = \{ x_1, x_2, x_4, x_5, x_6, x_8 \}$. According to Definition 12 and Proposition 3, the expanded dominance relation matrices $\mathbb {M}_U^{\succcurlyeq B}$, $\mathbb {M}_{X_1}^{\succcurlyeq B}$, $\mathbb {M}_{X_2}^{\succcurlyeq B}$, and $\mathbb {M}_{X_3}^{\succcurlyeq B}$ are calculated respectively as

$$\begin{aligned} & \mathbb {M}_U^{ \succcurlyeq B} = {\left[ {\begin{array}{*{20}{c}} 1& 1& 0& 1& 1& 0& 0& 0 \\ 0& 1& 0& 1& 0& 0& 0& 0 \\ 1& 1& 1& 1& 1& 1& 1& 1 \\ 0& 1& 0& 1& 0& 0& 0& 0 \\ 0& 0& 0& 0& 1& 0& 0& 0 \\ 1& 1& 0& 1& 1& 1& 0& 1 \\ 1& 1& 1& 1& 1& 1& 1& 1 \\ 1& 1& 0& 1& 1& 1& 0& 1 \end{array}} \right] _{8 \times 8}}, \mathbb {M}_{{X_1}}^{ \succcurlyeq B} = {\left[ {\begin{array}{*{20}{c}} 1& 0& 0& 0& 0 \\ 1& 1& 1& 1& 1 \\ 1& 0& 1& 0& 1 \\ 1& 1& 1& 1& 1 \\ 1& 0& 1& 0& 1 \end{array}} \right] _{5 \times 5}}, \\ & \mathbb {M}_{{X_2}}^{ \succcurlyeq B} = {\left[ {\begin{array}{*{20}{c}} 1& 0& 1& 0& 0 \\ 1& 1& 1& 1& 1 \\ 1& 0& 1& 0& 0 \\ 0& 0& 0& 1& 0 \\ 1& 1& 1& 1& 1 \end{array}} \right] _{5 \times 5}}, \mathbb {M}_{{X_3}}^{ \succcurlyeq B} = {\left[ {\begin{array}{*{20}{c}} 1& 1& 1& 1& 0& 0 \\ 0& 1& 1& 0& 0& 0 \\ 0& 1& 1& 0& 0& 0 \\ 0& 0& 0& 1& 0& 0 \\ 1& 1& 1& 1& 1& 1 \\ 1& 1& 1& 1& 1& 1 \end{array}} \right] _{6 \times 6}}. \end{aligned}$$

Subsequently, according to Corollary 1 the MIP between $c{l_i}$ and $c{l_j}$ under the attribute set B can be calculated via using matrices $\mathbb {M}_{X_1}^{\succcurlyeq B}$, $\mathbb {M}_{X_2}^{\succcurlyeq B}$, and $\mathbb {M}_{X_3}^{\succcurlyeq B}$ as

$MI{P_{(c{l_1},c{l_2})}} = \frac{{Sum(\mathbb {M}_{{X_1}}^{ \succcurlyeq B})}}{{{m^2}}} = 17/25$; $MI{P_{(c{l_1},c{l_3})}} = \frac{{Sum(\mathbb {M}_{{X_2}}^{ \succcurlyeq B})}}{{{m^2}}} = 15/25$; $MI{P_{(c{l_2},c{l_3})}} =$$\frac{{Sum(\mathbb {M}_{{X_3}}^{ \succcurlyeq B})}}{{{m^2}}} = 21/36$.

Next, according to Corollary 2, the MIND between $c{l_i}$ and $c{l_j}$ under the attribute set B are calculated as

$MIN{D_{(c{l_1},c{l_2})}}\! =\! 1 \!- \!MI{P_{(c{l_1},c{l_2})}} \!=\! 8/25$; $MIN{D_{(c{l_1},c{l_3})}} \!= \!1 \!- \!MI{P_{(c{l_1},c{l_3})}} \!= \!10/25$; $MIN{D_{(c{l_2},c{l_3})}}\! =$ $1 - MI{P_{(c{l_2},c{l_3})}} \! = \! 15/36$.

Finally, according to Corollary 3, WMIND of B can be calculated as $MWIN{D_U}(B,CL) =$$\frac{1}{n}\sum \limits _{i = 1}^n {MIN{D_i}} =$$\frac{1}{3} \times (\frac{8}{{25}} + \frac{{10}}{{25}} + \frac{{15}}{{36}}) = 0.3789$.

Corollary 4

In an IODS, the MWIND-Based inner significance measure of a in B is denoted as

$$\begin{aligned} Msig_{inner}^{ \succcurlyeq U}(a,B,d) = MWIN{D_U}(B,CL) - MWIN{D_U}(B - \{ a\} ,CL) \end{aligned}$$

(15)

The inner significance measures derived from WIND and MWIND are equivalent, and the results obtained from Eqs. 9 and 15 are also the same.

Corollary 5

In an IODS, the MWIND-Based outer significance measure of a in B is denoted as

$$\begin{aligned} Msig_{outer}^{ \succcurlyeq U}(a,B,d) = MWIN{D_U}(B \cup \{ a\} ,CL) - MWIN{D_U}(B,CL) \end{aligned}$$

(16)

The outer significance measures derived from WIND and MWIND are equivalent, and the results obtained from Eqs. 10 and 16 are also the same.

Heuristic attribute reduction algorithm based on MWIND

This subsection introduces a heuristic attribute reduction algorithm (HANDR) based on MWIND.

Here is a detailed breakdown of the steps involved in Algorithm 1, along with an analysis of their time complexity. Step 2 computes MWIND from $U$ with a time complexity of $O(|C||K||U|^2)$, where $K$ represents the number of decision classes. Steps 3 through 8 Obtain the indispensable attribute and its time complexity is$O(|C|^2|U|^2)$. In Steps 10 through 16, the algorithm selects the optimal attribute $a_k$ from the remaining attributes $C - B$ to include in subset $B$, also incurring a time complexity of $O(|C|^2|U|^2)$. Finally, Steps 17 to 21 remove redundant attributes from the relative reduct $B$, with a time complexity of $O(|B|^2|U|^2)$. Consequently, the total time complexity of the HANDR algorithm is given by $O(|C||K||U|^2 + |C|^2|U|^2 + |C|^2|U|^2 + |B|^2|U|^2)$.

Algorithm 1

A heuristic approach to non-dominance-basedattribute reduction (HANDR).

In addition, the running efficiency can be improved by using an incremental mechanism or parallel computing. In a dynamic data set, incremental computing can effectively reduce the running time. When adding an object, it is only necessary to calculate the dominance relationship between the new object and the existing object without starting from scratch; when deleting an object, it is only necessary to remove the corresponding rows and columns in the matrix. Through the incremental mechanism, the time complexity of the algorithm can be reduced to $O(|U| + |C||U||{U^ + }| + (|C| - |B|)|{U^ + }{|^2} + |B{|^2}|{U^ + }{|^2})$, Where ${U^ + }$ represents the number of added objects.

To illustrate the workings of the algorithm, we present an example demonstrating the steps involved in computing the reduct via HANDR

Example 8

Table 1 is an IODS, where $U = \{ {x_1},{x_2}, \cdots ,{x_8}\}$, and $C = \{ {a_1},{a_2},{a_3},{a_4}\}$.

Step 1::

Initialize $R = \emptyset$.

Step 2::

Calculate $MWIND_U(C, CL) = 0.3789$ using Corollary 3.

Step 3::

The inner significance measures of all attributes in C are respectively: $Msig_{inner}^{\succcurlyeq U}(a_1, C, d) = 0.0452$, $Msig_{inner}^{\succcurlyeq U}(a_2, C, d) = 0.0678$, $Msig_{inner}^{\succcurlyeq U}(a_3, C, d) = 0.0226$, $Msig_{inner}^{\succcurlyeq U}(a_4, C, d) = 0.0$. So we get $R = \{ a_1, a_2, a_3 \}$, then we let $B = R$.

Step 4::

Calculate $MWIND(B, CL) = MWIND(C, CL)=0.3789$. Therefore, we go to step 22 and output the final reduced result $R = \{ a_1, a_2, a_3 \}$.

Experimental analysis

This section verifies the effectiveness of the proposed algorithm through experiments conducted on twelve datasets from the UCI Machine Learning Repository, detailed in Table 2. Here, “object”refers to the number of instances,“attribute”denotes the number of conditional attributes, and“class”indicates the number of decision categories. To meet the needs of the IODS algorithm, the data preprocessing process includes the following steps: First, we identify and remove completely redundant duplicate samples from the dataset to avoid overfitting. Second, to simulate the issue of missing data in real-world scenarios, 30% of the conditional attributes are randomly selected for each dataset while ensuring the structural integrity of the dataset, and 10% of the sample values within these selected attributes are randomly marked as missing values (“*”). All algorithms in this paper are implemented in Python and are executed on a computer equipped with a 2.50GHz Intel(R) Core(TM) i5-13500 CPU, 16.0GB of RAM, and a 64-bit Windows 11 operating system.

Table 2 The details of twelve datasets in UCI.

To assess the performance of the HANDR algorithm, a comparison was made with four existing attribute reduction algorithms: IAR, Algorithm 2, Algorithm 4, and MIFS. The IAR algorithm serves as a method for attribute reduction tailored for ordered information systems based on dominant conditional entropy. Algorithm 2 focuses on attribute reduction leveraging conditional entropy in incomplete information systems. Algorithm 4 employs a heuristic approach based on feature dominance relationships within incomplete ordered information systems. Lastly, the MIFS algorithm represents a forward greedy attribute reduction technique rooted in mutual information within incomplete information systems. Furthermore, we evaluated the running times of these five algorithms across various data scales, along with their classification accuracies using three classifiers: SVM, KNN, and RF, while performing statistical analysis based on the classification accuracy outcomes.

Efficiency evaluations

In this subsection, we assess the efficiency of the HANDR algorithm by comparing the execution times of five algorithms as the sample size increases. We begin by selecting the first 50% of objects from each dataset in Table 2 as the original set, then incrementally add the remaining 10% to form datasets of sizes 60%, 70%, 80%, 90%, and 100%. The time consumed by each algorithm on these datasets is compared, with results illustrated in Fig. 1, where the horizontal axis represents dataset size and the vertical axis represents running time.

Fig. 1

Time consumption trend of different algorithms.

As depicted in Fig. 1, the execution time for the five algorithms rises as the sample size grows. Each sub-graph illustrates that the computation time for the algorithm HANDR is lower than that of the other four algorithms. This difference is particularly marked in larger datasets, where the runtime for HANDR is notably shorter compared to Algorithm 2 and the algorithm MIFS. This is mainly because Algorithm 2 calculates the reduction in a set manner, and the tolerance class needs to be calculated multiple times during the calculation process, resulting in a large time overhead. Algorithm MIFS uses mutual information as an evaluation index of attribute importance. Before calculating mutual information, information entropy and conditional entropy need to be calculated separately. Therefore, algorithm MIFS is also more time-consuming when facing a large data set. Compared with algorithm IAR and algorithm 4, algorithm IAR needs to calculate multiple matrices such as dominance relation matrices, diagonal matrices, inverse matrices, etc. when calculating conditional entropy, while algorithm HANDR only needs to calculate the expanded dominance matrices between different decision class groups in the process of calculating MWIND. Therefore, the operating efficiency of algorithm HANDR is slightly higher than that of algorithm IAR.

Effectiveness evaluations

This section evaluates the performance of the HANDR algorithm in comparison to four other algorithms. To assess the classification effectiveness of these five algorithms, we employed the ten-fold cross-validation method using SVM, KNN, and RF classifiers. The experimental outcomes are summarized in Tables 3, 4, and 5.

Table 3 Comparison of classification accuracy of different algorithms based on KNN.

Table 4 Comparison of classification accuracy of different algorithms based on SVM.

Table 5 Comparison of classification accuracy of different algorithms based on RF.

The data presented in Tables 3, 4, and 5 indicates that for the majority of datasets, the classification performance achieved by the reductions produced by the HANDR algorithm is comparable to or even surpasses that of reductions generated by the other four algorithms. This is evident in the average results as well. Thus, these findings suggest that the reductions produced by the HANDR algorithm are effective.

Statistical analysis

To assess significant differences in attribute reduction performance among the five algorithms, we apply the Friedman test⁵⁰ and the Bonferroni-Dunn test⁵¹. We rank the classification accuracy using KNN, SVM, and RF classifiers. Let $I$ denote the number of algorithms, $T$ the number of datasets, and $R_a$ the average rank of the $a$-th algorithm. The Friedman test confirms significant differences among the algorithms, calculated as follows:

$$\begin{aligned} \chi _F^2 = \frac{{12T}}{{I(I + 1)}}\left( \sum _{a = 1}^I R_a^2 - \frac{{I(I + 1)^2}}{4}\right) , \quad F = \frac{{(T - 1)\chi _F^2}}{{T(I - 1) - \chi _F^2}} \end{aligned}$$

(17)

The $F$ values obtained are $\chi _F^2 = 22.22, F = 3.45$ for KNN; $\chi _F^2 = 21.66, F = 3.29$ for SVM; and $\chi _F^2 = 21.79, F = 3.33$ for RF. Each $F$ exceeds the critical value $F_{(4,44)} = 2.077$ at a significance level of $\alpha = 0.1$, leading us to reject the null hypothesis that all algorithms have equivalent classification capabilities.

Next, we apply the Bonferroni-Dunn test to differentiate the algorithms further. The classification performance of two algorithms is considered significantly different if the distance between their average ranks exceeds the critical distance:

$$\begin{aligned} CD_\alpha = q_\alpha \sqrt{\frac{I(I + 1)}{6T}}, \end{aligned}$$

where $q_\alpha$ is the critical value and $\alpha$ is the significance level of the test. For $\alpha = 0.1$, $q_{0.1} = 2.241$, yielding $CD_{0.1} = 1.447$.

The $CD$ graph illustrates the relationships among the algorithms, as shown in Fig. 2. The average ranking of each algorithm is plotted, with the best ranks on the left. A thick black line segment connects pairs of algorithms whose distance is less than the critical distance $CD$. In Fig. 2a, HANDR significantly outperforms Algorithm 4, IAR, Algorithm 2, and MIFS using the KNN classifier. Figure 2b shows HANDR’s significant advantage over Algorithm 2 and Algorithm 4 with the SVM classifier, while the differences with IAR and MIFS are less clear. Similarly, Fig. 2c indicates that HANDR’s performance with the RF classifier is statistically better than Algorithm 2 and Algorithm 4, but distinctions from IAR and MIFS remain uncertain. Overall, these tests demonstrate the superior performance of the HANDR algorithm.

Fig. 2

Bonferroni–Dunn test results of different algorithms on three classifiers.

Conclusion and future work

In this paper, under the framework of IODS, the attribute reduction method based on inter-class non-dominance is studied. Firstly, the definitions of inter-class proximity and inter-class non-dominance in IODS are given, and then a calculation method based on extended dominance matrix (MIND) is proposed, and the average value is used as the evaluation index of attribute importance. On this basis, a heuristic attribute reduction algorithm (HANDR) is proposed, and the efficiency and feasibility of the proposed algorithm are proved by experiments.

However, the algorithm is currently only available for static datasets. Therefore, in future work, we will further extend the HANDR algorithm to dynamic datasets to study how to achieve efficient processing when attributes and objects change. This will greatly improve the applicability of the algorithm and make it better able to adapt to the dynamic nature of the data in real-world applications.