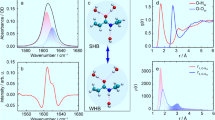
Abstract
IR spectra from 4000 to 100 cm–1 were measured for four kinds of alkali chloride solutions (LiCl, NaCl, KCl, CsCl solutions) with different concentrations. Their second derivative spectra revealed two bands around 3400 and 3160 cm–1 attributed to the OH stretching mode of weakly hydrogen-bonded (WHB) and strongly hydrogen-bonded (SHB) water species, respectively. Two-dimensional correlation spectroscopy (2D-COS) was applied to analyze the IR spectra. Two autopeaks in a 2D synchronous spectrum correspond to the WHB and SHB bands, respectively. Moreover, 2D-COS confirmed the existence of two bands around 700 and 350 cm–1 in the 1000 –100 cm–1 region. The bands at 700 and 350 cm–1 are assignable to liberational L2 modes and correlated with SHB (~ 3160 cm–1) and WHB band (~ 3400 cm–1), respectively, revealed by the hetero 2D-COS spectrum. These results suggest the two kinds of hydrogen-bonding networks are constructed by SHB or WHB water species in the alkali chloride solutions.
Similar content being viewed by others
Introduction
The structure and dynamics of water have long been investigated extensively due to its great importance in our life and various anomalies in physicochemical properties1,2,3,4,5,6,7 However, in spite of intensive physicochemical, spectroscopic, and theoretical studies, structure and dynamics of water and its anomalous behavior as liquid have not been fully explored yet1,2,3,4,5,6,7 There has been fundamental conflict in understanding water structures; mixture models consisting of the distributions of structural components reflecting the coexistence of two or more types of local structures and continuum models based on the distribution of continuous hydrogen-bonding networks8,9,10 The mixture model proposed by Bernal and Fowler8 was a simple one in which water is a mixture of two molecular states. Walrafen reported Raman spectroscopy studies of the effects of temperature on water in 1964 and 196611 They measured Raman spectra of water both in the OH-stretching and low-frequency regions. They concluded that the intermolecular vibrations of water are related to a five-molecule hydrogen-bonded C2ν model. Recently, Shi and Tanaka12 reported that two peaks exist within a diffraction peak in the X-ray scattering pattern. One of the hidden peaks was associated with the tetrahedral structure of water, and the other peak was found to arise from a distorted tetrahedral structure. This finding unambiguously proves the coexistence of the two states of local structures in liquid water, directly evidencing the two-state model. Recently, water’s tetrahedrality was probed by two-dimensional IR-Raman spectroscopy13.
Vibrational spectroscopy is powerful to investigate the structure and dynamics of water. Infrared (IR),13,14,15,16,17,18,19,20,21,22 Raman,13,23,24,25,26 near-infrared (NIR),27,28,29,30 and Terahertz31,32 spectroscopy have been used extensively to explore the water structure and dynamics because they are very sensitive to the structure of hydrogen bondings of water. One can use the frequencies, intensities and band widths of peaks to explore the structure and dynamics of water. The IR spectra of water and the Raman spectra of water are similar in the 4000 –3000 cm–1 region but they are markedly different in the low frequency region, giving rise to different information. The IR spectra of liquid water show four major bands in the regions of 4000 –3000 cm–1, 1700 –1600 cm–1, 1000 –300 cm–1, and 300 –100 cm–1.13−22 They are assigned to the OH stretching modes, HOH bending mode, liberation mode, and O・・O hydrogen-bonding stretching mode of water, respectively. In this study we investigate the 4000 –3000 cm–1 region and the 1000 –100 cm–1 region. The IR spectra of the 4000 –3000 cm–1 region of water and aqueous solutions show a very broad feature centered at around 3300 cm–113,14,15,16,17,18,19,20,21,−22. Using the second derivative one can divide the broad feature into two major bands at 3400 and 3160 cm–1. It is well known that these are due to OH stretching modes of weakly hydrogen-bonded (WHB) water species and strongly hydrogen-bonded (SHB) water species, respectively21,22 SHB and WHB water species correspond to tetrahedron structure and slightly distorted tetrahedron structure, respectively12 Thus, the 4000 –3000 cm–1 region is very suitable to investigate local hydrogen bond structure. In contrast to the 4000 –3000 cm–1 region the 1000 –100 cm–1 region has not been well analyzed18,19,20,21,22 In this study we have tried to deepen the spectral analysis in the 4000 − 3000 and 1000 –100 cm–1 regions. We have also explored the correlation between the two regions. One of the important novelties of this study is to use two-dimensional correlation spectroscopy (2D-COS)33,34,35 for the band analysis in the two regions and to investigate the relation between the two regions. This is a clearly different point between the present study and those reported in Refs21,22, where we did not employ 2D-COS. Second derivative and curve-fitting are also employed for band analysis. They are very useful to investigate the dynamics of water in liquid water and aqueous solutions because they offer information about the band widths of OH stretching modes and water liberational modes. Effects of ions in the aqueous solutions on the IR spectra are also studied. CsCl solutions show significantly different effects on the spectra from LiCl, NaCl, and KCl solutions.
In the 1000 –100 cm–1 region (IR/FIR region) one broad feature is observed around 500 cm–1, and it has been assigned to a liberation mode18,19,20,21,22. It was found by Ashihara et al.18. that the liberational L2 band with a maximum at 670 cm–1 reflects water structure18. Using MD calculations Cho et al. attributed this band to an intermolecular vibration of several to several hundred water molecules19. Both Ashihara et al.18. and Cho et al.19. indicated that the band in the 1000–100 cm–1 region arises from the cooperative vibrational mode of many water molecules. IR spectra in the 4000 –3000 cm–1 region are concerned with local vibrational modes (OH stretching modes). In contrast, the 1000–100 cm–1 region is for the cooperative vibrational mode of numerous water molecules. Therefore, the 1000–100 cm–1 region is suitable for exploring water hydrogen- bonding network structure.
It was not clear how many component bands are involved in the broad feature. Recently, Ishikawa et al. divided the broad band in the 1000–100 cm–1 region of NaCl solutions into two components using curve-fitting21 The base of the two components came from the existence of an isosbestic point near 600 cm–1.21 In the case of NaCl solutions the peak top of the two bands are identified at 673 and 403 cm–1. Based on the concentration-dependent spectra variations of NaCl solutions in both high- and low-frequency regions, Ishikawa et al. suggested that the 673 cm–1 band is correlated with the SHB band at 3210 cm–1 while the 403 cm–1 band is related with the WHB band at 3380 cm–1. The detailed spectra variations in the 1000 –100 cm–1 region for LiCl, KCl, NaCl, CsCl, CaCl2 and BaCl2 solutions were reported firstly by Ishikawa et al.21. They have found that an isosbestic point occurred in the 1000–100 cm–1 region, and that its wavenumber is correlated to the hydrated area of each ion21.
The purpose of the present study is to investigate the structure and dynamics of water by deepening the spectral analysis of both the 4000 –3000 cm–1 and the 1000 –100 cm–1 regions. To deepen the spectral analysis we used 2D-COS33,34,35 2D-COS is a powerful analytical technique that enhances spectral resolution by spreading peaks along a second dimension, allowing for the detection of correlations between spectral intensity changes under various perturbations, such as mechanical stress, electric fields, temperature, pH, and concentration, etc33,34,35 There are three main functions: (1) characterizing intermolecular interactions, (2) resolving overlapping peaks, and (3) probing the sequential order of physical and chemical processes. In our work, 2D-COS has been instrumental in revealing the correlations between different vibrational modes, providing strong evidence for distinct hydrogen-bonding environments in these aqueous systems. The 2D-COS has allowed us to confirm there are two components in the low-frequency region without any assumption and elucidate the correlation between two bands in the high frequency region and those in the low-frequency region. Another important point of the present study lies in the discussion of the changes in the bandwidth and shift of the components bands in the two regions caused by the changes in the kinds of alkali ions and their concentrations. This may be the first time that the band widths of water bands have ever been discussed. Based on these variations one can discuss changes in the structure and dynamics of water species. The present study has reached very important conclusion that two kinds of hydrogen-bonding networks consisting of the several to several hundred of SHB or WHB water species exist in the alkali chloride solutions.
Results
IR spectra of alkali chloride aqueous solutions in the high frequency region (4000–3000 cm–1)
Figure 1A, B, C, and D show concentration-dependent IR spectra and second derivative spectra in the 4000 –3000 cm–1 region of LiCl (2,10,22 w/v%), NaCl (2,10,22 w/v%), KCl (2,10,22 w/v%), and CsCl (2,10,22 w/v%) solutions, respectively. It is well known that the IR spectra of pure water and aqueous solutions consist mainly of two bands, a higher frequency band at around 3380 cm–1 and a lower frequency band at around 3210 cm–1 band21,22 The former is due to the OH stretching mode of WHB water species while the latter is assigned to the OH stretching mode of SHB species21,22 The SHB has tetrahedron structure while the WHB has slightly distorted tetrahedron structure12 It can be seen from Fig. 1A, B, C, and D that the intensity of the SHB band decreases with the increase in the concentration of aqueous solutions because the ions perturb tetrahedron structure of the SHB species. In contrast, the intensity of the WHB band band increases with the concentration. Of note is that the intensity changes are rather small for CsCl. The ion size of Cs+ (1.81Å) is significantly larger than those of others (Li+ (0.90Å), Na+ (1.16Å), K+ (1.52Å)). Thus, the effect of charge density is small for CsCl.
These frequencies of the two bands change as follows; LiCl:3371 and 3209 cm–1, NaCl: 3374 and 3210 cm–1, KCl; 3370 and 3209 cm–1, CsCl: 3371 and 3210 cm–1. These frequencies are fairly different for the corresponding frequencies in the power spectra of 2D-COS (Fig. 4). We will discuss this point later. The frequency of the SHB band decreases from 3212 to 3204 cm–1 with the increase in the concentration of LiCl while that of the WHB band changes a little (Fig. 1A). The similar results were obtained for NaCl and KCl (Fig. 1B, C). These indicate that the hydrogen bonding in the SHB species becomes weaker with the concentration and that the strength of the hydrogen-bonding in the WHB species changes little. However, for CsCl the corresponding band shifts are very small (Fig. 1D), indicating that the strength of the hydrogen bonds in the SHB species of CsCl changes little. Interestingly, the bandwidth of the SHB band becomes narrower significantly while that of the WHB band becomes wider slightly for LiCl, NaCl, and KCl solutions. These observations indicate that in the lower concentrations the water molecules behave more freely in the SHB species. On the other hand, they move less freely in the SHB species in the higher concentrations. In the WHB species the movement of water molecules changes little with concentration. The difference in the change in the bandwidth may come from the difference in the hydrogen-bonding structure between the SHB and WHB species. For CsCl solutions the bandwidth varies little for both the SHB and WHB bands, again indicating that in the case of CsCl solutions, the effect of charge is small compared with the other ions.
This may be the first time that the bandwidth of the second derivative spectra of aqueous solutions has ever been investigated.
IR/FIR spectra of alkali chloride aqueous solutions in the low frequency region (1000–100 cm–1)
Figure 2A, B, C, and D show concentration-dependent IR/FIR spectra in the 1000 –100 cm–1 region of LiCl (2,10,22 w/v%), NaCl (2,10,22 w/v%), KCl (2,10,22 w/v%), and CsCl (2,10,22 w/v%) solutions together with their curve-fitting spectra. All show a very broad band centered at around 600 –550 cm–1 with an isosbestic point of 591, 488, 477, and 410 cm–1 for the LiCl, NaCl, KCl, and CsCl solutions, respectively. The broad band was assigned to the liberation L2 mode and attributed to the intermolecular vibration which causes several water molecules to bond and vibrate collectively18,19 Ishikawa et al. reported that the spectra in the 1000 –100 cm–1 region of NaCl solutions consist of two peaks based on the curve-fitting results of the broad bands21 It was difficult for Ishikawa et al. to obtain good second derivative spectra of NaCl solutions, but they could calculate their curve-fitting spectra. It can be seen from the spectra in Fig. 2 that the same conclusion can be reached for other solutions. Figure 2 shows that the higher frequency band at around 700 cm–1 decreases while the lower frequency band at around 400 cm–1 increases with the increase in the concentration for all the solutions. In the case of the low-frequency region even CsCl solutions shows significant variations, although they are smaller. Thus, it seems that the higher frequency band is correlated with the band at 3200 cm–1 due to the SHB species while the lower frequency band is related to the WHB species band at around 3400 cm–1. As we will discuss later we can confirm this point using 2D-COS. Therefore, we have assigned the higher and lower frequency bands in the low frequency region to the librational L2 mode of the SHB and WHB species, respectively.
As in the case of the two bands in the 4000 –3000 cm–1 region, the band widths of the two bands at 700 and 400 cm–1 change. The higher frequency bands become narrower as the concentration increases as in the case of the SHB band at 3180 cm–1, while the lower frequency band becomes broader as in the case of the WHB band at 3380 cm–1 in the cases of the LiCl. NaCl, and KCl solutions. However, the changes in the bandwidths are small for the CsCl solutions. The same discussion as that for the 4000 –3000 cm–1 region can be made for the concentration-dependent variations of the band widths of the LiCl. NaCl, KCl, and CsCl solutions.
2D-COS of IR spectra of alkali chloride solutions in the 4000-3000 cm–1 region
LiCl
Figure 3A shows a synchronous 2D correlation spectrum in the 3900 –2600 cm–1 region of LiCl solutions with the concentrations of 2, 10, 22 w/v%. Two diagonal peaks appear at (3375, 3375) and (3156, 3156) cm–1 and two negative cross peaks develop at (3375, 3156) and (3375, 3156) cm–1. The two diagonal peaks correspond to the two peaks in the second derivative spectra of the 1D spectra. The two peaks at 3375 and 3156 cm–1 are due to OH stretching modes of WHB and SHB water species, respectively. It is of note that the frequencies of the two diagonal peaks (3375 and 3156 cm–1) are close to but significantly different from those of the second derivative peaks (3375 and 3220 cm–1). We will discuss this discrepancy latter. Figure 4A depicts a power spectrum in the 4000 –3000 cm–1 region developed from the 2D synchronous spectrum of LiCl solutions. It shows two peaks at 3375 and 3156 cm–1, corresponding to the two peaks in the synchronous spectrum. The former is stronger than the latter.
Autopower spectra of the two-dimensional synchronous correlation analysis in the 4000–2600 cm−1 region corresponding to Fig. 3. (A) LiCl, (B) NaCl, (C) KCl, and (D) CsCl.
NaCl
Figure 3B shows a synchronous 2D correlation spectrum in the 3900 –2600 cm–1 region of NaCl solutions with the concentrations of 2, 10, 22 w/v%. Two diagonal peaks appear at (3419, 3419) and (3171, 3171) cm–1 and two negative cross peaks develop at (3419, 3171) and (3171, 3419) cm–1. Figure 4B depicts a power spectrum in the 3900 –2600 cm–1 region developed from the 2D synchronous spectrum. It shows two peaks at 3419 and 3171 cm–1, corresponding to the two peaks in the synchronous spectra. Note that in contrast to the case of LiCl solutions, the former is weaker than the latter. The relative intensity of the two peaks in the power spectra changes significantly between LiCl and NaCl solutions. We will discuss this point later.
KCl, CsCl
Figures 3C and 4C show a synchronous 2D correlation spectrum in the 3900–2600 cm–1 region of KCl solutions with the concentrations of 2,10,22 mM and its power spectrum in the 3900 –2600 cm–1 region developed from the 2D synchronous spectrum, respectively. As in the cases of LiCl and NaCl solutions, two diagonal peaks appear at (3429, 3429) and (3156, 3156) cm–1 and two negative cross peaks develop at (3429, 3156) and (3156, 3429) cm–1. The power spectrum in the 3900 –3000 cm–1 region shows two peaks at 3429 and 3156 cm–1, corresponding to the two peaks in the synchronous spectra. A synchronous 2D correlation spectrum in the 3900 –2600 cm–1 region of CsCl solutions with the concentrations of 2, 10, 22 w/v% and its power spectrum in the 3900 –2600 cm–1 region generated from the 2D synchronous spectrum are shown in Figures. 3D and 4D, respectively. The power spectrum of CsCl solutions in the 3900 –2600 cm–1 region shows two peaks at 3425 and 3155 cm–1, corresponding to the two peaks in the synchronous spectra. It is noted that the relative intensity of the two peaks in the power spectra changes significantly among LiCl, NaCl, KCl, and CsCl solutions.
In the high-frequency region of LiCl, NaCl, KCl, and CsCl solutions there are significant differences between the autopeak positions and band positions in the second derivative spectra. The reason for the discrepancy is that the band position in the second derivative spectra and the autopeak in 2D synchronous spectra reflect different aspects. According to the reference33,34,35, autopeaks represent the total amount of spectral intensity variations observed at a specific spectral variable ν during the measurement. Thus, for a given perturbation, any region with significant intensity changes will exhibit strong autopeaks, while regions that remain relatively constant will show little or no autopeaks. On the other hands, the second derivative approach is a useful method for identifying the inflection points in the 1D spectrum, effectively indicating the positions of underlying peaks and shoulders. This means that the two approaches can provide different information depending on their mathematical underpinnings. This is the reason why the autopeak positions may not correspond to the peak positions in second derivative spectra, especially when the positions shift with changing concentrations of aqueous solutions.
The four kinds of the alkaline chloride solutions show interesting frequency shift behaviors of SHB and WHB bands. The shift of the WHB band is as follow (Fig. 4);
Only LiCl solutions give the lower frequency compared with other three. Li+ has a smaller ionic radius with high charge density. This indicates that there are strong interactions between Li+ ions and water molecules. These strong interactions can weaken the OH bonds in the WHB species, resulting in the lower frequency shift of the WHB band of LiCl solutions. As the ionic radius increases and charge density decreases (Li⁺ to Cs⁺), the interactions become weaker to allow OH bonds to vibrate at wavenumbers closer to those of free water molecules. For the SHB water species, the autopeak positions remain relatively stable (3155–3171 cm–1, Fig. 4). This behavior shows that the SHB water networks beyond the immediate vicinity of the ions maintain similar structural characteristics irrespective of the kinds of ions because the SHB water species have rather rigid tetragonal structure.
It can be seen from Fig. 4 that the intensity ratio of the WHB band and the SHB band (WHB/SHB) changes as follows;
Of note is that the LiCl solutions yield much larger intensity ratio compared with others, showing that much larger intensity variation of the WHB peak. This means that the intensity of the WHB band changes largely with the increasing the concentration. This is clear also from the 1D spectra and their second derivative spectra (Fig. 1A). This result suggests that Li+ ion interacts more strongly with the WHB water species than the SHB water species because the WHB water species have somewhat distorted structure.
2D-COS of IR/FIR spectra of alkali chloride solutions in the 1000 –100 cm–1 region
LiCl
Figures 5A and 6A show a synchronous 2D correlation spectrum in the 1000 –100 cm–1 region of LiCl solutions with the concentrations of 2, 10, 22 w/v% and its power spectrum generated from the synchronous spectrum, respectively. Two diagonal peaks appear at (758, 758) and (396, 396) cm–1 and two negative cross peaks develop at (758, 396) and (396, 758) cm–1. The two diagonal peaks correspond to the two peaks in the curve-fitting spectra of the 1D spectra (Fig. 2). The frequencies of the two diagonal peaks (758 and 396 cm–1) are close to but significantly different from those of the curve-fitted peaks (674 and 367 cm–1). As we mentioned in the session of the 1D spectra and their curve-fitting the two peaks at 758 and 396 cm–1 are concerned with the SHB and WHB water species, respectively. The 396 cm–1 band (WHB) is stronger than the band at 758 cm–1 (SHB) in the power spectrum (Fig. 6). This is consistent with the result of the high frequency region (Fig. 4).
Autopower spectra in the 1000 –100 cm–1 region derived from the two-dimensional synchronous correlation data presented in Fig. 5. (A) LiCl, (B) NaCl, (C) KCl, and (D) CsCl.
NaCl
Figures 5B and 6B shows a synchronous 2D correlation spectrum in the 1000 –100 cm–1 region of NaCl solutions with the concentrations of 2, 10, 22 w/v% and its power spectrum generated from the synchronous spectrum, respectively. Two diagonal peaks appear at (~666, ~ 666) and (364, 364) cm–1 and two negative cross peaks develop at (~666, 364) and (364, ~666) cm–1. The two diagonal peaks correspond to the two peaks in the curve fitting spectra of the 1D spectra (Fig. 2). The frequencies in the 2DCOS spectra are ~666 and 364 cm–1 while those in the curve fitting spectra are 673 and 403 cm–1. Thus, there is significant discrepancy in the frequency of the lower frequency band between the power spectrum and the curve-fitting spectrum.
KCl, CsCl
Figures 5C and 6C show a synchronous 2D correlation spectrum in the 1000 –100 cm–1 region of KCl solutions with the concentrations of 2, 10, 22 w/v% and its power spectrum in the 1000 –100 cm–1 region developed from the 2D synchronous spectrum, respectively. Figures 5D and 6D depict the corresponding synchronous spectrum of CsCl and its power spectrum, respectively. LiCl, NaCl, KCl, and CsCl all show two peaks in the power spectra. Their frequencies change as follows: 758-666-615–617 cm–1 and 396-364-324-324 cm–1. The frequencies of the LiCl solutions are much higher than those of others. The frequencies of KCl and CsCl are similar to each other, and those of NaCl are somewhat between the frequencies of LiCl and those of KCl and CsCl solutions. The relative intensity of the two autopeaks of LiCl solutions is markedly different from those of other solutions and those of the KCl and CsCl solutions are similar. Those results of frequencies and relative intensities suggest that due to the smaller ion size with high charge density Li+ interacts more strongly with WHB water species than other ions. The behavior of NaCl solutions is somewhat between the LiCl solutions and the KCl and CsCl solutions.
The autopeak positions around 700 cm–1 of KCl and CsCl solutions may not be very accurate due to the noise. However, it seems that these bands around 700 and 400 cm–1 are redshifted as the ionic radius increases (Li+→Na+→K+→Cs+). As the alkali metal ions increase in radius, their hydration strength decreases. That leads to weaker hydrogen bonding in the shells formed between water molecules and ions. Thus, the length and/or bond angles of hydrogen bonds increase. This result aligns with the study by Ashihara et al.18.
Hetero 2D-COS between the 4000 –3000 cm–1 region and the 1000–100 cm–1 region
Figure 7A, B, C and D exhibit hetero synchronous 2D correlation spectra between the 4000 –2600 cm–1 and 1000 − 100 cm–1 regions for LiCl, NaCl, KCl, and CsCl solutions, respectively. In the hetero 2D-COS spectrum of LiCl solutions there are four major cross peaks at (3375, ~758), (3375, ~ 396), (3156, ~758), and (3156, ~396) cm–1. Now, it is clear that the 3375 cm–1 band is positively correlated with the 396 cm–1 band, and the 3156 cm–1 band is positively correlated with the 758 cm–1 band. Therefore, the 340 cm–1 band is correlated with the WHB band while the 680 cm–1 band is corelated with the SHB band. Similar correlations can be found for the NaCl, KCl, and CsCl solutions (Fig. 7B, C, and D). Ishikawa et al. already reached to the same correlation based on the concentration-dependent intensity changes of the second derivative and curve-fitting spectra of the 1D spectra21 Their conclusion was based partly on the simulation (the curve-fitting spectra). In contrast, the present study confirms the same conclusion based on the solid mathematical calculations of the experimental data. It yields correlations quantitatively.
It seems from Fig. 7 that the hetero correlation between the 396 cm–1 band and the 3375 cm–1 band (both WHB bands) becomes weak upon going from LiCl to NaCl, KCl, and CsCl solutions. On the other hand, hetero correlation between the 758 cm–1 band and the 3156 cm–1 band (both SHB bands) becomes strong upon going from LiCl to NaCl, KCl and CsCl solutions.
Figure 8 shows slice spectra extracted from the heterogeneous 2D-COS spectra of alkali chloride solutions shown in Fig. 7. The slice positions correspond to wavenumber at (A) 360 and (B) 3425 cm–1, respectively. It can be seen clearly that the peak intensities near 3425 (Fig. 8A) and 360 cm–1 (Fig. 8B) gradually decrease in the order of LiCl, NaCl, KCl, and CsCl solutions. In all the cases the changes are very small for CsCl solutions.
The slice spectra extracted from the heterogeneous synchronous 2D-COS spectra of alkali chloride solutions shown in Fig. 7. The slice positions correspond to wavenumber at y = 360 (A), and x = 3425 (B) cm–1, respectively.
The trend of the intensity variations around (3425, 360) shown in Figs. 7 and 8A and B, follows the order; LiCl ≈ NaCl > KCl > CsCl. This trend can be explained by the hydration capacity of different alkali metal ions: Li+ and Na+ have a strong hydration ability and tend to form stable shells with water molecules, leading to increase the proportion of WHB species. However, the hydration capacity of K+ and Cs+ is weaker. They have less effect on the hydrogen bonding network, which leads to a relative decrease in the amounts of WHB species.
Discussion
The present study based on the 2D-COS analysis, the second derivative, and curve-fitting revealed that there are two major bands in both high frequency region (4000 –3000 cm–1) and low frequency region (1000 –100 cm–1) of IR spectra of the LiCl, NaCl, KCl, and CsCl solutions. The two bands at around 3400 and 3160 cm–1 are due to OH stretching modes of WHB and SHB water species, respectively, SHB and WHB correspond to tetrahedron structure and slightly distorted tetrahedron structure, respectively. Thus, the 4000 –3000 cm–1 region is very suitable to investigate local hydrogen bond structure.
Skinner et al.36 have demonstrated that the apparent presence of two bands in the 4000 –3000 cm–1 region stems from a Fermi resonance of the OH stretching vibration with the overtone of the H2O bending vibration. While this idea is interesting, the present result in the 4000 –3000 cm–1 region can be explained by 2D-COS and second derivative spectra. The 2D-COS analysis clearly reveals correlations between the 3400 cm–1 band and 370 cm–1 band, as well as between the 3160 cm–1 band and 700 cm–1 band irrespective of the kinds of ions. These correlations between the OH stretching and librational modes, in various alkali cations solutions, provide a strong evidence for the existence of distinct hydrogen-bonding environments in these solutions, complementing the spectral interpretations based on Fermi resonance.
Bands at around 700 and 370 cm–1 are assigned to the librational L2 modes of the SHB and WHB water species, respectively. The librational L2 band is collective vibration of several to several hundreds of molecules, and thus suitable for exploring network structure of water hydrogen bonds18,19 Therefore, there may be two kinds of hydrogen bonding networks of water molecules; the network consisting of the SHB species with tetrahedron structure and that involving the WHB species with slightly distorted tetrahedron structure. Both regions yield clear evidences for the existence of two kinds of water hydrogen bonding networks; the 4000 –3000 cm–1 region gives information about two kinds of water structures, tetrahedron structure (SHB) and distorted tetrahedron structure (WHB) through local vibrational mode (OH stretching mode). The 1000 –100 cm–1 region suggests that there are two kinds of the cooperative vibrational modes of many water molecules.
Materials and methods
Sample preparation
LiCl, NaCl, KCl, and CsCl were purchased from Fijifilm-Wako, Osaka, Japan, and their solutions were prepared based on the method described by Ishikawa et al.21.
IR and IR/FIR spectra measurements in the 4000–100 cm–1 region
ATR-IR/FIR spectra in the region of 4000–50 cm–1 were measured using an FT-IR spectrometer (FT/IR-6700FV, JASCO) with a high-intensity ceramic source, a Si beam splitter, and a DLATGS detector. An ATR accessory (ATR PRO ONE, JASCO) with a diamond crystal which transmits light in the wide wavenumber region was used for the IR/FIR measurements. In addition, a whole optical path was evacuated to avoid the interference of water vapor and carbon dioxide. Each spectrum was measured with a spectral resolution of 2 cm–1 and accumulated for 50 scans. The ATR method uses evanescent waves to obtain the absorption spectrum of a sample. Since the penetration depth of the evanescent wave depends on the wavelength, the ATR correction involved in the instrument was applied to all spectra prior to analysis.
All ATR spectra were treated with the correction of penatration depth. For confirmation of repeatability, each sample was subjected to the IR/FIR measurement twice and averaged spectra were used. To obtain second derivative spectra of ATR-IR, Savitzky-Golay method were used.
Calculation of 2DCOS
2D-COS spectra were calculated using the algorithm-based numerical method proposed by Noda33. The synchronous 2D correlation spectra were generated using MATLAB software (The MathWorks Inc.).
Curve-fitting spectra
The simulated spectra in the 1000–100 cm–1 region was calculated by a combination of Gauss and Lorentz functions. The procedure was performed using a curve fitting program of Spectral Manager (JASCO Co., Tokyo, Japan).
Data availability
The datasets used and/or analysed during the current study are available from the corresponding author on reasonable request.
References
Ball, P. Water—an enduring mystery. Nature 452, 291–292 (2008).
Pettersson, L. G. M., Henchman, R. H. & Nilson, A. Water—the most anomalous liquid. Chem. Rev. 116, 7459–7462 (2016).
Russo, J. & Tanaka, H. Understanding water’s anomalies with locally favored structures. Nat. Commun. 5, 3556 (2014).
Nilsson, A. & Pettersson, L. G. M. The structural origin of anomalous properties of liquid water. Nat. Commun. 6, 8998 (2015).
Bakker, H. J. & Skinner, J. L. Vibrational spectroscopy as a probe of structure and dynamics in liquid water. Chem. Rev. 110, 1498–1517. https://doi.org/10.1021/cr9001879 (2010).
Marcus, Y. Effect of ions on the structure of water: Structure-making and breaking. Chem. Rev. 109, 1346–1370 (2009).
Kontogeorgis, G. M. et al. Water structure, properties and some applications—a review. Chem. Thermodyn. Therm. Anal. 6, 100053 (2022).
Bernal, J. D. & Fowler, R. H. A theory of water and ionic solutions with particular reference to hydrogen and hydroxyl ions. J. Chem. Phys. 1, 515–548 (1933).
Do, H. & Beslev, N. A. Structure and bonding of ionized water cluster. J. Phys. Chem. A. 117, 5385–5391 (2013).
Pople, J. Molecular association in liquid II. Theory of water structure. Proc. R Soc. A: Math. Phys. Eng. Sci. 205, 163–178 (1951).
Walralen, G. E. Raman spectral studies of the effects of temperature on water and electrolyte solutions. J. Chem. Phys. 44, 1546–1558 (1966).
Shi, R. & Tanaka, H. Direct evidence in the scattering function for the coexistence of two types of local structures in liquid water. J. Am. Chem. Soc. 142, 2868–2875 (2020).
Begušić, T. & Blake, G. A. Two-dimensional infrared-Raman spectroscopy as a probe of water’s tetrahedralit. Nat. Commun. 14, 1950 (2023).
Brubach, J. B., Mermet, A., Filabozzi, A., Gerschel, A., Roy, P. & & Signatures of the hydrogen bonding in the infrared bands of water. J. Chem. Phys. 122, 184509 (2005).
De Ninno, A. & Francesco, M. D. ATR-FTIR study of the isosbestic point in water solution of electrolytes. Chem. Phys. 513, 266–272 (2018).
Vasylieva, A., Doroshenko, I., Vaskivskyi, Y., Chernolevska, Y. & Pogorelov, V. FTIR study of condensed water structure. J. Mol. Struct. 1167, 232–238 (2018).
Millo, A., Raichlin, Y. & Katzir, A. Mid-infrared fiber-optic attenuated total reflection spectroscopy of the solid–liquid phase transition of water. Appl. Spectrosc. 59, 460–466 (2005).
Ashihara, S., Huse, N., Espagne, A., Nibbering, E. T. J. & Elsaesser, T. Ultrafast structural dynamics of water induced by dissipation of vibrational energy. J. Phys. Chem. A 111, 743–746 (2007).
Cho, M., Fleming, G. R., Saito, S., Ohmine, I. & Stratt, R. M. Instantaneous normal mode analysis of liquid water. J. Chem. Phys. 100, 6672–6683 (1994).
Tassaing, T., Danten, Y. & Besnard, M. Infrared spectroscopic study of hydrogen-bonding in water at high temperature and pressure. J. Mol. Liq. 104, 149–158 (2002).
Ishikawa, D., Shinohara, R., Shichishima, N. & Fujii, T. Infrared spectra in the 1000–100 cm−1 region combined with 4000–3000 cm−1region to evaluate the states of water. Appl. Spectrosc. 77, 1087–1094 (2023).
Ishikawa, D., Shichisima, N., Shinohara, R., Yang, J. & Fujii, T. Investigating the water state in saccharide solutions by infrared/far-infrared spectra in the 1000–100 cm−1 region combined with a band in the 4000–3000 cm−1 region. J. Phys. Chem. C. (2025).
Nasu, T., Ozaki, Y. & Sato, H. Study of changes in water structure and interactions among water, CH, and COO– groups during water absorption in acrylic acid-based super absorbent polymers using Raman spectroscopy. Spectrochim Acta Part. A 250, 119305 (2021).
Okajima, H., Ando, M. & Hamaguchi, H. Formation of nano-ice and density maximum anomaly of water. Bull. Chem. Soc. Jpn. 91, 991–997 (2018).
Asano, H., Ueno, N., Ozaki, Y. & Sato, H. Temperature-dependent structural variations of water and supercooled water and spectral analysis of Raman spectra of water in the OH stretching band region and low-frequency region studied by two-dimensional correlation spectroscopy. J. Raman Spectrosc. 53, 1669–1678 (2022).
Rossi, B., Tommasini, M., Ossi, P. M. & Paolantoni, M. Pre-resonance-effects in deep UV Raman spectra of normal and deuterated water. Phys. Chem. Chem. Phys. 26, 22023–22030 (2024).
Maeda, M., Ozaki, Y., Tanaka, M., Hayashi, N. & Kojima, T. Near-infrared spectroscopy and chemometrics studies of temperature-dependent spectral variations of water; relationship between spectra changes and hydrogen bonds. J. Near-Infrared Spectrosc. 3, 191–201 (1995).
Segtnan, V. H., Sasic, S., Issakson, T. & Ozaki, Y. Studies on the structure of water using two-dimensional near-infrared correlation spectroscopy and principal component analysis. Anal. Chem. 73, 3153–3161 (2001).
Sasic, S., Segtnan, V. H. & Ozaki, Y. Self-modeling curve resolution study of temperature-dependent near-infrared spectra of water and the investigation of water structure. J. Phys. Chem. A 106, 760–766 (2002).
Ishigaki, M., Yasui, Y., Kajita, M. & Ozaki, Y. Assessment of embryonic bioactivity through changes in the water structure using near-infrared spectroscopy and imaging. Anal. Chem. 92, 8133–8141 (2020).
Shiraga, K., Suzuki, T., Kondo, N., De Baerdemaeker, J. & Ogawa, Y. Quantitative characterization of hydration state and destructuring effect of monosaccharides and disaccharides on water hydrogen bond network. Carbohydr. Res. 406, 46–54 (2015).
Shiraga, K., Tanaka, K., Arikawa, T., Saito, S. & Ogawa, Y. Reconsideration of the relaxational and vibrational line shapes of liquid water based on ultrabroadband dielectric spectroscopy. Phys. Chem. Chem. Phys. 20, 26200–26209 (2018).
Noda, I. & Ozaki, Y. Two-Dimensional Correlation Spectroscopy: Applications in Vibrational and Optical Spectroscopy (Chichester, 2004).
Noda, I., Dowrey, A. E., Marcott, C., Story, G. M. & Ozaki, Y. Generalized two-dimensional correlation spectroscopy. Appl. Spectrosc. 54, 236A–248A (2000).
Park, Y., Noda, I. & Jung, Y. M. Novel developments and progress in two-dimensional correlation spectroscopy (2D-COS). Appl. Spectrosc. 79, 13–35 (2025).
Kananenka, A. A. & Skinner, J. L. Fermi resonance in OH-stretch vibrational spectroscopy of liquid water and water hexamer. J. Chem. Phys. 148, 244107–244101 (2018).
Acknowledgements
We would like to acknowledge Mr. Kohei Tamura and M. Kenichi Akao for allowing us to use their FTIR instrument (FT/IR-6700FV) at Jasco at Hachioji.
Author information
Authors and Affiliations
Contributions
D.I. and T.F. developed the concept and designed the experimentation. D.I. carried out sample preparation of IR spectral measurements. Y.O., A.H., and Y.X. proposed to use 2D-COS. A.H. carried out the calculation of 2D-COS. Discussion on the results were made mainly by D.I.A.H. and Y.O. but T.F. and Y.X. also contributed to the discussion at the final stage. Y.O. prepared the draft of the manuscript, and the final version was prepared mainly by D.I.A.H. and Y.O. All the coauthors joined revising the final version.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Ishikawa, D., He, A., Xu, Y. et al. Evidence for two kinds of hydrogen-bonding networks in ionic solutions by 2D infrared correlation spectroscopy. Sci Rep 15, 16991 (2025). https://doi.org/10.1038/s41598-025-00774-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-025-00774-0