Development of a triangular Fermatean fuzzy EDAS model for remote patient monitoring applications

Abstract

Remote Patient Monitoring Systems (RPMS) are vital for tracking patients’ health outside clinical settings, such as at home or in long-term care facilities. Wearable sensors play a crucial role in these systems by continuously collecting and transmitting health data. However, selecting the optimal sensor is challenging due to the wide variety of available options and diverse patient needs. To address this paper, introduce score and accuracy functions for Triangular Fermatean Fuzzy Numbers (TFFNs) and propose a novel Triangular Fermatean Fuzzy Sugeno–Weber Weighted Average (TFFSWWA) aggregation operator. In this paper establish key properties of TFFSWWA, confirming its ability to manage fuzzy uncertainty effectively. Using TFFSWWA, we develop an improved Evaluation based on Distance from Average Solution (EDAS) method for multi-criteria group decision-making (MCGDM) under TFFN settings. A case study on wearable sensor selection demonstrates the proposed model’s efficiency. We present an algorithm and a flowchart to guide the decision-making process, alongside a computational example that verifies the method’s reliability. Sensitivity analysis and comparison with existing methods show that the proposed approach improves decision accuracy and stability, highlighting its practical utility in healthcare decision-making.

Introduction

Real-world circumstances are frequently complex, marked by confusion, inconsistency, and an inability of understanding, all of which can result in uncertain. Language statements specify the majority of the parameters in these challenges. Treating the decision makers’ knowledge as uncertain data is therefore more effective. The “uncertainty and ambiguity” inherent in human systems can be described using a method of mathematics known as fuzzy modelling. Zadeh¹ introduced the concept of fuzzy sets (FSs) to solve ambiguity in practical issues. However, it is clear that FS theory cannot describe the intricacies of fulfilment and discontent in human DM. In response to the identified limitations of traditional fuzzy sets, Atanassov² proposed an advancement in the form of intuitionistic fuzzy sets (IFS). This innovative framework integrates a nonmembership function, which is confined to the interval [0, 1], thereby facilitating the representation of the degree of discontent that may influence human DM processes. The model constrains both the added membership degree (${\mathcal{M}}$) and the non-membership degree (${\mathcal{N}}$) to values within the interval [0, 1]. In 2013, Yager³ proposed the Pythagorean fuzzy set (PFS), which introduced a relaxed condition by requiring that the $0 \le {\mathcal{M}}^{{{2}}} + {\mathcal{N}}^{{{2}}} \le {{1}}$. Senapati and Yager^4,5 introduced the Fermatean fuzzy set (FFS) theory as a generalization of PFS, addressing its limitations. In FFS, $0 \le {\mathcal{M}}^{{{3}}} + {\mathcal{N}}^{{{3}}} \le {{1}}$ Additional explanations and various applications of the FFS are provided in the cited references^6,7,8,9,10.

The FS, IFS, FFS, and Fermatean fuzzy linguistic variables¹¹, which are employed in existing MCDM issues that use the EDAS approach, are restricted to discrete environments. The Triangular IFS extends the concept of IFS by enabling the representation of decision information across multiple dimensions¹². The scope of the IFS is broadened through an extension from discrete to continuous sets¹³. The TFN and traditional IFN can be viewed as particular instances of the TIFN. By integrating the TFN into the IFN, TIFN improves the information available to decision makers, allowing it to surpass vague fuzzy terms like “excellent” or “good” and enabling a more precise expression^14,15. Li¹⁶ found and corrected numerous mistakes in Shu et al.¹²'s description of TIFN operational laws in the context of decision-making procedures. Sharma et al.¹⁷ defined MCGDM for Triangular PF environment. The concept of a Triangular Fermatean fuzzy number (TFFN) was introduced by Akram et al.¹⁸, characterized as a triplet denoted by (a, b, c). This representation expands the range space, allowing it to capture a greater level of ambiguity compared to a single value. For our study, we have selected TFFNs due to their superior ability to handle incomplete and uncertain information in decision-making.

Research background

Einstein geometric aggregation operators have been introduced for q-ROFSS to improve the accuracy and consistency of MCDM models¹⁹. Similarly, interval-valued Pythagorean fuzzy soft sets have been explored with aggregation operators to solve multi-attribute group decision-making problems²⁰. The use of Einstein aggregation operators in Pythagorean fuzzy soft sets has also demonstrated effectiveness in enhancing decision-making processes²¹. Furthermore, an interaction and feedback mechanism-based group decision-making approach using T-spherical fuzzy information has been proposed for the selection of emergency medical supplies suppliers²². In cloud service provider selection, correlation-based TOPSIS with interval-valued q-rung orthopair fuzzy soft sets has shown promising results²³. Algorithms for generalized multipolar neutrosophic soft sets with information measures have been applied to medical diagnosis and decision-making problems²⁴. The extension of Einstein average aggregation operators has also been utilized in medical diagnostic approaches under q-rung orthopair fuzzy soft sets²⁵. A novel multi criteria decision-making approach for interactive aggregation operators of q-rung orthopair fuzzy soft sets has further improved the decision-making framework²⁶. The selection of unmanned aerial vehicles (UAVs) for precision agriculture has been addressed using interval-valued q-rung orthopair fuzzy information-based TOPSIS methods²⁷. An integrated group decision-making technique under interval-valued probabilistic linguistic T-spherical fuzzy information has been applied to the selection of cloud storage providers²⁸. Einstein ordered weighted aggregation operators have also been used for Pythagorean fuzzy hypersoft sets to solve MCDM problems²⁹. In green supply chain management, correlation-based TOPSIS under a q-rung orthopair fuzzy soft environment has been employed for supplier selection³⁰. Further extensions of the correlation coefficient-based TOPSIS technique have been applied to interval-valued Pythagorean fuzzy soft sets in the context of extract, transform, and load (ETL) techniques³¹. The assessment of bio-medical waste disposal techniques using interval-valued q-rung orthopair fuzzy soft set-based EDAS methods has provided a structured decision-making framework³². An Einstein hybrid structure of q-rung orthopair fuzzy soft sets has been developed and applied to the diagnosis of waterborne infectious diseases³³. Transportation decisions in supply chain management have also benefited from interval-valued q-rung orthopair fuzzy soft information-based models³⁴. Hesitant fuzzy sets have been applied to ranking and balancing methods³⁵, expert evaluation systems³⁶, and construction safety assessment³⁷. Group decision-making approaches for green supply chain management³⁸ have further enhanced decision accuracy. A dynamic intuitionistic fuzzy³⁹ group decision analysis for sustainability risk assessment in surface mining operation projects. These methods demonstrate the effectiveness of fuzzy-based models in addressing real-world decision-making challenges.

Related works

MCGDM involves choosing the best option from a set of alternatives by evaluating them based on predefined criteria. Various AOs are utilized to tackle problems involving multiple criteria groups.

In the first approach, traditional methods are employed, while the second approach utilizes multiple AOs. Examples of these AOs include Sugeno–Weber, Yager, Frank, and Dombi, which represent various average and geometric operators, among others. Traditional methods typically offer only ratings. On the other hand, with AOs, every alternative is carefully assessed and ranked. It is more logical to fully assess the alternatives, considering the weights assigned to each attribute. Readers can review several existing studies by referring to Table 1, which presents comparisons based on the types of numbers used, the various methods employed by decision makers (DMs), the aggregation operators utilized, and the ranking methodologies applied.

Table 1 Literature comparison.

EDAS method

Several studies have explored Fermatean fuzzy-based decision-making approaches across different fields, highlighting their effectiveness in handling uncertainty and complex decision-making problems. For instance, the Fermatean fuzzy CRADIS approach based on triangular divergence has been applied for selecting an optimal online shopping platform, demonstrating the strength of Fermatean fuzzy models in addressing multi-criteria decision-making (MCDM) problems involving conflicting preferences⁵⁰. A confidence-based group decision-making method in an interval-valued Fermatean fuzzy environment was proposed for identifying sustainable strategies for electronic waste management, showcasing the robustness of Fermatean fuzzy methods in strategic decision-making⁵¹. Similarly, the SWARA-ARAS method was employed in a confidence level-based interval-valued Fermatean fuzzy environment to determine the best renewable energy sources in India, illustrating the adaptability of Fermatean fuzzy models in real-world energy selection problems⁵². Furthermore, an EDAS method based on a novel score function was introduced for selecting a vacant post in a company under a q-rung orthopair fuzzy environment, reinforcing the applicability of the EDAS technique in personnel selection⁵³.

The EDAS method is a distance-based MCDM method, comparable to TOPSIS and VIKOR. TOPSIS and VIKOR assess each alternative by measuring its distance from both the PIS and NIS, using this as a critical decision criterion. Therefore, it is necessary to define the PIS and NIS. The EDAS method eliminates the necessity of an additional procedural stage through the direct measurement of the distance separating an alternative from the Av solution. This implies that decision-makers are not required to calculate the PIS and NIS. They just need to compute the average score for each attribute. Consequently, the EDAS method simplifies distance calculations and efficiently reaches the final decision⁵⁴. By eliminating non-promising candidates, EDAS outperforms TOPSIS and VIKOR in terms of time complexity. Furthermore, this strategy is useful when information regarding the preferred average value of attribute assessments is available⁵⁵. Kahraman et al.⁵⁶ defined intuitionistic fuzzy EDAS method. Zhang et al.⁵⁷ applied the classic EDAS approach to the MAGDM problem in the picture fuzzy environment. Li et al.⁵⁸ adapted the EDAS method for MAGDM using q-rung orthopair fuzzy sets. Yanmaz et al.⁵⁹ extended the EDAS method for interval-valued Pythagorean fuzzy numbers. Batool et al.⁶⁰ established an EDAS method for Pythagorean probabilistic hesitant fuzzy information.

It is concluded from existing research that EDAS represents an effective, resilient, and precise methodology. Nevertheless, the application of this method in conjunction with TFFNs data has not been examined in detail.

Sugeno–Weber aggregation operator

In MCGDM, the AO plays a crucial role in identifying the optimal alternative. Essentially, it is a mathematical tool designed to combine a set of vectors into a single value. The Hamacher operations⁶¹, particularly the Hamacher T-norm (TN) and T-conorm (TCN), serve as robust alternatives to the traditional algebraic multiplication and summation. Many researchers have investigated Hamacher AOs and their applications to MCGDM problems^62,63. Dombi AOs for PFS were suggested by Akram et al.⁶⁴. Aydemir et al.⁴⁶ proposed the use of Dombi AOs and the TOPSIS method for FFS. SW triangular norms are regarded as one of the most important parameter groups of t-norms⁶⁵. The norms presented serve as dependable and efficient methods for aggregating information, thus addressing the ambiguity inherent in human assessments during the process of group decision-making. They can manage complex interactions with non-linear effects, whereas other aggregation operators may not be as adaptable and flexible. Sarkar et al.⁶⁶, developed the SW TN and TCN, AOs for t-spherical fuzzy hypersoft numbers. Ashraf et al.⁶⁷ introduced SW AOs for circular spherical fuzzy numbers. Wang et al.⁶⁸ introduced novel q-rung orthopair SW-power AOs, highlighting their key features. Additionally, they proposed a MCGDM method using these operators and applied it to assess solar panels. Ashraf et al.⁶⁹ introduced a series of SW AOs by integrating spherical fuzzy z-numbers with SW triangular norms.

The Sugeno–Weber aggregation operator is highly flexible due to its adjustable parameters, which allow it to balance conjunctive (AND-type) and disjunctive (OR-type) behaviors effectively. A key advantage is that its parameters are used four times during the aggregation process, enhancing its adaptability and accuracy in handling complex interactions among criteria. It can manage nonlinearity and correlation between criteria, making it suitable for complex decision-making problems. Its versatility extends to various fuzzy environments, including Intuitionistic Fuzzy Sets (IFSs), Pythagorean Fuzzy Sets (PFSs), and Fermatean Fuzzy Sets (FFSs), improving decision accuracy and consistency.

A review on remote patient monitoring systems

The popularity of RPMS is steadily growing, driven by factors such as the rise of highly infectious diseases like COVID-19, an aging population, and the increasing prevalence of health complications. A remote patient monitoring system collects physiological data using biomedical sensors to measure patients’ health away from a hospital setting⁷⁰. The objective encompasses the transformation of conventional clinical care practices to accommodate the environments in which patients reside, conduct their professional activities, and participate in their everyday lives. To enable appropriate decision-making, collected data is communicated to the healthcare provider using wireless technology^71,72. This form of telehealth allows for the measurement and transmission of physiological data, including heart rate, body temperature and blood pressure⁷³. RPMS benefits include the ability to detect illnesses in real time and continuously monitor patients’ health status. When potentially life-threatening conditions are detected, prompt intervention can be initiated. Furthermore, these systems use a range of communication technologies to help reduce healthcare expenditures. A patient can continue with their regular daily activities while undergoing treatment. Furthermore, the RPMS enhances emergency care for traffic accidents and mobility⁷⁴. Computers in hospitals were formerly linked to cable sensors as part of patient monitoring systems. The development of home-based care marked the introduction of RPMS in healthcare facilities. Initially, this device lacked user usability, similar to traditional patient monitoring approaches. Over the passage of time, advancements in technology have facilitated the development of solutions aimed at the remote monitoring of patients utilizing wireless connections. Significant progress is being made in the healthcare industry as more researchers and businesses use RPMS to improve care, which is causing company growth to accelerate^75,76,77.

Motivation of study

Aggregation operators play a crucial role in fuzzy decision-making problems by integrating the values of various criteria. Over time, researchers have explored different aggregation operators, such as Dombi, Hamacher, and Einstein, under various fuzzy environments, leading to significant advancements in fuzzy decision-making methodologies. The Sugeno–Weber operator is an important aggregation operator that has been defined for fuzzy sets (FSs) and their extensions, including intuitionistic fuzzy sets (IFSs), Pythagorean fuzzy sets (PFSs), and Fermatean fuzzy sets (FFSs). Triangular Fermatean fuzzy numbers (TFFNs) are a generalization of FSs that combine the features of FFSs and triangular fuzzy sets. However, a notable gap exists in the literature: the Sugeno–Weber operator has not yet been defined for TFFNs. Similarly, while the Evaluation based on Distance from Average Solution (EDAS) method has been successfully applied to FSs, IFSs, PFSs, and FFSs, it remains unexplored for TFFNs, presenting another gap in the literature. These gaps motivated us to introduce the Sugeno–Weber operator for TFFNs and extend the EDAS technique to the TFFN framework. In this study, we aim to address these gaps by developing a novel decision-making model that integrates the Sugeno–Weber operator with the EDAS method under a TFFN environment.

Objective of the paper

The primary objective of this study is to develop a novel decision-making framework for selecting the most suitable wearable sensor in Remote Patient Monitoring Systems (RPMS) under a Triangular Fermatean Fuzzy (TFF) environment. To achieve this, the study aims to:

• 1. Define score and accuracy functions for Triangular Fermatean Fuzzy Numbers (TFFNs) to enhance the handling of uncertainty and imprecision in decision-making.

• 2. Introduce and establish the properties of the Triangular Fermatean Fuzzy Sugeno–Weber Weighted Average (TFFSWWA) aggregation operator for effective information fusion under TFF settings.

• 3. Develop an extended version of the Evaluation based on Distance from Average Solution (EDAS) technique tailored for TFFNs to address multi-criteria group decision-making (MCGDM) problems.

• 4. Propose an algorithm and an illustrative flowchart to guide the decision-making process using the TFFSWWA-based EDAS approach.

• 5. Validate the proposed model through a case study on wearable sensor selection for RPMS, demonstrating its effectiveness and practical applicability.

• 6. Perform sensitivity analysis and comparative evaluation to highlight the superiority and consistency of the proposed method over existing approaches.

Contribution

The paper presents its key contributions and novel aspects as follows.

• 1. This paper introduce a novel MAGDM method within the TFF environment. TFFNs are utilized to allow decision makers (DMs) to convey their information more comprehensively, addressing the limitations of traditional Fermatean fuzzy numbers (FFNs) and offering a more adaptable approach to represent the cognitive data of DMs. Additionally, the relevant arithmetic operations and score functions for TFFNs are defined.

• 2. Establish the fundamental operations of TFFS information based on SW norms to lay a foundation for future research.

• 3. The Sugeno–Weber AO offers enhanced flexibility in information aggregation and decision-making due to its ability to handle high variability in operational parameters. To improve the aggregation of information provided by decision-makers (DMs), the Sugeno–Weber AO is extended to the triangular Fermatean fuzzy environment. The properties associated with this operator are further explored and analyzed.

• 4. This paper adapted the classical EDAS method to address MCGDM in a TFF environment.

• 5. The selection of optimal wearable sensors for RPMS constitutes a practical challenge that has been examined in order to validate the approach that has been proposed.

• 6. To handle a lack of clarity in decision-making, compare the recommended EDAS technique to existing method and aggregation operators.

Research questions

• 1. How do Triangular Fermatean Fuzzy Numbers (TFFNs) improve the modeling of uncertainty compared to other fuzzy sets like IFSs, PFSs, and FFSs?

• 2. Why is the EDAS method an effective approach for multi-criteria decision-making in fuzzy environments?

• 3. How does the incorporation of multiple parameters in the TFFSWWA operator enhance the decision-making process?

• 4. What are the main computational challenges when applying the TFFSWWA-based EDAS method to real-world healthcare decision-making problems?

• 5. How can the proposed model be adapted to address dynamic changes in patient conditions and healthcare technologies?

The structure of this article is as follows: Section “Preliminaries” covers the basic concepts related to TFFSs. Section “Triangular Fermatean fuzzy number under Sugeno–Weber operations” introduces the Sugeno–Weber operations for TFFSs. In Section “An EDAS method for MCGDM with TFFNs”, we discuss methodology based on EDAS approach for MCGDM problem. Section “Problem statement” demonstrates the problem statement of the proposed method for selection of the best Wearable Sensors for Remote Patient Monitoring System. Section “Results” presented results of the proposed method. Lastly, the conclusion of section “Conclusion” synthesizes the findings of the study and outlines avenues for future research as well as prospective contributions to the field.

Preliminaries

This section provides a succinct overview of fundamental concepts pertaining to TFFSs.

Definition 3

⁴³ A FFS defined on a universe $Y$ is expressed as an object in the form:

$${\breve{\mathcal{S}}} = \left\{ {y_{j} , \alpha_{{{\breve{\mathcal{S}}}}} \left( {y_{j} } \right),\beta_{{{\breve{\mathcal{S}}}}} \left( {y_{j} } \right) |y_{j} \in Y} \right\}$$

(1)

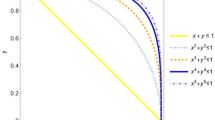
In this context, $\alpha_{{{\breve{\mathcal{S}}}}} \left( {y_{j} } \right)$ and $\beta_{{{\breve{\mathcal{S}}}}} \left( {y_{j} } \right)$ represent the MD and NMD of $y_{j} \in Y$, respectively, where $\alpha_{{{\breve{\mathcal{S}}}}} \left( {y_{j} } \right),\beta_{{{\breve{\mathcal{S}}}}} \left( {y_{j} } \right) \in \left[ {0, 1} \right]$, and the condition $0 \le \left( { \alpha_{{{\breve{\mathcal{S}}}}} \left( {y_{j} } \right)} \right)^{3} + \left( {\beta_{{{\breve{\mathcal{S}}}}} \left( {y_{j} } \right)} \right)^{3} \le 1$ holds. The degree of indeterminacy for $y_{j} \in Y$ is given by $\overline{\pi }_{{{\breve{\mathcal{S}}}}} = \sqrt[3]{{1 - \left( { \alpha_{{{\breve{\mathcal{S}}}}} \left( {y_{j} } \right)} \right)^{3} - \left( {\beta_{{{\breve{\mathcal{S}}}}} \left( {y_{j} } \right)} \right)^{3} }}$. Figure 1, we show that space comparison of IFS, PFS and FFS.

Fig. 1

Space comparison of IFS, PFS and FFS.

Triangular Fermatean fuzzy number

Definition 4

⁹ A TFFN ${\check{\mathcal{T}}} = \left( {\left( {\overline{\overline{a}} ,\overline{\overline{b}} ,\overline{\overline{c}} } \right);\alpha_{{\check{\mathcal{T}}}} ,\beta_{{\check{\mathcal{T}}}} } \right)$ represents a specific type of FFS defined over the set of real numbers R. The membership function (MF) associated with this FFS is formulated as follows:

$$\alpha_{{\check{\mathcal{T}}}} \left( y \right) = \left\{ {\begin{array}{*{20}l} {\frac{{\left( {y - \overline{\overline{a}} } \right)\alpha_{{\check{\mathcal{T}}}} }}{{\left( {\overline{\overline{b}} - \overline{\overline{a}} } \right)}},} \hfill & {\quad if\;\; \overline{\overline{a}} \le y < \overline{\overline{b}} } \hfill \\ {\alpha_{{\check{\mathcal{T}}}} ,} \hfill & {\quad if\;\; y = \overline{\overline{b}} } \hfill \\ {\frac{{\left( {\overline{\overline{c}} - y} \right)\alpha_{{\check{\mathcal{T}}}} }}{{\left( {\overline{\overline{c}} - \overline{\overline{b}} } \right)}},} \hfill & {\quad if\;\; \overline{\overline{b}} < y \le \overline{\overline{c}} } \hfill \\ {0,} \hfill & {\quad if\;\; y< {\overline{\overline{a}}\;\; or\;\; y} > \overline{\overline{c}} } \hfill \\ \end{array} } \right.$$

(2)

The (NMF) can be characterized as follows:

$$\beta_{{\check{\mathcal{T}}}} \left( y \right) = \left\{ {\begin{array}{*{20}l} {\frac{{\left( {\overline{\overline{b}} - y} \right) + \beta_{{\check{\mathcal{T}}}} \left( {y - \overline{\overline{a}} } \right)}}{{\left( {\overline{\overline{b}} - \overline{\overline{a}} } \right)}},} \hfill & {\quad if \;\;\overline{\overline{a}} \le y < \overline{\overline{b}} } \hfill \\ {\beta_{{\check{\mathcal{T}}}} ,} \hfill & {\quad if \;\;y = \overline{\overline{b}} } \hfill \\ {\frac{{\left( {y - \overline{\overline{b}} } \right) + \beta_{{\check{\mathcal{T}}}} \left( {\overline{\overline{c}} - y} \right)}}{{\left( {\overline{\overline{c}} - \overline{\overline{b}} } \right)}},} \hfill & {\quad if\;\; \overline{\overline{b}} < y \le \overline{\overline{c}} } \hfill \\ {1,} \hfill & {\quad if \;\;y< {\overline{\overline{a}} or y} > \overline{\overline{c}} } \hfill \\ \end{array} } \right.$$

(3)

where in triplet $\left( {\overline{\overline{a}} ,\overline{\overline{b}} ,\overline{\overline{c}} } \right)$, $\overline{\overline{a}}$, $\overline{\overline{b}}$, $\overline{\overline{c}}$ are real numbers such that $\overline{\overline{a}} < \overline{\overline{b}} < \overline{\overline{c}}$, $\alpha_{{\check{\mathcal{T}}}}$, $\beta_{{\check{\mathcal{T}}}}$ : $Y$ → [0, 1] represent the MF and NMF, respectively, for the element $y$ in ${\check{\mathcal{T}}}$, where it holds that $0 \le \alpha_{{\check{\mathcal{T}}}}^{3} + \beta_{{\check{\mathcal{T}}}}^{3} \le 1$ and $\overline{\pi }_{{\mathop {\mathcal{S}}\limits }} = \sqrt[3]{{1 - \alpha_{{\check{\mathcal{T}}}}^{3} - \beta_{{\check{\mathcal{T}}}}^{3} }}$ is the degree of hesitation. The MF and NMF are shown in Fig. 2.

Fig. 2

Graphical representation of TFFNs.

Example 1

Let ${\check{\mathcal{T}}} = \left( {\left( {1,3,5} \right);\alpha_{{\check{\mathcal{T}}}} ,\beta_{{\check{\mathcal{T}}}} } \right)$ be a TFFN. We can obtain the MF and NMF are follows as:

$$\alpha_{{\check{\mathcal{T}}}} \left( y \right) = \left\{ {\begin{array}{*{20}l} {\frac{{\left( {y - 1} \right)\alpha_{{\check{\mathcal{T}}}} }}{{\left( {3 - 1} \right)}},} \hfill & {\quad if \;\;1 \le y < 3} \hfill \\ {\alpha_{{\check{\mathcal{T}}}} ,} \hfill & {\quad if \;\;y = 3} \hfill \\ {\frac{{\left( {5 - y} \right)\alpha_{{\check{\mathcal{T}}}} }}{{\left( {5 - 3} \right)}},} \hfill & {\quad if \;\;3 < y \le 5} \hfill \\ {0, } \hfill & {\quad if \;\;y < 1\;or\;y > 5} \hfill \\ \end{array} } \right.$$

$$\beta_{{\check{\mathcal{T}}}} \left( y \right) = \left\{ {\begin{array}{*{20}l} {\frac{{\left( {3 - y} \right) + \beta_{{\check{\mathcal{T}}}} \left( {y - 1} \right)}}{{\left( {\overline{\overline{b}} - \overline{\overline{a}} } \right)}},} \hfill & {\quad if\;\; 1 \le y < 3} \hfill \\ {\beta_{{\check{\mathcal{T}}}} ,} \hfill & {\quad if\;\; y = 3} \hfill \\ {\frac{{\left( {y - 3} \right) + \beta_{{\check{\mathcal{T}}}} \left( {5 - y} \right)}}{{\left( {5 - 3} \right)}},} \hfill & {\quad if \;\;3 < y \le 5} \hfill \\ {1, } \hfill & {\quad if \;\;y < 1\;or\;y > 5} \hfill \\ \end{array} } \right.$$

The MF and NMF of TFFNs in example 3 are shown in Fig. 3.

Fig. 3

Geometrical representation of MF and NMF of TFFNs.

Definition 5

Consider the TFFN denoted as ${\check{\mathcal{T}}} = \left( {\left( {\overline{\overline{a}} ,\overline{\overline{b}} ,\overline{\overline{c}} } \right);\alpha_{{\check{\mathcal{T}}}} ,\beta_{{\check{\mathcal{T}}}} } \right)$. The definition of its score function is presented as follows:

$$S\left( {\check{\mathcal{T}}} \right) = \frac{{\overline{\overline{a}} + 2\overline{\overline{b}} + \overline{\overline{c}} }}{4}\left( {\alpha_{{\check{\mathcal{T}}}}^{3} - \beta_{{\check{\mathcal{T}}}}^{3} } \right)$$

(4)

The accuracy function can be defined as follows:

$$A\left( {\check{\mathcal{T}}} \right) = \frac{{\overline{\overline{a}} + 2\overline{\overline{b}} + \overline{\overline{c}} }}{4}\left( {\alpha_{{\check{\mathcal{T}}}}^{3} + \beta_{{\check{\mathcal{T}}}}^{3} } \right)$$

(5)

Definition 6

Let ${\check{\mathcal{T}}}_{1} = \left( {\left( {\overline{\overline{a}}_{1} ,\overline{\overline{b}}_{1} ,\overline{\overline{c}}_{1} } \right);\alpha_{{{\check{\mathcal{T}}}_{1} }} ,\beta_{{{\check{\mathcal{T}}}_{1} }} } \right)$ and ${\check{\mathcal{T}}}_{2} = \left( {\left( {\overline{\overline{a}}_{2} ,\overline{\overline{b}}_{2} ,\overline{\overline{c}}_{2} } \right);\alpha_{{{\check{\mathcal{T}}}_{2} }} ,\beta_{{{\check{\mathcal{T}}}_{2} }} } \right)$ be two TFFNs, then

• 1. If $S\left( {{\check{\mathcal{T}}}_{1} } \right) < S\left( {{\check{\mathcal{T}}}_{2} } \right) \Rightarrow {\check{\mathcal{T}}}_{1} < {\check{\mathcal{T}}}_{2};$

• 2. If $S\left( {{\check{\mathcal{T}}}_{1} } \right) > S\left( {{\check{\mathcal{T}}}_{2} } \right) \Rightarrow {\check{\mathcal{T}}}_{1} > {\check{\mathcal{T}}}_{2};$

• 3. If $S\left( {{\check{\mathcal{T}}}_{1} } \right) = S\left( {{\check{\mathcal{T}}}_{2} } \right),$ then

  • I. $A\left( {{\check{\mathcal{T}}}_{1} } \right) < A\left( {{\check{\mathcal{T}}}_{2} } \right) \Rightarrow {\check{\mathcal{T}}}_{1} < {\check{\mathcal{T}}}_{2}$;

  • II. $A\left( {{\check{\mathcal{T}}}_{1} } \right) > A\left( {{\check{\mathcal{T}}}_{2} } \right) \Rightarrow {\check{\mathcal{T}}}_{1} > {\check{\mathcal{T}}}_{2}$;

  • III. $A\left( {{\check{\mathcal{T}}}_{1} } \right) = A\left( {{\check{\mathcal{T}}}_{2} } \right) \Rightarrow {\check{\mathcal{T}}}_{1} \sim {\check{\mathcal{T}}}_{2}$.

Example 2

Let ${\check{\mathcal{T}}}_{1} = \left( {\left( {1,3,5} \right);0.8,0.4} \right)$ and ${\check{\mathcal{T}}}_{2} = \left( {\left( {2,3,4} \right);0.9,0.5} \right)$ be two TFFNs, we have $S\left( {{\check{\mathcal{T}}}_{1} } \right) = 1.34$, $S\left( {{\check{\mathcal{T}}}_{2} } \right) = 1.81$, then $S\left( {{\check{\mathcal{T}}}_{1} } \right) < S\left( {{\check{\mathcal{T}}}_{2} } \right) \Rightarrow {\check{\mathcal{T}}}_{1} < {\check{\mathcal{T}}}_{2}$ is obtained.

Example 3

Let ${\check{\mathcal{T}}}_{1} = \left( {\left( {2,3,5} \right);0.7,0.7} \right)$ and ${\check{\mathcal{T}}}_{2} = \left( {\left( {2,3,5} \right);0.6,0.6} \right)$ be two TFFNs, we have $S\left( {{\check{\mathcal{T}}}_{1} } \right) = 0$, $S\left( {{\check{\mathcal{T}}}_{2} } \right) = 0$, from definition 6 we apply accuracy function $A\left( {{\check{\mathcal{T}}}_{1} } \right) = 2.23$, $A\left( {{\check{\mathcal{T}}}_{2} } \right) = 1.40$, then $A\left( {{\check{\mathcal{T}}}_{1} } \right) > A\left( {{\check{\mathcal{T}}}_{2} } \right) \Rightarrow {\check{\mathcal{T}}}_{1} > {\check{\mathcal{T}}}_{2}$ is obtained.

Triangular Fermatean fuzzy number under Sugeno–Weber operations

This section discusses various operational laws and aggregation operator, including the Triangular Fermatean fuzzy Sugeno–Weber weighted average (TFFSWWA) operator. We will then examine specific desirable properties in detail, such as idempotency, monotonicity, and boundedness.

Definition 7

⁷⁸ Equations (6) and (7) define the SW TN and TCN for real numbers ξ and Ω.

$${\hat{\mathcal{T}}}_{SW} \left( {{\upxi } , {\Omega }} \right) = \left\{ {\begin{array}{*{20}l} {{\hat{\mathcal{T}}}_{D} \left( {{\upxi } , {\Omega }} \right), if \delta = - 1 } \\ {max\left( {0,\frac{{{\upxi } + {\Omega } - 1 + \delta }}{1 + \delta }} \right), if - 1 < \delta < + \infty } \\ {{\hat{\mathcal{T}}}_{P} \left( {{\upxi } , {\Omega }} \right), if\;\; \delta = + \infty . } \\ \end{array} } \right.$$

(6)

$${\hat{\mathcal{S}}}_{SW} \left( {{\upxi } , {\Omega }} \right) = \left\{ {\begin{array}{*{20}l} {{\hat{\mathcal{S}}}_{D} \left( {{\upxi } , {\Omega }} \right), if\;\; \delta = - 1 } \\ {min\left( {1,{\upxi } + {\Omega } - \frac{{\delta {{\xi \Omega }}}}{1 + \delta }} \right), if\;\; - 1 < \delta < + \infty } \\ {{\hat{\mathcal{S}}}_{P} \left( {{\upxi } , {\Omega }} \right), if\;\; \delta = + \infty . } \\ \end{array} } \right.$$

(7)

Operational laws for Triangular Fermatean fuzzy number based on Sugeno–Weber operator

Definition 8

If ${\check{\mathcal{T}}}_{1} = \left( {\left( {\overline{\overline{a}}_{1} ,\overline{\overline{b}}_{1} ,\overline{\overline{c}}_{1} } \right);\alpha_{{{\check{\mathcal{T}}}_{1} }} ,\beta_{{{\check{\mathcal{T}}}_{1} }} } \right)$ and ${\check{\mathcal{T}}}_{2} = \left( {\left( {\overline{\overline{a}}_{2} ,\overline{\overline{b}}_{2} ,\overline{\overline{c}}_{2} } \right);\alpha_{{{\check{\mathcal{T}}}_{2} }} ,\beta_{{{\check{\mathcal{T}}}_{2} }} } \right)$ are any two TFFNs, where $\rho \in \left[ {0, 1} \right]$ and $- 1 < \delta < + \infty$, be a real number. The following definition of operations will be employed:

• 1. ${\check{\mathcal{T}}}_{1} \oplus_{S} {\check{\mathcal{T}}}_{2} = \left( {\begin{array}{*{20}c} {\left( {\overline{\overline{a}}_{1} + \overline{\overline{a}}_{2} , \overline{\overline{b}}_{1} + \overline{\overline{b}}_{2} , \overline{\overline{c}}_{1} + \overline{\overline{c}}_{2} } \right);} \\ {\left( {\sqrt[3]{{\alpha_{{{\check{\mathcal{T}}}_{1} }}^{3} + \alpha_{{{\check{\mathcal{T}}}_{2} }}^{3} - \frac{{\delta \alpha_{{{\check{\mathcal{T}}}_{1} }}^{3} \alpha_{{{\check{\mathcal{T}}}_{2} }}^{3} }}{1 + \delta }}}, \sqrt[3]{{\frac{{\beta_{{{\check{\mathcal{T}}}_{1} }}^{3} + \beta_{{{\check{\mathcal{T}}}_{2} }}^{3} - 1 + \delta \beta_{{{\check{\mathcal{T}}}_{1} }}^{3} \beta_{{{\check{\mathcal{T}}}_{2} }}^{3} }}{1 + \delta }}}} \right)} \\ \end{array} } \right)$,

• 2. ${\check{\mathcal{T}}}_{1} \otimes_{S} {\check{\mathcal{T}}}_{2} = \left( {\begin{array}{*{20}c} {\left( {\overline{\overline{a}}_{1} .\overline{\overline{a}}_{2} , \overline{\overline{b}}_{1} .\overline{\overline{b}}_{2} , \overline{\overline{c}}_{1} .\overline{\overline{c}}_{2} } \right);} \\ {\left( {\sqrt[3]{{\frac{{\alpha_{{{\check{\mathcal{T}}}_{1} }}^{3} + \alpha_{{{\check{\mathcal{T}}}_{2} }}^{3} - 1 + \delta \alpha_{{{\check{\mathcal{T}}}_{1} }}^{3} \alpha_{{{\check{\mathcal{T}}}_{2} }}^{3} }}{1 + \delta }}}, \sqrt[3]{{\beta_{{{\check{\mathcal{T}}}_{1} }}^{3} + \beta_{{{\check{\mathcal{T}}}_{2} }}^{3} - \frac{{\delta \beta_{{{\check{\mathcal{T}}}_{1} }}^{3} \beta_{{{\check{\mathcal{T}}}_{2} }}^{3} }}{1 + \delta }}}} \right)} \\ \end{array} } \right)$,

• 3. $\rho \odot_{S} {\check{\mathcal{T}}}_{1} = \left( {\begin{array}{*{20}c} {\left( {\rho .\overline{\overline{a}}_{1} , \rho .\overline{\overline{b}}_{1} , \rho .\overline{\overline{c}}_{1} } \right);} \\ {\left( {\sqrt[3]{{\frac{1 + \delta }{\delta }\left( {1 - \left( {1 - \frac{{\delta \alpha_{{{\check{\mathcal{T}}}_{1} }}^{3} }}{1 + \delta }} \right)^{\rho } } \right)}}, \sqrt[3]{{\frac{1}{\delta }\left( {\left( {1 + \delta } \right)\left( {\frac{{\delta \beta_{{{\check{\mathcal{T}}}_{1} }}^{3} + 1}}{1 + \delta }} \right)^{\rho } - 1} \right)}}} \right)} \\ \end{array} } \right)$,

• 4. $\left( {{\check{\mathcal{T}}}_{1} } \right)^{\rho } = \left( {\begin{array}{*{20}c} {\left( {\overline{\overline{a}}_{1}^{\rho } , \overline{\overline{b}}_{1}^{\rho } , \overline{\overline{c}}_{1}^{\rho } } \right);} \\ {\left( {\sqrt[3]{{\frac{1}{\delta }\left( {\left( {1 + \delta } \right)\left( {\frac{{\delta \alpha_{{{\check{\mathcal{T}}}_{1} }}^{3} + 1}}{1 + \delta }} \right)^{\rho } - 1} \right)}}, \sqrt[3]{{\frac{1 + \delta }{\delta }\left( {1 - \left( {1 - \frac{{\delta \beta_{{{\check{\mathcal{T}}}_{1} }}^{3} }}{1 + \delta }} \right)^{\rho } } \right)}}} \right)} \\ \end{array} } \right)$;

Example 4

If ${\check{\mathcal{T}}}_{1} = \left( {\left( {2,3,4} \right);0.7,0.7} \right)$ and ${\check{\mathcal{T}}}_{2} = \left( {\left( {1,2,3} \right);0.8,0.7} \right)$ are any two TFFNs, then using SW operations on TFFNs as describe in definition 8, for $\rho = 0.6$ and $\delta = 3$, we get

• 1. ${\check{\mathcal{T}}}_{1} \otimes_{S} {\check{\mathcal{T}}}_{2} = \left( {\left( {3,5,7} \right);0.90,0.21} \right)$;

• 2. ${\check{\mathcal{T}}}_{1} \otimes_{S} {\check{\mathcal{T}}}_{2} = \left( {\left( {2,6,12} \right);0.46,0.84} \right)$;

• 3. $0.6{ } \odot_{S} {\check{\mathcal{T}}}_{1} = \left( {\left( {1.2,1.8,2.4} \right);0.60,0.90} \right)$;

• 4. $\left( {{\check{\mathcal{T}}}_{1} } \right)^{0.6} = \left( {\left( {1.52,1.93,2.30} \right);0.90,0.60} \right)$.

Triangular Fermatean fuzzy Sugeno–Weber weighted average (TFFSWWA) operator

Definition 9

Let ${\check{\mathcal{T}}}_{p} = \left( {\left( {\overline{\overline{a}}_{p} ,\overline{\overline{b}}_{p} ,\overline{\overline{c}}_{p} } \right);\alpha_{{{\check{\mathcal{T}}}_{p} }} ,\beta_{{{\check{\mathcal{T}}}_{p} }} } \right)\left( {p = 1,2, \ldots ,\overline{n}} \right)$ be set of TFFNs. Then, the Triangular Fermatean fuzzy Sugeno–Weber weighted average (TFFSWWA) operator is a function $TFFSWWA:{\check{\mathcal{T}}}^{{\overline{n}}} \to {\check{\mathcal{T}}} ,$ such that:

$${\text{TFFSWWA}}\left( {{\check{\mathcal{T}}}_{1} , {\check{\mathcal{T}}}_{2} , \ldots ,{\check{\mathcal{T}}}_{{\overline{n}}} } \right) = \oplus_{p = 1}^{{\overline{n}}} \left( {{\mathcal{W}}_{p} {\check{\mathcal{T}}}_{p} } \right)$$

(8)

where ${\mathcal{W}} = \left( {{\mathcal{W}}_{1} ,{\mathcal{W}}_{2} , \ldots ,{\mathcal{W}}_{{\overline{n}}} } \right)^{T}$, ${\mathcal{W}}_{p} > 0$, and $\mathop \sum \limits_{p = 1}^{{\overline{n}}} {\mathcal{W}}_{p} = 1.$

Theorem 1

If ${\check{\mathcal{T}}}_{p} = \left( {\left( {\overline{\overline{a}}_{p} ,\overline{\overline{b}}_{p} ,\overline{\overline{c}}_{p} } \right);\alpha_{{{\check{\mathcal{T}}}_{p} }} ,\beta_{{{\check{\mathcal{T}}}_{p} }} } \right)\left( {p = 1,2, \ldots ,\overline{n}} \right)$, representing a collection of TFFNs. The aggregated value of these TFFNs, when combined using the TFFSWWA operation, is also a TFFN.

$${\text{TFFSWWA}}\left( {{\check{\mathcal{T}}}_{1} , {\check{\mathcal{T}}}_{2} , \ldots ,{\check{\mathcal{T}}}_{{\overline{n}}} } \right) = \oplus_{p = 1}^{{\overline{n}}} \left( {{\mathcal{W}}_{p} {\check{\mathcal{T}}}_{p} } \right)$$

$$= \left( {\begin{array}{*{20}c} {\left( {\mathop \prod \limits_{p = 1}^{{\overline{n}}} \left( {\overline{\overline{a}}_{p} } \right)^{{{\mathcal{W}}_{p} }} , \mathop \prod \limits_{p = 1}^{{\overline{n}}} \left( {\overline{\overline{b}}_{p} } \right)^{{{\mathcal{W}}_{p} }} , \mathop \prod \limits_{p = 1}^{{\overline{n}}} \left( {\overline{\overline{c}}_{p} } \right)^{{{\mathcal{W}}_{p} }} } \right);} \\ {\left( {\sqrt[3]{{\frac{1 + \delta }{\delta }\left( {1 - \mathop \prod \limits_{p = 1}^{{\overline{n}}} \left( {1 - \frac{{\delta \alpha_{{{\check{\mathcal{T}}}_{p} }}^{3} }}{1 + \delta }} \right)^{{{\mathcal{W}}_{p} }} } \right)}}, \sqrt[3]{{\frac{1}{\delta }\left( {\left( {1 + \delta } \right)\mathop \prod \limits_{p = 1}^{{\overline{n}}} \left( {\frac{{\delta \beta_{{{\check{\mathcal{T}}}_{p} }}^{3} + 1}}{1 + \delta }} \right)^{{{\mathcal{W}}_{p} }} - 1} \right)}}} \right)} \\ \end{array} } \right)$$

(9)

${\mathcal{W}} = \left( {{\mathcal{W}}_{1} ,{\mathcal{W}}_{2} , \ldots ,{\mathcal{W}}_{{\overline{n}}} } \right)^{T}$ is the weight vector of ${\check{\mathcal{T}}}_{p} = \left( {p = 1,2, \ldots ,\overline{n}} \right)$ such that ${\mathcal{W}}_{p} > 0$ and $\mathop \sum \nolimits_{p = 1}^{{\overline{n}}} {\mathcal{W}}_{p} = 1$.

Proof

Apply mathematical induction to prove it.

For $\overline{n} = 2$

$${\text{TFFSWWA}}\left( {{\check{\mathcal{T}}}_{1} , {\check{\mathcal{T}}}_{2} } \right) = {\mathcal{W}}_{1} {\check{\mathcal{T}}}_{1} \oplus {\mathcal{W}}_{1} {\check{\mathcal{T}}}_{1}$$

$$= \left( {\begin{array}{*{20}c} {\left( {\left( {\overline{\overline{a}}_{1} } \right)^{{{\mathcal{W}}_{1} }} \left( {\overline{\overline{a}}_{2} } \right)^{{{\mathcal{W}}_{2} }} , \left( {\overline{\overline{b}}_{1} } \right)^{{{\mathcal{W}}_{1} }} \left( {\overline{\overline{b}}_{2} } \right)^{{{\mathcal{W}}_{2} }} , \left( {\overline{\overline{c}}_{1} } \right)^{{{\mathcal{W}}_{1} }} \left( {\overline{\overline{c}}_{2} } \right)^{{{\mathcal{W}}_{2} }} } \right);} \\ {\left( {\begin{array}{*{20}c} {\sqrt[3]{{\frac{1 + \delta }{\delta }\left( {1 - \left( {1 - \frac{{\delta \alpha_{{{\check{\mathcal{T}}}_{1} }}^{3} }}{1 + \delta }} \right)^{{{\mathcal{W}}_{1} }} \left( {1 - \frac{{\delta \alpha_{{{\check{\mathcal{T}}}_{2} }}^{3} }}{1 + \delta }} \right)^{{{\mathcal{W}}_{2} }} } \right)}},} \\ { \sqrt[3]{{\frac{1}{\delta }\left( {\left( {1 + \delta } \right)\left( {\frac{{\delta \beta_{{{\check{\mathcal{T}}}_{1} }}^{3} + 1}}{1 + \delta }} \right)^{{{\mathcal{W}}_{1} }} \left( {\frac{{\delta \beta_{{{\check{\mathcal{T}}}_{2} }}^{3} + 1}}{1 + \delta }} \right)^{{{\mathcal{W}}_{2} }} - 1} \right)}}} \\ \end{array} } \right)} \\ \end{array} } \right)$$

$$= \left( {\begin{array}{*{20}c} {\left( {\mathop \prod \limits_{p = 1}^{2} \left( {\overline{\overline{a}}_{p} } \right)^{{{\mathcal{W}}_{p} }} , \mathop \prod \limits_{p = 1}^{2} \left( {\overline{\overline{b}}_{p} } \right)^{{{\mathcal{W}}_{p} }} , \mathop \prod \limits_{p = 1}^{2} \left( {\overline{\overline{c}}_{p} } \right)^{{{\mathcal{W}}_{p} }} } \right);} \\ {\left( {\sqrt[3]{{\frac{1 + \delta }{\delta }\left( {1 - \mathop \prod \limits_{p = 1}^{2} \left( {1 - \frac{{\delta \alpha_{{{\check{\mathcal{T}}}_{p} }}^{3} }}{1 + \delta }} \right)^{{{\mathcal{W}}_{p} }} } \right)}}, \sqrt[3]{{\frac{1}{\delta }\left( {\left( {1 + \delta } \right)\mathop \prod \limits_{p = 1}^{2} \left( {\frac{{\delta \beta_{{{\check{\mathcal{T}}}_{p} }}^{3} + 1}}{1 + \delta }} \right)^{{{\mathcal{W}}_{p} }} - 1} \right)}}} \right)} \\ \end{array} } \right)$$

So, Eq. (9) holds true when $\overline{n} = 2$.

Equation (9) is assumed to apply for $\overline{n} = k$.

$${\text{TFFSWWA}}\left( {{\check{\mathcal{T}}}_{1} , {\check{\mathcal{T}}}_{2} , \ldots ,{\check{\mathcal{T}}}_{k} } \right) = \oplus_{p = 1}^{k} \left( {{\mathcal{W}}_{k} {\check{\mathcal{T}}}_{k} } \right)$$

$$= \left( {\begin{array}{*{20}c} {\left( {\mathop \prod \limits_{p = 1}^{k} \left( {\overline{\overline{a}}_{p} } \right)^{{{\mathcal{W}}_{p} }} , \mathop \prod \limits_{p = 1}^{k} \left( {\overline{\overline{b}}_{p} } \right)^{{{\mathcal{W}}_{p} }} , \mathop \prod \limits_{p = 1}^{k} \left( {\overline{\overline{c}}_{p} } \right)^{{{\mathcal{W}}_{p} }} } \right);} \\ {\left( {\sqrt[3]{{\frac{1 + \delta }{\delta }\left( {1 - \mathop \prod \limits_{p = 1}^{k} \left( {1 - \frac{{\delta \alpha_{{{\check{\mathcal{T}}}_{p} }}^{3} }}{1 + \delta }} \right)^{{{\mathcal{W}}_{p} }} } \right)}}, \sqrt[3]{{\frac{1}{\delta }\left( {\left( {1 + \delta } \right)\mathop \prod \limits_{p = 1}^{k} \left( {\frac{{\delta \beta_{{{\check{\mathcal{T}}}_{p} }}^{3} + 1}}{1 + \delta }} \right)^{{{\mathcal{W}}_{p} }} - 1} \right)}}} \right)} \\ \end{array} } \right)$$

Now, for $\overline{n} = k + 1$

$${\text{TFFSWWA}}\left( {{\check{\mathcal{T}}}_{1} , {\check{\mathcal{T}}}_{2} , \ldots ,{\check{\mathcal{T}}}_{k} ,{\check{\mathcal{T}}}_{k + 1} } \right) = \oplus_{p = 1}^{k} \left( {{\mathcal{W}}_{k} {\check{\mathcal{T}}}_{k} } \right) \oplus \left( {{\mathcal{W}}_{k + 1} {\check{\mathcal{T}}}_{k + 1} } \right)$$

$$= \left( {\begin{array}{*{20}c} {\left( {\mathop \prod \limits_{p = 1}^{k} \left( {\overline{\overline{a}}_{p} } \right)^{{{\mathcal{W}}_{p} }} , \mathop \prod \limits_{p = 1}^{k} \left( {\overline{\overline{b}}_{p} } \right)^{{{\mathcal{W}}_{p} }} , \mathop \prod \limits_{p = 1}^{k} \left( {\overline{\overline{c}}_{p} } \right)^{{{\mathcal{W}}_{p} }} } \right);} \\ {\left( {\sqrt[3]{{\frac{1 + \delta }{\delta }\left( {1 - \mathop \prod \limits_{p = 1}^{k} \left( {1 - \frac{{\delta \alpha_{{{\check{\mathcal{T}}}_{p} }}^{3} }}{1 + \delta }} \right)^{{{\mathcal{W}}_{p} }} } \right)}}, \sqrt[3]{{\frac{1}{\lambda }\left( {\left( {1 + \delta } \right)\mathop \prod \limits_{p = 1}^{k} \left( {\frac{{\delta \beta_{{{\check{\mathcal{T}}}_{p} }}^{3} + 1}}{1 + \delta }} \right)^{{{\mathcal{W}}_{p} }} - 1} \right)}}} \right)} \\ \end{array} } \right)$$

$$\oplus \left( {\begin{array}{*{20}c} {\left( {\left( {\overline{\overline{a}}_{k + 1} } \right)^{{{\mathcal{W}}_{k + 1} }} , \left( {\overline{\overline{b}}_{k + 1} } \right)^{{{\mathcal{W}}_{k + 1} }} , \left( {\overline{\overline{c}}_{k + 1} } \right)^{{{\mathcal{W}}_{k + 1} }} } \right);} \\ {\left( {\sqrt[3]{{\frac{1 + \delta }{\delta }\left( {1 - \left( {1 - \frac{{\delta \alpha_{{{\check{\mathcal{T}}}_{k + 1} }}^{3} }}{1 + \delta }} \right)^{{{\mathcal{W}}_{k + 1} }} } \right)}}, \sqrt[3]{{\frac{1}{\delta }\left( {\left( {1 + \delta } \right)\left( {\frac{{\delta \beta_{{{\check{\mathcal{T}}}_{k + 1} }}^{3} + 1}}{1 + \delta }} \right)^{{{\mathcal{W}}_{k + 1} }} - 1} \right)}}} \right)} \\ \end{array} } \right)$$

$$= \left( {\begin{array}{*{20}c} {\left( {\mathop \prod \limits_{p = 1}^{k + 1} \left( {\overline{\overline{a}}_{p} } \right)^{{{\mathcal{W}}_{p} }} , \mathop \prod \limits_{p = 1}^{k + 1} \left( {\overline{\overline{b}}_{p} } \right)^{{{\mathcal{W}}_{p} }} , \mathop \prod \limits_{p = 1}^{k + 1} \left( {\overline{\overline{c}}_{p} } \right)^{{{\mathcal{W}}_{p} }} } \right);} \\ {\left( {\sqrt[3]{{\frac{1 + \delta }{\delta }\left( {1 - \mathop \prod \limits_{p = 1}^{k + 1} \left( {1 - \frac{{\delta \alpha_{{{\check{\mathcal{T}}}_{p} }}^{3} }}{1 + \delta }} \right)^{{{\mathcal{W}}_{p} }} } \right)}}, \sqrt[3]{{\frac{1}{\delta }\left( {\left( {1 + \delta } \right)\mathop \prod \limits_{p = 1}^{k + 1} \left( {\frac{{\delta \beta_{{{\check{\mathcal{T}}}_{p} }}^{3} + 1}}{1 + \delta }} \right)^{{{\mathcal{W}}_{p} }} - 1} \right)}}} \right)} \\ \end{array} } \right)$$

Equation (9) holds true for $\overline{n} = k + 1$.

We will now define the properties of the TFFSWA operator.□

Property 1

“Idempotency” If all TFFNs are identical, i.e., ${\check{\mathcal{T}}}_{p} = \left( {\left( {\overline{\overline{a}}_{p} ,\overline{\overline{b}}_{p} ,\overline{\overline{c}}_{p} } \right);\alpha_{{{\check{\mathcal{T}}}_{p} }} ,\beta_{{{\check{\mathcal{T}}}_{p} }} } \right)$ $\left( {p = 1,2, \ldots ,\overline{n}} \right)$ $= \left( {\left( {\overline{\overline{a}} ,\overline{\overline{b}} ,\overline{\overline{c}} } \right);\alpha_{{\check{\mathcal{T}}}} ,\beta_{{\check{\mathcal{T}}}} } \right)$ for all $p$, ${\check{\mathcal{T}}}_{p} = {\check{\mathcal{T}}}$ then; ${\mathcal{W}} = \left( {{\mathcal{W}}_{1} ,{\mathcal{W}}_{2} , \ldots ,{\mathcal{W}}_{{\overline{n}}} } \right)^{T}$ is the weight vector of ${\check{\mathcal{T}}}_{p} = \left( {p = 1,2, \ldots ,\overline{n}} \right)$ such that ${\mathcal{W}}_{p} > 0$ and $\sum\nolimits_{p = 1}^{{\overline{n}}} {{\mathcal{W}}_{p} = 1}$.

Proof

Equation (9) assumes that ${\check{\mathcal{T}}}_{p} = {\check{\mathcal{T}}}$ for every $p$.

$${\text{TFFSWWA}}\left( {{\check{\mathcal{T}}}_{1} , {\check{\mathcal{T}}}_{2} , \ldots ,{\check{\mathcal{T}}}_{{\overline{n}}} } \right) = \oplus_{p = 1}^{{\overline{n}}} \left( {{\mathcal{W}}_{p} {\check{\mathcal{T}}}_{p} } \right)$$

$$= \left( {\begin{array}{*{20}c} {\left( {\mathop \prod \limits_{p = 1}^{{\overline{n}}} \left( {\overline{\overline{a}}_{p} } \right)^{{{\mathcal{W}}_{p} }} , \mathop \prod \limits_{p = 1}^{{\overline{n}}} \left( {\overline{\overline{b}}_{p} } \right)^{{{\mathcal{W}}_{p} }} , \mathop \prod \limits_{p = 1}^{{\overline{n}}} \left( {\overline{\overline{c}}_{p} } \right)^{{{\mathcal{W}}_{p} }} } \right);} \\ {\left( {\sqrt[3]{{\frac{1 + \delta }{\delta }\left( {1 - \mathop \prod \limits_{p = 1}^{{\overline{n}}} \left( {1 - \frac{{\delta \alpha_{{{\check{\mathcal{T}}}_{p} }}^{3} }}{1 + \delta }} \right)^{{{\mathcal{W}}_{p} }} } \right)}}, \sqrt[3]{{\frac{1}{\delta }\left( {\left( {1 + \delta } \right)\mathop \prod \limits_{p = 1}^{{\overline{n}}} \left( {\frac{{\delta \beta_{{{\check{\mathcal{T}}}_{p} }}^{3} + 1}}{1 + \delta }} \right)^{{{\mathcal{W}}_{p} }} - 1} \right)}}} \right)} \\ \end{array} } \right)$$

Since $\sum\nolimits_{p = 1}^{{\overline{n}}} {{\mathcal{W}}_{p} = 1}$ and for all $p = 1$ to $\overline{n}$, $\overline{\overline{a}}_{p} = \overline{\overline{a}}$, $\overline{\overline{b}}_{p} = \overline{\overline{b}}$, $\overline{\overline{c}}_{p} = \overline{\overline{c}}$, $\alpha_{{{\check{\mathcal{T}}}_{p} }}^{3} = \alpha_{{\check{\mathcal{T}}}}^{3}$ and $\beta_{{\check{\mathcal{T}}}}^{3}$, then we have

$$= \left( {\begin{array}{*{20}c} {\left( {\overline{\overline{a}} , \overline{\overline{b}} , \overline{\overline{c}} } \right);} \\ {\left( {\sqrt[3]{{\frac{1 + \delta }{\delta }\left( {1 - \left( {1 - \frac{{\delta \alpha_{{\check{\mathcal{T}}}}^{3} }}{1 + \delta }} \right)} \right)}}, \sqrt[3]{{\frac{1}{\delta }\left( {\left( {1 + \delta } \right)\left( {\frac{{\delta \beta_{{\check{\mathcal{T}}}}^{3} + 1}}{1 + \delta }} \right) - 1} \right)}}} \right)} \\ \end{array} } \right)$$

$$= \left( {\left( {\overline{\overline{a}} ,\overline{\overline{a}} ,\overline{\overline{c}} } \right);\alpha_{{\check{\mathcal{T}}}} ,\beta_{{\check{\mathcal{T}}}} } \right)$$

$$= {\check{\mathcal{T}}}$$

□

Property 2

“Boundedness” Assume ${\check{\mathcal{T}}}_{p} = \left( {\left( {\overline{\overline{a}}_{p} ,\overline{\overline{b}}_{p} ,\overline{\overline{c}}_{p} } \right);\alpha_{{{\check{\mathcal{T}}}_{p} }} ,\beta_{{{\check{\mathcal{T}}}_{p} }} } \right)\left( {p = 1,2, \ldots ,\overline{n}} \right)$ be a class of TFFNs. Let ${\check{\mathcal{T}}}^{ - } = \left( {\left( {min\overline{\overline{a}}_{p} ,min\overline{\overline{b}}_{p} ,min\overline{\overline{c}}_{p} } \right);min\alpha_{{{\check{\mathcal{T}}}_{p} }} ,max\beta_{{{\check{\mathcal{T}}}_{p} }} } \right) = \left( {\left( {\overline{\overline{a}}_{p}^{ - } ,\overline{\overline{b}}_{p}^{ - } ,\overline{\overline{c}}_{p}^{ - } } \right);\alpha_{{{\check{\mathcal{T}}}_{p} }}^{ - } ,\beta_{{{\check{\mathcal{T}}}_{p} }}^{ - } } \right)$ and ${\check{\mathcal{T}}}^{ + } = \left( {\left( {max\overline{\overline{a}}_{p} ,max\overline{\overline{b}}_{p} ,max\overline{\overline{c}}_{p} } \right);max\alpha_{{{\check{\mathcal{T}}}_{p} }} ,min\beta_{{{\check{\mathcal{T}}}_{p} }} } \right) = \left( {\left( {\overline{\overline{a}}_{p}^{ + } ,\overline{\overline{b}}_{p}^{ + } ,\overline{\overline{c}}_{p}^{ + } } \right);\alpha_{{{\check{\mathcal{T}}}_{p} }}^{ + } ,\beta_{{{\check{\mathcal{T}}}_{p} }}^{ + } } \right)$, Then.

$${\check{\mathcal{T}}}^{ - } \le {\text{TFFSWWA}}\left( {{\check{\mathcal{T}}}_{1} , {\check{\mathcal{T}}}_{2} , \ldots ,{\check{\mathcal{T}}}_{{\overline{n}}} } \right) \le {\check{\mathcal{T}}}^{ + }$$

(10)

Proof

$$\alpha_{{{\check{\mathcal{T}}}_{p} }}^{ - } \le \alpha_{{{\check{\mathcal{T}}}_{p} }} \le \alpha_{{{\check{\mathcal{T}}}_{p} }}^{ + }$$

$$\Rightarrow 1 - \frac{{\delta \alpha_{{{\check{\mathcal{T}}}_{p} }}^{ - 3} }}{1 + \delta } \le 1 - \frac{{\delta \alpha_{{{\check{\mathcal{T}}}_{p} }}^{3} }}{1 + \delta } \le 1 - \frac{{\delta \alpha_{{{\check{\mathcal{T}}}_{p} }}^{ + 3} }}{1 + \delta }$$

$$\Rightarrow \left( {1 - \frac{{\delta \alpha_{{{\check{\mathcal{T}}}_{p} }}^{ - 3} }}{1 + \delta }} \right)^{{{\mathop \sum \limits_{p = 1}{\overline{n}}} {\mathcal{W}}_{p} }} \le \mathop \prod \limits_{p = 1}^{{\overline{n}}} \left( {1 - \frac{{\delta \alpha_{{{\check{\mathcal{T}}}_{p} }}^{3} }}{1 + \delta }} \right)^{{{\mathcal{W}}_{p} }} \le \left( {1 - \frac{{\delta \alpha_{{{\check{\mathcal{T}}}_{p} }}^{ + 3} }}{1 + \delta }} \right)^{{{\mathop \sum \limits_{p = 1}{\overline{n}}} {\mathcal{W}}_{p} }}$$

$$\Rightarrow 1 - \frac{{\delta \alpha_{{{\check{\mathcal{T}}}_{p} }}^{ - 3} }}{1 + \delta } \le \mathop \prod \limits_{p = 1}^{{\overline{n}}} \left( {1 - \frac{{\delta \alpha_{{{\check{\mathcal{T}}}_{p} }}^{3} }}{1 + \delta }} \right)^{{{\mathcal{W}}_{p} }} \le 1 - \frac{{\delta \alpha_{{{\check{\mathcal{T}}}_{p} }}^{ + 3} }}{1 + \delta }$$

$$\Rightarrow \frac{{\delta \alpha_{{{\check{\mathcal{T}}}_{p} }}^{ - 3} }}{1 + \delta } \le 1 - \mathop \prod \limits_{p = 1}^{{\overline{n}}} \left( {1 - \frac{{\delta \alpha_{{{\check{\mathcal{T}}}_{p} }}^{3} }}{1 + \delta }} \right)^{{{\mathcal{W}}_{p} }} \le \frac{{\delta \alpha_{{{\check{\mathcal{T}}}_{p} }}^{ + 3} }}{1 + \delta }$$

$$\Rightarrow \alpha_{{{\check{\mathcal{T}}}_{p} }}^{ - 3} \le \frac{1 + \delta }{\delta }\left( {1 - \mathop \prod \limits_{p = 1}^{{\overline{n}}} \left( {1 - \frac{{\delta \alpha_{{{\check{\mathcal{T}}}_{p} }}^{3} }}{1 + \delta }} \right)^{{{\mathcal{W}}_{p} }} } \right) \le \alpha_{{{\check{\mathcal{T}}}_{p} }}^{ + 3}$$

$$\Rightarrow \alpha_{{{\check{\mathcal{T}}}_{p} }}^{ - } \le \sqrt[3]{{\frac{1 + \delta }{\delta }\left( {1 - \mathop \prod \limits_{p = 1}^{{\overline{n}}} \left( {1 - \frac{{\delta \alpha_{{{\check{\mathcal{T}}}_{p} }}^{3} }}{1 + \delta }} \right)^{{{\mathcal{W}}_{p} }} } \right)}} \le \alpha_{{{\check{\mathcal{T}}}_{p} }}^{ + }$$

Similarly,

$$\beta_{{{\check{\mathcal{T}}}_{p} }}^{ - } \le \sqrt[3]{{\frac{1}{\delta }\left( {\left( {1 + \delta } \right)\mathop \prod \limits_{p = 1}^{{\overline{n}}} \left( {\frac{{\delta \beta_{{{\check{\mathcal{T}}}_{p} }}^{3} + 1}}{1 + \delta }} \right)^{{{\mathcal{W}}_{p} }} - 1} \right)}} \le \beta_{{{\check{\mathcal{T}}}_{p} }}^{ + }$$

Then, by comparison we get

$${\check{\mathcal{T}}}^{ - } \le {\text{TFFSWWA}}\left( {{\check{\mathcal{T}}}_{1} , {\check{\mathcal{T}}}_{2} , \ldots ,{\check{\mathcal{T}}}_{{\overline{n}}} } \right) \le {\check{\mathcal{T}}}^{ + }$$

□

Property 3

“Monotonicity” Let ${\check{\mathcal{T}}}_{p}^{*} = \left( {\left( {\overline{\overline{a}}_{p}^{*} ,\overline{\overline{b}}_{p}^{*} ,\overline{\overline{c}}_{p}^{*} } \right);\alpha_{{{\check{\mathcal{T}}}_{p} }}^{*} ,\beta_{{{\check{\mathcal{T}}}_{p} }}^{*} } \right)$ and ${\check{\mathcal{T}}}_{p} = \left( {\left( {\overline{\overline{a}}_{p} ,\overline{\overline{b}}_{p} ,\overline{\overline{c}}_{p} } \right);\alpha_{{{\check{\mathcal{T}}}_{p} }} ,\beta_{{{\check{\mathcal{T}}}_{p} }} } \right)$ be two set of TFFNs with $\left( {p = 1,2, \ldots ,\overline{n}} \right)$ such that $\overline{\overline{a}}_{p} \le \overline{\overline{a}}_{p}^{*}$, $\overline{\overline{b}}_{p} \le \overline{\overline{b}}_{p}^{*}$, $\overline{\overline{c}}_{p} \le \overline{\overline{c}}_{p}^{*}$, $\alpha_{{{\check{\mathcal{T}}}_{p} }}^{*} \le \alpha_{{{\check{\mathcal{T}}}_{p} }}$ and $\beta_{{{\check{\mathcal{T}}}_{p} }}^{*} \ge \beta_{{{\check{\mathcal{T}}}_{p} }}$ then,

$${\text{TFFSWWA}}\left( {{\check{\mathcal{T}}}_{1} , {\check{\mathcal{T}}}_{2} , \ldots ,{\check{\mathcal{T}}}_{{\overline{n}}} } \right) \le {\text{TFFSWWA}}\left( {{\check{\mathcal{T}}}_{1}^{*} , {\check{\mathcal{T}}}_{2}^{*} , \ldots ,{\check{\mathcal{T}}}_{{\overline{n}}}^{*} } \right)$$

(11)

Proof is similarly to Property 2.

An EDAS method for MCGDM with TFFNs

In this section, we utilize the proposed EDAS method and TFFSWWA operator to develop a novel MCGDM model in the TFFNs context. The calculating technique for the developed model is described below and illustrated in Fig. 5.

Assume there are $\overline{m}$ alternatives $\left\{ {{\tilde{\chi }}_{1} ,{{ \tilde{\chi }}}_{2} , \ldots ,{{ \tilde{\chi }}}_{{\overline{m}}} } \right\}$, $\overline{n}$ be set of criteria $\left\{ {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\uppsi } }_{1} ,{ }{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\uppsi } }_{2} ,{ } \ldots ,{ }{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\uppsi } }_{{\overline{n}}} } \right\}$ and ${\mathcal{U}}$ experts $\left\{ {{\dot{\upvarepsilon}} _{1} , {\dot{\upvarepsilon}} _{2} , \ldots , {\dot{\upvarepsilon}} _{{\mathcal{U}}} } \right\}$, let ${\mathcal{W}} = \left( {{\mathcal{W}}_{1} ,{\mathcal{W}}_{2} , \ldots ,{\mathcal{W}}_{{\overline{n}}} } \right)^{T}$ and ${\text{e}} = \left( {{\text{e}}_{1} ,{\text{e}}_{2} , \ldots ,{\text{e}}_{f} } \right)^{T}$ be represent the vectors for criteria weights and expert weights that satisfy the following conditions. Let ${\mathcal{W}}_{p} { } \in \left[ {0,1} \right]$, ${\text{e}}_{g}$ ∈ [0,1] and $\mathop \sum \nolimits_{p = 1}^{{\overline{n}}} {\mathcal{W}}_{p} = 1$, $\mathop \sum \nolimits_{g = 1}^{f} {\text{e}}_{g} = 1$. Each decision-maker evaluates the provided alternatives across various attributes and expresses their preference values as TFFNs. Suppose ${\mathbb{D}} = \left( {{\check{\mathcal{T}}}_{pq}^{{\mathcal{U}}} } \right)_{{\overline{m} \times \overline{n}}}$ is the decision matrix, in which ${\check{\mathcal{T}}}_{pq}^{{\mathcal{U}}} = \left( {\left( {\overline{\overline{a}}_{pq}^{{\mathcal{U}}} ,\overline{\overline{b}}_{pq}^{{\mathcal{U}}} ,\overline{\overline{c}}_{pq}^{{\mathcal{U}}} } \right);\alpha_{{{\check{\mathcal{T}}}_{pq} }}^{{\mathcal{U}}} ,\beta_{{{\check{\mathcal{T}}}_{pq} }}^{{\mathcal{U}}} } \right)$ represents a TFFN. This TFFN quantifies the evaluation assigned to the $p th$ alternative concerning the $q th$ criterion, as provided by the decision maker (DM). The decision steps of the proposed the MCGDM model are as follows:

Step 1: Construction of decision matrices ${\mathbb{D}} = \left( {{\check{\mathcal{T}}}_{pq}^{{\mathcal{U}}} } \right)_{{\overline{m} \times \overline{n}}}$, where $p = 1,2, \ldots \overline{m}$, $q = 1,2, \ldots \overline{n}$ and ${\mathcal{U}} = 1,2, \ldots ,g$ using TFFN:

$${\mathbb{D}} = \left( { \begin{array}{*{20}c} {{\check{\mathcal{T}}}_{11}^{{\mathcal{U}}} {\check{\mathcal{T}}}_{12}^{{\mathcal{U}}} \cdots {\check{\mathcal{T}}}_{{1\overline{n}}}^{{\mathcal{U}}} } \\ {{\check{\mathcal{T}}}_{21}^{{\mathcal{U}}} {\check{\mathcal{T}}}_{22}^{{\mathcal{U}}} \cdots {\check{\mathcal{T}}}_{{2\overline{n}}}^{{\mathcal{U}}} } \\ { \vdots \vdots \ddots \vdots } \\ {{\check{\mathcal{T}}}_{{\overline{m}1}}^{{\mathcal{U}}} {\check{\mathcal{T}}}_{{\overline{m}2}}^{{\mathcal{U}}} \ldots {\check{\mathcal{T}}}_{{\overline{{m\overline{n}}} }}^{{\mathcal{U}}} } \\ \end{array} } \right)$$

(12)

Step 2: Using the TFFSWWA operator and the expert’s weighting vector $\left\{ {{\text{e}}_{1} ,{\text{e}}_{2} , \ldots ,{\text{e}}_{f} } \right\}$, we can calculate the overall ${\check{\mathcal{T}}}_{pq}^{{\mathcal{U}}}$ to ${\check{\mathcal{T}}}_{pq}$ according to the decision-making matrix ${\mathbb{D}} = \left( {{\check{\mathcal{T}}}_{pq}^{{\mathcal{U}}} } \right)_{{\overline{m} \times \overline{n}}}$. The computation results are as follows.

Step 3: Determine the average solution (AV) based on all presented attributes:

$$AV = \left( {AV_{q} } \right)_{{1 \times \overline{n}}} = \left( {\frac{{\mathop \sum \nolimits_{p = 1}^{{\overline{m}}} {\check{\mathcal{T}}}_{pq} }}{{\overline{m}}}} \right)_{{1 \times \overline{n}}}$$

(13)

$$AV = \left( {\begin{array}{*{20}c} {\left( {\mathop \prod \limits_{p = 1}^{{\overline{m}}} \left( {\overline{\overline{a}}_{p} } \right)^{{\frac{1}{{\overline{m}}}}} , \mathop \prod \limits_{p = 1}^{{\overline{m}}} \left( {\overline{\overline{b}}_{p} } \right)^{{\frac{1}{{\overline{m}}}}} , \mathop \prod \limits_{p = 1}^{{\overline{m}}} \left( {\overline{\overline{c}}_{p} } \right)^{{\frac{1}{{\overline{m}}}}} } \right);} \\ {\left( {\sqrt[3]{{\frac{1 + \delta }{\delta }\left( {1 - \mathop \prod \limits_{p = 1}^{{\overline{m}}} \left( {1 - \frac{{\delta \alpha_{{{\check{\mathcal{T}}}_{p} }}^{3} }}{1 + \delta }} \right)^{{\frac{1}{{\overline{m}}}}} } \right)}}, \sqrt[3]{{\frac{1}{\lambda }\left( {\left( {1 + \delta } \right)\mathop \prod \limits_{p = 1}^{{\overline{m}}} \left( {\frac{{\delta \beta_{{{\check{\mathcal{T}}}_{p} }}^{3} + 1}}{1 + \delta }} \right)^{{\frac{1}{{\overline{m}}}}} - 1} \right)}}} \right)} \\ \end{array} } \right)$$

(14)

Step 4: Based on the average solution (AV) values, we can calculate the PDA and NDA using the formula shown below.

$${\mathcal{Z}}^{ + } = \left( {{\text{PDA}}} \right)_{{\overline{m} \times \overline{n}}} = \frac{{max\left( {0,\left( {{\check{\mathcal{T}}}_{pq} - AV_{q} } \right)} \right)}}{{AV_{q} }}$$

(15)

$${\mathcal{Z}}^{ - } = \left( {{\text{NDA}}} \right)_{{\overline{m} \times \overline{n}}} = \frac{{max\left( {0,\left( {AV_{q} - {\check{\mathcal{T}}}_{pq} } \right)} \right)}}{{AV_{q} }}$$

(16)

To make things easier, we may use the scoring function of FFSs to compute the ${\mathcal{Z}}^{ + }$ and ${\mathcal{Z}}^{ - }$ outcomes as follows:

$${\mathcal{Z}}_{p}^{ + } = \left( {{\text{PDA}}} \right)_{{\overline{m} \times \overline{n}}} = \frac{{max\left( {0,\left( {S\left( {{\check{\mathcal{T}}}_{pq} } \right) - S\left( {AV_{q} } \right)} \right)} \right)}}{{S\left( {AV_{q} } \right)}}$$

(17)

$${\mathcal{Z}}_{p}^{ - } = \left( {{\text{NDA}}} \right)_{{\overline{m} \times \overline{n}}} = \frac{{max\left( {0,\left( {S\left( {AV_{q} } \right) - S\left( {{\check{\mathcal{T}}}_{pq} } \right)} \right)} \right)}}{{S\left( {AV_{q} } \right)}}$$

(18)

Step 5: Compute the value of $S{\text{PDA}}$ and $S{\text{NDA}}$, which represent the weighted sum of ${\mathcal{Z}}^{ + }$ and ${\mathcal{Z}}^{ - }$, using the following formula:

$${\mathcal{Q}}_{p}^{ + } = \mathop \sum \limits_{q = 1}^{{\overline{n}}} {\mathcal{W}}_{q} {\mathcal{Z}}_{pq}^{ + }$$

(19)

$${\mathcal{Q}}_{p}^{ - } = \mathop \sum \limits_{q = 1}^{{\overline{n}}} {\mathcal{W}}_{q} {\mathcal{Z}}_{pq}^{ - }$$

(20)

Step 6: The solutions of Eqs. (21) and (22) can be normalized as follows:

$${\mathcal{N}}_{p}^{ + } = \frac{{{\mathcal{Q}}_{p}^{ + } }}{{max\left( {{\mathcal{Q}}_{p}^{ + } } \right)}}$$

(21)

$${\mathcal{N}}_{p}^{ - } = 1 - \frac{{{\mathcal{Q}}_{p}^{ - } }}{{max\left( {{\mathcal{Q}}_{p}^{ - } } \right)}}$$

(22)

Step 7: Calculate the appraisal score values based on each alternative’s ${\mathcal{N}}_{p}^{ + } {\text{ and }}{\mathcal{N}}_{p}^{ - } :$

(23)

Step 8: The ranking of all of the alternatives according to the calculation findings; the higher the value of , the better the alternative selected.

Problem statement

Remote Patient Monitoring (RPM) has emerged as a crucial field in healthcare, especially with the increasing demand for continuous health tracking due to demographic changes, such as the growing aging population. The World Health Organization predicts that in the coming years, the number of people aged 65 and older will surpass the number of children under five. This shift has increased the demand for innovative healthcare solutions that can provide real-time patient monitoring outside of traditional clinical settings. Healthcare providers are increasingly relying on connected healthcare devices, such as Bluetooth-enabled Fitbits and wearable heart monitors, to enhance patient care and improve health outcomes. The wearable technology market is expanding rapidly, largely driven by the growing popularity of smartwatches and other health-focused devices. Among these, wearable medical technology plays a significant role by enabling real-time monitoring of physiological parameters such as heart rate, body temperature, and blood pressure. Initially, patient monitoring devices were limited to hospital use, where they were used to track vital signs. However, advancements in wireless technology have enabled the development of wearable sensors that allow remote monitoring, creating new opportunities for improved patient-provider communication and proactive healthcare management. Despite the advantages of wearable sensors, selecting the most suitable one for a specific patient remains a significant challenge. A wide variety of sensors are available, each differing in terms of accuracy, comfort, energy efficiency, and flexibility. The decision-making process is further complicated by patient-specific needs and the dynamic nature of healthcare conditions. Additionally, data collected from these devices often involve uncertainty and vagueness due to variability in patient responses, environmental factors, and technical limitations. Traditional decision-making methods struggle to handle this type of fuzzy information and conflicting criteria, making it difficult to identify the optimal sensor.

The challenge stems from the wide variety of available sensors, each differing in accuracy, comfort, energy efficiency, and flexibility. Moreover, patient-specific requirements and the dynamic nature of healthcare conditions further complicate the decision-making process. Traditional decision-making methods often fail to handle the uncertainty and vagueness associated with fuzzy patient data and conflicting evaluation criteria. To address this, an effective decision-making model that can manage fuzzy information and multiple conflicting criteria is needed. This study proposes a novel decision-making approach using TFFs information and the EDAS approach to handle fuzzy uncertainty and improve the accuracy and reliability of wearable sensor selection. The selection process for alternative there are five Wearable Sensors for RPMS that are;

${\tilde{\chi }}_{1}$: Smart Watch, ${\tilde{\chi }}_{2}$: Smart Ring, ${\tilde{\chi }}_{3}$: Smart Belt, ${\tilde{\chi }}_{4}$: Smart T-shirt and ${\tilde{\chi }}_{5}$:

In accordance with the previously defined criteria for deciding of the best suitable devices within the healthcare sector, the following five criteria are provided for consideration:

${\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\uppsi } }_{1}$: Reliable communication: Reliable communication in RPMS networks is critical in emergency situations, requiring low data rate errors and the use of proper routing methods to ensure quality.

${\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\uppsi } }_{2}$: Device mobility management: Adaptation of the communication network is essential to address variations in link quality. Such modifications are necessary to guarantee efficient distribution of data and to maintain equilibrium throughout the network. This requirement holds true irrespective of the speed of patients or relay nodes involved in the system.

${\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\uppsi } }_{3}$: Latency: Latency refers to the end-to-end delay in a communication network, indicating the time taken for data to travel from the source to the sink and vice versa. In RPMS (Real-time Patient Monitoring Systems), delays are unacceptable due to the critical nature of human lives, requiring immediate feedback. Latency is affected by factors such as load distribution and balancing within the network.

${\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\uppsi } }_{4}$: Scalability: Scalability refers to the ability of a network algorithm to adjust and respond effectively to changes in network size or external events. In the context of RPMS, patients can be monitored during transit, in vehicles, at home, or in shopping centers, whether in urban or rural areas. These varying locations can impact the number of nodes in the network and potentially affect events surrounding those nodes.

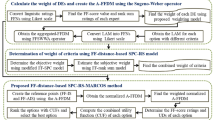
The calculating technique for the developed model is described below and illustrated in Fig. 4, see Boikanyo et al. ⁷⁴.

Fig. 4

Flow chart of the proposed model for Wearable Sensors for RPMS, Boikanyo et al.⁷⁴. (Figure generated using Microsoft Office.).

Results

Algorithm-1: Using EDAS method

Step 1: Construction of decision matrices ${\mathbb{D}} = \left( {{\check{\mathcal{T}}}_{pq}^{{\mathcal{U}}} } \right)_{5 \times 4}$, where $p = 1,2, \ldots 5$, $q = 1,2, \ldots 4$ and ${\mathcal{U}} = 1,2,3$ using TFFN shown in Table 2:

Table 2 Assessments from three DMs in the form of TFFNs.

Step 2: We combine all the data from ${\mathbb{D}} = \left( {{\check{\mathcal{T}}}_{pq}^{{\mathcal{U}}} } \right)_{5 \times 4}$ into one single matrix using the TFFSWWA operator. We set $\delta = 3$ and use the weight values from the experts ${\text{e}} = \left( {0.2,{ }0.3,{ }0.5} \right)$. The results of the calculations are presented in Table 3.

Table 3 Aggregated TFFNs using TFFSWWA.

Step 3: Based on all of the attributes that have been provided, we can calculate the AV value using Eq. (14) and Table 3. The results of the calculation are displayed in Table 4.

Table 4 Average value (AV).

Step 4: Using the Eqs. (17) and (18), calculate the PDA and NDA according to the findings of the average solution (AV). The results of the calculations are displayed in Tables 5 and 6.

Table 5 The results of PDA.

Table 6 The results of NDA.

Step 5: Using Eq. (19) and (20), the attribute weighting vector , to calculate the values of ${\mathcal{Q}}_{p}^{ + }$ and ${\mathcal{Q}}_{p}^{ - }$, the results of the calculations are displayed in Tables 7.

Table 7 Evaluation parameters of TFF-EDAS method.

Step 6: Using Eq. (21) and (22), to calculate ${\mathcal{N}}_{p}^{ + }$ and ${\mathcal{N}}_{p}^{ - }$, respectively in Table 7:

Step 7: Determine the appraisal score values by taking the ${\mathcal{N}}_{p}^{ + } {\text{ and }}{\mathcal{N}}_{p}^{ - }$ of each alternative:

Step 8: The outcomes of the computations are shown in Table 7, which ranks each choice in accordance with the .

Algorithm-2: Using aggregation methodology

Step 1 and Step 2 same as the algorithm-1.

Step 3: Combine all the TFFNs for each alternative ${\tilde{\chi }}_{{\text{p}}}$ using the TFFSWWA operator with $\delta = 3$, and apply the attribute weighting vector . The results of the calculations are displayed in Table 8.

Table 8 Aggregate all the TFFNs for each alternative ${\tilde{\chi }}_{{\text{p}}}$.

Step 4: We can get the collective overall score function values $S\left( {{\tilde{\chi }}_{p} } \right)$, as seen in shown in Table 9. Figure 5 shows the graphical ranking of alternatives by using algorithm-1 and algorithm-2.

Table 9 Ranking for TFFSWWA operator.

Fig. 5

Graphical representation of comparison EDAS method and TFFSWWA operator, Boikanyo et al.⁷⁴. (Figure generated using Microsoft Office.)

In the proposed decision-making model, Smart T-shirt is identified as the best wearable sensor using the Triangular Fermatean Fuzzy Sugeno–Weber Weighted Average (TFFSWWA) operator and the modified Evaluation Based on Distance from Average Solution (EDAS) method. The TFFSWWA operator aggregates decision-makers’ assessments, addressing uncertainty and interaction among criteria. The EDAS method computes the Positive Distance from Average Solution (PDAS) and Negative Distance from Average Solution (NDAS), where higher PDAS and lower NDAS indicate better performance. Smart T-shirt achieved the highest PDAS and lowest NDAS, confirming its superior performance. Sensitivity analysis validated this outcome, showing consistent ranking under varying input data. The selection of Smart T-shirt reflects its effectiveness in improving decision-making accuracy and operational efficiency in Remote Patient Monitoring Systems (RPMS).

Sensitivity analysis

Sensitivity analysis was conducted to examine the stability and robustness of the proposed Triangular Fermatean Fuzzy Sugeno–Weber Weighted Average (TFFSWWA) operator-based decision-making model under varying values of the operational parameter $\delta$. The parameter $\delta$ in the TFFSWWA operator controls the degree of aggregation and the influence of the criteria weights in the decision-making process. To evaluate the impact of this parameter on the ranking of alternatives, we calculated the rankings of the five alternatives ${\tilde{\chi }}_{1} ,{\tilde{\chi }}_{2} ,{\tilde{\chi }}_{3} ,{\tilde{\chi }}_{4} ,{\tilde{\chi }}_{5}$ for different values of $\delta$ ranging from 1 to 10. Table 10 presents the ranking results for each value of $\delta$, while Fig. 6 provides a graphical representation of the ranking behavior. The results demonstrate that the ranking order remains consistent throughout the range of $1 \le \delta \le 10$. Specifically, the ranking follows the order ${\tilde{\chi }}_{4} > {\tilde{\chi }}_{3} > {\tilde{\chi }}_{2} > {\tilde{\chi }}_{1} > {\tilde{\chi }}_{5}$ for all tested values of $\delta$. This consistency indicates that the proposed TFFSWWA operator exhibits strong stability and reliability under varying operational conditions. The fact that alternative ${\tilde{\chi }}_{4}$ remains the best-ranked option across the entire range of $\delta$ confirms the robustness of the decision-making model and the effectiveness of the aggregation process. These findings validate that the proposed model can maintain decision consistency and accuracy even under changing parameter conditions, reinforcing its practical applicability in complex decision-making environments.

Table 10 Sensitivity analysis of the parameter ${\varvec{\delta}}$.

Fig. 6

Graphical representation of Sensitivity analysis of the parameter ${\varvec{\delta}}$.

Comparison analysis with existing method

The suggested approaches for MCGDM are validated and compared to current methods, as indicated in Table 11. Applying different approaches is crucial to verifying the methodology created for the MAGDM problem. We have evaluated the suggested strategy using a variety of ranking techniques in a range of settings to show its resilience.

Table 11 Comparison analysis with existing method.

In this section, we evaluate the performance of the proposed approach by comparing it with several existing multi-criteria decision-making (MCDM) methods to demonstrate its advantages and effectiveness. The proposed method processes values as Triangular Fermatean Fuzzy Numbers (TFFNs) to handle uncertainty and hesitation more effectively. It integrates the Evaluation based on Distance from Average Solution (EDAS) method and the Triangular Fermatean Fuzzy Sugeno–Weber Weighted Average (TFFSWWA) operator to select the optimal wearable sensor for Remote Patient Monitoring Systems (RPMS) from a predefined set of alternatives. The EDAS method assesses the desirability of alternatives based on their distances from the average solution, while the TFFSWWA operator handles the interaction between criteria using Sugeno and Weber functions, enhancing decision accuracy. To validate the effectiveness of the proposed method, the same example and weight data are used for comparison with several established methods, including the FFDWA operator ⁴⁶, FFYWA operator ⁴⁴, FFAAWA operator ⁸³, TOPSIS method ¹⁰, GRA method ⁷⁹, CoCoSo method ⁸⁰, ELECTRE method ⁸¹, and WASPAS method. The comparative rankings are summarized in Table 12 and illustrated in Fig. 7. The results demonstrate that the proposed method consistently produces accurate and reliable rankings, outperforming existing methods by effectively managing complex criteria and uncertainty in wearable sensor selection under a TFFN-based framework.

Table 12 Comparison ranking with existing method.

Fig. 7

Graphical representation of Comparison analysis with existing method.

Discussion

The following conclusions are drawn from the comparison with the Fermatean fuzzy TOPSIS method:

• 1. Table 11 show the sensitivity analysis for the proposed techniques. Variations in score function values, yet the optimal outcome remains unchanged.

• 2. The outcomes of the TFFNs-EDAS method, alongside other approaches, are presented in Table 6. The data illustrates that, in both instances, the optimal solution is identified as ${\tilde{\chi }}_{4}$, thereby indicating the alignment of the proposed decision-making methodology with the desired results.

• 3. A graph showing the options and score values for the TFFNs-EDAS approach and the other method is shown in Fig. 7. The graph makes it evident that not only is the best alternative ranked the same, but the other alternatives are also in the same optimal order.

• 4. Both decision-making approaches are used to choose the suitable alternatives depending upon the given data and environment of the MAGDM problem.

• 5. The proposed TFFNs-EDAS approach has potential to handle Triangular Fermatean fuzzy number data. But the existing Fermatean fuzzy EDAS method cannot deal with only Triangular Fermatean fuzzy number. Therefore, this trait proves that our presented technique is more powerful and superior over Fermatean fuzzy EDAS method.

• 6. The growing demand for remote patient monitoring (RPM) due to chronic diseases and aging populations makes effective decision-making in selecting wearable sensors crucial. Traditional models often fail to handle the uncertainty and conflicting criteria involved in this process. Triangular Fermatean fuzzy sets (TFFSs) enhance uncertainty modeling, while the Sugeno–Weber weighted average (SWWA) operator improves aggregation by handling nonlinearity and interaction among criteria. The integration of TFFS-SWWA with the Evaluation Based on Distance from Average Solution (EDAS) method ensures more accurate and consistent ranking of alternatives. This novel approach provides a systematic framework for wearable sensor selection in RPM, improving decision accuracy and healthcare outcomes. Its adaptability to other healthcare decision problems increases its value to the scientific community.

Advantages of the proposed model

• 1. Triangular Fermatean fuzzy sets (TFFS) allow the representation of higher degrees of hesitation and uncertainty compared to intuitionistic and Pythagorean fuzzy sets, leading to more accurate modeling of complex decision environments.

• 2. TFFS provide a wider range for membership and non-membership values, improving the ability to capture complex and vague information in decision-making scenarios.

• 3. The Sugeno–Weber operator accounts for the interdependence and correlation among criteria, enhancing the consistency and reliability of the aggregated values.

• 4. The Sugeno–Weber aggregation operator’s adjustable parameters enable it to balance conjunctive (AND-type) and disjunctive (OR-type) behaviors, enhancing adaptability and accuracy in complex decision-making.

• 5. Its versatility allows it to handle nonlinearity and correlation among criteria in various fuzzy environments, such as IFSs, PFSs, and FFSs, improving decision accuracy and consistency.

• 6. The EDAS method evaluates alternatives based on positive and negative distances from the average solution, ensuring a balanced and objective ranking process.

• 7. Combining TFFSWWA with EDAS reduces information loss and enhances the accuracy of the final decision by considering both the degree of satisfaction and dissatisfaction.

• 8. The proposed model effectively supports the selection of wearable sensors for RPMS, improving real-time monitoring, patient outcomes, and healthcare efficiency.

Limitations

Despite the effectiveness of the proposed model in selecting wearable sensors for Remote Patient Monitoring Systems (RPMS), several limitations remain. First, the model is based on Triangular Fermatean Fuzzy Numbers (TFFNs), which may not fully capture more complex forms of uncertainty that exist in real-world healthcare scenarios, such as vague or conflicting data. Second, the TFFSWWA aggregation operator involves multiple parameters, which may increase computational complexity and require careful tuning to achieve optimal results. Third, the model’s applicability has been demonstrated only in the context of wearable sensor selection; its effectiveness in other healthcare decision-making problems, such as treatment planning or medical device selection, needs further validation. Fourth, the decision-making process assumes that the criteria and expert judgments are consistent over time, which may not hold in dynamic healthcare environments where patient conditions and technological advancements are constantly evolving. Lastly, the model relies on expert-provided inputs, which introduces the possibility of subjective bias and inconsistency in the decision-making process.

Future avenues of research do these limitations

Future research could extend the model to interval-valued or hesitant Fermatean fuzzy sets to handle complex uncertainty more effectively. Enhancing parameter optimization for the Sugeno–Weber operator could reduce computational complexity and improve accuracy. Expanding the model’s use to other healthcare decisions, such as hospital resource allocation and clinical diagnosis, would strengthen its applicability. Developing adaptive models to adjust to changing patient conditions and technological advances, along with integrating machine learning for automated input analysis, could improve consistency and reduce bias.

Conclusion

RPMS are effective for monitoring patients outside clinical settings, with wearable sensors playing a key role in continuous health tracking. However, selecting the optimal sensor remains challenging due to varying patient needs and sensor performance. To address this, we introduced score and accuracy functions for TFF numbers and proposed the TFFSWWA aggregation operator, establishing its key properties. We developed a modified EDAS technique for MCGDM under TFF environments using the TFFSWWA operator to identify the most suitable sensor. A case study demonstrated sensor selection based on patient-specific requirements, supported by an algorithm and a flowchart. Sensitivity analysis confirmed the model’s responsiveness to input data, and comparative analysis showed its superiority over existing methods. The model enhances decision consistency, reduces uncertainty, and improves healthcare efficiency, helping managers make better strategic decisions and optimize resource allocation in patient care.

The proposed approach can be extended to other real-life decision-making problems, such as electric vehicle (EV) adoption⁸², municipal solid waste management⁸⁴, supply chain management⁸⁵, etc. to evaluate complex criteria under Triangular Fermatean fuzzy environment like Triangular Fermatean fuzzy number for three way decision making problem, Triangular Fermatean Hesitant fuzzy set, Triangular Fermatean fuzzy neural network model etc.