Introduction

The rapid pace of anthropogenic climate change contrasts with the slower, natural climate variations observed over geological time scales. Increased greenhouse gas concentrations from human activities primarily drive this. The multiple indicators, such as rising global temperatures, sea level rise, ocean heat content, ice melt, and permafrost thaw, form a cohesive body of evidence showing the warming trend. A warming climate enhances the hydrological cycle because warmer air holds more moisture (following the Clausius-Clapeyron relation), leading to higher atmospheric water vapour levels, accelerated surface evaporation, and increased intensity of precipitation events under similar meteorological conditions, often resulting in heavier downpours or extreme rainfall. Significant changes in the hydrological cycle are anticipated due to climate change1,2. Altered rainfall patterns, such as less frequent but more intense storms, can profoundly affect ecosystem composition and productivity3. Intra-annual and inter-annual precipitation variability may have negative and positive impacts, depending on the ecosystem type4,5. Extreme wet or dry years are particularly detrimental to the productivity of crops like rice and grasslands, which rely on stable water availability6. Furthermore, research indicates that ecosystems respond to higher rainfall variability differently. Xeric habitats, which are adapted to arid conditions, tend to benefit more from such variability compared to mesic habitats, which rely on more consistent moisture availability5,6,7,8. Precipitation is important in regulating terrestrial carbon uptake because it influences ecosystem Gross Primary Productivity (GPP)9. GPP, defined as converting atmospheric carbon dioxide into organic matter by plant photosynthesis, emphasizes the complex relationship between the carbon and water cycles in terrestrial ecosystems10,11. Precipitation significantly influences vegetative productivity and ecological processes12. The sensitivity of GPP to precipitation demonstrates the ecosystem’s flexibility to changes in water supply13,14. The relationship between GPP and precipitation frequently shows complicated nonlinear properties. While more significant precipitation can raise productivity in some years, it can also reduce GPP due to interactions with system states and other factors, including temperature and local water availability15,16. These dynamics underscore the intricate coupling between precipitation and ecosystem processes. As climate patterns continue to shift, changes in precipitation amount, timing, and spatial distribution are expected to influence GPP significantly. Altered rainfall regimes may lead to both positive and negative outcomes depending on regional ecosystem conditions, plant water-use efficiency, and the availability of supplementary resources like soil moisture and nutrients14,17. GPP refers to the total amount of solar energy plants capture through photosynthesis, which is converted into organic matter (biomass). It is a key measure of ecosystem productivity and carbon fixation. GPP is influenced by various factors such as temperature, sunlight, carbon dioxide concentration, soil quality, and rainfall. Water is a crucial input for plant growth. In agricultural systems, rainfall determines crop yields and ecosystem productivity. Adequate rainfall supports plant growth by providing water for photosynthesis, nutrient uptake and transpiration. In excess rainfall, water can lead to waterlogging, root damage and reduced oxygen availability in the soil, ultimately affecting plant health and GPP. In contrast, insufficient rainfall can lead to drought stress, limiting photosynthesis and biomass production. Reduced water availability also hinders nutrient uptake and can stunt plant growth. So, threshold analysis is necessary to identify the specific range of an environmental factor, such as rainfall, which maximizes or optimizes a particular outcome, that is, GPP. The idea is to find the point at which GPP reaches its highest value in terms of varying levels of rainfall. However, outside of this range, GPP begins to decline due to the limiting or damaging effects of either excess or insufficient rainfall. Using this concept, threshold analysis is made for 15 districts under different agro-climatic zones of our study separately, and districts under different agro-climatic zones are shown in Fig. 1.

Fig. 1
figure 1

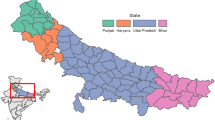
Ten agro-climatic zones comprising 30 districts of Odisha. (Source: Liansangpuii, F., Panigrahi, B., & Paul, J. C. (2019). Assessment of meteorological drought by standardized precipitation index for coastal agro-climatic zones of Odisha, India, Indian Journal of Soil Conservation, 47(3), pp 205–212).

Full size image

While previous studies have analyzed rainfall trends in India, fewer have specifically examined century-long (1901–2023) monsoon rainfall trends in Odisha’s agro-climatic zones. The non-linear response of GPP to rainfall variations has not been well explored in the context of Odisha’s diverse agro-climatic zones. Prior studies have not established an optimal rainfall threshold that maximizes GPP in Odisha’s agricultural districts. These gaps have been addressed in this paper. Moreover, this article’s scientific contributions and novelty are listed as monsoon rainfall trends in Odisha during 123 years have been examined using robust statistical techniques to detect shifts, variabilities, and monsoon rainfall influencing GPP at a district level has been investigated, which reveals non-linear relationships that have not been fully explored before. Besides these, by conducting threshold analysis, this study provides actionable insights for optimizing water resource management in agriculture. In addition, it demonstrates that forested regions show greater sensitivity to rainfall fluctuations than cropped areas, a finding with implications for climate adaptation strategies. Moreover, this research focuses on the variation in Kharif paddy output, considering the impacts of irregularities in the onset and duration of the rainy season. Key factors include the delayed arrival of potentially useful rains, the overall shortening of the rainy season, poor rainfall distribution, and the occurrence of floods18,19,20,21. So, our analysis of monthly and seasonal rainfall from 1901–2023 during the monsoon season will be dealt with for finding the trend in rainfall using the Mann–Kendall test and detecting the abrupt change point in the time frame by the Pettitt test. Analysis of precipitation trends in Cuttack District, Odisha, revealed insignificant overall changes. However, it highlighted a rising trend in precipitation during some months and a decreasing trend in others22.

Temperature and rainfall play a pivotal role in crop germination, growth, reproduction, and yield in subsequent agricultural production23. It is evidenced that the amount of monsoon rainfall is the prime factor for crop productivity as compared to temperature in some of the districts such as Kalahandi, Koraput and Bolangir districts24,25. Moreover, higher amounts of rainfall have been recorded in coastal Odisha than the country’s average, but its distribution is uneven, especially during the cropping season26. Efforts have been made to establish the relationship between GPP and rainfall by threshold analysis for the 15 studied districts.

This study discusses the importance of Kharif paddy production during the monsoon season, as paddy is the major crop. Kharif paddy in Odisha is predominantly rainfed, relying heavily on monsoon rainfall for its water requirements. However, limited irrigation coverage is available in many areas of Odisha. Several studies have shown that variations in monsoon rainfall, such as delayed onset or deficits and excess flooding, have significantly affected crop yield. Rainfall variations influence sowing dates, crop growth stages, and overall yield. Moreover, previous studies have demonstrated the direct relationship between monsoon rainfall and paddy yield in India, particularly in Odisha. Some reported cases have indicated that a drought-like situation was envisaged in Odisha when deficit rainfall of about 63% was recorded by 15 August 2021. However, paddy cultivation dropped by 40% until mid-July in the year 2022 due to the late arrival of monsoon as well as scanty rainfall in the month of June, and a similar situation occurred in Kalahandi district due to 66% deficit rainfall by mid-July of 2023. The influence of temperature on paddy growth is sensitive, as observed during break monsoon conditions due to scanty or lack of rain. Still, paddy is primarily a water-sensitive crop, and its response to temp is secondary to its water availability. Therefore, it is necessary to investigate the influence of rainfall in paddy production during monsoon season.

To visualize the status of agricultural productivity, mainly rice yield, an attempt was made to study the rainfall trend in selected districts under different agro-climatic zones using standard methods in climate change scenarios. One of the methods is the impact of rains in prior and post-change points of the year based on the Pettitt test and the role of GPP connected to rainfall using threshold analysis by selecting 15 districts from 10 agro-climatic zones of Odisha as shown in Fig. 1. Moreover, the characteristics of 10 agro-climatic zones briefly stated below as Odisha’s agricultural landscape categorized into ten distinct agro-climatic zones, each characterized by unique climatic conditions and soil types. The zonal diversity reflects the interplay of climatic and soil factors shaping the agricultural patterns in Odisha.

  1. 1.

    A hot, moist climate with red and yellow soils marks the Northwestern Plateau.

  2. 2.

    The Northcentral Plateau is hot and moist, featuring red loamy soils.

  3. 3.

    The Northeastern Coastal Plateau experiences a hot, moist sub-humid climate dominated by alluvial soils.

  4. 4.

    East and Southeastern Plateau has a hot and humid climate with coastal alluvial soils that turn saline near the coastline.

  5. 5.

    A hot, moist sub-humid climate with laterite and brown forest soils characterizes Northeastern Ghat.

  6. 6.

    The Eastern Ghat and Highland feature a warm and humid climate with red and brown soils.

  7. 7.

    The Southeastern Ghat shares a similar warm and humid climate but has black and mixed red–black soils.

  8. 8.

    The Western Undulating Zone has a warm and moist climate, with black and mixed red–black soils predominating.

  9. 9.

    The West Central Tableland is hot and moist, with heavy-textured red soils.

  10. 10.

    The Mid Central Tableland is defined by a hot and dry sub-humid climate with red loamy, laterite, and mixed red–black soils.

Study area

Odisha is located on the eastern coast of India, and agriculture is the main livelihood of people; a higher percentage of the population is either farmers or agricultural labourers involved in the agriculture sector. The location of Odisha is shown in Fig. 1. As a natural calamity-prone state, agriculture is significantly affected by cyclones, droughts, and floods with varying intensities, resulting in crop loss and poor productivity, as reported in some years. Agricultural production is strongly influenced by the variability and unpredictability of weather, including climate change, climate variability, and inherent biological uncertainties in crop management. Millions of farm households nationwide face significant yield uncertainty and risk due to factors like unpredictable rainfall patterns during the monsoon season (South-west monsoon, June to September), rising temperatures, recurrent climate-induced natural disasters like drought and floods, high variability in monsoon onset dates, prolonged dry spells, and unseasonal rain27,28,29,30. There are ten agro-climatic zones covering 30 districts. In this study, 15 districts are chosen out of 30 districts under different agro-climatic zones, as shown in Table 1. Odisha state lies roughly between latitudes 22° 36’ N and 17o 49’ N and longitudes 81° 36’ E and 87o 18’ E. The state has an area of 1, 55,707 square km. It is bounded by the districts Ranchi, Singbhum (of Jharkhand state) and Medinapur (of West Bengal state) on the north, by the districts Raigarh, Raipur, Bastar (of Chattishgarh state) on the west, by the districts Khammam, East Godavari, Visakhapatnam and Srikakulam (of Andhra Pradesh state) on the South and by the Bay of Bengal on the east. The state’s climate is categorized by hot summer and cold winter in the interior but a moist and equable climate in the coastal region near the Bay of Bengal.

Table 1 Districts with Agro-climatic zone for the study purpose.
Full size table

Data and methodology

Data collection and preprocessing

The month-wise rainfall data of 15 districts during the monsoon season from 1901 to 2023 are obtained from the National Data Centre, IMD, Pune and the website of the Special Relief Commissioner (SRC), Government of Odisha (www.srcodisha.nic.in). The inverse distance weight (IDW) method is used to the adjacent district’s known rainfall data to fill up the missing data of the concerned district. Month-wise rainfall data during the southwest monsoon season, June to September, and the whole monsoon season, about 15 districts, as shown in Table 1, for the period 1901 to 2023, were used in this study. Utmost care has been taken to scrutinize the data for its accuracy and reliability. Each district comprises some blocks, and rainfall is calculated based on rainfall recorded at blocks. Rainfall distribution during the southwest monsoon season is characterized by monsoon systems such as low-pressure areas (monsoon lows), depressions or deep depressions forming in the Bay of Bengal. Moreover, rainfall distribution depends upon the system’s track and life span. However, widespread rainfall is realized by low-pressure systems as compared to Depression or Deep Depression or, in rare cases, cyclonic storms during monsoon season. In contrast, depression or its further intensification process measures the higher intensity rainfall over certain areas as most of the monsoon system generally moves in a northwest direction31. Given these rainfall characteristics, verification of rainfall of the specific block day-wise as well as the whole month is made concerning the rainfall amount of adjacent blocks falling within the district and adjacent districts. Besides these checks, district-wise rainfall calculations of IMD and SRC were also referred to for verification. In case of more significant discrepancy, the monsoon system along with the track was taken into consideration, and then the correct rainfall amount of either SRC or IMD was accepted in case a similar amount or near to that is recorded in adjacent blocks of the same district or nearby districts falling in the region. Similar checking procedures were adopted for break-in monsoon conditions or insitu phenomena by monsoon current as a higher amount of rainfall does not happen widespread but in isolated blocks (one or two blocks) and light rainfall in adjacent blocks. Data about the total geographical area of each of the 15 districts, forest cover, and crop area during the monsoon season from 2000 to 2022 are collected from the Odisha Agriculture Statistics manual published by the Department of Agriculture and Farmers Empowerment, Government of Odisha for the years 2000 to 2022. The data is accessible at (http;//agri.odisha.gov.in).

District Gross Primary Productivity (GPP) of Odisha state was obtained from a Moderate Resolution Imaging Spectroradiometer (MODIS) GPP product with the help of the Google Earth Engine (GEE) platform. The MODIS GPP product, especially the MODI7 A2 dataset, provides vital information on vegetation productivity across various landscapes32. MODIS GPP dataset was filtered to encompass the desired temporal range relevant to this study. The dataset comprises images collected at a 1 km resolution expressed in gC/m2/day (grams of carbon per square meter per day). The shape file containing districts of Odisha was uploaded to the GEE platform, facilitating the clipping of the GPP dataset to focus exclusively on the area or district of interest. By applying the spatial filter, GPP values are extracted specifically for the districts of the Odisha region. To generate monthly GPP files, the dataset was aggregated by month, and then the GPP values were exported as GeoTIFF files, enabling future processing and analysis.

Homogenization process

The monthly rainfall data of 15 districts in Odisha are scrutinized for missing or incorrect entries. A district’s monthly rainfall is calculated using the number of block rain gauge stations. These rainfall data may be affected by non-meteorological factors such as instrumentation, growing trees near rain gauge stations, shifting of rain gauge sites and procedure of measuring rainfall every day using appropriate measuring glass and changes in the surrounding environment like urbanization as well as installation of rain gauge at a site33,34. These data may yield spurious results due to the influence of non-climatic factors obscuring the effects of climate change or variability35,36,37,38. Therefore, the month-wise rainfall data of the districts need homogenization to remove artificial discontinuities as homogeneous time series data of temperature or rainfall are used to study climate variability or trend because change patterns of observed data only by weather and climate39.

Each district’s monthly total rainfall from 1901 to 2023, from June to September, was homogenized separately using a homogenization software package known as RH tests V4 by relative homogeneity test. For the relative homogeneity test, a composite reference series will be created for the target time series (station or observatory data to be homogenized). The correlation coefficients were calculated for the time series data of the target station, and the rainfall time series data for the district or station exhibited a significant correlation coefficient of 99%. The probability of the two-tailed test was used to determine whether to include or reject the station or district to calculate the composite reference series. The concerned districts’ sorted-out time series data will be used to create a composite reference series for the target station by averaging these selective or sorted-out districts40. To evaluate the homogeneity of the target series in comparison to the composite reference series, the RH tests V4 software program was utilized. There has been extensive usage of this software package in climate studies41,42,43,44,45,46,47. Utilizing the composite reference series, the relative test uses the penalized maximal T (PMT) test48 to identify arbitrary shifts or sudden changes in the data. This approach addresses several change points and empirically takes into consideration the influence of the lag-1 auto-correlated noise by employing a recursive testing methodology49. (Wang, 2008b) states that the method lessens the impact of varying sample sizes before and after a specific time point by integrating an empirical function into each algorithm. The final homogenized rainfall time series data for each district, processed for monthly, seasonal, and annual periods, will be used in further research, including the Mann–Kendall, Pettitt, and GPP vs rainfall assessment. To further refine the analysis, the method minimizes the impact of unequal sample sizes before and after a specific time point using an empirical function embedded in each algorithm. The final homogenized rainfall time series data for each district, processed for monthly, seasonal, and annual periods, will be employed in subsequent analyses, including the Mann–Kendall, Pettitt, and GPP versus rainfall assessments.

Trend analysis: Mann- Kendall test and Sen’s slope estimator

Mann- Kendall (MK) test is a widely used non-parametric statistical method for detecting trends in time series data50,51. This test is particularly suitable for analyzing climatic and hydrological data as it does not assume a specific distribution for the data and is robust against missing values and outliers. Moreover, its use is more prevalent in environmental and climate data series to detect monotonic trends in long-term time series data that are either increasing or decreasing for parameters like temperature, rainfall, etc. In climatological research, the environmental variables, such as temperature, rainfall, etc., change over time due to natural variability or anthropogenic influences like climate change. Moreover, some climatological time series data do not follow a normal distribution so that this test will be applicable52. The Mann–Kendall (MK) test is based on a null hypothesis (H0), which assumes no trend, and an alternative hypothesis (Ha), which posits the existence of a trend53. The actual slope or rate of change per unit of time is estimated using Sen’s slope (SS) estimator54. To account for autocorrelation in the results of the MK test, serial correlation was assessed before applying the MK test. The lag-1 serial correlation coefficient r1 was computed for a two-tailed test at a 5% significance level using the following equation55,56:

$${r}_{1}=\frac{\sum_{i=1}^{n-1}\left({x}_{i}-\overline{x }\right)\left({x}_{i+1}-\overline{x }\right)}{\sum_{i=1}^{n}{\left({x}_{i}-\overline{x }\right)}^{2}}$$

where,

\({x}_{i}\)= Value of an observation in the time series.

\(\overline{x }\) = Mean of the sample.

n = Sample size.

The calculated autocorrelation co-efficient r1 was compared against the confidence interval defined by the following equation:

$${r}_{1}\left(95\%\right)=\frac{-1\pm 1.96\sqrt{n-2}}{n-1}$$

Suppose the lag-1 serial correlation coefficient (r1) falls outside the upper and lower bounds of the confidence interval; the time series is considered not serially correlated, and the MK test can be applied directly. However, if r1 falls within the bounds, the trend-free pre-whitening (TFPW) approach, a modified version of the MK test, is applied to remove the effects of serial correlation and ensure reliable trend detection57.

Mann–Kendall test statistic (S) can be computed to evaluate the trend S for each pair of data points \({x}_{j}\) and \({x}_{i}\) for i < j, then the sign of the difference between the values can be computed using the following expression:

$$S= \sum\nolimits_{i=1}^{n-1}\sum\nolimits_{j=i+1}^{n}sgn ({x}_{j}-{x}_{i})$$

where \(sgn ({x}_{j}-{x}_{i}\)) is the sign function, which is written as

$$sgn ({x}_{j}-{x}_{i}) = \left\{\begin{array}{c} 1 \:\text{if}\: {x}_{j}> {x}_{i}\\ 0\:\text{if}\:{x}_{j} = {x}_{i}\\ -1\:\text{if}\:{x}_{j} < {x}_{i}\end{array}\right.$$

The value of S indicates the overall direction of the trend. The + ve value of S suggests an upward trend, and the –ve value of S suggests a downward trend.

If there are tied values in the dataset, then the variance of S is calculated using the following expression:

$$Var \left(S\right)= \frac{n\left(n-1\right)\left(2n+5\right)- \sum_{i-1}^{m}{t}_{i}({t}_{i}-1)(2{t}_{i}+5)}{18}$$

where \({t}_{i}\) = represents the number of ties of length ‘i’ (data points with equal values), m is the number of tied groups and ‘n’ is the total number of observations.

The Z-score is evaluated to standardize S, and then the statistical significance of the trend can be determined:

$$\text{Z}= \left\{\begin{array}{l}\frac{S-1}{ \sqrt{Var (S)}} ,\; if\; S>0\\ 0 , \qquad \quad if\; S=0\\ \frac{S+1}{\sqrt{Var (S)}},\; if\; S<0\end{array}\right.$$

The trend can be interpreted as increasing or decreasing based on the positive or negative values of Z statistic. A Z value of 0 indicates no trend, suggesting that the data are typically distributed with no significant trend.

To know the magnitude of the trend, Sen’s slope is applied, where the median slope is calculated for all pairs of data points (\({x}_{j} ,\) \({x}_{i}\))

$$\widehat{\beta }=\text{Median}= \left(\frac{{x}_{j}-{x}_{i}}{j-i}\right)\text{ For all }1\le \text{ i}<\text{ j }\le \text{ n}$$

where \({x}_{j}\) and \({x}_{i}\) are data points at times j and i and j > i, the final estimate of the trend is the median of these slopes, providing a robust measure of the rate of change in the data.

Change point detection: Pettitt test

The Pettitt test is non-parametric, and it is used in hydrology and climatological series data to detect a single change point, especially for temperature, rainfall or streamflow. It is based on the data’s rank order and identifies when a significant shift occurs58,59,60. It is based on the rank order of data and identifies when a significant shift occurs in the time series.

Let a time series x1, x2, –––, xn consist of ‘n’ observations and ‘k’ is the potential change point in the time series data. So, there are two groups: one before ‘k’ (i.e. x1, x2, –––, xk) and one after ‘k’ (i.e. xk+1, xk+2, ––––, xn).

The Pettitt test statistics Uk is computed for each potential change point k as follows

$${U}_{k}= \sum\nolimits_{i=1}^{k}\sum\nolimits_{j=k+1}^{n}sgn ({x}_{j}-{x}_{i})$$

where \(sgn ({x}_{j}-{x}_{i}\)) is the sign function, which is

$$\begin{aligned}sgn ({x}_{j}-{x}_{i}) = 1\text{ if }{x}_{j}> {x}_{i}\\0\text{ if }{x}_{j} = {x}_{i}\\-1\text{ if }{x}_{j} < {x}_{i}\end{aligned}$$

The test statistic ‘K’ is the point where the absolute value of \({U}_{k}\) is maximized

$$\begin{aligned}\text{K}=&\text{Max} \left|{U}_{k}\right|\\ &\quad \text{k}\end{aligned}$$

If any exists, K represents the most likely point where the change occurs. Under the null hypothesis (no change point), K does not exceed specific critical values determined by approximate probability values or significance levels, typically derived using Monte Carlo simulations or asymptotic approximations. The significance of the change point is tested by calculating the p-value associated with the test statistics.

$$p\approx 2\text{exp}\left(\frac{-6{k}^{2}}{{n}^{3}+{n}^{2}}\right)$$

where ‘n’ is the total number of data points in the series. The null hypothesis is rejected if the p-value is less than the significance level ‘α’, indicating a significant change point in the series.

Gross primary productivity (GPP) and rainfall analysis

Gross Primary Productivity (GPP) represents the total amount of organic carbon assimilated by vegetation through photosynthesis per given unit of time and area. It is the most significant carbon flux in the carbon budget and plays a vital role in the global carbon cycle. The variation of GPP might intuitively represent the effect of climate and environmental change on plants and ecosystems. Water is a crucial input for plant growth. In agricultural systems, rainfall plays a vital role in determining crop yields and ecosystem productivity. Adequate rainfall supports plant growth by providing water for photosynthesis, nutrient uptake, and transpiration. While rainfall is essential, excess water can lead to waterlogging, root damage, and reduced oxygen availability in the soil, ultimately affecting plant health and GPP. On the other hand, too little rainfall can lead to drought stress, limiting photosynthesis and biomass production. Reduced water availability also hinders nutrient uptake and can stunt plant growth.

Threshold analysis

Threshold analysis is used to identify an ecological factor’s specific range; in our case, rainfall, which optimizes a particular outcome, is GPP61,62. Our purpose is to find the point at which GPP reaches its highest value in terms of varying levels of rainfall during the monsoon season concerning each district in our study. Outside this range, GPP begins to decline due to the limiting or damaging effects of either excess or insufficient rainfall.

The range of rainfall is divided into bins of equal width. Each rainfall point is categorized into a corresponding bin, and for each bin, the mean GPP is calculated by the formula63:

$$\text{Mean GPP in Bin}_\text{j}= [\sum\nolimits_{i=1}^{{n}_{j}}{GPP}_{i}]/{n}_{j}$$

\({n}_{j}\): Number of rainfall observations in the jth bin.

GPPi: GPP value for the ith observation in that bin.

The bin with the highest mean GPP is identified, and the formula extracts the rainfall range for the optimal bin.

$$\text{Optimal}\: \text{Bin} =\:\text{arg}\:\text{max}\:(\text{Mean}\:\text{GPP}\:\text{Bins})$$

Then, bar charts are plotted with rainfall bins on the X-axis and the mean GPP of each bin on the Y-axis.

Rainfall data are grouped into bins (e.g., 50 mm) to create categories for analysis. The monsoon seasonal rainfall of 15 districts and corresponding GPP data are generated. For each bin or rainfall range, the mean GPP value is calculated. It summarises how GPP responds to different levels of rainfall17,64. The rain range is identified to generate the maximum mean GPP. To visualize these things, bar charts are prepared to know the optimal rainfall range where GPP is maximized. Once the optimal range is created, interpret the findings to understand the rainfall conditions that best support plant growth and ecosystem productivity.

Results and discussions

Homogeneity of rainfall

Initially, homogeneity testing was made for monthly time series data from June to September of the Southwest monsoon season from 1901 to 2023 for 15 districts falling under different agro-climatic zones. Eighty percent of rainfall mainly occurs during the southwest monsoon season, the only season favourable for maximum rain. Our interest is to understand the variation of Kharif rice production year to year, so we will study the rainfall pattern during the monsoon season. Accordingly, an attempt has been made for homogenisation along with an analysis of rainfall for the months during the monsoon season. These homogenised rainfall data have been used in our study for the MK test, Pettitt test, GPP analysis and threshold value analysis in subsequent sub-sections.

Trend analysis-Mann–Kendall test

This section analyses the rainfall trend in districts across different agro-climatic zones by examining the intensity of Z values and trends at a 0.05 significance level. The analysis is based on the Mann–Kendall (MK) test applied to monsoon rainfall and monthly rainfall during the monsoon period. Mann- Kendall test was used to detect a monotonic trend in the 123-year rainfall series, and Sen’s slope estimator quantified the rate of change.

No serial correlation is observed in any of the individual months or the whole monsoon season of the respective districts. The trend with Z-score values of the MK test from June to September and for the entire monsoon period concerning 15 districts of Odisha are shown in Table 2.

Table 2 The Results of the Mann–Kendall (MK) test (Z), the trend for monthly rainfall from 1901 to 2023 and Sen’s slope are summarized below.
Full size table

On verifying the data, there is decreasing trend of rainfall in July of Angul with Z = −2.7, or at p = 0.01 at 95% significance level and rate of change = −0.75 mm per year whereas increasing trend of rainfall in August of Cuttack with Z = 2.22, p = 0.03 and rate of change 0.63 mm per year. However, analysis of rainfall in July of Sambalpur shows decreasing trend of rainfall with Z = −1.97, p = 0.05, rate of change = −0.7 mm per year. The decreasing trend of monsoon rainfall in Sundergarh with Z = −2.5, p = 0.01, rate of change = −1.30 mm per year and decreasing trend in July of Sundergarh with Z = −2.68, p = 0.01, rate of change = −0.83 mm per year. No trend observed in the rest of the months and monsoon period of the districts concerned in this study. During June month, most of the districts under study show a decreasing trend (varies from −0.007 to −0.303 mm/year) except Baragarh, Keonjhar, and Sambalpur, with an increasing tendency (varies from 0.106 to 0.179 mm/year). In July, a decreasing tendency was observed in most of the districts (varies from −0.007 to −0.829 mm/year) except Baragarh, Gajapati, Ganjam and Kalahandi, with an increasing tendency (varies from 0.024 to 0.505 mm/year). In the case of August month, the increasing tendency is realised in Angul, Bhadrak, Cuttack, Ganjam, Kalahandi, Kendrapara, Keonjhar, Khurda and Puri (varies from 0.012 to 0.628 mm/year). In contrast, a decreasing tendency noticed in the districts of Baragarh, Gajapati, Koraput, Malkanagiri, Sambalpur, and Sundergarh (varies from −0.079 to −0.650 mm/year). During the last month of the monsoon season in September, most of the districts indicate an increasing tendency of rainfall (varies from 0.008 to 0.315 mm/year) except Keonjhar, Koraput, Malkanagiri and Sambalpur (varies from −0.05 to −0.199 mm per). After taking into consideration of whole monsoon season, decreasing in rainfall has been observed in the districts of Angul, Bhadrak, Gajapati, Keonjhar, Koraput, Malkanagiri, Sambalpur and Sundergarh (varies from −0.194 to −1.364 mm per year) whereas rising tendency noticed in the districts of Baragarh, Cuttack, Ganjam, Kalahandi, Kendrapara, Khurda and Puri (varies from 0.04 to 0.8 mm per year).

The increasing trend in rainfall at Cuttack suggests a possible shift in regional climate pattern with a steady increase of precipitation in August over the last century. Moreover, it raises concerns about potential flooding or shifts in agricultural conditions due to water availability. If the trend continues, there might be a significant increase in August average rainfall, implying higher average annual rainfall over the next few decades. In a similar context, the decreasing trend of rainfall indicates a drought-like situation in July and the monsoon season in the districts. In case of decrease in monsoon rainfall as well as average annual rainfall, paddy production in respective districts has been affected, as rainfall in July and August is crucial for good harvesting of paddy crop in Odisha. Mann- Kendall test results suggest no significant trend in monthly and whole monsoon period rainfall in most of the districts, and this stability implies that regional rainfall patterns have not shown an upward or downward trajectory, which may be attributed to balancing natural variability. So, minimal long-term climate-driven shifts in precipitation. Districts with increasing rainfall trends in July and August indicate the growth of paddy, whereas there are potential risks for water availability in the districts with decreasing trends.

In the coastal state of West Bengal, the researchers have shown a similar rainfall pattern. Some districts exhibit an increasing trend, whereas others record a decreasing trend in the monsoon season65,66. Analysis of the MK test indicates that the overall rainfall pattern has remained relatively stable over the 123 years for most of the districts under study, and this finding aligns with studies in similar regions or districts that report stable rainfall patterns, suggesting minimal long-term climate-driven shifts in precipitation.

Change point analysis (Pettitt Test)

The selection of change points for monsoon rainfall in each of the 15 districts, determined based on the p-value performance of these tests, is presented in Table 3.

Table 3 The Results of the Pettitt test for change point analysis of monsoon rainfall from 1901 to 2023 summarized.
Full size table

This table describes the presence of the change point (true or false), the p-value (P), the probable change year, and the mean rainfall before and after the detected change point. In the Angul district, the change point is marked as accurate with a p-value of 0.04, indicating statistical significance. The probable change year is 1944, with a decrease in mean rainfall from 1175.01 mm to 1073.30 mm. It suggests a long-time decline in rainfall after 1944. In a similar context, the p-value of 0.00 in the Koraput district shows a highly significant change point in 1947 with a decrease in rainfall from a pre-change mean of 1470.13 mm to a post-change mean of 1152.37 mm, resulting in a substantial shift in rainfall patterns. While analysing Sundergarh district parameter, the p-value of 0.005 also points to a significant change with a year of probable change being 1963 indicating decrease in rainfall from 1286.91 mm before 1963 to 1134.78 mm after the year. Moreover, p-values are above 0.05 for Baragarh and Bhadrak with 0.36 and 0.55, respectively, suggesting no statistically significant change point, although probable change year and mean values are listed.

From the table, it is inferred that the probable change years vary by district, ranging from 1919 to 2009, suggesting that the different districts experienced shifts in rainfall at other times, possibly due to localised environmental changes or geographical factors affecting rainfall distribution. The districts with statistically significant changes showing shifts in rainfall patterns could affect water resource planning, agricultural practices and flood management strategies. Keeping in view the probable change year of all 15 districts, it is observed that the total mean rainfall increased after the change point in districts such as Cuttack (133.39 mm), Ganjam (52.38 mm), Kalahandi (179.11 mm), Kendrapara (95.60 mm) and Puri (69.30 mm) whereas a decrease in rainfall after post change point is observed in remaining districts. The shifts in rainfall patterns can be attributed to climate change and human impact, including land use changes in the region. In case rainfall increased or became more erratic after the change point, it might imply greater variability or risk for agriculture, flood control, or water management.

The Pettitt test successfully identified significant change points in rainfall across different districts from the districts under study (e.g., Angul in 1944, Koraput in 1947, and Sundergarh in 1963). The pre-and post-change rainfall means to confirm a shift in monsoon rainfall patterns, with some districts experiencing increased and others decreasing rainfall after the change point. The p-values were checked for statistical significance, ensuring the reliability of detected change points. The findings align with previous studies on climate variability and human-induced changes in land use, supporting the validity of the detected change points. By applying the Pettitt test, researchers indicated a shift in Kolkata of the coastal state of West Bengal during the monsoon season while analysing rainfall data from 1901 to 201967. The identified years coincide with major climate pattern shifts (e.g., post-1940 s monsoon weakening in India, early 1960 s El Nino episodes).

Gross primary productivity (GPP) analysis

The variation of GPP during the monsoon season in Odisha during the period 2000- 2022 is illustrated in Fig. 2.

Fig. 2
figure 2

Trend of GPP from 2000 to 2022 during monsoon season for the state of Odisha.

Full size image

The peak of monsoon GPP in the past 23 years was 1026.67 gC/m2 per season in 2015, and the state was 566.45 gC/m2 per season in 2001. It may happen due to global warming causing increased CO2 concentration and other persistent global climate changes resulting in vegetation growth68. Regression analysis was applied to understand the linear trend for the period from year 2000 to 2022. The GPP increased at a rate of 10.8764 gC/m2 during the monsoon season, and the correlation coefficient is 0.65. Trend analysis of GPP during the monsoon period indicates a gradual increase in rainfall from 2000 to 2022, but the coefficient of correlation is −0.45. The increasing trend with a negative correlation coefficient is attributed to the variability of rainfall distribution during the monsoon season, followed by occasional heavy rainfall.

The linear positive trend is attributed to the forest cover consistently enhancing rainfall efficiency, favouring increased GPP. Also, it may be additionally due to high-yielding paddy varieties, better irrigation facilities, and fertiliser use that might have favoured increasing GPP.

An attempt has also been made to understand the trend of GPP concerning rainfall for a month and the whole monsoon season separately for each district. The analysis reveals that the regression analysis trend of GPP shows an increase in rainfall, barring no change or insignificant trend in September for Gajapati, Koraput, Malkanagiri, and Sambalpur, while a decreasing trend was observed in Sambalpur in June. However, the coefficient of correlation during the whole monsoon months June to September between GPP and rainfall is almost negative or insignificant, barring positive for Koraput and Malkanagiri (0.27 and 0.20 respectively) and also positive CC for Baragarh, Gajapati, Ganjam, Koraput and Malkanagiri (0.26, 0.29, 0.09, 0.11 and 0.21 respectively) in June.

The lower value of the coefficient of correlation may be due to excess rainfall associated with cloud cover, causing reduced solar radiation available for photosynthesis and impacting GPP value as GPP depends on sunlight. Moreover, advanced agricultural practices, such as high-yielding paddy varieties, better irrigation facilities, and fertilisers, are favoured to boost GPP. Moreover, a negative correlation indicates that rainfall may not be a direct positive contributor to GPP in many cases. Instead, extreme rainfall might be detrimental, causing stress in paddy crops. Effective water management practices such as drainage systems and supplementary irrigation can mitigate these issues. Moreover, threshold analysis can help identify the optimal rainfall ranges for GPP in each district by examining the relationship between rainfall and GPP across varying ranges (“Gross primary productivity (GPP) and rainfall analysis” and “Threshold analysis”). As shown in Fig. 3, the intercept values increase progressively with each subsequent month, highlighting the impact of cumulative rainfall on GPP.

Fig. 3
figure 3

Comparison of intercept values on Bar Charts from the regression between GPP and Rainfall during monsoon season for specific districts of Odisha.

Full size image

The intercept values in districts such as Kalahandi, Sambalpur, and Gajapati are higher due to their excellent forest cover, which contributes to higher GPP values. Extensive forests enhance carbon assimilation through photosynthesis, leading to a more significant impact on GPP in these regions. However, the crop area percentage is higher in the Kendrapara and Bhadrak districts. It shows that GPP may not always respond linearly to rainfall. A high intercept could mean that factors other than rainfall, such as temperature, solar radiation and nutrient availability, substantially drive productivity, particularly at lower rainfall levels. Therefore, a higher intercept implies that external inputs (e.g. irrigation, fertilisers) significantly support productivity even in low rainfall conditions, that is, efficient agricultural practices and better adaptation to rainfall variability.

A region or district with high intercept values shows that irrigation or alternative water sources effectively maintain productivity. By comparing intercepts across regions or districts, someone can identify better or worse areas equipped to handle rainfall deficits. Higher forest cover (e.g., Gajapati, Koraput and Malkanagiri) enhances GPP, while excessive rainfall can reduce solar radiation and affect photosynthesis.

In Fig. 4, the positive correlation in June regarding Baragarh, Gajapati, Ganjam, Koraput, and Malkanagiri signifies that soil moisture from pre-monsoon showers or irrigation might sustain baseline GPP even before significant rainfall. The negative correlation may be due to uneven rainfall distribution in subsequent months, even with adequate total rainfall, which can stress crops during critical growth stages (e.g. tillering in July or flowering in August). The misalignment of rainfall timing and crop water demand reduces the positive impact of rainfall on GPP. Regions or districts with a low coefficient of correlation (CC) might be less sensitive to rainfall variability due to alternative water sources (e.g. irrigation), so irrigation systems can mitigate the impact of poor monsoons.

Fig. 4
figure 4

r- value for June, July, August and September for 15 districts of Odisha.

Full size image

GPP trends show increasing productivity despite inconsistent rainfall correlations and negative correlations suggest that extreme rainfall impairs paddy growth, emphasizing the need for efficient water management. In Odisha, excess rainfall, especially during the monsoon, can lead to waterlogging in paddy fields. This can reduce GPP due to oxygen stress in the soil, impairing root respiration and nutrient uptake. Waterlogged conditions may also favour pest infestations and diseases, further impacting productivity. Variability in rainfall distribution within the monsoon season might lead to periods of drought stress followed by heavy rainfall. This can disrupt crop growth stages, lowering overall GPP.

The plotting of r-values for the whole monsoon of 15 districts with the percentage of forest area and r-values versus the rate of crop area in Fig. 5(a) and 5(b), respectively, indicate the sensitivity of individual land use classes during the monsoon period.

Fig. 5
figure 5

Regression outputs of coefficient of correlation between Gross Primary Productivity (GPP) and rainfall with land use class (%) for the whole of Odisha (based on 15 districts). 5.(a). r values for monsoon months and forest area (%) and 5.(b). r values for monsoon months and cropped area (%).

Full size image

The linear trend line indicates that the GPP was more sensitive to forest area than to the crop area region. The r-value concerning forest area is more than 0.6 (= 0.73). In contrast, the crop area shows 0.32 because forest areas exhibit higher photosynthetic activity due to dense forest cover, significantly contributing to GPP. The forest area also increases yearly. In contrast, photosynthetic activity is limited by seasonal cropping patterns. Moreover, monsoon rain vigorously enhances the photosynthetic effect in forest areas compared to seasonal crop areas. Forests absorb and retain water, reducing runoff and ensuring consistent soil moisture availability. This moderates the impact of rainfall variability on GPP.

If forest cover consistently enhances the efficiency of rainfall in driving GPP, the graph will show a linear trend. Beyond a certain level of forest cover, the rainfall-GPP correlation might saturate, leading to a plateau in the graph. Districts with low forest cover may depend more on agricultural land for GPP, making the correlation between rainfall and GPP stronger in such districts. In contrast, forest-dominated districts may exhibit relationships that are more complex. It may be due to the ecological buffering provided by forests. Higher forest cover (e.g., Gajapati, Koraput and Malkanagiri) enhances GPP, while excessive rainfall can reduce solar radiation and affect photosynthesis.

The increasing GPP trend (2000–2022) with a correlation coefficient 0.65 suggests a significant positive trend in vegetation productivity, aligning with previous MODIS-based GPP studies. The correlation analysis between GPP and rainfall showed mixed relationships, indicating the complexity of rainfall impacts on productivity. The negative correlation in some districts suggests excessive rainfall and cloud cover may reduce available solar radiation, affecting photosynthesis. The variation in r-values with land use (forest vs cropped areas) confirms that forested regions are more sensitive to rainfall changes than cropped areas, validating the ecological role of forests in carbon assimilation.

Threshold analysis

The optimal rainfall range is generated during monsoon season for 15 districts of our study, and the corresponding maximize GPP is also sorted out from bar chart Fig. 6(a) to 6(o). This signifies the ideal crop growth or ecosystem condition in the concerned district. Too little or too much rainfall outside the optimal range leads to reduced GPP. Rainfall deficits can cause drought stress, while excess rain can result in excess rainfall, water logging, or flooding. The threshold value of GPP against the optimal rainfall range is shown in Table 4. The highest GPP threshold values are generated for Gajapati, Ganjam, Kalahandi, Koraput and Malkanagiri. However, the optimal rainfall range is higher for Kalahandi, Koraput and Malkanagiri, whereas the low range is for Gajapati and Ganjam. This is attributed to the higher percentage of forest area in Gajapati. As it is observed that the coefficient of correlation is negative for rainfall versus GPP, threshold analysis can identify any increasing trends where GPP rises with rains up to the optimal range. These are reflected in Table 4. and bar charts of each of the 15 districts in Figs. 6 (a) to 6 (o).

Fig. 6
figure 6

The Bar Chart highlights how GPP varies across different rainfall ranges.

Full size image
Table 4 Threshold Analysis of highest GPP based on Optimal Rainfall Range for 15 districts of Odisha.
Full size table

The threshold value provides a guideline for optimal agricultural practices, identifying ideal conditions for farming and crop yield predictions. Depending on soil, crop, and farming practices, different districts may have varying thresholds. The optimal rainfall range for GPP indicates that districts experiencing the optimal rainfall range are likely to exhibit peak agrarian productivity. Based on this information, agricultural planning and climate adaptation strategies can be considered for prospects, particularly in monsoon-dependent districts. As rainfall varies across regions and years, periodic reassessment of these thresholds is essential to ensure sustainable land and water management practices. Figure 7 shows the GPP value for the optimal range of rainfall during the monsoon season for Odisha using only 15 districts’ data. This analysis identified the rainfall range 950–1000 mm as optimal for maximizing GPP, with a peak mean GPP of 903.63 during the monsoon season for Odisha.

Fig. 7
figure 7

Bar chart highlights the variation of GPP across different optimal ranges of rainfall.

Full size image

Identifying optimal rainfall-GPP relationships helps in climate adaptation strategies. Efficient irrigation, drainage, and precision farming can mitigate risks from extreme rainfall variations. Periodic reassessment of threshold values is necessary for sustainable water and land management.

The threshold analysis identified optimal rainfall ranges for maximizing GPP, confirming that excess and deficit rainfall reduces GPP. The highest GPP values in forested districts like Gajapati, Koraput and Malkanagiri suggest a strong rainfall-driven productivity response in natural ecosystems. The statistical approach using rainfall bins and mean GPP values ensures an objective method to determine threshold values. The findings align with global studies on non-linear GPP responses to precipitation, supporting their validity.

Conclusion

This study highlights the intricate relationship between monsoon rainfall and GPP in Odisha’s diverse agro-climatic zones. While most of the districts exhibit stable rainfall trends. Some show significant declines, emphasizing the need for adaptive water resource planning. Higher intercept values in regression analysis of rainfall versus GPP indicate efficient agricultural practices. Better adaptation to rainfall variability and a low coefficient of correlation (r) imply that these regions are less sensitive to rainfall variability due to alternative water sources (e.g. irrigation). Threshold analysis identified optimal rainfall ranges for maximizing GPP across districts based on forest cover and crop type. Presumably, excessive rainfall diminishes GPP due to waterlogging, while deficit causes drought stress. The findings emphasize the importance of localized agricultural strategies tailored to rainfall thresholds for sustainable productivity. Future studies could integrate additional climatic factors such as temperature and CO2 concentration to refine the understanding of ecosystem productivity under changing climate conditions.

June rainfall sets the stage for the rest of the monsoon season. A significant departure (deficit or excess) in June affects soil moisture availability, sowing schedules, and early crop vigour, creating a cascade of effects throughout the growing season. For example, if there is a deficit of rainfall in June, then late sowing or poor establishment leads to shorter crop duration, reduced tillering, and lower overall productivity. While good rainfall in subsequent months can partially compensate for an early-season deficit, it often cannot fully recover the lost potential due to the critical role of June rainfall in establishing optimal growing conditions. Adaptive water resource planning is needed for districts with decreasing rainfall trends. GPP monitoring and forecasting tools should be developed to improve agricultural resilience. Long-term climatic land-use studies should be integrated to develop better climate adaptation policies.

Identifying the optimal range that maximises GPP helps make informed decisions for agricultural practices, resource management, and climate adaptation. This study contributes to scientific knowledge such as providing long-term spatiotemporal rainfall trend analysis (1901–2023) using robust statistical methods (Mann–Kendall and Pettitt tests), and establishing a direct link between monsoon rainfall variability and Gross Primary Productivity (GPP), offering insights into ecosystems responses to climate variability. Moreover, the optimal rainfall thresholds for maximising GPP can be identified, which is crucial for climate-adaptive agricultural strategies in Odisha and demonstrates how forested and cropped areas respond differently to rainfall fluctuations, highlighting the role of land use in climate resilience. Besides these advantages, it offers validated methodological approaches, including crosschecking data with ERA5 and in-situ observations, ensuring accuracy and applicability in future climate studies.

Further studies could explore the combined effects of rainfall, temperature and other climatic variables, to provide a more comprehensive understanding of their interactions and impacts on paddy yield.