Introduction

HIV, the human immunodeficiency virus, progressively debilitates the immune system, eventually resulting in Acquired Immune Deficiency Syndrome (AIDS), where the immune system is significantly impaired. A condition triggered by a pathogen that assaults and assaults lymphocytes, ensuing in a lessened defense against contaminated aliment, is also referred to as HIV. The latter stage, dubbed AIDS, can take a patient anywhere from 2 to 15 years to manifest. AIDS can be marked by particular cancers, ailments, or other devastating clinical manifestations. It is generally thought that over 30 million people perished from HIV over the span of 30 years and that 7000 fresh instances of the virus are contracted abroad entire day. An estimated 44% of new pathogens in 2015 were thought to have emanated from substantial groups and their spouses. Around one-fourth of all fatalities annually are triggered by accessible aliment, leading to severe repercussions for civilization1. According to HIV/AIDS data in 2021, over 38.4 million [33.9–43.8 million] individuals around the world are HIV positive, 1.5 million [1.1–2 million] individuals have been impacted with HIV, 650,000 [510,000–860,000] individuals expired from illness that associated with AIDS, and 28.7 million individuals are approaching antiretroviral therapy2.

Screening CD4 + lymphocytes is a frequently utilized approach to monitoring the immune system’s effectiveness. Various personal fluids, such as plasma, sperm, pre-coughing fluid, secretions from the genitals, and infant milk, are capable of enacting HIV from an HIV-positive individual to an AIDS-negative adult. HIV cannot momentarily be curable or averted, but it may be regulated with adequate medical assistance. ART diminishes the probability of conveying HIV, prolongs frequently destiny, and enhances well-being3. Drug resistance (DR) could hamper the therapeutic effect of ART agents, yet they have proven productive in lessening the prevalence of HIV as well as the associated mortality and morbidity. HIV-DR is marked by a mutation in the genetic code of HIV which renders it attainable to safely prevent the replication of the virus with a particular medication or a mixture of pharmaceuticals4,5. A deep understanding of HIV transmission dynamics is crucial for developing operative prevention and treatment approaches. Mathematical modeling plays a vigorous role in examining viral epidemiology, evaluating interventions, predicting future trends, and addressing serious social challenges.

In recent years, fractional calculus has appeared as a dominant tool for modeling complex systems, allowing the calculation of derivatives and integrals of any positive real order. This ability has significantly improved models by integrating non-local physiognomies and memory effects6. Several fractional derivative methods, such as the Riemann-Liouville, Katugampola, Hadamard, and Caputo derivatives, have proved their efficacy in improving the precision of simulations for Real-life occurrences8,28. The idea of fractional derivatives was initially introduced by Riemann-Liouville in 1832 and far ahead refined by Caputo in 1967. Caputo’s devising comprised initial and boundary conditions, making it more pertinent for solving practical problems5,7,10. Each derivative operator is intended to cater to precise system dynamics and present varying degrees of flexibility based on the requirements. Numerical, iterative methods and computational techniques have been widely applied to study fractional-order mathematical models9,29.

Recent studies have progressive numerical approaches, for instance, the A–B Forth Moulton approach presented by Baleanu8, under the context of the generalized Caputo operator (GCO). Mathematical models are characteristically classified as either deterministic or stochastic. For example, Li et al.11 estimated the dynamic behavior of models using both the SFD and NSFD methods. An ensemble-based approach with a temporal lag, reflecting the delay in a virus’s ability to infect healthy T cells, was discovered by Roy et al.12. Wu et al.8 examined the erratic conduct and permanency of fractional differential equations (FDEs) under a generalized Caputo derivative framework. Cai et al.13 examined a model that incorporated the phases of symptomatic and asymptomatic development for infected individuals, enabled by a variety of treatments. Goyal et al.14 evaluated disease dynamics using the fractal fractional derivative operators (FDOs) and the Caputo–Fabrizio. To study the spread of HIV/AIDS, Aslam et al.15 constructed an FDO with a Mittag–Leffler kernel. The concept of piecewise FDEs employing the Atangana–Baleanu derivative was introduced by Iqbal et al.16, and an integer-order nonlinear HIV/AIDS propagation model was constructed by Shaiful et al.17 as a modification of a non-integer model. Additional notable publications include Jan et al.18, who proposed a model explaining the dynamics of HIV/AIDS transmission between genders, and Naik et al.19, who evaluated novel HIV/AIDS models using Caputo fractional derivatives. Piqueira et al.20 developed a model that brought social network effects into account. Kumar et al.21 evaluated an HIV transmission model using fractional-order approaches.

Anjam et al.26 utilized fractal-fractional derivatives via the Caputo operator to investigate HIV transmission patterns across three infection levels. A TB-HIV co-infection model incorporating exogenous reinfection and recurrent TB was studied using a non-local operator with a Mittag–Leffler kernel27. New models have been developed to study disease transmission, including a reaction-diffusion model for HIV/AIDS, emphasizing its chronic nature and socioeconomic impacts34; a Chagas-HIV model with fractional operators35; and a reaction-diffusion framework for SARS-CoV-2 to enhance public health strategies37. Additionally, an Artificial Neural Network (ANN)-based framework was introduced to model Ebola transmission dynamics and long-term outcomes38.

Further advancements include mathematical models for Monkeypox transmission in humans and rodents39, Hepatitis B using fractional-order dynamics with memory effects40, and malaria in Africa incorporating treatment and vaccination strategies via the Atangana–Baleanu fractional derivative41. The study also explores the complex joint dynamics of bovine tuberculosis (bTB) and rabies, highlighting the challenges posed by their differing transmission mechanisms42. The versatility of fractional calculus in dynamic modeling, particularly in epidemiology, demonstrates its potential to address complex scientific problems and advanced computational techniques.

Several studies also have explored the mathematical modeling of HIV/AIDS dynamics using real-world data. A temporal fractional HIV/AIDS model with fractal dimensions was developed to examine the influence of awareness on the transmission dynamics of HIV/AIDS in India, utilizing actual data from 1990 to 2016 to validate the proposed model30. Similarly, Ref32. employed mathematical models to forecast the outbreaks of HIV/AIDS—one of the most critical public health challenges—in South Africa from 1990 to 2021, aiming to assess the country’s preparedness for combating the epidemic in the near future. Furthermore, a mathematical model was formulated to investigate the dynamics of HIV/AIDS in real-world scenarios, incorporating reported HIV/AIDS statistics from Pakistan (1992–2020) to analyze its transmission patterns and conduct a comprehensive mathematical assessment33.

In order to accurately model the long-term dynamics, crossover behavior, and memory effects of HIV transmission, it is necessary to choose the proper fractional operator and kernel type. The Caputo operator is an important decision in this situation because of its power-law kernel, which is exceptionally equipped for preserving these memory effects and long-term interactions. These features serve as vital for accurately modeling the intricate dynamics of HIV transmission because they enable a realistic depiction of the various elements that contribute to the virus’s spread. These components include individual behavior, social attitudes, healthcare restrictions, and the efficacy of treatments, each of which is important for analyzing and preventing HIV spread. As a result of this awareness, the study has shifted its attention to the findings’ deeper implications.

This research investigates the dynamics of HIV transmission by establishing a compartment for recovered persons, which accounts for the implementation of hospitalized patients to recovery. The model is dependent on a generalized Caputo fractional operator (CFO) with two fractional-order variables, considerably improving its potential to capture genetic and memory effects. Six different compartments are used to classify the population. The model’s dependability is verified by a thorough study that uses the fixed-point theory framework to verify the existence and uniqueness of solutions. The significance of the research is tackled by establishing a new numerical method for simulations based on the predictor–corrector approach, which is validated in MATLAB. Simulation results are graphically presented for various fractional orders, allowing for comparisons with integer-order models. This study underscores the efficacy of the fractional approach, highlighting the model’s sensitivity to changes in fractional orders.

The subsequent sections of the article are ordered as follows: “Essential preliminaries” offers a brief explanation of fractional-order calculus, whereas “Model construction” defines the model formulation and its fractional representation. “Qualitative analysis of model” concentrates on model analysis, and sensitivity analysis, and also discusses the stability aspects of the model under consideration. “Theoretical exploration of the FO HIV dynamics” provides the validation of the existence and uniqueness of the solution. “Numerical techniques for the devised model” offers specifics of the numerical simulations by using the novel predictor-corrector-based numerical technique and application to the proposed model. The numerical solutions are presented in “Results and discussion”, whereas the discussion of results is given. Finally, “Conclusion” offers a concise summary of the article.

Essential preliminaries

In this segment, the main definitions of generalized fractional operators from earlier research are reviewed, which will be applied in the study22,23,24.

Definition

The generalized fractional integral of a function \(z(\hat {p}),\)is specified as \(\delta \in (k - 1,k],\) while \(k \in N\) (if remains integral)

$$I_{{{a^+}}}^{{\delta ,\sigma }}z(\hat {p})=\frac{{{\sigma ^{(1 - \delta )}}}}{{\Gamma (\delta )}}\int\limits_{a}^{{\hat {p}}} {{\xi ^{(\sigma - 1)}}({{\hat {p}}^\sigma }} - {\xi ^\sigma }{)^{\delta - 1}}z(\xi )d\xi ,\hat {p}>a,$$
(1)

where \(\sigma >0,\) and \(a \geqslant 0.\)

Definition

The parameter order \(\delta\) of generalized Caputo derivative (GCD) for \(z(\hat {p})\) is specified that \(\delta \in (k - 1,k],\) while \(k \in N\) and \(\sigma >0,\) \(a \geqslant 0,\)then

$${}^{C}D_{{{a^+}}}^{{\delta ,\sigma }}z(\hat {p})=I_{{{a^+}}}^{{k - \delta ,\sigma }}({{\rm X}^k}z)(\hat {t})=\frac{{{\sigma ^{(\delta - k+1)}}}}{{\Gamma (k - \delta )}}\int\limits_{a}^{{\hat {p}}} {{\xi ^{(\sigma - 1)}}({{\hat {p}}^\sigma }} - {\xi ^\sigma }{)^{k - \delta - 1}}{{\rm X}^k}z(\xi )d\xi ,\hat {p}>a,$$
(2)

where \({\rm X}=({\xi ^{(1 - \sigma )}}\frac{d}{{d\xi }}),\) and approach the new derivative as an isolated case, when \(\delta \in (0,1)\) and \(a=0,\)the new form GCD is given as follows:

$${}^{C}D_{{{a^+}}}^{{\delta ,\sigma }}z(\hat {p})=\frac{{{\sigma ^{(\delta )}}}}{{\Gamma (1 - \delta )}}\int\limits_{0}^{{\hat {p}}} {({{\hat {p}}^\sigma }} - {\xi ^\sigma }{)^{ - \delta }}{z^\prime}(\xi )d\xi ,\hat {p}>0.$$
(3)

Model construction

Analyzing the dynamics of HIV transmission and establishing effective preventative and treatment strategies are both enhanced by the incorporation of mathematical models. It is essential to construct such models using epidemiological strategies in order to provide insight into the basic mechanisms of HIV transmission. It is essential to determine important factors to mitigate HIV transmission. The development of prevention and treatment strategies has benefited tremendously from the construction and documentation of several HIV transmission models that depend on infectious mechanisms.

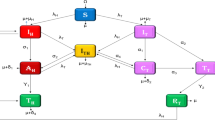
This research is centered on investigating the dynamics of HIV-AIDS transmission by presenting a compartment for recovered individuals, which accounts for the transition of hospitalized patients to recovery. The model construction distributes the whole populace of humanity into six distinct subsets those are outlined beneath: Susceptible uninformed populace (\(\tilde{S}_{u}\)), the Susceptible informed populace \((\tilde{S}_{i} ),\) the HIV-infected populace \((\tilde{I}),\) the AIDS-afflicted people \((\tilde{A}),\) the HIV-infected populace with ART medication \((\tilde{C}),\) and the recovered individuals \((\tilde{R}).\)Entirely population is indicated by \(\tilde{E}_{p}\) that is specified as:

$${\tilde {E}_p}={\tilde {S}_u}+{\tilde {S}_i}+\tilde {I}+\tilde {A}+\tilde {C}+\tilde {R}.$$

The rate at which susceptible individuals acquire the infection through interacting with infectious individuals is the force of infection in our model. It depicts the dynamics of disease transmission by quantifying the risk of infection per capita and capturing the interplay between susceptible and infected populations.

Moreover, the assumptions employed in formulating the mathematical model for the spread of HIV/AIDS are as follows:

  • The individuals \(\tilde{C}\) and \(\tilde{A}\) are assumed not to spread HIV due to their specific condition.

  • The population\(\tilde{A}\) is assumed not to spread HIV, as the AIDS population is considered too ill to transmit the virus (until isolated).

  • Unaware individuals\(\tilde{S}_{u}\) can transition to becoming aware\(\tilde{S}_{i}\), but the reverse is not possible.

  • Individuals with AIDS who begin antiretroviral therapy (ART) will transition into the treated population and will remain in this group if they consistently adhere to the therapy.

  • It is supposed that individuals suffering from HIV and AIDS have access to antiretroviral therapy (ART) treatment.

  • The mortality rate due to HIV/AIDS is assumed to occur only among individuals affected by AIDS.

Based on the aforementioned principles, Fig. 1 illustrates the flow pattern of interaction between the different stages of infectious diseases. Thus, the integer-order model with a consciousness alter regarding HIV-AIDS propagation is specified as:

$$S_{u}^{\prime }={\rm X} - \frac{{{{\tilde {S}}_u}\tilde {I}{\gamma _1}}}{{{{\tilde {E}}_p}}} - {\tilde {S}_u}(\omega _{{(1)}}^{ * }+{\rho _1}),$$
$$S_{i}^{\prime }={\tilde {S}_u}{\rho _1} - \frac{{{{\tilde {S}}_i}\tilde {I}{\gamma _1}}}{{{{\tilde {E}}_p}}}(1 - {\xi _1}) - {\tilde {S}_i}\omega _{{(1)}}^{ * },$$
$${I^\prime}=({\tilde {S}_i}(1 - {\xi _1})+{\tilde {S}_u})\frac{{\tilde {I}{\gamma _1}}}{{{{\tilde {E}}_p}}}+\tilde {C}{\phi _{(1)}}+\tilde {A}{\theta _1} - \tilde {I}(\omega _{{(1)}}^{ * }+{\nu _1}+{\eta _{(1)}}),$$
(4)
$${A^\prime}=\tilde {I}{\eta _{(1)}} - \tilde {A}({\varphi _1}+\omega _{{(1)}}^{ * }+{\theta _1}),$$
$${C^\prime}=\tilde {I}{\nu _1} - \tilde {C}(\omega _{{(1)}}^{ * }+{\phi _{(1)}}),$$
$${R^\prime}=\tilde {I}{\sigma _1}+\tilde {C}{\sigma _2}+\tilde {A}{\sigma _3} - \tilde {R}\omega _{{(1)}}^{ * }$$

Hence, the initial conditions are:

$${\tilde {S}_u}(0)={E_1},{\tilde {S}_i}(0)={E_2},\tilde {I}(0)={E_3},\tilde {C}(0)={E_4},\tilde {A}(0)={E_5},\tilde {R}(0)={E_6}.$$

This model (4) is constructed here using the newly introduced GCFD. The following is the apprised rendition of the proposed model:

$${}^{C}D_{0}^{{\delta ,\sigma }}{\tilde {S}_u}={\rm X} - \frac{{{{\tilde {S}}_u}\tilde {I}{\gamma _1}}}{{{{\tilde {E}}_p}}} - {\tilde {S}_u}(\omega _{{(1)}}^{ * }+{\rho _1}),$$
$${}^{C}D_{0}^{{\delta ,\sigma }}{\tilde {S}_i}={\tilde {S}_u}{\rho _1} - \frac{{{{\tilde {S}}_i}\tilde {I}{\gamma _1}}}{{{{\tilde {E}}_p}}}(1 - {\xi _1}) - {\tilde {S}_i}\omega _{{(1)}}^{ * },$$
$${}^{C}D_{0}^{{\delta ,\sigma }}\tilde {I}=({\tilde {S}_i}(1 - {\xi _1})+{\tilde {S}_u})\frac{{\tilde {I}{\gamma _1}}}{{{{\tilde {E}}_p}}}+\tilde {C}{\phi _{(1)}}+\tilde {A}{\theta _1} - \tilde {I}(\omega _{{(1)}}^{ * }+{\nu _1}+{\eta _{(1)}}),$$
(5)
$${}^{C}D_{0}^{{\delta ,\sigma }}\tilde {A}=\tilde {I}{\eta _{(1)}} - \tilde {A}({\varphi _1}+\omega _{{(1)}}^{ * }+{\theta _1}),$$
$${}^{C}D_{0}^{{\delta ,\sigma }}\tilde {C}=\tilde {I}{\nu _1} - \tilde {C}(\omega _{{(1)}}^{ * }+{\phi _{(1)}}),$$
$${}^{C}D_{0}^{{\delta ,\sigma }} \tilde{R} = \tilde{I}\sigma _{1} + \tilde{C}\sigma _{2} + \tilde{A}\sigma _{3} - \tilde{R}\omega _{{(1)}}^{ * } ,$$
Fig. 1
figure 1

Schematic flow of the proposed model.

Full size image

where the following is an outline of the model parameters mentioned above:

  • \({\rm X}\) indicates the susceptible uninformed,

  • \({\gamma _1}\) For the HIV acquisition rate,

  • \({\rho _1}\) symbolizes the rapid rate at which \({S_u}\) changes into \({S_i}\),

  • \(\omega _{{(1)}}^{ * }\) signifies the frequency of natural mortality,

  • \({\phi _{(1)}}\) shows the number of people in class C who go to class I.

  • \({\theta _1}\) symbolizes the clip at which A shifts to I.

  • \({\nu _1}\) illustrates the rate of improvement in class I subsequent toward class C.

  • \({\eta _{(1)}}\) depicts rapidity while A converts from I.

  • \({\varphi _1}\) reflects the mortality rate from AIDS.

  • \({\sigma _1}\),\({\sigma _2}\),\({\sigma _3}\) identify the extent of recurrence from infected people \({S_u}\) to \({S_i}\) and from hospitalized patients to recovered cases.

  • \({\xi _1}\) Indicates the proportion of \({S_i}\) those who get an infection.

Qualitative analysis of model

In the upcoming section, our study will emphasize the mathematical formulation encapsulated in the model (4). Our investigation will delve into the aspects of boundedness and positivity within the model. Additionally, we will determine the equilibrium points and compute the basic reproduction number. The sensitivity analysis and the local stability and global stability of the developed model at equilibrium points are also explored.

Positivity

Positivity constraints are imposed on both the initial conditions and parameters in the devised model, ensuring that their values remain non-negative or greater than zero throughout the modeling process. This imposition enhances the model’s reliability by minimizing the occurrence of unrealistic outcomes, thereby improving its applicability and making it more representative of real-world scenarios and behaviors.

Theorem 4.1

We assume a positive initial value for the problem specified in Eq. (4) and if the solutions to the model in Eq. (4) exist, they will be positive for all time \(\:\text{t}>0\).

Proof

Let us consider the first equation of the devised model (4) as

$$\:\frac{d{\stackrel{\sim}{S}}_{u}\:}{dt}=X-\frac{{\stackrel{\sim}{S}}_{u}I{\stackrel{\sim}{r}}_{1}}{{\stackrel{\sim}{E}}_{p}}-{\stackrel{\sim}{S}}_{u}\left({\omega\:}_{1}^{*}+{\rho\:}_{1}\right).$$

By constant formula of alternation provides the solution

$$\:{\stackrel{\sim}{S}}_{u}\left(t\right)={\stackrel{\sim}{S}}_{u}\left(0\right)exp\left[-\underset{0}{\overset{t}{\int\:}}\left({\omega\:}_{1}^{*}+{\rho\:}_{1}\right)dt-{\omega\:}_{1}^{*}t\right]+exp\left[-\underset{0}{\overset{t}{\int\:}}\left({\omega\:}_{1}^{*}+{\rho\:}_{1}\right)dt-{\omega\:}_{1}^{*}t\right]X$$
$$\:\left(X-\frac{{\stackrel{\sim}{S}}_{u}\stackrel{\sim}{I}{r}_{1}}{{\stackrel{\sim}{E}}_{p}}\right)\int\:exp\left[\underset{0}{\overset{t}{\int\:}}\left({\omega\:}_{1}^{*}+{\rho\:}_{1}\right)dt-{\omega\:}_{1}^{*}t\right]dt.$$

Hence, \(\:{\stackrel{\sim}{S}}_{u}\left(t\right)\ge\:0\) for all time \(\:\text{t}>0\).

Similarly, it can be shown that \(\:{\stackrel{\sim}{S}}_{i}\ge\:0,\:\stackrel{\sim}{I}\ge\:0,\:\stackrel{\sim}{A}\ge\:0,\:\stackrel{\sim}{C}\ge\:0,\:\stackrel{\sim}{R}\ge\:0.\)

Invariant region

We determined the invariant region where the solution of the proposed model is bounded. Now, consider the total population of the given model as:

$${\tilde {E}_p}={\tilde {S}_u}+{\tilde {S}_i}+\tilde {I}+\tilde {A}+\tilde {C}+\tilde {R}.$$
(6)

Now, differentiate Eq. (6) provides

$$\:\frac{d{\stackrel{\sim}{E}}_{p}}{dt}=\frac{d{\stackrel{\sim}{S}}_{u}}{dt}+\frac{d{\stackrel{\sim}{S}}_{i}}{dt}+\frac{d\stackrel{\sim}{I}}{dt}+\frac{d\stackrel{\sim}{A}}{dt}+\frac{d\stackrel{\sim}{C}}{dt}+\frac{d\stackrel{\sim}{R}}{dt}.$$
(7)

Substituting all the state equations from the model (4) into Eq. (7) yields

$$\:\frac{d{\stackrel{\sim}{E}}_{p}}{dt}=X-{\omega\:}_{1}^{*}{\stackrel{\sim}{E}}_{p}.$$
(8)

Taking integration on both sides of Eq. (8) with \(\:\text{t}\to\:{\infty\:},\) one obtains \(\:{\stackrel{\sim}{E}}_{p}\le\:\frac{\text{X}}{{{\upomega\:}}_{1}^{\text{*}}}\).

Thus, \(\:{\stackrel{\sim}{E}}_{p}\left(\text{t}\right)\le\:\frac{\text{X}}{{{\upomega\:}}_{1}^{\text{*}}}\:\text{a}\text{s}\:\text{t}\to\:{\infty\:}\)

$$\:\varOmega\:=\left\{{\stackrel{\sim}{S}}_{u},\:{\stackrel{\sim}{S}}_{i},\:\stackrel{\sim}{I},\:\stackrel{\sim}{A},\:\stackrel{\sim}{C},\:\stackrel{\sim}{R}\in\:{R}_{+}^{6}:\:{\stackrel{\sim}{S}}_{u}+{\stackrel{\sim}{S}}_{i}+\stackrel{\sim}{I}+\stackrel{\sim}{A}+\stackrel{\sim}{C}+\stackrel{\sim}{R}\le\:\frac{X}{{\omega\:}_{1}^{*}}\right\}.$$

Clearly, \(\:\varOmega\:\) is positively invariant.

Equilibrium points

Equilibrium points indicate in stable condition in the progression of the disease, where the occurrence of new infections is offset by combined occurrences of recoveries and deaths. Equilibrium points have two important types disease disease-free and endemic equilibrium. Disease Free Equilibrium (DFE) represents when there is no disease in the population. To calculate DFE \(\:{D}_{0}\), we put \(\:\frac{d\stackrel{\sim}{I}}{dt},\:\frac{d\stackrel{\sim}{A}}{dt},\:\frac{d\stackrel{\sim}{C}}{dt},\:\frac{d\stackrel{\sim}{R}}{dt}=0\). Expect the susceptible class \(\:{\stackrel{\sim}{\text{S}}}_{\text{u}},\:{\stackrel{\sim}{\text{S}}}_{\text{i}},\) which we set to its initial values.

This point helps us to compare disease behavior in the presence and absence of disease.

$$\:{D}_{0}=\left({\stackrel{\sim}{S}}_{u}\left(0\right),\:{\stackrel{\sim}{S}}_{i}\left(0\right),\:0,\:0,\:0,\:0\right),$$
$$\:{D}_{0}=\left(\frac{X}{{\omega\:}_{1}^{*}+{\rho\:}_{1}},\:\frac{{\stackrel{\sim}{S}}_{u}{\rho\:}_{1}}{{\omega\:}_{1}^{*}},\:0,\:0,\:0,\:0\right)$$

.

Now, the endemic equilibrium points are calculated as:

$$\:{D}^{*}=\left({\stackrel{\sim}{S}}_{u}^{*},\:{\stackrel{\sim}{S}}_{i}^{*},\:{\stackrel{\sim}{I}}^{*},\:{\stackrel{\sim}{A}}^{*},\:{\stackrel{\sim}{C}}^{*},\:{\stackrel{\sim}{R}}^{*}\right),$$

where,

$$\:{\stackrel{\sim}{S}}_{u}^{*}=\frac{X{\stackrel{\sim}{E}}_{p}}{\stackrel{\sim}{I}{r}_{1}+\left({\omega\:}_{1}^{*}+{\rho\:}_{1}\right)},$$
$$\:{\stackrel{\sim}{S}}_{i}^{*}=\frac{X{\stackrel{\sim}{E}}_{p}^{2}{\rho\:}_{1}}{\left[\stackrel{\sim}{I}{r}_{1}+\left({\omega\:}_{1}^{*}+{\rho\:}_{1}\right)\right]\left[\stackrel{\sim}{I}\:{r}_{1}\left(1-{\xi\:}_{1}\right)-{\omega\:}_{1}^{*}{\stackrel{\sim}{E}}_{p}\right]},$$
$$\:{\stackrel{\sim}{I}}^{*}=\frac{{\stackrel{\sim}{E}}_{\:p}\left({\omega\:}_{1}^{*}+{\varphi\:}_{1}\right)\left({\varphi\:}_{1}+{\omega\:}_{1}^{*}+{\theta\:}_{1}\right)\left({\omega\:}_{1}^{*}+{\upsilon\:}_{1}+{\eta\:}_{1}\right)-\left({\stackrel{\sim}{S}}_{i}^{*}\left(1-{\xi\:}_{1}\right)+{\stackrel{\sim}{S}}_{u}^{*}\right){r}_{1}+{\nu\:}_{1}+{\eta\:}_{1}}{\left({\stackrel{\sim}{S}}_{i}\left(1-{\xi\:}_{1}\right)+{\stackrel{\sim}{S}v}_{u}\right){r}_{1}+{\nu\:}_{1}+{\eta\:}_{1}},$$
$$\:{\stackrel{\sim}{A}\:}^{*}=\frac{\stackrel{\sim}{I}{\eta\:}_{1}}{\left({\varphi\:}_{1}+{\omega\:}_{1}^{*}+{\theta\:}_{1}\right)},$$
$$\:{\stackrel{\sim}{C}}^{*}=\frac{\stackrel{\sim}{I}\:{\nu\:}_{1}}{{\omega\:}_{1}^{*}+{\varphi\:}_{1}},$$
$$\:{\stackrel{\sim}{R}}^{*}=\frac{\left[{\sigma\:}_{1}\left({\varphi\:}_{1}+{\omega\:}_{1}^{*}+{\theta\:}_{1}\right)+{\nu\:}_{1}{\theta\:}_{1}+{\eta\:}_{1}\right]\stackrel{\sim}{I}}{{\omega\:}_{1}^{*}\left({\varphi\:}_{1}+{\omega\:}_{1}^{*}+{\theta\:}_{1}\right)}.$$

The basic reproduction number

The threshold value, or basic reproduction number \(\:{R}_{0}\), is a widely employed statistic for evaluating a communicable disease’s transmissibility or contagiousness. In a vulnerable group, it represents the average amount of people infected by a single infectious person. Biologically, it reflects the contagiousness and transmissibility of a pathogen. If \(\:{R}_{0}>1,\) it indicates that the disease has the potential to sustain transmission within the population, leading to an outbreak. Conversely, if \(\:{R}_{0}<1\), the infection is unlikely to establish a self-sustaining chain of transmission, and it may eventually die out in the population. Using the principle of the next-generation matrix, it is calculated as

$$\:F=\left[\begin{array}{ccc}\frac{\left({\stackrel{\sim}{\text{S}}}_{\text{i}}\left(1-{{\upxi\:}}_{1}\right)+{\stackrel{\sim}{\text{S}}}_{\text{u}}\right){\text{r}}_{1}}{{\stackrel{\sim}{\text{E}}}_{\text{p}}}&\:0&\:0\\\:0&\:0&\:0\\\:0&\:0&\:0\end{array}\right]$$

.

$$\:V=\left[\begin{array}{ccc}\left({{\upomega\:}}_{1}^{\text{*}}+{{\upupsilon\:}}_{1}+{{\upeta\:}}_{1}\right)&\:0&\:0\\\:0&\:\left({{\upvarphi\:}}_{1}+{{\upomega\:}}_{1}^{\text{*}}+{{\uptheta\:}}_{1}\right)&\:0\\\:0&\:0&\:\text{c}\left({{\upomega\:}}_{1}^{\text{*}}+{{\upvarphi\:}}_{1}\right)\end{array}\right].$$

Therefore, the reproduction number \(\:{R}_{0}\) for our devised model (5) is the spectral radius of the next generation matrix \(\:F{V}^{-1}\) and calculated as,

$$\:F{V}^{-1}=\left[\begin{array}{ccc}\frac{\left({\stackrel{\sim}{\text{S}}}_{\text{i}}\left(1-{{\upxi\:}}_{1}\right)+{\stackrel{\sim}{\text{S}}}_{\text{u}}\right){\text{r}}_{1}}{{\stackrel{\sim}{\text{E}}}_{\text{p}}\left({{\upomega\:}}_{1}^{\text{*}}+{{\upupsilon\:}}_{1}+{{\upeta\:}}_{1}\right)}&\:0&\:0\\\:0&\:0&\:0\\\:0&\:0&\:0\end{array}\right].$$
(9)

Therefore, from Eq. (9), the reproduction number \(\:{R}_{0}\) is calculated as:

$$\:{R}_{0}=\frac{\left({\stackrel{\sim}{\text{S}}}_{\text{i}}\left(1-{{\upxi\:}}_{1}\right)+{\stackrel{\sim}{\text{S}}}_{\:\:\text{u}}\right){\text{r}}_{1}}{{\stackrel{\sim}{\text{E}}}_{\text{p}}\left({{\upomega\:}}_{1}^{\text{*}}+{{\upupsilon\:}}_{1}+{{\upeta\:}}_{1}\right)}.$$

Now, by putting initial values yields

$$\:{R}_{0}=\frac{\left({E}_{2}\left(1-{\xi\:}_{1}\right)+{E}_{1}\right){y}_{1}}{{\stackrel{\sim}{E}}_{p}\left({\omega\:}_{1}^{*}+{\upsilon\:}_{1}+{\eta\:}_{1}\right)}.$$

Sensitivity analysis

The degree of influence of input parameters over the dynamics of infectious model is assets through the launch of sensitivity analysis. The sensitivity indices of the infectious disease model given in (4) are deduced by using the approach of Chitnis. Now, the normalized forward sensitivity indices of a parameter\(\:\:x\) of \(\:{R}_{0}\) is calculated as

$$\:{\varDelta\:}_{x}^{{R}_{0}}=\frac{\partial\:{R}_{0}}{\partial\:x}\frac{x}{{R}_{0}}.$$

The estimated sensitivity projected in reproduction number with respect to various parameters is given as

$$\:{\varDelta\:}_{{y}_{1}}^{{R}_{0}}=\frac{\partial\:{R}_{0}}{\partial\:{y}_{1}}.\frac{{y}_{1}}{{R}_{0}}=1,$$
$$\:{\varDelta\:}_{{\omega\:}_{1}^{*}}^{{R}_{0}}=\frac{\partial\:{R}_{0}}{\partial\:{\omega\:}_{1}^{*}}.\frac{{\omega\:}_{1}^{*}}{{R}_{0}}=-0.0729,$$
$$\:{\varDelta\:}_{{\upsilon\:}_{1}}^{{R}_{0}}=\frac{\partial\:{R}_{0}}{\partial\:{\upsilon\:}_{1}}.\frac{{\upsilon\:}_{1}}{{R}_{0}}=0.0017956,$$
$$\:{\varDelta\:}_{{\xi\:}_{1}}^{{R}_{0}}=\frac{\partial\:{R}_{0}}{\partial\:{\xi\:}_{1}}.\frac{{\xi\:}_{1}}{{R}_{0}}=-0.165,$$
$$\:{\varDelta\:}_{{\eta\:}_{1}}^{{R}_{0}}=\frac{\partial\:{R}_{0}}{\partial\:{\eta\:}_{1}}.\frac{{\eta\:}_{1}}{{R}_{0}}=0.5585.$$

Table 1 comprehends the directional projection of the parameters involved in the considered model explaining the viral infectious disease transmission flow. This analysis also shows the significance of various factors in the transmission of disease. The sensitivity indices indicate the set of parameters \(\:{S}_{1}=\left\{{y}_{1},\:{\nu\:}_{1},\:{\eta\:}_{1}\right\}\) and \(\:{R}_{0}\) have a direct relationship and the set of parameters \(\:{S}_{2}=\left\{{\omega\:}_{1}^{*},\:{\xi\:}_{1}\right\}\) has an inverse relationship with \(\:{R}_{0}\). This illustrates that the greater the value of the parameters \(\:{S}_{1}\) greatly maximize the threshold value \(\:{R}_{0}\), but \(\:{R}_{0}\) decreases by a greater value of \(\:{S}_{2}\).

Table 1 Sensitivity indices and parameters of the reproduction number \(\:{\varvec{R}}_{0}\)
Full size table

The existence of a positive relationship is voted through the plus sign whereas the negative sign acknowledges the showing of the negative relationship between the parameters and the transmission rate.

Stability analysis

The system’s local and global stability are studied in this section. The eigenvalues of the Jacobian matrix at the equilibrium point are evaluated in order to ascertain local stability. The equilibrium is locally stable when all of the eigenvalues have negative real parts. On the other hand, global stability requires analyzing the behavior of the system across the entire domain, which frequently calls for advanced mathematical methods like Lyapunov analysis.

Local stability

The purpose of local stability analysis is to determine whether a small perturbation in the disease system will lead to disease persistence or eradication. Understanding local stability at equilibrium points is crucial in epidemiological modeling, as it provides insights into disease transmission dynamics and population-level spread. To demonstrate the local asymptotic stability of both the endemic equilibrium and disease-free equilibrium, the following theorems are presented.

Theorem 4.2

The disease-free equilibrium \(\:{D}_{0}\) is locally asymptotically stable when \(\:{R}_{0}<1\), however, when \(\:{R}_{0}>1\), it is unstable.

Proof

The Jacobin matrix of disease-free equilibrium point for the proposed model is given as

$$\begin{gathered} \:J\left( {F_{0} } \right) = \left[ {\begin{array}{*{20}c} { - \left( {\omega \:_{1}^{*} + \rho \:_{1} } \right) - \frac{{\mathop I\limits^{\sim } r_{1} }}{{\mathop E\limits^{\sim } _{p} }}} & 0 \\ {\rho \:_{1} } & {\frac{{ - \mathop I\limits^{\sim } r_{1} }}{{\mathop E\limits^{\sim } _{{\:p}} }}\left( {1 - \xi \:_{1} } \right) - \omega \:_{1}^{*} } \\ {\frac{{Ir_{1} }}{{\mathop E\limits^{\sim } _{p} }}} & {\frac{{\left( {1 - \xi \:_{1} } \right)\mathop I\limits^{\sim } r_{1} }}{{\mathop E\limits^{\sim } _{p} }}} \\ 0 & 0 \\ 0 & 0 \\ \end{array} } \right. \hfill \\ \left. {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ {\left( {\mathop S\limits^{\sim } _{i} \left( {1 - \xi \:_{1} } \right) + \mathop S\limits^{\sim } _{u} } \right)\frac{{r_{1} }}{{\mathop E\limits^{\sim } _{p} }} - \left( {\omega \:_{1}^{*} + \nu \:_{1} + \eta \:_{1} } \right)} & {\theta \:_{1} } & {\varphi \:_{1} } \\ {\eta \:_{1} } & {\theta \:_{1} } & 0 \\ {\nu \:_{1} } & 0 & { - \left( {\omega \:_{1}^{*} + \varphi \:_{1} } \right)} \\ \end{array} } \right] \hfill \\ \end{gathered}$$

The evaluation of the Jacobin at disease-free equilibrium provides

$$\:J\left({F}_{0}\right)=\left[\begin{array}{ccccc}-\left({\omega\:}_{1}^{*}+{\rho\:}_{1}\right)&\:0&\:0&\:0&\:0\\\:{\rho\:}_{1}&\:-{\omega\:}_{1}^{*}&\:0&\:0&\:0\\\:0&\:0&\:\left({\stackrel{\sim}{S}}_{i}\left(1-{\xi\:}_{1}\right)+{\stackrel{\sim}{S}}_{u}\right)\frac{{r}_{1}}{{\stackrel{\sim}{E}}_{p}}-\left({\omega\:}_{1}^{*}+{\nu\:}_{1}+{\eta\:}_{1}\right)&\:{\theta\:}_{1}&\:{\varphi\:}_{1}\\\:0&\:0&\:{\eta\:}_{1}&\:-\left({\varphi\:}_{1}+{\omega\:}_{1}^{*}+{\theta\:}_{1}\right)&\:0\\\:0&\:0&\:{\nu\:}_{1}&\:0&\:-\left({\omega\:}_{1}^{*}+{\varphi\:}_{1}\right)\end{array}\right].$$
$$\begin{gathered} \:\left| {J\left( {F_{0} } \right) - \lambda \:I} \right| = \left[ {\begin{array}{*{20}c} { - \left( {\omega \:_{1}^{*} + \rho \:_{1} } \right) - \lambda } & 0 \\ {\rho \:_{1} } & { - \omega \:_{1}^{*} - \lambda } \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ \end{array} } \right. \hfill \\ \left. {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ \begin{gathered} \left( {\mathop S\limits^{\sim } _{i} \left( {1 - \xi \:_{1} } \right) + \mathop S\limits^{\sim } _{u} } \right)\frac{{r_{1} }}{{\mathop E\limits^{\sim } _{p} }} \hfill \\ - \left( {\omega \:_{1}^{*} + \nu \:_{1} + \eta \:_{1} } \right) - \lambda \hfill \\ \end{gathered} & 0 & {\varphi \:_{1} } \\ {\eta \:_{1} } & { - \left( {\varphi \:_{1} + \omega \:_{1}^{*} + \theta \:_{1} } \right) - \lambda \:} & 0 \\ {\nu \:_{1} } & 0 & { - \left( {\omega \:_{1}^{*} + \varphi \:_{1} } \right) - \lambda } \\ \end{array} } \right]. \hfill \\ \hfill \\ \end{gathered}$$

By using the Routh–Hurwitz Criterion, it is verified that each eigenvalue of the polynomial equation contains a non-positive real part when \(\:{R}_{0}<1\). As a result, the DFE point \(\:{D}_{0}\) is locally asymptotically stable.

Theorem 4.3

The endemic equilibrium point \(\:{D}^{*}\) will be locally asymptotically stable if the value \(\:{R}_{0}>1\), however, when \(\:{R}_{0}<1\), it is unstable.

Proof

\(\:J\left({F}^{*}\right)=\left[\begin{array}{ccccc}-\left({\omega\:}_{1}^{*}+{\rho\:}_{1}\right)-\frac{\stackrel{\sim}{I}{r}_{1}}{{\stackrel{\sim}{E}}_{p}}&\:0&\:0&\:0&\:0\\\:{\rho\:}_{1}&\:\frac{-\stackrel{\sim}{I}{r}_{1}}{{\stackrel{\sim}{E}}_{p}}\left(1-{\xi\:}_{1}\right)-{\omega\:}_{1}^{*}&\:0&\:0&\:0\\\:\frac{\stackrel{\sim}{I}{r}_{1}}{{\stackrel{\sim}{E}}_{p}}&\:\frac{\left(1-{\xi\:}_{1}\right)\stackrel{\sim}{I}{r}_{1}}{{\stackrel{\sim}{E}}_{p}}&\:\left({\stackrel{\sim}{S}}_{i}\left(1-{\xi\:}_{1}\right)+{\stackrel{\sim}{S}}_{u}\right)\frac{{r}_{1}}{{\stackrel{\sim}{E}}_{p}}-\left({\omega\:}_{1}^{*}+{\nu\:}_{1}+{\eta\:}_{1}\right)&\:{\theta\:}_{1}&\:{\varphi\:}_{1}\\\:0&\:0&\:{\eta\:}_{1}&\:-\left({\varphi\:}_{1}+{\omega\:}_{1}^{*}+{\theta\:}_{1}\right)&\:0\\\:0&\:0&\:{\nu\:}_{1}&\:0&\:-\left({\omega\:}_{1}^{*}+{\varphi\:}_{1}\right)\end{array}\right].\)

$$\:J\left({F}^{*}\right)=\left[\begin{array}{ccccc}-{\mu\:}_{1}&\:0&\:0&\:0&\:0\\\:{\rho\:}_{1}&\:-{\mu\:}_{2}&\:0&\:0&\:0\\\:\frac{\stackrel{\sim}{I}{r}_{1}}{{\stackrel{\sim}{E}}_{p}}&\:\frac{\left(1-{\xi\:}_{1}\right)I{\stackrel{\sim}{}r}_{1}}{{\stackrel{\sim}{E}}_{p}}&\:-{\mu\:}_{3}&\:0&\:0\\\:0&\:0&\:{\eta\:}_{1}&\:-{\mu\:}_{4}&\:0\\\:0&\:0&\:{\nu\:}_{1}&\:0&\:-{\mu\:}_{5}\end{array}\right].$$

where \(\:{\mu\:}_{1}=\left({\omega\:}_{1}^{*}+{\rho\:}_{1}\right)-\frac{\stackrel{\sim}{I}{r}_{1}}{{\stackrel{\sim}{E}}_{p}}\), \(\:{\mu\:}_{2}=\frac{\stackrel{\sim}{I}{r}_{1}}{{\stackrel{\sim}{E}}_{p}}\left(1-{\xi\:}_{1}\right)-{\omega\:}_{1}^{*}\), \(\:{\mu\:}_{3}=\left({\stackrel{\sim}{S}}_{i}\left(1-{\xi\:}_{1}\right)+{\stackrel{\sim}{S}}_{u}\right)\frac{{r}_{1}}{{\stackrel{\sim}{E}}_{p}}-\left({\omega\:}_{1}^{*}+{\nu\:}_{1}+{\eta\:}_{1}\right)\), \(\:{\mu\:}_{4}=\left({\varphi\:}_{1}+{\omega\:}_{1}^{*}+{\theta\:}_{1}\right)\), \(\:{\mu\:}_{5}=\left({\omega\:}_{1}^{*}+{\varphi\:}_{1}\right)\).

It is clear that all eigenvalues of \(\:J\left({F}^{*}\right)\) have negative and real if \(\:{R}_{0}>1\).

Global stability

Global stability analysis in a disease model determines whether the system converges to a stable equilibrium across all possible initial conditions. This analysis is crucial for understanding long-term disease dynamics and overall infection prevalence within a population. The following theorem establishes the conditions for globally asymptotically stable endemic and disease-free equilibrium points.

Theorem 4.4

The disease-free equilibrium point \(\:{\text{F}}_{0}\) is globally asymptotically stable for \(\:{R}_{0}<1\), otherwise, unstable for \(\:{R}_{0}>1\).

Proof

The subsequent Lyapunov function is precise and satisfies the settings of being positive definite with a negative definite derivative. To establish this result, we first present the Lyapunov function defined as:

$$\:\mathcal{L}={y}_{1}{\stackrel{\sim}{S}}_{u}+{y}_{2}{\stackrel{\sim}{S}}_{i}+{y}_{3}\stackrel{\sim}{I}+{y}_{4}\stackrel{\sim}{A}+{y}_{5}\stackrel{\sim}{C.}$$
(10)

where \(\:{y}_{1},\:{y}_{2},\:{y}_{3},\:{y}_{4},\:{y}_{5}\) are constants. Now, by differentiating Eq. (10), one obtains

$$\:{\mathcal{L}}^{{\prime\:}}={y}_{1}{\stackrel{\sim}{S}}_{u}^{{\prime\:}}+{y}_{2}{\stackrel{\sim}{S}}_{i}^{{\prime\:}}+{y}_{3}{\stackrel{\sim}{I}}^{{\prime\:}}+{y}_{4}{\stackrel{\sim}{A}}^{{\prime\:}}+{y}_{5}{\stackrel{\sim}{C}}^{{\prime\:}}.$$

Putting the values from the model and arranging them provides

$$\begin{aligned} \:{\mathcal{L}}^{{\prime \:}} & = \left\{ {y_{1} X - y_{1} \frac{{\mathop I\limits^{\sim } r_{1} }}{{\mathop E\limits^{\sim } _{p} }} - y_{1} \left( {\omega \:_{1}^{*} + \rho \:_{1} } \right) + y_{2} \rho \:_{1} + y_{3} \frac{{\mathop I\limits^{\sim } r_{1} }}{{\mathop E\limits^{\sim } _{p} }}} \right\}{\text{(}}\tilde{S}_{u} - \tilde{S}_{u}^{ \circ } ) \hfill \\ & \quad + \left\{ {y_{3} \left( {1 - \xi \:_{1} } \right)\frac{{\mathop I\limits^{\sim } r_{1} }}{{\mathop E\limits^{\sim } _{p} }} - y_{2} \frac{{\mathop I\limits^{\sim } r_{1} }}{{\mathop E\limits^{\sim } _{p} }}\left( {1 - \xi \:_{1} } \right) - y_{2} \omega \:_{1}^{*} } \right\}{\text{(}}\tilde{S}_{i} - \tilde{S}_{i}^{ \circ } ) \hfill \\ & \quad + \left\{ {y_{4} \eta \:_{1} - y_{3} \left( {\omega \:_{1}^{*} + \nu \:_{1} + \eta \:_{1} } \right)} \right\}\mathop I\limits^{\sim } + \left\{ {y_{3} \theta \:_{1} - y_{4} \left( {\varphi \:_{1} + \omega \:_{1}^{*} + \theta \:_{1} } \right)} \right\}\mathop A\limits^{\sim } \hfill \\ & \quad + \left\{ {y_{3} \varphi \:_{1} + y_{5} \left( {\omega \:_{1}^{*} + \varphi \:_{1} } \right)} \right\}\mathop {C.}\limits^{\sim } \hfill \\ \end{aligned}$$

where \(\:{D}_{0}=\left(\frac{X}{{\omega\:}_{1}^{*}+{\rho\:}_{1}},\frac{{\stackrel{\sim}{S}}_{u}{\rho\:}_{1}}{{\omega\:}_{1}^{*}}\right)\). It is observed that \(\:{\mathcal{L}}^{{\prime\:}}\left(t\right)\le\:0\) when \(\:{\stackrel{\sim}{S}}_{u}>{\stackrel{\sim}{S}}_{u}^{^\circ\:}\) and \(\:{\stackrel{\sim}{S}}_{i}>{\stackrel{\sim}{S}}_{i}^{^\circ\:}\) and \(\:{\stackrel{\sim}{R}}_{0}<1\:\)and \(\:{\mathcal{L}}^{{\prime\:}}=0\) if and only if \(\:{\stackrel{\sim}{S}}_{u}={\stackrel{\sim}{S}}_{u}^{^\circ\:},\:{\stackrel{\sim}{S}}_{i}={\stackrel{\sim}{S}}_{i}^{^\circ\:}\).

The Lasalle’s invariance principle and \(\:\stackrel{\sim}{I}=\stackrel{\sim}{A}=\stackrel{\sim}{C}=0\). The Lyapunov function is positive definite, its derivative is negative definite and all of the conditions for the Lyapunov function are positive definite. Consequently, the DFE is globally asymptotically stable.

Theorem 4.5

The endemic equilibrium point \(\:{D}^{*}\) is globally asymptotically stable if the value \(\:{R}_{0}>1\), however, when \(\:{R}_{0}<1\), it is unstable.

Proof

To prove the global stability of the proposed model at the endemic equilibrium point \(\:{D}^{*}\), the Castilo Chevez method is used. Further, we consider the model as

$$\:\left.\begin{array}{c}\frac{d{\stackrel{\sim}{S}}_{u}}{dt}=X-{\stackrel{\sim}{S}}_{u}\frac{\stackrel{\sim}{I}{r}_{1}}{{\stackrel{\sim}{E}}_{p}}-{\stackrel{\sim}{S}}_{u}\left({\omega\:}_{1}^{*}+{\rho\:}_{1}\right),\\\:\frac{d{\stackrel{\sim}{S}}_{i}}{dt}={\stackrel{\sim}{S}}_{i}{\rho\:}_{1}-{\stackrel{\sim}{S}}_{i}\frac{\stackrel{\sim}{I}{r}_{1}}{{\stackrel{\sim}{E}}_{p}}\left(1-{\xi\:}_{1}\right)-{\stackrel{\sim}{S}}_{i}{\omega\:}_{1,}^{*}\\\:\frac{d\stackrel{\sim}{I}}{dt}=\left({\stackrel{\sim}{S}}_{i}\left(1-{\xi\:}_{1}\right)+{\stackrel{\sim}{S}}_{u}\right)\frac{\stackrel{\sim}{I}{r}_{1}}{{\stackrel{\sim}{E}}_{p}}+\stackrel{\sim}{C}{\varphi\:}_{1}+\stackrel{\sim}{A}{\theta\:}_{1}-\stackrel{\sim}{I}\left({\omega\:}_{1}^{*}+{\upsilon\:}_{1}+{\eta\:}_{1}\right).\end{array}\right\}$$
(11)

Taking the Jacobin and the additive compound matrix of order 2 for the Eq. (4.6), the following matrix is obtained

$$\:J=\left[\begin{array}{ccc}-{a}_{11}&\:0&\:0\\\:{a}_{21}&\:-{a}_{22}&\:0\\\:{a}_{31}&\:{a}_{32}&\:-{a}_{33}\end{array}\right],$$
$$\:{J}^{\left|2\right|}=\left[\begin{array}{ccc}-\left({a}_{11}+{a}_{22}\right)&\:{a}_{23}&\:-{a}_{13}\\\:{a}_{32}&\:-\left({a}_{11}+{a}_{22}\right)&\:{a}_{12}\\\:-{a}_{31}&\:{a}_{21}&\:-\left({a}_{22}+{a}_{33}\right)\end{array}\right],$$
(12)

Let \(\:Q\left(x\right)=\left({\stackrel{\sim}{S}}_{u},\:{\stackrel{\sim}{S}}_{i},\:\stackrel{\sim}{I}\right)=diag\left\{\frac{{\stackrel{\sim}{S}}_{u}}{{\stackrel{\sim}{S}}_{i}},\:\frac{{\stackrel{\sim}{S}}_{u}}{{\stackrel{\sim}{S}}_{i}},\:\frac{{\stackrel{\sim}{S}}_{u}}{{\stackrel{\sim}{S}}_{i}}\right\}\) and then \(\:{Q}^{-1}\left(x\right)=diag\left\{\frac{{\stackrel{\sim}{S}}_{i}}{{\stackrel{\sim}{S}}_{u}},\:\frac{{\stackrel{\sim}{S}}_{i}}{{\stackrel{\sim}{S}}_{u}},\:\frac{{\stackrel{\sim}{S}}_{i}}{{\stackrel{\sim}{S}}_{u}}\right\}\), then the time derivative of the function \(\:{Q}_{f}\left(x\right)\), suggests that

$$\:{Q}_{f}\left(x\right)=diag\left\{\frac{\dot{{\stackrel{\sim}{S}}_{u}}}{{S}_{i}}-\frac{{\stackrel{\sim}{S}}_{u}\dot{{\stackrel{\sim}{S}}_{i}}}{{\stackrel{\sim}{S}}_{i}^{2}},\:\frac{\dot{{\stackrel{\sim}{S}}_{u}}}{{\stackrel{\sim}{S}}_{i}}-\frac{{\stackrel{\sim}{S}}_{u}\dot{{\stackrel{\sim}{S}}_{i}}}{{\stackrel{\sim}{S}}_{i}^{2}},\:\frac{\dot{{\stackrel{\sim}{S}}_{u}}}{{\stackrel{\sim}{S}}_{i}}-\frac{{\stackrel{\sim}{S}}_{u}\dot{{\stackrel{\sim}{S}}_{i}}}{{\stackrel{\sim}{S}}_{i}^{2}}\right\}.$$
(13)

Now, \(\:{Q}_{f}{Q}^{-1}=diag\left\{\frac{\dot{{\stackrel{\sim}{S}}_{u}}}{{\stackrel{\sim}{S}}_{u}}-\frac{\dot{{\stackrel{\sim}{S}}_{i}}}{{\stackrel{\sim}{S}}_{i}},\:\frac{\dot{{\stackrel{\sim}{S}}_{u}}}{{\stackrel{\sim}{S}}_{u}}-\frac{\dot{{\stackrel{\sim}{S}}_{i}}}{{\stackrel{\sim}{S}}_{i}},\:\frac{\dot{{\stackrel{\sim}{S}}_{u}}}{{\stackrel{\sim}{S}}_{u}}-\frac{\dot{{\stackrel{\sim}{S}}_{i}}}{{\stackrel{\sim}{S}}_{i}}\right\}\)

And \(\:Q{J}_{2}^{\left|2\right|}{Q}^{-1}={J}_{2}^{\left|2\right|}.A={Q}_{f}{Q}^{-1}+Q{J}_{2}^{\left|2\right|}{Q}^{-1}\), which can be described as

$$\:A=\left[\begin{array}{cc}{A}_{11}&\:{A}_{12}\\\:{A}_{21}&\:{A}_{22}\end{array}\right],$$
(14)
$$\:\left\{\begin{array}{c}{A}_{11}=\frac{\dot{{\stackrel{\sim}{S}}_{u}}}{{\stackrel{\sim}{S}}_{u}}-\frac{\dot{{\stackrel{\sim}{S}}_{i}}}{{\stackrel{\sim}{S}}_{i}}-\frac{\stackrel{\sim}{I}{r}_{1}}{{\stackrel{\sim}{E}}_{p}}-\left({\omega\:}_{1}^{*}+{\rho\:}_{1}\right)-\frac{\stackrel{\sim}{I}{r}_{1}}{{\stackrel{\sim}{E}}_{p}}\left(1-{\xi\:}_{1}\right)-{\omega\:}_{1}^{*},\:{\:A}_{12}=\left[\begin{array}{cc}0&\:0\end{array}\right],\:\\\:{A}_{21}=\left[\begin{array}{c}\left(1-{\xi\:}_{1}\right)\frac{\stackrel{\sim}{I}{r}_{1}}{{\stackrel{\sim}{E}}_{p}}\\\:\frac{\stackrel{\sim}{I}{r}_{1}}{{\stackrel{\sim}{E}}_{p}}\end{array}\right],{A}_{22}=\left[\begin{array}{cc}{x}_{11}&\:{x}_{12}\\\:{x}_{21}&\:{x}_{22}\end{array}\right],\:\:\:{x}_{11}=\frac{\dot{{\stackrel{\sim}{S}}_{u}}}{{\stackrel{\sim}{S}}_{u}}-\frac{\dot{{\stackrel{\sim}{S}}_{i}}}{{\stackrel{\sim}{S}}_{i}}-2\frac{\stackrel{\sim}{I}{r}_{1}}{{\stackrel{\sim}{E}}_{p}}-2{\omega\:}_{1}^{*}-{\rho\:}_{1}-\frac{\stackrel{\sim}{I}{r}_{1}}{{\stackrel{\sim}{E}}_{p}}{\xi\:}_{1},\:\:{x}_{12}={\rho\:}_{1},\\\:{x}_{21}=\frac{\dot{{\stackrel{\sim}{S}}_{u}}}{{\stackrel{\sim}{S}}_{u}}-\frac{\dot{{\stackrel{\sim}{S}}_{i}}}{{\stackrel{\sim}{S}}_{i}}-\frac{\stackrel{\sim}{I}{r}_{1}}{{\stackrel{\sim}{E}}_{p}}\left(1-{\xi\:}_{1}\right)-{\omega\:}_{1}^{*}-\left({\omega\:}_{1}^{*}+{\nu\:}_{1}+{\eta\:}_{1}\right),{x}_{22}=\frac{\dot{{\stackrel{\sim}{S}}_{u}}}{{\stackrel{\sim}{S}}_{u}}-\frac{\dot{{\stackrel{\sim}{S}}_{i}}}{{\stackrel{\sim}{S}}_{i}}-\frac{\stackrel{\sim}{I}{r}_{1}}{{\stackrel{\sim}{E}}_{p}}\left(1-{\xi\:}_{1}\right)-2{\omega\:}_{1}^{*}-{\nu\:}_{1}-{\eta\:}_{1}.\:\end{array}\right.$$

Let \(\:\left({b}_{1},\:{b}_{2},\:{b}_{3}\right)\) be a vector in \(\:{R}^{3}\) and \(\left\| . \right\|\) of \(\:\left({b}_{1},\:{b}_{2},\:{b}_{3}\right)\) is specified by

$$\left\| {b_{1} ,\:b_{2} ,\:b_{3} } \right\| = max\left\{ {\left\| {b_{1} } \right\| + \left\| {b_{2} } \right\| + \left\| {b_{3} } \right\|} \right\}$$

,

Now we yield the Lozinski measure,

$$\:l\left(A\right)\le\:sup\left\{{h}_{1},\:{h}_{2}\right\}=sup\left\{l\left({A}_{11}\right)+\left\|{A}_{12}\right\|,\:l\left({A}_{22}\right)+\left\|{A}_{21}\right\|\right\}.$$

where \(\:{h}_{i}=l\left({A}_{ii}\right)+\left\|{A}_{ij}\right\|,\:for\:i=1,\:2\:and\:i\ne\:j\), which implies that

$$\:{h}_{1}=l\left({A}_{11}\right)+\left\|{A}_{12}\right\|,\:{h}_{2}=l\left({A}_{22}\right)+\left\|{A}_{21}\right\|.$$
(15)

where

$$\:l\left({A}_{11}\right)=\frac{\dot{{\stackrel{\sim}{S}}_{u}}}{{\stackrel{\sim}{S}}_{u}}-\frac{\dot{{\stackrel{\sim}{S}}_{i}}}{{\stackrel{\sim}{S}}_{i}}-2\frac{\stackrel{\sim}{I}{r}_{1}}{{\stackrel{\sim}{E}}_{p}}-2{\omega\:}_{1}^{*}-{\rho\:}_{1}-\frac{\stackrel{\sim}{I}{r}_{1}}{{\stackrel{\sim}{E}}_{p}}{\xi\:}_{1}$$

.

$$\:l\left({A}_{22}\right)=max\left\{\frac{\dot{{\stackrel{\sim}{S}}_{u}}}{{\stackrel{\sim}{S}}_{u}}-\frac{\dot{{\stackrel{\sim}{S}}_{i}}}{{\stackrel{\sim}{S}}_{i}}-\frac{\stackrel{\sim}{I}{r}_{1}}{{\stackrel{\sim}{E}}_{p}}\left(1-{\xi\:}_{1}\right)-{\omega\:}_{1}^{*}-\left({\omega\:}_{1}^{*}+{\nu\:}_{1}+{\eta\:}_{1}\right),\:{\rho\:}_{1}\right\}=\left\{\frac{\dot{{\stackrel{\sim}{S}}_{u}}}{{\stackrel{\sim}{S}}_{u}}-\frac{\dot{{\stackrel{\sim}{S}}_{i}}}{{\stackrel{\sim}{S}}_{i}}-\frac{\stackrel{\sim}{I}{r}_{1}}{{\stackrel{\sim}{E}}_{p}}\left(1-{\xi\:}_{1}\right)-2{\omega\:}_{1}^{*}-{\nu\:}_{1}-{\eta\:}_{1}\right\},$$
$$\:\left\|{A}_{12}\right\|=0\:and\:\left\|{A}_{21}\right\|=max\left\{\left(1-{\xi\:}_{1}\right)\frac{\stackrel{\sim}{I}{r}_{1}}{{\stackrel{\sim}{E}}_{p}},\:\frac{\stackrel{\sim}{I}{r}_{1}}{{\stackrel{\sim}{E}}_{p}}\right\}=\left(1-{\xi\:}_{1}\right)\frac{\stackrel{\sim}{I}{r}_{1}}{{\stackrel{\sim}{E}}_{p}}$$

.

Therefore, \(\:{h}_{1}\:and\:{h}_{2}\) becomes, such that

$$\:{\text{h}}_{1}=\frac{\dot{{\stackrel{\sim}{\text{S}}}_{\text{u}}}}{{\stackrel{\sim}{\text{S}}}_{\text{u}}}-2{{\upomega\:}}_{1}^{\text{*}}-{{\upnu\:}}_{1}-{{\upeta\:}}_{1}\:\text{a}\text{n}\text{d}\:{\text{h}}_{2}=\frac{\dot{{\stackrel{\sim}{\text{S}}}_{\text{u}}}}{{\stackrel{\sim}{\text{S}}}_{\text{u}}}-\left(1-{{\upxi\:}}_{1}\right)-\text{m}\text{i}\text{n}\left\{\text{r}-\text{r}{{\upxi\:}}_{1}\right\}.$$

This shows that \(\:l\left(A\right)\le\:\left\{\frac{\dot{{\stackrel{\sim}{S}}_{u}}}{{\stackrel{\sim}{S}}_{u}}-\left(1-{\xi\:}_{1}\right)-min\left\{r-r{\xi\:}_{1}\right\}-2{\omega\:}_{1}^{*}\right\}\).

Hence, \(\:l\left(A\right)\le\:\frac{\dot{{\stackrel{\sim}{S}}_{u}}}{{\stackrel{\sim}{S}}_{u}}-\left(1-{\xi\:}_{1}\right)\). Taking the integral of \(\:l\left(A\right)\), one gets

$$\:\underset{t\to\:\infty\:}{{lim}}sup\:sup\:\frac{1}{t}\underset{0}{\overset{\infty\:}{\int\:}}l\left(A\right)dt<-2{\omega\:}_{1}^{*}.$$
$$\:k=\underset{t\to\:\infty\:}{{lim}}sup\:sup\:\frac{1}{t}\underset{0}{\overset{\infty\:}{\int\:}}l\left(A\right)dt<0.$$

Hence, the model is globally asymptotically stable.

Theoretical exploration of the FO HIV dynamics

In this section, a fixed-point theorem is applied to determine the existence and uniqueness of the devised fractional-order model (5). This approach provides insights into the likelihood of a solution’s existence. The relevant equation is derived by applying the generalized integral to one of the nodes in the model (5).

\({\tilde {S}_u}(\hat {p}) - {\tilde {S}_u}(0)=I_{{{0^+}}}^{{\delta ,\sigma }}\{ {\rm X} - \frac{{{{\tilde {S}}_u}\tilde {I}{\gamma _1}}}{{{{\tilde {E}}_p}}} - {\tilde {S}_u}(\omega _{{(1)}}^{ * }+{\rho _1})\} ,\)

\({\tilde {S}_i}(\hat {p}) - {\tilde {S}_i}(0)=I_{{{0^+}}}^{{\delta ,\sigma }}\{ {\tilde {S}_u}{\rho _1} - \frac{{{{\tilde {S}}_i}\tilde {I}{\gamma _1}}}{{{{\tilde {E}}_p}}}(1 - {\xi _1}) - {\tilde {S}_i}\omega _{{(1)}}^{ * }\} ,\)

$$\tilde {I}(\hat {p}) - \tilde {I}(0)=I_{{{0^+}}}^{{\delta ,\sigma }}\{ ({\tilde {S}_i}(1 - {\xi _1})+{\tilde {S}_u})\frac{{\tilde {I}{\gamma _1}}}{{{{\tilde {E}}_p}}}+\tilde {C}{\phi _{(1)}}+\tilde {A}{\theta _1} - \tilde {I}(\omega _{{(1)}}^{ * }+{\nu _1}+{\eta _{(1)}})\} ,$$
(16)
$$\tilde {A}(\hat {p}) - \tilde {A}(0)=I_{{{0^+}}}^{{\delta ,\sigma }}\{ \tilde {I}{\eta _{(1)}} - \tilde {A}({\varphi _1}+\omega _{{(1)}}^{ * }+{\theta _1})\}$$

,

$$\tilde {C}(\hat {p}) - \tilde {C}(0)=I_{{{0^+}}}^{{\delta ,\sigma }}\{ \tilde {I}{\nu _1} - \tilde {C}(\omega _{{(1)}}^{ * }+{\phi _{(1)}})\}$$

,

\(\tilde {R}(\hat {p}) - \tilde {R}(0)=I_{{{0^+}}}^{{\delta ,\sigma }}\{ \tilde {I}{\sigma _1}+\tilde {C}{\sigma _2}+\tilde {A}{\sigma _3} - \tilde {R}\omega _{{(1)}}^{ * }\}\)

For clarity, the kernel is assumed as follows:

\({F_1}(\hat {p},{\tilde {S}_u})={\rm X} - \frac{{{{\tilde {S}}_u}\tilde {I}{\gamma _1}}}{{{{\tilde {E}}_p}}} - {\tilde {S}_u}(\omega _{{(1)}}^{ * }+{\rho _1}),\)

\({F_2}(\hat {p},{\tilde {S}_i})={\tilde {S}_u}{\rho _1} - \frac{{{{\tilde {S}}_i}\tilde {I}{\gamma _1}}}{{{{\tilde {E}}_p}}}(1 - {\xi _1}) - {\tilde {S}_i}\omega _{{(1)}}^{ * },\)

$${F_3}(\hat {p},\tilde {I})=({\tilde {S}_i}(1 - {\xi _1})+{\tilde {S}_u})\frac{{\tilde {I}{\gamma _1}}}{{{{\tilde {E}}_p}}}+\tilde {C}{\phi _{(1)}}+\tilde {A}{\theta _1} - \tilde {I}(\omega _{{(1)}}^{ * }+{\nu _1}+{\eta _{(1)}}),$$
(17)
$${F_4}(\hat {p},\tilde {A})=\tilde {I}{\eta _{(1)}} - \tilde {A}({\varphi _1}+\omega _{{(1)}}^{ * }+{\theta _1}),$$
$${F_5}(\hat {p},\tilde {C})=\tilde {I}{\nu _1} - \tilde {C}(\omega _{{(1)}}^{ * }+{\phi _{(1)}}),$$
$$F_{6} (\hat{p},\tilde{R}) = \tilde{I}\sigma _{1} + \tilde{C}\sigma _{2} + \tilde{A}\sigma _{3} - \tilde{R}\omega _{{(1)}}^{ * } .$$

Thus,

$${\tilde {S}_u}(\hat {p}) - {\tilde {S}_u}(0)=\frac{{{\sigma ^{(1 - \delta )}}}}{{\Gamma (\delta )}}\int\limits_{0}^{{\hat {p}}} {{\xi ^{(\delta - 1)}}} {({\hat {p}^\sigma } - {\xi ^\sigma })^{\delta - 1}}{F_1}(\xi ,{\tilde {S}_u})d\xi ,$$
$${\tilde {S}_i}(\hat {p}) - {\tilde {S}_i}(0)=\frac{{{\sigma ^{(1 - \delta )}}}}{{\Gamma (\delta )}}\int\limits_{0}^{{\hat {p}}} {{\xi ^{(\delta - 1)}}} {({\hat {p}^\sigma } - {\xi ^\sigma })^{\delta - 1}}{F_2}(\xi ,{\tilde {S}_i})d\xi ,$$
$$\tilde {I}(\hat {p}) - \tilde {I}(0)=\frac{{{\sigma ^{(1 - \delta )}}}}{{\Gamma (\delta )}}\int\limits_{0}^{{\hat {p}}} {{\xi ^{(\delta - 1)}}} {({\hat {p}^\sigma } - {\xi ^\sigma })^{\delta - 1}}{F_3}(\xi ,\tilde {I})d\xi ,$$
(18)
$$\tilde {A}(\hat {p}) - \tilde {A}(0)=\frac{{{\sigma ^{(1 - \delta )}}}}{{\Gamma (\delta )}}\int\limits_{0}^{{\hat {p}}} {{\xi ^{(\delta - 1)}}} {({\hat {p}^\sigma } - {\xi ^\sigma })^{\delta - 1}}{F_4}(\xi ,\tilde {A})d\xi ,$$
$$\tilde {C}(\hat {p}) - \tilde {C}(0)=\frac{{{\sigma ^{(1 - \delta )}}}}{{\Gamma (\delta )}}\int\limits_{0}^{{\hat {p}}} {{\xi ^{(\delta - 1)}}} {({\hat {p}^\sigma } - {\xi ^\sigma })^{\delta - 1}}{F_5}(\xi ,\tilde {C})d\xi ,$$
$$\tilde{R}(\hat{p}) - \tilde{R}(0) = \frac{{\sigma ^{{(1 - \delta )}} }}{{\Gamma (\delta )}}\int\limits_{0}^{{\hat{p}}} {\xi ^{{(\delta - 1)}} } (\hat{p}^{\sigma } - \xi ^{\sigma } )^{{\delta - 1}} F_{6} (\xi ,\tilde{R})d\xi .$$

Theorem 5.1

The kernel’s \({F_1},{F_2},{F_3},{F_4},{F_5}\) and \({F_6}\) fulfil the subsequent inequality exists if the contraction and Lipschitz condition accomplished as

$$0 \leqslant {\Delta _1},{\Delta _2},{\Delta _3},{\Delta _4},{\Delta _5},{\Delta _6}<1.$$

Proof

Since \({\tilde {S}_u}\) and \(\tilde {S}_{u}^{*}\) for kernel \({F_1}\), yields

$$\parallel F_{1} (\hat{p},\tilde{S}_{u} ) - F_{1} (\hat{p},\tilde{S}_{u}^{*} )\parallel {\kern 1pt} {\kern 1pt} = {\kern 1pt} {\kern 1pt} \parallel - (\frac{{\tilde{I}\gamma _{1} }}{{\tilde{E}_{p} }} + (\omega _{{(1)}}^{ * } + \rho _{1} ))(\tilde{S}_{u} - \tilde{S}_{u}^{*} )\parallel ,$$
(19)
$$\parallel {F_1}(\hat {p},{\tilde {S}_u}) - {F_1}(\hat {p},\tilde {S}_{u}^{*})\parallel \leqslant (\frac{{\parallel \tilde {I}\parallel {\gamma _1}}}{{{{\tilde {E}}_p}}}+\omega _{{(1)}}^{ * }+{\rho _1})\parallel {\tilde {S}_u} - \tilde {S}_{u}^{*}\parallel ,$$
$$\leqslant (\frac{{{m_3}{\gamma _1}}}{{{{\tilde {E}}_p}}}+\omega _{{(1)}}^{ * }+{\rho _1})\parallel {\tilde {S}_u} - \tilde {S}_{u}^{*}\parallel ,$$
(20)
$$\leqslant {\Delta _1}\parallel {\tilde {S}_u} - \tilde {S}_{u}^{*}\parallel .$$

Here, it is supposed \({\Delta _1}=\frac{{{k_3}{\gamma _1}}}{{{{\tilde {E}}_p}}}+\omega _{{(1)}}^{ * }+{\rho _1}<1\) and \(\parallel \tilde {I}\parallel \leqslant {k_3}\)be the bounded function. Therefore, one obtains

$$\parallel {F_1}(\hat {p},{\tilde {S}_u}) - {F_1}(\hat {p},\tilde {S}_{u}^{*})\parallel \leqslant {\Delta _1}\parallel {\tilde {S}_u} - \tilde {S}_{u}^{*}\parallel .$$
(21)

The kernel \({F_1}\) fulfills the Lipschitz conditions (LC) then \(0<{\Delta _1}<1,\) so the criterion for contraction \({F_1}\) is also valid. Additionally, inequality for subsequent kernels is obtained as:

\(\parallel {F_2}(\hat {p},{\tilde {S}_i}) - {F_2}(\hat {p},\tilde {S}_{i}^{*})\parallel \leqslant {\Delta _2}\parallel {\tilde {S}_i} - \tilde {S}_{i}^{*}\parallel .\)

$$\parallel {F_3}(\hat {p},\tilde {I}) - {F_3}(\hat {p},{\tilde {I}^*})\parallel \leqslant {\Delta _3}\parallel \tilde {I} - {\tilde {I}^*}\parallel .$$
(22)
$$\parallel {F_4}(\hat {p},\tilde {A}) - {F_4}(\hat {p},{\tilde {A}^*})\parallel \leqslant {\Delta _4}\parallel \tilde {A} - {\tilde {A}^*}\parallel ,$$
$$\parallel {F_5}(\hat {p},\tilde {C}) - {F_5}(\hat {p},{\tilde {C}^*})\parallel \leqslant {\Delta _5}\parallel \tilde {C} - {\tilde {C}^*}\parallel .$$
$$\parallel {F_6}(\hat {p},\tilde {R}) - {F_6}(\hat {p},{\tilde {R}^*})\parallel \leqslant {\Delta _6}\parallel \tilde {R} - {\tilde {R}^*}\parallel .$$

Now implement the recursive formula on Eq. (8), one gets.

$${\tilde {S}_{{u_l}}}(\hat {p})={\tilde {S}_u}(0)+\frac{{{\sigma ^{(1 - \delta )}}}}{{\Gamma (\delta )}}\int\limits_{0}^{{\hat {p}}} {{\xi ^{(\delta - 1)}}} {({\hat {p}^\sigma } - {\xi ^\sigma })^{\delta - 1}}{F_1}(\xi ,{\tilde {S}_{{u_{(l - 1)}}}})d\xi ,$$
$${\tilde {S}_{{i_l}}}(\hat {p})={\tilde {S}_i}(0)+\frac{{{\sigma ^{(1 - \delta )}}}}{{\Gamma (\delta )}}\int\limits_{0}^{{\hat {p}}} {{\xi ^{(\delta - 1)}}} {({\hat {p}^\sigma } - {\xi ^\sigma })^{\delta - 1}}{F_2}(\xi ,{\tilde {S}_{{i_{(l - 1)}}}})d\xi ,$$
(23)
$${\tilde {I}_l}(\hat {p})=\tilde {I}(0)+\frac{{{\sigma ^{(1 - \delta )}}}}{{\Gamma (\delta )}}\int\limits_{0}^{{\hat {p}}} {{\xi ^{(\delta - 1)}}} {({\hat {p}^\sigma } - {\xi ^\sigma })^{\delta - 1}}{F_3}(\xi ,{\tilde {I}_{(l - 1)}})d\xi ,$$
$${\tilde {C}_l}(\hat {p})=\tilde {C}(0)+\frac{{{\sigma ^{(1 - \delta )}}}}{{\Gamma (\delta )}}\int\limits_{0}^{{\hat {p}}} {{\xi ^{(\delta - 1)}}} {({\hat {p}^\sigma } - {\xi ^\sigma })^{\delta - 1}}{F_4}(\xi ,{\tilde {C}_{(l - 1)}})d\xi ,$$
$${\tilde {A}_l}(\hat {p})=\tilde {A}(0)+\frac{{{\sigma ^{(1 - \delta )}}}}{{\Gamma (\delta )}}\int\limits_{0}^{{\hat {p}}} {{\xi ^{(\delta - 1)}}} {({\hat {p}^\sigma } - {\xi ^\sigma })^{\delta - 1}}{F_5}(\xi ,{\tilde {A}_{(l - 1)}})d\xi ,$$
$${\tilde {R}_l}(\hat {p})=\tilde {R}(0)+\frac{{{\sigma ^{(1 - \delta )}}}}{{\Gamma (\delta )}}\int\limits_{0}^{{\hat {p}}} {{\xi ^{(\delta - 1)}}} {({\hat {p}^\sigma } - {\xi ^\sigma })^{\delta - 1}}{F_6}(\xi ,{\tilde {R}_{(l - 1)}})d\xi ,$$

So, the initial conditions are given as per:

$$\tilde{S}_{u} (\hat{p}_{0} ) = \tilde{S}_{u} (0),\tilde{S}_{i} (\hat{p}_{0} ) = \tilde{S}_{i} (0),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \tilde{I}(\hat{p}_{0} ) = \tilde{I}(0),\tilde{C}(\hat{p}_{0} ) = \tilde{C}(0),{\kern 1pt} \tilde{A}(\hat{p}_{0} ) = \tilde{A}(0),\tilde{R}(\hat{p}_{0} ) = \tilde{R}(0).$$

Furthermore, by computing the difference between successive terms, the following lexes are obtained:

$$\psi _{l} (\hat{p}) = \tilde{S}_{{u_{l} }} (\hat{p}) - \tilde{S}_{{u_{{(l - 1)}} }} (\hat{p}) = \frac{{\sigma ^{{(1 - \delta )}} }}{{\Gamma (\delta )}}\int\limits_{0}^{{\hat{p}}} {\xi ^{{(\delta - 1)}} } (\hat{p}^{\sigma } - \xi ^{\sigma } )^{{\delta - 1}} (F_{1} (\xi ,\tilde{S}_{{u_{{(l - 1)}} }} ) - F_{1} (\xi ,\tilde{S}_{{u_{{(l - 2)}} }} ))d\xi ,$$
$$\xi _{l} (\hat{p}) = \tilde{S}_{{i_{l} }} (\hat{p}) - \tilde{S}_{{i_{{(l - 1)}} }} (\hat{p}) = \frac{{\sigma ^{{(1 - \delta )}} }}{{\Gamma (\delta )}}\int\limits_{0}^{{\hat{p}}} {\xi ^{{(\delta - 1)}} } (\hat{p}^{\sigma } - \xi ^{\sigma } )^{{\delta - 1}} (F_{2} (\xi ,\tilde{S}_{{i_{{_{{(l - 1)}} }} }} ) - F_{2} (\xi ,\tilde{S}_{{i_{{(l - 2)}} }} ))d\xi ,$$
$$\phi _{l} (\hat{p}) = \tilde{I}_{l} (\hat{p}) - \tilde{I}_{{(l - 1)}} (\hat{p}) = \frac{{\sigma ^{{(1 - \delta )}} }}{{\Gamma (\delta )}}\int\limits_{0}^{{\hat{p}}} {\xi ^{{(\delta - 1)}} } (\hat{p}^{\sigma } - \xi ^{\sigma } )^{{\delta - 1}} (F_{3} (\xi ,\tilde{I}_{{(l - 1)}} ) - (F_{3} (\xi ,\tilde{I}_{{(l - 2)}} ))d\xi ,$$
(24)
$$\chi _{l} (\hat{p}) = \tilde{A}_{l} (\hat{p}) - \tilde{A}_{{(l - 1)}} (\hat{p}) = \frac{{\sigma ^{{(1 - \delta )}} }}{{\Gamma (\delta )}}\int\limits_{0}^{{\hat{p}}} {\xi ^{{(\delta - 1)}} } (\hat{p}^{\sigma } - \xi ^{\sigma } )^{{\delta - 1}} (F_{4} (\xi ,\tilde{A}_{{(l - 1)}} ) - F_{4} (\xi ,\tilde{A}_{{(l - 2)}} ))d\xi ,$$
$$\theta _{l} (\hat{p}) = \tilde{C}_{l} (\hat{p}) - \tilde{C}_{{(l - 1)}} (\hat{p}) = \frac{{\sigma ^{{(1 - \delta )}} }}{{\Gamma (\delta )}}\int\limits_{0}^{{\hat{p}}} {\xi ^{{(\delta - 1)}} } (\hat{p}^{\sigma } - \xi ^{\sigma } )^{{\delta - 1}} (F_{5} (\xi ,\tilde{C}_{{(l - 1)}} ) - F_{5} (\xi ,\tilde{C}_{{(l - 2)}} ))d\xi ,$$
$$\varphi _{l} (\hat{p}) = \tilde{R}_{l} (\hat{p}) - \tilde{R}_{{(l - 1)}} (\hat{p}) = \frac{{\sigma ^{{(1 - \delta )}} }}{{\Gamma (\delta )}}\int\limits_{0}^{{\hat{p}}} {\xi ^{{(\delta - 1)}} } (\hat{p}^{\sigma } - \xi ^{\sigma } )^{{\delta - 1}} (F_{6} (\xi ,\tilde{R}_{{(l - 1)}} ) - F_{6} (\xi ,\tilde{R}_{{(l - 2)}} ))d\xi .$$
$${\tilde {S}_{{u_l}}}(\hat {p})=\sum\limits_{{i=1}}^{l} {{\psi _i}(\hat {p}),} {\tilde {S}_{{i_l}}}(\hat {p})=\sum\limits_{{i=1}}^{l} {{\xi _i}(\hat {p}),} {\tilde {I}_l}(\hat {p})=\sum\limits_{{i=1}}^{l} {{\phi _i}(\hat {p}),} {\tilde {A}_l}(\hat {p})=\sum\limits_{{i=1}}^{l} {{\chi _i}(\hat {p}),} {\tilde {C}_l}(\hat {p})=\sum\limits_{{i=1}}^{l} {{\theta _i}(\hat {p}),} {\tilde {R}_l}(\hat {p})=\sum\limits_{{i=1}}^{l} {{\varphi _i}(\hat {p}).}$$

Using the triangle inequality and Eq. (24) in norm form, after that, Eq. (24) is transformed into

$$\begin{gathered} \parallel \psi _{l} (\hat{p})\parallel = \parallel \tilde{S}_{{u_{l} }} (\hat{p}) - \tilde{S}_{{u_{{(l - 1)}} }} (\hat{p})\parallel \hfill \\ \le \frac{{\sigma ^{{(1 - \delta )}} }}{{\Gamma (\delta )}}\parallel \int\limits_{0}^{{\hat{p}}} {\xi ^{{(\delta - 1)}} } (\hat{p}^{\sigma } - \xi ^{\sigma } )^{{\delta - 1}} (F_{1} (\xi ,\tilde{S}_{{u_{{(l - 1)}} }} ) - F_{1} (\xi ,\tilde{S}_{{u_{{(l - 2)}} }} ))d\xi \parallel . \hfill \\ \end{gathered}$$
(25)

With the kernel LC, one attains;

$$\parallel {\tilde {S}_{{u_l}}}(\hat {p}) - {\tilde {S}_{{u_{(l - 1)}}}}(\hat {p})\parallel \leqslant \frac{{{\Delta _1}{\sigma ^{(1 - \delta )}}}}{{\Gamma (\delta )}}\int\limits_{0}^{{\hat {p}}} {{\xi ^{(\delta - 1)}}} {({\hat {p}^\sigma } - {\xi ^\sigma })^{\delta - 1}}\parallel {\tilde {S}_{{u_{(l - 1)}}}}(\hat {p}) - {\tilde {S}_{{u_{(l - 2)}}}}(\hat {p})\parallel d\xi .$$
(26)

Therefore, the following result is obtained: \(\parallel {\psi _l}(\hat {p})\parallel \leqslant \frac{{{\Delta _1}{\sigma ^{(1 - \delta )}}}}{{\Gamma (\delta )}}\int\limits_{0}^{{\hat {p}}} {{\xi ^{(\delta - 1)}}} {({\hat {p}^\sigma } - {\xi ^\sigma })^{\delta - 1}}\parallel {\psi _{(l - 1)}}(\xi )\parallel d\xi .\) (27)

In a similar manner, the subsequent expressions are obtained: \(\parallel {\xi _l}(\hat {p})\parallel \leqslant \frac{{{\Delta _2}{\sigma ^{(1 - \delta )}}}}{{\Gamma (\delta )}}\int\limits_{0}^{{\hat {p}}} {{\xi ^{(\delta - 1)}}} {({\hat {p}^\sigma } - {\xi ^\sigma })^{\delta - 1}}\parallel {\xi _{(l - 1)}}(\xi )\parallel d\xi .\)

$$\parallel {\phi _l}(\hat {p})\parallel \leqslant \frac{{{\Delta _3}{\sigma ^{(1 - \delta )}}}}{{\Gamma (\delta )}}\int\limits_{0}^{{\hat {p}}} {{\xi ^{(\delta - 1)}}} {({\hat {p}^\sigma } - {\xi ^\sigma })^{\delta - 1}}\parallel {\phi _{(l - 1)}}(\xi )\parallel d\xi .$$
(27)
$$\parallel {\chi _l}(\hat {p})\parallel \leqslant \frac{{{\Delta _4}{\sigma ^{(1 - \delta )}}}}{{\Gamma (\delta )}}\int\limits_{0}^{{\hat {p}}} {{\xi ^{(\delta - 1)}}} {({\hat {p}^\sigma } - {\xi ^\sigma })^{\delta - 1}}\parallel {\chi _{(l - 1)}}(\xi )\parallel d\xi .$$
$$\parallel {\theta _l}(\hat {p})\parallel \leqslant \frac{{{\Delta _5}{\sigma ^{(1 - \delta )}}}}{{\Gamma (\delta )}}\int\limits_{0}^{{\hat {p}}} {{\xi ^{(\delta - 1)}}} {({\hat {p}^\sigma } - {\xi ^\sigma })^{\delta - 1}}\parallel {\theta _{(l - 1)}}(\eta )\parallel d\eta .$$
$$\parallel {\varphi _l}(\hat {p})\parallel \leqslant \frac{{{\Delta _6}{\sigma ^{(1 - \delta )}}}}{{\Gamma (\delta )}}\int\limits_{0}^{{\hat {p}}} {{\xi ^{(\delta - 1)}}} {({\hat {p}^\sigma } - {\xi ^\sigma })^{\delta - 1}}\parallel {\varphi _{(l - 1)}}(\xi )\parallel d\xi .$$

Theorem 5.2

The considered system (5) has a solution if there exists a value \(t_{{\hbox{max} }}^{\sigma }\) such that

$$\frac{{{\Delta _1}}}{{\Gamma (\delta +1)}}{(\frac{{t_{{\hbox{max} }}^{\sigma }}}{\sigma })^\delta }<1.$$

Proof

It is acknowledged that the functions \({\tilde {S}_u}(\hat {t}),{\tilde {S}_i}(\hat {t}),\tilde {I}(\hat {t}),\tilde {C}(\hat {t})\), \(\tilde {A}(\hat {t})\) and \(\tilde {R}(\hat {t})\) are bounded then kernels fulfill the LC as well. Therefore, the following relations may be found by using provided Eq. (5.12) and (5.13)

$$\parallel {\psi _l}(\hat {p})\parallel \leqslant \parallel {\tilde {S}_u}(0)\parallel {[\frac{{{\Delta _1}}}{{\Gamma (\delta +1)}}{(\frac{{\hat {p}_{{\hbox{max} }}^{\sigma }}}{\sigma })^\delta }]^l},$$
$$\parallel {\xi _l}(\hat {p})\parallel \leqslant \parallel {S_i}(0)\parallel {[\frac{{{\Delta _2}}}{{\Gamma (\delta +1)}}{(\frac{{\hat {p}_{{\hbox{max} }}^{\sigma }}}{\sigma })^\delta }]^l},$$
$$\parallel {\phi _l}(\hat {p})\parallel \leqslant \parallel \tilde {I}(0)\parallel {[\frac{{{\Delta _3}}}{{\Gamma (\delta +1)}}{(\frac{{\hat {p}_{{\hbox{max} }}^{\sigma }}}{\sigma })^\delta }]^l},$$
(28)
$$\parallel {\chi _n}(\hat {p})\parallel \leqslant \parallel \tilde {A}(0)\parallel {[\frac{{{\Delta _4}}}{{\Gamma (\delta +1)}}{(\frac{{\hat {p}_{{\hbox{max} }}^{\sigma }}}{\sigma })^\delta }]^l},$$
$$\parallel {\theta _l}(\hat {p})\parallel \leqslant \parallel \tilde {C}(0)\parallel {[\frac{{{\Delta _5}}}{{\Gamma (\delta +1)}}{(\frac{{\hat {p}_{{\hbox{max} }}^{\sigma }}}{\sigma })^\delta }]^l},$$
$$\parallel {\varphi _l}(\hat {p})\parallel \leqslant \parallel \tilde {R}(0)\parallel {[\frac{{{\Delta _6}}}{{\Gamma (\delta +1)}}{(\frac{{\hat {p}_{{\hbox{max} }}^{\sigma }}}{\sigma })^\delta }]^l}.$$

Consequently, the model’s solution is real and continuous. To demonstrate that the function represents the system’s solutions, the assumption is made.

$${\tilde {S}_u}(\hat {p}) - {\tilde {S}_u}(0)={\tilde {S}_{{u_n}}}(\hat {p}) - H_{l}^{1}(\hat {p}),$$
$${\tilde {S}_i}(\hat {p}) - {\tilde {S}_i}(0)={\tilde {S}_{{i_l}}}(\hat {p}) - H_{l}^{2}(\hat {p}),$$
$$\tilde {I}(\hat {p}) - \tilde {I}(0)={\tilde {I}_l}(\hat {p}) - H_{l}^{3}(\hat {p}),$$
(29)
$$\tilde {A}(\hat {p}) - \tilde {A}(0)={\tilde {A}_l}(\hat {p}) - H_{l}^{4}(\hat {p}),$$
$$\tilde {C}(\hat {p}) - \tilde {C}(0)={\tilde {C}_l}(\hat {p}) - H_{l}^{5}(\hat {p}),$$
$$\tilde {R}(\hat {p}) - \tilde {R}(0)={\tilde {R}_l}(\hat {p}) - H_{l}^{6}(\hat {p}).$$

Since our purpose is to demonstrate that while \(l \to \infty\) the factor \(\parallel H_{l}^{1}(t)\parallel\) turns to zero. Taking the standard LC for the kernel \({F_1},\) provides,

$$\begin{aligned} & \parallel H_{l}^{1}(\hat {p})\parallel \leqslant \parallel \frac{{{\sigma ^{(1 - \delta )}}}}{{\Gamma (\delta )}}\int\limits_{0}^{{\hat {p}}} {{\xi ^{(\sigma - 1)}}} {({{\hat {p}}^\sigma } - {\xi ^\sigma })^{\delta - 1}}({F_1}(\xi ,{{\tilde {S}}_u}) - {F_1}(\xi ,{{\tilde {S}}_{{u_{(l - 1)}}}}))d\xi \parallel , \\ & \quad \leqslant \frac{{{\sigma ^{(1 - \delta )}}}}{{\Gamma (\delta )}}\int\limits_{0}^{{\hat {p}}} {{\xi ^{(\sigma - 1)}}} {({{\hat {p}}^\sigma } - {\xi ^\sigma })^{\delta - 1}}\parallel ({F_1}(\xi ,{{\tilde {S}}_u}) - {F_1}(\xi ,{{\tilde {S}}_{{u_{(l - 1)}}}})\parallel d\xi , \\ & \quad \leqslant \frac{{{\Delta _1}}}{{\Gamma (\delta +1)}}{(\frac{{{{\hat {p}}^\sigma }}}{\sigma })^\delta }\parallel {{\tilde {S}}_u} - {{\tilde {S}}_{{u_{(l - 1)}}}}\parallel . \\ \end{aligned}$$
(30)

Then, by repeating the same steps once more, the following result is obtained:

$$\parallel H_{l}^{1}(\hat {p})\parallel \leqslant \parallel {\tilde {S}_u}(0)\parallel {[\frac{1}{{\Gamma (\delta +1)}}{(\frac{{{{\hat {p}}^\sigma }}}{\sigma })^\delta }]^{(l+1)}}\Delta _{1}^{l}E,$$
(31)

at \({\hat {p}_{\hbox{max} }},\) yields

$$\parallel H_{l}^{1} (\hat{p})\parallel \le \parallel \tilde{S}_{l} (0)\parallel [\frac{1}{{\Gamma (\delta + 1)}}(\frac{{\hat{p}_{{\max }}^{\sigma } }}{\sigma })^{\delta } ]^{{(l + 1)}} \Delta _{1}^{l} E.$$
(32)

Taking the limit \(l \to \infty ,\) on Eq. (33), yields \(\parallel H_{l}^{1}(\hat {p})\parallel \to 0.\) Correspondingly, the following result can be attained: \(\parallel H_{l}^{2}(\hat {p})\parallel ,\) \(\parallel H_{l}^{3}(\hat {p})\parallel ,\) \(\parallel H_{l}^{4}(\hat {p})\parallel ,\) \(\parallel H_{l}^{5}(\hat {p})\parallel ,\) and \(\parallel H_{l}^{6}(\hat {p})\parallel\) tend to 0.

Another crucial component is proving that model solutions are unique. Because of this, it is inferred from the contradiction that alternative forms exist, \(\tilde{S}_{u}^{*} (\hat{t}),\tilde{I}^{*} (\hat{t}),\tilde{C}^{*} (\hat{t}),\tilde{S}_{a}^{*} (\hat{t}),\tilde{A}^{*} (\hat{t})\) and \({\tilde {R}^*}(\hat {t})\) then

$$\tilde{S}_{u} (\hat{p}) - \tilde{S}_{u}^{*} (\hat{p}) \le \frac{{\sigma ^{{(1 - \delta )}} }}{{\Gamma (\delta )}}\int\limits_{0}^{{\hat{p}}} {\xi ^{{(\sigma - 1)}} } (\hat{p}^{\sigma } - \xi ^{\sigma } )^{{\delta - 1}} (F_{1} (\xi ,\tilde{S}_{u} ) - F_{1} (\xi ,\tilde{S}_{u}^{*} ))d\xi .$$
(33)

By applying the norm to Eq. (34), the following result is gained:

$$\parallel {\tilde {S}_u}(\hat {p}) - \tilde {S}_{u}^{*}(\hat {p})\parallel \leqslant \frac{{{\sigma ^{(1 - \delta )}}}}{{\Gamma (\delta )}}\int\limits_{0}^{{\hat {p}}} {{\xi ^{(\sigma - 1)}}} {({\hat {p}^\sigma } - {\xi ^\sigma })^{\delta - 1}}\parallel ({F_1}(\xi ,{\tilde {S}_u}) - {F_1}(\xi ,\tilde {S}_{u}^{*})\parallel d\xi ,$$
(34)

By extending LC to kernels, the following result is attained:.

$$\parallel {\tilde {S}_u}(\hat {p}) - \tilde {S}_{u}^{*}(\hat {p})\parallel \leqslant \frac{{{\Delta _1}}}{{\Gamma (\delta +1)}}{(\frac{{{{\hat {p}}^\sigma }}}{\sigma })^\delta }\parallel {\tilde {S}_u}(\hat {p}) - \tilde {S}_{u}^{*}(\hat {p})\parallel ,$$
(35)
$$\parallel {\tilde {S}_u}(\hat {p}) - \tilde {S}_{u}^{*}(\hat {p})\parallel [1 - \frac{{{\Delta _1}}}{{\Gamma (\delta +1)}}{(\frac{{{{\hat {p}}^\sigma }}}{\sigma })^\delta }] \leqslant 0,$$
(36)
$$\parallel {\tilde {S}_u}(\hat {p}) - \tilde {S}_{u}^{*}(\hat {p})\parallel =0, \to {\tilde {S}_u}(\hat {p})=\tilde {S}_{u}^{*}(\hat {p}).$$
(37)

Thus, the uniqueness of the devised system’s solution is established. Consequently, it is shown that

$${\tilde {S}_u}(\hat {p})=\tilde {S}_{u}^{*}(\hat {p}),{\tilde {S}_i}(\hat {p})=\tilde {S}_{i}^{*}(\hat {p}),\tilde {I}(\hat {p})={\tilde {I}^*}(\hat {p}),\tilde {A}(\hat {p})={\tilde {A}^*}(\hat {p}),\tilde {C}(\hat {p})={\tilde {C}^*}(\hat {p}),$$
(38)
$$\tilde {R}(\hat {p})={\tilde {R}^*}(\hat {p}).$$

Numerical techniques for the devised model

When all other existing analytical methods fail, numerical techniques are employed to find a solution. Numerical approaches are considered the most suitable method for representing solutions to models using fractional-order calculus. In this section, the newly adaptive Predictor–Corrector (P–C) approach is presented, anticipated by4 beneath the Generalized Caputo Operator (GCO), which extends the P–C method outlined in5. Consider the initial value problem (IVP) stated as:

$$\begin{gathered} {}^{C}D_{{{a^+}}}^{{\delta ,\sigma }}z(\hat {p})=f(t,{\rm Z}(\hat {p})),\quad \hat {p} \in [0,T], \hfill \\ {{\rm Z}^l}(a)={\rm Z}_{0}^{l},\quad l=0,1,.,[\delta ]. \hfill \\ \end{gathered}$$
(39)

where \(\delta \in ((k - 1),k],\) \(a \geqslant 0,\) and \(\sigma > 0.\) Through applying the generalized integral, Eq. (40) can be stated as a Volterra integral equation:

$${\rm Z}(\hat{p}) = q(\hat{p}) + \frac{{\sigma ^{{(1 - \delta )}} }}{{\Gamma (\delta )}}\int\limits_{a}^{{\hat{p}}} {\xi ^{{(\sigma - 1)}} (\hat{p}^{\sigma } } - \xi ^{\sigma } )^{{\delta - 1}} f(\xi ,{\rm Z}(\xi ))d\xi .$$
(40)

where, \(q(\hat {p})=\sum\limits_{{r=0}}^{{(k - 1)}} {\frac{1}{{{\sigma ^r}r!}}} {({\hat {p}^\sigma } - {a^\sigma })^r}[{({x^{1 - \sigma }}\frac{d}{{dx}})^r}{\rm Z}(x)]{|_{x=a}}.\)

Based on the theory, the first stage in our method is where the function Z such that there is a unique solution on a certain interval \([a,\hat {P}],\) comprises of splitting the interval \([a,\hat {P}]\) into N subintervals \(\{ [{\hat {p}_l},{\hat {p}_{l+1}}],\) \(l=0,1,\ldots,N - 1\}\) integrating the mesh points:

$$\begin{gathered} {{\hat {p}}_0}=a, \hfill \\ {{\hat {p}}_{l+1}}={(p_{l}^{\sigma }+h)^{\frac{1}{\sigma }}},\quad l=0,1,\ldots,(N - 1), \hfill \\ \end{gathered}$$
(41)

where \(h=\frac{{({{\hat {P}}^{(\sigma )}} - {a^{(\sigma )}})}}{N}\) and natural number is N. To solve our devised initial value problem numerically, Now, the approximation will be extended \({{\rm Z}_l},\) \(l=0,1,\ldots,N.\) The fundamental behavior, assuming that the previous investigation of the estimation has been conducted\({{\rm Z}_w} \approx {\rm Z}({\hat {p}_w}),\) \(w=1,2,\ldots,n,\) is that an estimate solution needs to be obtained \({{\rm Z}_{(l+1)}} \approx {\rm Z}({\hat {p}_{(l+1)}})\) with an integral equation 

$${\rm Z}({\hat {p}_{(l+1)}})=q({\hat {p}_{(l+1)}})+\frac{{{\sigma ^{(1 - \delta )}}}}{{\Gamma (\delta )}}\int\limits_{a}^{{{{\hat {p}}_{(l+1)}}}} {{\xi ^{(\sigma - 1)}}} {(\hat {p}_{{l+1}}^{\sigma } - {\xi ^\sigma })^{\delta - 1}}f(\xi ,{\rm Z}(\xi ))d\xi ,$$
(42)

By substitution \({\eta ^\sigma }=\lambda ,\) one get

$${\rm Z}({\hat {p}_{(l+1)}})=q({\hat {p}_{(l+1)}})+\frac{{{\sigma ^{( - \delta )}}}}{{\Gamma (\delta )}}\int\limits_{{{a^\sigma }}}^{{\hat {p}_{{(l+1)}}^{\sigma }}} {(\hat {p}_{{l+1}}^{\sigma }} - \lambda {)^{\delta - 1}}f({\lambda ^{\frac{1}{\sigma }}},{\rm Z}({\lambda ^{\frac{1}{\sigma }}}))d\lambda ,$$
(43)
$${\rm Z}(\hat{p}_{{(l + 1)}} ) = q(\hat{p}_{{(l + 1)}} ) + \frac{{\sigma ^{{( - \delta )}} }}{{\Gamma (\delta )}}\sum\limits_{{j = 0}}^{l} {\int\limits_{{t_{j}^{\sigma } }}^{{\hat{p}_{{(j + 1)}}^{\sigma } }} {(\hat{p}_{{l + 1}}^{\sigma } } - \lambda )^{{\delta - 1}} f(\lambda ^{{\frac{1}{\sigma }}} ,{\rm Z}(\lambda ^{{\frac{1}{\sigma }}} ))d\lambda .}$$
(44)

Then, if the weight function-related trapezoidal quadrature rule is utilized \({(\hat {p}_{{(l+1)}}^{\sigma } - \lambda )^{\delta - 1}}\) to replace the function with an approximation integral on the right-hand sides of (6.6)\(f({\lambda ^{\frac{1}{\sigma }}},{\rm Z}({\lambda ^{\frac{1}{\sigma }}}))\) using its piecewise linear interpolator and suitable nodes at the \(\hat {p}_{w}^{\sigma }(w=0,1,\ldots,(l+1)),\) then one obtain,

$$\begin{gathered} \int\limits_{{t_{w}^{\sigma } }}^{{\hat{p}_{{(w + 1)}}^{\sigma } }} {(\hat{p}_{{(l + 1)}}^{\sigma } } - \lambda )^{{(\delta - 1)}} f(\lambda ^{{\frac{1}{\sigma }}} ,{\rm Z}(\lambda ^{{\frac{1}{\sigma }}} ))d\lambda \approx \frac{{h^{{(\delta )}} }}{{\delta (\delta + 1)}}\{ ((l - w)^{{(\delta + 1)}} - (l - w - \delta ) \hfill \\ (l - (w + 1))^{\delta } )f(\hat{p}_{{(w)}} ,{\rm Z}(\hat{t}_{{(w)}} )) + ((l - w + 1)^{{\delta + 1}} \hfill \\ - (l - (w) + \delta + 1)(l - (w))^{\delta } f(\hat{p}_{{(w + 1)}} ,{\rm Z}(\hat{p}_{{(w + 1)}} ))\} . \hfill \\ \end{gathered}$$
(45)

The corrector formulae for the function \({\rm Z}({\hat {p}_{(l+1)}}),\) \(l=0,1,\ldots,N - 1,\) are attained from (46) and (47) and are documented as follows:

$${\rm Z}(\hat{p}_{{(l + 1)}} ) \approx q(\hat{p}_{{(l + 1)}} ) + \frac{{\sigma ^{{( - \delta )}} h^{{(\delta )}} }}{{\Gamma (\delta + 2)}}\sum\limits_{{j = 0}}^{{(l)}} {\nabla _{{j,(l + 1)}} f(\hat{p}_{w} ,{\rm Z}(\hat{p}_{w} )) + } \frac{{\sigma ^{{( - \delta )}} h^{{(\delta )}} }}{{\Gamma (\delta + 2)}}f(\hat{p}_{{(l + 1)}} ,{\rm Z}(\hat{p}_{{(l + 1)}} )).$$
(46)

When the weight function appears \({\nabla _{w,(l+1)}}\) is described as:

$${\nabla _{w,(l+1)}}=\begin{array}{*{20}{c}} {{l^{(\delta +1)}} - (l - \delta ){{(l+1)}^\delta }} \\ {{{(l - w+2)}^{(\delta +1)}}+{{(l - w)}^{(\delta +1)}} - 2{{(l - w+1)}^{(\delta +1)}},} \end{array}{\text{if}}\,\begin{array}{*{20}{c}} {w=0} \\ {1 \leqslant (w) \leqslant l.} \end{array}$$
(47)

Now, utilizing our approach on the quantity \({\rm Z}({\hat {p}_{(l+1)}})\) provides the quantity \({{\rm Z}^P}({\hat {p}_{(l+1)}})\) in (47) which is known as predictor value. It is also attainable from (44) using the Adams-Bashforth approach. In this regard, \(f({\lambda ^{\frac{1}{\sigma }}},{\rm Z}({\lambda ^{\frac{1}{\sigma }}}))\) substituted by \(f({\hat {p}_{(w)}},{\rm Z}({\hat {p}_{(w)}}))\) in (45) on every integral, then the predictor value \({{\rm Z}^P}({\hat {p}_{(l+1)}}) \approx {{\rm Z}^P}{\hat {p}_{(l+1)}}\) is obtained as per:

$$\begin{aligned} {\rm Z}_{{(l+1)}}^{P} & \approx q({{\hat {p}}_{(l+1)}})+\frac{{{\sigma ^{ - \delta }}}}{{\Gamma (\delta )}}\sum\limits_{{w=0}}^{l} {\int\limits_{{t_{{(w)}}^{\sigma }}}^{{\hat {p}_{{(w+1)}}^{\sigma }}} {(\hat {p}_{{l+1}}^{\sigma }} - \lambda {)^{(\delta - 1)}}f({{\hat {p}}_{(w)}},{\rm Z}({{\hat {p}}_{(w)}}))d\lambda ,} \\ & =q({{\hat {p}}_{(l+1)}})+\frac{{{\sigma ^{( - \delta )}}{h^{(\delta )}}}}{{\Gamma (\delta +1)}}\sum\limits_{{w=0}}^{{(l)}} {{\Pi _{w,(l+1)}}f({{\hat {p}}_{(w)}},{\rm Z}({{\hat {p}}_{(w)}}))} . \\ \end{aligned}$$
(48)

where.

\({\Pi _{w,(l+1)}}=[{(l+1 - (w))^\delta } - {(l - w)^\delta }]\)\(0 \leqslant w \leqslant l.\)

Consequently, the Adaptive-P-C method for assessing estimation \({{\rm Z}_{(l+1)}} \approx {\rm Z}({\hat {p}_{(l+1)}})\) is completely indicated by the formula

$${{\rm Z}_{(l+1)}} \approx q({\hat {p}_{(l+1)}})+\frac{{{\sigma ^{( - \alpha )}}{h^{(\alpha )}}}}{{\Gamma (\alpha +2)}}\sum\limits_{{w=0}}^{{(l)}} {{\nabla _{w,l+1}}f({{\hat {p}}_{(w)}},{\rm Z}({{\hat {p}}_{(w)}})} +\frac{{{\sigma ^{( - \alpha )}}{h^{(\alpha )}}}}{{\Gamma (\alpha +2)}}f({\hat {p}_{(l+1)}},{\rm Z}_{{(l+1)}}^{P}).$$
(49)

Diethelm et al.25 offered where \(\sigma =1,\)the A-P-C technique is dropped to decrease to P-C approach.

Adaptive P–C approach for modeling HIV/AIDS propagation within a fractional-order framework

The estimation of the corrected values is now implemented \({\tilde {S}_{{u_{(l+1)}}}},{\tilde {S}_{{i_{(l+1)}}}},{\tilde {I}_{(l+1)}},{\tilde {A}_{(l+1)}},{\tilde {C}_{(l+1)}}\) in the implied model (4) to perform the Adaptive-P-C approach:

$$\begin{gathered} {{\tilde {S}}_{{u_{(l+1)}}}} \approx {E_1}+\frac{{{\sigma ^{( - \delta )}}{h^{(\delta )}}}}{{\Gamma (\delta +2)}}\sum\limits_{{w=0}}^{{(l)}} {{\nabla _{w,(l+1)}}} {B_1}({{\hat {p}}_{(w)}},{{\tilde {S}}_{{u_{(w)}}}},{{\tilde {S}}_{{i_{(w)}}}},{{\tilde {I}}_{(w)}},{{\tilde {A}}_{(w)}},{{\tilde {C}}_{(w)}},{{\tilde {R}}_{(w)}}) \hfill \\ +\frac{{{\sigma ^{( - \delta )}}{h^{(\delta )}}}}{{\Gamma (\delta +2)}}{B_1}({{\hat {p}}_{(l+1)}},\tilde {S}_{{{u_{(l+1)}}}}^{P},\tilde {S}_{{{i_{(l+1)}}}}^{P},\tilde {I}_{{(l+1)}}^{P},\tilde {A}_{{(l+1)}}^{P},\tilde {C}_{{(l+1)}}^{P},\tilde {R}_{{(l+1)}}^{P}), \hfill \\ \end{gathered}$$
$$\begin{gathered} {{\tilde {S}}_{{i_{(l+1)}}}} \approx {E_2}+\frac{{{\sigma ^{( - \delta )}}{h^{(\delta )}}}}{{\Gamma (\delta +1)}}\sum\limits_{{w=0}}^{{(l)}} {{\nabla _{w,(l+1)}}} {B_2}({{\hat {p}}_{(w)}},{{\tilde {S}}_{{u_{(w)}}}},{{\tilde {S}}_{{i_{(w)}}}},{{\tilde {I}}_{(w)}},{{\tilde {A}}_{(w)}},{{\tilde {C}}_{(w)}},{{\tilde {R}}_{(w)}}) \hfill \\ +\frac{{{\sigma ^{( - \delta )}}{h^{(\delta )}}}}{{\Gamma (\delta +1)}}{B_2}({{\hat {p}}_{(l+1)}},\tilde {S}_{{{u_{(l+1)}}}}^{P},\tilde {S}_{{{i_{(l+1)}}}}^{P},\tilde {I}_{{(l+1)}}^{P},\tilde {A}_{{(l+1)}}^{P},\tilde {C}_{{(l+1)}}^{P},\tilde {R}_{{(l+1)}}^{P}), \hfill \\ \end{gathered}$$
$$\begin{gathered} {{\tilde {I}}_{(l+1)}} \approx {E_3}+\frac{{{\sigma ^{( - \delta )}}{h^{(\delta )}}}}{{\Gamma (\delta +1)}}\sum\limits_{{w=0}}^{{(l)}} {{\nabla _{w,(l+1)}}} {B_3}({{\hat {p}}_{(w)}},{{\tilde {S}}_{{u_{(w)}}}},{{\tilde {S}}_{{i_{(w)}}}},{{\tilde {I}}_{(w)}},{{\tilde {A}}_{(w)}},{{\tilde {C}}_{(w)}},{{\tilde {R}}_{(w)}}) \hfill \\ +\frac{{{\sigma ^{( - \delta )}}{h^{(\delta )}}}}{{\Gamma (\delta +1)}}{B_3}({{\hat {p}}_{(l+1)}},\tilde {S}_{{{u_{(l+1)}}}}^{P},\tilde {S}_{{{i_{(l+1)}}}}^{P},\tilde {I}_{{(l+1)}}^{P},\tilde {A}_{{(l+1)}}^{P},\tilde {C}_{{(l+1)}}^{P},\tilde {R}_{{(l+1)}}^{P}), \hfill \\ \end{gathered}$$
(50)
$$\begin{gathered} {{\tilde {A}}_{(l+1)}} \approx {E_4}+\frac{{{\sigma ^{( - \delta )}}{h^{(\delta )}}}}{{\Gamma (\delta +2)}}\sum\limits_{{w=0}}^{{(l)}} {{\nabla _{w,l+1}}} {B_4}({{\hat {p}}_{(w)}},{{\tilde {S}}_{{u_{(w)}}}},{{\tilde {S}}_{{i_{(w)}}}},{{\tilde {I}}_{(w)}},{{\tilde {A}}_{(w)}},{{\tilde {C}}_{(w)}},{{\tilde {R}}_{(w)}}) \hfill \\ +\frac{{{\sigma ^{( - \delta )}}{h^{(\delta )}}}}{{\Gamma (\delta +2)}}{B_4}({{\hat {p}}_{(l+1)}},\tilde {S}_{{{u_{(l+1)}}}}^{P},\tilde {S}_{{{i_{(l+1)}}}}^{P},\tilde {I}_{{(l+1)}}^{P},\tilde {A}_{{(l+1)}}^{P},\tilde {C}_{{(l+1)}}^{P},\tilde {R}_{{(l+1)}}^{P}), \hfill \\ \end{gathered}$$
$$\begin{gathered} {{\tilde {C}}_{(l+1)}} \approx {E_5}+\frac{{{\sigma ^{( - \delta )}}{h^{(\delta )}}}}{{\Gamma (\delta +2)}}\sum\limits_{{w=0}}^{l} {{\nabla _{w,(l+1)}}} {B_5}({{\hat {p}}_{(w)}},{{\tilde {S}}_{{u_{(w)}}}},{{\tilde {S}}_{{i_{(w)}}}},{{\tilde {I}}_{(w)}},{{\tilde {A}}_{(w)}},{{\tilde {C}}_{(w)}},{{\tilde {R}}_{(w)}}) \hfill \\ +\frac{{{\sigma ^{( - \delta )}}{h^{(\delta )}}}}{{\Gamma (\delta +1)}}{{\rm E}_5}({{\hat {p}}_{(l+1)}},\tilde {S}_{{{u_{(l+1)}}}}^{P},\tilde {S}_{{{i_{(l+1)}}}}^{P},\tilde {I}_{{(l+1)}}^{P},\tilde {A}_{{(l+1)}}^{P},\tilde {C}_{{(l+1)}}^{P},\tilde {R}_{{(l+1)}}^{P}), \hfill \\ \end{gathered}$$
$$\begin{gathered} \tilde{R}_{{(l + 1)}} \approx E_{6} + \frac{{\sigma ^{{( - \delta )}} h^{{(\delta )}} }}{{\Gamma (\delta + 2)}}\sum\limits_{{w = 0}}^{{(l)}} {\nabla _{{w,(l + 1)}} } B_{6} (\hat{p}_{{(w)}} ,\tilde{S}_{{u_{{(w)}} }} ,\tilde{S}_{{i_{{(w)}} }} ,\tilde{I}_{{(w)}} ,\tilde{A}_{{(w)}} ,\tilde{C}_{{(w)}} ,\tilde{R}_{{(w)}} ) \hfill \\ + \frac{{\sigma ^{{ - \delta }} h^{\delta } }}{{\Gamma (\delta + 2)}}B_{6} (\hat{p}_{{(l + 1)}} ,\tilde{S}_{{u_{{(l + 1)}} }}^{P} ,\tilde{S}_{{i_{{(l + 1)}} }}^{P} ,\tilde{I}_{{(l + 1)}}^{P} ,\tilde{A}_{{(l + 1)}}^{P} ,\tilde{C}_{{(l + 1)}}^{P} ,\tilde{R}_{{(l + 1)}}^{P} ). \hfill \\ \end{gathered}$$

So, predictor values \(\tilde {S}_{{{u_{(l+1)}}}}^{P},\tilde {S}_{{{i_{(l+1)}}}}^{P},\tilde {I}_{{(l+1)}}^{P},\tilde {A}_{{(l+1)}}^{P},\tilde {C}_{{(l+1)}}^{P}\), and \(\tilde {R}_{{(l+1)}}^{P}\) are indicated as:

$$\tilde {S}_{{{u_{(l+1)}}}}^{P} \approx {E_1}+\frac{{{\sigma ^{( - \delta )}}{h^{(\delta )}}}}{{\Gamma (\delta +1)}}\sum\limits_{{j=0}}^{{(l)}} {{\Pi _{j,(l+1)}}} {{\rm E}_1}({\hat {p}_{(w)}},{\tilde {S}_{{u_{(w)}}}},{\tilde {S}_{{i_{(w)}}}},{\tilde {I}_{(w)}},{\tilde {A}_{(w)}},{\tilde {C}_{(w)}},{\tilde {R}_{(w)}}),$$
$$\tilde {I}_{{(l+1)}}^{P} \approx {E_3}+\frac{{{\sigma ^{( - \delta )}}{h^{(\delta )}}}}{{\Gamma (\delta +1)}}\sum\limits_{{w=0}}^{{(l)}} {{\Pi _{w,l+1}}} {B_3}({\hat {p}_{(w)}},{\tilde {S}_{{u_{(w)}}}},{\tilde {S}_{{i_{(w)}}}},{\tilde {I}_{(w)}},{\tilde {A}_{(w)}},{\tilde {C}_{(w)}},{\tilde {R}_{(w)}}),$$
(51)
$$\tilde {A}_{{(l+1)}}^{P} \approx {B_4}+\frac{{{\sigma ^{( - \delta )}}{h^{(\delta )}}}}{{\Gamma (\delta +1)}}\sum\limits_{{w=0}}^{{(l)}} {{\Pi _{w,(l+1)}}} {B_4}({\hat {p}_{(w)}},{\tilde {S}_{{u_{(w)}}}},{\tilde {S}_{{i_{(w)}}}},{\tilde {I}_{(w)}},{\tilde {A}_{(w)}},{\tilde {C}_{(w)}},{\tilde {R}_{(w)}}),$$
$$\tilde {C}_{{(l+1)}}^{P} \approx {E_5}+\frac{{{\sigma ^{( - \delta )}}{h^{(\delta )}}}}{{\Gamma (\delta +1)}}\sum\limits_{{w=0}}^{{(l)}} {{\Pi _{w,(l+1)}}} {B_5}({\hat {p}_{(w)}},{\tilde {S}_{{u_{(w)}}}},{\tilde {S}_{{i_{(w)}}}},{\tilde {I}_{(w)}},{\tilde {A}_{(w)}},{\tilde {C}_{(w)}},{\tilde {R}_{(w)}}),$$
$$\tilde{R}_{{(l + 1)}}^{P} \approx E_{6} + \frac{{\sigma ^{{( - \delta )}} h^{{(\delta )}} }}{{\Gamma (\delta + 1)}}\sum\limits_{{w = 0}}^{{(l)}} {\Pi _{{w,(l + 1)}} } B_{6} (\hat{p}_{{(w)}} ,\tilde{S}_{{u_{{(w)}} }} ,\tilde{S}_{{i_{{(w)}} }} ,\tilde{I}_{{(w)}} ,\tilde{A}_{{(w)}} ,\tilde{C}_{{(w)}} ,\tilde{R}_{{(w)}} ).$$

where \({B_1},{B_2},{B_3},{B_4},{B_5}\) and \({B_6}\) are given as:

$${B_1}(\hat {p},{\tilde {S}_u},{\tilde {S}_i},\tilde {I},\tilde {C},\tilde {A},\tilde {R}):={\rm X} - \frac{{{{\tilde {S}}_u}\tilde {I}{\gamma _1}}}{{{{\tilde {E}}_p}}} - {\tilde {S}_u}(\omega _{{(1)}}^{ * }+{\rho _1}),$$
$${B_2}(\hat {p},{\tilde {S}_u},{\tilde {S}_i},\tilde {I},\tilde {C},\tilde {A},\tilde {R}):={\tilde {S}_u}{\rho _1} - \frac{{{{\tilde {S}}_i}\tilde {I}{\gamma _1}}}{{{{\tilde {E}}_p}}}(1 - {\xi _1}) - {\tilde {S}_i}\omega _{{(1)}}^{ * },$$
$${B_3}(\hat {p},{\tilde {S}_u},{\tilde {S}_i},\tilde {I},\tilde {C},\tilde {A},\tilde {R}):=({\tilde {S}_i}(1 - {\xi _1})+{\tilde {S}_u})\frac{{\tilde {I}{\gamma _1}}}{{{{\tilde {E}}_p}}}+\tilde {C}{\phi _1}+\tilde {A}{\theta _1} - \tilde {I}(\omega _{{(1)}}^{ * }+{\nu _1}+{\eta _{(1)}}),$$
(52)
$${B_4}(\hat {p},{\tilde {S}_u},{\tilde {S}_i},\tilde {I},\tilde {A},\tilde {C},\tilde {R}):=\tilde {I}{\eta _{(1)}} - \tilde {A}({\varphi _1}+\omega _{{(1)}}^{ * }+{\theta _1}),$$
$${B_5}(\hat {p},{S_u},{S_i},I,A,C,R):=I{\nu _1} - C(\omega _{{(1)}}^{ * }+{\phi _1}),$$
$${B_6}(\hat {p},{\tilde {S}_u},{\tilde {S}_i},\tilde {I},\tilde {A},\tilde {C},\tilde {R}):=\tilde {I}{\sigma _1}+\tilde {C}{\sigma _2}+\tilde {A}{\sigma _3} - \tilde {R}\omega _{{(1)}}^{ * }.$$

Results and discussion

In this section, the graphical representation of the dynamic behavior of an HIV-AIDS model is evaluated. The initial values taken in the simulation are defined as: \({E_1}=129,789,089,{E_2}=1 \times {10^8},{E_3}=7195,{E_4}=3716,{E_5}=0,{E_6}=0.\)

Moreover, the solution behavior of the dynamic model (5) for \({\tilde {S}_u},{\tilde {S}_i},\tilde {I},\tilde {A},\tilde {C}\) and \(\tilde {R}\) are simulated via fractional Adaptive-P-C technique against the real data given in Table 2, corresponding varying values of fractional order \(\delta .\) The following values of the model parameters are considered as \({\alpha _1}=0.3465,{\alpha _2}=0.4865,\)\({\alpha _3}=0.5465,{\alpha _4}=0.6165\) and the initial conditions are \({\tilde {S}_u}(0)=129,789,089,\) \({\tilde {S}_i}(0)=1 \times {10^8},\) \(\tilde {I}(0)=7195,\) \(\tilde {A}(0)=3716,\) \(\tilde {C}(0)=0\)and \(\tilde {R}(0)=0,\) and h = 0.01.

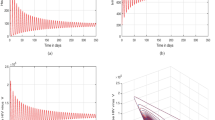
Table 2 Parameters and their values.
Full size table

The numerical results shown in Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 and 13 indicate the numerical simulation of the model relating to time T = 50 years and \(E=675\) for values of \(\:\sigma\:=0.9,\:1.2\) and various values of \(\delta =0.70,0.80,0.90,1\). The dynamic behavior of different class subpopulations of the model (5) with \(\:\sigma\:=0.9\) for distinct values \(\delta\)are shown in Figs. 2, 3, 4, 5 and 7.

Fig. 2
figure 2

Dynamical numerical simulation of susceptible uniformed.

Full size image
Fig. 3
figure 3

Dynamical numerical simulation of susceptible informed.

Full size image
Fig. 4
figure 4

Dynamical simulation of HIV infected.

Full size image
Fig. 5
figure 5

Dynamical simulation of AIDS afflicted.

Full size image
Fig. 6
figure 6

Dynamical simulation of ART medication.

Full size image
Fig. 7
figure 7

Dynamical simulation of recovered individuals.

Full size image

The dynamical behavior of the varying subpopulation classes in the proposed model (5) with \(\:\sigma\:=1.2\) for distinct values of \(\delta\) as shown in Figs. 8, 9, 10, 11, 12 and 13.

Fig. 8
figure 8

Dynamical simulation of susceptible uninfected.

Full size image
Fig. 9
figure 9

Dynamical simulation of susceptible informed.

Full size image
Fig. 10
figure 10

Dynamical simulation of HIV infected.

Full size image
Fig. 11
figure 11

Dynamical simulation of AIDS afflicted.

Full size image
Fig. 12
figure 12

Dynamical simulation of ART medication.

Full size image

A spectrum of subpopulation behavior of the model with \(\:\sigma\:=1.2\) for significant measures \(\delta\) is depicted in the following Fig. 13 below.

Fig. 13
figure 13

Dynamical simulation of recovered individual.

Full size image

Figures 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 and 13 illustrate the graphical depiction of the transmission of the HIV disease model via our considered numerical scheme, along with a comparison between fractional and integer orders. Now, Fig. 2 demonstrates in what manner the number of susceptible uninformed individuals decreases over time, and this decrease is influenced by the fractional order parameter \(\:\delta\:\). For the small value of \(\:\delta\:\), the decline in the susceptible uninformed population occurs more gradually. This could imply a slower rate of transition from susceptible to informed or infected states. A gradual decline might suggest that interventions or information dissemination are affecting the uninformed population slowly.

Figure 3 signifies the dynamics of the susceptible informed population. This figure shows that the number of susceptible informed individuals S increases and then stabilizes after a few years. The initial rise in the susceptible informed population could be due to a period of increased information dissemination or initial exposure to preventive measures. This could imply that more individuals are becoming informed and thus moving into this category. After some years, the number of susceptible informed individuals reaches a stable level. This stability might indicate that the population of susceptible informed individuals has reached an equilibrium, where the rate of becoming informed equals the rate of leaving this category. The pattern of growth followed by stabilization suggests that the system is approaching a new steady state after an initial period of change. This could be reflective of a successful information campaign reaching saturation or a balance being struck between new information and other dynamics. Fig. 4 displays that the number of HIV-positive individuals declines as the value of \(\:\delta\:\) decreases. The decline in the HIV-positive population with decreasing fractional order suggests that the dynamics of the HIV-positive population are less aggressive or more stable when the system has less memory or inertia. This could mean that interventions or changes in behavior might have a more gradual or less pronounced impact in systems with smaller fractional order parameters. A smaller value of \(\:\delta\:\) might imply a slower or less pronounced response to treatment or intervention, potentially leading to a slower decline in the HIV-positive population compared to a system with a higher fractional order.

As Fig. 5 demonstrates, as the value of the fractional order decreases, correspondingly falls the number of people with AIDS. As lower the fractional order in the proposed model influences the rate of decline of AIDS-afflicted individuals, exactly as it does for the HIV-positive population. In systems with lower values of δ, the dynamics controlling the progression or transition to AIDS may be less aggressive or more stable, as shown by the drop in AIDS-afflicted persons with smaller fractional order.

Figure 6 depicts how the fractional order decreases when the proportion of HIV-positive people taking ART drops. Less memory or inertia in the system is usually represented by a drop in fractional order. In the context of ART, this might suggest that the system’s response to ART is slower or less impactful with a lower fractional order. As the system becomes less responsive, the effectiveness or uptake of ART may become less obvious, as seen by the steady throw in the ratio of HIV-positive people getting ART with decreasing fractional order. This may arise from softer dynamics during the transition to treatment or from a slower rate of adaptation to treatment. The finding indicates a system with a smaller fractional order could not see as much continuous growth in the number of people using ART. Improved ART distribution strategies and more responsive medical treatments may be created with an understanding of these dynamics.

Figure 7 demonstrates that the number of recovered persons drops with time. A decreasing number of recovered individuals may indicate that recovery rates are not keeping pace with new infections or that the duration of recovery is limited. This might represent an instance where patients do not remain in a recovered condition for long or if recovery rates are inadequate relative to the number of new cases. If the model incorporates fractional order, this decline might be influenced by the \(\:\delta\:\). For instance, a lower value of \(\:\delta\:\) might mean slower or less pronounced recovery dynamics, leading to a slower accumulation of recovered individuals. This result highlights the need for continuous and effective interventions to ensure that more individuals transition to a recovered state. If the decline is significant, it may indicate the need for revisiting treatment or intervention strategies to improve recovery rates and ensure sustainable health outcomes.

Similarly, when with \(\:\sigma\:=1.2\) Fig. 8 shows the susceptible uninformed populace increased slowly with a smaller fractional order. According to Fig. 9, the number of susceptible informed populace increases for the different fractional order. Figure 10 shows the populace with HIV infected gradually increasing over time. Figure 11 displays the number of AIDS-afflicted people increased with a smaller fractional order. Figure 12 illustrates that the populace receiving ART gradually increased over time and it indicates the great impact on society. Figure 13 shows that the recovered individual increased with a smaller fractional order. The numerical simulation, shown in Figs. 8, 9, 10, 11, 12 and 13, demonstrates that early detection and treatment are effective in eradicating the disease. Public awareness about HIV-AIDS prevention has increased, and the use of contraception and microbicides has been explored as additional control measures. As a result, more people are aware of the disease, and receiving ART, and the number of AIDS patients recovering has increased. The study could be further expanded by considering a hypothetical vaccine and the reduction of intimate activities by some individuals with AIDS. It was observed that varying the value of δ leads to different trajectories, and the graphs indicate that the system’s dynamic behavior is modified by a fractional derivative of order two. Understanding these dynamics through the figures provides valuable insights into how mathematical models can inform public health strategies and improve the management of HIV/AIDS.

Conclusion

Mathematical modeling plays an important role in understanding and handling infectious diseases such as HIV. Comparing nonlinear compartmental models to traditional models, the first offers a more sophisticated understanding of disease transmission. In order to investigate numerical insights into the transmission dynamics of the HIV disease, a fractional order model by incorporating antiretroviral treatment (ART) is introduced. The rate at which the infected population getting ART transitions to recovered persons (R) and the frequency of hospitalized patients’ recovery progress are specifically measured via the devised model. We applied the fractional derivative operators to capture more natural phenomena of the proposed model. A more realistic and exact understanding of how procedures impact different populations and how recovery dynamics change over time is also made possible by this model.

Throughout the investigation, a comprehensive analysis is conducted, covering key aspects such as positivity, boundedness, equilibrium points, the basic reproduction number, stability, and sensitivity. The model ensures boundedness and positivity by incorporating constraints and selecting appropriate functional forms, preventing unrealistic variable growth, and aligning the model with real-world constraints. This precautionary approach enhances the model’s reliability and applicability, providing policymakers with an accurate representation that supports well-informed decision-making within practical limitations.

The analysis of stability in the model indicates that when R0 < 1, the system is both locally and globally asymptotically stable at the disease-free equilibrium D0. Conversely, if R0 > 1, the system exhibits an endemic equilibrium \(\:{D}^{*}\), at which point it is locally and globally asymptotically stable. Furthermore, a sensitivity analysis is conducted to assess the impact of various compartmental parameters on the basic reproduction number. The existence and uniqueness of the fractional-order model are established using the framework of fixed-point theory. To solve the nonlinear differential equations, a modified fractional Caputo operator is employed alongside an adaptive predictor-corrector approach. A quantitative study is performed to compare the effects of integer-order and fractional-order models, and numerical results are obtained using the adaptive predictor-corrector strategy. The graphical results demonstrated that the outcomes are significantly influenced by the fractional order parameters σ and \(\:\delta\:\). Numerical simulations at different fractional orders, along with a comparative analysis against integer-order models, further illustrate the model’s predictive capability. The numerical implementation using a predictor-corrector scheme in MATLAB enhances computational efficiency, improving the validation of theoretical findings. The results suggest that both susceptible informed and susceptible ignorant individuals significantly impact the number of infected individuals. The overall infection rate exhibits smoother transitions and prolonged peaks in the infected population due to the interplay between fractional-order dynamics in susceptible and ignorant individuals. Additionally, individuals who recover from the virus or transition through antiretroviral therapy (ART) are classified as recovered. The process of recovery is influenced by infection rates and interactions between compartments which leads to a more gradual increase in the recovered population and potentially longer periods of recovery dynamics. Moreover, the extended compartment \(\:\stackrel{\sim}{R}\)(t) demonstrates that the infected population under ART progresses toward recovery, reinforcing the importance of treatment interventions in managing disease spread.

This model offers a more precise and realistic depiction of disease transmission, the impact of interventions on different populations, and the evolution of recovery dynamics over time. The existing analysis can be extended by integrating various fractional operators that integrate non-local and non-singular kernels, enhancing the mathematical modeling of HIV/AIDS and improving future predictions and intervention strategies. Moreover, future directions for a temporal fractional HIV/AIDS model with fractal dimensions comprise refining parameter estimation, incorporating socioeconomic factors, and leveraging machine learning to enhance forecasting accuracy. Expanding the model to multiple locations, enabling real-time monitoring, and exploring different intervention scenarios can further increase its effectiveness. The model’s adaptability allows for customization based on regional needs, and its implementation in public health education can contribute to raising awareness. This research advances the field of fractional epidemiology, paving the way for similar methodologies to be applied in studying other infectious diseases.