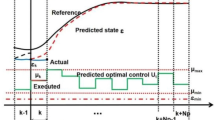
Abstract
Trajectory tracking control, as the core component of the autopilot system, is essential for achieving high-performance autopilot functionality. Therefore, to design a trajectory-tracking controller that is stable, reliable, accurate, fast, and robust, this paper proposes three lateral control schemes and two longitudinal control schemes for comparative analysis. In lateral control, a lateral control strategy of linear quadratic regulator (LQR) based on feedforward and feedback is designed. Subsequently, a lateral controller utilizing a linear parametric time-varying model predictive control (MPC) approach is proposed, and the constrained optimization problem is addressed using a quadratic programming (QP) solver. Finally, a lateral control method based on nonlinear integral sliding mode control (NISMC) is developed, which realizes zero steady-state error by substituting saturation function for symbolic function and introducing integral action. The MPC and PID speed-tracking controllers are compared within the longitudinal control scheme. The effectiveness of these controllers and their respective performance metrics are validated through step speed tracking tests. Furthermore, the efficacy of the three proposed controllers, along with their advantages, disadvantages, and applications, is assessed by designing three distinct road surface adhesion coefficients for the double lane change test, and the circular path test under medium-low adhesion conditions. At the same time, in order to display the control characteristics of the three controllers more directly, this paper designed a 5 score chart according to various performance indicators listed in Table 2 to quantitatively compare and analyze the comprehensive performance of various controllers.
Similar content being viewed by others
Introduction
As a burgeoning trend in the future development of the automotive industry, the core intelligent features of autonomous driving technology are reflected in the field of intelligent and safe driving. Given the challenges posed by a concerning traffic safety situation, excessive energy consumption, and increased environmental pollution, intelligent vehicles, as an integral component of the intelligent transportation system, are garnering increasing attention and significanc1,2. The functional architecture of automated vehicles can be primarily divided into three major components: comprehensive perception, decision planning, and motion control. Among these, the motion control system is responsible for executing specific actuator commands based on the desired driving path derived from comprehensive sensing and decision planning, as well as real-time feedback on the vehicle’s status. This ensures that the vehicle can navigate smoothly along the intended trajectory. Trajectory tracking control serves as a crucial link between the planning layer and the execution layer, playing a vital role in determining the stability and safety of the vehicle system3. Its performance directly influences both the safety of the vehicle and the overall passenger experience. Therefore, conducting in-depth research on vehicle trajectory-tracking control systems is particularly important.
In recent years, numerous studies have focused on trajectory-tracking control. In lateral control, kinematic model-based trajectory tracking methods include pure tracking algorithms4 and Stanley’s algorithm5. However, these methods often inadequately account for vehicle dynamics, resulting in significant model mismatch issues under conditions of large or variable curvature and medium to high speeds. This mismatch can lead to instability during the trajectory-tracking process. To enhance the vehicle’s tracking performance under such conditions, it is essential to incorporate vehicle dynamics into the controller design. The trajectory tracking controllers based on the dynamics model include PID control6, LQR control7, sliding mode control8,9,10,11, fuzzy control12, model predictive control13, etc. Although some results have been achieved in some previous research, there are still some challenges, which mainly lie in the highly nonlinear nature of the vehicle dynamics model and the interference of time-varying parameters; and the trade-off between the computational efficiency and the accuracy of the vehicle model14. In longitudinal control, PID is widely used in industry because it does not depend on the accurate model and the control principle is simple, in addition, sliding mode adaptive speed control15, optimal pre-scanning speed tracking control16, MPC speed tracking control17 and so on in vehicle speed tracking control have all have achieved certain results, but the working conditions involved are relatively simple for the nonlinear characteristics of tires and the longitudinal coupling characteristics of the vehicle are relatively insufficient consideration. Therefore, we expect to design stable, reliable, accurate, fast, and robust lateral and longitudinal controllers based on the trajectory tracking control of automated vehicles.
In this paper, we design and compare three lateral control schemes, namely LQR, MPC, and NISMC to track the reference trajectory. For longitudinal control, we design and compare two schemes: MPC speed tracking control and PID control to track the reference vehicle speed. The main contributions of this paper are as follows:
-
1.
Three kinds of lateral controllers, LQR, MPC, and NISMC, are designed based on a three-degree-of-freedom vehicle model and a tracking error model. The current design enhances the feedforward link in conjunction with feedback control to eliminate steady-state lateral displacement errors, thereby improving control accuracy. Secondly, a linear time-varying MPC controller is developed, employing a QP solver to process the objective function with constraints for effective trajectory tracking. Finally, a nonlinear integral sliding mode lateral controller is proposed, building upon traditional sliding mode control. This new controller achieves zero steady-state error by replacing the sign function with a saturation function while incorporating integral action.
-
2.
In order to achieve longitudinal motion control for trajectory tracking, an MPC speed-tracking controller is designed. Through a layered control approach, the upper layer calculates the desired acceleration based on the current speed, current acceleration, and desired speed, and then transmits this information to the lower layer. The lower layer is governed by a drive-brake switching logic and a PI controller to generate the drive-brake input necessary for effective speed tracking. Additionally, a PID controller is employed as a benchmark to compare the control effectiveness of the two controllers.
The remainder of the paper is organized as follows: “Model description” describes the model, specifically deriving the vehicle dynamics model and the tracking error model. “Lateral controller design” details the design of the lateral controller using LQR, MPC, and NISMC based on the established model. “Longitudinal controller design” outlines the design of the longitudinal controller utilizing MPC and PID control. “Simulation results and discussion” demonstrates the control performance of each controller through simulation analysis and quantifies the results in combination with the six-dimensional score graph for comprehensive evaluation. Finally, conclusions are presented in “Conclusion”.
Model description
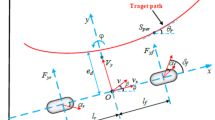
As shown in Fig. 114, this section presents the design of the 3DOF vehicle dynamic model and a tracking error model for further analysis and the development of a corresponding control strategy.
Dynamic modeling of trajectory tracking systems14.
Vehicle dynamics model
To ensure a better characterization of vehicle dynamics, as well as to enhance the accuracy and responsiveness of trajectory tracking, this study employs a three-degree-of-freedom dynamics model for vehicles. The equations of motion18 in the longitudinal, lateral, and transverse pendulum directions are formulated based on Newton’s second law, which is expressed as follows:
where m represents the mass of the vehicle; γ is the yaw angular velocity of the vehicle; vx, vy are the longitudinal and lateral velocities of the vehicle, respectively; Fx is the total tire force along the longitudinal axis of the vehicle; Fr is the rolling resistance, Fw is the air resistance, Fg is the ramp resistance, and Fj is the acceleration resistance; Fyf, Fyr are the lateral tire forces of the front and rear wheels; lf, lr are the distances from the center of mass to the front and rear axles; and δf denotes the angle of the front wheels; Iz signifies the yaw moment of inertia.
Where rolling resistance, air resistance, slope resistance, and acceleration resistance19 are expressed as follows:
where f denotes the rolling resistance coefficient, CD is the air resistance coefficient, A represents the vehicle windward area, \({\theta }_{g}\) is the measured or estimated road slope, \(\tau\) signifies the conversion coefficient of the vehicle rotating mass, \(\tau >1\), \(\frac{dV}{dt}\) is the vehicle driving speed.
According to the wheel torque balance relationship, the equation governing wheel dynamics can be derived as follows:
where \({I}_{\omega i}\) is the moment of inertia of the wheel, \(\upomega\) is the angular speed of the wheel, R signifies the equivalent rolling radius of the wheel, \({T}_{di}\) and \({T}_{bi}\) respectively denote the driving torque and braking torque of the wheel, \({F}_{xi}\) is the longitudinal tire force of the wheel, and \({F}_{Ri}\) is the rolling resistance of the wheel.
Because the nonlinear model impacts the computational complexity of the controller, it has been further simplified. First, we assume that the front wheel angle is small. Second, the tire model is simplified to represent a linear relationship between the tire side deflection force and the side deflection angle. The side force20 is expressed as follows:
where Caf represents the lateral stiffness of the front wheel and Car denotes the lateral stiffness of the rear wheel. αf is the side deflection angle of the front wheel, and αr is the side deflection angle of the rear wheel.
The front and rear wheel side deflections of the vehicle are determined using the small angle assumption as follows:
Considering that the lateral declination angle and yaw velocity of the center of mass effectively represent the lateral stability of the vehicle, the lateral dynamics model is derived from the force balance equation perpendicular to the vehicle’s longitudinal axis and the moment balance equation around the center of mass:
where \(\beta\) is the centroid side deflection angle of the vehicle.
Tracking error model
The tracking error model is a fundamental concept in vehicle trajectory tracking control. For a vehicle to achieve autonomous navigation and driving along a predetermined trajectory or path, the tracking error model aids in understanding the discrepancies that arise when the vehicle follows the reference trajectory. This understanding is essential for designing an appropriate controller that minimizes these errors and enhances tracking performance.
As illustrated in Fig. 1, the lateral error \(y_{e}\) is defined as the straight-line distance from the vehicle’s center of mass to the point where the reference trajectory is projected. The heading deviation is expressed as follows:
where \(\varphi\) and \(\varphi_{d}\) are the heading angles of the longitudinal axis of the body and the tangent to the reference track at point P, respectively.
For lateral velocity error \(\dot{{y}_{e}}\) and lateral acceleration error \(\ddot{{y}_{e}}\) satisfy the relationship:
When the effect of the heading angular acceleration error is disregarded under conditions of small curvature, the heading angular velocity error and the heading angular acceleration error exhibit the following relationship:
The state equation is formulated based on the vehicle’s trajectory tracking error. The state variables are defined as the lateral tracking error ye, heading error φe, lateral speed error \(\dot{{y}_{e}}\), heading angular speed error \(\dot{{\varphi }_{e}}\), and the input variable is the front wheel angle δf. By integrating the vehicle dynamics relations with the error calculation equations, the trajectory tracking state equation can be derived as follows:
In Eq. (10), error space state equation \(x={\left[\begin{array}{ccc}{y}_{e}& \begin{array}{cc}\dot{{y}_{e}}& {\varphi }_{e}\end{array}& \dot{{\varphi }_{e}}\end{array}\right]}^{T}\), input variables \(u={\delta }_{f}\), output variable \(y={\left[\begin{array}{cc}{y}_{e}& {\varphi }_{e}\end{array}\right]}^{T}\), and the specific forms of each matrix A, B, C and D are expressed as
Lateral controller design
In this section, we will design LQR, MPC, and NISMC controllers based on the trajectory tracking model established earlier. By comparing the three lateral control methods, we will assess the effectiveness of each controller. This evaluation will be based on several criteria, including trajectory tracking accuracy, robustness to parameter uncertainty, reliability in handling curvature discontinuities, and the actual control input.
LQR controller design
As the optimal control, the LQR control algorithm has a relatively stable control effect. It can effectively reduce system error to zero using minimal control input while simultaneously stabilizing unstable systems. The closed-loop optimal control system is established through an all-state linear feedback control law. The linear quadratic optimal control problem has a standardized solution process, allowing for the derivation of an analytical expression for the optimal solution, which can incorporate various performance indicators21. Consequently, this paper applies the LQR controller to the design of a lateral controller.
Theoretical basis of LQR trajectory tracking control
LQR controller comprises several components: the AB calculation module, the LQR module, the prediction module, the tracking error calculation module, the feedforward control calculation module, and the optimal control module. Initially, the optimal control feedback matrix K is obtained by calculating the vehicle dynamics parameters AB and inputting them into the LQR module. Subsequently, to ensure control smoothness and enhance accuracy, the dynamic information obtained from the prediction module is augmented. The status information is gathered by the tracking error calculation module, and the optimal control rate is calculated by the optimal control module. Finally, based on the original control law, an appropriate feedforward control quantity is added to eliminate the steady-state error in lateral displacement. Fig. 2 illustrates the algorithmic flow of the LQR trajectory tracking controller.
Consider a linear error system:
By establishing the optimal control \({u}^{\boldsymbol{*}}\left(t\right)\), the quadratic performance index cost function is minimized:
where Q is a 4 × 4 semi-definite real symmetric constant matrix, reflecting the weight of the state quantity, and R is a Positive definite matrix, reflecting the weight of the control quantity. Through iterative tuning to obtain the weight matrices \(Q=diag\left\{30, 1, 5, 1\right\}\), \(R=10\).
Constructing Hamilton function:
Ignoring the constraints of the input signal, the derivation of Eq. (14) is conducted to determine the extreme value, allowing the optimal control to be expressed as follows:
where \(\lambda \left( t \right) = P\left( t \right)x\left( t \right)\), P is the positive definite solution of the Riccati equation:
The necessary and sufficient conditions for obtaining the optimal control signal are as follows:
Application of LQR in trajectory tracking control
For LQR, in order to facilitate calculation and avoid multi-value problems, the expected trajectory is discretized to obtain a series of reference trajectory points22, as shown in Fig. 3.
Schematic of discrete reference trajectory points22.
The error matrix and curvature of discrete trace points are calculated as follows:
-
1.
At any given time, the tuple of reference track points is represented by \(\left[\begin{array}{cc}\begin{array}{cc}{x}_{d}& {y}_{d}\end{array}& \begin{array}{cc}{\varphi }_{d}& {k}_{d}\end{array}\end{array}\right]\), traversing reference track point \(\left[\begin{array}{cc}\begin{array}{cc}{x}_{d}& {y}_{d}\end{array}& \begin{array}{cc}{\varphi }_{d}& {k}_{d}\end{array}\end{array}\right]\) to find the closest point to the real position \(\left[\begin{array}{cc}\begin{array}{cc}x& y\end{array}& \begin{array}{cc}\varphi & k\end{array}\end{array}\right]\) of the vehicle, which is called the matching point. Define the sequence where the matching points are located as \(\left[\begin{array}{cc}\begin{array}{cc}{x}_{m}& {y}_{m}\end{array}& \begin{array}{cc}{\varphi }_{m}& {k}_{m}\end{array}\end{array}\right]\) and the unit tangent vector and normal vector of the matching points are expressed as
$$\begin{gathered} \vec{\tau }_{m} = \left[ {\begin{array}{*{20}c} {\cos \left( {\varphi_{m} } \right)} \\ {\sin \left( {\varphi_{m} } \right)} \\ \end{array} } \right] \hfill \\ \vec{n}_{m} = \left[ {\begin{array}{*{20}c} { - \sin \left( {\varphi_{m} } \right)} \\ {\cos \left( {\varphi_{m} } \right)} \\ \end{array} } \right] \hfill \\ \end{gathered}$$(18) -
2.
Let the curvature from the matching point to the projection point remain unchanged. According to the geometric relationship, the longitudinal position deviation and lateral displacement error can be obtained as follows:
$$\begin{gathered} x_{e} = - \left( {x - x_{m} } \right)\cos \varphi_{m} + \left( {y - y_{m} } \right)\sin \varphi_{m} \hfill \\ y_{e} = - \left( {x - x_{m} } \right)\sin \varphi_{m} + \left( {y - y_{m} } \right)\cos \varphi_{m} \hfill \\ \end{gathered}$$(19) -
3.
Define s as the arc length between point P and a reference point on the reference track. The speed of point P moving along the reference track, denoted as s, can be expressed as:
$$\dot{s} = \frac{1}{{1 - k_{d} y_{e} }}\left( {v_{x} \cos \varphi_{e} + v_{y} \sin \varphi_{e} } \right) = \frac{{V\cos \left( {\varphi - \varphi_{e} } \right)}}{{1 - k_{d} y_{e} }}$$(20) -
4.
The expected course angle can be obtained from the definitions of curvature and arc length, measured from the matching point to the projection point:
$$\varphi_{d} = \varphi_{m} + k_{m} x_{e}$$(21) -
5.
The course deviation can be determined based on the course angle at the projection point. The derivatives of course deviation and velocity deviation are expressed as follows:
$$\begin{gathered} \varphi_{e} = \varphi - \varphi_{d} \hfill \\ \dot{y}_{e} = v_{y} \cos \varphi_{e} + v_{x} \sin \varphi_{e} = V\sin \left( {\varphi - \varphi_{d} } \right) \hfill \\ \dot{\varphi }_{d} = k_{d} \dot{s} = k_{m} \dot{s} \hfill \\ \dot{\varphi }_{e} = \dot{\varphi } - k_{m} \frac{{v_{x} \cos \varphi_{e} - v_{y} \sin \varphi_{e} }}{{1 - k_{m} y_{e} }} \hfill \\ \end{gathered}$$(22)
Finally, the error space state \(x={\left[\begin{array}{ccc}{y}_{e}& \begin{array}{cc}\dot{{y}_{e}}& {\varphi }_{e}\end{array}& \dot{{\varphi }_{e}}\end{array}\right]}^{T}\) and the curvature kd are obtained. To further enhance real-time performance and operational smoothness, while considering the hysteresis of the algorithm, the prediction time is defined as tm. The position after tm is predicted in advance, and this prediction information is updated to the discrete trajectory reference point to obtain the control quantity at the subsequent moment. The forecast information is expressed as follows:
where \({x}_{pre}, {y}_{pre},{\varphi }_{pre},{v}_{{x}_{pre}},{v}_{{y}_{pre}},{\dot{\varphi }}_{pre}\) are respectively the predicted lateral and longitudinal position, yaw angle, lateral and longitudinal velocity, and yaw angle velocity.
In order to improve the response speed of the trajectory tracking control system to the reference signal and reduce the lateral steady-state error, a feedforward control strategy is introduced. This approach enables the system to better handle various complex conditions, improves control performance, reduces steady-state error, and achieves the desired control effect. The feedforward control law is defined as follows:
Substituting into the state-space equation of the system, there is:
When the system is stabilized, there is:
Let x = 0, the appropriate feedforward control quantity is expressed as follows:
where kd is the path curvature and K3 is the third term of the optimal control law feedback matrix.
MPC controller design
The MPC controller exhibits high adaptability in the realm of intelligent vehicle motion control, as it systematically incorporates predictive information and addresses multiple constraints and multi-objective optimization challenges. However, due to the computational speed limitations of MPC when handling nonlinear model optimization problems, this paper employs linear parameter varying model predictive control (LPV-MPC) to ensure both tracking accuracy and real-time computation23.
Model discretization and augmented system representation
The MPC trajectory tracking controller is founded on the dynamics model of tracking error. To facilitate the design of the MPC algorithm, it is necessary to discretize the tracking error dynamics model. In this context, the vehicle model, after discretization, is expressed using the midpoint Euler method as follows:
where \({A}_{1}={\left(I-\frac{AT}{2}\right)}^{-1}\left(I+\frac{AT}{2}\right)\), \({B}_{1}=BT\), \({C}_{2}=C\dot{{\varphi }_{d}}T\), \({D}_{1}=D\) and T is the sampling time.
In general, in order to eliminate steady-state error and ensure vehicle stationarity, the constraint of control increment should be considered. From \(\Delta u\left(k\right)=u\left(k\right)-u\left(k-1\right)\), state quantity \(x\left(k\right)\) and control quantity \(u\left(k\right)\) are augmented into a new state variable, which is represented as \(\xi \left(k\right)={\left[\begin{array}{cc}x\left(k\right)& u\left(k-1\right)\end{array}\right]}^{\text{T}}\). The augmented system is represented as follows:
In which:
Define the input increment and the output representation at future moments as follows:
The states in the predicted time domain are calculated iteratively using the generalized discrete state space equations as follows:
where Np and Nc represent the prediction and control time domains, respectively. Moreover \({N}_{c}\le {N}_{p}\), the output in the predicted time domain can be obtained according to the iteration as follows:
Organizing Eq. (33) yields the predicted output as follows:
With:
Finally, the discretization of the model makes the model suit the MPC algorithm in the system. Moreover, enhancing the system representation improves the performance and adaptability of MPC control. Through these operations, we establish a more accurate and efficient foundational model for the application of MPC in trajectory tracking control.
Application of MPC in trajectory tracking control
In order to enable the MPC trajectory tracking controller to follow the reference path smoothly and accurately within the prediction time domain, while also accounting for potential errors that may arise during actual tracking, errors that could hinder the timely identification of the optimal solution, a relaxation factor ρ is introduced24. The cost function is defined as follows:
where \(\varepsilon\) is the weight coefficient of the relaxation factor, and the diagonal matrices \(\widetilde{Q}\) and \(\widetilde{R}\) are positive definite weight matrices, where \(\widetilde{Q}\) represents the tracking error between the predicted output and the reference trajectory, and \(\widetilde{R}\) is a penalty on the control inputs, which helps to make the control process smoother.
Substituting the predicted output into the cost function:
where \(G\left(k\right)=\psi \xi \left(k\right)+\Gamma \Theta \left(k\right)\), and \({G}^{T}\left(k\right)\widetilde{Q}G\left(k\right)\) are constants independent of \(\Delta U\). The cost function is expressed as
where \(H = 2\left[ {\begin{array}{*{20}c} {\left( {\Phi^{T} \tilde{Q}\Phi + \tilde{R}} \right)} & 0 \\ 0 & \varepsilon \\ \end{array} } \right],g^{T} = \left[ {\begin{array}{*{20}c} {2\Phi^{T} \tilde{Q}G\left( k \right)} & 0 \\ \end{array} } \right].\)
Consider the physical constraints on the front wheel angle, specifically the rigid limitations imposed on the actuator.
In which:
Consider the environmental conditions that impose certain restrictions on the output variables.
Consider that the predicted output constraint exists:
The MPC trajectory tracking problem is reformulated as a quadratic programming problem by defining appropriate cost functions and constraints. QuadProg, a widely used quadratic programming solver, efficiently and accurately addresses the optimization problem. The optimization is solved at any time step k, and the optimal solution \(\Delta {u}^{*}\left(k\right)\) is obtained and applied to the system to obtain the optimal control law:
In this design, in order to ensure the accuracy of the acquired vehicle information set the adoption time T to be 0.02. To improve the computational efficiency, set the prediction step size \({N}_{p}=20\) and the control step size \({N}_{c}=3\). Through iterative tuning to obtain the weight matrices \(\widetilde{Q}=diag\left\{20,0; 0,5\right\}\), \(\widetilde{R}=600\), the weights of the relaxation factors \(\upvarepsilon =10\).
Design of nonlinear conditional integral sliding mode controller
Sliding mode control is widely utilized in intelligent driving motion control due to its inherent discontinuity in the sliding mode surface25, which provides significant robustness against external perturbations and variations in system modeling parameters. However, when confronted with switching delays or high-frequency dynamics, jitter phenomena may arise, adversely affecting the tracking performance. To address this issue, this paper introduces the third lateral controller NISMC26, which effectively eliminates steady-state errors caused by model inaccuracies or external disturbances, thanks to its lower feedback gain. In comparison to the basic sliding mode controller, the inclusion of the integral term allows the system to rectify steady-state errors resulting from model inaccuracies or external interference, thereby ensuring accurate, smooth, and rapid tracking. Additionally, due to its low feedback gain, the controller can achieve anti-saturation of the integral operation, thereby enhancing the stability and robustness of the tracking performance.
Reference to yaw velocity calculation
From the vehicle dynamics equation of state Eq. (6), the transfer function of the second-order system relating the front wheel angle input to the transverse pendulum angular velocity response is expressed as follows:
With:
The steady-state gain of the system for the front wheel angle is obtained to be designed as follows:
Where Kg is the gain coefficient and L is the vehicle wheelbase. The reference transverse pendulum angular velocity can be expressed as:
where Kw is the stability factor coefficient. Meanwhile, considering the limitation of the road surface condition and the small side deflection angle of the center of mass, the value of the reference transverse pendulum angular velocity limited by the road surface condition is obtained as follows27:
Application of NISMC to trajectory tracking
The design of the NISMC feedback control law is grounded in the yaw dynamics model. By regulating the front wheel angle, the vehicle’s yaw velocity is maintained, allowing it to adhere to the expected yaw velocity derived from Eq. (44). This ensures that the vehicle can navigate along the predetermined trajectory.
The yaw dynamics model obtained from Eq. (6) is expressed as follows:
Defining the pendulum angle tracking error \({\gamma }_{e}=\gamma -{\gamma }_{ref}\) transforms the trajectory tracking problem into an error calibration problem:
With:
To simplify the problem, we assert that by considering the centroid side deflection angle estimation error term and combining Eqs. (41) through (45), Eq. (47) can be expressed as follows:
where \(\Delta \left(\bullet \right)\) is the combination term of the error term of centroid side deflection angle estimation and the reference yaw angle.
In order to enhance chatter reduction near the sliding mode surface, minimize tracking error, and prevent integral saturation28, a nonlinear integral sliding mode controller has been designed.
First, set up the surface of the slip mold as follows:
where k0 is the error integral control coefficient and k0 > 0, \(\sigma\) is the integral of the error, which satisfies the relation \(\dot{\sigma }={\gamma }_{e}\). Zero steady-state error can be achieved by incorporating integral action. The derivation of the above equation exists:
The sliding mode control law can be expressed as follows:
In the actual control process, in order to eliminate jitter and ensure continuous smoothness in control, the saturation function \(sat\left(\bullet \right)\) instead of the sign function \(sgn\left(\bullet \right)\). The formula above can be expressed as follows:
where \(\kappa\) is the boundary layer thickness. \(sat\left(\frac{s}{\kappa }\right)\) is defined as follows:
The final error is represented dynamically as:
Satisfaction \(|\sigma \left(0\right)|\le \frac{\kappa }{{k}_{0}}\).
When \(|s|\ge \kappa\), \({\delta }_{f}=-{k}_{p}sgn\left(\frac{s}{\kappa }\right)\). Therefore, outside the saturation function boundary, the front wheel angle is not influenced by the tracking error integral. The tracking error of the transverse pendulum’s angular velocity is asymptotically stabilized, which ensures both the robustness and response speed of the sliding mode control.
When \(|s|<\kappa\), \({\delta }_{f}=-{k}_{p}\frac{s}{\kappa }=-\frac{{k}_{p}}{\kappa }{\gamma }_{e}-\frac{{k}_{p}{k}_{0}}{\kappa }\sigma\). That is, following the introduction of the conditional integral within the bounds of the saturation function, the motion tracking control law incorporates an integral component of the tracking error. This addition enhances the controller’s response performance and decreases the tracking error of the transverse pendulum’s angular velocity.
Longitudinal controller design
In the trajectory tracking control of intelligent driving vehicles, it is essential to emphasize tracking accuracy, smoothness, and driving comfort while ensuring lateral control precision. Consequently, the smoothness and high accuracy of longitudinal speed control are also critical performance indicators in tracking control. As illustrated in Fig. 4, this section is based on the MPC hierarchical speed tracking controller29, where the upper layer employs the MPC controller to calculate the desired acceleration. The lower layer determines the driving and braking modes by switching logic and computes the driving or braking inputs using a simple proportional-integral control method to achieve high-precision speed tracking. Additionally, PID controllers, which are straightforward to implement and do not depend on precise vehicle models, are considered benchmarks for comparison.
MPC speed tracking controller design
During the longitudinal movement of the vehicle, due to the inertial delays in the drive train and control system, the first-order inertial system is considered30,31,32 in the longitudinal control denoted as follows:
where \({K}_{a}=1\) is the system gain; \({\tau }_{d}=0.2\) is the inertia time constant; a is the actual acceleration; ades is the desired acceleration. The space equation of state for the longitudinal motion of the vehicle can be expressed as follows:
With:
where the system state vector \(\chi ={\left[\begin{array}{cc}v& a\end{array}\right]}^{T}\),control input \({u}_{s}={a}_{des}\). Using the Forward Euler method for Eq. (60), the discretized state space representation of the system can be expressed as follows:
With:
To accurately and smoothly track the target velocity, the objective function is defined as follows:
where \({Q}_{s}\) is the weight matrix of the system output, reflecting the tracking accuracy of the reference speed, and \({R}_{s}\) is the weight matrix of the control input increment, reflecting the penalty for acceleration changes. The primary objective of the function is to achieve a stable and rapid speed that effectively tracks the target speed.
Considering the smoothness and comfort of driving, the constraints imposed on the control inputs and their increments are expressed as follows:
where \({u}_{smax}\) and \({u}_{smin}\) denote the maximum and minimum values of acceleration respectively, \(\Delta {u}_{smax}\) and \(\Delta {u}_{smin}\) denote the maximum and minimum values of acceleration increment respectively.
Transforming the MPC problem into a quadratic programming problem.
The QP solver in MATLAB is utilized to address quadratic programming problems, and the optimal control input is determined by calculating the optimal control increment.
The control input at time k is substituted into the system’s state-space equation. At time k + 1, the system recalculates the output for the next time step based on the predicted information. It then obtains the control increment sequence for time k + 1 through calculations, completing the control process of the entire system cyclically. The design weights matrix \({Q}_{s}=200\) and \({R}_{s}=0.5\).
Considering the actual situation of vehicle operation, driving, and braking are generally independent processes that do not occur simultaneously. Furthermore, to ensure a smooth driving experience, it is advisable to minimize frequent transitions between driving and braking modes. The switching buffer parameter, denoted as athr, should be carefully selected. Consequently, the design of the driving and braking switching logic is articulated as follows:
where ades is the expected acceleration, the drive or braking mode is determined by comparing with athr, atdes is the expected throttle opening, Pbdes is the expected brake master cylinder pressure.
PID speed tracking controller design
At present, PID control remains widely utilized in various longitudinal control systems due to its independence from precise modeling and its applicability to most control systems33,34. In this section, we will design a speed-tracking controller based on the PID algorithm and the control rate will be expressed as follows:
In the formula, proportional coefficient \({k}_{p}=1\), integral coefficient \({k}_{i}=0.001\), differential coefficient \({k}_{d}=0.1\), \(\Delta v\) is the velocity tracking error, \({U}_{pid}\) is the velocity error measurement, when \({U}_{pid}\ge 0\), apply the driving torque, when \({U}_{pid}<0\), apply the braking pressure.
Simulation results and discussion
In this section, a series of simulation experiments are conducted to compare the trajectory-tracking performance of three lateral controllers and the velocity-tracking effectiveness of two longitudinal controllers. First, “Lateral controller performance comparison” assesses the tracking performance of the three lateral controllers under variable or large curvature conditions by comparing the results of the double lane change test and the circular path test. Next, “Step speed tracking test” presents step speed-tracking tests to evaluate the speed-tracking performance of the two longitudinal controllers. Finally, “Comprehensive evaluation” analyzes the results and provides a comprehensive evaluation of the control performance of the lateral and longitudinal controllers designed in this paper. The relevant parameters of the autonomous vehicle used in this simulation are detailed in Table 1.
Lateral controller performance comparison
Case A: double lane change test
In this example, the automated vehicles are programmed to conduct a double lane change test at an initial speed of 36 km/h. The road surfaces are classified based on their adhesion coefficients: 0.85 for regular road conditions and 0.35 for icy or snowy conditions. The transient control capabilities and stability of the three controllers are compared under varying road environments and low lateral acceleration conditions, simulating challenging driving scenarios.
The test on the 0.85 adhesion coefficient road
The simulation results of the double lane change test conducted on a conventional high-adherence road (coefficient of friction = 0.85) are presented in Fig. 5. All three proposed controllers effectively track the reference trajectory. Among them, the LQR controller exhibits the largest maximum lateral displacement error of 0.08 m. The MPC controller has the second-largest maximum lateral displacement error, which aligns well with the reference curvature of the double lane change test, demonstrating excellent control performance. In contrast, the proposed nonlinear integral sliding mode controller achieves the smallest maximum lateral displacement error of 0.025 m. However, it is important to note that the actual steering angle of the wheel and the lateral deviation angle of the center of mass are larger, resulting in a smoother control process. While the nonlinear integral sliding mode controller provides the best tracking effect with the smallest maximum lateral displacement error of 0.025 m, it also exhibits larger actual steering angles and centroid side deflection angles, leading to a less smooth control process. In terms of heading error angles, the LQR controller achieves the smallest maximum heading error of only 0.045 radians, followed by the MPC controller and the nonlinear integral sliding mode controller. As illustrated in Fig. 5b, using the QP solver and computer with AMD R9 7945HX CPU, the average real-time computation time for the MPC controller is 0.002 seconds, which meets the real-time computation requirements for effective control.
The test on the 0.5 adhesion coefficient road
The simulation results of the double lane change test on a wet road (coefficient of friction = 0.5) are presented in Fig. 6. At this point, the tires remain within the linear region, and the path tracking performance is similar to that observed on conventional road surfaces. The tracking effectiveness of the LQR and MPC controllers is comparable; however, the maximum lateral displacement error for the MPC is significantly smaller. The lateral error of the nonlinear integral sliding-mode controller remains relatively stable, staying within 0.02 m. Nevertheless, as the road surface attachment coefficient decreases, both the center of mass side deflection angle and the actual wheel steering angle exhibit more pronounced changes.
The test on the 0.35 adhesion coefficient road
As road conditions deteriorate, the tires enter a nonlinear region, which significantly tests the performance requirements of the controller. The simulation results of the double lane change test conducted on snow and ice (coefficient of friction = 0.35) are presented in Fig. 7. All three controllers are generally able to follow the reference path; however, the LQR controller demonstrates the best performance, maintaining a maximum heading angle error within 0.05 radians. In contrast, the lateral error of the nonlinear integral sliding mode controller increases noticeably, performing poorly compared to the high and medium adhesion surfaces. The MPC controller exhibits minimal lateral displacement error during the 4–9 s interval. Specifically, during this period, the lateral displacement error of the MPC controller is very small, and the actual turning angle of the wheels is less than that of both the LQR and nonlinear integral sliding mode controllers, indicating a more effective path tracking capability with reduced control inputs. These results suggest that the MPC controller exhibits high robustness under the challenging conditions of the external road environment.
Case B: circular path test
In order to demonstrate the steady-state characteristics of the proposed three lateral controllers on low and medium-adhesion road surfaces, a circular path test condition is selected. The vehicle enters the test road with an initial speed of 54 km/h, the road adhesion coefficient is 0.5, and the radius of the reference path’s circumference is 60 m. The reference path is illustrated in Fig. 8a.
The control results for the circumferential path are presented in Fig. 8. In both the middle and low adhesion road surfaces, all three controllers effectively track the reference path. The actual steering angle, centroid side deflection angle, and heading angle errors among the three controllers are relatively similar, with the heading error ultimately stabilizing at − 0.03 radians. Notably, the MPC exhibits the smallest lateral displacement error and converges rapidly to zero, achieving stable tracking. In contrast, the nonlinear integral sliding mode control converges more slowly but ultimately reaches a zero steady-state error. The maximum lateral displacement error for the LQR is − 0.06 m, with a final steady-state error of approximately 0.03 m, which is less favorable compared to the tracking steady-state characteristics of the other controllers.
Step speed tracking test
In order to verify the steady-state tracking performance of the proposed two longitudinal controllers for speed tracking, a step vehicle speed response experiment was conducted. The road surface adhesion coefficient was set at 0.8, the initial front wheel angle was zero, and the initial vehicle speed was also zero. As illustrated in Fig. 9a, the vehicle was accelerated twice before reaching 70 s. The speed increased to 30 km/h at 10 s, and then the vehicle continued to accelerate to 50 km/h by 30 s. After 70 s, the speed decreased to 10 km/h and subsequently maintained a constant speed.
The simulation results are shown in Fig. 9. Both longitudinal controllers effectively track the reference speed, with the steady-state speed tracking error approaching zero. The average rise time is approximately 2 s. However, the MPC controller exhibits a jittering effect when the speed changes, which is attributed to constraint issues.
Comprehensive evaluation
Both proposed longitudinal controllers can track the reference speed quickly and accurately, demonstrating good steady-state tracking performance. During the speed tracking process, the PID controller provides a rapid response in both driving and braking modes, making it more suitable for longitudinal speed tracking control due to its relatively intuitive design and ease of parameter tuning. In contrast, the proposed Model Predictive Control (MPC) controller can quickly track the reference speed in driving mode; however, it exhibits a slower braking response due to constraints encountered in braking mode. As shown in Fig. 9b, the MPC controller also suffers from a jitter effect. Generally, the MPC controller has higher requirements for the accuracy of system modeling, making adjustments more challenging and increasing computational complexity. Therefore, when selecting a speed-tracking controller, the simpler and more user-friendly PID controller is often the more appropriate choice.
To facilitate the analysis of the trajectory tracking effectiveness of the three proposed lateral controllers, the root mean square error (RMSE) is included as one of the metrics. The equation is expressed as follows:
Where N denotes the length of the sampling period, yi denotes the measured output, and yd indicates the reference output. The comprehensive performance of the controllers is evaluated by analyzing the maximum lateral displacement error, heading angle error, maximum front wheel turning angle, and the root mean square value of each controller under three different road adhesion coefficient conditions during the double lane change test. The results are presented in Table 2.
In order to more intuitively compare the comprehensive performance of the three lateral controllers, each performance indicator is presented under three different adhesion coefficients. At the same time, to enhance the clarity of the graph, the data is displayed with two significant digits, as illustrated in Fig. 10.
In terms of the lateral tracking effect, both the maximum lateral displacement error and the root mean square error of the MPC controller decrease as the adhesion coefficient of the road surface declines from 0.85 to 0.5, indicating improved control performance. However, when the adhesion coefficient further decreases to 0.35, both the maximum lateral displacement error and the root mean square error increase. In contrast, the maximum lateral displacement error of the NISMC controller on medium to high adhesion road surfaces is only 0.028 m, with the root mean square error stabilizing within 0.01 m. This demonstrates excellent control performance on good road surfaces. Nevertheless, the control effectiveness significantly diminishes on icy and snowy road surfaces, where the maximum lateral displacement error and root mean square error increase by approximately 0.1 m and 0.03 m, respectively, indicating relatively poor robustness on low-adhesion road surfaces. The maximum lateral error of the LQR controller remains around 0.07 m across the three road conditions, and interestingly, the lateral displacement error decreases as the road surface adhesion coefficient decreases.
In terms of heading tracking performance, the MPC controller and the LQR controller exhibit similar effectiveness, with the maximum heading error and the root mean square error stabilized at approximately 0.06 radians and 0.02 radians, respectively. This level of performance ensures effective heading tracking. In contrast, the NISMC controller demonstrates slightly inferior performance, with its maximum heading error exceeding 0.06 m and the root mean square of the heading error greater than 0.02 radians.
In terms of control inputs, the maximum wheel turning angle of the MPC controller is less than 6 degrees on both medium and low traction surfaces. As the road adhesion coefficient decreases to 0.35, the maximum wheel turning angle increases by only about 1.5°, with a maximum root mean square error of 2.39° on icy and snowy road surfaces. The LQR controller maintains a smaller wheel turning angle on medium and low traction surfaces, and its control inputs are comparable to those of the MPC. However, when the road adhesion coefficient is reduced to 0.35, the control inputs significantly increase to 16.7° and 3.3°, respectively. The NISMC controller does not fully account for the influence of control inputs; to ensure effective tracking, its wheel angle increases as the road surface adhesion coefficient decreases, particularly in poor road conditions, resulting in a maximum wheel angle of 2.39°. The LQR controller can ensure a small wheel angle on medium to low traction road surfaces, with control inputs similar to those of the MPC. Notably, when the road environment deteriorates, the maximum wheel angle and root mean square error reach 22.2° and 4.67°, respectively.
To accurately assess the control potential of the three controllers, six performance indicators were selected to evaluate them under a road adhesion coefficient of 0.35. A lower value indicates better performance, resulting in a higher score. The scoring system operates on a scale from 0 to 10, where 10 represents the best performance and 0 signifies the worst. For each indicator, we will identify the maximum and minimum values among the three controllers and apply the following formula to assign scores:
In this formula, \({\mathbb{R}}_{value}\) indicates the current controller indicator value, and \({\mathbb{R}}_{min}\) refers to the minimum value among the values of the three controllers for this indicator, which is also regarded as the best value.
The index scores of the three controllers obtained through calculation are shown in Table 3.
According to the performance index scores of the three controllers presented in Table 3, a six-dimensional radar chart has been created, as illustrated in Fig. 11. Under extreme adhesion road conditions, the MPC achieved an overall performance score of 9.24 points. It excelled in heading error control and front wheel angle control, demonstrating only a slight disadvantage compared to the LQR in lateral error control. Notably, the MPC’s overall performance improved by 11% and 63% compared to the LQR and NISMC, respectively. The comprehensive performance score for the LQR is 8.32; its primary advantage lies in maintaining stability in lateral error. However, this comes at the cost of excessive front wheel angle output, which may lead to comfort issues such as abrupt steering and potential collisions during actual driving. The NISMC recorded the lowest overall performance score of only 5.66 points, exhibiting poor robustness and immunity to extreme driving conditions, with its performance deteriorating by 87% compared to conventional driving conditions.
In general, the MPC controller can accurately and smoothly track the upper reference trajectory while maintaining small control inputs. It addresses the road’s large curvature or curvature discontinuities through model prediction, rolling optimization, and real-time computation. This approach balances inputs and outputs to achieve optimal control and demonstrates improved robustness. However, the comprehensive consideration of the vehicle dynamics model and constraints increases the complexity of optimization and solution processes. Consequently, this necessitates significant computational capability from the controller, and real-time computation remains a critical factor limiting the application of MPC in motion control. In contrast, the LQR controller is generally less effective than MPC in managing system dynamics and nonlinear issues. Nevertheless, it ensures system stability and can achieve optimal solutions within a fixed time frame. The proposed NISMC controller outperforms both MPC and LQR under normal operating conditions, ensuring rapid and smooth tracking of the reference path. However, when road conditions become severe or when there are sudden changes in curvature, the control effectiveness of NISMC diminishes compared to MPC. Despite this, it still guarantees system stability and can find optimal solutions within a fixed time domain. It is important to note that under adverse road conditions or sudden curvature changes, tracking accuracy may decline due to overshooting caused by the integral term. Additionally, it takes time for the system to recover from a zero steady-state error. In summary, MPC demonstrates the most comprehensive performance and maintains effective control even under extreme conditions, making it suitable for high-precision control scenarios. The lateral control of the LQR is outstanding, but the load capacity of the actuator needs to be optimized. It can also perform well under certain conditions. The control performance of Nonlinear Integral Sliding Mode Control (NISMC) tends to deteriorate significantly as the driving environment worsens, limiting its applicability to certain characteristic scenarios and conventional working conditions.
Conclusion
In this paper, we present a comparative study of three lateral controllers, MPC, LQR, and NISMC as well as two longitudinal controllers, MPC and PID, focusing on trajectory tracking and speed tracking. This study is based on a three-degree-of-freedom vehicle dynamics model and a trajectory-tracking error-based model.
In comparing the lateral controllers, the comprehensive performance of three different lateral controllers is evaluated through two scenarios: a double lane change test, and a circular path test, each conducted on surfaces with varying road adhesion coefficients. Considering the system’s capability to handle multiple constraints, the first lateral controller is designated as the MPC controller, which demonstrates excellent tracking performance and resistance to interference in simulation experiments, yielding the best overall performance. The second lateral controller employs LQR control, which exhibits slightly inferior comprehensive performance compared to the MPC but offers advantages in real-time processing and computational complexity, effectively maintaining control stability during simulations. The third controller introduces a lateral controller that employs sliding mode control based on a nonlinear conditional integrator. Simulation results demonstrate that the NISMC controller outperforms the others in terms of accuracy and response time under both optimal and normal road conditions. At the same time, in order to reflect the control potential of the three controllers, we employed a six-dimensional scoring system for evaluating the controllers’ performance on low-adhesion pavement with a coefficient of 0.35, allowing for a more direct assessment of their overall performance. The results indicated that the MPC achieved the highest comprehensive performance score of 9.24. Furthermore, the MPC’s performance was 11% and 63% superior to that of the LQR and NISMC, respectively. In contrast, the NISMC recorded the lowest comprehensive performance score of only 5.66, which was 87% lower than the performance observed on high-adhesion pavement with a coefficient of 0.85. In the comparison of longitudinal controllers, the steady-state performance of speed tracking between MPC and PID control is evaluated through a step speed tracking test. The simulation results reveal that the PID controller responds quickly to track the reference speed, while the MPC can also follow the vehicle’s speed but exhibits a jitter effect due to tuning parameter constraints and other issues. Therefore, PID control is recommended as the preferred choice for longitudinal speed-tracking controllers.
It is important to note that the control algorithms proposed in this paper have been validated through simulation. In the future, we plan to establish a real-vehicle experimental platform to further evaluate the control methods presented in this study. In addition, we will pay attention to the problem of actuator saturation and consider issues such as active disturbance rejection and parameter observation and estimation in the subsequent research.
Data availability
The datasets used and analysed during the current study available from the corresponding author on reasonable request.
References
Chen, L. et al. Milestones in autonomous driving and intelligent vehicles: survey of surveys. IEEE Trans. Intell. Veh. 8, 1046–1056 (2023).
Cao, D. et al. Future directions of intelligent vehicles: potentials, possibilities, and perspectives. IEEE Trans. Intell. Veh. 7, 7–10 (2022).
Zhao, G., Chen, Z. & Liao, W. Reinforcement-tracking: an end-to-end trajectory tracking method based on self-attention mechanism. Int. J. Automot. Technol. 25, 541–551 (2024).
Wang, M., Lv, X., Chen, J. & Su, X. Improved pure pursuit algorithm based path tracking method for autonomous vehicle. J. Adv. Comput. Intell. Inform. 28, 1034–1042 (2024).
Thrun, S. et al. Stanley: the robot that won the darpa grand challenge. J. Field Robot. 23, 661–692 (2006).
Nie, L., Guan, J., Lu, C., Zheng, H. & Yin, Z. Longitudinal speed control of autonomous vehicle based on a self-adaptive pid of radial basis function neural network. IET Intell. Transp. Syst. 12, 485–494 (2018).
Yang, T., Bai, Z., Li, Z., Feng, N. & Chen, L. Intelligent vehicle lateral control method based on feedforward + predictive Lqr algorithm. Actuators. 10, (2021).
Dai, P., Taghia, J., Lam, S. & Katupitiya, J. Integration of sliding mode based steering control and Pso based drive force control for a 4Ws4Wd vehicle. Auton. Robots. 42, 553–568 (2018).
Hameed, A. H., Al-Samarraie, S. A., Humaidi, A. J. & Saeed, N. Backstepping-based quasi-sliding mode control and observation for electric vehicle systems: a solution to unmatched load and road perturbations. World Electr. Veh. J. 15, 419. https://doi.org/10.3390/wevj15090419 (2024).
Abbas, S., Husain, S., Al-Wais, S. & Humaidi, A. Adaptive integral sliding mode controller (SMC) design for vehicle steer-by-wire system. SAE Int. J. Veh. Dyn. Stab. NVH. 8(3), 383–396. https://doi.org/10.4271/10-08-03-0021 (2024).
Husain, S. S., Al-Dujaili, A. Q., Jaber, A. A., Humaidi, A. J. & Al-Azzawi, R. S. Design of a robust controller based on barrier function for vehicle steer-by-wire systems. World Electr. Veh. J. 15, 17. https://doi.org/10.3390/wevj15010017 (2024).
Wang, X., Fu, M., Ma, H. & Yang, Y. Lateral control of autonomous vehicles based on fuzzy logic. Control Eng. Pract. 34, 1–17 (2015).
Wu, H., Si, Z. & Li, Z. Trajectory tracking control for four-wheel independent drive intelligent vehicle based on model predictive control. IEEE Access. 8, 73071–73081 (2020).
Yang, X., Xiong, L., Leng, B., Zeng, D. & Zhuo, G. Design, validation and comparison of path following controllers for autonomous vehicles. Sensors (Basel, Switzerland). 20, 6052 (2020).
Hang, P., Chen, X., Zhang, B. & Tang, T. Longitudinal velocity tracking control of a 4Wid electric vehicle. Ifac-Papersonline. 51, 790–795 (2018).
Xu, S., Peng, H., Song, Z., Chen, K. & Tang, Y. Accurate and smooth speed control for an autonomous vehicle. In IEEE Symposium on Intelligent Vehicle. Changshu 1976–1982 (IEEE, 2018).
Zhu, M., Chen, H. & Xiong, G. A model predictive speed tracking control approach for autonomous ground vehicles. Mech. Syst. Signal Proc. 87, 138–152 (2017).
Xia, X. et al. Autonomous vehicle kinematics and dynamics synthesis for sideslip angle estimation based on consensus Kalman filter. IEEE Trans. Control Syst. Technol. 31(1), 179–192 (2022).
Kieckhafer, K., Walther, G., Axmann, J. & Spengler, T. Integrating Agent-Based Simulation and System Dynamics to Support Product Strategy Decisions in the Automotive Industry. In Proceedings of the 2009 Winter Simulation Conference (WSC) 1433–1443 (IEEE, 2009).
Xiong, L. et al. IMU-based automated vehicle body sideslip angle and attitude estimation aided by GNSS using parallel adaptive Kalman filters. IEEE Trans. Veh. Technol. 69(10), 10668–10680 (2020).
Zhang, W. A robust lateral tracking control strategy for autonomous driving vehicles. Mech. Syst. Signal Proc. 150, 107238 (2021).
Li, H., Li, P., Yang, L., Zou, J. & Li, Q. Safety research on stabilization of autonomous vehicles based on improved-Lqr control. Aip Adv. 12, 15313 (2022).
Cheng, S., Li, L., Chen, X., Wu, J. & Wang, H. Model-predictive-control-based path tracking controller of autonomous vehicle considering parametric uncertainties and velocity-varying. IEEE Trans. Ind. Electron. 68, 8698–8707 (2021).
Jeong, Y. Model predictive control based integrated fault tolerant controller for autonomous vehicles with four-wheel independent steering, driving and braking systems. Veh. Syst. Dyn. 1–24 (2024).
Ma, B., Pei, W. & Zhang, Q. Trajectory tracking control of autonomous vehicles based on an improved sliding mode control scheme. Electronics. 12, (2023).
Hu, C., Wang, R. & Yan, F. Integral sliding mode-based composite nonlinear feedback control for path following of four-wheel independently actuated autonomous vehicles. IEEE Trans. Transp. Electrif. 2, 221–230 (2016).
Xie, F., Liang, G. & Chien, Y. Highly robust adaptive sliding mode trajectory tracking control of autonomous vehicles. Sensors. 23, (2023).
Yu, Z., Zhang, R., Xiong, L. & Fu, Z. Robust hierarchical controller with conditional integrator based on small gain theorem for reference trajectory tracking of autonomous vehicles. Veh. Syst. Dyn. 57, 1143–1162 (2019).
Cheng, S., Li, L., Guo, H., Chen, Z. & Song, P. Longitudinal collision avoidance and lateral stability adaptive control system based on Mpc of autonomous vehicles. IEEE Trans. Intell. Transp. Syst. 21, 2376–2385 (2020).
Mekala, G. K., Sarugari, N. R. & Chavan, A. Speed control in longitudinal plane of autonomous vehicle using Mpc. In 2020 IEEE International Conference for Innovation in Technology (INOCON) 1–5 (IEEE, 2020).
He, H. et al. Mpc-based longitudinal control strategy considering energy consumption for a dual-motor electric vehicle. Energy 253, 124004 (2022).
Yao, Q. & Tian, Y. A model predictive controller with longitudinal speed compensation for autonomous vehicle path tracking. Appl. Sci. 9, (2019).
Abdullah, M., Idros, S., Toha, S. F. & Md Said, M. S. Modelling of vehicle longitudinal dynamics for speed control. J. Adv. Res. Appl. Mech. 123, 56–74 (2024).
Shaju, A., Southward, S. & Ahmadian, M. Pid-based longitudinal control of platooning trucks. Machines. 11, (2023).
Acknowledgements
This work was supported in part by The Ganpo Talent Support Program-Leading Academic and Technical Personnel in Major Disciplines of Jiangxi Province (Grant No.20232BCJ23091), the National Natural Science Foundation of China (Grant No. 52462053), the Jiangxi Province Government Special Fund for Graduate Innovation (Grant No. YC2023-B207), the Natural Science Foundation of Jiangxi Province (Grant No.20232BAB214092; Grant No.20224BAB214045), and The 03 Special Program and 5G Project of Jiangxi Province (Grant No.20232ABC03A30).
Funding
This work was supported in part by The Ganpo Talent Support Program-Leading Academic and Technical Personnel in Major Disciplines of Jiangxi Province (Grant No. 20232BCJ23091), the National Natural Science Foundation of China (Grant No. 52462053), the Jiangxi Province Government Special Fund for Graduate Innovation (Grant No. YC2023-B207), the Natural Science Foundation of Jiangxi Province (Grant No.20232BAB214092; Grant No. 20224BAB214045), and The 03 Special Program and 5G Project of Jiangxi Province (Grant No. 20232ABC03A30).
Author information
Authors and Affiliations
Contributions
D.Z. and S.P. in the research design, data analyses, and drafting of this article; Y.Y., Y.H. and J.Y. participated in experiments drafting of this article; P.Z., L.X., G.C. and L.G. participated in research and reviewing of this article.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Zeng, D., Pan, S., Yu, Y. et al. A comparative study on trajectory tracking control methods for automated vehicles. Sci Rep 15, 17073 (2025). https://doi.org/10.1038/s41598-025-01365-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-025-01365-9