Robust super-twisting algorithm-based single-phase sliding mode frequency controller in power systems integrating wind turbines and energy storage systems

Abstract

Frequency regulation in multi-area power systems (MPSs) faces increasing challenges due to the integration of renewable energy sources, such as wind power, and the dynamic behavior of energy storage systems (ESSs). These challenges are further compounded by disturbances from tie-line power exchanges, wind power fluctuations, and variations in battery and flywheel storage. To address this, this paper proposes a robust sliding mode control (SMC) strategy based on a proportional-derivative sliding surface (PD-SS) structure for load frequency control (LFC), leveraging a single-phase approach enhanced by an improved super-twisting algorithm (ISTA). A reduced-order LFC model is introduced to effectively characterize the frequency dynamics. The proposed model explicitly considers lumped disturbances including tie-line power exchanges, wind power fluctuations, and power variations in ESSs of battery and flywheel. A novel SMC scheme is therefore designed based on the simplified model, where the PD-SS structure and single-phase approach eliminate reaching time, ensure immediate trajectory convergence and improve transient performance. An improved super-twisting control law is developed to further enhance robustness by effectively mitigating chattering and oscillation in system dynamics under uncertainties. The global stability of the proposed control strategy is mathematically verified via Lyapunov stability theory. Simulation results under step and stochastic load variations show that the proposed method achieves up to 56% and 84.5% reduction in overshoot compared to PD and PI SMC schemes, respectively, along with a 54.5% improvement in settling time over the PI SMC scheme, thereby confirming its enhanced performance and robustness relative to existing control strategies.

Introduction

Load Frequency Control (LFC) is vital for maintaining the frequency stability of modern power systems (PSs), especially as renewable energy sources (RESs) like wind turbine generators (WTG) become more popular in multi-area power systems (MPSs)^1,2. WTG under various wind conditions are intermittent, leading to frequent and unpredictable power fluctuations. This variation challenges both short-term and long-term balance between generation and demand³. Energy storage systems (ESSs), including flywheels (FESSs) and batteries (BESSs), introduce significant support to mitigate generation-load imbalances. FESSs respond rapidly to short-term fluctuations, while BESSs offer flexible and scalable storage for both short- and long-term regulation. Their integration smooths power fluctuations and enhances the stability and resilience of MPSs, which is crucial for sustainable and reliable future systems^4,5.

Numerous studies on LFC of various methods to enhance MPS stability and reliability have been conducted over the years. Among them, the derivatives of Among these, proportional-integral-derivative (PID) controllers are widely used for their simplicity, cost-effectiveness, and strong performance in linear systems^{6,7,8,9,10,11,12,13,14}. In⁶, particle swarm optimization and genetic algorithms were used to optimize PID parameters for LFC in MPSs with both renewable and conventional energy sources. The study in¹² introduces the one-to-one-based optimizer-optimized PI-PD controller for a four-area PSs under load disturbances and system nonlinearities. In¹³, a Jaya-optimized cascade fractional order fuzzy PID-integral double derivative controller using de-loaded tidal turbines was proposed to enhance LFC under uncertainties. In¹⁴, an arithmetic optimized African vulture’s optimization algorithm-tuned type-2 fuzzy PD–2DOF PID controller improved LFC performance in systems with thermal and RESs under practical constraints. However, due to the nonlinearities and uncertainties in MPSs, combined with the growing integration of RESs, PID controllers and their variations face increasing limitations. The fixed design in control parameter hinder adaptability under dynamic conditions, often lead to suboptimal performance in scenarios of disturbances or variable RESs.

Advanced techniques such as optimal and model predictive control (MPC) have been explored^15,16,17 to overcome these challenges. In¹⁵, two robust LFC schemes based linear quadratic regulator method, and its variation was introduced for microgrids with high RESs, using BESS-based virtual inertia control under load and RES disturbances. In¹⁷, a Harris Hawks Optimization-tuned MPC scheme was proposed in MPS, demonstrating enhanced LFC and robustness under stochastic load variations and system nonlinearities. However, its dependence on accurate models and high computational requirements makes it less suitable for complex or highly dynamic grids, particularly those with a high penetration of RESs.

Adaptive control methods have gained attention for their ability to adjust control parameters in real time, making them suitable for MPSs experiencing dynamic changes^18,19. In¹⁸, an adaptive controller using a hybrid Jaya-Balloon optimizer for frequency stabilization in a single-area smart microgrid, which manages flexible loads such as heat pumps and electric vehicles, was proposed. However, their computational complexity and algorithmic requirements may hinder real-time deployment in large-scale systems. Similarly, model predictive control (MPC) and artificial intelligence (AI)-based approaches have shown promise in managing the variability and uncertainty of RESs^{20,21,22,23,24}. Study²⁰ presented a fuzzy adaptive MPC approach for LFC in an isolated microgrid, enhancing response speed and adaptability by adjusting the tuning parameter. A distributed secondary LFC method for islanded microgrids, using artificial neural networks for spatial load power forecasting to optimize power outputs and stabilize frequency without the need for frequency measurement is developed in²³. While MPC optimizes control using predictive models, it is limited by forecasting and computational demands, whereas AI techniques manage nonlinearities but require extensive datasets and tuning.

Sliding mode control (SMC) is proposed for LFC scheme to enhance system robustness and stability, particularly in the presence of disturbances and parameter variations. By leveraging its robustness against model uncertainties and external disturbances, SMC can effectively mitigate frequency deviations in MPSs. Its implementation in LFC ensures fast response times and maintains system performance under dynamic load variations, making it a viable solution for MPSs with fluctuating load and high penetration of RESs^{25,26,27,28,29,30,31,32,33,34,35,36}. First-order SMC schemes are widely recognized for their simplicity and ease of implementation, making them particularly well-suited for LFC in MPSs. The straightforward design enables rapid implementation with relatively low computational cost, as demonstrated in numerous studies applying first-order SMCs. These schemes typically utilize various sliding surfaces (SSs)^{26,27,28,29,30,31,32}, allowing the system to achieve effectively frequency regulation with minimal complexity. For instance, in^26,28, a traditional SMCs-based PI SS was introduced for decentralized LFC under both matched and mismatched uncertainties. Additionally³⁰, developed a modified SMC approach based on a double PI SS using a state observer for decentralized LFC, while³¹ proposed a novel SMC method with a PD SS for LFC considering nonlinear MPSs. In³², an advanced PID SS was utilized for decentralized frequency regulation for MPSs with hydropower turbines. Despite these advantages, first-order SMCs suffer from the significant drawback of chattering. This phenomenon, characterized by high-frequency oscillations in the control input, can undermine the system’s stability and performance, especially in the presence parameter variations or external disturbances.

To mitigate chattering, advanced SMC strategies were proposed^33,34,35,36. For example³³, introduced a super-twisting-based SMC for two-area PSs³⁴, used second-order SMC with disturbance observers, and³⁵ optimized higher-order SMC using the Honey Badger algorithm. Despite their robustness, these methods face sensitivity to model uncertainties and complex tuning processes. Moreover, the reaching phase leaves the system vulnerable to disturbances. Table 1 compares various SMC approaches for LFC in MPSs, detailing SMC types, sliding surfaces (SSs), sensor usage, and system models, offering a clear perspective on their structures, capabilities, and limitations.

Table 1 Comparison of reported and suggested papers of SMC for LFC in MPSs.

LFC in MPSs involves challenges like nonlinear dynamics, load disturbances, wind power intermittency, and fluctuations from ESSs and tie-line power exchanges. Controllers must ensure frequency stability under such uncertainties, with fast transient response and high robustness.

This paper proposes a novel super-twisting-based single-phase PD SMC scheme aimed at enhancing robustness and reducing chattering. The single-phase method ensures that the system trajectory is immediately constrained within the predefined PD SS, effectively suppressing transient oscillations and improving system stability. Furthermore, the improved super-twisting algorithm (ISTA) is developed to mitigate chattering while maintaining the fast response and strong disturbance rejection capabilities of conventional SMCs. The proposed strategy is validated through comprehensive case studies on MPSs with RES variations and ESS integrations, demonstrating its effectiveness under various operating conditions, including step and random load disturbances. Comparative assessments with recently developed SMC approaches highlight the superiority of the proposed scheme in terms of settling time, overshoot reduction, and robustness to uncertainties. With its enhanced performance, the proposed controller offers a reliable and high-performance solution for LFC in modern MPSs.

The paper’s key contributions are as below:

• A simplified yet accurate reduced-order LFC model is developed for MPSs, combining tie-line power exchanges, wind power fluctuations, and ESS output variations into a single lumped disturbance term. This formulation improves model tractability while retaining essential dynamic behavior;

• A novel PD SMC-based controller is proposed by integrating the single-phase sliding mode approach with an improved super-twisting control law. This eliminates reaching time, mitigates chattering, and ensures finite-time convergence under system uncertainties;

• Unlike existing SMC methods, the proposed controller achieves faster dynamic response and greater robustness, with simulation results showing up to 84.5% overshoot reduction and 54.5% faster settling time across a wide range of operating conditions;

• The effectiveness and robustness of the proposed strategy are validated through comprehensive case studies in MPSs with renewable integration, demonstrating superior performance over several recently developed SMC-based methods.

The rest of the paper is structured as follows: Section II presents system modeling and the reduced-order LFC model. Section III describes the proposed control design. Section IV presents simulation results. Section V concludes the study.

MPS frequency response model

WTG model

Considering the MPS with penetration of RES, the WTG is included as a variable source of power input³⁷. The mechanical and output power generated by the WTG are expressed through Eq. (1) and Eq. (2) as follows:

$${P_{wd}}=\theta {P_w}$$

(1)

and

$${P_w}=\frac{1}{2}{C_p}(\lambda ,\beta )A\rho V_{{wd}}^{3}$$

(2)

where ${P_{wd}}$ is turbine’s output power, $\theta$ is turbine’s efficiency, ${C_p}$is turbine coefficient, $\lambda$ is blade tip speed ratio, $\beta$ is blade’s pitch angle (deg), A is turbine swept area (${m^2}$), $\rho$is air density ($kg/{m^3}$), ${V_{{\text{w}}d}}$ is speed of wind (m/s).

Particularly, in the LFC scheme displayed in Fig. 1, the WTG is represented by a first-order transfer function as

$${G_{WT}}(s)=\frac{{\Delta {P_{WT}}}}{{{P_{wd}}}}=\frac{{{K_{wt}}}}{{1+s{T_{wt}}}}$$

(3)

where ${K_{wt}}=1$ and ${T_{wt}}=1s$ are WTG gain and constant, respectively.

Fig. 1

Dynamic model of MPSs integrating wind turbines and ESSs with proposed SMC scheme.

ESS models

BESS and FESS are critical for regulating system frequency by providing quick power transfer³⁷. While BESSs store energy using electrochemical processes, FESSs store kinetic energy while minimizing frictional losses. In the LFC scheme displayed in Fig. 1, the transfer function for both BESSs and FESSs is described in Eqs. (4) and (5):

$${G_{BE}}(s)=\frac{{\Delta {P_{BE}}}}{{\Delta F}}=\frac{1}{{1+s{T_{be}}}}$$

(4)

and

$${G_{FE}}(s)=\frac{{\Delta {P_{FE}}}}{{\Delta F}}=\frac{1}{{1+s{T_{fe}}}}$$

(5)

where ${T_{be}}=0.1s$ and ${T_{fe}}=0.1s$ are BESS and FESS constants.

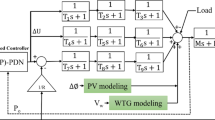
MPS frequency response model

The proposed LFC model includes thermal MPSs, WTG, FESSs, and BESSs is illustrated in Fig. 1. To ensure effective coordination and control between RESs and ESSs, a robust super-twisting-based PD SMC scheme without reaching phase is utilized, providing robust performance and high adaptability to various operational disturbances and uncertainties.

Each region of MPS dynamics can be presented by different equations as follows:

$$\Delta {\dot {F}_i}= - \frac{1}{{{T_{ppi}}}}\Delta {F_i}+\frac{{{K_{ppi}}}}{{{T_{ppi}}}}\Delta {P_{VPi}} - \frac{{{K_{ppi}}}}{{{T_{ppi}}}}\Delta {P_{BEi}} - \frac{{{K_{ppi}}}}{{{T_{ppi}}}}\Delta {P_{FEi}} - \frac{{{K_{ppi}}}}{{{T_{ppi}}}}\Delta {P_{Tie,ij}} - \frac{{{K_{ppi}}}}{{{T_{ppi}}}}\Delta {P_{LDi}}+\frac{{{K_{ppi}}}}{{{T_{ppi}}}}\Delta {P_{{\text{W}}Ti}}$$

(6)

$$\Delta {\dot {P}_{VPi}}= - \frac{1}{{{T_{vpi}}}}\Delta {P_{VPi}}+\frac{1}{{{T_{vpi}}}}\Delta {P_{GVi}}$$

(7)

$$\Delta {\dot {P}_{GVi}}= - \frac{1}{{{T_{gvi}}{R_i}}}\Delta {F_i} - \frac{1}{{{T_{gvi}}}}\Delta {P_{GVi}}+\frac{1}{{{T_{gvi}}}}\Delta {P_{SMCi}}$$

(8)

$$\Delta {\dot {P}_{Ei}}={K_{ei}}{B_i}\Delta {F_i}+{K_{ei}}\Delta {P_{Tie,{\text{ij}}}}$$

(9)

$$\Delta {\dot {P}_{BEi}}=\frac{1}{{{T_{bei}}}}\Delta {F_i} - \frac{1}{{{T_{bei}}}}\Delta {P_{BEi}}$$

(10)

$$\Delta {\dot {P}_{FEi}}=\frac{1}{{{T_{fei}}}}\Delta {F_i} - \frac{1}{{{T_{fei}}}}\Delta {P_{FEi}}$$

(11)

$$\Delta {\dot {P}_{Tie,ij}}=2\pi \sum\limits_{{i \ne j}}^{{i=1}} {{T_{ij}}(\Delta {F_i} - \Delta {F_j})}$$

(12)

where $i=1,.,N$ is area number in MPS; $\Delta {F_i}(t)$ is frequency deviation; $\Delta {P_{VPi}}(t)$ is turbine output deviations, $\Delta {P_{GVi}}(t)$ is governor output change; $\Delta {P_{Ei}}(t)$ represents the frequency error integral component, which is typically used to provide integral action in the LFC loop, improving steady-state accuracy; $\Delta {P_{BEi}}(t)$ and $\Delta {P_{FEi}}(t)$ are output powers of BESSs and FESSs; $\Delta {P_{tie,ij}}(t)$ is a power change of neighborhood areas and $\Delta {P_{WTi}}(t)$ is a output power of WTG; $\Delta {P_{LDi}}$ is load disturbances; $\Delta {P_{SMCi}}$ is output control signal of SMC.

Based on Eqs. (6)-(12), the MPS model with the proposed SMC scheme presented in Fig. 1 can be derived in the following state-space equation below

$${\bar {x}_i}(t)={\bar {A}_i}{x_i}(t)+{\bar {B}_i}{u_i}(t)+{\bar {C}_{ij}}{x_j}(t)+{\bar {D}_i}{\bar {\Omega }_i}(t)$$

(13)

where.

${\bar {x}_i}(t)={\left[ {\begin{array}{*{20}{c}} {\bar {x}_{i}^{1}(t)}&{\bar {x}_{i}^{2}(t)}&{\Delta {P_{Tie,ij}}(t)} \end{array}} \right]^T}$; ${\bar {\Omega }_i}(t)=\Delta {P_{LDi}}+\Delta {P_{WTi}}$

and.

$x_{i}^{1}(t)=\left[ {\begin{array}{*{20}{c}} {\Delta {F_i}(t)}&{\Delta {P_{VPi}}(t)}&{\Delta {P_{GVi}}(t)} \end{array}} \right]$; $x_{i}^{2}(t)=\left[ {\begin{array}{*{20}{c}} {\Delta {P_{Ei}}(t)}&{\Delta {P_{BEi}}(t)}&{\Delta {P_{FEi}}(t)} \end{array}} \right]$

where ${\bar {x}_i}(t)$ is system state vector of the i^th area including $\Delta {P_{Ei}}$; ${u_i}(t)$ is control input; ${x_j}$ is state vector of the j^h interconnected area; ${\bar {\Omega }_i}(t)$ is external disturbances; ${\bar {A}_i}$,${\bar {B}_i}$,${\bar {C}_{ij}}$ and ${\bar {D}_i}$ are the system, input, interconnection, and disturbance matrices, respectively.

From these equations, we can consider the matrices ${\bar {A}_i},\,\,{\bar {B}_i},\,{\bar {C}_{ij}},\,{\bar {D}_i}$ for MPSs as follows:

$\begin{gathered} \bar{A}_{i} = \left[ {\begin{array}{*{20}l} { - \frac{1}{{T_{{ppi}} }}} \hfill & {\frac{{K_{{ppi}} }}{{T_{{ppi}} }}} \hfill & 0 \hfill & 0 \hfill & { - \frac{{K_{{ppi}} }}{{T_{{ppi}} }}} \hfill & { - \frac{{K_{{ppi}} }}{{T_{{ppi}} }}} \hfill & { - \frac{{K_{{ppi}} }}{{T_{{ppi}} }}} \hfill \\ 0 \hfill & { - \frac{1}{{T_{{vpi}} }}} \hfill & {\frac{1}{{T_{{vpi}} }}} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ { - \frac{1}{{T_{{gvi}} R_{i} }}} \hfill & 0 \hfill & { - \frac{1}{{T_{{gvi}} }}} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ {K_{{ei}} B_{i} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {K_{{ei}} } \hfill \\ {\frac{1}{{T_{{bei}} }}} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & { - \frac{1}{{T_{{bei}} }}} \hfill & 0 \hfill & 0 \hfill \\ {\frac{1}{{T_{{fei}} }}} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & { - \frac{1}{{T_{{fei}} }}} \hfill & 0 \hfill \\ {2\pi \sum\limits_{{i \ne j}}^{{i = 1}} {T_{{ij}} } } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right]\;\bar{B}_{i} = \left[ {\begin{array}{*{20}c} 0 & 0 & {\frac{1}{{T_{{gvi}} }}} & 0 & 0 & 0 & 0 \\ \end{array} } \right] \hfill \\ \bar{C}_{i} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ {2\pi \sum\limits_{{i \ne j}}^{{i = 1}} {T_{{ij}} } } & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right]\;\bar{D}_{i} = \left[ {\begin{array}{*{20}l} { - \frac{{K_{{ppi}} }}{{T_{{ppi}} }}} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right] \hfill \\ \end{gathered}$

The effect of tie-line power, WTG, BESS and FESS powers are considered as other disturbances for decentralized control.

$${\Omega _i}(t)=\Delta {P_{LDi}}+\Delta {P_{Tie,ij}}+\Delta {P_{WTi}}+\Delta {P_{BEi}}+\Delta {P_{FEi}}$$

.

Then, the MPS model can also be refined in the conventional form below:

$${\dot {x}_i}(t)={A_i}{x_i}(t)+{B_i}\Delta {P_{SMCi}}(t)+{D_i}{\Omega _i}(t)$$

(14)

where

$$A_{i} = \left[ {\begin{array}{*{20}c} { - \frac{1}{{T_{{ppi}} }}} & {\frac{{K_{{ppi}} }}{{T_{{ppi}} }}} & 0 & 0 \\ 0 & { - \frac{1}{{T_{{vpi}} }}} & {\frac{1}{{T_{{vpi}} }}} & 0 \\ { - \frac{1}{{R_{i} T_{{ppi}} }}} & 0 & { - \frac{1}{{T_{{gvi}} }}} & 0 \\ {B_{i} K_{{ei}} } & 0 & 0 & 0 \\ \end{array} } \right];\;B_{i} = \left[ {\begin{array}{*{20}c} 0 & 0 & {\frac{1}{{T_{{gvi}} }}} & 0 \\ \end{array} } \right]^{T} ;\;D_{i} = \left[ {\begin{array}{*{20}c} { - \frac{{K_{{ppi}} }}{{T_{{ppi}} }}} & 0 & 0 & 0 \\ \end{array} } \right]^{T}$$

where ${T_{gvi}}=0.08s$ is a governor time constant; ${T_{vpi}}=0.03s$ is a turbine time constant; ${K_{ppi}}=120$ and ${T_{ppi}}=20s$ are respectively PS gain and time constant; ${T_{ij}}=0.545pu.MW/Hz$ is the tie-line factor of j^th area;${B_i}=0.425pu.MW/Hz$ is frequency feedback factor of i^th area; ${R_i}=0.05$ is a governor’s speed drop.

According to these functions, the state-space form of system model is achieved as

$$\left[ {\begin{array}{*{20}{c}} {\Delta {{\dot {F}}_i}(t)} \\ {\Delta {{\dot {P}}_{VPi}}(t)} \\ {\Delta {{\dot {P}}_{GVi}}(t)} \\ {\Delta {{\dot {P}}_{Ei}}(t)} \end{array}} \right]=\left[ {\begin{array}{*{20}{r}} { - 0.05}&{6.00}&0&0 \\ 0&{ - 33.33}&{33.33}&0 \\ { - 1.00}&0&{ - 12.50}&0 \\ {4.25}&0&0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\Delta {F_i}(t)} \\ {\Delta {P_{VPi}}(t)} \\ {\Delta {P_{GVi}}(t)} \\ {\Delta {P_{Ei}}(t)} \end{array}} \right]+{\left[ {\begin{array}{*{20}{c}} 0&0&{12.5}&0 \end{array}} \right]^T}\Delta {P_{SMCi}}(t)+{\left[ {\begin{array}{*{20}{c}} { - 6}&0&0&0 \end{array}} \right]^T}{\Omega _i}(t)$$

(15)

Remark 1

Decentralized LFC offers significant advantages over centralized approaches, particularly in large-scale MPSs. By allowing each area to independently manage its frequency with localized information and control, it enhances system flexibility, fault tolerance, and scalability, while also improving the handling of matched and mismatched uncertainties. This approach reduces reliance on global data exchange, making it more robust and cost-effective in dynamic operating conditions.

Novel single-phase PD sliding surface and improved super-twisting controller

Existing SMCs have limits, particularly the chattering phenomenon in first-order model^{26,27,28,29,30,31,32} and oscillation issues owing to reaching phase in higher-order model^33,34,35., By developing a novel single-phase PD sliding surface (PD-SS) enhanced with the improved super-twisting control law, the proposed control aim at overcoming these challenges. Therefore, it enhances transient performance, reduces oscillations, and minimizes chattering. Leveraging SMC’s robustness in handling nonlinear dynamics and system variations, the proposed solution can be applied to other applications to improve the modeling and control of complicated nonlinear systems.

A novel SS utilizes a single-phase approach-based PD structure in³⁴ for the MPSs is proposed as:

$${G_i}(t)=\underbrace {{{K_i}{x_i}(t)}}_{{Proportional}}+\underbrace {{{K_i}{{\dot {x}}_i}(t)}}_{{Derivative}}+\underbrace {{{K_i}{x_i}\left( 0 \right){e^{ - {\beta _i}t}}}}_{{Single - phase}}$$

(16)

where ${K_i}$ is designed to guarantee that ${K_i}{B_i}$ is invertible.

Differentiate ${G_i}(t)$ in Eq. (16) and integrated with Eq. (14), we obtain

$${\dot {G}_i}(t)={K_i}{A_i}{x_i}(t)+{K_i}{B_i}\Delta {P_{SMCi}}(t)+{K_i}{D_i}{\Omega _i}(t)+{K_i}{\ddot {x}_i}(t)+{K_i}{\dot {x}_i}\left( 0 \right){e^{ - {\beta _i}t}}$$

(17)

Establishing ${K_i}{A_i}{x_i}(t)+{K_i}{B_i}\Delta {P_{SMCi}}(t)+{K_i}{D_i}{\Omega _i}(t)+{K_i}{\ddot {x}_i}(t)+{K_i}{\dot {x}_i}\left( 0 \right){e^{ - {\beta _i}t}}=0$, then the control law can be defined as:

$$\Delta {P_{SMCi}}(t)= - {({K_i}{B_i})^{ - 1}}[{K_i}{A_i}{x_i}(t)+{K_i}{D_i}{\Omega _i}(t)+{K_i}{\ddot {x}_i}(t)+{K_i}{\dot {x}_i}\left( 0 \right){e^{ - {\beta _i}t}}]$$

(18)

In the presence of system uncertainties $\Delta {x_i}(t)$, including disturbances, unmodeled dynamics, and other factors, if these uncertainties are bounded, the SS can be maintained through a control law based on the ISTA.

Then, to regulate the system frequency, the PD SMC law combined with the improved super-twisting control law is formulated as:

$$u_{i}^{{PC}}=\underbrace {{\Delta {P_{SMCi}}(t)}}_{{Equivalent}}+\underbrace {{u_{i}^{{st}}(t)}}_{{Super - twisting}}$$

(19)

and

$$u_{i}^{{st}}(t)= - {({K_i}{B_i})^{ - 1}}[{\rho _{i1}}{\Phi _{i1}}(t)+{\rho _{i2}}{\Phi _{i2}}(t)+\int_{0}^{t} {{\rho _{i3}}} {\Phi _{i3}}(t)d\tau ]$$

(20)

where:

${\Phi _{i1}}(t)=sat[{G_i}(t)]$; ${\Phi _{i2}}(t)={\left| {{G_i}(t)} \right|^{1/2}}sat[{G_i}(t)]$; ${\Phi _{i3}}(t)=\frac{{sat[{G_i}(t)]}}{2}$;

and $sat[{G_i}(t)]=\left\{ {\begin{array}{*{20}{c}} {\,\,\,1,\,\,\,\,\,\,{G_i}(t)>0} \\ {\,\,\,0,\,\,\,\,\,\,{G_i}(t)=0} \\ { - 1,\,\,\,\,\,\,\,{G_i}(t)<0} \end{array}} \right.$

Remark 2

The proposed ISTA introduces a novel modification to the classical super-twisting structure by adding the traditional signum-based terms with a smoothed formulation using saturation functions, as highlighted in the control law in Eq. (20). This adjustment reduces chattering and enhances numerical stability while preserving robustness against uncertainties. By incorporating a saturation-based gradient and a scaled discontinuous term, ISTA ensures smoother control action, finite-time convergence, and compatibility with reduced-order models, offering a practical and efficient alternative to traditional super-twisting method for decentralized LFC in MPSs.

Combining Eqs. (18), (19), (20), the final form of control signal is presented as:

$$\begin{gathered} u_{i}^{{PC}}= - {({K_i}{B_i})^{ - 1}}[{K_i}{A_i}{x_i}(t)+{K_i}{D_i}{\Omega _i}(t)+{K_i}{{\ddot {x}}_i}(t)+{K_i}{{\dot {x}}_i}\left( 0 \right){e^{ - {\beta _i}t}}] - {({K_i}{B_i})^{ - 1}}[{\rho _{i1}}sat[{G_i}(t)] \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,+{\rho _{i2}}{\left| {{G_i}(t)} \right|^{1/2}}sat[{G_i}(t)]+\int_{0}^{t} {{\rho _{i3}}} \frac{{sat[{G_i}(t)]}}{2}d\tau ] \hfill \\ \end{gathered}$$

(21)

Substituting Eq. (18) into Eq. (14), we achieve:

$${\ddot {x}_i}(t)= - {\dot {x}_i}\left( 0 \right){e^{ - {\beta _i}t}} - {\dot {x}_i}(t)$$

(22)

Supporting that

$${\bar {x}_i}(t)={\dot {\bar {x}}_i}(t)$$

(23)

Then, Eq. (22) become

$${\dot {\bar {x}}_i}(t)=\mu {\bar {x}_i}(t)+\Upsilon (t)$$

(24)

where.

$\mu = - 1$ and $\Upsilon (t)= - {\bar {x}_i}\left( 0 \right){e^{ - {\beta _i}t}}$

Proof

To prove the MPS’s stability, we choose the Lyapunov function as:

$$\upsilon ({x_i})=\bar {x}_{i}^{T}(t){P_i}\,{\bar {x}_i}(t)$$

(25)

where ${P_i}>0$ satisfied Eq. (25).

Derivative of $\upsilon ({x_i})$ can be presented as:

$$\dot {\upsilon }({x_i})=\dot {\bar {x}}_{i}^{T}(t){P_i}\,{\bar {x}_i}(t)+\bar {x}_{i}^{T}(t){P_i}\,{\dot {\bar {x}}_i}(t)$$

(26)

By using ${\dot {\bar {x}}_i}(t)$ in Eq. (24), we obtain

$$\dot {\upsilon }({x_i})={\mu ^T}\bar {x}_{i}^{T}(t){P_i}\,{\bar {x}_i}(t)+{\Upsilon ^T}(t){P_i}\,{\bar {x}_i}(t)+\bar {x}_{i}^{T}(t){P_i}\,\mu {\bar {x}_i}(t)+\bar {x}_{i}^{T}(t){P_i}\,\Upsilon (t)$$

(27)

Lemma³⁰

Selecting N and M are positive matrices. Then, for any scalar $\tau >0$, the following matrix inequality obtain: ${N^{\mathbf{T}}}M+{M^{\mathbf{T}}}N \leqslant \tau {N^{\mathbf{T}}}N+{\tau ^{ - 1}}{M^{\mathbf{T}}}M.$

By applying above Lemma, Eq. (27) become:

$$\dot {\upsilon }({x_i})={\mu ^T}\bar {x}_{i}^{T}(t){P_i}\,{\bar {x}_i}(t)+\bar {x}_{i}^{T}(t){P_i}\,\mu {\bar {x}_i}(t)+\tau \bar {x}_{i}^{T}(t){P_i}{P_i}\,{\bar {x}_i}(t)\,+{\tau ^{ - 1}}{\Upsilon ^T}(t)\Upsilon (t)$$

(28)

Then, Eq. (28) become:

$$\dot {\upsilon }({x_i})=\bar {x}_{i}^{T}(t)({\mu ^T}{P_i}+{P_i}\mu +\tau {P_i}{P_i}){\bar {x}_i}(t)+{\tau ^{ - 1}}{\Upsilon ^T}(t)\Upsilon (t)$$

(29)

Letting ${\mu ^T}{P_i}+{P_i}\mu +\tau {P_i}{P_i}= - {\Theta _i}$, Eq. (28) can be reduce as

$$\dot {\upsilon }({x_i})= - \bar {x}_{i}^{T}(t){\Theta _i}{\bar {x}_i}(t)+{\tau ^{ - 1}}{\Upsilon ^T}(t)\Upsilon (t)$$

(30)

Then, Eq. (30) is defined as

$$\dot {\upsilon }({x_i})= - {\lambda _{\hbox{min} }}({\Theta _i}){\left\| {{{\bar {x}}_i}} \right\|^2}+{\delta _i}$$

(31)

where ${\delta _i}={\tau ^{ - 1}}{\Upsilon ^T}(t)\Upsilon (t)$ and the eigenvalues of ${\lambda _{\hbox{min} }}({\Theta _i})>0$, then consequently $\dot {\upsilon }({x_i})<0$ with $\left\| {{{\bar {x}}_i}} \right\|>\sqrt {{\delta _i}/{\lambda _{\hbox{min} }}({\Theta _i})}$.

Figure 2 illustrates the block diagram of the proposed LFC scheme incorporating the improved super-twisting-based advanced SMC. The control structure consists of an equivalent control component and the ISTA, which work together to generate the control input for the MPSs.

Fig. 2

Block diagram of the proposed LFC in MPSs with designed SMC approach.

Remark 3

The ISTA employs a continuous control law that forces the system trajectory to reach and remain on the SS without chattering. It consists of three terms: the first and second terms gradually reduce trajectory deviation using a nominal and fractional power term, ensuring a smooth control action, while the second term introduces an internal state that dynamically compensates for disturbances, maintaining sliding motion under uncertainties. Additionally, the single-phase technique directly embeds the PD SS into the initial system trajectory, eliminating the reaching phase. This integration ensures that the system starts and remains on the SS from the beginning, further reducing transient oscillations and improving response time, making it highly effective for LFC in MPSs.

Simulated results

This section presents the simulated results, which are analyzed and compared with those obtained using newly published methods in^28,31. To evaluate the performance comprehensively, three simulation scenarios are conducted: the first and second considers a single-area PS (SAPS) with and without WTG, while the third involves MPSs. All scenarios include the integration of BESSs and FESSs to enhance frequency stability. The simulations account for various load disturbances (LDs) and wind power fluctuations (WPFs), reflecting real-world operating challenges. The comparison highlights the effectiveness of the proposed control strategy in maintaining stability and performance under dynamic and uncertain conditions.

Then, the sliding matrix in Eq. (16) is designed as ${K_i}=\left[ {\begin{array}{*{20}{c}} {0.9}&{1/155}&{2.5}&{0.4} \end{array}} \right]$ and power factors including ${\rho _{i1}}$, ${\rho _{i2}}$, and ${\rho _{i3}}$ (if any) in Eq. (21) are set respectively as 0.015, 0.15 and 0.03 for all comparison methods.

SAPS under single LD

In this case, external step disturbance is set as 0.01 p.u at 1s. The Bode plot of the proposed controller, shown in Fig. 3, illustrates its dynamic response characteristics. The magnitude plot displays a gain peak of approximately − 28 dB around 10 rad/s, indicating enhanced responsiveness in the mid-frequency range. As frequency increases, the gain consistently decreases, reaching around − 110 dB at 1000 rad/s, effectively attenuating high-frequency components and thereby suppressing chattering. The phase response transitions smoothly from + 90° to about − 270°, confirming stable phase behavior and robust performance across a wide frequency range. It is evident from Fig. 4 that the deviations in frequency error under the step LD remain well within the permissible limits. This demonstrates the effectiveness of the proposed scheme in quickly stabilizing the system after the LD.

Fig. 3

Bode diagram of the proposed SMC scheme in SAPS.

Fig. 4

Comparison of frequency deviations in a SAPS under different controllers.

From the simulation results, it is also evident that the proposed controller successfully eliminates the chattering issue, a limitation in compared SMC methods. In Fig. 5, the control signal generated by the proposed scheme shows smooth transitions without high-frequency oscillations. This is achieved thanks to the ISTA, which offers an advanced solution to chattering by introducing a smooth switching law. The reduction in chattering not only enhances PS stability but also prevents excessive stress on system components, such as actuators, contributing to improved durability and operational reliability.

Fig. 5

Comparison of control signals in a SAPS under different controllers.

By comparing the obtained results with the newly published other SMCs^28,31 in Fig. 6, the proposed controller shows improved performance in terms of faster settling time and better stability, highlighting its superiority in handling single LD.

Fig. 6

Summary of frequency deviation responses in SAPS.

SAPS integrated WTG

In second case, the external step demand is still set the same value with previous case. In Fig. 7, the WTG (above), as a factor impacting system stability, and the ESS power (below) including BESS and FESS, as a supporting solution for LFC, are both illustrated.

Fig. 7

WTG and ESS power in SAPS.

Figure 8 presents the frequency errors of three methods under two different conditions. The result in Fig. 9 indicates that the proposed scheme, which includes an ESS regulator, effectively mitigates both step LDs and WPFs while maintaining PS stability. The simulation results further demonstrate that the system performs better when supplemented with both BESS and FESS, suggesting the enhanced effectiveness of combined energy storage solutions in LFC. In comparison to the other SMC schemes, which exhibit higher frequency deviations, the proposed scheme shows superior performance in reducing frequency fluctuations and improving stability.

Fig. 8

Comparison of frequency deviations in SAPS with WTG under different controllers.

Fig. 9

Summary of frequency deviation responses in SAPS integrated WTG.

MPS integrated WTG under multiple disturbances

In the last case, the performance of the proposed control strategy is evaluated under MPSs considering the integration of WPFs and random LDs. This case simulates real-world operational challenges where both LDs and power generation from RES exhibit stochastic behavior.

The load variations in this scenario are set to random values, as displayed in Fig. 10, while Fig. 11 depicts the WPFs in areas 1 and 3. From Figs. 12, 13, 14 and 15, the main responses of frequency fluctuations under three different methods are illustrated. It is easy to observe that the suggested approach achieves the best performance in terms of smaller overshoots and faster settling time. Finally, Figs. 16, 17, 18 and 19 present the lumped disturbances of the MPSs, including LDs, WPFs, tie-line power variations, BESS, and FESS.

Fig. 10

Random load conditions in four-area PSs.

Fig. 11

WPFs in four-area PSs.

Fig. 12

Comparison of frequency deviations in 1st area of MPSs under different controllers.

Fig. 13

Comparison of frequency deviations in 2nd area of MPSs under different controllers.

Fig. 14

Comparison of frequency deviations in 3rd area of MPSs under different controllers.

Fig. 15

Comparison of frequency deviations in 4th area of MPSs under different controllers.

Fig. 16

Comparison of Lumped disturbances in 1st area of MPSs under different controllers.

Fig. 17

Comparison of Lumped disturbances in 2nd area of MPSs under different controllers.

Fig. 18

Comparison of Lumped disturbances in 3rd area of MPSs under different controllers.

Fig. 19

Comparison of Lumped disturbances in 4th area of MPSs under different controllers.

The proposed control strategy demonstrates exceptional performance and adaptability, making it particularly well-suited for large-scale PS with multiple areas. By leveraging the complementary strengths of BESS and FESS, the controller effectively mitigates disturbances caused by LDs, WPFs, and tie-line power exchanges. BESS provides high-energy support for sustained disturbances, while FESS offers high-power capabilities to suppress rapid transients. This synergy ensures smoother frequency profiles, smaller overshoots, and faster settling times, as evidenced in Figs. 12, 13, 14 and 15.

Additionally, the proposed controller significantly reduces the reliance on conventional synchronous generators by balancing dynamic fluctuations, thereby extending their operational lifespan and enhancing overall system efficiency. Its ability to adapt to stochastic behaviors of WPFs and LDs across area ensures reliable operation in complex, real-world scenarios. This solution provides a robust, scalable framework for modern PSs, ensuring stability and efficiency even in systems with high renewable energy integration and multi-area coordination requirements.

Power systems with nonlinearities

To investigate the performance of the proposed control scheme under practical operating conditions, the simulation model is extended to include two key nonlinearities: governor dead-band (GDB) and generation rate constraint (GRC). These nonlinearities reflect common physical limitations in real-world power generation systems that can significantly impact LFC performance. An external step disturbance of 0.02 p.u, the same value with³⁶, is applied to assess the controller’s ability to stabilize frequency under sudden load changes. Furthermore, the PS parameters used in the simulation setup are also adopted directly from³⁶ to ensure consistency and fair comparison. Simulation results demonstrate that the proposed ISTA-based PD-SS SMC maintains strong robustness and fast dynamic response despite the presence of GRC and GDB, validating its effectiveness under realistic nonlinear operating conditions.

The simulation results presented in Fig. 20; Table 2 clearly demonstrate the effectiveness of the proposed ISTA-based PD-SS SMC in handling power system nonlinearities, specifically GRC and GDB. As shown in Fig. 20, the controller maintains frequency deviations within a narrow range and ensures fast convergence following a 0.02 p.u. step disturbance. Compared to the adaptive HOSMC method in³⁶, the proposed scheme achieves significantly lower overshoot (–7.073 × 10⁻³ vs. − 2.17) and faster settling time (87.73s vs. 150s), confirming its superior dynamic performance and robustness under realistic operating conditions. Finally, Fig. 21 shows ACE signal of proposed SMC method in SAPS with nonlinearity.

Fig. 20

Frequency deviations in PS with nonlinearities.

Fig. 21

Area control error (ACE) in PS with nonlinearities.

Table 2 Frequency deviations in single area Ps with nonlinearities.

Remark 4

The overall comparison between systems with and without nonlinearities reveals that while the presence of GRC and GDB slightly slows the dynamic response and increases frequency deviation, the proposed scheme still maintains excellent performance. This demonstrates the controller’s strong robustness and adaptability, effectively mitigating the adverse effects of nonlinear elements and ensuring reliable frequency regulation in practical scenarios.

Discussion

The simulation results underscore the robustness and effectiveness of the robust super-twisting-based single-phase PD SMC scheme in LFC for MPSs. Case A evaluates the proposed controller in a SAPS under a single LD. The results demonstrate the controller’s ability to achieve faster settling times, reduced overshoots, and enhanced frequency stability compared to other SMC schemes. A key highlight in this case is the controller’s ability to effectively mitigate the chattering issue commonly seen in traditional SMC methods. By leveraging the ISTA, the proposed scheme generates a smooth control signal, eliminating high-frequency oscillations and ensuring stable and efficient operation.

In Case B, the controller is applied to a SAPS integrated with WTG subjected to LD. The proposed scheme exhibits outstanding adaptability to the inherent variability of WTG, ensuring stable frequency responses and improved system dynamics. Additionally, its optimized performance underscores the reliability of the controller in scenarios involving WPFs.

In Case C, the proposed scheme is tested in four-area PSs integrated with WTG under random LDs. The controller consistently outperformed other SMC strategies by achieving faster settling times, reduced overshoots, and robust frequency stability. Its optimized integration of BESS and FESS further enhanced the system’s adaptability and reliability in addressing dynamic WGT scenarios.

Across all cases, the proposed controller proved to be a robust, efficient, and practical solution for decentralized LFC in both SAPS and MPSs. Its consistent superiority over other SMC strategies, coupled with its ability to handle chattering effectively, makes it a desired approach for ensuring stable grid operation, particularly in modern MPSs with high WTG integration and dynamic LDs.

Furthermore, the proposed single-phase PD-based super-twisting SMC significantly reduces computational complexity by adopting a streamlined control structure. Unlike higher-order or multi-loop controllers, the design avoids complex dynamics and auxiliary estimation processes, enabling faster execution and easier integration into real-time control platforms. Additionally, the use of a reduced-order system model—where disturbances from tie-line power, wind generation, and ESSs are aggregated into a single term—further simplifies controller computation. The single-phase method’s ability to eliminate the reaching phase ensures finite-time convergence with fewer iterations, offering improved performance without increasing the processing burden.

Remark 5

The proposed ISTA-based PD-SS SMC controller features a simplified structure. However, hardware limitations such as limited processing power, memory, and potential communication delays in embedded systems may challenge high-speed execution, especially under rapid transients. Moreover, practical issues like signal noise and numerical stability require careful consideration. To ensure feasibility, future work will focus on implementing the controller on a real-time HIL platform to assess performance under hardware constraints and validate its practical deployment in real-world power systems.

Conclusion

This paper proposes a novel SMC approach based on a single-phase PD-SS structure and ISTA for decentralized LFC in MPSs incorporating WTG, BESSs, and FESSs. The work presents a reduced-order LFC model that integrates dynamic disturbances, by combining tie-line power exchanges, WPFs, and variations in two types of ESSs, into lumped disturbance. Then, a new single-phase PD-SS design is introduced, eliminating the reaching phase and improving system performance. Additionally, the improved super-twisting control law is introduced to mitigate chattering in the PS’s dynamics. Based on these features, the proposed control scheme shows superior robustness and stability in handling LDs and uncertainties, outperforming existing SMC approaches in terms of settling time, reduced overshoot, and overall stability. Simulation results demonstrate the effectiveness of the approach, making it a desired solution for decentralized LFC in MPSs with WPFs and ESS integrations. However, the absence of an observer in the proposed controller limits its capability to estimate unmeasurable states and external disturbances, which may affect control precision and robustness under partially observed or rapidly changing system conditions. Incorporating an observer in future designs could enhance disturbance estimation, improve state feedback, and further strengthen the system’s resilience against uncertainties. Future work will focus on validating the proposed method using more comprehensive power system models to assess its practical applicability under real-world operating conditions. Additionally, the controller will be implemented on a real-time simulation platform such as OPAL-RT to evaluate hardware-in-the-loop (HIL) performance, ensuring its feasibility and effectiveness for practical deployment.