Instruction

With the development of trans-regional long distance transmission project, the application of high voltage shunt reactor in power grid is more and more extensive. The noise generated during the operation of shunt reactor has attracted much attention, and the substation noise exceeding the standard and complaints caused by it are very common. This issue has emerged as a key factor restricting the siting of substation1. Reactor noise mainly includes body noise and radiator noise. The body noise, which is caused by vibration of core, winding, oil tank and oil pillow, makes a greater contribution2. Reactor vibration could also accelerate the aging of equipment, and even cause serious equipment failure3. In recent years, indoor shunt reactors have appeared in urban areas, which are more sensitive to vibration problems.

The unbalance forces that cause reactor vibration are complex, and primarily include the Maxwell force on the surface of the core, the magnetostrictive effect of the core, and the Lorentz force within the winding4. Previous studies mainly focused on the first two factors5,6, but paid less attention to the Lorentz force acting on the winding. The air gap of the reactor core column is relatively large, and the number is also quite large. During normal operation, in addition to the main magnetic flux generated by the current in the winding, the leakage magnetic flux produced by it is also large. Compared with the transformer winding, the reactor winding is subjected to much greater Lorentz force, so the effect of its Lorentz force on winding vibration should not be ignored7.

The disk⁃type winding is widely used in large reactors8. This type of winding is characterized by arranging the wires into a round disk, and then connecting disks in series to form the whole of winding. A number of insulation blocks are placed between each adjacent disk to play an insulating role and form a cooling oil passage between the disks. The “block” hereinafter refers to winding block unless otherwise specified. The winding vibration is manifested as periodic vibration generated by the alternating Lorentz force of each disk in the leakage magnetic field, and its fundamental frequency is 100 Hz9.

Since the 1960s, TOURNIER, MADINA, WATTS et al.10,11,12. established and improved the dynamic model of transformer winding. Then SWIHART and WRIGHT13 proposed the mass-spring-damping model of winding vibration and established the equivalent single-degree-of-freedom model. HORI and OKUYAMA14 proposed a method for predicting and calculating the axial nonlinear vibration of transformer winding. With the development of multi-physical field simulation technology and tools, SHI, JIN et al.15,16 applied the electromagnetic-mechanical coupling field to the vibration simulation of transformer winding. ZHANG et al.17,18,19,20 carried out a lot of research on the natural frequency of transformer winding by using modal analysis. ZHANG et al.21 established the electromagnetic-mechanical coupling field model of reactor winding, which set the disks and blocks as a whole and adopted unified material parameters. WU et al.22 also adopted a similar method in their study. Although this method could reduce the simulation calculation time and complexity, the simulation structure is very different from the actual structure. The winding could be regarded as a mechanical system composed of multiple elastic elements (disk and block)18, and its true motion process could not be simulated if it is set as a whole and unified material parameters are adopted. Meanwhile, the current density and force of the winding are concentrated on the disks, and the real force of the winding could not be reflected if the disks and blocks are set as a whole. The prediction accuracy of the model needs to be improved.

This study focused on a shunt reactor as the research object and established a simulation model of electromagnetic-mechanical coupling field according to the structural characteristics of winding disks and blocks. After verifying the simulation modeling method by using the actual reactor manufactured according to the scaled model, the unbalance force - Lorentz force acting on the winding was obtained through simulation calculation, and the vibration of the winding was analyzed. The influence of structural parameters such as elastic modulus and quantity of blocks on winding vibration was explored. Finally, the vibration control strategy was proposed.

Theoretical calculation method of the reactor winding vibration

The magnetic field model of the reactor is proposed based on Maxwell equations. The differential form of Faraday’s induction law is as follows:

$$\:\nabla\:\times\:\varvec{E}=-\frac{\partial\:\varvec{B}}{\partial\:t}$$
(1)

Where ∇ is the Hamiltonian operator; E is the electric field strength, V/m.

The differential form of Ampere’s loop law is as follows:

$$\:\nabla\:\times\:\varvec{B}=\mu\:\varvec{J}$$
(2)

Where B is magnetic flux density, T; µ is permeability, H/m; J is the current intensity, A/m2.

For isotropic media:

$$\:\varvec{B}={\mu\:}_{0}{\mu\:}_{\text{r}}\varvec{H}=\mu\:\varvec{H}$$
(3)

Where µ0 is vacuum permeability, H/m; µr is relative permeability, H/m; H is the magnetic field strength, A/m.

The conservation equation is as follows:

$$\:\nabla\:\times\:\varvec{J}=0$$
(4)

Introducing vector magnetic potential A, it could be obtained:

$$\:\nabla\:\times\:\varvec{A}=\varvec{B}$$
(5)

Substituting Eq. (5) into Eq. (2), it could be obtained:

$$\:{\nabla\:\times\:(\mu\:}^{-1}\nabla\:\times\:\varvec{A})=\varvec{J}$$
(6)

The microscopic expression of Ohm’s law is as follows:

$$\:\varvec{J}=\delta\:\varvec{E}$$
(7)

Where δ is material conductivity, S/m. Then substituting Eq. (1) and Eq. (5) into Eq. (7), it could be obtained:

$$\:\varvec{J}=-\delta\:\frac{\partial\:\varvec{A}}{\partial\:t}$$
(8)

Based on Eq. (6) and Eq. (8), with the help of the method for solving vector magnetic potential A by three-dimensional eddy current field, it could be obtained:

$$\:\nabla\:\times\:{(\mu\:}^{-1}\nabla\:\times\:\varvec{A})+\delta\:\frac{\partial\:\varvec{A}}{\partial\:t}=\nabla\:\times\:{(\mu\:}_{0}^{-1}{\mu\:}_{r}^{-1}\nabla\:\times\:\varvec{A})+\delta\:\frac{\partial\:\varvec{A}}{\partial\:t}={\varvec{J}}_{\mathbf{s}}$$
(9)

Where Js is the impressed excitation current density, A/m2. In this model Js is the winding current density.

The winding current is approximated to the ring current. Based on the Lorentz force formula, the force f could be calculated by Eq. (10)23:

$$\:\varvec{f}=\left[\begin{array}{c}\begin{array}{c}{f}_{\text{r}}\\\:{f}_{{\upphi\:}}\end{array}\\\:{f}_{\text{z}}\end{array}\right]={\varvec{J}}_{\mathbf{s}}\times\:\varvec{B}=\left[\begin{array}{c}\begin{array}{c}0\\\:{J}_{{\upphi\:}}\end{array}\\\:0\end{array}\right]\times\:\left[\begin{array}{c}\begin{array}{c}{B}_{\text{r}}\\\:0\end{array}\\\:{B}_{\text{z}}\end{array}\right]=\left[\begin{array}{c}\begin{array}{c}{{J}_{{\upphi\:}}B}_{\text{r}}\\\:0\end{array}\\\:{{-J}_{{\upphi\:}}B}_{\text{z}}\end{array}\right]$$
(10)

Where Js is the current density flowing through the winding; fr, fφ and fz are the forces in the radial, circumferential and axial directions respectively, N/m3; Jφ is the current density, A/m2; Br and Bz are the radial and axial magnetic flux density respectively, T.

In a system of multi-degree-of-freedom, the differential equation of motion could be expressed as:

$$\:\varvec{M}\ddot{\varvec{x}}+\varvec{C}\dot{\varvec{x}}+\varvec{K}\varvec{x}=\varvec{F}\left(t\right)+\varvec{M}g+{\varvec{F}}_{\text{p}\text{r}}$$
(11)

Where M is the mass matrix; C is damping matrix; K is the stiffness matrix; x is the displacement matrix; \(\:\dot{\varvec{x}}\) and \(\:\ddot{\varvec{x}}\) are the matrixes of first and second derivative displacement with respect to time, i.e., velocity and acceleration. F(t) is the system excitation force matrix; g is the acceleration of gravity; Fpr is the compression force matrix. In this model, F(t) is the Lorentz force f of the winding. Then the winding vibration displacement x could be obtained by solving Eq. (11).

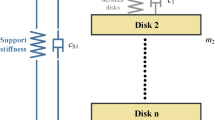
The whole winding system is regarded as a mechanical system, and its dynamic model is shown in (Fig. 1)19. According to the structural characteristics of the winding, it could be approximated that the disk is the concentrated mass and the block is the elastic element.

Fig. 1
figure 1

The dynamic model of the winding.

Full size image

Simulation modeling method and rationality verification

Simulation model and its establishment method

The shunt reactor of a certain manufacturer was taken as the modeling object, whose rated current and rated voltage were 669.9 A and 16.9 kV respectively. The number of turns of the winding wire was 210. The winding had a total of 35 disks. There were 20 blocks in each layer between the adjacent disks or the disk and the magnetic shield, and the magnetic shield also acted as a pressing board for the winding. The core was mainly composed of a core limb, yokes and magnetic shields. The core limb was composed of 5 core cakes. The blocks of core limb were arranged in the gaps between the adjacent core cakes and the gaps between the core cakes and magnetic shields. The number of core limb blocks in each layer was 22. The model is shown in (Fig. 2), with key structural parameters of the core highlighted in the diagram. Detailed specifications of other components are systematically summarized in (Table 1).

Fig. 2
figure 2

The model of shunt reactor core and winding. The unit of length data in the figure is mm.

Full size image
Table 1 Structural parameters of components.
Full size table

In this paper, an electromagnetic-mechanical coupling field analysis model was established by multi-physics simulation software. The Lorentz force of the winding was calculated through the electromagnetic field analysis model. Then the Lorentz force was taken as the input condition of the structural field analysis model to calculate the vibration result.

In the model, the core cake, magnetic shield and yoke were made of oriented silicon steel, the wire disk was made of copper, the core limb block was made of marble, and the winding block was made of insulating cardboard. Because the insulation paper used for wrapping wire disk was thin, its effect on the structure field was not considered in the model20, but its insulating property was taken into account.

In order to improve the convergence, blocks (refers specifically to winding blocks) of the same layer were set as a whole that was in full contact with the disk or magnetic shield, which was also known as the equivalent block (Fig. 3). Its equivalent elastic modulus and equivalent density were calculated by Eq. (12) and Eq. (13)18:

$$\:{E}_{\text{e}}=\frac{{E}_{\text{b}}\sum\:_{i=1}^{n}{A}_{\text{b}}}{\pi\:\left({r}_{\text{e}\text{x}}^{2}-{r}_{\text{i}\text{n}}^{2}\right)}$$
(12)
$$\:{\rho\:}_{\text{e}}=\frac{{\rho\:}_{\text{b}}\sum\:_{i=1}^{n}{A}_{\text{b}}}{\pi\:\left({r}_{\text{e}\text{x}}^{2}-{r}_{\text{i}\text{n}}^{2}\right)}$$
(13)

Where Ee is the equivalent elastic modulus, Pa; Eb is the elastic modulus of the block material, Pa; Ab is the contact area between a single block and the disk, m2; n is the number of blocks in each layer; rin and rex are the inner radius and external radius of the disk, m. ρe is the equivalent density, kg/m3; ρb is the density of the block material, kg/m3. According to Eq. (12) and Eq. (13), the equivalent elastic modulus of the equivalent block was 2.1 × 107 Pa and the equivalent density was 682.45 kg/m3.

The main parameters of model materials are shown in (Table 2).

Fig. 3
figure 3

The geometry model of the winding.

Full size image
Table 2 Main parameters of model materials.
Full size table

The material parameters of insulating cardboard are equivalent elastic modulus and equivalent density.

According to the design parameters of the reactor, the compression forces of 470,000 N were set at the top and bottom of the core. In order to simulate the fixed effect of the bottom of the core, the contact surface between the core and the foot was set as a fixed constraint.

After the model was completed, a mesh within 293,685 elements was generated in the software.

Reasonableness verification of the simulation modeling method

In order to verify the accuracy of the simulation modeling method, an actual device was built according to the reactor scaling model, as shown in (Fig. 4). The rated capacity and voltage of the reactor were 10 kVar and 550 kV. This winding was within a total of 24 disks, and its top and bottom were arranged with pressure boards. The winding would be affected by the vibration of the core during the operation. The reactor structure characteristics and the vibration source characteristics of the core determine that the influence was mainly axial vibration4,5. In order to reduce this effect, the winding fixing blocks were connected to the yoke clamp instead of directly connected to the core.

Fig. 4
figure 4

The field verification object and its test point location.

Full size image

Three test points (T1, T2 and T3 in Fig. 4) were set in front of the top three disks, and the testing parameter was y-displacement. A test point (T4 in Fig. 4) was set at the upper surface of the top pressure board, and its testing parameter was z-displacement. The test instrument was LV-S01 single point laser vibrometer.

Each disk was equipped with 6 blocks. Model A was established according to the actual structure of blocks, and Model B was established by the modeling method in Sect. 3.1, as shown in (Fig. 5).

Fig. 5
figure 5

Setting method of winding blocks in simulation model of actual verification object. (a) Model A, (b) Model B.

Full size image

The test values of test points are compared with those calculated by simulation in (Fig. 6). As shown in (Fig. 6), the calculated values of Model A and Model B are close to each other at the test points of T1 to T4, and the differences are within the range of ± 0.026 μm. The relative error of the calculated value of Model A at each test point is within the range of ± 4.405%, and the relative error of Model B at each test point is within the range of ± 4.360%. It could be seen that the relative errors between the calculated values and the test values of all test points are less than 5%, which indicated that the consistency is good. Therefore, the modeling method proposed in this study is reasonable.

Fig. 6
figure 6

Comparison of test values and calculated values at test points of the winding.

Full size image

The analysis and discussion of simulation results

Simulation results analysis

Taking the result at 0.025s (at peak current) as an example, Fig. 7 shows the winding flux density and Lorentz force distribution. As shown in Fig. 7, the maximum values of flux density and Lorentz force both appear in the central inner region of the winding, with values of 0.328 T and 1.056 × 106 N/m3, respectively. Because the winding current is approximately a ring current, the overall direction of the Lorentz force is radial outward along the winding, and the axial (z-direction) Lorentz force is less than the radial Lorentz force. The Lorentz force decreases from inside to outside along the winding radial direction, which is consistent with the distribution of magnetic flux density. Figure 8 further shows the volume average of axial Lorentz force of each disk. Combined with (Figs. 7c and 8), it could be seen that the axial Lorentz force is distributed symmetrically up and down, and the maximum values of 1.689 × 105 N/m3 are distributed at the top and bottom of the winding. If the direction of the force is considered, the disks’ axial Lorentz forces are distributed in an S-shape along the axis of the winding, and the values are close to zero at about 1/6, 1/2, and 5/6 heights.

Fig. 7
figure 7

The flux density and Lorentz force distribution of the winding. (a) Flux density, (b) Total Lorentz force, (c) Lorentz force in the z-direction.

Full size image
Fig. 8
figure 8

The volume average of axial Lorentz force of each disk.

Full size image

Figure 9 shows the typical distribution when the winding reaches its maximum displacement. As shown in Fig. 9, the winding displacement is mainly axial. It could be seen that although the radial Lorentz force is greater than the axial Lorentz force, the deformation of the winding is mainly axial. The main reason is that the stiffness of the block is obviously less than that of the disk, and it is also affected by the compression force and gravity in its axial direction. The deformation of each disk in front of the core (y-direction) is larger than that in side (x-direction), which is mainly related to the constraints placed on the winding by the core. At the same time, due to the fixed constraints of the core feet, the displacement of the winding is gradually reduced from top to bottom, and the minimum value appears at 1/4 height.

Fig. 9
figure 9

Typical distribution of the winding displacement. (a) Total displacement (deformation ratio = 2000), (b) Axial displacement.

Full size image

One point in the y-direction and the other one in the x-direction on the side of each disk are selected as the analysis points, as shown M-point and N-point in (Fig. 3). Figure 10 shows the axial amplitudes at M-point and N-point of each disk, as well as the volume average. As shown in (Fig. 10), the volume averages of the disk axial amplitudes range from 14.340 μm to 28.374 μm, the results of M-point range from 16.631 to 34.631 μm, and the results of N-point range from 8.826 to 24.811 μm. Therefore, the amplitude of M-point is significantly greater than that of N-point, which is mainly related to the inhibitory effect of the core. It could also be seen from Fig. 10 that the winding axial amplitude as a whole presents an M-shape distribution along its axis, with an obvious trough at 1/2 of its height.

Fig. 10
figure 10

Axial amplitudes at M-point and N-point and the volume average of each disk.

Full size image

Discussion

The natural frequency of winding

For the vibration reduction design of winding, the natural frequency is a very important performance index. When the natural frequency is close to the exciting force, the resonance phenomenon would occur, resulting in a large increase in vibration. LIU et al.20 found through research that the mode of vibration corresponding to the first-order natural frequency in the axial direction of the transformer winding presents a V-shape distribution, and the mode corresponding to the second-order natural frequency presents an M-shape distribution. Then they proposed that the winding amplitude distribution might be dominated by the natural frequency approached by the excitation force. Modal analysis of the reactor winding model in this study was carried out in software. As the results, the first three natural frequencies of the winding axis are 368.8, 631.1, and 1251.0 Hz, which are far away from the excitation force frequency of 100 Hz. Therefore, although the winding axial amplitude is distributed in an M-shape as shown in (Fig. 10), it has little relationship with the natural frequency. As could be seen from (Fig. 8), the disks’ axial Lorentz forces are distributed in an S-shape along the winding axis, and the force is close to zero at 1/2 height, so the axial amplitude troughs there. In addition, the axial amplitude of the winding gradually decreases when it is close to its two ends. This is because the equivalent stiffnesses of the core and magnetic shield are much larger than that of the block19, so their inhibition effect on winding vibration is more obvious.

Effect of elastic modulus and the number of blocks on winding vibration

As could be seen from the dynamic model in (Fig. 1), as an elastic element in the winding system, the equivalent stiffness of the block is a key parameter. The equivalent stiffness could be adjusted by adjusting the elastic modulus and the number of blocks in each layer. Increasing the equivalent stiffness of the block could not only increase the axial natural frequency of the winding20,24, but also enhance the inhibition effect on the axial displacement of the disks. In this study, Eq. (12) and Eq. (13) were used to calculate the equivalent elastic modulus and equivalent density of the equivalent blocks corresponding to different elastic modulus and number of blocks, as shown in (Tables 3 and 4). Then, these parameters were input into the model to calculate the relationship between the elastic modulus and number of the blocks and the axial amplitude of the 1# and 35# disks. The results are shown in (Figs. 11 and 12).

Table 3 The relationships between the elastic modulus of blocks and relevant parameters of equivalent blocks.
Full size table
Table 4 The relationships between the number of blocks and relevant parameters of equivalent blocks.
Full size table
Fig. 11
figure 11

The relationship between the elastic modulus of blocks and the volume mean axial amplitudes of 1# and 35# disks.

Full size image
Fig. 12
figure 12

The relationship between the number of blocks and the volume mean axial amplitudes of 1# and 35# disks.

Full size image

As shown in Figs. 11 and 12, with the increase of elastic modulus or number of blocks, axial amplitudes of 1# and 35# disks both show a downward trend. When the elastic modulus of blocks increases from 8.00 × 107 Pa to 2.00 × 108 Pa, the axial amplitude of the 1# disk decreases from 14.340 μm to 9.453 μm, and the axial amplitude of the 35# disk decreases from 14.492 μm to 7.760 μm, with an average decrease of 40.265%. When the number of blocks increased from 20 to 45, the axial amplitude of 1# disk decreases from 14.340 μm to 9.030 μm, and the axial amplitude of 35# disk decreases from 14.492 μm to 8.279 μm, with an average decrease of 39.951%. It could also be seen from Figs. 11 and 12 that the axial amplitudes of 1# and 35# disks gradually slow down with the increase of elastic modulus or number of blocks, and the determination coefficients (R2) of the fitting curves are all above 0.910.

Taking 1# disk as an example, Fig. 13 compares the influence of the elastic modulus of blocks on the time-domain signal of its axial displacement, and Fig. 14 compares the influence of the number of blocks on the time-domain signal of its axial displacement. As could be seen from (Figs. 13 and 14), the displacement of 1# disk during the operating cycle is less than zero, which is because the winding itself has a certain axial compression due to the action of the compression force. Due to the increase of equivalent elastic modulus of blocks, the compression inhibition ability of winding is enhanced. Thus, as the elastic modulus of blocks increases or the number of blocks increases, the peak value and amplitude of axial displacement of 1# disk tend to decrease.

Fig. 13
figure 13

Influence of elastic modulus of blocks on the time-domain signal of axial displacement of 1# disk.

Full size image
Fig. 14
figure 14

Influence of the number of blocks on the time-domain signal of axial displacement of 1# disk.

Full size image

From the above analysis results, in the process of vibration damping design of winding, increasing the elastic modulus or the number of blocks could achieve the purpose of reducing winding vibration. Due to the limitation of insulation, structural strength, corrosion resistance and other factors, it is difficult to continue to increase the elastic modulus of blocks. However, the elastic modulus of the blocks is positively correlated with the compression force they are subjected to20, so it is a considered idea to increase the elastic modulus of blocks in the design process of the winding structure’s compression force. It is less difficult to increase the number of blocks, which could be used as one of the priority measures in the design of winding vibration reduction. On the one hand, the compression resistance of the winding is enhanced by adding blocks. On the other hand, the increase of the number of blocks is conducive to the increase of the axial natural frequency of the winding20, so the axial natural frequency is further removed from its excitation frequency of 100 Hz.

However, from the results that the axial amplitudes of 1# and 35# disks gradually slow down with the increase of elastic modulus or number of blocks, the economy of measures should not be ignored in the design process, which means that the increase of investment cost should be considered while realizing the target of vibration reduction.

In addition, controlling temperature rise is one of the keys of reactor design. Thermal performance in the oil-immersed reactor is governed by the flow of oil25,26. The adding of winding blocks might impede oil circulation within the tank, potentially leading to localized hotspots and an overall increase in reactor temperature. Consequently, the design of winding block for vibration suppression requires a holistic evaluation that incorporates thermal effects. Future studies will employ coupled thermal-fluid analysis to quantitatively assess the temperature rise induced by blocks. This comprehensive methodology is expected to balance vibration attenuation performance, investment cost and thermal constraints.

Conclusions and recommendations

A shunt reactor was used as the research object in this study. The simulation modeling method of winding vibration based on electromagnetic-mechanical coupling field was proposed and verified by actual measurement. The vibration caused by the alternating Lorentz force acting on the winding was analyzed by the simulation model. The results indicate that:

  1. 1)

    The simulation model could be properly simplified by setting multiple blocks of the same layer as an equivalent block. The validation results show that the calculated value of each test point is in good agreement with the test values, and the relative errors are less than 5%. Therefore, the modeling method proposed and adopted in this paper is reasonable.

  2. 2)

    The maximum values of the winding flux density and Lorentz force both appear in its central inner region. The axial Lorentz force is distributed symmetrically up and down, and the maximum values are distributed at the top and bottom of the winding. The axial Lorentz forces of disks are distributed in an S-shape along the axis of the winding, and the forces approach zero at about 1/6, 1/2, and 5/6 heights.

  3. 3)

    The axial direction is the main direction of winding deformation and amplitude. The volume averages of the disk axial amplitudes range from 14.340 μm to 28.374 μm, the results of M-point range from 16.631 to 34.631 μm, and the results of N-point range from 8.826 to 24.811 μm. On the whole, the axial amplitude of the winding presents an M-shape distribution along its axis, which is mainly related to the characteristics of the axial Lorentz force distribution and the suppression effect of the core and magnetic shielding.

  4. 4)

    The axial amplitudes of 1# and 35# disks decrease with the increase of the elastic modulus or the number of blocks. When the elastic modulus of blocks increases from 8.00 × 107 Pa to 2.00 × 108 Pa, the axial amplitude of 1# and 35# disks decreases by 40.265% on average. When the number of blocks increase from 20 to 45, the axial amplitude of 1# and 35# disks decrease by 39.951% on average. However, the axial amplitudes of 1# and 35# disks gradually slow down with the increase of elastic modulus or number of blocks, so the vibration reduction target and investment cost should be considered comprehensively in the vibration reduction design of winding. In addition, the design of winding block for vibration suppression should induce the thermal effect.