An efficient semantic segmentation method for road crack based on EGA-UNet

Abstract

Road cracks affect traffic safety. High-precision and real-time segmentation of cracks presents a challenging topic due to intricate backgrounds and complex topological configurations of road cracks. To address these issues, a road crack segmentation method named EGA-UNet is proposed to handle cracks of various sizes with complex backgrounds, based on efficient lightweight convolutional blocks. The network adopts an encoder-decoder structure and mainly consists of efficient lightweight convolutional modules with attention mechanisms, enabling rapid focusing on cracks. Furthermore, by introducing RepViT, the model’s expressive ability is enhanced, enabling it to learn more complex feature representations. This is particularly important for dealing with diverse crack patterns and shape variations. Additionally, an efficient global token fusion operator based on Adaptive Fourier Filter is utilized as the token mixer, which not only makes the model lightweight but also better captures crack features. Finally, to demonstrate the method’s effectiveness and accuracy, we compare the proposed approach with some existing methods on three public datasets. Experimental results demonstrate that the proposed method outperforms existing approaches in detecting cracks of diverse shapes and sizes within complex backgrounds, satisfying the requirements for both high precision and real-time segmentation.

Introduction

Cracks constitute the most prevalent road defects. As urbanization accelerates and infrastructure construction advances, the detection and segmentation of cracks exhibit extensive application value in road safety assessments and maintenance. Unrepaired cracks can pose severe threats to traffic safety¹. The timely detection and repair of cracks represent a significant responsibility for transportation departments. Traditional crack detection methods rely heavily on manual inspections—a process that is cumbersome, labor-intensive, and inefficient, with accuracy further compromised by operator experience and subjective judgment. Consequently, there is an urgent need for high-precision and real-time segmentation methods. Segmenting cracks poses significant challenges due to their erratic intensity, erratic contrast, and densely packed backgrounds. Moreover, diverse road textures resembling cracks and their inherently low contrast complicate crack recognition. The advent of deep learning has facilitated the emergence of computer vision techniques, presenting researchers with novel solutions to these problems. Researchers have increasingly directed their focus on automated crack segmentation methods grounded in computer vision techniques.

Crack segmentation serves as a critical preprocessing step for quantitative structural health assessment, aiming to precisely extract crack morphologies from complex backgrounds. Crack segmentation methodologies are primarily categorized into traditional image processing methods^2,3,4,5,6,7 and deep learning methods^{9,10,11,12,13}. Traditional frameworks typically employ edge detection algorithms, morphological operations, and threshold segmentation strategies. Ron et al.² introduced the concept of gravitational field intensity as a substitute for image gradient and proposed an adaptive threshold selection approach based on the mean and standard deviation of image gradient magnitude. Yan-Yin et al.³ presented an image segmentation algorithm leveraging an adaptive weighted mathematical morphology edge detector. Cuevas et al.⁴ introduced an image segmentation algorithm based on an automated threshold determination technique. These methods exhibit efficacy in handling images with simple backgrounds and distinct cracks but falter in images with complex backgrounds, blurred and microscale crack, and cannot fulfill real-time segmentation demands. Recently, advancements in deep learning technology, particularly the pervasive application of convolutional neural networks⁸ in image processing, have significantly propelled crack segmentation methods based on deep learning^{14,15,16,17,18,19,20}. Deep learning-based crack segmentation demonstrates superior accuracy and computational efficiency through three fundamental advantages. Firstly, deep learning models exhibit robust feature learning capabilities, enabling automatic learning of crack feature representations, thereby enhancing segmentation accuracy. Secondly, deep learning models possess excellent generalization ability, achieving effective segmentation across different scenarios and crack types. Finally, deep learning models can be trained and optimized end-to-end, simplifying the segmentation process and improving segmentation efficiency. Liu et al.⁹ proposed a deep level of convolutional neural network (CNN) called DeepCrack which predicted pixel-wise crack segmentation in an end-to-end approach, achieving high performance. Choi et al.¹⁰ proposed a semantic damage detection network (SDDNet), which was trained on a manually created crack dataset, achieving a high mean Intersection over Union (mIoU) on the test set and demonstrating a certain degree of real-time performance. Qu et al.¹¹ combined a novel multi-scale convolutional feature fusion module and proposed a crack detection method based on a deeply supervised convolutional neural network, which achieved better performance in terms of F1 score and mean IoU. These crack segmentation methods demonstrate satisfactory performance but struggle with accurately segmenting topological cracks and lack real-time segmentation capabilities. Real-time segmentation is crucial for enhancing efficiency and ensuring segmentation integrity. Real-time denotes an algorithm’s ability to complete a task within a specified time frame without significantly increasing the number of parameters to improve accuracy. Our focus is on real-time segmentation methods that preserve semantic information during transmission, as this information tends to degrade over time. Employing lightweight convolutions, residual connections, and the Spatial Pyramid Pooling Fast (SPPF) module in deep network layers can address these challenges, enhancing multi-scale information representation and overcoming limitations of single spatial hierarchy in feature maps. This paper mainly has the following contributions:

• 1. An Efficient Ghost Sparse Convolution(GSConv) Block (EG-Block) is proposed, consisting of three lightweight convolutions with kernel sizes of 3 × 3, incorporating residual connections and an efficient multi-scale attention (EMA) module. This module enhances the extraction and transmission of crack features and reduces the loss of crack information.

• 2. The A-RepViT Block module is proposed, wherein the original token mixer is substituted by Adaptive Frequency Filtering (AFF). AFF facilitates the model in capturing crack features more effectively, enhances crack segmentation accuracy, and diminishes a certain quantity of parameters, thereby achieving an improved equilibrium between accuracy and efficiency.

• 3. The EGA-UNet network is proposed, which embeds the proposed Efficient GSConv Block into UNet and incorporates the SPPF module and A-RepViT Block into the deeper layers of the encoder. EGA-UNet improves the effectiveness of crack segmentation while being a lightweight network, meeting the requirements for real-time and high-precision crack segmentation.

The rest of the paper is organized as follows: Sect. 2 presents the related work; Sect. 3 presents the proposed algorithm and designed methodology; Sect. 4 explores the experimental results and discussion. Finally, conclusions are drawn in Sect. 5.

Related works

This section mainly explains the practical application of semantic segmentation technology in road crack detection, as well as the historical development of transformers and attention mechanisms and their practical application in crack detection.

Road crack detection based on semantic segmentation

Semantic segmentation of road cracks is predominantly implemented through deep convolutional neural networks (CNNs). In this paper, it is possible to learn the complex relationships between crack pixels in an image and generate a crack prediction map of the same size as the input image by training the network, ensuring that each pixel is assigned a specific category label. Leveraging the advantages of CNN in feature representation, various semantic segmentation techniques for crack image detection have emerged. Cheng et al.²² proposed an automatic crack detection method based on the U-Net deep convolutional neural network, achieving excellent results. A supervised method²³ based on deep learning was proposed, which had the ability to handle different road surface conditions. However, the encoder of the traditional UNet network had relatively weak feature extraction capabilities and a large number of parameters. This had prompted efforts to enhance the encoder’s feature extraction capabilities and to make the entire network more lightweight. Yu et al.²⁴ proposed a U-shaped encoder-decoder semantic segmentation network that combined UNet and ResNet for pixel-level road surface crack image segmentation, improved crack detection performance. Zhang et al.²⁵ proposed a customized deep learning model architecture named Efficient Crack Segmentation Network to accelerate real-time pavement crack detection and segmentation without compromising performance. Building upon the work of previous researchers, the algorithm proposed in this paper, named EGA-UNet, integrates efficient lightweight convolutional blocks to quickly and precisely segment topological cracks of varying shapes with complex backgrounds.

The application of transformers in semantic segmentation

Since Transformer architecture was introduced by Vaswani et al. in 2017²⁶, it was initially primarily used for natural language processing tasks. However, over time, the powerful capabilities of Transformer have also been applied to the field of computer vision, including object detection²⁷ and image segmentation²⁸. Conventional convolutional neural networks (CNNs) predominantly utilize local receptive fields for image processing, whereas Transformers leverage self-attention mechanisms to capture global dependencies. This enables effective integration of features across various levels, enhancing the model’s ability to comprehend global image information and inter-regional relationships. At the same time, the self-attention mechanism of Transformers²⁹ also facilitates self-supervised learning, which is particularly useful in image segmentation since labeling a large amount of image data is both time-consuming and labor-intensive. Through self-supervised learning, the model can be trained with little to no labeled data. Therefore, scholars have begun applying the Transformers architecture to image segmentation. Gao Y et al.³⁰ proposed UTNet, which integrated the self-attention mechanism into convolutional neural networks to enhance medical image segmentation. Cheng B et al.³¹ proposed a new architecture capable of solving any image segmentation task (panoptic, instance, or semantic), which achieved excellent results on public datasets like COCO. Xie E et al.³² proposed a semantic segmentation framework called SegFormer, which combined transformers with a lightweight multi-layer perceptron (MLP) decoder, improving segmentation performance. While Transformers have demonstrated strong performance, they have also incurred significant computational costs and inference speed trade-offs. The advancement of Transformers has traditionally been credited to the attention-based mechanism for token mixing. Yu T et al.³³ completely replaced the attention-based module with Spatial MLPs as the token mixer and discovered that the derived MLP-like model could easily achieve competitive performance on image classification benchmarks. Yu W et al.³⁴ further abstracted the entire Transformer as a general architecture MetaFormer by viewing the attention module as a specific token mixer. They did not specify a token mixer, as they believe that MetaFormer is the key to achieving superior results in visual task models similar to Transformers and MLPs. Huang Z et al.³⁵ developed an efficient global token fusion operator named Adaptive Fourier Filter to replace the self-attention module in Transformers. To address the computational complexity of Transformers, Wang et al.³⁶ proposed a lightweight Transformer architecture with a slight increase in the number of parameters and inference speed, which accuracy has been improved. In the task of crack segmentation, Liu et al.³⁷ proposed a Transformer-based crack detection network called CrackFormer, and conducted experiments on three public datasets, all of which achieved good results. Building upon prior research, this study enhances the RepViT Block, introduces the A-RepViT Block, and incorporates it into the EGA-UNet al.gorithm. This integration aims to deepen image comprehension and enhance the precision of crack segmentation.

Attention mechanisms

In recent years, attention mechanisms have been widely applied in various fields of deep learning, including object detection^38,39, semantic segmentation^40,41, object tracking⁴², and face recognition⁴³, among others. The core principle of the attention mechanism is to emulate human information processing by selectively prioritizing important information based on task requirements, while disregarding irrelevant information, rather than treating all information equally. Hu et al.⁴⁴ proposed the Squeeze-and-Excitation Network (SENet) to model the interdependencies between feature channels. Wang et al.⁴⁵ introduced an Efficient Channel Attention (ECA) module, overcoming the trade-off between performance and complexity. Xu et al.⁴⁶ presented an Efficient Local Attention (ELA) method that effectively utilized spatial information without reducing channel dimensions or increasing the complexity of the neural network, meeting the demands of various vision tasks. Ouyang et al.⁴⁷ proposed an Efficient Multi-Scale Attention(EMA) module that focused on retaining information of each channel while reducing computational overhead. Additionally, the method further aggregates the output features of two parallel branches through cross-dimensional interaction. The results show that EMA significantly outperforms several recent attention mechanisms without changing the network depth. In the task of crack detection, Qiao et al.⁴⁸ and Liang et al.⁴⁹ respectively proposed a pavement crack detection method using the attention mechanism, both having good performances. This illustrates the capability of the attention mechanism to integrate multi-scale feature data and identify distinctive features. Building upon prior work, the present study introduces the EG-block, incorporating an attention mechanism to facilitate rapid identification of cracks within the network.

Methods

In this section, the proposed EGA-UNet network is introduced firstly, and then the EG-block, A-RepViT Block, SPPF module and finally the loss function in detail.

The structure of EGA-UNet

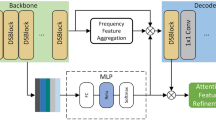
EGA-UNet consists mainly of EG-block, A- RepViT Block and SPPF module. Input a road crack image into the segmentation model and divide all the pixels in the image into crack pixels and background pixels based on the corresponding probability values. Crack pixels have higher probability values, while background pixels have lower probability values. Therefore, crack segmentation can be seen as a pixel-by-pixel binary classification problem. Figure 1 shows the architecture of the EGA-UNet. Based on the encoder-decoder structure, the EGA-UNet network model is proposed. It utilizes a combination of residual connections and attention mechanism modules to form the EG-block, replacing the convolutional parts in the encoder and decoder to extract feature information from different layers. Integrating the SPPF module into the encoder’s lower layers enables the network to better capture spatial hierarchies in images. This enhancement improves multi-scale crack feature perception while boosting flexibility and robustness. Following the SPPF module, the A-RepViT Block is included to help the model better capture crack features and handle multi-scale features. The decoder integrates multi-layer feature information in the form of feature pyramid to achieve accurate crack segmentation.

Fig. 1

The structure of EGA-UNet.

The structure of EG-Block

The EG-Block comprises three 3 × 3 lightweight convolutions and a single 1 × 1 standard convolution. It also incorporates a residual connection mechanism and an EMA module, as shown in the Fig. 2. This process can be represented as Eq. (1). Increasing the network depth can enhance crack recognition in models. The EG-Block structure employs three concatenated lightweight convolutional layers to extract features efficiently. Stacking convolutional layers augments the number of parameters, hence lightweight convolutions were utilized. Each convolutional layer captures distinct levels of features from input data, enabling the network to amalgamate simple features into complex representations. Moreover, stacking convolutional layers enhances the network’s robustness against translations and minor deformations in the input data, thereby enhancing generalization. However, excessive convolutional layer stacking can degrade network performance. To address this issue, the residual method is employed after three lightweight convolutional layers, directly incorporating input features into the feature map. This approach facilitates feature reuse, minimizes information loss, and sustains robust feature extraction capabilities with increased network depth. Furthermore, an EMA module is integrated after the initial lightweight convolutional layer to integrate multi-scale feature information and select discriminative features. This module reconstructs some channels into batch dimensions and groups the channel dimensions into multiple sub-features to ensure that spatial semantic features are evenly distributed within each feature group, which can be represented by Eq. (2)⁴⁷. The purpose of this is not only to encode global information to recalibrate the channel weights in each parallel branch but also to further aggregate the output features of the two parallel branches through cross-dimensional interaction. To capture pixel-level paired relationships, it can retain more crack pixels.

$${f_{out}}={f_C}({f_{GS}}({f_{GS}}({f_{GS}}(x)))+{f_{EMA}}({f_{GS}}(x)))$$

(1)

where x represents the input, ${f_{out}}$ represents the output, ${f_{EMA}}$ represents the channel through the EMA module, ${f_{GS}}$ represents the operation of GSConv with a kernel size of 3 × 3, ${f_C}$ represents the result of a standard convolution operation with a kernel size of 1 × 1.

$$X=[{X_0},{X_i},\cdots,{X_{G - 1}}],{X_i} \in {{\mathbb{R}}^{C//G \times W \times H}}$$

(2)

where C//G represents division into G groups along the channel direction, and W and H represent the width and height of the feature map.

Fig. 2

The structure of Efficient GSConv Block(EG-Block).

The structure of A-RepViT block

The RepViT Block is the main structure in the lightweight convolutional neural network RepViT³⁶, and it uses structural re-parameterization techniques to separate the Token mixer and Channel mixer. This preserves the original expressive capacity by decreasing parameters and computational complexity, thereby enhancing the model’s learning and inference efficiency. Moreover, the expansion ratio in the Channel mixer is adjusted to 2, augmenting network width, improving model performance, and decreasing computational burden. A 3 × 3 kernel convolution is employed alongside the SE layer arranged in a cross-block configuration akin to the Token mixer to decrease latency without compromising model performance. Despite the reduction in delay, the SE layer exhibits lower precision for target segmentation compared to the self-attention mechanism in the conventional Transformer architecture. Therefore, the efficient global token fusion operator based on AFF proposed in [35] is adopted in this paper instead of the SE layer as the Token mixer in RepViT Block, and the A-RepViT Block is proposed, as shown in Fig. 3(a). The adaptive frequency filtering can help the model better capture the crack characteristics and deal with multi-scale features better. The AFF(as shown in the Fig. 3(b)) based efficient global Token fusion operator is mathematically equivalent to using a dynamic convolution kernel with the same spatial resolution as the Token set to perform Token fusion in the original domain (as shown in the Fig. 3(c)), and has the function of content adaptive Token fusion in the global scope. Thus, the depth of the image understanding and the accuracy of crack segmentation can be improved. Moreover, AFF optimizes computational resource utilization by prioritizing crucial information, leading to improved model performance.

Fig. 3

The structures of A-RepViT Block, Adaptive Frequency Filters and Dynamic Large-kernel Mixers.

The structure of SPPF

SPPF is improved on the basis of Spatial Pyramid Pooling(SPP), as shown in Fig. 4. SPP uses three maximum pooling layers with different kernel sizes to maximize feature maps, thus obtaining multi-scale feature maps. Finally, these feature maps are joined together to enrich the spatial hierarchy of the feature map. SPPF is modified from SPP by changing it into three max pooling layers of the same kernel size and transforming it into a serial structure for computation. This reduces redundant calculations and enhances the model’s speed while better handling multi-scale objects and improving robustness to scale variations.

Loss function

The loss function is the most fundamental and crucial element in deep learning, as it measures the quality of predictions. EGA-UNet is regarded as a per-pixel classifier and generates a prediction map. Firstly, binary cross-entropy loss is introduced for training the EGA-UNet. The predicted probability for the pixel is denoted by $P=\{ {P_i},i=1,2,\cdots,N\}$, where N represents the number of pixels in the image. $Y=\{ {y_i},i=1,2,\cdots,N\} ,{y_i} \in \{ 0,1\}$ is the true label. The binary cross-entropy loss function is defined as:

$${L_{bce}}= - \sum\limits_{{i=1}}^{N} {{y_i}\log ({p_i}) - (1 - {y_i})\log (1 - {p_i})}$$

(3)

Dice loss can handle severely imbalanced classes, improving the balance between accuracy and recall during training. Dice loss is defined as:

$${L_{dice}}=1 - \frac{{2\sum\nolimits_{{i=1}}^{N} {{p_i}{y_i}+1 \times {{10}^{ - 6}}} }}{{\sum\nolimits_{{i=1}}^{N} {y_{i}^{2}+} \sum\nolimits_{{i=1}}^{N} {p_{i}^{2}+1 \times {{10}^{ - 6}}} }}$$

(4)

Add $1 \times {10^{ - 6}}$ to both the numerator and denominator to smooth out fluctuations across epochs and enhance stability. Considering that most of the pixels in the image are non-crack (background), binary cross-entropy loss and Dice loss are combined for network training. The overall loss is the weighted sum of binary cross-entropy loss and Dice loss.

$$L=r{L_{bce}}+(1 - r){L_{dice}}$$

(5)

where r is the weighting factor that controls the contribution of the two losses to the total loss. In this paper, r is set to 0.5.

Results and discussion

In order to verify the performance of the proposed EGA-UNet on crack segmentation, three public data sets are used to train and test the algorithm, and the EGA-UNet is compared with other mainstream detection algorithms. It is verified that the proposed algorithm shows good performance on topological cracks with different shapes and complex backgrounds. Finally, the ablation experiments are carried out to verify the effectiveness of the improved modules.

Experimental detail

The proposed method is implemented by PyTorch, and CUDA is used to accelerate the algorithm. The algorithm adopts batch normalization after each convolutional layer to accelerate the convergence speed during training. After batch normalization, SiLU is used to add the nonlinear relationship between the layers of the network to overcome the problems of overfitting and gradient disappearance. The following Table 1 lists the specific information.

Table 1 Experimental configurations.

Dataset

Crack500⁵⁰: This dataset consists of 500 images of road surface cracks, each with a size of 2000 × 1500 pixels. These images often blend with similar backgrounds with their complex background noise and foreground, which make detection difficult. Due to the small dataset, the images in the dataset are divided into 3368 road surface crack images, and each size of image is 640 × 360 pixels, as shown in Fig. 5(a). These images were then split into 1896 training images, 348 validation images, and 1124 test images. The cracks in this dataset are diverse, including single and topological cracks, as well as thick and thin cracks.

DeepCrack⁹: This dataset consists of 537 complex crack images with a resolution of 544 × 384, as shown in Fig. 5(b), which 300 images are for the training set and 237 images for the test set. The image samples contain cracks with various textures, different scenes and varying scales with crack widths ranging from 1 to 180 pixels. This allows for testing the network’s performance in handling multi-scale cracks in different scenarios.

CrackTree206⁵¹: This dataset contains 206 images of road cracks with a resolution of 800 × 600 pixels, as shown in Fig. 5(c), which 126 images are for training and 80 images are for validation. The cracks in the dataset are relatively thin and there are obstructions and shadow interferences. It can test the generalization performance of network models.

CFD⁵²: This dataset contains 118 images of size 480 × 320 pixels, as shown in Fig. 5(d). And these images contain background noises such as shadows and stains. All the images have manually labeled ground truth contours. The CFD dataset was used to test model generalization performance.

Fig. 4

The structure of SPPF

Evaluation metrics

Pixel-level crack detection can be regarded as a form of binary semantic segmentation, aiming to divide the image into foreground (cracks) and background (non-crack features). Therefore, Dice coefficient and mean intersection over union (mIoU) are used as evaluation metrics for segmentation performance. Dice coefficient is a statistic method used for comparing the similarity of two samples, while mIoU measures the ratio of the intersection to the union of the predicted results and the ground truth labels to assess model performance. Model Parameters and FLOPs are used simultaneously as standards for measuring model complexity. The equations are defined as follows.

$$Dice=\frac{{2\sum\nolimits_{{i=1}}^{N} {{p_i}{g_i}} }}{{\sum\nolimits_{{i=1}}^{N} {p_{i}^{2}+} \sum\nolimits_{{i=1}}^{N} {g_{i}^{2}} }}$$

(6)

$$mIoU=\frac{1}{2} \times (Io{U_b}+Io{U_f})$$

(7)

where ${p_i}$ and ${g_i}$ represent the predicted and ground truth values for pixel i respectively, and N is the total number of pixels. $Io{U_b}$represents Intersection over Union (IoU) of the true background and the predicted background. $Io{U_f}$represents Intersection over Union of actual cracks and predicted cracks.

The effectiveness of the attention mechanism

To verify the effectiveness of the attention mechanism in the EG-Block, we conducted experiments on EG-Block(without attention mechanism), EG-Block(with SE), EG-Block(with ECA), EG-Block(with CBAM) and EG-Block(with EMA) respectively in Crack500. Then it can be seen from Table 2 that the segmentation performance of EG-Block(with EMA) is the best.

Table 2 Test the effectiveness of the attention mechanism in the EG-Block on Crack500.

Evaluation

To evaluate the effectiveness of the proposed method, this paper conducts comparative experiments between the proposed method and five mainstream methods—FCN, U-Net, SegNet, PSPNet, and DeepLabV3—on three public datasets. To ensure the comparability of the experiments, all compared methods were applied with their default parameter settings and underwent the same training process. A total of 100 rounds of training were conducted, followed by qualitative and quantitative analysis of the resulting models to evaluate the performance of each method. Firstly, we display the loss curve to determine whether the model overfits the current data as shown in Fig. 6.

Fig. 5

Samples of four datasets.

Fig. 6

Loss curve of the training process of the different network.

Then, this paper qualitatively analyzes method performance through the detection results of different models. The detection results of FCN, UNet, SegNet, PSPNet, and DeepLabV3, compared to the method proposed in this paper on the Crack500, DeepCrack, and CrackTree206 public datasets are shown in the Fig. 7. The experiment selected images with topological, coarse, normal and fine cracks. For the images with topological and coarse cracks, it can be seen from the first row that FCN, UNet, SegNet, PSPNet, and DeepLabV3 all missed some detections; from the sixth row, it can be observed that the FCN and UNet networks had incomplete detections, while the other networks performed well. For topological and normal cracks, it can be seen from the second row that in the presence of edge stone influence, all comparison networks show missed detections; from the third row, it can be seen that the comparison networks are less effective in segmenting cracks; from the fourth row, it can be seen that the comparison networks are poor at identifying scattered cracks; from the fifth row, it can be seen that FCN, UNet, PSPNet, and DeepLabv3 have incomplete segmentation of fine cracks at the edges. The last three rows show images of topological and fine cracks. It is evident from these images that FCN exhibits insensitivity towards fine cracks, rendering it incapable of their identification. Conversely, UNet, SegNet, PSPNet, and DeepLabV3 demonstrate a tendency to overlook numerous fine cracks. In contrast, the approach introduced in this study successfully detects nearly all fine cracks. In summary, the method proposed in this paper surpasses these methods in segmenting topological cracks of diverse shapes against intricate backgrounds, thereby meeting the practical demands for crack segmentation.

Fig. 7

Comparison pictures of various methods test results (The first three rows are for the crack500, the middle three rows are for the DeepCrack, and the last three rows are for the CrackTree206).

To better verify the effectiveness of the method proposed in this paper, quantitative analysis is conducted using three datasets. The experimental results for different methods are shown in the Tables 3, 4 and 5, which include Dice coefficient, background intersection over union ($Io{U_b}$), crack intersection over union ($Io{U_f}$), mean intersection over union (mIoU), parameters, FLOPs and FPS. On the Crack500 dataset, the proposed EGA-UNet achieves a Dice coefficient of 77.8%, which is 5.2%, 2.3%, 3.0%, 1.8% and 2.5% higher than FCN, U-Net, SegNet, PSPNet and DeepLabV3 respectively. The mIoU of EGA-UNet reaches 83.9%, which is higher than FCN, U-Net, SegNet, PSPNet and DeepLabV3 by 3.1%, 1.3%, 1.3%, 1.1% and 2.0% respectively. On the DeepCrack dataset, the proposed EGA-UNet achieves a Dice coefficient of 82.6%, which is higher than FCN, U-Net, SegNet, PSPNet and DeepLabV3 by 14.9%, 3.4%, 2.8%, 5.1% and 3.7% respectively. The mIoU of EGA-UNet reaches 86.4%, which exceeds FCN, U-Net, SegNet, PSPNet and DeepLabV3 by 8.8%, 1.5%, 1.9%, 3.0% and 2.2% respectively. On the CrackTree206 dataset, because the FCN network is too deep and does not make good use of the shallow information, the fine crack information is not extracted. The proposed EGA-UNet achieves a Dice coefficient of 73.1%, which is higher than U-Net, SegNet, PSPNet and DeepLabV3 by 3.1%, 11.9%, 44.9% and 52.3% respectively. The mIoU of EGA-UNet reaches 78.9%, surpassing U-Net, SegNet, PSPNet and DeepLabV3 by 1.3%, 4.7%, 21.1% and 23.4% respectively. Moreover, the number of parameters and FLOPs of EGA-UNet are significantly lower than those of models like FCN, SegNet, PSPNet, and DeepLabV3, thus EGA-UNet meets the requirements for real-time and high-precision crack segmentation. Additionally, it can be seen that EGA-UNet has a faster detection speed than other mainstream methods from FPS, which proves the high efficiency of this method. Finally, we compared EGA-UNet with the latest methods on three datasets in Table 6, and EGA-UNet has a highest mIoU that it meets the requirement of real-time segmentation of road cracks.

Table 3 Comparison of the performance of different models on the Crack500.

Table 4 Comparison of the performance of different models on the deepcrack.

Table 5 Comparison of the performance of different models on the CrackTree206.

Table 6 mIoU comparison of the latest models on three datasets.

Furthermore, the model’s generalization performance will be evaluated by testing on the CFD dataset. We performed quantitative and qualitative analyses on this dataset. And the experimental setting is exactly the same as the training to ensure the fairness of the experiment. Firstly, quantitative analysis as shown in Table 7, we can see that EGA-UNet has higher accuracy and speed than the compared network. And as shown in Fig. 8, it can be seen that EGA-UNet can basically segment pavement cracks, which reflects the good generalization performance of the model.

Table 7 Comparison of the performance of different models on the CFD.

Fig. 8

Test on the CFD dataset

Finally, the superiority of the proposed method is demonstrated through comparisons on various complex background images, as illustrated in Fig. 9, showcasing its capability to accurately segment cracks amidst intricate backgrounds.

Fig. 9

Compare the segmentation of various complex background images.

Ablation

In this section, ablation experiments are designed on the Crack500 dataset to examine the roles of different mechanisms in the U-Net architecture. The contribution of various improved modules to the final model’s performance is evaluated, and the results are shown in Table 8. Among them, U-Net (c = 32) indicates that the channel parameters are 32, 64, 128, 256 respectively; U-Net (c = 64) indicates that the channel parameters are 64, 128, 256, 512 respectively. By comparing the first row and the second row, it can be seen that U-Net(c = 32) achieves higher metrics with fewer parameters. Comparing the last four lines with the first line, it can be seen that the added EG-Block module, SPPF module and A-RepViT Block module all effectively improve the model’s performance in segmenting images. According to the results of the ablation experiments, compared to the basic U-Net network, the Dice coefficient increased by 2.3% and the mIoU increased by 1.3%, with almost no change in the number of parameters, which satisfies the requirements for detecting cracks of various sizes in complex backgrounds.

Table 8 Effectiveness of each improved module.

Conclusion

This research presented an innovative and efficient crack segmentation method. Specifically, lightweight modules are proposed, EG-Block and A-RepViT Block, which address the issue of feature loss in transmission and retains crack features better, while also improving the segmentation performance and efficiency of the network. This method addresses critical limitations of traditional crack segmentation methods, such as relying on slow and error-prone manual segmentation. Extensive experimentation on three publicly available datasets has confirmed that EGA-UNet outperforms in terms of higher mIoU and reduced computational demands, thereby affirming the efficacy and versatility of the approach. This research holds significant implications by offering a streamlined approach for road maintenance personnel to expedite and enhance the accuracy of crack detection, thereby optimizing road maintenance operations. Future endeavors will focus on further refining crack segmentation techniques for roads and enhancing algorithmic efficiency. Moreover, efforts will be directed towards enhancing the model’s generalizability across various segmentation domains.