Abstract
The results of this study indicate that a rear adjustable spoiler significantly improves the aerodynamic performance of a fastback vehicle. Computational fluid dynamics simulations were conducted in ANSYS Fluent to optimize the spoiler’s height and angle for enhanced stability and aerodynamic efficiency. The NACA 4412 airfoil was selected due to its superior lift-to-drag ratio compared to other airfoils. Simulations were performed at three Reynolds numbers (4.87 × 106, 9.75 × 106, and 14.61 × 106), with spoiler heights ranging from 5 to 15 cm. The findings revealed that a 10 cm height provides an optimal balance between drag reduction and increased downforce. At this height, a 0° angle resulted in the lowest drag under normal driving conditions, improving aerodynamic efficiency without significantly affecting downforce. However, in sudden braking conditions, increasing the spoiler angle to 45°–60° significantly enhanced downforce, thereby improving tire grip and braking performance. The results confirm that an adjustable rear spoiler can effectively reduce lift, thereby increasing road adhesion at high speeds and enhancing braking performance without compromising aerodynamic efficiency. However, higher spoiler angles also increase drag, which may impact fuel consumption. These findings provide valuable insights into optimizing high-performance and energy-efficient vehicle designs, offering a foundation for future advancements in vehicle aerodynamics.
Similar content being viewed by others
Introduction
Today, a significant part of automotive design focuses on the body’s aerodynamics. The airflow movement over the body and wheels generates drag and lift forces, which should be minimized for optimal design. Researchers and engineers have mitigated these forces by refining the body shape and controlling the boundary layer flow and vortices surrounding vehicles. Since nearly half of the energy produced by the engine is used to overcome these aerodynamic forces1, the primary and most important effect of this optimization is the reduction of fuel consumption or reliance on other energy sources. Other subsequent effects include increased speed and better controllability, which are also among users’ desires, given the rapid advancement of technology. Modern body designs and various devices to alter and control the airflow around vehicles can directly impact their aerodynamics2. These measures fall under airflow control methods around the vehicle, including active and passive aerodynamic control3. The application of computational methods for optimizing aerodynamic shapes has garnered significant research attention in various engineering fields, particularly in aviation4,5 and automotive fields6,7. Aerodynamic shape optimization in road vehicle applications is generally aimed at reducing aerodynamic drag8,9, increasing downforce10,11, or reducing lateral force due to crosswinds12,13. Reducing vehicle drag is a common approach in nearly all aerodynamic optimizations. Improving downforce is usually used for high-performance vehicles where high-speed handling is a concern, and optimizing lateral forces caused by crosswinds13,14 primarily becomes a concern for large vehicles such as tractor-trailers, trains, buses, or trucks. A road vehicle generally has a body shape where the generated aerodynamic force is primarily due to pressure components, with less attention given to skin friction forces. Therefore, efforts to improve a vehicle’s aerodynamic performance mainly involve suppressing or delaying separation on the vehicle’s body and controlling the structures behind the vehicle15. This reduction in base drag can be achieved by applying passive aerodynamic devices to improve aerodynamic properties, which can range from a simple to a complex overall form, such as a flap16, vortex generator17, circular cylinder arrays18, rounded edges19, base blowing20, base cavity21, boat tails21, and rear spoiler15. Among the aerodynamic devices mentioned, the rear spoiler is one of the most widely used applications in road vehicles22. On the other hand, in active control methods, equipment that requires energy consumption controls the airflow over the vehicle’s body. This equipment needs sensors to measure the current flow conditions over the body and its auxiliary equipment and then relay this information to the relevant equipment. If a change is required, the equipment will apply it to the system. At the moment, one of the most important active aerodynamic control devices is the rear wing of some vehicles, which adjusts its angle and position according to the current situation to direct the airflow behind the car in a way that is favorable for both the vehicle and the driver. The rear spoiler changes the angle depending on whether the car accelerates, decelerates, or turns23 to increase downforce during acceleration and drag during deceleration for quicker stopping. Sometimes, the pressure under the vehicle rises at high speeds, leading to higher lift coefficients and causing the vehicle to tend to lift off the ground24. At this moment, the speed control sensor informs the rear spoiler to adjust the wing’s angle of attack, increasing the air pressure above the vehicle and creating a reactive downward force to keep the vehicle pressed to the road.
The history of using rear spoilers dates back to racing cars when, in 1965, Jim Hall invented the aerodynamic brake to reduce lift in modern racing cars by using inverted movable airfoils on Chaparral cars25. Yuping and Ayyagari26 analyzed the aerodynamic performance of an active rear spoiler designed to improve the lateral stability of high-speed road vehicles. Simulations were conducted for a high-speed car with and without a spoiler at different angles of attack and speeds. The result showed that the angle should be controlled within the range of 10 to 15 degrees to achieve maximum downforce and minimum drag. Sakib et al.27 also examined the effect of a spoiler with an NACA 4412 cross-section on the aerodynamic indices of a sedan car. Initially, they found that increasing the Reynolds number leads to higher drag and lift coefficients. They observed changes in drag and lift coefficients by considering four attack angles: 8, 10, 12, and 14 degrees for the spoiler. The highest negative lift and drag forces occurred at a 14-degree attack angle. In another research paper, Eftekhari et al.28 used numerical and experimental methods to study and analyze three spoilers with NACA 0012, NACA 4412, and S1223 cross-sections on their geometric model, named ERC, with and without spoilers at various adjustment angles and a Reynolds number of 2 × 106. Based on the results, it was concluded that using a spoiler significantly reduces the lifting and drag forces on racing cars. Specifically, using S1223 on a racing car creates higher downforce compared to NACA 0012 and NACA 4412, and the drag coefficient of the ERC model with the S1223 spoiler is lower than the other models, leading to higher speed for the racing car. In another study, Roslan et al.24 concluded that a car’s performance improves with the presence of a rear spoiler, as they observed a significant reduction in drag and an increase in downforce across both turbulence models they examined. Nepali et al.29 analyzed the impact of rear spoilers using computational fluid dynamics (CFD) and found that while spoilers improve vehicle stability and downforce, they also increase drag, especially at higher speeds. Sharma et al. studied various airfoil designs for spoilers in race cars, utilizing CFD simulations to identify shapes that optimize downforce and drag characteristics for competitive performance30. Gupta et al. explored the development of adaptive smart spoilers that adjust according to vehicle speed, demonstrating that these dynamic spoilers can maintain vehicle stability without significant increases in drag, thereby offering efficiency gains31. Das et al. applied CFD combined with machine learning techniques to optimize the rear spoilers for the Volkswagen Vento model, identifying configurations that effectively balance downforce and drag reduction32. Finally, Kumar et al.33 conducted simulations to investigate the effects of rear spoilers on commercial vehicles, emphasizing their role in enhancing vehicle stability and efficiency by better-managing lift and drag.
Despite various advancements in passive and active aerodynamic control, most rear spoiler designs are either fixed or limited to single-degree-of-freedom adjustments. A comprehensive solution that optimally adjusts both the height and angle of the spoiler for different driving scenarios has yet to be developed. Additionally, an Audi vehicle with a fastback rear configuration has been used to propose a suitable rear spoiler design. According to previous research34, the Audi A5 has the highest aerodynamic lift coefficient due to its rear configuration. Compared to other rear configurations, such as notchback and estate models, it requires greater improvements in this coefficient to enhance stability, especially at high speeds34. Another reason for selecting this vehicle is that the body of standard DrivAer models is derived from the designs of BMW and Audi35, making the initial validation process easier with the available experimental data for the fastback DrivAer model36.
This study aims to summarize previous findings in this field and propose a spoiler with two degrees of freedom height and angle to optimize two key design objectives: maximizing stability during cruising and ensuring quick and safe vehicle stopping in emergency situations through effective aerodynamic braking.
Achieving these two design objectives requires determining the optimal spoiler height in relation to the vehicle body and the optimal angle relative to the airflow at various Reynolds numbers. This study calculates key aerodynamic parameters through simulations, considering flows at various Reynolds numbers, to establish the best design limits for maximum stability in motion and effective aerodynamic braking. The process typically involves conducting numerical simulations of a 3D vehicle in ANSYS, analyzing the aerodynamic effects of spoiler adjustments at various heights and angles, and ultimately selecting the optimal configuration by evaluating the aerodynamic efficiency of different designs based on drag and lift coefficients.
Governing equations
Reynolds averaging Navier–Stokes (RANS)
This method uses the time-averaged Navier–Stokes equation, and the turbulent flow is calculated through modeling. For example, this can be written for the velocity quantity, which \({u}_{i}\) has two components: the fluctuating part \({u}_{i}^{\prime}\) and the mean part \({\overline{u} }_{i}\)37.
Similarly, following the form of Eq. 1, this decomposition can be applied to pressure or other scalar quantities. After substituting these new variables into the continuity and momentum equations, the general averaged continuity and momentum equations in the Cartesian coordinate system can be expressed as Eqs. 2 and 337 where ρ is the density (assumed constant in this study), \(\overline{p }\) is the averaged pressure and \({\delta }_{ij}\) kronecker delta37.
The equations mentioned above are known as the Reynolds-Averaged Navier–Stokes (RANS) equations. These equations retain the general form of the complete Navier–Stokes equations, with the variables expressed in terms of their mean or averaged values. The only additional term that appears in these equations is \((-\rho \overline{{u }_{i}^{\prime}{u}_{j}^{\prime}})\), which is referred to as the Reynolds stress. This term arises due to the turbulence of the flow. Solving the turbulent flow problem in this context involves developing a method to compute these Reynolds stresses and incorporating them into the RANS equations37,38.
The Boussinesq hypothesis and the Reynolds stress transport method
To model turbulent flows using the RANS approach, it is essential to accurately determine and compute the Reynolds stresses that appear in Eq. (3). A general method for achieving this is to use the Boussinesq hypothesis, where the Reynolds stresses are calculated as follows based on the gradients of the mean velocity37,38:
The Boussinesq theory is used in the Spalart–Allmaras, k-ε, and k-ω models. The advantage of this theory is its relatively low computational cost, which is attributed to the calculation of turbulent viscosity. In the Spalart–Allmaras model, only a single equation is used to calculate turbulent viscosity \(({\mu }_{t})\). But in the k–ε and k–ω models, two equations are solved to calculate turbulent kinetic energy (k) and either the turbulence dissipation rate (ε) or the specific dissipation rate (ω). In these cases, \({\mu }_{t}\) becomes a function of k and ε, or k and ω37.
The k-ω model
All industrial-relevant two-equation models use the equation for the turbulence kinetic energy, k, to provide one of the two scales required. The k-equation (Eq. 5) can be derived by summing up half of the diagonal of the exact RSM (Reynolds Stress Model) equations, where \({P}_{k}\) is the production term of the turbulent kinetic energy39.
This study uses the SST version of the k-ω turbulence model to obtain the turbulent viscosity. This model was introduced by Menter39 to blend the k-ω method, which performs well in near-wall regions with the k-ε method. In other words, this model can simultaneously utilize the capability of the k-ω model for accounting for low Reynolds number regions and the capability of the k-ε model for accounting for high Reynolds number regions37. Equations 7 and 8 represent the governing equations for the model under consideration. Further details regarding the quantities written in these equations (\(\beta ,{\beta }^{*},\gamma ,{\sigma }_{\omega 2}\), etc.) are precisely available in references38,39.
The SST k-ω model is very similar to the standard k-ω model, in which the standard k-ω model and the transformed version of the k-ε model are both multiplied by blending functions (\({F}_{1}\),\({F}_{2}\)) and then combined. The blending functions are designed to have a value of one near the wall, thereby activating the k-ω model in those regions, and a value of zero far from the wall, thereby activating the transformed version of the k-ε model. It should be noted that although this approach can enhance the capabilities of both models, switching from one model to another is often accompanied by instabilities or weak convergence behaviors37.
Numerical simulation
Computational model geometry
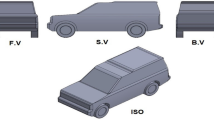
The geometry in question is a car from the Audi automotive group, which, in terms of rear configuration, corresponds to the standard DrivAer Fastback model35. The car model is the Audi A5, designed using the Blueprint method in the SolidWorks 2020 software environment. In Fig. 1a, the Audi car is shown from different views, with its body displayed. The DrivAer fastback model, as shown in Fig. 1b, is a generic vehicle model developed at the Institute of Aerodynamics and Fluid Mechanics at the Technical University of Munich to facilitate aerodynamic research on passenger vehicles36,40. The Fastback configuration, one of the model variants, has been shown through research41,42 to result in lower air pressure on the rear section compared to similar configurations like the notchback36, due to the smoother airflow passing over the rear end. However, since the airflow passes over the vehicle with less turbulence, it benefits from reduced drag force, placing it in a favorable position in terms of drag.
The two-dimensional schematic views of : (a) The designed body of the Audi A5, modeled in SolidWorks 2020 using blueprint drawings, (b) The DrivAer fastback model, created in SolidWorks 2020 based on the available 3D models from the Technical University of Munich40.
Computational domain
Based on the problem conditions, the governing equations must be solved within a specified domain, referred to as the computational domain. The boundaries of this domain should be placed at a sufficient distance from the computational model body so that further increasing them does not affect the results. According to previous research35, this domain was selected based on the ratio of the model’s length (L), width (W), and height (H). Specifically, the inlet boundary of the flow is set 2L away from the front bumper, the outlet boundary 7L away from the rear bumper, and the domain’s height and width are set to 8H and 11W, respectively. Additionally, a subdomain was established around the computational model to calculate the vortices more accurately. The presence of this subdomain increases the mesh density around the computational model. In this setup, the front and top boundaries of the flow are set 30 cm away from the front bumper and the vehicle’s roof, while the rear boundary is placed at a distance of L from the rear bumper, as shown in Fig. 2 The reason for this distance from the rear bumper is the significance of this part of the domain, where vortices and flow separation occur, and thus, greater accuracy is required.
Computational domain meshing
The computational domain meshing was performed in the ANSYS Meshing 2019 environment. Given the numerous geometric complexities of the body, an unstructured triangular mesh was used. Additionally, due to the presence of the viscous sublayer in the boundary layer around the body and the SST k-ω turbulence model, a special mesh with the condition y+ ≤ 143 must be created in this region. Considering a y+ = 144 and a Reynolds number of 4.87 × 106, the distance of the first cell from the wall was calculated to be 0.0254 mm. Moreover, 10 boundary layers with a growth rate of 1.2 were specified. According to Fig. 3, the computational domain meshing around the DrivAer fastback model in the symmetric plane is illustrated, with a zoomed-in view of the vehicle’s front and rear areas.
Boundary conditions and solver settings
In the aerodynamic analysis of vehicles, the air is considered incompressible because the airspeed-to-sound-speed ratio (Mach number) is typically less than 0.3, resulting in negligible density variations, typically less than 5%45. Therefore, the air density and dynamic viscosity are assumed to be constant, with values of 1.225 kg/m3 for density and 0.000017894 N · s/m2 for dynamic viscosity, according to Fluent’s default settings. Additionally, using the Silhouettet feature in SolidWorks, the exact frontal area of the Audi A5 vehicle facing the airflow was determined to be 2.185 m2. However, due to symmetry, only half of the domain is defined for the solution in Fluent. The numerical solution was performed based on pressure and in a steady state. A second-order method was used to discretize the equations, and the SIMPLEC algorithm was employed to couple velocity and pressure. The Green Gauss Cell-Based method was also chosen for estimating derivatives, as it offers high accuracy in unstructured tetrahedral meshes37. According to Fig. 2, the inlet boundary condition is defined as a velocity inlet corresponding to a Reynolds number (e.g., 15.126 m/s for Re = 4.87 × 106), while the outlet boundary condition is set as a pressure outlet with a relative pressure of 0 Pa. A symmetry boundary condition is applied to the midplane of the vehicle. The side and top boundaries of the computational domain are assigned a zero-gradient condition for all flow variables, such as velocity, ensuring zero flux. The vehicle body is modeled as a stationary wall with a no-slip condition, while the ground is defined as a moving wall with a velocity equal to the freestream velocity. Additionally, a rotating wall boundary condition is applied to the wheels, assuming no slip. Under the specified Reynolds number, the wheel rotational speed (\(\dot{\theta }\)) is calculated based on a wheel radius of 33 cm, resulting in 45.836 rad/s.
Grid size independence
Before performing numerical simulations of airflow around the Audi A5, achieving mesh independence for the DrivAer Fastback model under the same turbulence model and boundary conditions is essential. The number and size of cells in the computational domain significantly impact the accuracy and reliability of the results. If the cells are not sufficiently small, the solution will lack precision. On the other hand, excessive mesh refinement increases computational costs41. Therefore, by gradually reducing cell size and increasing the number of cells, as shown in Fig. 4a, the drag coefficient was calculated after achieving stable residual fluctuations for each equation. The drag coefficient stabilized at approximately 0.242 after approximately 2.354 million cells, which showed no difference from the experimentally measured drag coefficient in the wind tunnel (also 0.242)36. Additionally, for better validation, the distribution of the local pressure coefficient was examined based on the number of mesh cells. As depicted in Fig. 5, when the mesh size exceeded approximately 2.3 million cells, the alignment of the pressure coefficient curves (orange and pink) with the experimental results (black circular points) improved. Furthermore, Fig. 5 clearly illustrates the difference in pressure coefficients between the front and rear of the vehicle body, highlighting pressure drag as the primary resistive force against motion.
The distribution of the static pressure coefficient on the upper surface of the fastback body at different mesh densities, compared with the experimental wind tunnel results36 along its centerline.
Reynolds number independence
The study of Reynolds number independence in aerodynamic simulations of cars is crucial to ensure that numerical results accurately represent real-world aerodynamic behavior. Reynolds number independence occurs when aerodynamic coefficients, such as drag (Cd) and lift (Cl), remain relatively constant despite further increases in Reynolds number, indicating that the flow is fully turbulent and no longer affected by viscosity-dominated effects. Studies on-road vehicles, including the DrivAer model, suggest that this independence is typically achieved at Reynolds numbers above 5 × 106, where changes in Cd and Cl become negligible with further increases in Re36. For fastback-style vehicles like the Audi A5, which exhibit strong wake structures, independence is often reached between 5 × 106 and 7 × 106, depending on surface roughness and flow separation effects42. Moreover, the critical Reynolds number, which marks the transition from laminar to turbulent flow over a vehicle, varies depending on body shape and flow conditions. While streamlined bodies often experience transition at Re ≈ 5 × 105 to 1 × 106, the complex geometry of cars results in a higher critical Reynolds number, generally in the range of 3 × 106 to 5 × 106, where flow instability and vortex formation significantly alter aerodynamic characteristics29. According to Fig. 4b, the variations in the total drag coefficient of the standard fastback vehicle, as simulated, are plotted in the Reynolds number range from 0.3 to 7 million. As observed, in the range of 3 to 5 million Reynolds numbers, the changes in the total drag coefficient are minimal, and beyond 5 million, it approaches zero. It can be concluded that the critical Reynolds number is around 5 million, after which the flow regime becomes fully turbulent, and aerodynamic parameters can be considered independent of the Reynolds number.
Results
The rear configuration of the Audi A5 is similar to the standard DrivAer Fastback model, offering two key advantages for aerodynamic simulations of the Audi A5. First, the numerical simulation approach for the Audi A5 can be validated using experimental data from the standard fastback model46. Second, due to the similarity in their configurations, valuable aerodynamic insights can be gained about the Audi A547. According to previous studies48, the fastback rear configuration yields a lower pressure differential between the front and rear of the vehicle, resulting in reduced drag. However, since the airflow behind the fastback faces no significant obstacles and experiences minimal flow separation, it generates a smoother airflow over the body, reducing the static pressure in the upper regions of the vehicle and consequently reducing the downforce compared to the notchback and estate model configurations49. Numerically, the drag coefficient and lift coefficient of the vehicle were calculated to be 0.304 and 0.037, respectively, at a Reynolds number of 4.87 × 106. The positive lift coefficient indicates an upward force on the moving vehicle. However, since this force is significantly smaller than the vehicle’s weight, it does not pose a stability issue. For further analysis, as shown in Fig. 6, the pressure coefficient distribution on the upper and lower surfaces of the Audi A5 was plotted after simulation at 4.87 × 106. The results showed that the pressure coefficient on the rear body remained close to zero. However, as the airflow passes beneath the vehicle, it interacts with the underbody components, resulting in a higher pressure coefficient in the lower regions compared to the upper surfaces. This pressure difference generates an upward force that increases at higher speeds and may reduce the vehicle’s stability50. Additionally, in sudden braking conditions, previous studies51 and experimental observations suggest that due to dynamic weight transfer, the front of the vehicle temporarily drops relative to the rear. To improve this condition, the installation of a rear wing or spoiler52 has been proposed as a method to enhance aerodynamic control, which will be examined in this study.
Rear spoiler design and its design parameters
The first step in designing the rear spoiler is selecting the airfoil shape. Initially, three airfoils, NACA 0012, NACA 4412, and S1223, were considered for the spoiler section. After comparing and analyzing them, NACA 4412 was chosen for the rear spoiler design due to its superior aerodynamic performance27,28 compared to NACA 0012 and S1223. The NACA 4412, with its cambered design, generates more downforce at lower angles of attack24, which is crucial for improving tire traction and stability at high speeds in automotive applications. It strikes a balance between lift and drag, offering a good lift-to-drag ratio, while its gradual stall characteristics ensure stability at varying speeds, making it ideal for a spoiler. In contrast, the NACA 0012, a symmetrical airfoil, provides lower lift and more abrupt stall characteristics, making it less suitable for downforce applications. The S1223, while efficient at high Reynolds numbers, is more specialized for aircraft and UAVs, where smooth airflow and low drag are prioritized. Therefore, the NACA 4412 was chosen as the most appropriate airfoil for automotive rear spoilers due to its blend of downforce, stability, and performance at the relevant Reynolds numbers53,54. The next step is to determine the airfoil’s chord length and the total length of the spoiler, which were set to 0.3 m and 1.18 m, respectively. The criterion for selecting a 0.3-m chord length was to ensure a minimum size sufficient to impact the separation zone (i.e., the distance it extends beyond the rear of the body). Additionally, the length of the spoiler was designed such that its projection, when viewed from above, fully covers the trunk without extending beyond the body or risking collisions with external objects during vehicle movement.
After designing the 3D model of the spoiler with roller supports and lift jacks, which allow for the adjustment of the angle and height while the vehicle is in motion, it was necessary to determine the optimal installation location for maximum effect. Referring to the pressure coefficient diagram on the car body, it was observed that the rearmost edge of the trunk lid, where the pressure suddenly drops, is the ideal location for the jack-mounted spoiler supports. In Fig. 7, the configuration of the spoiler and its attachment to the body is visible. After modeling the geometry of the spoiler, three variables were defined for its aerodynamic simulation under different conditions based on its degrees of freedom: (1) Spoiler height (the distance between the airfoil chord and the trunk lid in the central plane of the vehicle): The minimum height was set at 5 cm due to geometric constraints. To illustrate height determination, a view of the spoiler at a height of 150 mm is presented in Fig. 7c. (2) Spoiler angle (the angle between the airfoil chord and the airflow direction): This angle can be adjusted counterclockwise from 0 to 90 degrees, thanks to its roller-supported mechanism. (3) Reynolds number of the surrounding airflow.
Design point determination
In reality, a vehicle’s speed constantly changes while driving, meaning that the height and angle of the spoiler should also continuously adjust. However, a spoiler is not always necessary in all driving conditions because its height and angle adjustments require energy, which in turn increases fuel consumption. Therefore, it is more efficient to determine the optimal spoiler positions only for two critical driving scenarios discussed in the previous sections. These design points include (a) setting the height and angle of the spoiler while driving at high speeds, a common occurrence on highways and open roads, and (b) adjusting the spoiler during sudden braking, where it functions as an air brake. Moreover, since this study is based on experimental data and does not employ optimization algorithms, it is not feasible to analyze airflow across all possible Reynolds numbers. Consequently, the simulation of the vehicle with a spoiler was conducted at three Reynolds numbers: 4.87 × 106, 9.75 × 106, and 14.61 × 106, which correspond to vehicle speeds of 54.45 km/h, 108.90 km/h, and 163.36 km/h, respectively. The variation in speed range ensures coverage of the two design points. It is essential to note that these specific Reynolds numbers were selected because experimental data for the DrivAer Fastback model are available for 4.87 × 106 and 9.75 × 106, while 14.61 was chosen as a multiple of 4.87 to maintain consistency with these conditions. Since various heights and angles need to be examined, and the angle has a more significant effect compared to height, the spoiler was first analyzed at heights ranging from 5 to 15 cm in 2.5 cm increments. As observed in Fig. 8, at all three Reynolds numbers, the lowest total drag coefficient is achieved at a height of 10 cm. Additionally, at this height, the total lift coefficient remains negative and within an acceptable range for all three Reynolds numbers. For these reasons, this height was selected for further investigation of different angles.
In this section, the spoiler angle is examined in the counterclockwise direction at the optimal height of 10 cm, from zero degrees to higher angles that align with the design specifications. Given the continuous range of angle variations, the angles are discretized in increments of 5 and 10 degrees. Based on Fig. 9, the simulation results under identical boundary conditions and three Reynolds numbers are reported at a height of 10 cm with various spoiler angles. The increase in drag for the vehicle with a spoiler, even with a zero-degree angle, compared to the vehicle without a spoiler, can be observed by comparing the velocity distribution Fig. 10a, d, g to the velocity distribution Fig. 10b, e, h. This is because, at all three Reynolds numbers, the wake region’s width has increased, which means a decrease in pressure in this region, leading to an increase in the pressure differential between the front and rear of the vehicle, and consequently, an increase in the drag coefficient.
Flow velocity contours around the Audi car at Reynolds number 4.87 × 106: (a) without spoiler, (b) with spoiler at 10 cm height and 0 degree angle, (c) with spoiler at 10 cm height and 45 degree angle, at Reynolds number 9.75 × 106: (d) without spoiler, (e) with spoiler at 10 cm height and 0 degree angle, (f) with spoiler at 10 cm height and 60 degree angle, at Reynolds number 14.61 × 106: (g) without spoiler, (h) with spoiler at 10 cm height and 0 degree angle, (i) with spoiler at 10 cm height and 55 degree angle, in the plane passing through the center of the vehicle.
Additionally, The results in Fig. 9a show that as the angle of attack increases from zero to higher values, the total drag coefficient follows a completely increasing trend. This is due to the increase in pressure in the front region of the spoiler exposed to airflow at higher angles of attack and the expansion of the wake region and negative pressure behind the spoiler. This phenomenon is clearly visible in the velocity contour diagrams in Fig. 10c, f, i, where the width of the wake region is significantly larger compared to Fig. 10b, e, h, where the spoiler is at zero degrees. In Fig. 9b, the lift coefficient increases up to angles of 45, 60, and 55 degrees for Reynolds numbers 4.87 × 106, 9.75 × 106, and 14.61 × 106, respectively, and then starts to decrease beyond these points. This occurs because, as shown in Fig. 10c, f, i, with the increase in the angle of attack in the counterclockwise direction, the airflow is directed upward due to the spoiler angle instead of flowing directly over the body. According to the principle of momentum conservation, this change in airflow direction exerts a force from the airflow onto the spoiler, which is then transferred to the vehicle body through the spoiler mounts. Beyond these angles, the lift coefficient begins to decline due to the loss of kinetic energy in the incoming airflow to the spoiler region, which is used to overcome pressure drag. For instance, at Reynolds number 14.61 × 106 and an angle of 55 degrees, flow separation increases at the trailing edge of the spoiler, and separation also occurs underneath it. This leads to a decrease in pressure on the vehicle body, reducing the effectiveness of the spoiler in generating negative lift while increasing its contribution to drag.
After determining the total lift and drag coefficients for the three Reynolds numbers at different angles, the optimal angle for the design point under road conditions can be identified as 0 degrees. This is because it produces the lowest drag coefficient across all three Reynolds number cases. Although its negative lift coefficient is the lowest compared to other angles, it remains negative, which is beneficial for the vehicle’s aerodynamic performance. For the second design point, based on the graphs in Fig. 9a, b, the most suitable angles for the emergency braking design point are 45, 60 and 55 degrees for Reynolds numbers 4.87 × 106, 9.75 × 106, and 14.61 × 106, respectively. Despite the high total drag coefficient, which enhances braking efficiency, a greater downforce improves vehicle stability compared to other angles, leading to better overall performance55. Finally, a comprehensive summary of the appropriate spoiler height and angle.
for the two design points is provided in Table 1.
The impact of the spoiler on stability improvement
The rear spoiler of a vehicle plays a crucial role in enhancing vehicle stability, especially at high speeds. By controlling airflow, spoilers can reduce lift force and increase downforce, thereby improving tire grip and overall vehicle performance56. Recent studies in computational fluid dynamics have highlighted the specific effects of rear spoilers. One of the main effects is the increase in downforce, as the rear spoiler creates a high-pressure zone over the trunk, effectively replacing the low-pressure region that typically forms there. This change enhances vehicle stability by improving its road adhesion57. However, spoilers can also increase aerodynamic drag, which may impact fuel consumption and vehicle acceleration. The design and angle of the spoiler significantly influence these effects, as adjustable spoilers allow for an optimal balance between downforce and drag, optimizing vehicle performance according to driving conditions57. In summary, a well-designed rear spoiler can significantly enhance vehicle stability, but the potential increase in drag must also be considered to ensure that its benefits outweigh its drawbacks. To better understand this, a force analysis has been conducted for the vehicle with and without a spoiler. In this analysis, it is assumed that the wheels are in a purely rolling motion, the vehicle mass is 1600 kg58, the mass of the spoiler is negligible, and frictional drag is disregarded. In this scenario, according to Eqs. 9 and 10, the total drag force and total downforce of the vehicle with the spoiler are equal to the sum of the drag and downforce of the vehicle and the spoiler. Thus, using the total lift and drag coefficients obtained in the previous sections, the total drag force (\({D}_{total}\)) and total downforce (\({L}_{total}\)) can be calculated based on these equations and are shown in Fig. 11a, b as functions of the spoiler angle. According to these graphs, the presence of the spoiler in the first design point, where the objective was to improve stability, has performed effectively. For example, in the case of Reynolds number 14.61 × 106, the spoiler has changed the total lift force from -402.38 N in the no-spoiler condition to a total downforce of 51.09 N. In other words, although the spoiler angle relative to the airflow is zero, it has resulted in a 112.7% increase in total downforce. Additionally, the total drag force has increased from 837.79 N to 862.27 N, which amounts to only a 2.92% increase in air resistance. For the second design point, where the goal was rapid braking along with increased stability, it is observed that the total drag force has increased from 837.89 N in the no-spoiler condition to 1600 N at a spoiler angle of 55 degrees, equivalent to a 90.9% increase. Meanwhile, the total downforce has increased from -402.38 N to 1327.87 N, representing a 430% increase. Therefore, given that similar trends hold for other Reynolds numbers, it can be concluded that the presence of the spoiler contributes to greater stability for this Audi vehicle. Finally, it is noteworthy that as the Reynolds number increases, the rate of upward changes in both downforce and drag force with increasing spoiler angle also rises.
The impact of the spoiler on fuel consumption
According to the Fig. 11a, it was observed that the presence of a spoiler and an increase in the rear spoiler angle can nearly double the total drag force, especially at higher speeds. This significantly increases the required engine thrust for movement and leads to higher fuel consumption.In addition to aerodynamic drag, the total rolling resistance force (\({F}_{r})\) of the wheels (both front and rear) exists, which is obtained by multiplying the rolling resistance coefficient (\({C}_{r}\)) by the total vertical force on the surface (\({N}_{tot}\))59. On the other hand, according to Eq. 12, the total vertical force is equal to the sum of the vehicle’s weight and the total downforce. Additionally, based on the Fig. 11b, an increase in total downforce is observed with an increase in the spoiler angle, which also leads to an increase in rolling resistance force. This, in turn, results in a higher required driving force and increased fuel consumption. Consequently, the spoiler at high angles can be considered an aerodynamic brake. Next, assuming the vehicle moves at a constant speed (without braking or clutch engagement by the driver) and neglecting frictional losses and other electrical consumptions, the effects of the two resistance forces on vehicle motion are calculated in the form of the required driving force. For this purpose, the rolling resistance coefficient, which can range between 0.005 and 0.015 for passenger vehicles60, is assumed to be 0.01 in this study. By equating the sum of aerodynamic drag and rolling resistance force with the engine thrust force (\({F}_{engine}\)) along the x-axis, the total thrust required for vehicle motion can be estimated.
Equation 13, in the absence of a spoiler, are written as follows:
After estimating the total force required for motion, the total energy needed, which equals the total work done by the engine and is obtained by multiplying the total engine force by the vehicle’s displacement61, was calculated according to Eq. 15 Since the efficiency of the engines in this Audi model is reported to be between 28 and 32%58, an efficiency of 30% was assumed. With the total required energy, engine efficiency, and the assumption that the energy content of gasoline is 33 MJ per liter62, the fuel volume required for different displacements of the vehicle can be estimated using Eq. 16. In Fig. 12a, b, the variations in the total required engine force and the percentage change in fuel consumption compared to the no-spoiler case at different spoiler angles are presented.
As shown in Fig. 12a, an increase in the Reynolds number leads to an exponential rise in the required engine thrust. This indicates that the rear spoiler, by adjusting its angle in higher Reynolds number flows, performs more effectively in terms of enhancing stability and reducing speed more rapidly. Figure 12b illustrates the fuel consumption implications of using a spoiler. While the spoiler demonstrates optimal performance in achieving the design objectives at higher Reynolds numbers, it also demands higher fuel consumption. For instance, in the design point under road conditions at a Reynolds number of 14.61 × 106, the presence of a spoiler results in a 2.92% increase in fuel consumption, whereas in the same design point at a Reynolds number of 4.87 × 106, the fuel consumption increase is only 0.95%.
Conclusions
The results of this study demonstrate that an adjustable rear spoiler significantly enhances the aerodynamic performance of a fastback vehicle under various driving conditions. Simulations of the Audi A5 revealed that a 10 cm spoiler height and a 0° angle produced the lowest drag under normal driving conditions, thereby increasing aerodynamic efficiency while maintaining stability. In contrast, during sudden braking, increasing the spoiler angle to 45°–60° significantly improved downforce, reducing braking distance and enhancing vehicle control. Specifically, at a Reynolds number of 14.61 × 106, a 55° spoiler angle resulted in a 430% increase in downforce and a 90.9% increase in drag, demonstrating the spoiler’s effectiveness in enhancing braking performance. The comparison between a vehicle without a spoiler and one with an optimized spoiler revealed that, in the absence of a spoiler, positive lift forces can compromise stability at high speeds. However, with the optimized spoiler settings, lift forces were reduced or even reversed, improving road grip and handling. Nevertheless, increasing the spoiler angle also increases aerodynamic drag, which may affect fuel consumption and should be considered in urban vehicle designs. To further enhance accuracy and aerodynamic performance, future research should investigate the impact of yaw angle adjustments on spoiler performance, particularly in crosswind conditions and on winding roads. Additionally, optimization algorithms, such as genetic algorithms and neural networks, could be implemented to refine spoiler positioning under different driving scenarios. The integration of active aerodynamic control systems would enable real-time adjustments to spoilers based on vehicle speed, road conditions, and braking maneuvers. Moreover, wind tunnel testing and real-world experiments are recommended to validate CFD simulations and enhance the accuracy of numerical models. The use of lightweight materials, such as carbon fiber composites, should also be explored to optimize spoiler performance without adding excess weight. Overall, the development of intelligent aerodynamic control systems and adaptive spoiler technologies can contribute to the advancement of next-generation, high-performance, fuel-efficient, and stable vehicles.
Data availability
The datasets used and/or analysed during the current study available from the corresponding author on reasonable request.
References
Passaggia, P. Y., Mazellier, N. & Kourta, A. Aerodynamic drag modification induced by free-stream turbulence effects on a simplified road vehicle. Phys. Fluids 33, 1010 (2021).
Sudin, M. N., Abdullah, M. A., Shamsuddin, S. A., Ramli, F. R. & Tahir, M. M. Review of research on vehicles aerodynamic drag reduction methods. Int. J. Mech. Mechatron. Eng. 14, 37–47 (2014).
Joshi, S. N. & Gujarathi, Y. S. A review on active and passive flow control techniques. Int. J. Rec. Technol. Mech. Electr. Eng. 3, 1–6 (2016).
Martinelli, L. & Jameson, A. Computational aerodynamics: solvers and shape optimization. J. Heat Transf. 135, 011002 (2013).
Skinner, S. N. & Zare-Behtash, H. State-of-the-art in aerodynamic shape optimization methods. Appl. Soft Comput. 62, 933–962 (2018).
Othmer, C. Adjoint methods for car aerodynamics. J. Math. Ind. 4, 6 (2014).
Gunadi, G. et al. On the options for bus aerodynamic profile optimization. AIP Conf. Proc. 2671, 1 (2023).
Altaf, A., Omar, A. A. & Asrar, W. Passive drag reduction of square back road vehicles. J. Wind Eng. Ind. Aerodyn. 134, 30–43 (2014).
Putra, R. P., Yuvenda, D., Setiyo, M., Andrizal, A. & Martias, M. Body city car design of two passengers capacity: a numerical simulation study. Automot. Exp. 5, 163–172 (2022).
Szudarek, M., Piechna, A. & Piechna, J. Feasibility study of a fan-driven device generating downforce for road cars. Energies 15, 5549 (2022).
Arifin, Z. et al. Aerodynamic characteristics of Ahmed body with inverted airfoil Eppler 423 and Gurney flap on fastback car. Automot. Exp. 5, 355–370 (2022).
Baker, C. et al. Crosswind effects on road and rail vehicles. Veh. Syst. Dyn. 47, 983–1022 (2009).
Yudianto, A., Setiawan, W., Julianto, F. & Aminudin, U. Aerodynamic study of vehicles in formation under crosswind. AIP Conf. Proc. 2671, 1 (2023).
Yudianto, A., Adiyasa, I. W. & Yudantoko, A. Aerodynamics of bus platooning under crosswind. Automot. Exp. 4, 119–130 (2021).
Cheng, S. Y., Chin, K. Y. & Mansor, S. Experimental study of yaw angle effect on the aerodynamic characteristics of a road vehicle fitted with a rear spoiler. J. Wind Eng. Ind. Aerodyn. 184, 305–312 (2019).
Beaudoin, J. F. & Aider, J. L. Drag and lift reduction of a 3D bluff body using flaps. Exp. Fluids 44, 491–501 (2008).
Aider, J. L., Beaudoin, J. F. & Wesfreid, J. E. Drag and lift reduction of a 3D bluff-body using active vortex generators. Exp. Fluids 48, 771–789 (2010).
Pujals, G., Depardon, S. & Cossu, C. Drag reduction of a 3D bluff body using coherent streamwise streaks. Exp. Fluids 49, 1085–1094 (2010).
Thacker, A., Aubrun, S., Leroy, A. & Devinant, P. Effects of suppressing the 3D separation on the rear slant on the flow structures around an Ahmed body. J. Wind Eng. Ind. Aerodyn. 107, 237–243 (2012).
Howell, J., Sheppard, A. & Blakemore, A. Aerodynamic drag reduction for a simple bluff body using base bleed. SAE Trans. 1085–1091 (2003).
Yi, W., SaGong, W. & Choi, H. C. Drag reduction of a three-dimensional car model using passive control device. Proc. KSME Conf. 2868–2872 (2007).
Yudianto, A. Application of multi-objective adjoint-based aerodynamic optimisation on generic road vehicle with rear spoiler. Automot. Exp. 7, 28–47 (2024).
Rijns, S., Teschner, T. R., Blackburn, K. & Brighton, J. Effects of cornering conditions on the aerodynamic characteristics of a high-performance vehicle and its rear wing. Phys. Fluids 36, 1010 (2024).
Roslan, M. H. et al. Effect of a spoiler on the aerodynamic performance of a race car on track using two different turbulence models. J. Des. Sustain. Environ. 5, 28–37 (2023).
Pritchard, P. J. & Mitchell, J. W. Fox and McDonald’s Introduction to Fluid Mechanics (Wiley, 2016).
Ayyagari, D. T. & He, Y. Aerodynamic analysis of an active rear split spoiler for improving lateral stability of high-speed vehicles. Int. J. Veh. Syst. Model. Test. 12, 217–239 (2017).
Sakib, M. H. & Mahmud, M. S. CFD analysis of car using NACA 4412 spoiler. Int. Conf. Mech. Ind. Energy Eng. (2022).
Eftekhari, H., Al-Obaidi, A. S. & Eftekhari, S. The effect of spoiler shape and setting angle on racing cars aerodynamic performance. Indones. J. Sci. Technol. 5, 11–20 (2020).
Nepali, R. et al. Computational analysis of rear spoilers: effects on vehicle stability and drag. J. Automot. Aerodyn. 12, 45–58 (2023).
Sharma, P. et al. Optimization of airfoil-based spoilers for race cars using CFD. Int. J. Race Car Eng. 18, 112–129 (2022).
Gupta, A. et al. Smart adaptive spoilers: a CFD study on dynamic aerodynamics. Adv. Veh. Technol. 9, 78–91 (2021).
Das, S. et al. Machine learning-assisted CFD optimization of Volkswagen Vento rear spoilers. J. Comput. Fluid Dyn. Appl. 15, 203–217 (2023).
Kumar, V. et al. Aerodynamic effects of rear spoilers on commercial vehicles. Transp. Eng. J. 7, 34–47 (2022).
Varney, M., Passmore, M., Wittmeier, F. & Kuthada, T. Experimental data for the validation of numerical methods: DrivAer model. Appl. Sci. 10, 8732 (2020).
Heft, A. I., Indinger, T. & Adams, N. A. Experimental and numerical investigation of the DrivAer model. Fluids Eng. Div. Summer Meet. 44755, 41–51 (2012).
Heft, A.I., Indinger, T. & Adams, N. A. Introduction of a new realistic generic car model for aerodynamic investigations. SAE Tech. Pap. 2012, 2012-01-0168 (2012).
Dehghani, M. & Shabihsazi, A. NarmAfzar Fluent 6.3 4th edn. (Naqos Publications, 2015).
Menter, F. Zonal two equation k-w turbulence models for aerodynamic flows. In 23rd Fluid Dyn. Plasmadyn. Lasers Conf. 2906 (1993).
Menter, F. R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 32, 1598–1605 (1994).
Technical University of Munich. DrivAer Model Download. Available at: https://www.epc.ed.tum.de/en/aer/research-groups/automotive/drivaer/download/. Accessed 26 March 2025.
Aultman, M. & Duan, L. Flow topology of the bi-stable wake states for the DrivAer fastback model. Flow Turbul. Combust. 1, 1–31 (2024).
Qin, P., Ricci, A. & Blocken, B. CFD simulation of aerodynamic forces on the DrivAer car model: Impact of computational parameters. J. Wind Eng. Ind. Aerodyn. 248, 105711 (2024).
Yu, X., Jia, Q. & Yang, Z. Comprehensive study of the aerodynamic influence of ground and wheel states on the notchback DrivAer. Energies 15, 1124 (2022).
Baek, S. W. & Lee, S. W. Aerodynamic drag reduction on a realistic vehicle using continuous blowing. Microsyst. Technol. 1, 11–23 (2020).
Roohi, E. Dynamics of Gases (Ferdowsi Mashhad University Publications, 2018).
Heft, A. I., Pfitzner, L. & Schäfer, A. Experimental validation of a DrivAer fastback model for aerodynamic simulations. SAE Int. J. Passeng. Cars Mech. Syst. 8, 52–60 (2015).
Rossitto, S. et al. Aerodynamic performance of a fastback vehicle: Insights and comparisons. Proc. Inst. Mech. Eng. D J. Automob. Eng. 230, 1440–1455 (2016).
Zhang, W. et al. Aerodynamic effects of rear-end configurations in passenger vehicles. J. Wind Eng. Ind. Aerodyn. 146, 15–28 (2015).
Elrefaie, M. et al. Aerodynamic analysis of car body configurations at high Reynolds numbers. J. Fluid Mech. 904, 143–160 (2024).
Zhang, W., et al. Numerical and experimental investigation of fastback vehicle aerodynamics. Res. Gate (2015).
Zhang, W. et al. Dynamic weight transfer effects in vehicle braking. Automot. Eng. 40, 112–124 (2021).
Li, C., et al. Enhancement of aerodynamic stability in fastback vehicles with rear wing installations. Springer Link (2022). https://doi.org/10.1007/s12239-022-0110-2.
Geppert, E. & Miele, A. Aerodynamic design of rear spoilers for passenger vehicles. J. Veh. Eng. 45, 153–162 (2015).
Anderson, J. D. Introduction to Flight 8th edn. (McGraw-Hill Education, 2017).
Hucho, W. H. Aerodynamics of Road Vehicles: From Fluid Mechanics to Vehicle Engineering (Elsevier, 2013).
Hamut, H. S. et al. Effects of rear spoilers on ground vehicle aerodynamic drag. Int. J. Numer. Methods Heat Fluid Flow 24, 627–642 (2014).
Maji, D. S. & Mustaffa, N. CFD analysis of rear-spoilers effectiveness on sedan vehicle in compliance with Malaysia national speed limit. J. Automot. Powertrain Transp. Technol. 2, 26–36 (2022).
Audi A5. Wikipedia. https://en.wikipedia.org/wiki/Audi_A5. Accessed 19 March 2025.
Pacejka, H. B. Tire and Vehicle Dynamics (Elsevier, 2006).
Oppenheim, Y. H. & Chao, M. S. P. The Mechanics of Vehicle Tires (Wiley, 2010).
Merriam, J. L. Dynamics 6th edn. (Wiley, 2011).
Turns, S. R. & Pauley, L. L. Thermodynamics: Concepts and Applications (Cambridge University Press, 2020).
Author information
Authors and Affiliations
Contributions
M.K.: Writing—original draft, Visualization, Validation, Software, Methodology, Investigation. E.R.: Writing—review & editing, Supervision, Project administration, Funding acquisition, Conceptualization. M.P.: Writing—review & editing, Supervision, Project administration, Funding acquisition, Conceptualization.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Kheirkhah, M., Roohi, E. & Pasandidehfard, M. Improving the aerodynamics of a fastback car body using a spoiler. Sci Rep 15, 17756 (2025). https://doi.org/10.1038/s41598-025-02080-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-025-02080-1