Investigation of heat transfer performance in heat exchangers using hybrid nanofluids and twisted tape inserts with fixed special rings

Abstract

This study examines the thermo-hydraulic performance of a heat exchanger tube equipped with special fixed ring inserts and twisted tape elements, using a hybrid nanofluid composed of Al₂O₃-CuO/water. Simulations are carried out under turbulent flow conditions, covering Reynolds numbers from 6000 to 14,000. The impact of varying twisted tape torsion ratios (TR = 5, 10, and 15) and hybrid nanofluid volume concentrations (ϕ = 0.3%, 0.6%, and 0.9%) is systematically evaluated. A validated CFD model in ANSYS Fluent demonstrates strong agreement with benchmark data. The results show that, at Re = 14,000, inserting a twisted tape (TR = 5) into a plain tube boosts the Nusselt number (Nu) by 36.28% and the convective heat-transfer coefficient (h) by 36.3% compared to pure water. The tape promotes turbulence and disrupts the thermal boundary layer, enhancing convective heat transfer. However, these gains incur an 8.0% pressure-drop penalty (ΔP). Furthermore, the study highlights the critical role of nanofluid concentration in optimizing heat-exchanger performance. At a 0.9% volume fraction of Al₂O₃–CuO/water nanofluid added to the twisted-tape (TR = 5) configuration, the Nusselt number climbs an additional 3.2%, while the convective heat‐transfer coefficient rises by 18.2%. This nanofluid boost comes with a modest 6.1% pressure-drop penalty (ΔP increases from 284.8 to 302.2 Pa) yet drives the thermal performance factor (TPF) from 1.38 to 3.29. These findings provide a comprehensive understanding of how synergistic passive heat transfer methods and nanofluids can be strategically utilized to enhance the efficiency of industrial heat exchangers.

Introduction

Due to the increasing thermal load and the improvement in science and technology, the traditional design of heat exchangers and working fluids can no longer meet the demand in the very limited heat exchanging area; therefore, it is urgent to develop new technology to enhance heat transfer^1,2. Among these methods, the improvement of thermal conductivity of the working fluid is one of the most important, and nanofluids as an innovative, highly efficient energy transport medium have huge potential in applications for many fields. Passive or active techniques can enhance heat exchanger efficiency^3,4. Some common passive techniques are wire coil inserts^5,6, conical rings^7,8, helical screw tapes⁹, louvered strips¹⁰, vortex generators^11,12, gear ring turbulators¹³, and twisted tape inserts^14,15. Twisted tapes can generate turbulence or swirl flows, especially in the near-wall regions. Furthermore, better heat exchanger performance can be achieved for nanofluids as working fluids. Nanofluids used in conjunction with twisted tape inserts give higher heat transfer enhancement. Recently, passive techniques to enhance heat transfer rates have attracted much attention, among which turbulators of different geometries are widely used to enhance heat transfer. Besides, much research has been performed on nanofluid applications in recent decades^16,17. Hamza et al.¹⁸ and Razzaq et al.¹⁹ demonstrated that combining twisted tape inserts with Al₂O₃-CuO/water nanofluids can significantly enhance heat transfer, achieving a Nusselt number increase of over 45% and thermal performance factors approaching 1.7. These findings confirm the superior convective efficiency of hybrid nanofluids, particularly at moderate nanoparticle concentrations (1.8%) and optimized twist ratios (around 9.25). Qi et al.²⁰ examined TiO₂-H₂O nanofluids in a circular tube with spinning and static twisted tapes. Spinning tapes enhanced heat transfer by 101.6% at Re = 4500, with a performance index of 1.519, but reduced exergy efficiency. Hamza and Aljabair²¹studied Al₂O₃-CuO/water nanofluids in a copper heat exchanger with twisted tapes. At 1.8% concentration and a twist ratio of 9.25, the double V-cut tape increased the Nusselt number by 47.17%, achieving a thermal performance factor of 1.69. Tahmasebi et al.²² analyzed twisted tape effects on thermo-hydraulic performance in a parabolic solar collector (PSC) with magnetic nanofluids. At Re = 6000–24,000, hybrid magnetic nanofluids improved PEC by 27%, surpassing mono nanofluids (22%). Hamali et al.²³ combined swirl flow devices, four-way twisted tapes, and helical tapes to enhance mixing and reduce exergy loss. MWCNT + Fe₃O₄ nanofluids improved thermal properties, with exergy drop reduced by 88.43% and 32.6% due to higher inlet velocity and revolution number. Ghalambaz et al.²⁴ investigated twisted tape configurations under both turbulent and laminar flows, highlighting how truncation, overlap, and swirl direction affect PEC values ranging from 1.08 to 1.76, with optimal designs achieving up to 151% improvement in Nu. Kumar et al.²⁵ assessed hybrid nanofluids (Al₂O₃-CuO, 70:30) in heat exchangers with twisted tapes at twist ratios of 4 and 3. At 3% concentration, the Nusselt number increased by 370%, while the friction factor rose by 294%, with a 3.52-fold increase in thermal performance at a twist ratio of 3. Patel et al.²⁶ analyzed graphene nanoplatelet (GNP)/water nanofluids in tubes with twisted tapes. The anticlockwise-clockwise twisted tape (ACCT) improved the heat transfer coefficient by 67.8%, with peak performance factors of 2.03, 1.93, and 1.84 for GNP concentrations of 0.1%, 0.075%, and 0.05% at Re = 26,600. Khafaji et al.²⁷ experimentally evaluated a tubular heat exchanger with basket turbulators and basket-twisted tape inserts under turbulent flow (Re = 6000–19,500). The Nusselt number improved by 131.8–206.5%, with the highest efficiency 1.63 times that of a plain heat exchanger at y/w = 2.

Despite extensive research on twisted tape inserts and nanofluids, most studies have considered either conventional nanofluids or single-component flow modifiers in isolation. Studies focusing on hybrid nanofluids, especially those involving Al₂O₃–CuO/water mixtures, remain relatively limited, and even fewer investigations have combined such fluids with internal fixed ring structures. The role of fixed rings in enhancing turbulence and disrupting boundary layers remains underexplored, particularly when used alongside advanced nanofluids. Therefore, this study addresses a clear gap in the literature by evaluating the combined effects of hybrid nanofluids, twisted tape inserts, and fixed rings under varying Reynolds numbers.

Methodology

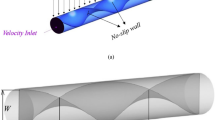
This study examines a heat exchanger’s hydraulic and thermal performance equipped with twisted tape inserts and a hybrid nanofluid as the working medium. The simulations were carried out using ANSYS Fluent 2023 R2. The pressure-based solver with steady-state conditions was employed. The flow was assumed to be turbulent, and the k-ε realizable turbulence model was selected due to its reliability for internal flows with swirl and curvature effects, such as those caused by twisted tapes and fixed rings. The standard wall function was applied for near-wall treatment.

The velocity inlet boundary condition was imposed at the inlet, with specified mean velocities corresponding to Reynolds numbers of 6000 and 14,000. The pressure outlet boundary condition was applied at the outlet. A uniform heat flux was applied to the tube wall, and the remaining walls were treated as no-slip and adiabatic.

Second-order upwind schemes were used for discretizing momentum and energy equations, while the SIMPLE algorithm was adopted for pressure–velocity coupling. Convergence was considered achieved when residuals dropped below $\:1\:\times\:\:{10}^{-6}$ for energy and $\:1\:\times\:\:{10}^{-3}$ for continuity and momentum equations. Grid independence was validated through a mesh refinement study.

Figure 1 presents the geometric configuration of a novel special ring insert intended for internal placement within heat exchanger tubes to augment thermal performance. The design strategically balances flow disruption and pressure drop management to enhance convective heat transfer. The use of such an insert structure results in significant improvement in heat exchanger performance, making it suitable for applications demanding high thermal efficiency without major modifications to the base system. The insert consists of the following key geometric features:

• The ring has a full circular profile with a central axial opening of the same diameter to ensure unobstructed core fluid flow, maintaining continuity in bulk flow momentum and minimizing excessive pressure loss.

• A series of evenly spaced radially oriented slots extends from the inner boundary toward the outer edge. These slots are critical in inducing flow separation and reattachment, which promote turbulent eddies and secondary swirl motions, significantly enhancing convective heat transfer by disrupting the thermal boundary layer near the tube wall.

• Strategically positioned elliptical holes (12 × 6 mm and 6 × 4 mm) are placed between the radial slots. These serve to further disturb the boundary layer by introducing localized velocity gradients and micro-scale vortices, leading to improved mixing and uniform temperature distribution across the flow cross-section.

• Successive inserts are arranged along the tube’s axis with a defined axial pitch (5D), allowing sufficient development of flow structures between each insert. This spacing is optimized to ensure sustained turbulence without inducing excessive pressure penalties.

Overall, this insert geometry is purposefully engineered to increase fluid turbulence near the tube walls, disrupt and thin the thermal boundary layer, induce secondary and swirling flows, and enhance thermal homogeneity, thereby improving overall heat transfer efficiency.

Fig. 1

Geometric structure of the special ring inserts for heat exchanger enhancement.

Figure 2 illustrates an internal configuration of a heat exchanger tube equipped with twisted tape inserts and specially shaped rings. This hybrid enhancement approach is designed to significantly improve thermal performance through disruption of boundary layers, flow swirling, and increased turbulence intensity. The twisted tape is a passive insert technique that forces the fluid to follow a helical path along the tube wall. This swirling motion increases the flow contact with the wall, enhancing heat transfer by promoting stronger fluid mixing across the cross-section, delaying thermal boundary layer development, and increasing the effective heat transfer surface area. The rings serve as periodic flow obstructions, placed at specific pitch intervals along the tube. These specially designed rings generate localized turbulence and recirculation zones, which break thermal boundary layers periodically, interrupt laminar sublayers that may form between the twisted tape and wall, and enhance axial mixing, leading to higher Nusselt numbers. The distance between consecutive rings (pitch) is a critical geometric parameter. Shorter pitches increase the frequency of disturbance, leading to higher heat transfer but also increased pressure drop. Larger pitches offer a balance between performance and hydraulic efficiency. The interaction of swirling flow induced by the twisted tape with the flow separations induced by the rings results in a synergistic enhancement mechanism. The tube wall acts as the main heat transfer interface, and this configuration ensures more uniform wall temperature and higher local convective heat transfer coefficients.

Fig. 2

Schematic of a heat exchanger tube with twisted tape and specially shaped ring inserts.

The twist ratio, defined as the length of tape required to complete a 180-degree twist divided by the Width of the twisted strip, is a key parameter in the study. The twisted tape was modeled and implemented in numerical simulations with three different twist ratios: 5, 10, and 15. Figures 3 illustrate the twisted tape configurations used in the study, showing three distinct twist ratios: 5, 10, and 15. The lower twist ratio means the twists are closer, implying increased turbulence to enhance heat transfer by promoting fluid flow mixing. However, tighter twists also result in a higher pressure drop due to increased flow resistance. The three configurations were systematically studied to evaluate the trade-off between enhanced heat transfer and increased pressure loss.

Fig. 3

Twisted tape configurations with different twist ratios (5, 10, 15).

Figure 4 shows the microscopic morphology of the Al₂O₃ and CuO nanoparticles used in the hybrid nanofluid. The nanoparticles were dispersed in water to create a stable hybrid nanofluid, which was utilized to enhance the thermal properties of the fluid flowing inside the pipe. The figure highlights the nanoparticles’ uniform distribution and size characteristics, which contribute to the hybrid nanofluid’s improved heat transfer efficiency and thermal conductivity.

Fig. 4

Structure of nanoparticles (Al₂O₃ and CuO) used in the hybrid nanofluid.

In the first phase of the study, water was used as the test fluid to evaluate the baseline performance of the heat exchanger under turbulent flow conditions, with the Re varying from 6000 to 14,000. A constant heat flux was applied to the pipe’s external surface, ensuring a steady thermal boundary condition for all cases. The fluid velocity and twist ratio were systematically varied during the simulations to consider their influence on convective heat transfer and flow resistance. Once the numerical simulations stabilized, key thermal and hydraulic parameters were extracted for analysis, including pressure drop, Nu number, and convective heat transfer coefficient.

In the second phase, the study was extended to examine the effects of replacing water with a hybrid nanofluid consisting of Al₂O₃ and CuO nanoparticles suspended in water, as illustrated in Fig. 4. Table 1 presents the base fluid (water) thermophysical properties and the Al₂O₃ nanoparticle and CuO nanoparticles. These properties involve specific heat capacity, thermal conductivity, and density, which are critical parameters influencing the heat transfer performance of the hybrid nanofluid. This hybrid nanofluid was chosen because of its superior thermal conductivity and lower cost when compared to other sophisticated nanofluids.

Table 1 Thermophysical properties of water (base fluid), copper oxide (CuO), and aluminum oxide (Al₂O₃)^28,29.

While the present study provides valuable insights into heat exchangers’ thermal and hydraulic behavior using hybrid nanofluids with twisted tape inserts and fixed rings, several limitations must be acknowledged. First, the results are based entirely on CFD simulations and assume ideal boundary conditions (e.g., steady flow, uniform heat flux). Second, using a single nanofluid mixture and fixed geometric configurations restricts generalizability. Additionally, the thermophysical properties of the nanofluids were considered constant, and they may not hold under varying temperature and flow conditions.

Mathematical modeling

Governing equations

The mathematical formulation governing fluid dynamics and heat transfer in the system represents steady three-dimensional incompressible flow with turbulence. The RNG k-ε turbulence model with increased wall treatment is used to reasonably simulate the characteristics of heat exchanger tubes with twisted tape (TT) inserts. It can accurately record turbulence events, particularly in the near-wall area with significant velocity gradients. The governing equations, which include the continuity equation, momentum equation, and energy equation, are defined as follows^30,31:

$$\:\frac{\partial\:}{\partial\:{x}_{i}}\left(\rho\:{u}_{i}\right)=0$$

(1)

$$\:\frac{\partial\:}{\partial\:{x}_{j}}\left({u}_{j}\rho\:{u}_{i}\right)=-\frac{\partial\:p}{\partial\:x}+\frac{\partial\:}{\partial\:{x}_{j}}\left\{\mu\:\left[\frac{\partial\:{u}_{i}}{\partial\:{x}_{j}}-\overline{\rho\:{u}_{i}^{{\prime\:}}{u}_{j}^{{\prime\:}}}\right]\right\}$$

(2)

$$\:\frac{\partial\:}{\partial\:{x}_{j}}\left(\rho\:{u}_{i}T\right)=\frac{\partial\:}{\partial\:{x}_{i}}\left\{\left[\frac{\mu\:}{Pr}+\frac{{\mu\:}_{t}}{P{r}_{t}}\right]\frac{\partial\:{T}^{{\prime\:}}}{\partial\:{x}_{i}}\right\}$$

(3)

Where ρ is fluid density, u is the fluid velocity; $\:{\mu\:}_{t}\:$is the turbulent viscosity.

Parameter definition

The non-dimensional parameters utilized in this analysis, including Reynolds number (Re), Prandtl number (Pr), Nusselt number (Nu), friction factor (f), and thermal performance factor (TPF), are determined using the following expressions:

$$\:\text{R}\text{e}=\frac{{\uprho\:}\text{u}D}{\mu\:}$$

(4)

​

$$\:\text{P}\text{r}=\frac{\mu\:{c}_{p}}{k}$$

(5)

​

$$\:\text{N}\text{u}=\frac{hD}{k}$$

(6)

​

$$\:f=\frac{\varDelta\:P}{\left(\frac{L}{D}\right)\left(\frac{\rho\:{u}^{2}}{2}\right)}$$

(7)

$$\:TPF=\frac{\text{N}\text{u}/{\text{N}\text{u}}_{s}}{{\left(f/{f}_{s}\right)}^{\frac{1}{3}}}$$

(8)

In these equations, $\:{\text{N}\text{u}}_{s}$ and $\:{f}_{s}$ refer to the Nu number and friction factor, respectively, for a smooth tube, while TPF represents the thermal performance factor of the system.

Thermal specifications of hybrid nanofluids

The following equations describe the fundamental thermophysical characteristics of hybrid nanofluids, including thermal conductivity, density, heat capacitance, and dynamic viscosity^28,32.

Volume fraction of nanoparticles in the nanofluid:

$$\:{{\varnothing}}_{hnf\text{}}={{\varnothing}}_{np\text{}1}+{{\varnothing}}_{np\text{2}}$$

(9)

Density of hybrid nanofluid:

$$\:{\rho\:}_{hnf}={\rho\:}_{np1}{{\Phi\:}}_{np1}+{\rho\:}_{np2}{{\Phi\:}}_{np2}+\left(1-{{\Phi\:}}_{hnf}\right){\rho\:}_{bf}$$

(10)

Specific heat of hybrid nanofluid:

$$\:C{p}_{hnf}=\frac{{{\Phi\:}}_{np1}{\rho\:}_{np1}C{p}_{np1}+{{\Phi\:}}_{np2}{\rho\:}_{np2}C{p}_{np2}+{\left(1-{{\Phi\:}}_{hnf}\right)}_{\rho\:bf}C{p}_{bf}}{{\rho\:}_{hnf}}$$

(11)

Thermal conductivity of hybrid nanofluid.

$$\:{K}_{hnf}={K}_{bf}\frac{\left.\left(\frac{\left.{{\varnothing}}_{np1}{k}_{np1}+{{\varnothing}}_{np2}{k}_{np2}\right)}{{{\varnothing}}_{total}}\right)+2{k}_{bf}+2\left({{\varnothing}}_{np1}{k}_{np1}+{{\varnothing}}_{np2}{k}_{np2}\right)-2{{\varnothing}}_{total}{k}_{bf}\right)}{\left.\left(\frac{{{\varnothing}}_{np1}{k}_{np1}+{{\varnothing}}_{np2}{k}_{np2}}{{{\varnothing}}_{total}}\right)+2{k}_{bf}-\left({{\varnothing}}_{np1}{k}_{np1}+{{\varnothing}}_{np2}{k}_{np2}\right)+{{\varnothing}}_{total}{k}_{bf}\right)}$$

(12)

​Viscosity of hybrid nanofluid:

$$\:{\mu\:}_{hnf}=\frac{{\mu\:}_{bf}}{{\left(1-{{\varnothing}}_{np1}-{{\varnothing}}_{np2}\right)}^{2.5}}$$

(13)

The parameters used in this study define the thermophysical properties of hybrid nanofluids and their constituent nanoparticles. The volume fraction of the hybrid nanofluid is denoted as $\:{{\Phi\:}}_{hnf}$, while $\:{{\Phi\:}}_{np1}$ and $\:{{\Phi\:}}_{np2}$represent the volume fractions of the first and second nanoparticles, respectively. The density of the hybrid nanofluid is denoted as $\:{\rho\:}_{hnf}$(kg/m³), whereas $\:{\rho\:}_{hnf}$, while $\:{\rho\:}_{np1}$ (kg/m³) indicate the densities of nanoparticles 1 and 2. The specific heat capacity of the hybrid nanofluid is expressed as $\:C{p}_{hnf}\:$(J/kg·K), while $\:C{p}_{np1}$and $\:C{p}_{np2}$(J/kg·K) correspond to the specific heat capacities of nanoparticles 1 and 2, respectively.

The thermal conductivity of the hybrid nanofluid is given as $\:{K}_{hnf}$(W/m·K), with $\:{k}_{np2}$ and $\:{k}_{np2}$ (W/m·K) representing the thermal conductivities of nanoparticles 1 and 2. Additionally, the viscosity of the hybrid nanofluid is denoted as $\:{\mu\:}_{hnf}$(Pa·s). The thermophysical properties of CuO and Al₂O₃ nanoparticles, along with their corresponding hybrid nanofluids, are provided in Table 2.

Table 2 Thermal properties of the hybrid nanofluid²⁸.

Numerical analysis

A Grid Independence Test (GIT) was performed to ensure the reliability and accuracy of the numerical simulations. This test checks if the results obtained from the numerical analysis are stable and independent of the mesh resolution, ensuring that the computational model adequately represents the physical problem. The numerical simulations were performed using ANSYS Fluent 2023 R2, where the computational domain was discretized into a structured mesh system. Node distribution, arrangement, and composition in the grid configuration are of great importance in terms of solution accuracy and stability. Quality and efficiency in the mesh were improved by refining different mesh parameters, such as grid smoothing, element size, and nodal distribution. Since mesh resolution directly affects simulation accuracy, an iterative approach was employed whereby the mesh was further refined until further refinement did not influence the simulation results. Nu was adopted as the main convergence parameter, and its values were compared with the experimental temperature measurements at the outlet of the heat exchange tube. The numerical values attained a stable value at the optimum mesh configuration and did not vary appreciably on further mesh refinement. Figure 5 represents the meshing process, where the computational domain is discretized. Figure 6 shows the Nusselt number (Nu) plotted against the number of mesh elements. A noticeable drop in Nu occurs as the mesh is refined up to 1,000,000 elements. Beyond this point, further refinements result in minimal variation (< 0.5%), indicating that the solution has reached grid independence. Based on this, a mesh size of ~ 1 million elements were adopted in all subsequent.

Fig. 5

Mesh generation and grid structure of the heat exchanger with twisted tape inserts and ring elements.

Fig. 6

Grid independence test results.

Figure 7 illustrates a numerical simulation of heat transfer analysis and boundary layer distribution inside a pipe containing a twisted spiral ribbon using ANSYS 2023 R1. The analysis shows the temperature distribution and heat diffusion inside the fluid as it flows through the pipe. The design was conducted with an inlet fluid temperature of 25 °C, a Reynolds number of 6000 (indicating turbulent flow), a nanoparticle concentration of 0.9 (volume ratio), and a spiral ribbon twist ratio of 5, influencing the twisting effect inside the pipe. The key thermal results indicate that the fluid temperature at the pipe outlet reached 5.4 °C, with a distinct heat distribution pattern inside the tube. A temperature rise characterizes the inner surface, while the edges remain less hot due to gradual heat transfer. The presence of the spiral ribbon enhances turbulence inside the fluid, which leads to improved heat transfer and increased heat exchange efficiency. This leads to a more homogeneous heat distribution across the tube section, as shown in the red areas in the figure. Nanoparticles improve the fluid’s thermal conductivity, which increases heat transfer efficiency compared to conventional fluids.

Fig. 7

Heat transfer analysis and boundary layer distribution inside a pipe.

Figure 8 shows a numerical representation of the velocity distribution and interaction of fluid layers inside a tube containing internal discs and a spiral ribbon. The simulation shows how the fluid boundary layers are formed and how geometric modifications such as perforated discs and a spiral ribbon affect the flow dynamics and heat transfer. The tube operates under fully turbulent flow (Reynolds number 14,000) with an inner disc-to-tube diameter ratio of 0.7, 250 mm spacing between inner discs, a spiral ribbon twist ratio of 5, and perforated inner discs to enhance fluid flow and minimize pressure loss. The flow becomes fully turbulent at a Reynolds number of 14,000, resulting in enhanced heat transfer due to increased boundary layer mixing. This higher-pressure drop may necessitate optimized disc design and the formation of complex vortices and flow structures within the tube. The analysis demonstrates that incorporating internal discs and a spiral tape enhances heat transfer efficiency by intensifying turbulence and minimizing the thermal boundary layer effect. In contrast, perforated inner discs help regulate flow and reduce pressure loss, improving overall thermal system performance. Figure 8a shows the initial shape of the fluid layers upon entering the tube, where the layers are arranged in regular rings without any external influences. The color gradient indicates the velocity distribution inside the tube, where high velocities are in the center (light blue to green), while low velocities are near the walls (dark blue). The flow begins to interact with the internal discs, redistributing the fluid in the tube. Figure 8b shows a cross-section of the tube, where the effect of the inner disc on the fluid flow can be seen. The red areas in the center indicate high speed, while the blue areas at the edges indicate low speed due to friction with the walls. This velocity distribution shows that the inner disc creates turbulence in the flow, which increases heat exchange inside the tube. Figure 8c illustrates the moment when the fluid hits the teeth of one of the inner discs, which leads to the formation of vortices and velocity shifts. There is an increase in turbulence, which is beneficial for heat transfer but may lead to increased pressure loss inside the tube. It also shows how the inner design enhances vortex flow, which improves heat transfer efficiency. The inner discs guide the fluid through specific paths, enhancing mixing and heat transfer. In contrast, perforations in the discs help reduce pressure loss, and the spacing between the discs significantly influences the level of turbulence within the tube. The spiral ribbon enhances flow turbulence, reducing the thermal boundary layer thickness and improving heat transfer efficiency while also ensuring homogeneous heat distribution inside the tube. However, it may increase pressure drop, necessitating system design optimizations for optimal performance.

Fig. 8

Fluid dynamics analysis inside a tube using internal discs and a spiral tape.

Figure 9 shows the numerical simulation of fluid flow lines inside a pipe containing internal rings. The figure presents how vortices form and increase flow turbulence, which improves heat transfer and reduces deposit accumulation inside the pipe. The flow lines inside the pipe are shown in Fig. 9a, as they follow the paths of the fluid as it passes through the internal rings. The fluid moves through circular layers at varying speeds, which enhances the mixing of thermal layers, leading to improved heat transfer. It can be seen how the flow forms in organized ring patterns around the internal discs. Figure 9b shows the moment when the flow collides with the internal rings, which leads to the formation of vortices and turbulence in the fluid. These vortices cause increased flow resistance but also improve the thermal mixing process. The effect of vortices appears at the points of collision, indicating that the design of the inner rings directly affects the fluid flow. The geometric design of the tube, particularly the incorporation of inner rings, significantly influences fluid flow dynamics. These rings force the fluid into complex circular paths, enhancing thermal layer mixing and improving heat exchange efficiency. However, they also increase flow resistance, potentially leading to higher pressure loss inside the tube. Additionally, they aid in removing accumulated deposits, reducing the need for frequent maintenance. The vortices generated by these structures further contribute to turbulent flow, which minimizes the thermal boundary layer thickness, thereby enhancing heat transfer. These vortices also improve energy exchange between the fluid and the tube walls, optimizing thermal system performance. At the same time, their turbulent nature helps prevent impurity buildup, naturally cleaning the inner surface of the tube and maintaining system efficiency over time.

Fig. 9

Analysis of fluid flow lines and the effect of vortices on heat transfer inside a tube.

Uncertainty analysis

The uncertainty analysis presented in Table 3 confirms the accuracy and reliability of the numerical results, with all parameters maintaining error margins below 4.5%, ensuring confidence in the predictions of heat transfer and hydraulic performance. The Nusselt number (Nu) ranged between 172.02 and 288.49, with an uncertainty of ± 5.15 and an error margin of ± 2.24%. Similarly, the heat transfer coefficient (h) varied from 2088.94 W/m²K to 4012.41 W/m²K, with an uncertainty of ± 55.79, while the error remained at ± 2%, ensuring numerical accuracy. For fluid flow resistance, the pressure drop (ΔP) exhibited a minimum value of 50.04 Pa and a maximum of 302.22 Pa, with an uncertainty of ± 3.8%. The thermal performance factor (TPF) varied from 1.32479 to 5.74171, with an uncertainty of ± 4.2%, demonstrating the effectiveness of the hybrid nanofluid and twisted tape configuration. The friction factor (f) ranged from 0.00054 to 0.1134, with an uncertainty between ± 0.00054 to ± 0.1134 and an error margin of ± 3.5%.

Table 3 Uncertainty and error analysis of key parameters in heat transfer study.

Results and conclusions

The reliability of the computational results in this study was verified by comparing the Nu values derived from simulations with those estimated using the Gnielinski and Dittus-Boelter correlations. Similarly, $\:\frac{\text{f}}{8}\:$has been compared with Blasius and Petukhov Eqs^33,34.

Gnielinski correlations:

$$\:{\text{N}\text{u}}_{s}=\frac{\frac{\text{f}}{8}\left(\text{Re}-1000\right)\text{P}\text{r}}{1+12\cdot\:7{\left(\frac{\text{f}}{8}\right)}^{{0}^{0.5}}\left({\text{P}}_{\text{r}}^{\frac{2}{3}}-1\right)}$$

(14)

​Dittus-Boelter equation:

$$\:{\text{N}\text{u}}_{s}=0.\:023\:{\text{R}\text{e}}^{0.8}{\:\text{P}\text{r}}^{0.4}$$

(15)

Blasius Eq. 

$$\:{f}_{s}=0.316R{e}^{-0.25}$$

(16)

​Petukhov Eq. 

$$\:{f}_{s}=(0.79\text{l}\text{n}Re-1.64{)}^{-2}$$

(17)

The validation results presented in Fig. 10 compare the findings of the present study with standard empirical correlations for Nusselt number (Nu) and friction factor (f) as functions of Reynolds number (Re). The present study’s results show good agreement with standard empirical correlations for both heat transfer (Nu) and pressure drop (f). The Nusselt number’s results are compared with the Dittus-Boelter equation and the Gnielinski equation. The results of the present study closely follow the Gnielinski equation, slightly deviating from the Dittus-Boelter equation. Also, the friction factor’s results are compared with the Blasius equation and the Petukhov equation. The present study’s friction factor aligns more closely with the Blasius equation at lower Reynolds numbers but follows the Petukhov equation at higher Reynolds numbers.

Fig. 10

Validation of the present study results with the standard correlations.

Figure 11 presents the relationship between the Nu and the Re number for a heat exchanger under different torsion ratio (TR) configurations, including a baseline case without torsion. The findings showed the use of twisted tape (especially TR = 5) greatly enhances heat transfer due to the increased turbulence and disruption of the boundary layer, and Lower torsion ratios (e.g., TR = 5) provide superior heat transfer but come at the cost of increased pressure drops, which are not visible in this figure but must be considered in practical applications. The improvement in Nu due to torsion ratios is more pronounced at higher Re, where turbulence is already significant, amplifying the effect of twisted tape. Applications without torsion are suitable for systems prioritizing low-pressure drops and energy efficiency over maximum heat transfer, and they are ideal for low-to-moderate Re ranges. It is also clear from the findings that TR = 5 is recommended for maximizing heat transfer in high-Re systems where pressure drop is less critical, and TR = 10 provides a compromise between improved Nu and manageable pressure drops, making it suitable for a wider range of applications. It is also clear that without the torsion ratio, Nu values are consistently the lowest across all Re. This indicates that the absence of torsion limits turbulence and mixing, resulting in lower heat transfer. TR = 15 provides a modest improvement over the baseline, showing Nu increases of ~ 10–15% depending on Re, and represents a balanced approach with moderate turbulence and relatively lower pressure drops. TR = 10 Further improves Nu, showing an increase of ~ 25–30% over the baseline. TR = 5 consistently outperforms all other configurations, delivering the highest Nu values. These findings align with those reported in previous research^35,36.

Fig. 11

Effect of torsion ratio on Nu variation with Re in a heat exchanger.

Figure 12 demonstrates the effect of the torsion ratio (TR) on the convective heat transfer coefficient (h) as a function of the Re in a heat exchanger, comparing a baseline case without torsion to cases with torsion ratios of 15, 10, and 5. As Re increases, h improves across all configurations due to greater flow velocity and turbulence. The baseline case, lacking torsion, consistently shows the lowest h values, while applying torsion significantly enhances heat transfer, particularly at lower TR values. For instance, at Re = 6000, TR = 5 achieves the highest h (2964.77), a 42% improvement over the baseline (2088.94). Lower TR values (e.g., TR = 5) generate higher turbulence, disrupting the boundary layer and improving heat transfer. However, they result in increased pressure drops, which may limit their use in energy-sensitive applications. At Re = 14,000, TR = 5 achieves the highest h (3394.61), demonstrating superior performance. However, TR = 10 provides a balanced option, offering significant heat transfer improvements while maintaining manageable pressure drops. The impact of torsion ratios is particularly pronounced at lower Re, where the enhanced turbulence from twisted tape has a greater influence on flow dynamics.

Fig. 12

Impact of torsion ratio on convective heat transfer coefficient variation with Re in a heat exchanger.

Figure 13 evaluates the effect of torsion ratio (TR) on pressure loss (dp) at both ends of the heat exchanger as a function of Re. Lower torsion ratios, such as TR = 5, enhance heat transfer efficiency but lead to significantly higher-pressure losses due to increased turbulence and tighter twists. At Re = 6000, TR = 5 records the highest-pressure loss (dp = 57.15, ~ 14% higher than the baseline), while TR = 15 results in a smaller increase (dp = 53.68, ~ 7%). Similarly, at Re = 14,000, TR = 5 experiences a pressure loss of dp = 284.81, approximately 8% higher than the baseline, whereas TR = 15 shows a modest increase of ~ 1.4%. The baseline configuration minimizes pressure loss, making it energy-efficient for systems prioritizing low flow resistance, but it compromises heat transfer due to reduced turbulence and mixing. TR = 15 introduces a slight pressure loss while balancing flow resistance and turbulence improvement. TR = 10 offers a middle ground with moderate pressure losses (~ 4.7–11% above the baseline) and improved thermal performance, making it suitable for general-purpose applications. In contrast, TR = 5 delivers maximum heat transfer efficiency but incurs the highest-pressure losses, making it ideal for systems where energy consumption is less of a concern. These findings underscore the trade-offs between turbulence-induced heat transfer enhancement and increased pressure losses in selecting torsion ratios.

Fig. 13

Effect of torsion ratio on pressure loss variation with Re in a heat exchanger.

Figure 14 examines the effect of torsion ratio (TR) on the Thermal Performance Factor (TPF) as a function of Re in a heat exchanger. TPF decreases by increasing Re across all configurations, starting at 1.933 for Re = 6000 and dropping to 1.324 at Re = 14,000 in the baseline case. The system shows the lowest TPF without torsion due to minimal turbulence and limited heat transfer enhancement. In contrast, configurations with torsion ratios improve TPF, with TR = 15 increasing by ~ 25% and TR = 5 achieving ~ 58% higher TPF than the baseline at Re = 6000. Lower torsion ratios, such as TR = 5, consistently deliver the highest TPF across all Re, particularly at lower flow rates, as they enhance turbulence and heat transfer efficiency. However, their benefits diminish at higher Re due to increased flow resistance. TR = 10 offers a balanced option, providing consistent improvements over the baseline and higher TPF values than TR = 15 across all Re. At Re = 14,000, TR = 10 achieves a TPF of 1.236, slightly lower than TR = 5 but still better than TR = 15 and the baseline. While minimizing pressure drops and being energy-efficient, the baseline configuration sacrifices heat transfer efficiency, leading to reduced TPF, especially at lower Re. Torsion ratios are most effective at lower Re, where turbulence enhances heat transfer. At higher Re, the dominance of frictional losses makes higher torsion ratios or the baseline more suitable for energy-efficient applications. These results are consistent with previous research findings³⁵.

Fig. 14

Effect of torsion ratio on TPF variation with Re in a heat exchanger.

Figure 15 reveals the relationship between the Re number and the Nu coefficient for hybrid nanofluids with three different concentrations of nanoparticles (ϕ = 0.9%, 0.6%, 0.3%). It is clear from the figure that at low Re (6000–8000), the Nu is high for all concentrations, indicating good thermal efficiency of the hybrid nanofluid. As the Re increases up to 12,000, a gradual decrease in the Nu is observed, which may be due to the effect of the thin thermal boundary layer, where the heat transfer rate begins to stabilize at certain values ​​of turbulence. At Re14000, a significant decrease in the Nu is seen for all concentrations, indicating that the positive effect of turbulence on heat transfer begins to decrease at this point. It is also evident from the figure that the fluid with the highest concentration (ϕ = 0.9%) achieves the highest Nu values ​​at all Re values, which means that increasing the proportion of nanoparticles leads to improved heat transfer. When comparing the results between the three concentrations, we find that the hybrid fluid with a concentration of 0.9% outperforms the other two concentrations (0.6% and 0.3%) in heat transfer efficiency. Still, the gap decreases with the increasing Re. At Re 14,000, the difference in Nu between different concentrations is less obvious, which may indicate that the effect of nanoparticles on improving heat transfer becomes less effective at very high flows.

Fig. 15

Effect of concentration of hybrid nanoparticles on Nu with Re in a heat exchanger.

Figure 16 shows the relationship between Re number and convective heat transfer coefficient (h) for hybrid nanofluids with different nanoparticle concentrations (ϕ = 0.9%, 0.6%, 0.3%). The figure shows how increasing the nanoparticle concentration improves the convective heat transfer coefficient, with the highest values for the fluid with ϕ = 0.9%, followed by ϕ = 0.6%, and then ϕ = 0.3%. It is clear from the figure that with increasing Re, a slight decrease in the convective heat transfer coefficient is observed for all concentrations. This may be due to the improvement of thermal mixing at medium turbulence, while the effect of nanoparticles begins to saturate at very high flows. Increasing the nanoparticle concentration enhances the thermal conductivity of the fluid, which leads to improved convective heat transfer, with the fluid with ϕ = 0.9% showing the highest thermal efficiency. When comparing the results between different concentrations, we find that the gap in the heat transfer coefficient between ϕ = 0.9% and ϕ = 0.6% is small but larger than that at ϕ = 0.3%, indicating that increasing the concentration gives a gradual improvement but becomes less pronounced at high values. At the Re of 14,000, the difference between the three concentrations is less pronounced, indicating that the effect of nanoparticles becomes limited at very high flows due to the short heat transfer time between the fluid and the tube surface.

Fig. 16

Effect of concentration of hybrid nanoparticles on convective heat transfer coefficient (h) with Re in a heat exchanger.

Figure 17 shows the relationship between Reynolds number (Re) and pressure loss when using hybrid nanofluids with different concentrations of nanoparticles (ϕ = 0.9%, 0.6%, 0.3%). It is noted from the figure that the pressure loss increases with increasing Re for all concentrations, indicating that increasing the flow velocity leads to an increase in the fluid resistance inside the tube. The effect of nanoparticle concentration on pressure loss is very limited, as the curves overlap significantly, indicating that the difference in viscosity and density between different concentrations does not substantially affect flow resistance. As the Re increases up to 14,000, the pressure loss increases approximately linearly, indicating that increasing the flow velocity increases fluid resistance without unexpected effects. It can also be seen that the difference between different concentrations (ϕ = 0.9%, ϕ = 0.6%, ϕ = 0.3%) is very small, indicating that the effect of nanoparticles on pressure loss is insignificant compared to the effect of Re. When comparing the results between different concentrations, we find that increasing the concentration of nanoparticles does not lead to a significant increase in pressure loss, which means that improving heat transfer using nanofluids does not come at the expense of a significant increase in hydraulic resistance.

Fig. 17

Effect of concentration of hybrid nanoparticles on pressure loss with Re in a heat exchanger.

Figure 18 shows the relationship between Re and thermal performance factors (TPF) when using hybrid nanofluids with different concentrations of nanoparticles (ϕ = 0.9%, 0.6%, 0.3%). It is noted from the figure that with increasing Re, there is a gradual decrease in the TPF for all concentrations, which may be due to the improvement of thermal mixing at medium turbulence. Still, the pressure loss becomes more pronounced at high flows. It can also be noted that the fluid with the highest concentration (ϕ = 0.9%) achieves the highest values of TPF at all values of Re, which means that increasing the percentage of nanoparticles leads to a clear improvement in thermal performance, but it decreases with increasing flow velocity. When comparing the results of the three concentrations, we find that the hybrid fluid with a concentration of 0.9% outperforms the other two concentrations (0.6% and 0.3%) in thermal performance. Still, it becomes less effective at very high flows due to pressure loss. At Re 14,000, the difference in thermal performance coefficient between different concentrations is less pronounced, indicating that the increase in nanoparticles loses its positive effect when pressure loss becomes the most influential factor.

Fig. 18

Effect of concentration of hybrid nanoparticles on thermal performance factor (TPF) with Re in a heat exchanger.

Figure 19 analyzes the impact of torsion ratio (TR) and hybrid nanofluid (Al2O3-CuO/water) on the Nu as a function of Re in a heat exchanger. The study compares three configurations: a baseline without torsion or nanofluid, TR = 5 without nanofluid, and TR = 5 with hybrid nanofluid. Across all cases, Nu increases with Re due to enhanced turbulence and higher flow velocities, with the effects of torsion and nanofluid becoming more pronounced at higher Re. This trend is in agreement with previous literature³⁷. The baseline case, offering minimal flow resistance and pressure drop, achieves the lowest heat transfer efficiency, reflected in the smallest Nu values. Introducing TR = 5 significantly enhances Nu, particularly at lower Re, where turbulence improves convective heat transfer. At Re = 6000, this configuration achieves Nu = 244.14, a ~ 42% improvement over the baseline, while at Re = 14,000, Nu = 279.53, a ~ 36% increase. However, the absence of nanofluid limits further enhancement. The combination of TR = 5 with a hybrid nanofluid achieves the highest Nu values, maximizing heat transfer efficiency. At Re = 6000, Nu = 248.12, representing a ~ 44% improvement over the baseline, and at Re = 14,000, Nu = 288.49, a ~ 41% increase over the baseline and ~ 3% higher than TR = 5 without nanofluid. This configuration, however, incurs increased pressure drops due to the combined effects of torsion and the denser nanofluid, highlighting a trade-off between improved heat transfer and higher flow resistance. These findings emphasize the combined benefits of torsion and hybrid nanofluid for enhancing thermal performance, especially at higher Re.

Fig. 19

Effect of torsion ratio and hybrid nanofluid on nu variation with Re in a heat exchanger.

The analysis in Fig. 20 investigates the impact of a torsion ratio (TR = 5) and a hybrid nanofluid (Al₂O₃-CuO/water) on the convective heat transfer coefficient (h) across varying Reynolds numbers (Re). Three configurations were examined: the baseline setup without torsion or nanofluid, the addition of TR = 5 without nanofluid, and the combination of TR = 5 with the hybrid nanofluid. The baseline design, which lacked torsion and nanofluid, had the worst heat transfer efficiency despite an increase in h with Re, owing to the lack of turbulence and increased thermal conductivity. TR = 5 increased h by ~ 42% at Re = 6000 and ~ 36% at Re = 14,000, indicating that turbulence damaged the thermal boundary layer. The combination of TR = 5 and the hybrid nanofluid resulted in the greatest performance, with a maximum h of 4012.41 W/m²K at Re = 14,000. This arrangement improved efficiency by around 71% at Re = 6000 and 61% at Re = 14,000 when turbulence and thermal conductivity were combined relative to the baseline. The tradeoff between heat transfer efficiency and pressure decrease was clear. While the hybrid nanofluid with TR = 5 performed better in heat transfer, it also had larger pressure drops, which might impact efficiency. The basic arrangement is appropriate for applications with a focus on energy savings and minimum pressure losses. In contrast, the hybrid nanofluid with TR = 5 achieves the highest heat transfer efficiency at high Re. TR = 5 without nanofluid provides a balanced approach by giving considerable heat transfer increases while maintaining reasonable pressure drops, making it a flexible option for practical applications.

Fig. 20

Effect of torsion ratio and hybrid nanofluid on convective heat transfer coefficient (h) with Re in a heat exchanger.

Figure 21 analyzes the effect of torsion ratio (TR = 5) and hybrid nanofluid (Al₂O₃-CuO/water) on the pressure drop (dp) in a heat exchanger under varying Reynolds numbers (Re). The study considers three configurations: a baseline without torsion or nanofluid, TR = 5 without nanofluid, and TR = 5 with the hybrid nanofluid. The baseline setup has the lowest dp, increasing from 50.04 Pa at Re = 6000 to 263.57 Pa at Re = 14,000 due to low flow resistance and absence of turbulence. Introducing TR = 5 causes a significant increase in dp, with a 14% rise at Re = 6000 and 8% at Re = 14,000 over the baseline since torsion-induced turbulence enhances heat transfer while raising flow resistance. The combination of TR = 5 with hybrid nanofluid yields the highest dp, with values 15% higher than the baseline at Re = 6000 and Re = 14,000 and 6% higher than TR = 5 without nanofluid. This is owing to the denser hybrid nanofluid’s increased viscosity and flow resistance. These results demonstrate a trade-off between better heat transfer efficiency and higher-pressure decreases. While the basic arrangement reduces energy usage, it sacrifices increased turbulence and thermal conductivity. TR = 5 enhances heat transmission with a slight increase in dp, making it a good choice for systems that need both efficiency and performance. The combination of TR = 5 with a hybrid nanofluid provides the best heat transfer efficiency but has the greatest energy expenditure owing to increased flow resistance.

Fig. 21

Effect of torsion ratio and hybrid nanofluid on the pressure drop with Re in a heat exchanger.

Figure 22 explores the impact of a torsion ratio (TR = 5) and hybrid nanofluid (Al₂O₃-CuO/water), alongside the baseline configuration without torsion or nanofluid, on the Thermal Performance Factor (TPF) in a heat exchanger across varying Reynolds numbers (Re). The TPF represents heat transfer efficiency relative to pressure drop, with higher values indicating better overall performance. In the baseline configuration, TPF decreases as Re increases, starting at 1.933 (Re = 6000) and dropping to 1.324 (Re = 14000), reflecting the lowest performance due to minimal turbulence and limited thermal conductivity. The introduction of TR = 5 significantly enhances TPF, with a 58% increase at Re = 6000 and a 4% increase at Re = 14,000 compared to the baseline. This improvement is attributed to turbulence, which boosts heat transfer efficiency but becomes less effective at higher Re due to increased pressure losses. Combining TR = 5 with hybrid nanofluid achieves the highest TPF values across all configurations, showing a remarkable 197% improvement at Re = 6000 and a 149% increase at Re = 14,000 compared to the baseline. This superior performance results from the combined effects of turbulence and the enhanced thermal conductivity provided by the nanofluid, allowing high TPF values even at elevated Re where frictional losses usually dominate. The performance comparison underscores the trade-offs between efficiency and energy costs. The baseline configuration minimizes pressure drops and energy consumption but delivers the lowest TPF. TR = 5 improves TPF substantially, particularly at lower Re, but its potential is constrained without nanofluids. The combination of TR = 5 with hybrid nanofluid optimizes TPF, particularly at higher Re, but incurs greater energy costs due to increased pressure drops. The analysis suggests that systems prioritizing thermal performance should use TR = 5 with hybrid nanofluid, especially at low-to-moderate Re, while systems focused on energy efficiency may find the baseline or TR = 5 without nanofluid more suitable.

Fig. 22

Effect of torsion ratio and hybrid nanofluid on the thermal performance factor (TPF) with Reynolds number in a heat exchanger.

Table 4 presents a comparative summary of key thermal and hydraulic performance parameters for various heat exchanger configurations using twisted tapes, hybrid nanofluids, and different Reynolds numbers. The configurations are benchmarked against a baseline case (no torsion, no nanofluid) and evaluated using key performance indicators, including Nusselt number (Nu), friction factor (f), pressure drop (ΔP), heat transfer coefficient (h), and thermal performance factor (TPF). The comparison reveals that both twisted tape inserts and hybrid nanofluids contribute significantly to heat transfer enhancement, with their combination providing synergistic thermal benefits. However, this comes at the cost of increased friction factor and pressure drop. At Re = 6000, the baseline configuration exhibits the lowest Nusselt number (172.02) and convective heat transfer coefficient (2088.94 W/m²·K). Introducing twisted tape with a twist ratio (TR) of 5 significantly increases Nu to 244.14 and h to 2964.77 W/m²·K, reflecting intensified turbulence and boundary layer disruption. When a hybrid nanofluid (Al₂O₃-CuO/water) is used with the twisted tape, Nu and h increase further to 248.12 and 3567.00 W/m²·K, respectively, while the friction factor rises slightly. The TPF value of 3.93 suggests a strong net performance gain despite added pressure losses. At Re = 14,000, performance improvements continue. The hybrid nanofluid + twisted tape configuration achieves the highest Nu (288.49), f (0.1134), and h (4012.41 W/m²·K), with a TPF of 5.74, confirming enhanced heat transfer effectiveness at higher flow rates. Notably, even the baseline and TR = 5 cases at Re = 14,000 (newly added) outperform their Re = 6000 counterparts due to increased turbulence and flow velocity.

Table 4 Comparative thermal and hydraulic performance of heat exchanger configurations at Reynolds numbers 6000 and 14,000.

Conclusion

In this study, the thermal and hydraulic performance of a heat exchanger tube equipped with twisted tape (TT) inserts and special fixed rings was investigated using a hybrid Al₂O₃–CuO/water nanofluid. A CFD simulation approach was employed under turbulent flow conditions with Reynolds numbers ranging from 6000 to 14,000. The effects of varying torsion ratios (TR = 5, 10, and 15) and nanofluid volume concentrations (ϕ = 0.3%, 0.6%, and 0.9%) were analyzed. The model was validated against published data, confirming its accuracy.

The key findings are summarized as follows:

• The TT and fixed ring combination promoted turbulence and secondary flows, which improved fluid mixing and thermal homogeneity. The hybrid nanofluid further enhanced heat transfer due to increased thermal conductivity and viscosity.

• For twisted tape alone (TR = 5), the Nusselt number increased by 36.3% compared to a plain tube. When combined with 0.9% hybrid nanofluid, the enhancement rose by an additional 3.2%, leading to a cumulative increase in the heat transfer coefficient (h) by 18.2%.

• Temperature contour analysis revealed that the inserts disrupted the boundary layer and increased near-wall fluid temperatures, improving local heat transfer effectiveness.

• The system experienced an increase in pressure drop as a trade-off for improved heat transfer. The rise in pressure was attributed to both the inserted elements and the increased viscosity of the nanofluid.

• Among the tested configurations, the combination of twisted tape inserts, fixed rings, and Al₂O₃–CuO/water nanofluid provided the most significant performance gains, with a thermal performance factor (TPF) reaching up to 3.29.

Future research should incorporate experimental validation to complement the CFD results and assess model accuracy under actual operating conditions. Exploring a broader range of nanofluid combinations, volume concentrations, and ring geometries may uncover further enhancements in heat transfer. Moreover, optimization algorithms (e.g., genetic algorithms, machine learning) can be integrated to determine the best-performing configurations for different industrial applications.