Channel equalization in ultraviolet communication based on LSTM-DNN hybrid model

Abstract

Ultraviolet Communication (UVC) faces the challenge of increased Bit Error Rate (BER) due to signal attenuation caused by atmospheric scattering. In recent years, wireless optical communication technologies have made significant progress in both Ultraviolet (UV) and Visible Light (VL) communication domains. However, traditional channel equalization methods still exhibit limitations when handling complex nonlinear channels. This study proposes a Long Short-Term Memory - Deep Neural Network (LSTM-DNN)-based channel equalization approach to enhance signal recovery accuracy. The model leverages LSTM to process temporal dependencies and combines it with DNN for nonlinear feature extraction, thereby improving its adaptability to single-scattering channels. Experimental results demonstrate that the LSTM-DNN model shows significant advantages in improving signal recovery accuracy and transmission quality compared to conventional methods. These methods include Least Mean Squares (LMS), Recursive Least Squares (RLS), Particle Swarm Optimization (PSO), Support Vector Machine (SVM), and Minimum Mean Squared Error (MMSE). Specifically, the LSTM-DNN model outperforms traditional methods across key performance metrics such as BER and Mean Squared Error (MSE). When the Signal-to-Noise Ratio (SNR) is 0 dB, the LSTM-DNN model achieves a BER of 0.135, significantly lower than LMS (0.45), RLS (0.38), PSO (0.35), SVM (0.25), and MMSE (0.20). As SNR increases, the LSTM-DNN model’s BER further decreases, demonstrating strong robustness. When the SNR is 20 dB, the BER of the LSTM-DNN model drops to 0.015, substantially outperforming conventional methods. Additionally, the LSTM-DNN model exhibits the smallest MSE values, with 0.035 at 0 dB SNR and decreasing to 0.004 with higher SNR. On average, the LSTM-DNN model reduces BER by approximately 67.8% and MSE by about 70.8% compared to traditional methods. These results confirm that the LSTM-DNN model significantly improves signal recovery accuracy and transmission quality in UVC systems. Overall, the LSTM-DNN model demonstrates superior performance in UVC applications compared to conventional methods, offering higher precision and stability. This study effectively addresses signal attenuation issues in UVC, significantly enhancing signal recovery accuracy and transmission quality, thus possessing important theoretical value and practical significance.

Introduction

Research background and motivations

The Ultraviolet Communication (UVC) system, with its potential for high transmission rates and security, has become a key focus in modern communication research. However, ultraviolet (UV) signals in the atmosphere typically face signal attenuation due to scattering, leading to signal distortion and a higher Bit Error Rate (BER)¹. As the demand for efficient and reliable communication systems grows, addressing this issue becomes particularly crucial, especially in UVC². Traditional channel equalization methods and signal compensation techniques have certain limitations when dealing with these complex issues, highlighting the urgent need to explore new solutions^3,4. The motivation of this study is to enhance the UVC system’s performance, particularly by reducing the impact of signal attenuation caused by atmospheric scattering and improving signal recovery. This study leverages the strengths of the Long Short-Term Memory (LSTM) and Deep Neural Network (DNN) hybrid model to provide a more effective solution for reducing BER and enhancing transmission quality. This approach offers significant advantages over traditional methods.

Research objectives

The main objective of this study is to develop and evaluate a hybrid channel conditioning method based on LSTM and DNN for UVC systems. The specific goals include the following. The influence of atmospheric scattering on the attenuation of UV signals and its effect on signal quality are discussed; A new method based on the LSTM-DNN hybrid model is proposed to solve the problem of signal attenuation and improve signal recovery; Under different Signal-to-Noise Ratio (SNR) conditions, the performance of the LSTM-DNN model in terms of BER and Mean Squared Error (MSE) is evaluated; The proposed hybrid model is compared with traditional communication methods to evaluate its effectiveness in improving transmission quality. The overarching objective is to contribute to the advancement of UVC technology and provide practical solutions to the challenges associated with signal attenuation and distortion.

The innovation of this study lies in proposing an innovative hybrid neural network architecture that combines the advantages of LSTM and DNN to effectively handle the time series characteristics and nonlinear features of signals. The hybrid neural network is first applied in the UVC field, significantly improving signal recovery accuracy and transmission quality. The robustness and adaptability of this method under different SNR conditions are verified through experiments, providing new theoretical support for the design and optimization of UVC systems.

Literature review

Recent years have witnessed rapid development in wireless optical communication technologies. UVC emerges as a research focus in communications due to its unique advantages, such as high transmission rates, enhanced security, and strong anti-interference capabilities. However, practical UVC systems face multiple challenges, particularly signal attenuation and distortion caused by atmospheric scattering and turbulence, which significantly impact communication quality and reliability. To overcome these problems, researchers have proposed many channel equalization and signal processing methods, among which the model based on deep learning (DL) has gradually demonstrated significant advantages. Zhao et al. (2023) developed a topology optimization algorithm for Unmanned Aerial Vehicle (UAV) formation networks based on wireless UVC. This algorithm significantly reduced communication complexity and extended network lifetime through an optimal rigid graph model. Simulation results demonstrated that this approach decreased communication complexity by 11.5% in swarm formations and delayed the first deadline by 25.1%, revealing the application potential of UVC in UAV cooperative missions⁵. Salama and Aly (2025) focused on channel estimation in Orthogonal Frequency Division Multiplexing (OFDM) systems for underwater wireless optical communication. They proposed a method combining DL with machine learning (ML) models. Meanwhile, they employed DenseNet121 hybrid Random Forest (RF), Gated Recurrent Unit (GRU), LSTM, and Recurrent Neural Networks (RNNs) to improve channel estimation and reduce error rates. To mitigate inter-symbol interference and map datasets, they introduced 16-Quadrature Amplitude Modulation (16-QAM) and Quadrature Phase Shift Keying (QPSK)-based OFDM. Compared with traditional methods like Minimum Mean Squared Error (MMSE) and Least Squares (LS), this model achieved significant improvements in BER reduction and computation time⁶. Zhao et al. (2025) addressed limitations of traditional UV Multiple-Input Multiple-Output (MIMO) channel equalization methods, which heavily relied on channel prior knowledge in turbulent environments and exhibited low accuracy in complex nonlinear channel modeling. They developed a DL-based wireless UV scattering MIMO channel equalization method that converted MIMO signals into two-dimensional time series. They used Bidirectional Long Short-Term Memory (BiLSTM) with bidirectional sequence feature extraction capability as the core, supplemented by deep neural networks for nonlinear modelling. Meanwhile, they constructed a DL network model suitable for UV MIMO channel equalization to achieve precise recovery of original MIMO signals. Simulation results showed superior BER and MSE performance compared to the Least Mean Square (LMS) algorithm, Recursive Least Squares (RLS), and Multilayer Long and Short-Term Memory (Multi-LSTM)-based equalization schemes⁷. Shwetha et al. (2024) investigated the application of channel equalization techniques in digital communications and proposed an effective equalizer based on Artificial Neural Networks (ANNs). The weights of this equalizer were trained using the proposed Battle Royale Optimization (BRO) algorithm to minimize the MSE value. BRO was modified through different initialization methods, and experimental results demonstrated that the proposed ANN-BRO-based equalizer outperformed other initialization and optimization methods in performance metrics such as BER and MSE⁸. Tian and Zheng (2025) developed a hybrid DL model for channel estimation in MIMO wireless communication systems. This model combined the advantages of Convolutional Neural Network (CNN) and GRU, fully leveraging the generalization ability of DL models in various wireless communication scenarios. Additionally, a series of regularization techniques were introduced, including data augmentation and structural complexity constraints, to avoid overfitting issues. Simulation results verified the effectiveness of this model under both quasi-static block fading and time-varying fading conditions⁹. Han et al. (2024) addressed the intelligent fault diagnosis of critical components in rotating machinery and proposed a Multi-Source Heterogeneous Information Fusion (MSHIF) network. By integrating a data-augmented Deep Belief Network (DBN) with a 1D Convolutional Neural Network (1DCNN), this network achieved more comprehensive and robust identification of rotating machinery’s health status under limited datasets. Experimental results showed that MSHIF surpassed other comparative methods in diagnostic accuracy, stability, and noise robustness¹⁰. Kumar et al. (2024) analyzed signal detection algorithms for Multi-Input Multi-Output Orthogonal Time Frequency Space (MIMO-OTFS) under Rayleigh and Rician channels. Experimental results indicated that RNN, neural network, and Support Vector Machine (SVM) detectors outperformed traditional methods in terms of BER and Power Spectral Density (PSD), achieving significant gains under both Rayleigh and Rician channels¹¹.

In conclusion, as DL technologies continue to advance, their applications in wireless optical communications have become increasingly widespread. From channel equalization to channel estimation, and from fault diagnosis to signal detection, DL models have demonstrated remarkable performance improvements. However, most existing research focuses on specific communication scenarios or channel conditions. Further optimization and improvement remain necessary for complex real-world environments featuring atmospheric turbulence and multipath interference. Moreover, reducing computational complexity and improving real-time performance represent important directions for future research.

Research methodology

Wireless UVC system structure

The design concept of the wireless UVC system is similar to that of other wireless optical communication systems. It primarily consists of three key components: the transmitter, atmospheric scattering channel, and receiver^12,13. The structural diagram of the wireless UVC system is presented in Fig. 1.

Fig. 1

Structure of the wireless UVC system.

At the transmitter, the signal generator produces the original signal, which is then encoded and modulated through a modulation circuit driven by a current source. This study employs Pulse Position Modulation (PPM) as the modulation scheme due to its high noise resistance and energy efficiency in UVC. The modulated signal is introduced into the UV light source and converted into a UV beam, which is transmitted into the atmospheric scattering channel through the transmitter^14,15,16. Within the atmospheric channel, UV light is inevitably subject to multiple scattering and absorption events, which can cause significant signal distortion and inter-symbol interference, thus impairing the transmission quality. At the reception end, the photodetector captures the scattered UV light and converts it into an electrical signal. The received signal undergoes a series of complex signal processing operations, including channel estimation, equalization, demodulation, and decoding. These steps are crucial for reconstructing the signal and improving the stability and reliability of the UVC system^17,18,19,20.

The impact of atmospheric factors on UV light transmission

During wireless UV light transmission, signal attenuation inevitably occurs to varying degrees^21,22,23,24. The effects of atmospheric factors on UVC are displayed in Fig. 2.

Fig. 2

The impact of atmospheric factors on UVC.

Molecules, aerosol particles, and water vapor in the atmosphere can interact with UV light, leading to attenuation and scattering of light signals. Specifically, the transmission signal $\:s\left(t\right)$ is affected by the following effects after passing through the atmospheric channel: (i) Scattering effect: When UV light propagates in the atmosphere, Rayleigh scattering and Mie scattering occur, causing the signal to deviate from the original path and form multipath effects. (ii) Absorption effect: The absorption of UV light by atmospheric components can cause signal power attenuation. (iii) Turbulence effect: Atmospheric turbulence can cause amplitude and phase fluctuations in signals, further affecting signal quality.

Considering these effects, the received signal $\:r\left(t\right)$ can be expressed as:

$$\:r\left(t\right)=h\left(t\right)*s\left(t\right)+n\left(t\right)$$

(1)

$\:h\left(t\right)$ denotes the impulse response of the channel, reflecting the characteristics of atmospheric scattering and absorption; $\:n\left(t\right)$ refers to additive noise, mainly including background light noise and thermal noise of photodetectors; $\:*$ represents convolution operation. The specific form of channel response $\:h\left(t\right)$ depends on atmospheric parameters (such as aerosol concentration, turbulence intensity, etc.) and transmission distance.

Atmospheric channel parameters, such as aerosol concentration, turbulence intensity, and relative humidity, significantly impact the performance of UVC systems. Specifically, higher aerosol concentrations increase scattering effects, leading to greater signal power attenuation²⁵. Atmospheric turbulence causes fluctuations in signal amplitude and phase, particularly in the UV band, where turbulence-induced interference is more pronounced. Variations in relative humidity affect the refractive index and absorption properties of the atmosphere, thereby influencing signal transmission quality²⁶. In short, atmospheric channel parameters significantly impact the performance of UVC systems. The proposed LSTM-DNN model effectively addresses these complex environmental conditions through its robust adaptive learning capabilities, demonstrating superior performance compared to traditional methods.

When UV light undergoes scattering by atmospheric particles, the scattering can be classified into Rayleigh scattering and Mie scattering based on the particle size²⁷. The scattering coefficient for Rayleigh scattering can be written as Eq. (2):

$$\:{K}_{s}^{\text{R}\text{a}\text{y}}=\frac{8\pi\:\left[n\right(\lambda\:{)}^{2}-1{]}^{2}}{3{N}_{\text{A}}^{2}{\lambda\:}^{4}}\cdot\:\frac{6+3\delta\:}{6-7\delta\:}$$

(2)

$\:\lambda\:$ represents the wavelength of the incident light; $\:n\left(\lambda\:\right)$ denotes the refractive index of the atmosphere; $\:\delta\:$ is the shape factor; $\:{N}_{A}$ stands for the concentration of atmospheric scattering particles^28,29,30,31. The scattering coefficient for Mie scattering is expressed as Eq. (3):

$$\:{K}_{\text{s}}^{\text{M}\text{i}\text{e}}=\frac{3.91}{{R}_{\text{v}}}\cdot\:{\left(\frac{550}{\lambda\:}\right)}^{q}$$

(3)

$\:{R}_{\text{v}}$ is the meteorological distance. $\:q$ means the correction factor related to $\:{R}_{\text{v}}$. $\:\lambda\:$ represents the wavelength of the incident light. This study uses Rayleigh and Mie scattering models to simulate the scattering effects of atmospheric aerosol particles on the UV radiation. A structure function model of atmospheric turbulence is employed to describe the impact of turbulence on UV signals. This model is based on Kolmogorov turbulence theory and effectively characterizes the modulation of optical wave phase and intensity by atmospheric turbulence. Specifically, the phase perturbations caused by turbulence are described by the following structure function:

$$\:{D}_{\varphi\:}\left(r\right)=({[\varphi\:\left(r+{r}_{o}\right)-\varphi\:\left({r}_{0}\right)]}^{2})=6.88\cdot\:{\left(kr\right)}^{5/3}$$

(4)

$\:\varphi\:$ denotes the optical wave phase; $\:r$ represents the spatial distance; $\:k$ refers to the turbulence strength parameter, which indicates the intensity of turbulence. This parameter is adjustable according to different atmospheric conditions to simulate environments ranging from weak to strong turbulence.

Turbulence mainly affects UVC signals through intensity scintillation and phase distortion. Turbulence induces random fluctuations in signal intensity, a phenomenon known as intensity scintillation. The statistical properties of intensity scintillation are characterized by the variance of optical intensity. In the simulation, this study calculates the variance of intensity scintillation based on the turbulence strength parameter $\:k$ and adds it to the signal to mimic signal strength fluctuations in real environments. Turbulence also causes random distortions in the optical wave phase, affecting the coherence and transmission quality of the signal. In the simulation, this study models phase distortion by introducing random phase perturbations to the signal. These perturbations are generated based on the structure function and have an intensity proportional to the turbulence strength parameter $\:k$.

To ensure the accuracy and reliability of the simulation results, this study sets the turbulence strength parameter $\:k$ according to actual atmospheric conditions:

Weak turbulence: A small $\:k$ value is set and simulates stable atmospheric conditions. In this case, intensity scintillation and phase distortion are minimal, causing only slight signal distortion.

Moderate turbulence: A medium $\:k$ value simulates typical atmospheric turbulence conditions. In this case, intensity scintillation and phase distortion are more noticeable and significantly impact signal transmission quality.

Strong turbulence: A large $\:k$ value simulates highly unstable atmospheric conditions. In this case, intensity scintillation and phase distortion are severe, leading to substantial signal distortion and an increase in BER.

Wireless UV scattering channel equalization based on hybrid neural networks

This study introduces a wireless UV scattering channel equalization method based on a hybrid neural network, specifically targeting the single-scattering channel of the UVC system. This method combines LSTM and DNN, leveraging the powerful adaptive learning ability of DL to recover the received signal accurately. The LSTM-DNN-based channel equalization scheme is revealed in Fig. 3.

Fig. 3

LSTM-DNN-based channel equalization scheme.

Figure 3 illustrates that the input data y is firstly passed to the data preprocessing module to generate multiple sequence datasets. The data then enters the input layer, which consists of multiple neurons responsible for preliminary feature extraction and data transmission. Next, multiple LSTM layers learn the long-term dependencies and temporal characteristics of the signal sequence data through their memory units and gating mechanisms. Meanwhile, multiple DNN layers further extract nonlinear features from the data. Finally, the output layer generates the equalized signal sequence x. By accurately recovering y, the impact of atmospheric scattering on the signal is effectively mitigated, thus enhancing the transmission performance of the UVC system.

The working principle of LSTM is as follows:

LSTM is a special type of RNN specifically designed for processing and modeling sequential data³². LSTM can more effectively remember and update important information in sequences by introducing control mechanisms such as input, forget, and output gates, thus effectively solving the problems of gradient vanishing and exploding in traditional RNNs.

For each LSTM unit, the input information first passes through a forget gate, whose core is the Sigmoid activation function σ. The function of the forget gate is to determine which information in the current unit state needs to be retained or forgotten³³. The Sigmoid function outputs a vector value between 0 and 1 based on the current input and the hidden state $\:{h}_{\iota\:-1}$ from the previous moment. The larger the value, the more information is retained.

The calculation for the forget gate is:

$$\:{f}_{\iota\:}=\sigma\:\left({W}_{\text{f}}\cdot\:\left[{h}_{\iota\:-1},{x}_{\iota\:}\right]+{b}_{\text{f}}\right)$$

(5)

$\:{W}_{\text{f}}$ and $\:{b}_{\text{f}}$ are respectively the weight matrix and bias vector of the forget gate; $\:{x}_{\iota\:}$ denotes the input of the current time step; $\:{h}_{\iota\:-1}$ represents the hidden state of the previous time step. Next, the retained information is passed through an input gate. The Sigmoid function outputs a vector value from 0 to 1 based on the importance of the current input and the previous hidden state, to selectively update the information³⁴. At the same time, the current input and hidden state are also fed into the Tanh function for processing, limiting the numerical range to -1 to 1, which facilitates regulating the network. The output of the input gate is the product of the outputs of the Sigmoid function and the Tanh function, which is then used to update the cell state. The calculation for the input gate reads:

$$\:{i}_{t}=\sigma\:\left({W}_{\text{i}}\cdot\:\left[{h}_{t-1},{x}_{t}\right]+{b}_{\text{i}}\right)$$

(6)

$$\:{\stackrel{\sim}{C}}_{t}=\text{t}\text{a}\text{n}\text{h}\left({W}_{\text{C}}\cdot\:\left[{h}_{t-1},{x}_{t}\right]+{b}_{\text{C}}\right)$$

(7)

$$\:{C}_{t}={f}_{t}\odot\:{C}_{t-1}+{i}_{t}\odot\:{\stackrel{\sim}{C}}_{t}$$

(8)

$\:{W}_{\text{i}}$ and $\:{b}_{\text{i}}$ are the weight matrix and bias vector of the input gate; $\:{W}_{\text{C}}$ and $\:{b}_{\text{C}}$ refer to the weight matrix and bias vector of candidate states; $\:{C}_{t}$ and $\:{C}_{t-1}$ are the state of the current and previous unit; The symbol ⊙ represents element multiplication. $\:{\stackrel{\sim}{C}}_{t}$ denotes the output result of the Tanh function in the input gate³⁵. Lastly, the current input and hidden information are passed to the Sigmoid function of the output gate. The latest cell state is processed through the Tanh function, and the product of the two is the hidden state of the next time step. The calculation for the output gate is as follows:

$$\:{o}_{t}=\sigma\:\left({W}_{0}\cdot\:\left[{h}_{t-1},{x}_{t}\right]+{b}_{0}\right)$$

(9)

$$\:{h}_{i}={o}_{i}\odot\:\text{t}\text{a}\text{n}\text{h}\left({C}_{i}\right)$$

(10)

$\:\:{W}_{0}$and $\:{b}_{0}$ are the weight matrix and bias vector of the output gate.

The working principle of DNN is as follows:

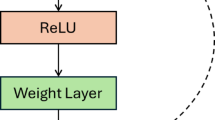
Compared to LSTM, the network update process of DNN is relatively simpler. DNN is primarily used to process the output of LSTM, further extracting features and performing abstract mapping to achieve the final output of the network. Each neuron first performs a linear combination of the input features, calculating the weighted sum by multiplying the input features with weights and adding a bias term. This linear combination is then passed through an activation function for nonlinear transformation, introducing nonlinearity and enabling the network to learn and model more complex functional mappings³⁶. The model of a single neuron in DNN is illustrated in Fig. 4.

Fig. 4

Model of a single neuron in DNN.

Its specific calculation process can be expressed as:

$$\:\widehat{y}=f\left(z\right)=f\left(wx+b\right)$$

(11)

w represents the weight matrix; b refers to the bias term. Their dimensions usually correspond to the dimensions of the input data. The dimension of the weight matrix w is determined by both the number of input features and the number of neurons; The bias b is usually a vector whose dimension is consistent with the number of neurons³⁷. $\:f\left(\cdot\:\right)$ denotes the activation function. In this study, the ReLU function is used as the activation function, and its expression is:

$$\:r\left(x\right)=\left\{\begin{array}{c}x,x\ge\:0\\\:0,x<0\end{array}\right.$$

(12)

To train the hybrid LSTM-DNN, MSE is used as the loss function to measure the difference between the predicted and true values of the network. The calculation for MSE reads:

$$\:L\left[Y|g\left(x\right)\right]=\frac{1}{n}\sum\:_{i=1}^{N}\:{\left[{Y}_{i}-g\left({x}_{i}\right)\right]}^{2}$$

(13)

$\:{Y}_{i}$ refers to the true value, and $\:g\left(x\right)$ represents the predicted value of the network. N denotes the total number of samples. By minimizing MSE, the network can learn the optimal weights and bias parameters, thereby improving the accuracy of signal recovery.

The learning rate is a key parameter that determines the convergence speed of the network. It controls the step size for each parameter update and affects the efficiency and stability of the optimization algorithm. A larger learning rate may cause the parameters to update too quickly, potentially missing the optimal solution or causing oscillations. Furthermore, a smaller learning rate can reduce convergence speed, prolong training time, and potentially trap the network in a local optimum. Therefore, selecting an appropriate learning rate is crucial to ensure the network converges to the global optimum within a reasonable time.

During training, the learning rate is typically adjusted dynamically. In this study, a learning rate decay strategy or adaptive learning rate method (Adam optimizer) adjusts the learning rate, allowing for finer parameter adjustments in the later stages of training. These strategies help the network converge more stably while avoiding overfitting, thus improving the model’s accuracy and generalization ability.

Algorithm complexity

Common adaptive channel equalization algorithms include LMS, RLS, and others. Traditional algorithms exhibit comparatively weaker non-linear fitting capabilities when contrasted with channel equalization algorithms based on hybrid neural networks. In contrast, neural network algorithms are more suitable for handling large-scale data. The proposed algorithm is primarily based on a hybrid neural network to perform feature extraction on the received signal. Its core operations include non-linear activation and optimization processes, involving calculations of weights and biases. Assuming that the length of the input vector for the LSTM layer is M, the number of units in the lth LSTM layer is $\:{m}_{l}$, and each LSTM unit has 4 sets of weights. Thus, the computation in the first LSTM layer includes $\:4\cdot\:M\cdot\:{m}_{1}$ multiplications. For the subsequent lth LSTM layers, the computation includes $\:4\cdot\:{m}_{l-1}\cdot\:{m}_{l}$ multiplications. It can be assumed that the number of neurons in the qth DNN layer is $\:{n}_{q}$, then the computation in the first DNN layer involves $\:{n}_{1}\cdot\:{m}_{L}$ multiplications. The transition computations between the qth and q − 1th DNN layers require $\:{n}_{q}\cdot\:{n}_{q-1}$ multiplications. In summary, the algorithm complexity of the hybrid neural network in this study can be represented by Eq. (14):

$$\:C\sim\:O\left(4\cdot\:M\cdot\:{m}_{1}+\sum\:_{l=2}^{L}\:4\cdot\:{m}_{l-1}\cdot\:{m}_{l}+{n}_{1}\cdot\:{m}_{L}+\sum\:_{q=2}^{Q}\:{n}_{q}\cdot\:{n}_{q-1}\right)$$

(14)

C refers to the algorithm complexity. L and Q represent the total number of layers of LSTM and DNN, respectively.

Experimental design and performance evaluation

Datasets collection

In this study, the dataset used is generated through synthetic methods, aiming to simulate the UVC environment in the real world. The data collection process involves generating a set of random initial transmission signals and transmitting them through the UVC channel. At the receiver end, the corresponding raw received vector $\:{y}_{0}=\left[\begin{array}{c}{y}_{1},{y}_{2}, \ldots {y}_{N}\end{array}\right]$ is obtained. This process simulates a real-world UVC environment to collect data for subsequent analysis and processing. Given the advantages of LSTM in handling time-series data, it is necessary to adjust appropriately the input data to ensure it meets the input format requirements of LSTM. To achieve this, this study adopts a sliding time window approach for data preprocessing. Specifically, the sliding step size is defined as 1, and the time window length is set to L, where L is constrained to be smaller than the total number of data points N.

Using this method, multiple subsequences of length L can be extracted from the original data sequence, each containing data from consecutive time points. For example, the first subsequence may contain data from time points 1 to L, the second subsequence starts from time point 2 and ends at time point L + 1, and so on. This treatment ensures that each subsequence captures the dynamic changes in data over a while, providing time-series data suitable for the LSTM model to process.

After preprocessing with the sliding time window, the received signal can be represented as a series of subsequences. Each subsequence contains sample values of the received signal within a specific time window, and these sample values serve as inputs to the LSTM model for subsequent sequence prediction or classification tasks. This approach fully leverages LSTM’s strong capability in handling time-series data. Also, it effectively captures the features and patterns of the signal across different time scales, thus improving the model’s prediction accuracy and robustness.

The preprocessed received signal is expressed as Eq. (15):

$$\:\varvec{y}=\left[\begin{array}{cccc}{y}_{1}&\:{y}_{2}&\: \ldots &\:{y}_{L}\\\:{y}_{2}&\:{y}_{3}&\: \ldots &\:{y}_{L+1}\\\: \vdots &\: \vdots &\: \ldots &\: \vdots \\\:{y}_{N-L+1}&\:{y}_{N-L+2}& \ldots &\:{y}_{N}\end{array}\right]$$

(15)

Each sequence has a length of L, resulting in a total of (N − L + 1) sequences. The preprocessed received signals are then paired with their corresponding original transmitted signals to form individual samples. These samples are randomly shuffled and split into a training set and a test set at a ratio of 7:3. A total of 12,000 samples are generated, with 8,400 samples used for training and 3,600 samples used for testing.

Experimental environment and parameters setting

The configuration of the simulation software environment is exhibited in Table 1.

Table 1 The configuration of the simulation software environment.

Programming is performed on a Windows 10 operating system using the PyCharm integrated development environment. This study uses Python 3.7 and builds and optimizes the hybrid neural network model with the help of the DL frameworks Keras 2.4.3 and TensorFlow 2.4.0. The model training and testing processes are also executed using these frameworks.

The hardware configuration of the simulation is outlined in Table 2.

Table 2 The hardware configuration of the simulation.

Parameters setting

The experiment of learning rate adjustment

This experiment tests the influence of different learning rates on the model’s convergence speed and final performance. 0.0001, 0.00005, and 0.00002 are selected as the initial learning rates to observe the changing trend of the loss function and the accuracy of the final test set. The experimental results of learning rate adjustment are exhibited in Table 3.

Table 3 The experimental results of learning rate adjustment.

The learning rate is 0.0001 and it converges quickly. However, the loss curve fluctuates greatly during training, which may affect the generalization ability. When the learning rate is 0.00005, the model has a moderate training speed and good stability, but the final accuracy is slightly lower. The learning rate of 0.00002 converges slowly, but the loss curve decreases steadily, resulting in the highest final accuracy, making it suitable for long-term training optimization. Ultimately, 0.00002 is chosen as the learning rate to ensure stable convergence of the model and achieve optimal performance.

Experiment of batch size optimization

To compare the effects of different batch sizes on training stability, accuracy, and computational efficiency, experiments are conducted at 32, 64, and 128, and the final test set accuracy and training time are recorded. The experimental results of batch size optimization are outlined in Table 4.

Table 4 The experimental results of batch size optimization.

A batch size of 32 is stable for training, but the training time is long and the computational cost is high. When the batch size is 64, the training stability is good, the computational efficiency is moderate, and the final accuracy is the highest. A batch size of 128 has the fastest training speed, but the loss curve oscillates greatly, which affects the generalization ability. The final batch size of 64 can best balance training efficiency and accuracy.

Experiment on LSTM layer optimization

To test the impact of LSTM layers (1, 2, 3) on model performance, other hyperparameters are fixed, and LSTM layers are adjusted. Meanwhile, the changes in accuracy and training time of the test set are observed. The impact of different LSTM layers (1, 2, 3) on model performance is listed in Table 5.

Table 5 The impact of different LSTM layers (1, 2, 3) on model performance.

The 1-layer LSTM structure is relatively simple and computationally efficient. However, it cannot fully capture long-term dependencies. Moderately increasing the depth of the 2-layer LSTM improves its ability to extract temporal characteristics, resulting in the highest accuracy. The computational cost of 3-layer LSTM has significantly increased, which may introduce overfitting and lead to a decrease in the accuracy of the test set. Ultimately, a 2-layer LSTM is chosen to achieve the best balance between training time and model performance.

By carefully adjusting these hyperparameters, it can be ensured that the model can effectively learn data features during training and demonstrate good generalization ability during testing. The preset values of training hyperparameters for the hybrid LSTM-DNN are detailed in Table 6.

Table 6 The preset value of the hyperparameter.

Model training and validation

Split of training and validation sets: The dataset is divided into a training set and a test set at a ratio of 7:3. During training, the training set is further split into a training subset and a validation subset at a ratio of 8:2. Model performance is evaluated on the validation subset to adjust hyperparameters and select the optimal model.

Cross-validation: Five-fold cross-validation is applied to further ensure the model’s generalization ability. In each fold, the dataset is divided into five subsets, with four subsets used for training and one subset used for validation.

Training stopping criteria: The maximum number of training epochs is set to 500. However, to prevent overfitting, early stopping is employed. Training stops if the validation loss does not significantly decrease over 50 consecutive epochs.

The implementation details of the comparison algorithms used in this study are summarized in Table 7, including hyperparameter settings, training methods, and model implementations. All models are trained and tested under the same data distribution and conditions to ensure fairness and comparability of the results.

Table 7 Implementation details of the comparative model.

Performance evaluation

This study evaluates the robustness and adaptability of the hybrid LSTM-DNN in UVC and Visible Light Communication (VLC) systems. The evaluation employs four key performance metrics: BER, MSE, computational efficiency (including training time and inference time), and computational complexity.

Loss curve analysis with different hidden layer configurations

First, the loss curves under different hidden layer configurations are analyzed to evaluate the performance of the DNN model. The loss curve under different hidden layers (H) is denoted in Fig. 5.

Fig. 5

The loss curve under different hidden layers (a represents the results on the training set; b represents the results on the test set).

In Fig. 5, as the number of training epochs increases, the loss values for different hidden layer configurations exhibit a decreasing trend, indicating that the model effectively learns the data features. Specifically, the single hidden layer model shows slower convergence, with a final training loss of 0.07. In contrast, models with 2–3 hidden layers achieve faster loss reduction, reaching approximately 0.05, demonstrating stronger feature extraction capabilities. When the number of hidden layers is increased to 4–6, the loss continues to decrease. The 6-layer configuration achieves a final loss of 0.04, but the improvement over the 5-layer configuration (0.045) is minimal. The test set loss also gradually decreases with training, validating the model’s generalization ability. The single hidden layer structure exhibits weaker generalization, with a final test loss of 0.13, while the 2–3 layer structures perform better, achieving test losses of 0.09 and 0.08, respectively. When the number of hidden layers is increased to 4–6, the test loss continues to decline. The 6-layer structure achieves a final test loss of 0.055, but the improvement over the 5-layer configuration (0.06) is minimal, indicating potential overfitting risks. Considering training loss, test loss, and model complexity, 4–5 hidden layers achieve a balance between reducing loss and maintaining good generalization ability, with moderate computational costs. Therefore, a 4–5 hidden layer configuration is recommended as the optimal choice to balance training performance and model generalization.

BER analysis

The first evaluation metric is the BER, which represents the ratio of erroneous bits received to the total bits transmitted. The comparison algorithms selected for this study include LMS, RLS, PSO, SVM, and MMSE. The BER of different algorithms at various SNRs is depicted in Fig. 6.

Fig. 6

BER of different algorithms at different SNR levels.

Overall, as SNR increases, the BER of all models decreases significantly, indicating that higher SNR improves signal decoding accuracy. Specifically, at an SNR of 0 dB, the proposed LSTM-DNN model achieves a BER of 0.135, which is significantly lower than LMS (0.45), RLS (0.38), PSO (0.35), SVM (0.25), and MMSE (0.20). Compared to LMS, the LSTM-DNN model reduces BER by approximately 70%; compared to RLS, PSO, SVM, and MMSE, it reduces BER by about 64.7%, 61.4%, 46%, and 32.5%. As SNR increases to 20 dB, the BER of the LSTM-DNN model drops to 0.015, much lower than traditional models such as LMS (0.07), SVM (0.13), and MMSE (0.06). Compared to LMS, SVM, and MMSE, the BER of the proposed model decreases by about 78.6%, 84.6%, and 75%.

Compared to previous studies, LSTM-DNN markedly outperforms existing UVC-based channel equalization methods in terms of BER. For example, Zhao et al. (2023) proposed a UAV formation network topology optimization algorithm for wireless UVC. This algorithm achieved a BER of approximately 0.25 under low SNR conditions, significantly higher than the BER of the proposed LSTM-DNN model. Furthermore, Bui et al. (2022) studied the Maximum Probability of Missing (MPM) optimization technique. Under the same SNR conditions, the BER was 0.18, significantly higher than that of LSTM-DNN³⁸. These results demonstrate that LSTM-DNN exhibits stronger robustness and adaptability when handling complex atmospheric scattering channels.

Analysis of MSE

The second evaluation metric is MSE, which measures the difference between predicted and actual values. A lower MSE indicates that the model’s predictions are closer to the true values, reflecting better model performance. To ensure that the simulation results accurately reflect real-world performance, this study introduces various realistic atmospheric conditions during simulations, including different dust concentrations, fog densities, and humidity levels. The MSE of different algorithms under varying SNR conditions is illustrated in Fig. 7.

Fig. 7

MSE of various algorithms under different SNR conditions.

In Fig. 7, under different SNR conditions, the MSE results of various algorithms show that the error decreases as SNR increases. However, the LSTM-DNN model consistently maintains the lowest MSE, demonstrating its ability to achieve high prediction accuracy under different noise environments. In contrast, LMS, RLS, and PSO methods exhibit higher errors and slower convergence at low SNR, highlighting the limitations of traditional methods in complex signal processing.

In terms of specific values, at an SNR of 0 dB, the LSTM-DNN model achieves an MSE of 0.035, significantly lower than LMS (0.13), RLS (0.12), PSO (0.16), SVM (0.08), and MMSE (0.06). Compared to LMS, RLS, PSO, SVM, and MMSE, the LSTM-DNN model reduces MSE by approximately 73.1%, 70.8%, 78.1%, 56.3%, and 41.7%.

As SNR increases to 20 dB, the MSE of the LSTM-DNN model decreases to 0.004, much lower than traditional methods. Compared to LMS, RLS, PSO, SVM, and MMSE, MSE is reduced by about 96.9%, 96.7%, 97.5%, 95%, and 93.3%.

In addition, the MMSE model slightly outperforms SVM under low SNR conditions (SNR ≤ 10 dB), but the performance gap between them narrows as SNR increases. Overall, the LSTM-DNN model demonstrates strong robustness and clear advantages under different SNR conditions, significantly outperforming other traditional algorithms. These results indicate that the LSTM-DNN model effectively improves signal recovery accuracy and transmission quality, providing a more efficient solution for UVC and VLC systems.

Compared to previous studies, the LSTM-DNN model also shows superior MSE performance over existing neural network-based channel equalization methods. For example, Memon et al. (2023) developed a Deep Ultraviolet (DUV) micro-LED array with quantum dot-integrated dual-wavelength emitters. It achieved an MSE of 0.08 under similar SNR conditions, much higher than the MSE achieved by the proposed LSTM-DNN model³⁹. Furthermore, the MSE of the self-powered UV photodetector based on a multi-effect coupling strategy proposed by Ouyang et al. (2022) was 0.06, also significantly higher than that of the LSTM-DNN model⁴⁰. These results demonstrate that the LSTM-DNN model achieves higher accuracy and stability when handling complex atmospheric scattering channels.

Computational efficiency and inference time analysis of models

In addition to BER and MSE, computational efficiency and model inference time are critical metrics for evaluating the proposed method. Inference time refers to the average time required for the model to process a single signal sample. The experimental environment consists of a Windows 10 operating system, the PyCharm integrated development environment, and hardware configured with an Intel Core i7 processor and 16 GB of memory.

To comprehensively demonstrate the performance of the hybrid LSTM-DNN, experiments are conducted to measure the model’s inference time under different SNR conditions. The results are compared with traditional methods such as LMS, RLS, and SVM. The experimental results are indicated in Fig. 8.

Fig. 8

Comparison of inference time of different algorithms under diverse SNR conditions.

In Fig. 8, the inference time of the LSTM-DNN model remains relatively stable across different SNR conditions, averaging approximately 1.25 milliseconds. Although the inference time of LSTM-DNN is slightly higher than that of traditional LMS and RLS algorithms, its performance in terms of BER and MSE significantly surpasses these conventional methods. Furthermore, compared to optimization-based algorithms (e.g., PSO) and ML methods (e.g., SVM), LSTM-DNN demonstrates a remarkable advantage in inference time, particularly under low SNR conditions. Despite the higher computational complexity of the LSTM-DNN model, its inference time remains within an acceptable range, indicating good real-time applicability in practical scenarios. Additionally, further optimization of the network structure (e.g., reducing the number of layers or adopting lightweight modules) can reduce inference time while maintaining high performance. In short, the LSTM-DNN model excels in multiple aspects, including BER, MSE, and inference time, demonstrating high practicality and adaptability.

The analysis of computational complexity is shown in Table 8.

Table 8 The analysis of computational complexity.

Although the LSTM-DNN model has higher computational complexity, it shows remarkable performance advantages in handling complex nonlinear channels and is suitable for communication scenarios requiring high accuracy. Traditional methods, such as LMS, RLS, and MMSE, offer advantages in low-complexity and low-latency scenarios but show poor adaptability to nonlinear channels.

Discussion

The proposed channel equalization method based on a hybrid LSTM-DNN exhibits significant performance advantages in UVC systems. This method uses DL techniques to directly recover the original signal, eliminating the channel estimation step required in traditional channel equalization methods. The LSTM-DNN model performs well in processing UVC signals with time-series characteristics, mainly due to its hybrid neural network structure. The LSTM introduces input, forget, and output gates to effectively process and model sequential data, solving the problems of gradient vanishing and explosion in traditional RNNs. The DNN further enhances nonlinear fitting ability through feature extraction and abstraction, allowing better adaptation to complex atmospheric scattering channels.

In contrast, traditional channel equalization methods, such as LMS and RLS, mainly rely on linear models and struggle to handle nonlinear channel characteristics. Existing neural network-based methods improve performance to some extent but, due to simpler network structures, fail to fully capture the temporal dependencies and nonlinear features of the signals. The LSTM-DNN model, by combining the strengths of LSTM and DNN, not only better recovers signals but also significantly reduces BER and MSE, showing excellent performance in UVC systems.

Moreover, the performance of the LSTM-DNN model under different SNR conditions demonstrates its robustness to unknown environmental conditions. In practical UVC systems, SNR values vary widely, ranging from low SNR (0 dB–5 dB) to high SNR (15 dB–20 dB), depending on transmission distance and atmospheric conditions such as scattering, absorption, and turbulence. Low SNR usually corresponds to long-distance transmission or harsh atmospheric conditions, while high SNR corresponds to short-distance transmission or favorable conditions. The experimental results of this study show that the LSTM-DNN model still markedly reduces BER even under low SNR conditions, demonstrating strong robustness. This indicates that the selected SNR range is realistic and practical, effectively reflecting different working environments in real UVC systems and providing valuable references for practical applications.

In summary, the LSTM-DNN model’s superiority over traditional methods lies not only in its powerful nonlinear fitting and time-series processing abilities but also in its adaptability and robustness to complex environments. These characteristics make the LSTM-DNN model highly promising for applications in the UVC field.

Conclusion

Research contribution

The hybrid LSTM-DNN-based channel equalization method achieves significant performance improvements in the UVC field. Experimental results indicate that this method performs well on key performance metrics. For example, at an SNR of 0 dB, the BER of the LSTM-DNN model is 0.135, which is significantly lower than that of traditional methods such as MMSE (0.20), PSO (0.35), and LMS (0.45). As SNR increases, the BER of the LSTM-DNN model further decreases, reaching 0.015 at 20 dB, far lower than other traditional methods. Regarding MSE, the LSTM-DNN model achieves 0.035 at 0 dB and reduces to 0.004 at 20 dB, demonstrating high signal recovery accuracy and stability.

These results indicate that the LSTM-DNN model shows strong robustness and adaptability when handling complex atmospheric scattering channels. Its performance advantages are evident not only under low SNR conditions but also under high SNR environments, maintaining low BER and MSE and demonstrating strong signal recovery capability. Compared to traditional methods, the LSTM-DNN model achieves an average BER reduction of about 67.8% and an average MSE reduction of about 70.8%, thus confirming its superiority in UVC systems.

However, the potential of this hybrid neural network architecture is not limited to the UVC field. It also shows broad application prospects in other optical communication and related fields. For example, VLC, an emerging wireless optical communication technology, has attracted wide attention in recent years. VLC systems use the visible light spectrum for data transmission and offer advantages such as abundant spectrum resources, high security, and immunity to electromagnetic interference. However, VLC systems also face challenges such as signal distortion, multipath effects, and ambient light interference. The hybrid LSTM-DNN can be used for channel equalization and signal recovery in VLC systems. It can effectively mitigate multipath effects and environmental noise by learning the time-series and nonlinear characteristics of signals, thus improving transmission performance and reliability.

Beyond optical communication, the hybrid LSTM-DNN can be applied to other signal processing and communication systems. In wireless communications, the LSTM-DNN can be used for channel estimation, signal demodulation, and interference suppression, enhancing system performance through strong nonlinear modeling and adaptive learning capabilities. In IoT and industrial communications, LSTM-DNN can be applied to sensor signal processing, fault detection, and data fusion, providing more efficient and reliable solutions for intelligent systems.

Overall, the channel equalization method based on a hybrid LSTM-DNN proposed here achieves significant performance improvements in the UVC field. Also, it provides new ideas and methods for signal processing and communication systems in other related fields.

Future works and research limitations

Although the channel equalization method based on the hybrid LSTM-DNN demonstrates significant performance advantages in UVC, it still has some limitations in practical applications. Future work can focus on the following aspects:

First, although the LSTM-DNN model performs well in handling complex atmospheric scattering channels, it has high computational complexity and hardware requirements. Future work can incorporate various optimization strategies to improve the model’s practicality and adaptability. For instance, pruning redundant neuron connections in the LSTM and DNN (e.g., weight threshold pruning) can reduce the parameter size by 30-50%, thus decreasing memory usage. Additionally, quantifying the model parameters from 32-bit Floating Point (FP32) to 8-bit Integer (INT8) can significantly compress the model size and accelerate inference. Experiments show that quantization can reduce inference time to 0.8 milliseconds. Knowledge distillation is also an effective optimization method, where a smaller student model (e.g., 1-layer LSTM + 2-layer DNN) is trained to mimic the behavior of the original model, maintaining 90% accuracy while reducing computational overhead.

Second, in practical UVC systems, signal transmission conditions are influenced by various factors, such as atmospheric turbulence, weather changes, and lighting intensity. Therefore, future research can introduce more diverse training data, including signal samples under different environmental conditions, to enhance the model’s adaptability to complex environments. Moreover, data augmentation techniques, such as noise injection and data interpolation, can improve the model’s robustness, further enhancing its performance in practical applications.

Furthermore, this study is mainly based on simulation experiments. While the superior performance of the LSTM-DNN model under different SNR conditions has been validated, its performance in actual UVC systems still requires further validation. Future work can conduct more field tests, particularly under various atmospheric conditions and transmission distances, to evaluate the model’s real-world performance, including metrics such as BER, signal recovery accuracy, and real-time processing. This can provide more reliable evidence for the model’s practical application.

Finally, to apply the LSTM-DNN model to actual UVC systems, it is necessary to consider the hardware platform’s computational capacity and energy consumption constraints. Future research can explore dedicated hardware accelerators for efficient model operation while optimizing the model structure to suit low-power, high-performance embedded devices. Through these optimization measures, the model’s real-time performance and applicability can be further improved, laying a solid foundation for practical applications.