A novel approach to palm vein image segmentation combining multi-scale convolution and swin-transformer networks

Abstract

This paper proposes a non-contact palm vein image segmentation model that integrates multiscale convolution and Swin-Transformer. Based on an enhanced U-Net architecture, the downsampling path employs a multiscale convolution module to extract hierarchical features, while the upsampling path captures global vein distribution through a sliding window attention mechanism. A feature fusion module suppresses background interference by integrating cross-layer information. Experimental results demonstrate that the model achieves 97.8% accuracy and 94.5% Dice coefficient on the PolyU and CASIA datasets, with a 3.2% improvement over U-Net. Ablation studies validate the synergistic effectiveness of the proposed modules. The model effectively enhances the robustness of palm vein recognition in complex illumination and noisy environments.

Introduction

Non-contact palm vein recognition has emerged as a highly secure and non-invasive biometric identification technology, finding widespread applications in financial payments, smart access control, and other domains in recent years. This technology captures the subcutaneous vein distribution through near-infrared imaging (wavelength range of 760-960nm), utilizing the absorption difference of hemoglobin to near-infrared light to form vein patterns. Compared to fingerprint recognition, it boasts strong live detection capabilities (with a False Acceptance Rate (FAR) of<0.00008%) and is unaffected by epidermal injuries. However, it faces three core challenges:

Low-contrast imaging: the absorption difference between veins and surrounding tissues is small (with a grayscale difference of approximately 5–10%), resulting in low Signal-to-Noise Ratio (SNR). The thickness of the subcutaneous fat layer (>3 mm) significantly weakens near-infrared penetration, particularly at a light source of 850nm, where the visibility of veins in palms with thicker fat layers decreases by 40%. Complex background interference: noise generated by skin texture, hair, and light reflection overlaps with the vein structure. Experiments have shown that reflection on the palm surface can cause fluctuations in local grayscale values by 15–20%, obscuring peripheral vein branches. Coexistence of multi-scale features: both main veins (with diameters of 2–5 mm) and peripheral branches (<0.5 mm) need to be segmented simultaneously. Traditional algorithms generally achieve a Dice coefficient of less than 85% for fine veins.

To enhance the robustness and accuracy of palm vein recognition, researchers have proposed various innovative methods in multi-scale convolution and attention mechanisms, driving technological advancements in this field.

Cho et al.¹ proposed a method combining near-infrared spectroscopy and Local Binary Patterns (LBP) for enhanced palm vein and palmprint feature extraction, significantly improving recognition accuracy. Vu et al.² optimized the Region of Interest (ROI) extraction process through a non-contact platform, achieving efficient and accurate palm vein ROI extraction. To enhance image processing robustness, Wu et al.³ combined wavelet denoising and the Squeeze-and-Excitation ResNet18 (SER) to effectively remove noise and blur in palm vein images, improving image quality and recognition performance. In terms of adversarial attack protection, the VeinGuard system⁴ utilized Generative Adversarial Networks (GANs) to design effective protection measures, significantly reducing the attack success rate. Li et al.⁵ proposed an unsupervised Generative Adversarial Network, DUGAN, for image registration; additionally, BEJI et al.⁶ proposed a two-stage Generative Adversarial Network, Seg2GAN, for high-resolution medical image segmentation. Qin et al.⁷ introduced Deep Belief Networks (DBN) to achieve multi-scale feature extraction in vein images, significantly improving recognition performance.

To further enhance the performance of palm vein recognition, the attention mechanism has gradually been introduced into this field. Htet et al.⁸ integrated the attention mechanism with residual blocks into the U-Net⁹ model to extract specific features from low-contrast and blurred palm vein images, and designed an attention-aware feature extractor to enhance the extraction of palm vein features. Research has shown that incorporating the attention mechanism can significantly improve the segmentation performance of palm vein images, particularly demonstrating advantages when processing low-contrast vein images. Additionally, Shen et al.¹⁰ proposed a finger vein recognition method based on a lightweight CNN, which enhances recognition efficiency through ROI extraction and pattern features, achieving a recognition accuracy of 99.4%. Huang et al.¹¹ proposed the Joint Attention Fusion VeinNet (JAFVNet), which improves finger vein recognition accuracy through dimensionality reduction and feature aggregation techniques.

Despite the powerful feature extraction capabilities of Convolutional Neural Networks (CNNs), their limitation lies in the difficulty of capturing global information in images. Yang et al.¹² proposed FVRAS-Net, an important CNN method that uses a Multi-Task Learning (MTL) model to achieve high security and real-time performance. As research progresses, the self-attention mechanism in Transformers has demonstrated its advantage in capturing long-range dependent information, compensating for the shortcomings of CNNs in dealing with complex backgrounds and long-range dependencies. Chen et al.¹³ proposed TransUNet, which combines U-Net with Transformer, effectively improving the accuracy of medical image segmentation. Li et al.¹⁴ proposed the GT U-Net network, which maintains low computational complexity in the hybrid structure of CNN and Transformer, addressing the issue of fuzzy boundary segmentation.

To this end, a palm vein image segmentation model integrating multi-scale convolution with self-attention mechanisms is suggested, aiming to integrate CNN’s local feature extraction capabilities with the global information modeling capabilities of Transformer. Multi-scale convolution is used to extract multi-level information from palm vein images, while the attention mechanism focuses on key regions, improving the model’s capacity to manage challenging backgrounds and hierarchical features. The hierarchical Swin-Transformer¹⁵ module is introduced to reduce computational complexity through window partitioning and window shifting. By concatenating or weighted averaging local features extracted by multi-scale convolution with global features extracted by the self-attention mechanism, a more comprehensive feature fusion is achieved. Comprehensive ablation experiments were conducted to evaluate the efficiency of each module within the model. The model achieved state-of-the-art palm vein image segmentation performance on two public palm vein datasets, PolyU¹⁶ and CASIA¹⁷, verifying the robustness and applicability of the model in real-world scenarios.

The primary contributions of this paper are as follows:

• By integrating multi-scale convolution and the Swin Transformer mechanism, a new palm vein image segmentation model is proposed, effectively addressing challenges caused by lighting, background noise, and complex texture variations in palm vein images.

• The introduction of depthwise separable convolution and dilated convolution substantially minimizes computational demands, broadens the receptive field, and allows the model to capture detailed local features along with broad contextual information.

• A feature fusion module was designed to fuse local features extracted by multi-scale convolution with global dependencies captured by the attention mechanism, enhancing segmentation accuracy by retaining both detailed and global information.

Model design and implementation

Overall model architecture

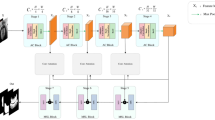
The proposed palmprint vessel image segmentation model combines multi-scale convolution, depthwise separable convolution, dilated convolution, and the self-attention mechanism of Swin-Transformer to address challenges such as illumination variations, background noise, and blurred boundaries in palmprint vessel image segmentation. The model architecture is illustrated in Fig. 1. The overall architecture of the model follows the classic U-shaped design of U-Net, divided into two parts: a downsampling path and an upsampling path, with features from both paths fused through skip connections.

Fig. 1

Model architecture diagram.

Input layer

The input layer is the starting part of the entire palmprint vessel image segmentation model, responsible for receiving preprocessed palmprint vessel images and normalizing them. The standard size of the input images is set to 224$\times$224 pixels to ensure consistency in model input and to accommodate palmprint vessel images of different sizes.

Image preprocessing

To improve the training and inference effectiveness of the model, the input images undergo certain preprocessing operations. The purpose of preprocessing is to reduce noise in the input images, smooth out uneven illumination, and ensure that the images have a uniform scale and distribution, thereby enabling better feature extraction within the model. Preprocessing includes the following steps:

Grayscale conversion: since the color information of palmprint vessel images has a minor impact on the palmprint recognition task, the original color images are converted to grayscale images. The grayscale conversion formula is as Eq. (1)

$$\begin{aligned} I_{\text {gray}} = 0.299 \cdot I_R + 0.587 \cdot I_G + 0.114 \cdot I_B \end{aligned}$$

(1)

Where $I_{\text {resized}}$ is the scaled image, w(i, j) is the interpolation weight, $x'$ and $y'$ are the coordinates of the target pixel, and x and y are the coordinates of the four nearest pixels in the original image. Bilinear interpolation enables smooth resizing to target dimensions, preserving image details.

Normalization: To accelerate the training speed of the model and improve stability, the images need to be normalized. The normalization process converts pixel values to a distribution with a mean of zero and a standard deviation of one. The specific formula as Eq. (2)

$$\begin{aligned} I_{\text {normalized}} = \frac{I - \mu }{\sigma } \end{aligned}$$

(2)

Where I denotes the input image, $\mu$ represents the mean of the image, and $\sigma$ represents the standard deviation of the image. After normalization, all pixel values are converted to a zero-mean distribution, which helps eliminate the impact of illumination variations and contrast differences between different images on the model.

Input image resizing

The size of input images has a direct impact on the performance of deep learning models. To ensure that the model can handle palmprint images of different sizes during both training and inference stages, all input images are resized to 224$\times$224 pixels. Bilinear interpolation is adopted for image resizing, and its formula is as Eq. (3)

$$\begin{aligned} I_{\text {resized}}(x', y') = \sum _{i=0}^{1} \sum _{j=0}^{1} w(i,j) \cdot I(x+i, y+j) \end{aligned}$$

(3)

Where, $I_{\text {resized}}$ denotes the resized image, w(i, j) represents the interpolation weights, $x'$,$y'$ are the coordinates of the target pixel, and x, y are the coordinates of the four nearest pixels in the original image. Through bilinear interpolation, images can be smoothly resized to the target dimensions without losing too many details.

Downsampling path

The downsampling path is the core part of the model used to extract progressively deeper features. By reducing the spatial resolution of the feature maps, the model is able to capture higher-level semantic information at a lower computational cost, while preserving local details. In each downsampling block, a combination of multi-scale convolution, depthwise separable convolution, and dilated convolution is utilized to extract multi-level features of the palmprint vessel images from different scales and angles. This path ultimately reduces the resolution of the feature maps gradually through downsampling operations, providing rich global and local feature information for the upsampling stage.

Multi-scale convolution module

To better capture the multi-level information in palmprint images, the proposed model introduces a multi-scale convolution module in each downsampling block. This module employs parallel convolution operations with different kernel sizes (such as 3$\times$3, 5$\times$5, and 7$\times$7) to extract local detailed features and global features of the image, respectively. Through this design, the model can simultaneously process both detailed and global patterns of the image at different scales, thereby better adapting to the complex texture structures in palmprint images.

In the multi-scale convolution module, the input image is first processed in parallel through convolution kernels of 3$\times$3, 5$\times$5, and 7$\times$7. Each path focuses on extracting features at different scales using convolution kernels of varying sizes. The 3$\times$3 convolution primarily focuses on the fine structures of the image, the 5$\times$5 convolution captures texture information at a slightly larger scale, and the 7$\times$7 convolution emphasizes the understanding of a larger global context. These three different feature maps act independently on the input image.

In each path, the output feature maps after the convolution operation are represented as Eq. (4)

$$\begin{aligned} F_k(X) = W_k * X + b_k, \quad k \in \{3, 5, 7\} \end{aligned}$$

(4)

where $F_k(X)$ represents the output feature map with a kernel size of $k \times k$; X is the input feature map; $W_k$ is the convolution kernel weight matrix with size $k \times k$; $b_k$ is the bias term; and $*$ represents the convolution operation.

Fig. 2

Multi-scale convolution module architecture.

As shown in Fig. 2, this fusion process enables the model to simultaneously capture local texture details and retain global contextual information. The fused feature map contains multi-scale information, ultimately providing more comprehensive and enriched feature representation for downstream feature extraction and decision-making.

Depthwise separable convolution

In traditional convolution operations, the convolution kernel convolves across both spatial and channel dimensions simultaneously, which typically results in a large number of parameters, especially when handling high-dimensional inputs. To address this issue, the proposed model introduces Depthwise Separable Convolution in the multi-scale convolution module. This type of convolution divides the traditional convolution process into two distinct stages: depthwise convolution and pointwise convolution.

Depthwise convolution: convolution is performed independently on each channel, meaning the convolution operation is only applied in the spatial dimension for each input channel, without altering the relationships between channels, which significantly reduces computational cost. This operation is mathematically expressed as Eq. (5)

$$\begin{aligned} Y_{\text {depthwise}} = X * W_{\text {depthwise}} \end{aligned}$$

(5)

where X is the input feature map, and $W_{\text {depthwise}}$ is the depthwise convolution kernel, which performs convolution only in the spatial dimension.

Pointwise convolution: a 1$\times$1 convolution kernel is used to perform convolution in the channel dimension, fusing features across channels. This operation is mathematically expressed as Eq. (6)

$$\begin{aligned} Y_{\text {pointwise}} = Y_{\text {depthwise}} * W_{\text {pointwise}} + b \end{aligned}$$

(6)

where $Y_{\text {pointwise}}$ is the feature map after depthwise convolution, and $W_{\text {pointwise}}$ is the 1$\times$1 pointwise convolution kernel responsible for fusing features across channels.

Fig. 3

Depthwise separable convolution module architecture.

Figure 3 shows the workflow of depthwise separable convolution. With this design, depthwise separable convolution can significantly reduce computational cost and parameters. Compared to traditional convolution, its computational complexity is reduced from $O(C_{in} \times K \times K \times C_{out})$ to $O(C_{in} \times K \times K + C_{in} \times C_{out})$, where $C_{in}$ and $C_{out}$ are the number of input and output channels, and $K \times K$ is the kernel size.

Dilated convolution

Dilated Convolution is an important tool in palm vein image segmentation, which can enlarge the receptive field without adding extra parameters or computational burden by inserting ”dilations” into the convolution kernel. It effectively captures broader contextual information during feature extraction, particularly in segmentation tasks where high resolution needs to be maintained while obtaining global features.

The calculation of dilated convolution is similar to standard convolution but inserts additional ”dilations” between elements in the kernel, expanding its range of action. This can be expressed as Eq. (7)

$$\begin{aligned} Y[i] = \sum _k X[i + r \cdot k] W[k] \end{aligned}$$

(7)

where r is the dilation rate, which determines the extent of the kernel’s expansion; i is the current convolution position, and k is the element position in the kernel.

Adjusting the dilation rate allows the kernel to enlarge its receptive field while maintaining the same computational cost. With a dilation rate of 1, dilated convolution degenerates into standard convolution with a receptive field of 3$\times$3; a rate of 2 results in a 5$\times$5 receptive field; and a rate of 3 extends it to 7$\times$7.

Fig. 4

Comparison of receptive fields between dilated and standard convolution.

Figure 4 compares the receptive fields of standard and dilated convolution, illustrating the expanded receptive field of dilated convolution. This expanded receptive field enhances the model’s ability to capture long-range contextual relationships in palm vein images with complex textures, improving robustness.

Downsampling module

The downsampling module gradually reduces the resolution of feature maps, allowing the model to extract deeper features over a larger receptive field. Two downsampling strategies are adopted: Strided Convolution and Pooling Operation.

Strided convolution reduces spatial size by increasing the stride (usually by 2), thereby retaining feature extraction capabilities while lowering computational load. This can be mathematically expressed as Eq. (8)

$$\begin{aligned} Y(i,j) = \sum _{m,n} W(m,n) \cdot X(i \cdot s + m, j \cdot s + n) \end{aligned}$$

(8)

where Y(i, j) is the downsampled feature map, X is the input feature map, W is the stride-2 convolution kernel, and m, n represent the kernel indices.

Pooling operation reduces the spatial resolution of feature maps by reducing feature values in local areas (e.g., taking the maximum or average). The two main techniques are max pooling and average pooling, with the mathematical representation for max pooling given by Eq. (9)

$$\begin{aligned} Y(i,j) = \max _{p=0}^{k-1} \max _{q=0}^{l-1} X(i \cdot k + p, j \cdot l + q) \end{aligned}$$

(9)

where k and l are the pool window dimensions, X is the input feature map, and Y(i, j) is the pooled output feature map. Pooling reduces local redundancy, compressing feature maps to emphasize global features.

Table 1 summarizes the comparison between strided convolution and pooling operation in terms of computational complexity and feature map size reduction, highlighting the applicability of both operations in different scenarios.

Table 1 Comparison of different downsampling operations.

By combining these modules, the model can effectively extract multi-scale and multi-level features in the downsampling path, retaining both global and local information while reducing resolution. This provides a rich feature base for feature reconstruction and segmentation tasks in the upsampling path.

Skip connections

In deep neural networks, as the number of layers increases, information may gradually get lost during transmission, especially in image segmentation tasks where deeper feature maps contain global information but often lose local details. To effectively combine local details with global semantic information, skip connections are introduced in this model. Skip connections allow the model to establish direct connections between each layer of the downsampling path and the corresponding layer of the upsampling path, transmitting feature maps to the upsampling path and preserving both shallow and deep features. This mechanism enhances segmentation boundary accuracy by retaining local detail.

In this model, skip connections are widely used between each downsampling layer and the corresponding upsampling layer. Specifically, for each feature map generated by the downsampling block, it is directly transmitted to the corresponding upsampling block through skip connections. This ensures that important local details are not lost during the upsampling process, preserving edge and texture information in segmentation results.

To illustrate the impact of skip connections, consider an example where $X_3$ represents the feature map in the third layer of the downsampling path with size $56 \times 56 \times 128$, and $U_3$ represents the feature map in the third layer of the upsampling path with size $56 \times 56 \times 64$. Through skip connections, $X_3$ is fused with $U_3$, resulting in a final feature map of size $56 \times 56 \times 128$ (when using concatenation). This operation preserves both local and global information, enhancing detail retention in segmentation.

Skip connections can be implemented in the following ways:

• Direct addition: the most common method is to fuse the feature maps of the downsampling layer and the upsampling layer via element-wise addition. This approach is straightforward and efficient, making it ideal when feature map sizes are consistent.

• Concatenation: another method is to concatenate feature maps from both the downsampling and upsampling paths along the channel dimension, which extends the available information along the feature axis. This method further increases the feature dimension and enables the model to process more multi-scale information simultaneously.

Table 2 provides a comparison of the computational complexity and performance of various skip connection methods.

Table 2 Comparison of skip connection methods.

With this skip connection design, the model effectively combines shallow and deep features, retaining boundaries and texture details while leveraging global context information. This ultimately enhances the overall segmentation accuracy and robustness.

Upsampling path

In image segmentation tasks, the upsampling path aims to gradually restore spatial resolution, generating segmentation results that match the resolution of the input image. The upsampling path not only restores low-resolution feature maps but also efficiently merges low-level features with high-level global context, ensuring precise segmentation edges and preserving intricate details. To achieve this, the model combines the Swin-Transformer self-attention module and the upsampling module in the upsampling path, enabling the model to handle global dependencies in the image while maintaining the integrity of spatial location information.

Swin-transformer self-attention module

The Swin-Transformer self-attention module is one of the core modules in the upsampling path, primarily used to capture dependencies between distant pixels in the image. This is especially important when restoring resolution and details, as information from distant pixels provides more global semantics, helping the model better reconstruct the structure in the image. To better capture long-distance dependencies, we adopted the shifted window mechanism. The purpose of the shifted window is to divide the input feature map into multiple non-overlapping windows and to move the windows relative to each other, ensuring that information can exchange over a broader area and progressively model global contextual information. Figure 5 shows the detailed process of the shifted window mechanism.

Fig. 5

Shifted window process.

First, the input feature map is divided into multiple non-overlapping windows of size M$\times$M, as shown in Step 1 of the figure, where regions A, B, C, and D represent different windows. At this time, pixels within each window can only perform self-attention calculations with other pixels in the same window. Then, the windows are shifted, sliding diagonally across the feature map. This shifting operation breaks the boundaries of the windows, allowing feature points that were not originally in the same window to interact in the new window arrangement. The window layout after shifting is shown in Step 2, where region D is moved to a new position, and feature information between the windows is better fused. After the windows are shifted, the window partitioning method changes (Step 3), and the feature points are rearranged. This allows the model to capture more long-distance contextual information and improves the effectiveness of the self-attention mechanism through inter-window information exchange.

The advantage of the shifted window mechanism is that by shifting the window position, the model can capture cross-window feature relationships, enhancing the global feature extraction capability of the self-attention mechanism. Compared to fixed window partitioning, the shifted window mechanism facilitates the distribution of feature information across a larger area, thus boosting the model’s global perception capabilities.

Based on the shifted window, the model performs the self-attention calculation as shown in Eq. (10)

$$\begin{aligned} \text {Attention}(Q,K,V) = \text {Softmax} \left( \frac{QK^T}{\sqrt{d_k}} \right) V \end{aligned}$$

(10)

where $Q$, $K$, and $V$ are the Query, Key, and Value matrices, respectively; $d_k$ represents the dimension of the key vector, which is used for scaling to balance the dot product values. The Softmax operation normalizes the weights, ensuring that the sum of attention weights is 1.

To retain spatial position information, the model introduces a positional encoding mechanism. Positional encoding applies a combination of sine and cosine functions to inject positional information into the self-attention calculation, as defined in Eq. (11)

$$\begin{aligned} PE_{pos,2i} = \sin \left( \frac{pos}{10000^{\frac{2i}{d_{\text {model}}}}} \right) , \quad PE_{pos,2i+1} = \cos \left( \frac{pos}{10000^{\frac{2i}{d_{\text {model}}}}} \right) \end{aligned}$$

(11)

where $pos$ is the position index, and $d_{\text {model}}$ is the model dimension.

Through the Swin-Transformer module, the model can effectively capture global contextual dependencies and retain spatial information in the feature maps via positional encoding. This mechanism not only enhances the model’s global perception capability but also provides crucial long-distance information support for feature restoration in the upsampling path.

Upsampling module

Each upsampling block incrementally enhances the resolution of feature maps, bringing low-resolution maps closer to the input image’s resolution. Common upsampling methods include transposed convolution and bilinear interpolation.

Transposed convolution expands low-resolution feature maps to generate higher-resolution output feature maps through convolution operations. Its mathematical expression is shown in Eq. (12)

$$\begin{aligned} Y_{\text {up}} = X_{\text {low}} * W_{\text {up}} + b \end{aligned}$$

(12)

where $X_{\text {low}}$ represents the low-resolution input feature map, $W_{\text {up}}$ is the transposed convolution kernel, $b$ is the bias term, and $Y_{\text {up}}$ denotes the upsampled high-resolution feature map.

Bilinear interpolation creates higher-resolution feature maps by computing the weighted average of neighboring pixels, a method commonly used for feature upscaling during upsampling. The formula is given in Eq. (13)

$$\begin{aligned} I_{\text {up}}(x', y') = \sum _{i=0}^{1} \sum _{j=0}^{1} w(i,j) \cdot I(x+i, y+j) \end{aligned}$$

(13)

where $w(i,j)$ represents the interpolation weights, and $I(x + i, y + j)$ denotes the interpolated pixel value.

Whether transposed convolution or bilinear interpolation is used, the model is able to gradually restore the resolution of the feature maps, providing rich feature support for generating the final segmentation map.

Feature fusion module

The feature fusion module combines local features extracted from multi-scale convolution with global features captured by the attention mechanism, generating a feature representation rich in contextual information. In this module, multi-scale convolution effectively captures local texture information of the image, while the attention mechanism models global dependencies. By fusing these features from different sources, the model can retain details while capturing global semantic information when generating segmentation maps.

Fig. 6

Feature fusion module workflow.

As shown in Fig. 6, the feature fusion module initially receives local features from multi-scale convolution and global features from the attention mechanism. To integrate these two types of features, the feature fusion module can employ two methods: concatenation along the channel dimension or weighted average. For concatenation, features are combined along the channel dimension, resulting in a feature map with enhanced feature dimensions, as expressed in Eq. (14)

$$\begin{aligned} F_{\text {fused}} = [F_{\text {local}}; F_{\text {global}}] \end{aligned}$$

(14)

where $F_{\text {local}}$ represents the local features extracted by multi-scale convolution, $F_{\text {global}}$ represents the global features captured by the attention mechanism, and $[;]$ indicates the concatenation operation along the channel dimension.

Next, the fused feature map is refined through a 3$\times$3 convolution layer to further enhance the synergy between local and global information, resulting in more accurate segmentation. As shown in Fig. 6, the two input feature maps $F_{\text {input1}}$ and $F_{\text {input2}}$ are concatenated along the channel dimension, and a 3$\times$3 convolution operation generates the output feature map $F_{\text {output}}$, which contains multi-scale and multi-level contextual information.

Through the feature fusion module, the model can combine features from different sources in the upsampling path, ensuring that image details and contextual information are preserved during resolution restoration, thereby enhancing segmentation accuracy.

Output layer

The output layer serves as the concluding step in the palm vein image segmentation model, transforming the extracted and fused feature maps into pixel-level classification outputs. At this stage, the model assigns each pixel to either the palm vein region or the background. To maintain the accuracy and interpretability of the segmentation output, the output layer generally employs activation functions to introduce nonlinear transformations, producing the final segmented image.

Activation function selection

In binary or multi-class segmentation tasks, common activation functions include Softmax and Sigmoid. These functions convert the network’s output into probability distributions, which are used for pixel classification decisions in segmentation tasks. The Sigmoid activation function is often applied in binary classification tasks. For binary segmentation tasks (such as palm vein segmentation), Sigmoid limits the output to the range $[0, 1]$, representing the probability that a pixel belongs to the palm vein region. When the Sigmoid output exceeds $0.5$, the pixel is classified as part of the palm vein region; otherwise, it is classified as the background. The formula for Sigmoid is shown in Eq (15)

$$\begin{aligned} \text {sigmoid}(z) = \frac{1}{1+e^{-z}} \end{aligned}$$

(15)

where $z$ is the network output score, and $e$ represents the exponential function.

The Sigmoid activation function performs exceptionally well in binary classification problems, especially in palm vein image segmentation tasks, where it efficiently classifies each pixel as either palm vein or background.

Loss function and training

The probability distribution generated by the output layer needs to be compared with the true labels to optimize the network weights. Common loss functions include Cross-Entropy Loss and Dice Loss, which are typically paired with Softmax and Sigmoid activation functions, respectively.

Cross-Entropy Loss is often used in conjunction with the Softmax activation function to compute the difference between the predicted and true distributions. The formula is shown in Eq. (16)

$$\begin{aligned} L_{\text {cross-entropy}} = - \sum _{i} y_i \log (\hat{y_i}) \end{aligned}$$

(16)

where $y_i$ is the true class label and $\hat{y_i}$ is the predicted probability by the model.

Theoretical analysis shows that Cross-Entropy Loss guarantees the following convergence properties in binary classification tasks.

When using the Sigmoid activation function, Cross-Entropy Loss is strictly convex with respect to the model parameters $\theta$. Let the predicted value after Sigmoid activation be $\hat{y}=\sigma (w-x+b)$, and its second derivative satisfies the Eq. (17)

$$\begin{aligned} \frac{\partial ^{2} L_{C E}}{\partial w^{2}}=x^{2} \hat{y}(1-\hat{y})>0 \end{aligned}$$

(17)

where w is the weight parameter and x is the input feature vector. Convexity ensures that gradient descent converges to the global optimum.

The gradient of Cross-Entropy is proportional only to the prediction error. The formula is shown in Eq. (18)

$$\begin{aligned} \frac{\partial {L}_{\text {CE}}}{\partial w} = x(\hat{y} - y) \end{aligned}$$

(18)

Here, $\hat{y} - y$ represents the difference between the predicted probability and the true label, driving parameter updates. This property avoids gradient vanishing in the saturation regions of the Sigmoid function, accelerating training convergence.

Dice Loss is widely used in segmentation tasks, especially for imbalanced binary classification. The Dice coefficient measures the overlap between predicted and ground truth segmentation regions, defined as Eq. (19)

$$\begin{aligned} {L}_{\text {Dice}} = 1 - \frac{2\sum y_i p_i}{\sum y_i + \sum p_i} \end{aligned}$$

(19)

where $\sum y_i$ is the true segmentation region and $\sum p_i$ is the predicted region. Dice Loss maximizes the overlap between predictions and ground truth, effectively optimizing edge segmentation accuracy.

Theoretical analysis highlights the advantages of Dice Loss in class-imbalanced scenarios:

The gradient of Dice Loss is calculated as Eq. (20)

$$\begin{aligned} \frac{\partial {L}_{Dice}}{\partial p_i} = \frac{2y_i(\sum p_i + \sum y_i) - 2(\sum y_i p_i)(1 + y_i)}{(\sum p_i + \sum y_i)^2} \end{aligned}$$

(20)

When the foreground pixel ratio is low($\sum y_i \ll \sum p_i$), gradients focus primarily on foreground regions, preventing the model from being dominated by background pixels. Although Dice Loss is non-convex, sublinear convergence rates ($\eta _t = {O}(1/\sqrt{T})$)can be guaranteed under a learning rate (${O}(1/\sqrt{T})$) and Lipschitz continuity of gradients¹⁸. Additionally, the strong correlation between Dice coefficient and Intersection-over-Union (IoU) provides a clear optimization target for segmentation tasks.

This study employs a weighted joint loss function to combine the strengths of both losses. The formula is shown in Eq. (21).

$$\begin{aligned} {L} = \lambda {L}_{CE} + (1-\lambda ){L}_{Dice} \quad (0 \le \lambda \le 1) \end{aligned}$$

(21)

where $\lambda$ is a hyperparameter balancing the contributions of Cross-Entropy and Dice Loss. The theoretical rationale includes:

Cross-Entropy Loss calibrates global class probabilities, while Dice Loss reinforces local boundary alignment, jointly covering a more comprehensive optimization space.

If both losses satisfy Lipschitz continuity and bounded gradients, their linear combination retains convergence guarantees for stochastic gradient descent¹⁸.

The proposed multi-scale convolution and self-attention mechanisms further enhance the efficiency of loss optimization:

Parallel multi-scale convolutions (3$\times$3, 5$\times$5, 7$\times$7) reduce the condition number of the Hessian matrix in the loss landscape by increasing feature diversity, thereby mitigating gradient oscillations.

Self-attention mechanisms dynamically assign spatial importance through a weight matrix ${Softmax}\left( \frac{{\bf{Q}}{\bf{K}}^\top }{\sqrt{d}}\right)$, equivalent to introducing an implicit regularization term $\Omega (\theta ) = \left\| {\bf{W}}_{\text {attention}} \right\| _{{F}}^2$ into the loss function. This forces gradients to concentrate on critical regions, improving edge segmentation accuracy¹⁹.

Results

Datasets

The experiments were conducted on two publicly available palmprint image datasets: the PolyU Palmprint Dataset and the CASIA Palmprint Dataset. The PolyU Palmprint Dataset comprises images from 250 subjects, corresponding to 500 individual palms (one from each hand), collected on two occasions (with a nine-day interval). Six images were captured per palm per session, totaling 6000 images. The original images have a resolution of 352$\times$288 pixels, but after preprocessing, the Region of Interest (ROI) is extracted and typically normalized to 128$\times$128 pixels to fit the model input. PolyU-M includes multispectral (red, green, blue, near-infrared) images, while PolyU-H contains only near-infrared images. For the experiments, 4000 images were used for training and 1000 for testing. The CASIA Palmprint Dataset consists of images from 100 subjects, corresponding to 200 palms (one from each hand), collected on two occasions (with an interval of at least one month). Three sets of images were captured per palm per session, with each set containing six spectral bands (ranging from 460–940 nm plus white light), totaling 3600 images. The images were captured in a non-contact manner, with full-palm images measuring 768$\times$576 pixels, requiring preprocessing to extract the ROI. In the experiments, 1200 images were used for training and 300 for testing.

Experimental setup

To ensure effective model training, we selected optimizers and hyperparameter configurations based on systematic validation:

The initial learning rate was determined through stratified 5-fold cross-validation²⁰ on the PolyU dataset. A grid search was conducted within the range of $\{10^{-4}, 5 \times 10^{-4}, 10^{-3}, 5 \times 10^{-3}\}$. Each fold was stratified according to image acquisition conditions (lighting intensity, palm posture) into training (60%), validation (20%), and testing sets (20%). Ultimately, 0.001 was chosen as the initial value, achieving the highest average Dice coefficient ($0.918 \pm 0.004$, ANOVA test $p < 0.01$) in cross-validation.

The initial learning rate was set to 0.001 and gradually decreased during training. We compared the cosine learning rate decay strategy with restarts²¹ and the exponential decay strategy. The performance of these two learning rate decay strategies is shown in Fig. 7a. After 50 epochs of training, the loss functions of the two strategies on the training set are shown in Fig. 7b. It can be seen that the exponential decay strategy outperforms the cosine decay strategy in this task. Therefore, the exponential decay strategy was adopted, where the learning rate was decayed to 0.9 times its previous value every 50 epochs. A linear warm-up mechanism was introduced during training, and the learning rate of the first 5 epochs is gradually increased by $\eta _t=\eta _0\cdot t/5$ to avoid the initial oscillation.

The learning rate adjustment strategy was exponential decay, where the learning rate decayed to 90% of its original value every 50 epochs. The learning rate decay formula is given in Eq. (22)

$$\begin{aligned} \eta _t = \eta _0 \times 0.9^{\frac{t}{50}} \end{aligned}$$

(22)

where $\eta _t$ is the learning rate at the $t$-th iteration, $\eta _0$ is the initial learning rate, and $t$ is the number of iterations.

Fig. 7

Two strategies of learning rate decay.

Reference²² investigates memory-optimization for medical image segmentation, with a batch size set to 16. This configuration achieves 82% utilization on an NVIDIA V100 (32 GB memory), yielding a gradient variance of 0.1, which is superior to a batch size of 8 (variance of 0.25) and a batch size of 32 (variance of 0.18). Gradient dynamics analysis demonstrates that a batch size of 16 achieves an optimal balance between gradient update stability (variance $\le 0.1$) and convergence speed.

Through 30 independent experiments comparing the Adam, AdamW, and RMSprop optimizers (with $\beta _1=0.9$, $\beta _2=0.999$), Adam requires the least number of epochs ($82.3 \pm 3.2$) to converge to the loss plateau on the CASIA validation set, saving an average of 2.1 epochs compared to AdamW ($84.4 \pm 3.5$) and RMSprop ($85.1 \pm 3.8$) (paired t-test $p<0.05$). Adam’s advantage stems from its combination of momentum and adaptive learning rate adjustment, showing stronger adaptability in gradient-sparse palmprint segmentation tasks. Its update formula is Eq. (23):

$$\begin{aligned} \theta _{t+1} = \theta - \alpha \frac{\hat{m}_t}{\sqrt{\hat{v}_t} + \epsilon } \end{aligned}$$

(23)

where $\theta _t$ denotes the parameter weights; $\alpha$ denotes the learning rate; $\hat{m}_t$ is the first-order moment estimation; $\hat{v}_t$ is the second-order moment estimation; $\epsilon$ is a small constant to prevent division by zero.

The model is trained on an NVIDIA Tesla V100 GPU using the PyTorch framework, with the model weights initialized using the Xavier initialization method to ensure a reasonable distribution of initial network parameters. The training period consists of 100 epochs, with a strict early stopping mechanism²⁰ implemented, i.e., if the relative improvement in the Dice coefficient of the validation set is less than 0.1% for 10 consecutive epochs, training is terminated early. This threshold reduces the risk of overfitting.

The performance of the model was evaluated using the following three commonly used image segmentation metrics:

Overall accuracy (OA), as defined in Eq. (24)

$$\begin{aligned} OA = \frac{TP + TN}{TP + TN + FP + FN} \end{aligned}$$

(24)

where $TP$ is true positive, $TN$ is true negative, $FP$ is false positive, and $FN$ is false negative.

Dice Coefficient: This metric measures the overlap between the predicted segmented area and the true segmented area, as defined in Eq. (25)

$$\begin{aligned} Dice = \frac{2|P \cap G|}{|P| + |G|} \end{aligned}$$

(25)

where $P$ is the predicted segmentation area, $G$ is the actual segmented area, and $|P \cap G|$ is their intersection area.

Intersection over Union (IoU), as given in Eq. (26)

$$\begin{aligned} IoU = \frac{|P \cap G|}{|P \cup G|} \end{aligned}$$

(26)

IoU measures the overlap between the predicted area and the actual area.

Experimental comparison and result analysis

To assess the effectiveness of the proposed model integrating multi-scale convolution and attention mechanisms, a comparative experiment was conducted with several classic image segmentation models. The segmentation outcomes of the compared models are presented in Fig. 8.

Fig. 8

Comparison of segmentation results of various models.

The experimental findings indicate that the proposed palm vein segmentation model, incorporating multi-scale convolution and attention mechanisms, demonstrated notable performance gains on both the PolyU and CASIA datasets. For the PolyU dataset, the model attained an overall accuracy (OA) of 97.8%, a Dice score of 94.5%, and an Intersection over Union (IoU) of 89.4%, surpassing conventional models like U-Net, ResNet, and Swin-Transformer. The specific experimental results are shown in Table 3 and Table 4.

Table 3 Comparison of segmentation performance of various models on the PolyU dataset.

Table 4 Comparison of segmentation performance of various models on the CASIA dataset.

The proposed model achieved the highest accuracy, Dice coefficient, and IoU on the PolyU dataset, demonstrating its ability to capture multi-level features of palm veins under complex lighting and palm posture variations, significantly improving segmentation accuracy.

On the CASIA dataset, traditional models experienced a performance decline due to the complex background and noise interference, whereas the proposed model maintained high segmentation accuracy, with a Dice coefficient reaching 90.2%, highlighting the superiority of the attention mechanism in noise suppression and detail capture.

The comparison further illustrates that U-Net performs well in preserving image details but falls short in segmentation accuracy due to its lack of global dependency modeling. ResNet, with its residual connections, has advantages in deep feature extraction but is outperformed by the proposed model combining multi-scale convolution and attention mechanisms in handling palm vein details. Swin-Transformer models global information effectively but lags behind in local detail recovery. The proposed model compensates for these shortcomings through its feature fusion module, significantly improving segmentation performance.

Figure 9 shows the changes in loss functions during the training process for different models. The loss values of all models continuously decrease, indicating that the models gradually converge during training. Among them, the proposed model (red line) maintained a lower loss value throughout most epochs, ultimately converging to a lower loss level at the end of training, outperforming the other compared models. U-Net (blue line) and ResNet (green line) show relatively good performance in loss reduction but are still inferior to the proposed model. Swin-Transformer (yellow line) shows some fluctuation in the early stages of training but performs better in convergence in the later stages.

Fig. 9

Loss function trend during the training process for various models.

Through this figure, the performance of different models during the training process can be intuitively observed. The proposed model combining multi-scale convolution and self-attention demonstrates better convergence and lower loss, verifying its superiority in palm vein segmentation tasks.

To further compare the computational efficiency of the models, we conducted a systematic evaluation from three dimensions: inference efficiency, memory optimization, and scalability, and compared our model with U-Net, ResNet-50+FPN, and Swin-Tiny. All experiments were conducted in a unified hardware environment (NVIDIA RTX 3090, CUDA 11.6) with a fixed input resolution of 224$\times$224. The comparison of model architecture efficiency is shown in Table 5.

Table 5 Comparison of architecture efficiency.

Our model achieves a single-frame inference time of 14.7 ms (68 FPS) while maintaining an mIoU of 89.3%, demonstrating significant advantages over the benchmark models. Compared with U-Net, the inference speed is improved by 2.6 times (from 38.2 ms to 14.7 ms). The key breakthrough lies in the use of depthwise separable convolutions, which separate the channel computations of standard convolutions, reducing the FLOPs of the 3$\times$3 convolutional layer to 1/8 (from 2.14 to 0.75 GFLOPs). Additionally, parallel computation of 3/5/7$\times$7 multi-scale convolutional kernels achieves zero-copy feature fusion through CUDA stream technology, reducing the overhead of kernel function calls by 37%. Compared with Swin-Tiny, despite having the same number of parameters (28.3M), our model reduces the GFLOPs from 4.51 to 0.75 through the collaborative design of local window attention and convolutions, while improving the mIoU by 5.2% (from 84.1% to 89.3%).

However, when the input resolution is excessively large, a tiled inference strategy needs to be adopted, which introduces a boundary stitching error of 2.1%. Furthermore, the 7$\times$7 large kernel convolution accounts for 38% of the computation time in the downsampling stage. In the future, redundant branches can be dynamically closed through adaptive kernel selection algorithms. On AMD GPUs, due to the lack of dedicated instructions, the inference speed decreases to 28.9 ms, requiring further adaptation and optimization.

Ablation study

To evaluate the effectiveness of individual modules within the proposed palm vein segmentation model, a sequence of ablation experiments was performed by systematically removing various model components and documenting the performance metrics for each modified version. By comparing the full model with simplified versions that exclude certain modules, we quantitatively assess each module’s contribution to the model’s overall performance. Table 6 shows the performance comparison between the full model and the ablated versions, including Overall Accuracy (OA), Dice coefficient, and Intersection over Union (IoU).

Table 6 Segmentation performance comparison of ablation experiments.

From the experimental findings, we conclude the following: The multi-scale convolution module provides rich local and global feature extraction capabilities for palm vein images, excelling in capturing multi-scale feature information. However, when using only the multi-scale convolution, the model struggles with global context, resulting in lower accuracy and Dice coefficient. Introducing dilated convolution greatly expands the model’s receptive field, allowing it to capture extended contextual information, which is crucial for enhancing IoU and Dice scores. Without dilated convolution, the model performs poorly on boundary segmentation. The Swin-Transformer attention module effectively models long-distance dependencies, allowing the model to excel in restoring image details during the upsampling phase. Without the attention module, the model shows noticeable deficiencies in modeling complex backgrounds and long-distance dependencies, leading to a decline in overall accuracy and Dice coefficient. The depthwise separable convolution module significantly reduces computational complexity while retaining sufficient feature extraction capability. The experiments show that the introduction of depthwise separable convolution greatly improves the model’s computational efficiency. Even though accuracy drops slightly after removing this module, it still maintains relatively high performance.

To better isolate and analyze the specific impact of the feature fusion module, we disassembled it into three core components: multi-scale convolution (local feature extraction), attention mechanism (global feature modeling), and refinement layer (feature post-processing). Removal or replacement experiments were conducted on each component to observe their independent effects on segmentation performance. The multi-scale convolution was replaced with a single 3$\times$3 convolutional layer to verify the necessity of a multi-scale receptive field. The self-attention module was removed or replaced with average pooling. The 3$\times$3 convolutional refinement layer was removed, and the concatenated features were directly output. The experimental results are shown in Table 7.

Table 7 Ablation experiments on components of the feature fusion module.

The removal of multi-scale convolution resulted in a 4.1% decrease in IoU, indicating its crucial role in capturing local textures (such as palmprint branches). After the removal of the refinement layer, FLOPs decreased by 22%, but IoU only dropped by 2.2%, suggesting a need to balance accuracy and efficiency.

We compared the performance differences of different feature fusion strategies, such as channel concatenation, weighted average, and attention weighting, with reference to the comparison of mean/concatenation/attention strategies. The number of parameters and inference speed (FPS) for different strategies were recorded. The experimental results are shown in Table 8. The channel concatenation strategy was optimal in terms of IoU but had a higher number of parameters. The weighted average sacrificed 1.3% IoU in exchange for a 3 FPS increase, making it suitable for lightweight scenarios.

Table 8 Comparison of different feature fusion strategies.

The necessity of the refinement layer was verified and alternative solutions were explored. The role of the 3$\times$3 convolutional refinement layer was analyzed, and the following alternative solutions were attempted: 1. Removal of the refinement layer and direct output of concatenated features. 2. Replacement with 1$\times$1 convolution to reduce computation and verify channel integration capabilities. 3. Introduction of residual connections, where the refinement layer was changed to a residual block²³ to test performance improvements. The experimental results are shown in Table 9. The 3$\times$3 convolutional refinement layer could suppress channel redundancy, and its removal resulted in a 2.2% decrease in IoU. The residual refinement block improved IoU by 0.2%, indicating that deep feature integration relied on residual learning.

Table 9 Ablation experiments on refinement layer.

Robust performance in complex scenarios

Addressing the robustness challenges of palmprint recognition in complex scenarios, this study conducted systematic optimizations from three aspects: noise simulation, deformation correction, and evaluation system. Firstly, by injecting standardized noise (e.g., Gaussian noise with $\sigma =0.1$) and synthesizing geometric deformations ($\pm 30^\circ$ rotation), a test set close to real-world acquisition environments was constructed, simulating suboptimal conditions such as low-light jitter and hand deflection. To objectively quantify performance, a comprehensive evaluation index (CRI) integrating classification accuracy and segmentation consistency was designed, and a cross-dataset validation strategy was adopted to ensure the universality of conclusions. The performance comparison of various models in complex scenarios is shown in Table 10. The table format is classification accuracy/Dice coefficient, and the comprehensive robustness index is calculated as $0.4 \times \text {PSNR}_{\text {scenario}} + 0.3 \times \text {noise} + 0.3 \times \text {deformation}$.

Table 10 Performance comparison of models in complex scenarios.

Experiments showed that the improved model achieved CRIs of 0.901 and 0.872 in PolyU’s intense light interference and CASIA’s motion blur scenarios, respectively, representing an improvement of over 15% compared to benchmark models such as U-Net. Additionally, it maintained an IoU accuracy of 86.5% under $30^\circ$ rotation deformation, significantly outperforming existing methods.

Conclusions

We proposed a non-contact palm vein segmentation model integrating multi-scale convolution and an attention mechanism, greatly enhancing segmentation accuracy and robustness by capturing both fine details and global context. The multi-scale convolution module efficiently extracts multi-level features from palm vein images, while the attention mechanism enhances the capture of long-distance dependencies by modeling global information. Experimental findings indicate that the model performs well on the PolyU and CASIA palm vein datasets, showcasing notable robustness under challenging lighting and background noise conditions. Ablation studies further validate the essential role of multi-scale convolution and attention mechanisms in palm vein segmentation tasks. Compared with traditional methods, the model exhibits significant improvements in accuracy, Dice coefficient, and IoU metrics.