Impact of incubation and gestation periods on the dynamics of a spatially heterogeneous eco-epidemiological model

Abstract

This study investigates a spatiotemporal eco-epidemic model describing prey–predator dynamics in which the infectious disease affects only the prey population. The model incorporates prey refuge and intraspecific competition among predators and focuses on the stability of the interior equilibrium to analyse disease-driven ecological interactions. Methodologically, this study first derived conditions for Turing instability in the non-delayed system, revealing how diffusion-driven spatial heterogeneity can destabilise homogeneous states. Subsequently, for both non-delayed and delayed systems, Hopf bifurcation analysis is performed to investigate the interaction of incubation and gestation delays both separately and together. Qualitative numerical simulations are conducted to validate the theoretical results. Key findings show that incubation delay causes Hopf bifurcation, therefore changing stability in non-diffusive as well as diffusive systems. Gestation delay may cause stability switching in non-diffusive environments by means of mismatched prey–predator growth-consumption rates. Spatial heterogeneity reduces the destabilisation effect of the gestation delay but loses this stabilising power under fixed incubation delay, stressing complicated delay-space interactions. These results highlight the vital impact of biological delays and spatial heterogeneity on eco-epidemic systems. The study underlines the importance of including temporal lags and spatial processes in forecasts of the effects of disease on ecological dynamics, therefore providing knowledge for conservation and outbreak management strategies.

Introduction

The intricate connection between environmental changes and the proliferation of infectious diseases can be more comprehensively analysed through the application of eco-epidemic models^1,2,3,4. To investigate the ways in which diseases affect the persistence, stability, and interactions of species in ecosystems, these models combine concepts from epidemiology and population ecology. It is fascinating to observe how infectious diseases impact predator behaviour, population sizes, and ecosystem health when they primarily impact the prey population in a predator–prey system. This adds an extra layer of complexity to the dynamics at play. In these types of systems, the pathogen mostly infects the prey population, leaving the predator population unharmed. Complex feedback loops can change predation rates, resource availability, and ecosystem stability after a disease is introduced into a prey population. An example of this would be a drop in predator populations caused by a decrease in food resources, such as a disease-induced drop in prey numbers. However, predators may gain short-term advantages at the expense of prey populations if the sickness makes animals more susceptible to predation. In order to preserve ecosystems, control diseases, and protect species, it is essential to understand these processes. Researchers can learn more about the ways infectious diseases affect ecological groups, how to anticipate and prepare for outbreaks, and how to lessen their effects by looking at the eco-epidemic system in which the disease solely affects the prey population.

A mathematical model is very useful to analyse any real-world problems^{5,6,7,8,9,10,11,12,13}. Similarly, to better comprehend the intricate relationships between ecological systems and infectious diseases, an intriguing intersection of mathematical ecology and epidemiology has been working toward the creation of eco-epidemic models. Over the course of several decades, these models have developed, incorporating the foundational work in population dynamics by Lotka¹⁴ and Volterra¹⁵, as well as disease transmission theory by Kermack–McKendric¹⁶. Diseases within prey–predator systems have recently garnered significant interest from researchers in ecology and epidemiology^17,18,19. The author of the article²⁰ studied a predator–prey system where they consider a microparasite infecting the prey population. They have investigated the condition that caused Hopf bifurcation. Additionally, they validated the requirement for consistent persistence of all species. Gupta and Dubey examined an eco-epidemic model²¹. This model presents a scenario where the prey suffers from an incurable disease while the predator is presented with the choice to consume the additional food available to them. Multiple kinds of bifurcation have been detected in their system. They have also discovered that the extra food adds to the intricate system dynamics. A stage-structured eco-epidemic model with intraspecific competition of the adult predator is examined by Shi et al.²². They discovered that the maturation delay determines the stability switches.

All the above studies assume a well-mixed environment with no spatial heterogeneity and solely consider population changes over time (i.e., ordinary differential equations (ODEs)). In contrast, partial differential equations (PDEs) can jointly consider space and time^{23,24,25,26,27}. Also, species distribution, resource availability, climate, and habitat structure all show notable geographic variation in real-world ecosystems. Most of the time, predators follow groups of prey, focusing on areas where prey density is high. This causes over-predation, which may reduce prey in that area but allow prey to persist in other areas, preventing extinction. Again, when prey species are faced with threats from predators or changes in resource availability, they choose to migrate or disperse^28,29,30,31. When trying to explain population persistence, temporal models (ODEs) fall short since they don’t account for how organisms migrate across different environments. Therefore, disregarding spatial factors (PDEs) may result in inaccurate forecasts and a lack of knowledge about ecological processes³². In order to create wildlife corridors, protected areas, and habitat restoration plans, spatiotemporal models are crucial from the standpoints of conservation and ecosystem management^33,34. Maintaining species connection across landscapes is the goal of many conservation initiatives in order to ensure genetic diversity and lower the danger of extinction. For example, spatiotemporal models can be used to analyse the movement patterns and habitat preferences of large mammals, such as tigers and elephants, which is necessary when building wildlife corridors for them. On the other hand, hosts, vectors, and pathogens frequently migrate between different locations, affecting transmission rates and persistence. In reality, diseases spread more quickly in specific regions (hotspots), where the infected individuals move more frequently or the environmental conditions favour pathogen survival. So, disease dynamics are also influenced by movement and dissemination. Therefore, spatiotemporal models are useful for understanding the spread of diseases^35,36,37.

Spatiotemporal eco-epidemic models provide a potent tool for tackling some of the most important issues in ecosystem management, wildlife conservation, and public health by bridging the gap between ecology, epidemiology, and spatial analysis. A study conducted by Upadhyay et al.³⁸ examined a space-induced eco-epidemiological system including pelicans and tilapia in the Salton Sea, California. They deduced the Turing instability condition due to species migration. Additionally, they discovered that the rate of interaction between vulnerable and sick tilapia fish greatly influences the spread of the infection. Raw et al.³⁹ examined a spatiotemporal prey–predator model whereby an infection influences the prey population. They have investigated a variety of bifurcation forms without diffusion. They have also obtained all feasible Turing instability conditions for the spatiotemporal system. However, their model does not account for the gestation or incubation periods. Melese and Feyissa examined a spatiotemporal eco-epidemic model⁴⁰. They demonstrate that criteria on the parameters of the system’s local interaction can be used to control the diffusion effect. Using toxin-producing and infectious phytoplankton species, Kaur et al.⁴¹ investigated a spatially homogenous and inhomogeneous planktonic system. They have investigated the Turing instability of the endemic equilibrium with zero flux boundary constraints. Neither prey refuge nor any delay is taken into account in their computation.

Delay differential equations (DDEs) become crucial whenever a system’s future rate of change relies not only on its present state but also on its past history^42,43,44. Time delays occur naturally in nonlinear dynamics, and they fundamentally change system behaviour in ways that ODEs or PDEs cannot catch. There are various forms of time lags or delays in ecological interaction^45,46 and disease transmission. Incubation delay arises when an infectious disease affects the prey population, leading to a time lag between exposure and the onset of infectiousness. This delay influences disease transmission dynamics. A prolonged incubation period can allow infected hosts to interact with other populations before becoming symptomatic. This “hidden” phase often complicates the prediction and control of outbreaks. On the other hand, gestation delay occurs in predator populations, representing the time to introduce newborn predators after consuming prey. A longer gestation delay implies that even if there is an abundance of prey, the predator population cannot immediately capitalize on the surplus because new offspring require time to develop and contribute to the population. A classic real-world example of an eco-epidemic system illustrating the interplay of incubation and gestation delays is the interaction between European rabbits, the myxoma virus, and predators (like foxes). The Myxoma virus, introduced in Australia in the 1950s to control rabbit overpopulation⁴⁷, is highly lethal to rabbits, with an initial mortality rate close to 99%. The disease (myxomatosis) does not directly affect predators (like foxes); however, it indirectly influences their dynamics by reducing their primary food source. In this case, myxomatosis imposes an incubation delay of 2–10 days, during which infected prey remains asymptomatic but contagious, facilitating viral spread via fleas before lethal symptoms manifest⁴⁸. Concurrently, predators such as foxes experience a gestation delay, delaying their reproductive response to fluctuations in prey availability. Therefore, incorporating these delays into prey–predator models offers a more realistic representation of eco-epidemiological interactions. The introduction of delays can result in complex dynamical behaviours, such as sustained oscillations, multi-stability, and even chaotic dynamics. Understanding the effects of incubation and gestation delays is crucial for predicting population fluctuations, assessing ecosystem stability, and designing effective management strategies in ecological and epidemiological contexts. An eco-epidemic model that included both incidence and gestation delays was examined by Jana et al.⁴⁹. Their research leads them to the conclusion that in order to keep the prey–predator system stable, it needs to slow down the prey’s consumption, death, or incidence delay rates while speeding up their recovery rates from infections. The author of article⁵⁰ analyses their eco-epidemiological system with and without incubation and predator’s gestation delay. They found that the system’s stable configuration is significantly impacted by both delays. However, prey refuge and the spatial movements of both prey and predators are not considered.

Thakur et al.⁵¹ analyse the dynamics of interacting Tilapia fish and Pelican bird populations in the Salton Sea. They have investigated the stability switching through the Hopf bifurcation of the gestation delay. They analysed the non-delayed diffusive system. The authors of the articles³⁸ analyse the diffusive eco-epidemic system. Another article³⁹ considers the intraspecific competition of the predator and studies the diffusive system. However, these articles did not consider any delay term for diffusive systems in their calculation. A thorough comparison of this current study with the existing literature is given in Table 1. Unlike the existing studies, which mainly focused on (i) a diffusive eco-epidemic system without any gestation and incubation delay, (ii) the eco-epidemic model with any one or both gestation and incubation delay in the absence of diffusion, or (iii) a diffusive eco-epidemic system without intraspecific competition of predators, this study focuses on the analysis of the diffusive eco-epidemic system with both delays and intraspecific competition of predators. Consequently, based on the aforementioned literature review, it can be concluded that investigating the integral impacts of spatial heterogeneity, two-time delays (namely, incubation and gestation delays), prey refuge, and intraspecific competition within a spatiotemporal eco-epidemic model that addresses an infectious disease that solely affects the prey population represents a novel contribution. The present study shall, therefore, concentrate on the dynamics of spatial systems both with and without the gestation and incubation lengths. Here are a few of the key queries that are directing this research:

• to investigate the occurrence of Hopf bifurcation due to prey refuge,

• to investigate the mathematical conditions that result in the emergence of spatial patterns as a consequence of diffusion-driven instability in the system,

• to investigate the impact of intraspecific competitions between predators on the spatial structure of the ecosystem,

• to investigate the impact of the incubation and gestation periods on the system’s stability and bifurcation behaviour.

Table 1 A comparative study among some existing eco-epidemiological systems in literature.

The following is a breakdown of the article’s structure: Section “Formulation of the model” provides the formulation of the spatiotemporal model and the necessary rationale for it. The next section gives the existence and uniqueness of the solution of the model formulated in the previous section. Section “Equilibrium points” analyses every potential equilibrium point. All the potential scenarios of Turing instability in the system without delays are analytically shown in Section “Analysis of spatiotemporal system”. Here, whether the delayed diffusive system exhibits Hopf bifurcation has also been examined. Section “Algorithm for solution of spatiotemporal system with time delays” provides a detailed algorithm for solving the spatiotemporal system with a time delay. Section “Numerical simulation” studies the spatiotemporal system qualitatively and shows the onset of various types of patterns. The last section contains the concluding observations of this study.

Formulation of the model

This section intends to form the model with proper justification. First, it is considered that S(x, y, t) and I(x, y, t) are the susceptible and infected prey populations, respectively; on the other hand, P(x, y, t) is the predator population at any point (x, y) of their habitat and at any time $t>0$. Furthermore, the logistically increasing prey population with a carrying capacity of K without the presence of infection and predator is considered. Here, a situation is considered in which the sick prey populations cannot reproduce because they die before reaching their reproduction age. So, only the susceptible prey population is responsible for increasing the prey population logistically at the rate of r. However, their carrying capacity is influenced by both vulnerable and unhealthy prey populations. In the real-world scenario, there are many diseases that mostly affect the prey population, leaving the predator population unharmed. For example, the “myxoma virus” may be considered, which is very specific to species. This virus is able to infect a certain species of rabbits (European rabbits), but it is unable to do so for the predator of this species (foxes)⁵⁵. For this reason, the present study intends to analyse the situation where the infection only affects the prey populations. The cohabitation of sick and susceptible prey causes the disease to propagate over the susceptible prey population. Here, $\beta$ may be considered as the disease transmission rate. The standard bilinear or non-linear form of the disease transmission term indicates that every susceptible individual has an equal probability of encountering an infected individual. Conversely, in actual situations, the expansion of the susceptible population may result in a lack of freedom of interaction among individuals as a result of space constraints, behavioural modifications, or diminished social interactions. In regions with a high population density, the saturated form is more feasible due to its ability to restrict excessive transmission when S is larger. So, the disease transmission term may be considered in saturated form as $\frac{\beta S I}{1+a I}$, which represents the crowding effects of the infectious prey with a saturation constant $a>0$. After the contact of a susceptible prey with an infected prey, it does not infect immediately. For most diseases, there is a time lag between exposure to a pathogen and the onset of noticeable symptoms or signs of disease. So, this time lag is denoted by $\tau _1$, which is known as the incubation period. $\mu$ denotes the death rate of the sick prey resulting from the illness.

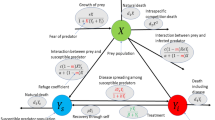
Holling type-II functional responses reflect the biological constraint that predators cannot consume prey indefinitely. As prey density increases, predation rates saturate due to handling time (time spent capturing, eating, and digesting prey), which is ecologically realistic. For this reason, the present study considers that predators consume both susceptible and infected prey, with Holling type-II functional responses as $\frac{\alpha _1 S P}{1+b S}$ and $\frac{\alpha _2 I P}{1+c I}$, respectively. The killing of prey during a predatory strike is likely to be immediate, but it takes some time to increase the predator’s population. Let that time lag be $\tau _2$, which is also known as the gestation period. Here, both $\tau _1$ and $\tau _2$ are discrete in nature. It may be assumed that the susceptible prey population employs behavioural techniques or seeks refuge to avoid predation and protect themselves. And the prey refugee rate is $\rho (\in [0,1])$. Due to the infection, infected prey are unable to employ this behavioural technique. Define $\gamma _1$ and $\gamma _2$ as the conversion coefficients that quantify how effectively predators transform the consumption of susceptible and infected prey, respectively, into their own biomass. Additionally, let d be the inherent mortality rate of the predator. It is frequently seen that predator species compete for limited resources such as food, space, or mating opportunities^56,57,58. In classical prey–predator models, predator growth is often assumed to be proportional to prey availability without accounting for competition among predators. However, in reality, as predator density increases, the availability of prey per predator decreases, leading to reduced hunting efficiency and territorial disputes. So, taking the intraspecific competition coefficient $\delta$ into the calculation will be more realistic. Therefore, based on the above assumption, a schematic diagram representing the interaction among the susceptible prey, infected prey and predators is given in Fig. 1 and the eco-epidemic model can be written as follows:

Fig. 1

Schematic diagram depicts the interactions among susceptible prey, infected prey and predators in homogeneous environments.

$$\begin{aligned} \frac{\partial S}{\partial t}&=r S \left( 1-\frac{S+I}{K}\right) -\frac{\beta S I}{1+a I}-\frac{\alpha _1 (1-\rho ) S P}{1+b (1-\rho ) S}+d_1 \nabla ^2 S\nonumber \\ \frac{\partial I}{\partial t}&= \frac{\beta S(t-\tau _1) I(t-\tau _1)}{1+a I(t-\tau _1)}-\frac{\alpha _2 I P}{1+c I}-\mu I+d_2 \nabla ^2 I\nonumber \\ \frac{\partial P}{\partial t}&=\frac{\gamma _1 \alpha _1 (1-\rho ) S(t-\tau _2) P(t-\tau _2)}{1+b (1-\rho ) S(t-\tau _2)}+\frac{\gamma _2 \alpha _2 I(t-\tau _2) P(t-\tau _2)}{1+c I(t-\tau _2)}-d P-\delta P^2+d_3 \nabla ^2 P \end{aligned}$$

(1)

where $d_1$, $d_2$, and $d_3$ correspond accordingly to the diffusive coefficients of susceptible and infected prey and predator. A large value of $d_i$ represents the rapid movements of the corresponding species. As the infected prey is weakened, $d_2$ will be less than $d_1$. Also, without loss of generality, it may be considered that the movement rate of the predator will be higher than that of the healthy prey (i.e., $d_3>d_1>d_2$). Here, $\nabla ^2\equiv \frac{\partial ^2~}{\partial x^2}+\frac{\partial ^2~}{\partial y^2}$ be the Laplacian operator. The initial circumstances of the aforementioned system can be written as:

$$\begin{aligned} S(x,y,0)>0,\quad I(x,y,0)>0,\quad P(x,y,0)>0,\quad \forall (x,y)\in \Sigma \end{aligned}$$

(2)

and the boundary conditions can be written as:

$$\begin{aligned} \frac{\partial S}{\partial \epsilon }=\frac{\partial I}{\partial \epsilon }=\frac{\partial P}{\partial \epsilon }=0,\quad \forall (x,y) \in \partial \Sigma \quad \text {and}\quad t>0. \end{aligned}$$

(3)

Applying the zero-flux border condition guarantees that no individual traverses the boundaries of their habitat. In this case, $\partial \Sigma$ denotes the smooth boundary of the presumed bounded domain $\Sigma \in \mathbb {R}^2$, and $\epsilon$ represents the outward normal to $\partial \Sigma$. Also, the following assumptions are considered throughout this work:

• A1. $d_i(i=1,2,3)$ are non-negative on $\Sigma$.

• A2. $r(\cdot ),K(\cdot ),\beta (\cdot ),a(\cdot ),\alpha _1(\cdot ),\alpha _2(\cdot ),\rho (\cdot ),b(\cdot ),c(\cdot ),\mu (\cdot ),\gamma _1(\cdot ),\gamma _2(\cdot ),d(\cdot ),\delta (\cdot )\in C^2(\Sigma )$ and exhibit strict positivity.

Existence and uniqueness of solution of the system (1)

This section intend to prove that the system (1) with (2) and (3) has a unique solution. For this, we first consider the differential operators as $\chi _i^0=d_i \nabla ^2$ for $i=1,2,3$ on the domain defined as

$$\begin{aligned} D(\chi _i^0)=\left\{ \phi \in C^2(\Sigma )\cap C^1(\bar{\Sigma }):\chi _i^0\phi \in C(\bar{\Sigma }), \frac{\partial \phi (x)}{\partial \epsilon }=0, x\in \partial \Sigma \right\} . \end{aligned}$$

According to⁵⁹, the closer $\chi _i$ of $\chi _i^0$ generates a $C_0$-semigroup $\left\{ T_i(t)\right\} _{t\ge 0}$→ such that $y(t)=T_i(t)\phi$ is a solution of $y_i'(t)=\chi _i y_i(t),t>0$ with $y_i(0)=\phi \in D(\chi _i)$, where

$$\begin{aligned} D(\chi _i)=\left\{ \phi \in C(\bar{\Sigma }):\lim _{t\rightarrow 0^{+}}\frac{[T_i(t)-I_d]\phi }{t}\text { exists}\right\} . \end{aligned}$$

Here, $I_d$ is the identity operator. Now, the following oparators can be defined on $\Sigma \times \mathbb {R}^3$ as

$$\begin{aligned} H_1(\mathcal {X},\mathbf{m})&=r m_1 \left( 1-\frac{m_1+m_2}{K}\right) -\frac{\beta m_1 m_2}{1+a m_2}-\frac{\alpha _1 (1-\rho ) m_1 m_3}{1+b (1-\rho ) m_1},\\ H_2(\mathcal {X},\mathbf{m})&=\frac{\beta m_1(t-\tau _1) m_2(t-\tau _1)}{1+a m_2(t-\tau _1)}-\frac{\alpha _2 m_2 m_3}{1+c m_2}-\mu m_2,\\ H_3(\mathcal {X},\mathbf{m})&=\frac{\gamma _1 \alpha _1 (1-\rho ) m_1(t-\tau _2) m_3(t-\tau _2)}{1+b (1-\rho ) m_1(t-\tau _2)}+\frac{\gamma _2 \alpha _2 m_2(t-\tau _2) m_3(t-\tau _2)}{1+c m_2(t-\tau _2)}-d m_3-\delta m_3^2, \end{aligned}$$

where $\mathcal {X}\in \Sigma$, $\mathbf{m}=(m_1,m_2,m_3)\in \mathbb {R}^2$. Now, the following sets can be defined as

$$\begin{aligned} \mathbb {X}=C(\Sigma ,\mathbb {R}),\quad \mathbb {Y}=C(\Sigma ,\mathbb {R})\times C(\Sigma ,\mathbb {R})\times C(\Sigma ,\mathbb {R}), \end{aligned}$$

where $C(\Sigma ,\mathbb {R})$ denotes the space of all continuous real valued functions defined on $\Sigma$, equipped with the following norm

$$\begin{aligned} ||\pi ||_{\mathbb {X}}=\max \left\{ \sup _{\mathcal {X}\in \Sigma }|\pi _1(\mathcal {X})|,\sup _{\mathcal {X}\in \Sigma }|\pi _2(\mathcal {X})|,\sup _{\mathcal {X}\in \Sigma }|\pi _3(\mathcal {X})|\right\} ,\quad \pi =(\pi _1,\pi _2,\pi _3)\in \mathbb {Y}. \end{aligned}$$

Now, the system (1) with (2) and (3) can be written in its abstract form as

$$\begin{aligned} y'(t)=\chi y(t)+ \mathcal {N}(y(t)),\quad t>0 \end{aligned}$$

(4)

where $y(t)=\begin{pmatrix} S(\cdot ,\cdot ,t)\\ I(\cdot ,\cdot ,t)\\ P(\cdot ,\cdot ,t)\end{pmatrix}\in \mathbb {Y}$, $y(0)=\begin{pmatrix}S_0(\cdot ,\cdot )\\ I_0(\cdot ,\cdot )\\ P_0(\cdot ,\cdot )\end{pmatrix}\in \mathbb {Y}^+$, $\chi y(t)=\begin{pmatrix}\chi _1 S\\ \chi _2 I\\ \chi _3 P\end{pmatrix}$ and $\mathcal {N}(\cdot )=\begin{pmatrix}H_1(\mathcal {X},\cdot )\\ H_2(\mathcal {X},\cdot )\\ H_3(\mathcal {X},\cdot )\end{pmatrix}$.

A mild solution of the abstract form (4) of the system (1) can be obtained as a continuous solution of the following integral equation,

$$\begin{aligned} y(t)=T(t) y(0)+\int _{0}^{t} T(t-s) \mathcal {N}(y(s)) ds,\quad t>0,\quad \text {where}\quad T(\cdot )=\begin{pmatrix} T_1(\cdot )\\ T_2(\cdot )\\ T_3(\cdot )\end{pmatrix}. \end{aligned}$$

(5)

Now, if $\mathbb {Y}^+$ be the positive cone of $\mathbb {Y}$, then the following Lemma may be stated by the Theorem 3.1 and Corollary 3.3 of chapter 7 of⁵⁹.

Lemma 1

There exist a $t_\infty \le \infty$, such that the initial value problem (4) has a unique mild solution y on $[0,t_\infty )$. Moreover, if $t_\infty <\infty$, then $\lim _{t\rightarrow t_\infty -0}||y(t)||\rightarrow +\infty$.

Proof

From Corollary 3.3 of chapter 7 of⁵⁹, it is sufficient to show that $H_i(\mathcal {X},\mathbf{m})\ge 0$ for $i=1,2,3$, $\mathcal {X}\in \Sigma$ and $\mathbf{m}\in \mathbb {R}_{+}^3$ with $m_i=0$. By the assumption (A2), it is obvious. This complete the proof. $\square$

Next theorem will prove the existence and uniqueness of the classical solution of the system (1).

Theorem 3.1

The abstract form (4) of the system (1) has the unique positive classical solution y(t) on $[0,\infty )$.

Proof

By the Lemma 1, it is sufficient to show that $t_\infty =\infty$. First, it can be supposed that $t_\infty <\infty$, then from the first equation of system (1) can be written as

$$\begin{aligned} \frac{\partial S}{\partial t}\le r S +d_1 \nabla ^2 S. \end{aligned}$$

It follows from Proof of Theorem 1 of the article⁶⁰ and the comparison principle, a positive constant $M_1$ may be found such that

$$\begin{aligned} 0\le S(\mathcal {X},t)<M_1,\quad \mathcal {X}\in \Sigma ,\quad t\in [0,t_\infty ). \end{aligned}$$

Therefore, S dose not blow up at $t=t_\infty$. Now, suppose that $\frac{\beta S(\cdot ,t) I(\cdot ,t)}{1+a I(\cdot ,t)}\rightarrow +\infty$ as $t\rightarrow t_\infty -0$. Then the first equation of system (1) gives $\frac{\partial S}{\partial t}\rightarrow -\infty$, which implies $S(\mathcal {X},t)<0$ in the neighbourhood of $t_\infty$, which contradicts to the positivity of S. Thus, $\frac{\beta S(\cdot ,t) I(\cdot ,t)}{1+a I(\cdot ,t)}<+\infty$ for $t\in [0,t_\infty )$. Therefore, the second equation of system (1) can be written as

$$\begin{aligned} \frac{\partial I}{\partial t}\le N_1^+ +d_2 \nabla ^2 I \end{aligned}$$

where $N_1^+=\sup _{(\mathcal {X},t)\in \Sigma \times [0,t_\infty )} \frac{\beta S(\mathcal {X},t) I(\mathcal {X},t)}{1+a I(\mathcal {X},t)}<\infty$. Now, similar argument as above, a positive $M_2$ may be found such that

$$\begin{aligned} 0\le I(\mathcal {X},t)<M_2,\quad \mathcal {X}\in \Sigma ,\quad t\in [0,t_\infty ). \end{aligned}$$

Thus, I does not blow up at $t=t_\infty$. As similar to the previous case, it may be claimed that $\frac{\gamma _1 \alpha _1 (1-\rho ) S(\cdot ,t) P(\cdot ,t)}{1+b (1-\rho ) S(\cdot ,t)}+\frac{\gamma _2 \alpha _2 I(\cdot ,t) P(\cdot ,t)}{1+c I(\cdot ,t)}<+\infty$. So, the third equation of system (1) may be rewritten as

$$\begin{aligned} \frac{\partial P}{\partial t}\le N_2^+ +d_3 \nabla ^2 P \end{aligned}$$

where $N_2^+=\sup _{(\mathcal {X},t)\in \Sigma \times [0,t_\infty )} \frac{\gamma _1 \alpha _1 (1-\rho ) S(\mathcal {X},t) P(\mathcal {X},t)}{1+b (1-\rho ) S(\mathcal {X},t)}+\frac{\gamma _2 \alpha _2 I(\mathcal {X},t) P(\mathcal {X},t)}{1+c I(\mathcal {X},t)}$. Thus, similar to the previous argument, a positive constant $M_3$ may be found such that

$$\begin{aligned} 0\le P(\mathcal {X},t)<M_3,\quad \mathcal {X}\in \Sigma ,\quad t\in [0,t_\infty ). \end{aligned}$$

Therefore, P also does not blow up at $t=t_\infty$. These contradicts the assumption $t_\infty <\infty$. Thus, $t_\infty =\infty$ and this complete the proof. $\square$

Equilibrium points

Here, we are interested in finding all possible equilibrium points of our formulated system. It is well known that the equilibrium points of a spatiotemporal system and the corresponding temporal system are the same. Therefore, the aforementioned spatiotemporal system (1) possesses the following equilibrium points:

• (i) The trivial equilibrium (0, 0, 0).

• (ii) Diseased prey and predator free equilibrium (K, 0, 0).

• (iii) Predator free equilibrium $(S_1,I_1,0)$, where $S_1=\frac{\mu }{\beta }(1+a I_1)$ and $I_1$ represents the positive root of $a(\beta +a\mu )r I_1^2+\{\beta ^2 K+2a\mu r+\beta r (1-a K)\} I_1+r(\mu -\beta K)=0$.

• (iv) Infected prey free equilibrium $(S_2,0,P_2)$, where $S_2$ and $P_2$ are the positive root of the following simultaneous equations:

  $$\begin{aligned}&r \left( 1-\frac{S_2+I_2}{K}\right) -\frac{\alpha _1 (1-\rho ) P_2}{1+b (1-\rho ) S_2}=0,\nonumber \\&\frac{\gamma _1 \alpha _1 (1-\rho ) S_2}{1+b (1-\rho ) S_2}-d-\delta P_2=0. \end{aligned}$$

  (6)

• (v) The interior equilibrium $E^*(S^*,I^*,P^*)$, can be determined by solving the following simultaneous equations involving $S^*$, $I^*$ and $P^*$:

  $$\begin{aligned}&r \left( 1-\frac{S^*+I^*}{K}\right) -\frac{\beta I^*}{1+a I^*}-\frac{\alpha _1 (1-\rho ) P^*}{1+b (1-\rho ) S^*}=0,\nonumber \\&\frac{\beta S^*}{1+a I^*}-\frac{\alpha _2 P^*}{1+c I^*}-\mu =0,\nonumber \\&\frac{\gamma _1 \alpha _1 (1-\rho ) S^*}{1+b (1-\rho ) S^*}+\frac{\gamma _2 \alpha _2 I^*}{1+c I^*}-d-\delta P^*=0. \end{aligned}$$

  (7)

Natural ecosystems rarely exhibit total extinction of species in stable conditions. By studying the interior equilibrium, we prioritize scenarios where prey (both healthy and infected) and predators persist over time. This aligns with real-world systems where disease, predation, and resource limitations interact to maintain dynamic balance, even if population sizes fluctuate. Furthermore, interior equilibria provide insights into how disease in prey affects predator survival and overall ecosystem stability, aligning with the ecological motivation of the study. For this reason, the present study will only focus on the interior equilibrium.

Analysis of spatiotemporal system

Studying stability analysis in eco-epidemic systems, which combine predator–prey interactions with disease dynamics, is crucial for understanding how ecosystems respond to disturbances, predict long-term outcomes, and inform conservation or disease management strategies. It reveals whether species (predators, susceptible prey, infected prey) can coexist indefinitely or face extinction. For example, a stable equilibrium suggests balanced interactions where predation and disease regulate populations without collapse. So, this section intends to study the stability analysis of the interior equilibrium.

By linearising the system (1) about the spatially homogeneous coexisting steady state $E^*(S^*,I^*,P^*)$ with the help of small spatiotemporal perturbations $X_1=S-S^*$, $X_2=I-I^*$, and $X_3=P-P^*$, where $|X_i|<<1$ for $i=1,2,3$, it can write

$$\begin{aligned} \frac{\partial X(x,y,t)}{\partial t}=\mathcal {J}_1 X(x,y,t) + \mathcal {J}_2 X(x,y,t-\tau _1) + \mathcal {J}_3 X(x,y,t-\tau _2) + \mathcal {D} \nabla ^2 X(x,y,t), \end{aligned}$$

(8)

where $X(x,y,t)=\left( X_1(x,y,t),X_2(x,y,t),X_3(x,y,t)\right) ^T$, $\mathcal {J}_1=(a_{ij})_{3\times 3}$, $\mathcal {J}_2=(b_{ij})_{3\times 3}$, $\mathcal {J}_3=(c_{ij})_{3\times 3}$, and $\mathcal {D}=\left( \begin{array}{ccc} d_1 & 0 & 0\\ 0 & d_2 & 0\\ 0 & 0 & d_3 \end{array} \right)$, with

$$\begin{aligned} a_{11}&=-\frac{r S^*}{K}+\frac{b \alpha _1 (1-\rho )^2 S^* P^*}{(1+b (1-\rho ) S^*)^2},\quad a_{12}=-\frac{r S^*}{K}-\frac{\beta S^*}{(1+a S^*)^2},\quad a_{13}=-\frac{\alpha _1 (1-\rho ) S^*}{1+b (1-\rho ) S^*},\\ a_{21}&=0,\quad a_{22}=-\frac{\alpha _2 P^*}{(1+c I^*)^2}-\mu ,\quad a_{23}=-\frac{\alpha _2 I^*}{1+c I^*},\\ a_{31}&=0,\quad a_{32}=0,\quad a_{33}=-d-2\delta P^*,\\ b_{11}&=b_{12}=b_{13}=0,\\ b_{21}&=\frac{\beta I^*}{1+a I^*},\quad b_{22}=\frac{\beta S^*}{(1+a I^*)^2},\quad b_{23}=0,\\ b_{31}&=b_{32}=b_{33}=0,\\ c_{11}&=c_{12}=c_{13}=0,\\ c_{21}&=c_{22}=c_{23}=0,\\ c_{31}&=\frac{\gamma _1 \alpha _1 (1-\rho ) P^*}{(1+b (1-\rho ) S^*)^2},\quad c_{32}=\frac{\gamma _2 \alpha _2 P^*}{(1+c I^*)^2},\quad c_{33}=\frac{\gamma _1 \alpha _1 (1-\rho ) S^*}{1+b (1-\rho ) S^*}+\frac{\gamma _2 \alpha _2 I^*}{1+c I^*}. \end{aligned}$$

Now, it is assumed that the solutions of the above system (8) are of the forms $X_j(x,y,t)=\varepsilon _j e^{\lambda t} e^{i \overrightarrow{k}\cdot \overrightarrow{q}}$ for $j=1,2,3$ with $i^2=-1$, $(\varepsilon _1,\varepsilon _2,\varepsilon _3)\ne 0$, $\overrightarrow{k}=(k_x,k_y)$ and $\overrightarrow{q}=(x,y)$ (for more details see the book⁶¹). Here, $k(=|\overrightarrow{k}|)$ and $\lambda$ are the wave number and wave frequency, respectively. Then, the characteristic equation may be written below as

$$\begin{aligned} P_1 - P_2 e^{-\lambda \tau _1} -P_3 e^{-\lambda \tau _2}+P_4 e^{-\lambda (\tau _1+\tau _2)}=0 \end{aligned}$$

(9)

where

$$\begin{aligned} P_1&=\lambda ^3-\eta _1(k) \lambda ^2+\eta _2(k) \lambda -\eta _3(k),\\ P_2&=\eta _4(k) \lambda ^2-\eta _5(k) \lambda +\eta _6(k),\\ P_3&=\eta _7(k) \lambda ^2-\eta _8(k) \lambda +\eta _9(k),\\ P_4&=\eta _{10}(k) \lambda -\eta _{11}(k), \end{aligned}$$

with

$$\begin{aligned} \eta _1(k)&=a_{11}+a_{22}+a_{33}-(d_1+d_2+d_3) k^2,\\ \eta _2(k)&=a_{11} a_{22} + a_{11} a_{33} + a_{22} a_{33} -\{a_{33} (d_1 + d_2) + a_{22} (d_1 + d_3) + a_{11} (d_2 + d_3)\} k^2 \\&\quad +(d_1 d_2 + d_1 d_3 + d_2 d_3) k^4,\\ \eta _3(k)&=a_{11} a_{22} a_{33}-(a_{22} a_{33} d_1 + a_{11} a_{33} d_2 + a_{11} a_{22} d_3) k^2+(a_{33} d_1 d_2 +a_{22} d_1 d_3 +a_{11} d_2 d_3) k^4\\&\quad -d_1 d_2 d_3 k^6,\\ \eta _4(k)&=b_{22},\\ \eta _5(k)&= a_{11} b_{22} + a_{33} b_{22} -a_{12} b_{21} - (b_{22} d_1 + b_{22} d_3) k^2,\\ \eta _6(k)&=a_{33} ( a_{11} b_{22}-a_{12} b_{21})-(a_{33} b_{22} d_1 + a_{11} b_{22} d_3 - a_{12} b_{21} d_3) k^2 + b_{22} d_1 d_3 k^4,\\ \eta _7(k)&=c_{33},\\ \eta _8(k)&=a_{11} c_{33} + a_{22} c_{33} -a_{13} c_{31} - a_{23} c_{32} - c_{33} (d_1 + d_2) k^2,\\ \eta _9(k)&=a_{12} a_{23} c_{31} + a_{11} a_{22} c_{33} - a_{11} a_{23} c_{32} -a_{13} a_{22} c_{31} \\&\quad - (a_{22} c_{33} d_1 + a_{11} c_{33} d_2- a_{13} c_{31} d_2 - a_{23} c_{32} d_1) k^2 + c_{33} d_1 d_2 k^4,\\ \eta _{10}(k)&=b_{22} c_{33},\\ \eta _{11}(k)&= a_{11} b_{22} c_{33} + a_{13} b_{21} c_{32} - a_{12} b_{21} c_{33} -a_{13} b_{22} c_{31} - b_{22} c_{33} d_1 k^2. \end{aligned}$$

Analysis in the absence of delays

In this situation, the characteristic Eq. (9) becomes

$$\begin{aligned} \lambda ^3+\xi _1(k) \lambda ^2+\xi _2(k) \lambda +\xi _3(k)=0 \end{aligned}$$

(10)

where

$$\begin{aligned} \xi _1(k)&=-\{\eta _1(k)+\eta _4(k)+\eta _7(k)\},\\ \xi _2(k)&=\eta _2(k)+\eta _5(k)+\eta _8(k)+\eta _{10}(k),\\ \xi _3(k)&=-\{\eta _3(k)+\eta _6(k)+\eta _9(k)+\eta _{11}(k)\}. \end{aligned}$$

Clearly, the above characteristic Eq. (10) (polynomial equation) has three eigenvalues, and stability is straightforward to assess by checking if all eigenvalues lie in the left half of the complex plane. But the inclusion of delays in dynamical systems transforms the characteristic equation into a transcendental form (9), which gives infinite poles and complicates stability analysis.

Hopf bifurcation of the non-diffusive system

In the present section, it will be checked whether the non-diffusive system without delays corresponds to the diffusive system (1) experience Hopf bifurcation or not. Here, if $\rho$, the prey refuge rate, is considered as a bifurcation parameter, subsequently one may derive the following theorem:

Theorem 5.1

If there exists a critical value $\rho ^{[C]}$ of $\rho$ such that $\xi _1(0)>0$, $\xi _3(0)>0$, and $\Omega (\rho ^{[C]})=0$, with $\left. \frac{d \Omega }{d \rho } \right| _{\rho =\rho ^{[C]}}\ne 0$, where $\Omega (\rho )=\xi _1(0)\xi _2(0)-\xi _3(0)$, then the non-diffusive system without delays corresponding to the diffusive system (1) experiences a Hopf bifurcation at the interior equilibrium $E^*$ when $\rho =\rho ^{[C]}$.

Proof

As $\Omega (\rho ^{[C]})=0$, so the characteristic Eq. (10) can be written as

$$\begin{aligned} \{\lambda ^2+\xi _2(0)\}\{\lambda +\xi _1(0)\}=0, \end{aligned}$$

(11)

and the eigenvalues will be $\lambda _{1,2}=\pm i\sqrt{\xi _2(0)}$ and $\lambda _3=-\xi _1(0)$, where $i^2=-1$.

As there exists a pair of purely imaginary eigenvalues for $\rho =\rho ^{[C]}$, the Hopf bifurcation may exist if the transversality condition is satisfied. To check the transversality condition, a point in the $\varepsilon -$neighbourhood of $\rho ^{[C]}$ such that $\lambda _{1,2}=\phi (\rho )\pm i\omega (\rho )$ is the pair of imaginary eigenvalues. Then, after separating real and imaginary parts, the characteristic Eq. (10) can be written as

$$\begin{aligned}&\phi ^3-3\phi \omega ^2+(\phi ^2-\omega ^2)\xi _1(0)+\phi \xi _2(0)+\xi _3(0)=0,\end{aligned}$$

(12)

$$\begin{aligned}&3\phi ^2\omega -\omega ^3+2\phi \omega \xi _1(0)+\omega \xi _2(0)=0. \end{aligned}$$

(13)

Differentiating both equation with respect to $\rho$, the above equations can be written as

$$\begin{aligned}&h_1(\rho ) \phi '-h_2(\rho ) \omega '+f_1(\rho )=0,\nonumber \\&h_2(\rho ) \phi '+h_1(\rho ) \omega '+f_2(\rho )=0, \end{aligned}$$

(14)

where

$$\begin{aligned} h_1(\rho )&=3 (\phi ^2-\omega ^2)+2 \xi _1(0) \phi +\xi _2(0),\\ h_2(\rho )&=6\phi \omega +2 \xi _1(0) \omega ,\\ f_1(\rho )&=\xi _1'(0) (\phi ^2-\omega ^2)+\xi _2'(0) \phi +\xi _3'(\rho ),\\ f_2(\rho )&=2 \xi _1'(0) \phi \omega +\xi _2'(0) \omega . \end{aligned}$$

Now, solving the above two equations of (14) for $\phi '$ and substituting $\phi (\rho ^{[C]})=0, \omega (\rho ^{[C]})=\sqrt{\xi _2(0)}$, it can be written as

$$\begin{aligned} \phi '\left( \rho ^{[C]}\right)&= {Re}\left[ \frac{d \lambda \left( \rho ^{[C]}\right) }{d \rho }\right] \\&=-\frac{h_1\left( \rho ^{[C]}\right) f_1\left( \rho ^{[C]}\right) +h_2\left( \rho ^{[C]}\right) f_2\left( \rho ^{[C]}\right) }{\left\{ h_1\left( \rho ^{[C]}\right) \right\} ^2+\left\{ h_2\left( \rho ^{[C]}\right) \right\} ^2}\\&=-\frac{\xi _1'\left( \rho ^{[C]}\right) \xi _2\left( \rho ^{[C]}\right) +\xi _1\left( \rho ^{[C]}\right) \xi _2'\left( \rho ^{[C]}\right) -\xi _3'\left( \rho ^{[C]}\right) }{2\{\xi _1^2\left( \rho ^{[C]}\right) +\xi _2\left( \rho ^{[C]}\right) \}}\\&=-\frac{\Omega '\left( \rho ^{[C]}\right) }{2\{\xi _1^2\left( \rho ^{[C]}\right) +\xi _2\left( \rho ^{[C]}\right) \}} \end{aligned}$$

Thus, $\Omega '(\rho ^{[C]})\ne 0$ implies ${Re}\left[ \frac{d \lambda (\rho ^{[C]})}{d \rho }\right] \ne 0$. Therefore, this complete the proof. $\square$

Note 1

If the values of parameters are chosen from Eq. (46), then $\Omega (\rho )=0$ gives $\rho =0.008278$. It can also be shown that at $\rho =0.008278$, the condition of the existence of Hopf bifurcation is satisfied. Furthermore, Fig. 2b clearly shows that the non-delayed, non-diffusive system corresponding to (1) becomes stable from unstable for crossing the value of $\rho =0.008278$ through the Hopf bifurcation where other parameters are fixed as in Eq. (46).

Fig. 2

Bifurcation diagram for (a) $\beta$ versus $\rho$ space, (b) $\delta$ versus $\rho$ space, and (c) $\delta$ versus $\beta$ space for the parameters as in Eq. (46), where the green region indicates Turing, the red region indicates Hopf–Turing, the blue region indicates stable, and the cyan region indicates pure Hopf.

Turing bifurcation of the diffusive system

Studying Turing bifurcation in eco-epidemic systems is much more than a mathematical exercise-it gives us powerful insights into how and why spatial patterns of disease and populations emerge and what they mean for real ecosystems. As the system approaches the Turing threshold, small spatial perturbations are capable of making different spatial structures. In this situation, to control the disease or conservation of the species, localised measures (like introducing barriers, selective culling) will be more effective than blanket measures (like mass vaccination, broad culling). So, this section intends to find the condition of Turing instability.

Turing instability arises only when a stable temporal system becomes unstable due to diffusion. The mathematical expression for this circumstance is the same as if all the conditions of C1 were satisfied, but for any positive k, at least one condition of C2 was violated. Here, C1 and C2 are as follows:

$$\begin{aligned} & C1:\xi _i(0)>0\quad \text {for}\quad i=1,2,3\quad \text {and}\quad \xi _1(0)\xi _2(0)>\xi _3(0),\end{aligned}$$

(15)

$$\begin{aligned} & C2:\xi _i(k)>0\quad \text {for}\quad i=1,2,3\quad \text {and}\quad \xi _1(k)\xi _2(k)>\xi _3(k). \end{aligned}$$

(16)

It can be easily shown that $\xi _1(k)>0$ for all $k\ge 0$. Therefore, instability due to the diffusion will occur if either $\xi _3(k)<0$ or $\xi _1(k)\xi _2(k)<\xi _3(k)$ for some positive k. Clearly, both $\Omega _1=\xi _3(k)$ and $\Omega _2=\xi _1(k)\xi _2(k)-\xi _3(k)$ can be expressed as a cubic polynomial of $k^2$ as

$$\begin{aligned} \Omega _i(k^2)=\Omega _1^i (k^2)^3 + \Omega _2^i (k^2)^2 + \Omega _3^i k^2 + \Omega _4^i, \end{aligned}$$

(17)

where $\Omega _j^i$ for $j=1,2,3,4$ are the coefficients of $\Omega _i$. It can be shows that both $\Omega _1^i$ and $\Omega _4^i$ for $i=1,2$ are positive if C1 holds. Therefore, to make $\Omega _i(k^2)$ negative for $i=1,2$, either one or both of $\Omega _2^i$ and $\Omega _3^i$ have to negative.

Next, in order to find the minimum value of $\Omega _i(k^2)$, $\frac{d \Omega _i}{d k^2}=0$ gives $k_{\pm }^2=\frac{-\Omega _2\pm \sqrt{\Omega _2^2 - 3 \Omega _1\Omega _3}}{3\Omega _1}$. As $k^2$ is a non-negative real number, so it is possible for either $\Omega _3^i<0$ or $\Omega _2^i<0$ with $(\Omega _2^i)^2-3 \Omega _1^i \Omega _3^i>0$. Also, it can be shown that at $k_+^2=\frac{-\Omega _2 + \sqrt{\Omega _2^2 - 3 \Omega _1\Omega _3}}{3\Omega _1}$, $\frac{d^2 \Omega _i}{d (k^2)^2}>0$. Therefore, $k_+^2$ gives the minimum value, and the Turing instability will occur if $\Omega _i(k_+^2)=\frac{2(\Omega _2^i)^3-9 \Omega _1^i \Omega _2^i \Omega _3^i-2\{(\Omega _2^i)^2-3 \Omega _1^i \Omega _3^i\}^{3/2}+27 (\Omega _1^i)^2 \Omega _4^i}{27 \Omega _1^2}<0$ for either $i=1$ or $i=2$. From this discussion, one can conclude the following:

Theorem 5.2

Assume that all the requirements of C1 are satisfied. Then, the conditions that are necessary for the diffusive system (1) without delays to experience Turing instability are (i) $\Omega _3^i<0$ or $\Omega _2^i<0$ with $(\Omega _2^i)^2-3 \Omega _1^i \Omega _3^i>0$ and (ii) $2(\Omega _2^i)^3-9 \Omega _1^i \Omega _2^i \Omega _3^i-2\{(\Omega _2^i)^2-3 \Omega _1^i \Omega _3^i\}^{3/2}+27 (\Omega _1^i)^2 \Omega _4^i<0$, for $i=1$ or $i=2$.

Turing instability causes different types of spatial patterns in the ecosystem, which will be seen in the next section. These patterns make things more stable and resilient by managing resource flows, feedback, and recovery processes. Their loss, on the other hand, can cause quick changes. This means that managing and keeping an eye on spatial heterogeneity is a powerful way to keep ecosystems alive in the face of global change. Now, one can give the following two straightforward lemmas:

Lemma 2

If both Theorems 5.1and 5.2are true at the same time, the diffusive system (1) will show that the Hopf–Turing instability is present.

Lemma 3

The pure Hopf instability can be observed in the diffusive system (1) when the conditions of Theorem 5.1are satisfied, but the Turing instability condition is not satisfied.

Hopf bifurcation analysis of delayed spatiotemporal system

Under this part, the delay-induced Hopf bifurcation of the spatiotemporal system (1) around $E^*$ will be studied. The analytical investigation of Hopf bifurcations analysis in delayed spatiotemporal systems proceeds through a sequence of well-defined steps^45,46,62: (a) linearising the system around the equilibrium $E^*$ to derive a transcendental characteristic equation; (b) determining the critical delays and frequencies at which a conjugate pair of eigenvalues crosses the imaginary axis; (c) verifying the transversality condition to ensure a genuine bifurcation. For systems with more than one delay, the characteristic equations are transcendental and naturally complicated because they include terms for $e^{-\lambda \tau _1}$ and $e^{-\lambda \tau _2}$. It is hard to solve these kinds of equations analytically because they have an infinite number of roots, which makes it hard to keep track of eigenvalues that cross the imaginary axis. Fixing one delay and changing the other reduces the problem to a single-delay case, which allows well-known methods to be used to find critical bifurcation thresholds. This simplification makes it easier to figure out the limits of stability and shows how each delay affects the stability of individual equilibrium states. Changing both delays at the same time, on the other hand, causes nonlinear interactions that make it hard to see how each delay contributes in its own way, which makes both analytical and numerical work harder. Therefore, depending on the values of two delays ($\tau _1$ and $\tau _2$, where at least one of $\tau _1$ and $\tau _2$ is non-zero), the following four cases may be considered.

For $\tau _1>0$ and $\tau _2=0$

In this situation, the characteristic Eq. (9) becomes

$$\begin{aligned} \lambda ^3-a_1^1 \lambda ^2+a_2^1 \lambda -a_3^1-\left\{ b_1^1 \lambda ^2-b_2^1 \lambda +b_3^1\right\} e^{-\lambda \tau _1}=0, \end{aligned}$$

(18)

where

$$\begin{aligned} a_1^1&=\eta _1(k)+\eta _7(k),\quad a_2^1=\eta _2(k)+\eta _8(k),\quad a_3^1=\eta _3(k)+\eta _9(k),\\ b_1^1&=\eta _4(k),\quad b_2^1=\eta _5(k)+\eta _{10}(k),\quad b_3^1=\eta _6(k)+\eta _{11}(k). \end{aligned}$$

Substituting $\lambda =i\omega _1$ in Eq. (18) and separating real and imaginary parts, it can be written as

$$\begin{aligned} & a_1^1 \omega _1^2 -a_3^1 - \left( b_3^1 - b_1^1 \omega _1^2\right) \cos (\omega _1\tau _1)+b_2^1\omega _1\sin (\omega _1\tau _1)=0,\end{aligned}$$

(19)

$$\begin{aligned} & -\omega _1^3+a_2^1 \omega _1+\left( b_3^1 - b_1^1 \omega _1^2\right) \sin (\omega _1\tau _1)+b_2^1\omega _1\cos (\omega _1\tau _1)=0. \end{aligned}$$

(20)

Solving these two equations, the following results are obtained:

$$\begin{aligned} & \sin (\omega _1\tau _1)=\frac{-b_2^1 \omega _1\left( a_1^1\omega _1^2-a_3^1\right) +\left( b_3^1-b_1^1\omega _1^2\right) \left( \omega _1^3-a_2^1\omega _1\right) }{\left( b_2^1\right) ^2\omega _1^2+\left( b_3^1-b_1^1\omega _1^2\right) ^2}:=S_1(\omega _1), \end{aligned}$$

(21)

$$\begin{aligned} & \cos (\omega _1\tau _1)=\frac{-b_2^1 \omega _1\left( \omega _1^3-a_2^1\omega _1\right) -\left( b_3^1-b_1^1\omega _1^2\right) \left( a_1^1\omega _1^2-a_3^1\right) }{\left( b_2^1\right) ^2\omega _1^2+\left( b_3^1-b_1^1\omega _1^2\right) ^2}:=C_1(\omega _1). \end{aligned}$$

(22)

By eliminating the trigonometric functions, one can write

$$\begin{aligned} \left( \omega _1^3-a_2^1\omega _1\right) ^2+\left( a_1^1\omega _1^2-a_3^1\right) ^2=\left( b_2^1\right) ^2\omega _1^2+\left( b_3^1-b_1^1\omega _1^2\right) ^2, \end{aligned}$$

(23)

which can be written as

$$\begin{aligned} \Theta _1(\theta )\equiv \theta ^3+\Psi _1^1 \theta ^2+\Psi _2^1 \theta +\Psi _3^1=0 \end{aligned}$$

(24)

where $\theta =\omega _1^2$, $\Psi _1^1=(a_1^1)^2-2 (a_2^1)-(b_1^1)^2$, $\Psi _2^1=(a_2^1)^2-2a_1^1 a_3^1-(b_2^1)^2+2 b_1^1 b_3^1$, $\Psi _3^1=(a_3^1)^2-(b_3^1)^2$.

If at least one of the coefficients of the above cubic Eq. (24) is negative, then it will have at least one positive root, say $\theta _0$, and consequently a positive root for $\omega _1$, say $\omega _1^0(=\sqrt{\theta _0})$. Then, the critical value of $\tau _1$ may be found from Eqs. (21) and (22) as

$$\begin{aligned} \tau _1^j=\left\{ \begin{array}{ll} \frac{1}{\omega _{1}^0}\left\{ \cos ^{-1} \left[ C_1\left( \omega _{1}^0\right) \right] +2 j \pi \right\} , & \quad \text {if}\quad S_1\left( \omega _{1}^0\right) >0\\ \frac{1}{\omega _{1}^0}\left\{ 2 \pi - \cos ^{-1} \left[ C_1\left( \omega _{1}^0\right) \right] +2 j \pi \right\} , & \quad \text {if}\quad S_1\left( \omega _{1}^0\right) <0,\quad j=0,1,2,\ldots . \end{array}\right. \end{aligned}$$

(25)

After finding the critical values $\tau _1$, it is necessary to figure out whether the eigenvalues on the imaginary axis alter their signs when $\tau _1$ crosses the threshold values $\tau _1=\tau _1^j$ for $j=0,1,2,\ldots$. Thus, in order to confirm the criterion of transversality, the Eq. (18) is differentiated with respect to $\tau _1$, considering $\lambda$ as a function of $\tau _1$, yielding

$$\begin{aligned} \left( \frac{d\lambda }{d \tau _1}\right) ^{-1}=-\frac{3\lambda ^2-2a_1^1\lambda +a_2^1}{\lambda \left( \lambda ^3-a_1^1 \lambda ^2+a_2^1 \lambda -a_3^1\right) }+\frac{2 b_1^1\lambda -b_2^1}{\lambda \left( b_1^1\lambda ^2-b_2^1\lambda +b_3^1\right) }-\frac{\tau _1}{\lambda }. \end{aligned}$$

Thus, at the critical values of $\tau _1$, the following is obtained:

$$\begin{aligned} {Re}\left[ \left( \frac{d\lambda }{d \tau _1}\right) ^{-1}\right] _{\tau _1=\tau _1^j}&= {Re}\left[ -\frac{3\lambda ^2-2a_1^1\lambda +a_2^1}{\lambda \left( \lambda ^3-a_1^1 \lambda ^2+a_2^1 \lambda -a_3^1\right) }+\frac{2 b_1^1\lambda -b_2^1}{\lambda \left( b_1^1\lambda ^2-b_2^1\lambda +b_3^1\right) }-\frac{\tau _1}{\lambda }\right] _{\lambda =i\omega _1^0}\\&=-\frac{\{-3\left( \omega _1^0\right) ^2+a_2^1\}\{\left( \omega _1^0\right) ^2-a_2^1\}-2 a_1^1 \{a_1^1 \left( \omega _1^0\right) ^2-a_3^1\}}{\{\left( \omega _1^0\right) ^3-a_2^1 \omega _1^0\}^2+\{a_1^1 \left( \omega _1^0\right) ^2-a_3^1 \}^2}\\&\quad +\frac{-\left( b_2^1\right) ^2+2 b_1^1 \{-b_1^1 \left( \omega _1^0\right) ^2+b_3^1\}}{\left( b_2^1\right) ^2 \left( \omega _1^0\right) ^2+\{-b_1^1 \left( \omega _1^0\right) ^2+b_3^1\}^2}\\&=\frac{\Theta _1'\{\left( \omega _1^0\right) ^2\}}{\left( b_2^1\right) ^2 \left( \omega _1^0\right) ^2+\{-b_1^1 \left( \omega _1^0\right) ^2+b_3^1\}^2}. \end{aligned}$$

Now, it can be observed that

$$\begin{aligned} \text {sign}\left\{ \left[ \frac{d( {Re}\lambda )}{d \tau _1}\right] _{\tau _1=\tau _1^j}\right\}&=\text {sign}\left\{ {Re}\left[ \left( \frac{d\lambda }{d \tau _1}\right) ^{-1}\right] _{\tau _1=\tau _1^j}\right\} \nonumber \\&=\text {sign}\left\{ \Theta _1'\left\{ \left( \omega _1^0\right) ^2\right\} \right\} \ne 0\quad \text {if}\quad \Theta _1'\left\{ \left( \omega _1^0\right) ^2\right\} \ne 0. \end{aligned}$$

(26)

From the above, one may conclude the following:

Theorem 5.3

For $\tau _2=0$, the delayed spatiotemporal system (1) undergoes a Hopf bifurcation at the interior equilibrium $E^*$ when $\tau _1=\tau _1^j$ provided $\Theta _1'\{(\omega _1^0)\}\ne 0$, where the expression of $\tau _1^j$ and $\Theta _1$ are given in Eqs. (25) and (24), respectively.

Lemma 4

If the Eq. (24) has two positive roots, say $\theta _1$, $\theta _2$, so consequently two positive roots for $\omega _1$, say $\omega _1^1$ and $\omega _1^2$ ($\omega _1^1>\omega _1^2$), then

$$\begin{aligned} \tau _1^{(1,j)}&=\frac{1}{\omega _{1}^1}\left\{ \cos ^{-1} \left[ C_1\left( \omega _{1}^0\right) \right] +2 j \pi \right\} ,\\ \tau _1^{(2,j)}&=\frac{1}{\omega _{1}^2}\left\{ 2 \pi - \cos ^{-1} \left[ C_1\left( \omega _{1}^0\right) \right] +2 j \pi \right\} , \end{aligned}$$

where $\tau _1^{(1,0)}<\tau _1^{(2,0)}<\tau _1^{(1,1)}<\tau _1^{(2,1)}<\cdots .$

If the Eq. (24) has three positive roots, say $\theta _1$, $\theta _2$, and $\theta _3$, so consequently three positive roots for $\omega _1$, say $\omega _1^1$, $\omega _1^2$, and $\omega _1^3$ ($\omega _1^1>\omega _1^2>\omega _1^3$), then $\tau _1^{(i,j)}=\tau _1^j(\omega _1^i)$ for $i=1,2,3$ where $\tau _1^{(1,0)}<\tau _1^{(2,0)}<\tau _1^{(3,0)}<\tau _1^{(1,1)}<\tau _1^{(2,1)}<\tau _1^{(3,1)}<\cdots .$

For $\tau _1=0$ and $\tau _2>0$

In this situation, the characteristic Eq. (9) becomes

$$\begin{aligned} \lambda ^3-a_1^2 \lambda ^2+a_2^2 \lambda -a_3^2-\left\{ b_1^2 \lambda ^2-b_2^2 \lambda +b_3^2\right\} e^{-\lambda \tau _1}=0, \end{aligned}$$

(27)

where

$$\begin{aligned} a_1^2&=\eta _1(k)+\eta _4(k),\quad a_2^2=\eta _2(k)+\eta _5(k),\quad a_3^2=\eta _3(k)+\eta _6(k),\\ b_1^2&=\eta _7(k),\quad b_2^2=\eta _8(k)+\eta _{10}(k),\quad b_3^2=\eta _9(k)+\eta _{11}(k). \end{aligned}$$

By a similar type of calculation as in Section “For τ₁ > 0 and τ₂ = 0”, the critical values of $\tau _2$ can be determined as

$$\begin{aligned} \tau _2^j=\left\{ \begin{array}{ll} \frac{1}{\omega _{2}^0}\left\{ \cos ^{-1} \left[ C_2\left( \omega _{2}^0\right) \right] +2 j \pi \right\} , & \quad \text {if}\quad S_2\left( \omega _{2}^0\right) >0\\ \frac{1}{\omega _{2}^0}\left\{ 2 \pi - \cos ^{-1} \left[ C_2\left( \omega _{2}^0\right) \right] +2 j \pi \right\} , & \quad \text {if}\quad S_2\left( \omega _{2}^0\right) <0,\quad j=0,1,2,\ldots , \end{array}\right. \end{aligned}$$

(28)

where

$$\begin{aligned} & \sin (\omega _2\tau _2)=\frac{-b_2^2 \omega _2\left( a_1^2\omega _2^2-a_3^2\right) +\left( b_3^2-b_1^2\omega _2^2\right) \left( \omega _2^3-a_2^2\omega _2\right) }{\left( b_2^2\right) ^2\omega _2^2+\left( b_3^2-b_1^2\omega _2^2\right) ^2}:=S_2(\omega _2), \end{aligned}$$

(29)

$$\begin{aligned} & \cos (\omega _2\tau _2)=\frac{-b_2^2 \omega _2\left( \omega _2^3-a_2^2\omega _2\right) -\left( b_3^2-b_1^2\omega _2^2\right) \left( a_1^2\omega _2^2-a_3^2\right) }{\left( b_2^2\right) ^2\omega _2^2+\left( b_3^2-b_1^2\omega _2^2\right) ^2}:=C_2(\omega _2), \end{aligned}$$

(30)

and $\omega _2^0$ be the positive root of the cubic polynomial

$$\begin{aligned} \Theta _2(\theta )\equiv \theta ^3+\Psi _1^2 \theta ^2+\Psi _2^2 \theta +\Psi _3^2=0, \end{aligned}$$

(31)

with $\theta =\omega _2^2$, $\Psi _1^2=(a_1^2)^2-2 (a_2^2)-(b_1^2)^2$, $\Psi _2^2=(a_2^2)^2-2a_1^2 a_3^2-(b_2^2)^2+2 b_1^2 b_3^2$, $\Psi _3^2=(a_3^2)^2-(b_3^2)^2$. For the transversality condition, a similar approach to the previous case is followed as

$$\begin{aligned} \text {sign}\left\{ \left[ \frac{d( {Re}\lambda )}{d \tau _2}\right] _{\tau _2=\tau _2^j}\right\}&=\text {sign}\left\{ {Re}\left[ \left( \frac{d\lambda }{d \tau _2}\right) ^{-1}\right] _{\tau _2=\tau _2^j}\right\} \\&=\text {sign}\left\{ \Theta _2'\left\{ \left( \omega _2^0\right) ^2\right\} \right\} \ne 0~\text {provided}~\Theta _2'\left\{ \left( \omega _2^0\right) ^2\right\} \ne 0. \end{aligned}$$

Therefore, one may conclude the following theorem:

Theorem 5.4

For $\tau _1=0$, the delayed spatiotemporal system (1) undergoes a Hopf bifurcation at the interior equilibrium $E^*$ when $\tau _2=\tau _2^j$ provided $\Theta _2'\{(\omega _2^0)\}\ne 0$, where the expression of $\tau _2^j$ and $\Theta _2$ are given in Eqs. (28) and (31), respectively.

Lemma 5

If the Eq. (31) has two positive roots, say $\theta _1$, $\theta _2$, so consequently two positive roots for $\omega _2$, say $\omega _2^1$ and $\omega _2^2$ ($\omega _2^1>\omega _2^2$), then

$$\begin{aligned} \tau _2^{(1,j)}&=\frac{1}{\omega _{2}^1}\left\{ \cos ^{-1} \left[ C_2\left( \omega _{2}^1\right) \right] +2 j \pi \right\} ,\\ \tau _2^{(2,j)}&=\frac{1}{\omega _{2}^2}\left\{ 2 \pi - \cos ^{-1} \left[ C_2\left( \omega _{2}^2\right) \right] +2 j \pi \right\} , \end{aligned}$$

where $\tau _2^{(1,0)}<\tau _2^{(2,0)}<\tau _2^{(1,1)}<\tau _2^{(2,1)}<\cdots .$

If the Eq. (31) has three positive roots, say $\theta _1$, $\theta _2$, and $\theta _3$, so consequently three positive roots for $\omega _2$, say $\omega _2^1$, $\omega _2^2$, and $\omega _2^3$ ($\omega _2^1>\omega _2^2>\omega _2^3$), then $\tau _2^{(i,j)}=\tau _2^j(\omega _2^i)$ for $i=1,2,3$ where $\tau _2^{(1,0)}<\tau _2^{(2,0)}<\tau _2^{(3,0)}<\tau _2^{(1,1)}<\tau _2^{(2,1)}<\tau _2^{(3,1)}<\cdots .$

For $\tau _1>0$ and $\tau _2$ is fixed in $(0,\tau _2^0)$

Substituting $\lambda =i\omega _3$ in Eq. (9) and dividing into real and imaginary components, it can be written as

$$\begin{aligned} & l_{11}-m_1 \cos (\omega _3\tau _1)+ n_1 \sin (\omega _3\tau _1)=0, \end{aligned}$$

(32)

$$\begin{aligned} & l_{21}+m_1 \sin (\omega _3 \tau _1)+ n_1 \cos (\omega _3 \tau _1)=0, \end{aligned}$$

(33)

where

$$\begin{aligned} l_{11}&=\eta _1 \omega _3^2-\eta _3 + (\eta _7 \omega _3^2- \eta _9 ) \cos (\tau _2 \omega _3) + \eta _8 \omega _3 \sin (\tau _2 \omega _3),\\ l_{21}&= - \omega _3^3+ \eta _2 \omega _3 + \eta _8 \omega _3 \cos (\tau _2 \omega _3)- (\eta _7 \omega _3^2-\eta _9) \sin (\tau _2 \omega _3),\\ m_1&= - \eta _4 \omega _3^2+\eta _6 - \eta _{10} \omega _3 \sin (\tau _2 \omega _3) + \eta _{11} \cos (\tau _2 \omega _3),\\ n_1&=\eta _5 \omega _3 + \eta _{10} \omega _3 \cos (\tau _2 \omega _3) + \eta _{11} \sin (\tau _2 \omega _3). \end{aligned}$$

Solving the above two Eqs. (32) and (33), the following is obtained

$$\begin{aligned} \sin (\omega _3\tau _1)&=-\frac{l_{21} m_1+l_{11} n_1}{m_1^2+n_1^2}:=S_3(\omega _3),\nonumber \\ \cos (\omega _3\tau _1)&=\frac{l_{11} m_1-l_{21} n_1}{m_1^2+n_1^2}:=C_3(\omega _3). \end{aligned}$$

(34)

Squaring and adding the above two equations to eliminate $\tau _1$, it can be written as

$$\begin{aligned} l_{11}^2+l_{21}^2-\left( m_1^2+n_1^2\right) =0 \end{aligned}$$

(35)

which is a transcendental equation. Now, if $\omega _{3}^0$ is a positive root of the Eq. (35), then from Eq. (34), it can be written as

$$\begin{aligned} \tau _1^j=\left\{ \begin{array}{ll} \frac{1}{\omega _{3}^0}\left\{ \cos ^{-1} \left[ C_3\left( \omega _{3}^0\right) \right] +2 j \pi \right\} , & \quad \text {if}\quad S_3\left( \omega _{3}^0\right) >0\\ \frac{1}{\omega _{3}^0}\left\{ 2 \pi - \cos ^{-1} \left[ C_3\left( \omega _{3}^0\right) \right] +2 j \pi \right\} , & \quad \text {if}\quad S_3\left( \omega _{3}^0\right) <0,\quad j=0,1,2,\ldots . \end{array}\right. \end{aligned}$$

(36)

After finding the critical values $\tau _1$, it is necessary to identify whether the eigenvalues on the imaginary axis alter their signs when $\tau _1$ crosses the threshold values $\tau _1=\tau _1^j$ for $j=0,1,2,\ldots$. To achieve this, the Eq. (9) is differentiated with respect to $\tau _1$, considering $\lambda$ as a function of $\tau _1$, resulting in

$$\begin{aligned} \frac{d\lambda }{d\tau _1}=\frac{M}{N}, \end{aligned}$$

(37)

where

$$\begin{aligned} M&=\lambda \left\{ - P_2 e^{-\lambda \tau _1} + P_4 e^{-\lambda (\tau _1+\tau _2)}\right\} ,\\ N&=3 \lambda ^2-2 \eta _1 \lambda +\eta _2-\{(2 \eta _4 \lambda -\eta _5)-\tau _1 P_2\}e^{-\lambda \tau _1}\\&\quad -\{(2 \eta _7 \lambda -\eta _8)-\tau _2 P_3\}e^{-\lambda \tau _2}+\{\eta _{10}-(\tau _1+\tau _2) P_4\} e^{-\lambda (\tau _1+\tau _2)}. \end{aligned}$$

Now, at the critical values of $\tau _1$ after eliminating $e^{-\lambda \tau _1}$ using the Eq. (9) from the Eq. (37), it can be written as

$$\begin{aligned} \left. \frac{d\lambda }{d\tau _1}\right| _{\tau _1=\tau _1^j}=\frac{\omega _3^0 Q_1\left( \omega _3^0,\tau _1^j\right) }{Q_2\left( \omega _3^0,\tau _1^j\right) } \end{aligned}$$

(38)

where

$$\begin{aligned} Q_1\left( \omega _3^0,\tau _1^0\right)&=\left\{ (P_2 P_3 + P_1 P_4) \sin \left( \tau _2 \omega _3^0\right) - P_3 P_4 \sin \left( 2 \tau _2 \omega _3^0\right) \right\} \\&\quad -i \left\{ P_1 P_2 - (P_2 P_3 + P_1 P_4) \cos \left( \tau _2 \omega _3^0\right) + P_3 P_4 \cos \left( 2 \tau _2 \omega _3^0\right) \right\} ,\\ Q_2\left( \omega _3^0,\tau _1^0\right)&=P_2 \eta _2 + P_1 \eta _5 + P_1 P_2 \tau _1 - 3 P_2 \left( \omega _3^0\right) ^2 + \left\{ -P_4 \eta _2 - P_3 \eta _5 + P_2 \eta _8 - P_2 P_3 \tau _1 + P_2 P_3 \tau _2 \right. \\&\quad \left. + P_1 (\eta _{10} - P_4 (\tau _1 + \tau _2)) + 3 P_4 (\omega _3^0)^2\right\} \cos (\tau _2 \omega _3^0) - (P_3 \eta _{10} + P_4 \eta _8 - P_3 P_4 \tau _1) \cos \left( 2 \tau _2 \omega _3^0\right) \\&\quad + (2 P_4 \eta _1 + 2 P_3 \eta _4 - 2 P_2 \eta _7) \omega _3^0 \sin \left( \tau _2 \omega _3^0\right) + 2 P_4 \eta _7 \omega _3^0 \sin \left( 2 \tau _2 \omega _3^0\right) \\&\quad +i \left\{ -2 P_2 \eta _1 \omega _3^0 - 2 P_1 \eta _4 \omega _3^0 + 2 (P_4 \eta _1 + P_3 \eta _4 - P_2 \eta _7) \omega _3^0 \cos (\tau _2 \omega _3^0) + 2 P_4 \eta _7 \omega _3^0 \cos (2 \tau _2 \omega _3^0) \right. \\&\quad +\left( - P_1 \eta _{10} + P_4 \eta _2 + P_3 \eta _5 - P_2 \eta _8 + P_2 P_3 \tau _1 + P_1 P_4 \tau _1 - P_2 P_3 \tau _2 + P_1 P_4 \tau _2 - 3 P_4 \left( \omega _3^0\right) ^2\right) \\&\quad \left. \sin \left( \tau _2 \omega _3^0\right) + (P_3 \eta _{10} + P_4 \eta _8 - P_3 P_4 \tau _1) \sin \left( 2 \tau _2 \omega _3^0\right) \right\} . \end{aligned}$$

Thus, the real parts can be written as

$$\begin{aligned} {Re}\left[ \left. \frac{d\lambda }{d\tau _1}\right| _{\tau _1=\tau _1^j}\right] =\omega _3^0 \left( \frac{ {Re}(Q_1) {Re}(Q_2)+Im(Q_1)Im(Q_2)}{\{ {Re}(Q_2)\}^2+\{Im(Q_2)\}^2}\right) \end{aligned}$$

(39)

Therefore, the transversality condition may be stated as

$$\begin{aligned} \left. \frac{d {Re}(\lambda )}{d\tau _1}\right| _{\tau _1=\tau _1^j}= {Re}\left[ \left. \frac{d\lambda }{d\tau _1}\right| _{\tau _1=\tau _1^j}\right] \ne 0,~\text {provided}~ {Re}(Q_1) {Re}(Q_2)+Im(Q_1)Im(Q_2) \ne 0. \end{aligned}$$

Based on the above, the following theorem can be concluded:

Theorem 5.5

For fixed $\tau _2(\in (0,\tau _2^0))$, the delayed spatiotemporal system (1) undergoes a Hopf bifurcation at the interior equilibrium $E^*$ when $\tau _1=\tau _1^j$ provided $Re(Q_1) Re(Q_2)+Im(Q_1)Im(Q_2)\ne 0$, where the expression of $\tau _1^j$ is given in Eq. (36).

For $\tau _2>0$ and $\tau _1$ is fixed in $(0,\tau _1^0)$

In this case, separating real and imaginary components after substituting $\lambda =i\omega _4$ in the Eq. (9) results in:

$$\begin{aligned}&l_{12}-m_2 \cos (\tau _2 \omega _4)+n_2 \sin (\tau _2 \omega _4)=0\\&l_{22}+ m_2 \sin (\tau _2 \omega _4)+n_2 \cos (\tau _2 \omega _4) =0 \end{aligned}$$

where

$$\begin{aligned} l_{12}&=\eta _1 \omega _4^2-\eta _3 + (\eta _4 \omega _4^2-\eta _6) \cos (\tau _1 \omega _4) + \eta _5 \omega _4 \sin (\tau _1 \omega _4),\\ l_{22}&=- \omega _4^3 + \eta _2 \omega _4 + \eta _5 \omega _4 \cos (\tau _1 \omega _4) - (\eta _4 \omega _4^2 - \eta _6) \sin (\tau _1 \omega _4),\\ m_2&=- \eta _7 \omega _4^2 + \eta _9 - \eta _{10} \omega _4 \sin (\tau _1 \omega _4) + \eta _{11} \cos (\tau _1 \omega _4),\\ n_2&=\eta _8 \omega _4 + \eta _{10} \omega _4 \cos (\tau _1 \omega _4) + \eta _{11} \sin (\tau _1 \omega _4). \end{aligned}$$

By a similar calculation as in the previous case, the critical values of $\tau _2$ can be obtained as

$$\begin{aligned} \tau _2^j=\left\{ \begin{array}{ll} \frac{1}{\omega _{4}^0}\left\{ \cos ^{-1} [C_4(\omega _{4}^0)]+2 j \pi \right\} , & \quad \text {if}\quad S_4(\omega _{4}^0)>0\\ \frac{1}{\omega _{4}^0}\left\{ 2 \pi - \cos ^{-1} [C_4(\omega _{4}^0)]+2 j \pi \right\} , & \quad \text {if}\quad S_4(\omega _{4}^0)<0,\quad j=0,1,2,\ldots , \end{array}\right. \end{aligned}$$

(40)

where

$$\begin{aligned} \sin (\omega _4\tau _2)&=-\frac{l_{22} m_2+l_{12} n_2}{m_2^2+n_2^2}:=S_4(\omega _4),\nonumber \\ \cos (\omega _4\tau _2)&=\frac{l_{12} m_2-l_{22} n_2}{m_2^2+n_2^2}:=C_4(\omega _3), \end{aligned}$$

(41)

and $\omega _{4}^0$ is the positive root (if it exists) of the transcendental equation $l_{12}^2+l_{22}^2-(m_2^2+n_2^2)=0$.

Now, for the transversality condition, the Eq. (9) is differentiated with respect to $\tau _2$ and obtained

$$\begin{aligned} \frac{d\lambda }{d\tau _2}=\frac{\bar{M}}{N} \end{aligned}$$

(42)

where $\bar{M}=\lambda \{- P_3 e^{-\lambda \tau _2} + P_4 e^{-\lambda (\tau _1+\tau _2)}\}$ and N is given in previous case.

Now, at the critical values of $\tau _2$ after eliminating $e^{-\lambda \tau _2}$ using the Eq. (9) from the Eq. (42), it can be written as

$$\begin{aligned} \left. \frac{d\lambda }{d\tau _2}\right| _{\tau _2=\tau _2^j}=\frac{\omega _4^0 Q_3(\omega _4^0,\tau _2^j)}{Q_4(\omega _4^0,\tau _2^j)} \end{aligned}$$

(43)

where

$$\begin{aligned} Q_3\left( \omega _4^0,\tau _2^0\right)&=(P_2 P_3 + P_1 P_4) \sin \left( \tau _1 \omega _4^0\right) - P_2 P_4 \sin \left( 2 \tau _1 \omega _4^0\right) \\&\quad -i\left\{ P_1 P_3 - (P_2 P_3 + P_1 P_4) \cos \left( \tau _1 \omega _4^0\right) + P_2 P_4 \cos \left( 2 \tau _1 \omega _4^0\right) \right\} ,\\ Q_4(\omega _4^0,\tau _2^0)&=P_3 \eta _2 + P_1 \eta _8 + P_1 P_3 \tau _2 - 3 P_3 (\omega _4^0)^2 + \left\{ -P_4 \eta _2 + P_3 \eta _5 - P_2 \eta _8 + P_2 P_3 \tau _1 - P_2 P_3 \tau _2 \right. \\&\quad \left. +P_1 (\eta _{10} - P_4 (\tau _1 + \tau _2)) + 3 P_4 (\omega _4^0)^2\right\} \cos \left( \tau _1 \omega _4^0\right) - (P_2 \eta _{10} + P_4 \eta _5 - P_2 P_4 \tau _2) \cos \left( 2 \tau _1 \omega _4^0\right) \\&\quad +(2 P_4 \eta _1 - 2 P_3 \eta _4 + 2 P_2 \eta _7) \omega _4^0 \sin \left( \tau _1 \omega _4^0\right) + 2 P_4 \eta _4 \omega _4^0 \sin \left( 2 \tau _1 \omega _4^0\right) \\&\quad +i\left\{ -2 P_3 \eta _1 \omega _4^0 - 2 P_1 \eta _7 \omega _4^0 + 2 (P_4 \eta _1 - P_3 \eta _4 + P_2 \eta _7) \omega _4^0 \cos (\tau _1 \omega _4^0) + 2 P_4 \eta _4 \omega _4^0 \cos (2 \tau _1 \omega _4^0) \right. \\&\quad +\left( -P_1 \eta _{10} +P_4 \eta _2 - P_3 \eta _5 +P_2 \eta _8 -P_2 P_3 \tau _1 + P_1 P_4 \tau _1 +P_2 P_3 \tau _2 +P_1 P_4 \tau _2 -3 P_4 (\omega _4^0)^2\right) \\&\quad \left. \sin \left( \tau _1 \omega _4^0\right) + (P_2 \eta _{10} +P_4 \eta _5 - P_2 P_4 \tau _2) \sin \left( 2 \tau _1 \omega _4^0\right) \right\} . \end{aligned}$$

Thus, the real parts can be written as

$$\begin{aligned} {Re}\left( \left. \frac{d\lambda }{d\tau _2}\right| _{\tau _2=\tau _2^j}\right) =\omega _4^0 \left( \frac{ {Re}(Q_3) {Re}(Q_4)+Im(Q_3)Im(Q_4)}{\{ {Re}(Q_4)\}^2+\{Im(Q_4)\}^2}\right) . \end{aligned}$$

(44)

Therefore, the transversality condition may be stated as

$$\begin{aligned} \left. \frac{d {Re}(\lambda )}{d\tau _2}\right| _{\tau _2=\tau _2^j}= {Re}\left[ \left. \frac{d\lambda }{d\tau _2}\right| _{\tau _2=\tau _2^j}\right] \ne 0,~\text {provided}~ {Re}(Q_3) {Re}(Q_4)+Im(Q_3)Im(Q_4) \ne 0. \end{aligned}$$

From the above, the following theorem can be stated:

Theorem 5.6

For fixed $\tau _1(\in (0,\tau _1^0))$, the delayed spatiotemporal system (1) undergoes a Hopf bifurcation at the interior equilibrium $E^*$ when $\tau _2=\tau _2^j$ provided ${Re}(Q_3) {Re}(Q_4)+Im(Q_3)Im(Q_4)\ne 0$, where the expression of $\tau _2^j$ is given in Eq. (40).

Algorithm for solution of spatiotemporal system with time delays

The next intent of this study is to solve the spatiotemporal system numerically. For this purpose, the algorithm is provided in this section as follows:

First of all, a spatiotemporal system with delay is considered as

$$\begin{aligned} \frac{\partial u}{\partial t}=f(t,u,u_{\tau })+d \nabla ^2 u \end{aligned}$$

(45)

with $(x,y)\in \Sigma$, $u(t,x,y)\ge 0$ for $t\in [-\tau ,0]$ and Neumann boundary conditions $\frac{\partial u}{\partial \nu }=0$ on $\partial \Sigma$, for all $t>0$, where $u\in \mathbb {R}^n$. Here $u_\tau =u(t-\tau ,x,y)$. Now, to solve the delayed spatiotemporal system (45), the Forward Time Centered Space (FTCS) scheme and the explicit Euler method will be used. The general layout of the algorithm is as follows:

• 1. Define the spatial domain $L\times L$ and temporal domain [0, T] .

• 2. Discretise the spatial domain with step size $h=\Delta x=\Delta y$ and time step size $\Delta t$. Consider $N^2$ as the total spatial grid points and $N_t$ as the number of time steps.

• 3. Ensure stability for the diffusion term by using the condition: $\Delta t\le \frac{h^2}{4 d}$.

• 4. Initialise $u(t=0,x,y)$ by giving a small random perturbation around the equilibrium and its delayed value $u(t\in [-\tau ,0],x,y)$.

• 5. For $n=0$ to $n=N_t-1$, do the following steps:

  • i. Apply the Neumann boundary condition for u.

  • ii. For diffusion terms, use the FTCS scheme:

    $$\begin{aligned} \nabla ^2 u\approx \frac{u_{i+1,j}^n+u_{i-1,j}^n+u_{i,j+1}^n+u_{i,j-1}^n-4 u_{i,j}^n}{h^2}. \end{aligned}$$

  • iii. For the reaction term, use the explicit Euler method: $\Delta t\cdot f(t,u,u_\tau )$.

  • iv. Update $u_{i,j}$ for $i,j=1,2,3,\ldots ,N-1$:

    $$\begin{aligned} u_{i,j}^{n+1}=u_{i,j}^n+\Delta t\cdot f(t,u,u_\tau )+d\cdot h\cdot \left( \frac{u_{i+1,j}^n+u_{i-1,j}^n+u_{i,j+1}^n+u_{i,j-1}^n-4 u_{i,j}^n}{h^2}\right) . \end{aligned}$$

  • v. Store the computed u value at each time step for accessing delayed terms $u_\tau$. If $t-\tau$ does not align with the grid, use linear interpolation to compute the delayed values.

• 6. Visualise u at desired time steps to analyse the spatiotemporal evolution of u.

Numerical simulation

Due to the inaccessibility of the real-world data, some physiologically significant parameter values are considered here for the numerical verification of the theoretical outcomes of the previous section. So, the reader should keep in mind that the numerical findings of this research will be qualitative, not quantitative. For this perspective, the parameter values are considered as follows:

$$\begin{aligned} r&=0.5;\quad K=20;\quad \beta =0.04;\quad a=0.1;\quad \alpha _1=0.04;\quad \rho =0.1;\quad b=1;c=1;\nonumber \\ \mu&=0.012;\quad \alpha _2=0.06;\nonumber \\ \gamma _1&=0.7;\quad \gamma _2=0.6;\quad d=0.02;\quad \delta =0.005;\quad d_1=1;\quad d_2=0.002;\quad d_3=3. \end{aligned}$$

(46)

The method as given in Section “Algorithm for solution of spatiotemporal system with time delays” is used to solve the spatiotemporal system (1) numerically. For this, $h=\Delta x=\Delta y=0.25$ and $\Delta t=0.005$ are taken to demonstrate the diffusive distributions of the populations in a $101\times 101$ grid points. Numerical simulations are conducted until the pattern attains its stationary state, enabling the observation of diverse spatial dynamics. It is observed that the species distributions are essentially similar. Therefore, only the pattern formation of the susceptible prey species is considered for clarity.

Diffusion driven instability without any delay

The primary objective of this part is to analyse the instability brought about by diffusion as a result of species’ random migrations, ignoring delays (i.e., $\tau _1=\tau _2=0$). The system must be stable when diffusion is absent (i.e., for $k=0$) for the Turing instability. For the parameters as in (46), it can be shown that $\xi _1(0)>0$, $\xi _2(0)>0$, $\xi _3(0)>0$, and $\xi _1(0)\xi _2(0)-\xi _3(0)>0$. So, the Turing instability may occur for these parameters near the interior equilibrium point $E^*(2.4233,7.7671,6.2183)$. Using the Theorems 5.1, 5.2 and Lemmas 2, 3, the stable, Turing, Hopf–Turing, and Pure–Hopf regions of the non-delayed spatiotemporal system corresponding to (1) are plotted in Fig. 2 for (a) $\beta$ versus $\rho$ space, (b) $\delta$ versus $\rho$ space, and (c) $\delta$ versus $\beta$ space. To verify these regions, the maximum of the real parts of the eigenvalues is also plotted in Fig. 3 for the parameters taken from different regions of Fig. 2. This figure shows that when the parameters are taken from the green region of Fig. 2, the maximum of the real parts of the eigenvalues starts at negative and cuts the $x-$axis two times. So, in the green region, Turing instability will occur. Again, if the parameters are taken from the red region of Figs. 2 and 3 shows that the maximum of the real parts of the eigenvalues starts at positive and cuts the x-axis thrice. So, the red region represents the Hopf–Turing. But, when the parameters are taken from the blue region, Fig. 3 shows that the maximum of the real parts of the eigenvalues starts at negative, and after that, it does not cut the x-axis any more (for cyan, it starts at positive and cuts the x-axis only one time). Thus, due to diffusion, no instability is observed in these regions (i.e., blue and cyan regions). Therefore, in the green and red regions of Fig. 2, some stationary patterns may be expected.

Fig. 3

The maximum of the real part of the eigenvalues against the wave-number for parameters taken from different regions of Fig. 2.

Figure 4 shows four distinct patterns for four distinct $\delta$ values when there is no delay. Figure 4a shows cold spot type patterns for $\delta =0.0015$. When $\delta$ is increased to 0.002, a combination of a cold spot and a strip emerges, as depicted in Fig. 4b. Next, purely strip-type patterns are shown for $\delta =0.0035$ in Fig. 4c. Figure 4d shows a transition from strip to hot spot type pattern for the increment of $\delta$ from 0.0035 to 0.005.

Fig. 4

Snapshots of the stationary patterns of susceptible prey for (a) $\delta =0.0015$, (b) $\delta =0.002$, (c) $\delta =0.0035$, (d) $\delta =0.005$ and other parameters as in (46). This figure shows that higher intraspecific competition reduces predator fitness, indirectly promoting prey survival and altering ecosystem spatial structure.

Now, the ecological and epidemiological implications of these patterns are discussed here. Spot-type patterns indicate that the prey is concentrated in isolated spots or patches (hot spots) separated by regions of lower density (cold spots). On the other hand, strip-type patterns indicate that the prey population is self-organising into elongated, alternating regions of high and low density. These types of high-density patterns can be thought of as “refuges” where prey may concentrate, either because the local conditions are more favourable (for instance, due to lower predation pressure or reduced disease transmission) or because they benefit from positive local interactions (like facilitation or cooperative behaviour). These highly dense patterns (spot or strip) might favour local epidemic outbreaks because higher local densities can increase transmission rates. On the other hand, if the patterns are sufficiently isolated, the disease may have a harder time spreading from one patch to another, potentially reducing the overall epidemic impact. Therefore, the adjacent low-density areas of these patterns (cold spots or alternating bands with low density) might limit the spread of a disease or the efficiency of predators, acting as a buffer zone.

Stripes suggest a more connected landscape compared to spots, where individuals might have more continuous movement along the bands. For this reason, strips potentially lead to more directional or wave-like epidemic propagation than spots. From a management or conservation perspective, recognising that prey is organised into spots or strips can help in designing targeted interventions. For example, if an epidemic is spreading primarily within these hotspots or high-density strips, then localised control measures (such as targeted vaccination or culling) may be more effective than blanket strategies.

Effect of cross diffusion

This section intends to study the impact of cross-diffusion on the system (1) in the absence of any delay. As the infected prey populations are weak in nature, it may be treated that the infected prey is unable to move away from predators. Therefore, by considering the cross-diffusion term on susceptible prey and predator populations, the system (1) may be written in the absence of any delay as

$$\begin{aligned} \frac{\partial S}{\partial t}&=r S \left( 1-\frac{S+I}{K}\right) -\frac{\beta S I}{1+a I}-\frac{\alpha _1 (1-\rho ) S P}{1+b (1-\rho ) S}+d_1 \nabla ^2 S+d_{13} \nabla ^2 P,\nonumber \\ \frac{\partial I}{\partial t}&= \frac{\beta S I}{1+a I}-\frac{\alpha _2 I P}{1+c I}-\mu I+d_2 \nabla ^2 I,\nonumber \\ \frac{\partial P}{\partial t}&=\frac{\gamma _1 \alpha _1 (1-\rho ) S P}{1+b (1-\rho ) S}+\frac{\gamma _2 \alpha _2 I P}{1+c I}-d P-\delta P^2+d_3 \nabla ^2 P+d_{31} \nabla ^2 S, \end{aligned}$$

(47)

where $d_{13}$ and $d_{31}$ represent the cross-diffusion coefficients of the susceptible prey and predator population, respectively. The initial and the boundary conditions are the same as of the system (1).

Figure 5 shows different types of patterns for different cross-diffusion coefficients. When the cross diffusion is not considered (i.e., $d_{13}=0,d_{31}=0$), Fig. 5a shows a strip-type pattern. As the cross-diffusion for predator is considered (i.e., $d_{13}=0,d_{31}=1$), Fig. 5b gives a mixture of strip and hot spot-type patterns. Finally, when both cross-diffusion coefficients are considered (i.e., $d_{13}=2,d_{31}=1$), Fig. 5c shows a hot spot-type pattern. At lower cross-diffusion values, strip patterns show a more even or directional organisation of space, which could be related to differences in the environment, like the amount of available resources. As cross-diffusion coefficients rise, hot spots appear, which are places where species gather into small groups. This shows that the behavioural responses are stronger. For example, prey might avoid areas with many more predators, which would spread them out more evenly. This shift from strips to hot spots underscores how movement behaviour modulates spatial heterogeneity, influencing coexistence and stability.

Fig. 5

Snapshots of the stationary patterns for $\delta =0.0035$, other parameters as in Eq. (46) and different cross diffusion coefficient: (a) $d_{13}=0,d_{31}=0$, (b) $d_{13}=0,d_{31}=1$ and (c) $d_{13}=2,d_{31}=1$. These changes underscore how movement behaviour modulates spatial heterogeneity, influencing the coexistence and stability of the ecosystem.

Pattern formation of delayed spatiotemporal system

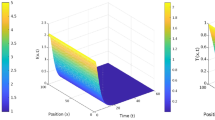
Next, the impact of incubation and gestational delay on the development of spatiotemporal patterns will be investigated. For an incubation delay of $\tau _1=0.6$ and a gestation delay of $\tau _2=0.8$, Fig. 6a shows the snapshot of spatial emergence of susceptible prey population at the end of simulation, and Fig. 6b shows the time series of spatial average of susceptible prey population during the simulation. After half of the simulation time, no changes are observed in the spatial average of the susceptible prey population. So, for these values of delays, the system (1) produces a stationary pattern. However, when $\tau _1=1$ and $\tau _2=1$, Fig. 7b exhibits oscillatory behaviour. Though Fig. 7a shows a spot-like pattern, during the simulation time, the range of the colour bar changes all the time. So, this pattern is not stationary. So, the delays have the power to change the stationary pattern (Fig. 6a) to the quasi-periodic pattern (Fig. 7a). These changes happen because of Hopf bifurcation, as discussed in Section “Hopf bifurcation analysis of delayed spatiotemporal system”.

Fig. 6

(a) Snapshot of the spatial pattern, and (b) time series plot of the spatial average of susceptible prey for $\tau _1=0.6$, $\tau _2=0.8$, and other parameters as in (46).

Fig. 7

(a) Snapshot of the spatial pattern, and (b) time series plot of the spatial average of susceptible prey for $\tau _1=1$, $\tau _2=1$, and other parameters as in (46).

For single delay

For $k=0$, i.e., the non-diffusive system, only one positive root of the Eq. (24) is obtained ($\omega _1^0=\sqrt{\theta _0}=0.1269$), and the corresponding critical value of $\tau _1$ is $\tau _1^0=0.2157$. Also, the Eq. (26) gives that the transversality condition $\left[ \frac{d(Re\lambda )}{d \tau _1}\right] _{\tau _1=\tau _1^0}>0$. Therefore, all conditions of Theorem 5.3 satisfy. Figure 8a also shows that at $\tau _1=0.2157$, a pair of eigenvalues crosses $\mathbb {C}^0$. Thus, for $\tau _2=0$, the non-diffusive system loses its stability at $\tau _1=0.2157$ through the Hopf bifurcation. Similarly, the Eq. (31) has two roots, $\omega _2^1=\sqrt{\theta _1}=0.1281$ and $\omega _2^2=\sqrt{\theta _2}=0.1221$. Therefore, the corresponding critical $\tau _2$ ($\tau _2^{(1,0)}=5.0583$ and $\tau _2^{(2,0)}=40.0451$) has the transversality conditions $\left[ \frac{d(Re\lambda )}{d \tau _2}\right] _{\tau _2=\tau _2^{(1,0)}}>0$ and $\left[ \frac{d(Re\lambda )}{d \tau _2}\right] _{\tau _2=\tau _2^{(2,0)}}<0$ respectively, as stated in Theorem 5.4. Also, all the threshold values of $\tau _2$ can be obtained as follows:

$$\begin{aligned} 0<\tau _2^{(1,0)}=5.0583<\tau _2^{(2,0)}=40.0451<\tau _2^{(1,1)}=54.175<\tau _2^{(2,1)}=91.5641<\cdots . \end{aligned}$$

Consequently, it may be deduced from Lemma 5 that $E^*$ experiences stability changes with respect to the increase of $\tau _2$. Figure 8b also illustrates the stability scenario in terms of eigenvalue variation of the characteristic Eq. (27) with respect to $\tau _2$. In this case, all the eigenvalues have positive real parts for $\left( \tau _2^{(1,0)},\tau _2^{(2,0)}\right) \cup \left( \tau _2^{(1,1)},\tau _2^{(2,1)}\right)$. So, the equilibrium $E^*$ becomes unstable when $\tau _2\in \left( \tau _2^{(1,0)},\tau _2^{(2,0)}\right) \cup \left( \tau _2^{(1,1)},\tau _2^{(2,1)}\right)$ for $\tau _1=0$.

Fig. 8

Variation of ${Re}(\lambda )$ with respect to (a) $\tau _1$ of the characteristic Eq. (18) and (b) $\tau _2$ of the characteristic Eq. (27) demonstrating delay-induced stability switching for $k=0$ with parameters as in (46).

Here, it is observed that if $\tau _1$ exceeds $\tau _1^0$, the system exhibits periodic behaviour. This is because a greater incubation period $\tau _1$ allows the disease to accumulate in the population silently. This is primarily due to the silent accumulation of the disease within the prey population during the incubation phase, where infected individuals do not yet show symptoms but can contribute to the spread of the disease. In this situation, normal control strategies become ineffective, requiring more aggressive or targeted measures to stabilise the situation. Also, when the infection label is at its peak, predators can consume more prey (infected prey) easily. So, the prey population goes down rapidly, which creates a shortage of resources for predators. Again, due to the shortage of resources, the predator population decreases. At this time, the prey population reproduces more due to lower predation pressure, and in this way, the period occurs. Thus, the incubation delay $\tau _1$ not only alters disease transmission dynamics but also introduces oscillatory patterns in the interacting species through eco-epidemiological feedback mechanisms.

Again, a stability switching is observed for the gestation delay $\tau _2$ (as in Fig. 8b). The ecological implication of this switching is that the timing of reproduction of predators plays a pivotal role in determining the overall stability of the ecosystem. This stability switching may happen for many reasons. When $\tau _2$ falls within the unstable intervals, the prey’s population growth may not synchronise well with the predator’s consumption rate. For large gestation delay, predators over-consume prey before reproducing, leading to prey collapse and subsequent predator crashes. On the other hand, for small gestation delays, predators overreact to prey increases, causing destabilising overcompensation. This mismatch can lead to an overabundance or a deficit of prey relative to the predator’s needs, disrupting the balance. For ecological management and conservation, understanding these critical delay values is essential. If the gestation delay is naturally or environmentally altered (e.g., due to stress, climate change, or habitat alteration), it might push the system into an unstable regime, resulting in dramatic fluctuations in population sizes.

When the delayed diffusive system (i.e., $k>0$) is considered, Fig. 9 shows the spatial behaviours of $E^*$ of the delayed diffusive system (1) for different values of $\tau _1$ with $\tau _2=0$. The left side of this figure shows the changes in the pattern formation (stationary hot spot$\rightarrow$quasi-periodic hot spot$\rightarrow$quasi-periodic strip), and the right side shows the changes in the time series plot of the spatial average of susceptible prey for increasing values of $\tau _1$. These changes reflect the growing spatial complexity and instability in the prey population distribution. Initially, when the incubation delay is small, stationary hot spots form, representing stable, localised clusters of susceptible prey. These regions persist over time due to a balance between predation, reproduction, and disease transmission. However, as $\tau _1$ increases, the hidden spread of infection during the incubation period disrupts this balance. This results in quasi-periodic hot spots, where prey densities fluctuate over both space and time. With a further increase in $\tau _1$, the infection’s delayed feedback becomes strong enough to cause a coherent shift in spatial structures, forming quasi-periodic strips. From this figure, it can be claimed that the critical value of $\tau _1$ must lie between 0.6 and 0.8. The critical values of a single delay have been calculated in Table 2 for different wave numbers with the help of Theorems 5.3 and 5.4. Here, the second and third columns represent the critical values of $\tau _1$ and $\tau _2$, respectively, for different values of k. As Fig. 9 indicates that the critical value of $\tau _1$ lies between 0.6 and 0.8, Table 2 suggests that the critical value of k for the parameter set (46) falls within the interval (0.075, 0.095). Again, Fig. 10 shows the spatial behaviour of $E^*$ for different values of $\tau _2$ with $\tau _1=0$. This figure shows that though $\tau _2$ shows the stability switching behaviour for the non-diffusive system, it has no power to change the stability of the spatial system (1) for the set of parameters (46). Thus, Table 2 confirms that the critical value of k lies within the interval (0.08, 0.095). By setting $k=0.085$, the real parts of the eigenvalues of the characteristic Eqs. (18) and (27) are plotted in Fig. 11a and b respectively. Figure 11a shows that at $\tau _1=0.7161$, a pair of eigenvalues crosses $\mathbb {C}^0$ for $\tau _2=0$. Therefore, if the critical value of k is 0.085, then $E^*$ lost its stability at $\tau _1=0.7161$ for $\tau _2=0$. Similarly, Fig. 11b shows that no eigenvalue crosses $\mathbb {C}^0$ for increasing $\tau _2$ and $\tau _1=0$. Hence, for the parameters in (46), the stability of the spatiotemporal system is unaffected by $\tau _2$ when $\tau _1$ is not present.

Fig. 9

Left: Snapshot of the spatial pattern, and Right: time series plot of the spatial average of susceptible prey for (a, b) $\tau _1=0.6$, (c, d) $\tau _1=0.8$, (e, f) $\tau _1=6$ and other parameters as in (46) with $\tau _2=0$. Temporal oscillations destabilise the Turing mechanism as the incubation delay increases, leading to large-scale wave-like patterns.

Table 2 Critical delay for different wave numbers and parameters as in Eq. (46).

Fig. 10

Left: Snapshot of the spatial pattern, and Right: time series plot of the spatial average of susceptible prey for (a, b) $\tau _2=5$, (c, d) $\tau _2=8$, (e, f) $\tau _2=28$ and other parameters as in (46) with $\tau _1=0$. This figure shows that spatial heterogeneity acts as a buffering mechanism.

Fig. 11

Variation of ${Re}(\lambda )$ with respect to (a) $\tau _1$ of the characteristic Eq. (18) and (b) $\tau _2$ of the characteristic Eq. (27) for $k=0.085$ with parameters as in (46).

Further, incorporating spatial structure into the model demonstrates that spatial movements (diffusion) dampen the overall effect of the gestation delay, $\tau _2$. In essence, spatial heterogeneity acts as a buffering mechanism-populations in different regions can “rescue” each other through dispersal, and local fluctuations do not synchronise globally. As a result, the destabilising thresholds observed in the purely temporal model vanish. Therefore, spatial heterogeneity and dispersal provide a stabilising mechanism that mitigates the effects of gestation delay, preventing the emergence of sharp critical thresholds.

For both delays

Figure 12 shows the spatial behaviour of $E^*$ for different values of $\tau _2$ and fixed $\tau _1=0.6$. The left-hand side of this figure shows the changes in pattern formation (stationary hot spot$\rightarrow$quasi-periodic mixture of hot spot and strip$\rightarrow$quasi-periodic strip) and the right-hand side shows the changes in the time series plot of the spatial average of susceptible prey for an increased value of $\tau _2$ and fixed $\tau _1=0.6$. From this figure, it can be concluded that the critical value of $\tau _2$ lies between 1 and 2. Theorem 5.6 gives the critical value of $\tau _2$ is 1.645. Figure 13b also support the same, i.e., this figure shows that at $\tau _2=1.645$, a pair of eigenvalues of the characteristic Eq. (9) crosses $\mathbb {C}^0$ for $\tau _1=0.6$ with $\left. \frac{d {Re}(\lambda )}{d\tau _2}\right| _{\tau _2=1.645}>0$.

Fig. 12

Left: Snapshot of the spatial pattern, and Right: time series plot of the spatial average of susceptible prey for (a, b) $\tau _2=1$, (c, d) $\tau _2=2$, (e, f) $\tau _2=3$ and other parameters as in (46) with $\tau _1=0.6$. This figure shows that temporal oscillations destabilise the Turing mechanism as the gestation period increases, leading to large-scale wave-like patterns.

Fig. 13

Variation of ${Re}(\lambda )$ with respect to (a) $\tau _1$ for $\tau _2=0.8$, $\delta =0.0015$ (b) $\tau _2$ for $\tau _1=0.6$, $\delta =0.005$ of the characteristic Eq. (9) with other parameters as in (46).

This phenomenon occurs because a non-zero incubation delay makes sure that the disease spreads evenly over time, so affected individuals all over the space domain either become infected or die at the same time. There are system-wide shocks caused by this synchronisation, like a sudden loss of prey or predator resources, that spatial diffusion can’t absorb. As a result, the system again exhibits sensitivity to the gestation delay, with instability emerging when it falls within critical intervals. Ecologically, the disease process “overrides” the natural desynchronisation provided by spatial spread, reintroducing the conditions for destabilising the system with gestation delay.

Also, Figs. 9 and 12 show that increasing incubation and gestation delays alter the dominant instability mechanism-from diffusion-driven (Turing) to delay-driven (Hopf)-reshaping patterns from localised to wave-like. This happens because, at low delays, the system is governed by the Turing instability, where the spatial movement of the species creates a localised pattern (hot spot). As delays increase, temporal oscillations induced by incubation or gestation periods destabilise the Turing mechanism, leading to large-scale wave-like patterns (strips).

Similarly, for $\delta =0.0015$, Fig. 14 shows the behavioural changes for different values of $\tau _1$ with fixed $\tau _2=0.8$. Here, the left-hand side represents the spatial patterns, and the right-hand side represents the time series of the spatial average of the susceptible prey. From this figure, it is clearly shown that the value of critical $\tau _1$ lies between 3.5 and 4. Figure 13a also shows that at $\tau _1=3.7189$ (Theorem 5.5 gives the same critical value), the real part of an eigenvalue crosses the $y=0$ line with $\left. \frac{d {Re}(\lambda )}{d\tau _1}\right| _{\tau _1=3.7189}>0$. So, at $\tau _1=3.7189$, the interior equilibrium $E^*$ of the spatiotemporal system loses its stability through Hopf bifurcation.

Fig. 14

Left: Snapshot of the spatial pattern, and Right: time series plot of the spatial average of susceptible prey for (a, b) $\tau _1=0.6$, (c, d) $\tau _1=0.3.5$, (e, f) $\tau _1=4$ and other parameters as in (46) with $\tau _2=0.8$. This figure shows that temporal oscillations destabilise the Turing mechanism as the incubation delay increases.

Conclusion

In this article, a spatiotemporal eco-epidemic model is developed that incorporates prey refuge and intraspecific competition among predators while addressing an infectious disease affecting only the prey population. Additionally, the incubation and gestation periods are incorporated into the spatiotemporal system. All possible equilibria of the spatiotemporal system have been obtained here. However, for all species present, only the stability and bifurcation analysis of the interior equilibrium is performed. Al-Jubouri and Naji⁶³ studied the transmission dynamics of the Crimean-Congo hemorrhagic fever virus using delay differential equations. Ghosh et al.⁶⁴ analyse an immuno-epidemiological model with distributed recovery and death rates. Both of the articles show rich results. However, they do not show the effects of spatial heterogeneity, which we have considered here. Acharya et al.⁶⁵ studied an SI epidemic model in space and time, incorporating the Allee effect. They found different types of results, but they did not consider any of the incubation or gestation delays in their calculation. Ghorai et al.⁶⁶ studied spatiotemporal pattern formation of a diffusive prey–predator interaction of zooplankton and two phytoplankton populations. Their studies show that selective predation causes various Turing and non-Turing patterns. However, they did not consider any type of delay. Also, a comparative study of recent eco-epidemic systems is presented in Table 1. Based on this comparative study, it may be concluded that the results of the current study-investigating the impact of both incubation and gestation delays on a spatially heterogeneous eco-epidemic system-demonstrate a novel and rich dynamical behaviour in the spatiotemporal eco-epidemiological system.

For the non-delayed system, the existence of Hopf bifurcation has been investigated. The system is found to move from instability to stability via a Hopf bifurcation, owing to the integration of prey refuge behaviour (see Theorem 5.1 and Note 1). High predator density leads to prey depletion, which in turn causes predator starvation and population decline, allowing prey to recover-resulting in oscillations. When a fraction of the prey takes refuge, predation pressure is reduced. This prevents excessive prey depletion, ensuring a more stable prey population. Consequently, the population of predators does not undergo significant swings, which promotes a steady coexistence. All possible conditions under which the non-delayed spatiotemporal system exhibits instability due to diffusion (i.e., Turing instability) have also been determined. Numerically, the Turing, Hopf–Turing, and Pure–Hopf regions have been obtained, as shown in Fig. 2. These regions are further verified by plotting the maximum of the real parts of the eigenvalues, as illustrated in Fig. 3. Changes in pattern formation are observed, transitioning from cold spot to mixed cold plot and strip, then to strip, and finally to hot spot, as the intraspecific competition among predators increases (see Fig. 4). Initially, cold spots emerge where predators effectively suppress prey populations, indirectly limiting disease spread by reducing host density and contact rates. But, as intraspecific rivalry among predators intensifies, predation pressure becomes inadequate to control prey populations over larger areas. Reflecting directional disease spread driven by prey movement and aggregation, striped patterns may predominate. The system finally moves to hot spots where predator absence or inefficiency lets prey populations flourish. In these areas, increased host density promotes regular contact, hastening disease spread. Also, these changes demonstrate that predator-intraspecific interactions are crucial in shaping ecosystem dynamics. In other words, intra-specific competition within the predator species implies that the predator species are quite stronger in their nature. Hence, it can be concluded that the above phenomena occur due to the stronger nature of the predator.

Later, when the incubation and gestation periods are included in the calculation, the non-diffusive delayed system (i.e., for $k=0$) exhibits unstable behaviour after crossing the critical value of the incubation delay $\tau _1$ via the Hopf bifurcation (see Fig. 8a). Additionally, a stability switching of the non-diffusive delayed system is observed for the gestation delay $\tau _2$ (see Fig. 8b). This may happen because when $\tau _2$ falls within the unstable intervals, the prey’s population growth is not synchronised well with the predator’s consumption rate. However, when spatial effects are introduced, diffusion mitigates the system’s unstable behaviour for $\tau _2$ (see Fig. 11b). In this case, spatial heterogeneity (diffusion) acts as a buffering mechanism. However, $\tau _1$ has similar types of unstable behaviour for spatial systems also (see Fig. 11a). Also, both stationary and quasi-periodic patterns are observed for different values of single delay (i.e., when $\tau _1>0$ for $\tau _2=0$ and $\tau _2>0$ for $\tau _1=0$). Due to the effect of incubation delay, for fixed $\tau _1$, $\tau _2$ shows stability switching behaviour again (see Fig. 13b). However, other than the length of the critical value, spatial heterogeneity (diffusion) or gestation delay does not change the system’s behaviour for $\tau _1$ (as in Figs. 8a, 11a, 13a).

The ecological significance of the above findings may be stated as the incubation delay ($\tau _1$) and gestation delay ($\tau _2$) act as critical early warning indicators for population collapse or outbreak in eco-epidemic systems. Exceeding the critical threshold of $\tau _1$ triggers a Hopf bifurcation, destabilizing the system, even in spatially heterogeneous environments. This makes $\tau _1$ a robust predictor of instability, requiring close monitoring of population management. In contrast, $\tau _2$ exhibits stability switching behaviour (alternating stable/unstable regimes) due to mismatched predator–prey dynamics, but spatial diffusion can buffer these instabilities, reducing collapse risks. However, when combined with fixed $\tau _1$, $\tau _2$ reintroduces instability, emphasizing the need to assess delays jointly. Now, some of the key findings of this study may be summarised as follows:

• Refuge behaviour of prey species may stabilized the system;

• Species movements may push the system towards the Turing instability and form different types of patterns in their habitat;

• Intraspecific competitions among the predators are able to change the structure of the ecosystem;

• The incubation delay has the potential to change the stability behaviour of both temporal and spatiotemporal system;

• Though the gestation delay of predators shows the stability switching for the temporal system, spatial heterogeneity mitigates it.

Some of the management recommendations from this study may be summarised as: (a) it needs to design refuge habitats for prey (e.g., protected areas) to stabilise ecosystems and reduce predator-driven collapses; (b) it needs to implement disease surveillance and adaptive control (e.g., timed vaccinations, harvesting, culling) to account for incubation delays and reduce risks; (c) it needs to increase the habitat diversity to buffer against instability due to predator gestation delay.

This research demonstrates the spatial impacts of incubation and gestation periods on an eco-epidemic model that assumes the infection spreads solely within the prey population via local interactions. Some of the limitations of this study may be listed as follows: (a) this study neglects environmental fluctuation, (b) due to the inaccessibility of the real data, this study presents only qualitative results, and (c) this study does not consider the cross-diffusion. In future work, these limitations may be overcome. Additionally, this work may be extended in future by incorporating distributed delays, multiple predator species, seasonality, or non-local interaction.