Introduction

As Moore’s law approaches physical and economic limits, traditional silicon-based computing faces critical challenges from leakage currents, device variability, and interconnect delays. While incremental solutions like 3D integration and carbon-based electronics1,2,3 temporarily extend CMOS viability4,5, they merely postpone inevitable bottlenecks such as memory and power walls. Resistive-switching memristors offer a potentially transformative solution through in-memory computing architectures6,7,8,9. These nanoscale devices offer exceptional performance metrics, combining durability, rapid switching capabilities, and high scalability10,11,12. A particularly compelling feature is their unique ability to both store and process information within the same physical space, enabling energy-efficient computing for both in-memory and parallel processing applications13,14,15,16,17,18,19,20,21,22,23,24.

The fundamental structure of oxide-based memristors consists of three layers: an insulating oxide layer sandwiched between top and bottom electrodes. The device operation relies on conductive filaments (CFs) that form within the oxide layer, creating paths for electrical conduction. These CFs can be repeatedly switched between high resistance states (HRS) and low resistance states (LRS) through processes of formation, breaking, and re-formation under applied voltage.

Based on their CF ionic composition, memristors fall into two categories: Electrochemical Metallization (ECM) devices, where CFs form from metal cations originating from electrochemically active electrodes25,26,27, and Valence Change Memory (VCM) devices, where CFs comprise material defects, primarily oxygen vacancies (VO), within metal oxide-based memristors28,29,30,31,32.

VCM devices require an initial electroforming step to create a CF connecting the electrodes33,34,35. This process depends on two fundamental mechanisms: the creation of oxygen vacancies at the oxide-electrode interface through chemical reactions, and the subsequent migration of these vacancies through the bulk material36,37, driven by both electric field forces and temperature gradients.

Extensive research has explored various metal oxides as insulating layers in memristors, also known as resistive random-access memory (RRAM) devices. Kamiya et al.38 demonstrated that switching processes are governed by transitions between unified and separated oxygen vacancies, with electrode materials affecting carrier injection. Clima et al.39 investigated oxygen movement in amorphous hafnia (HfOx) using molecular dynamics simulations that aligned with experimental observations. Yang et al.40 examined electroforming mechanisms in metal oxide switches, describing how oxygen vacancies form under strong electric fields to create conductive channels. Nandi et al.41 revealed different electroforming behaviors in Nb/NbOx/Pt devices depending on NbOx film conductivity.

Despite these advances, a critical gap remains in understanding how the physical properties of metal oxides—particularly their electrical and thermal conductivity—affect CF growth during electroforming and subsequent switching operations. These properties likely play a crucial role in determining switching reliability and uniformity42. Previous studies on TaOx-based RRAM have primarily focused on device fabrication43, switching mechanisms44, or basic electrical characterization45. For example, Lee et al. demonstrated asymmetric Ta2O5−x/TaO2−x bilayer structures for high endurance10, while Wei et al. investigated redox reaction mechanisms46. The work by Kim et al.47 presented a physical model for dynamic resistive switching but did not explore the fundamental relationship between material transport properties and switching uniformity. Similarly, Lee et al.48 developed a quantitative model for TaOx memristors but focused mainly on programming dynamics rather than material property effects. While these studies have advanced our understanding of TaOx-based devices, the crucial relationship between oxide transport properties (electrical and thermal conductivities) and device performance metrics (uniformity, forming voltage, and resistance ratio) remains unexplored.

Fig. 1
figure 1

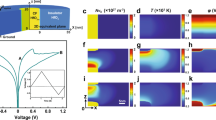
a Schematic of Pd/Ta2O5/TaOx/Pd bilayer memristor device. At the initial state, we assume a uniform doping concentration of nD = 1 × 1022 cm−3 within the conductive TaOx layer, which serves as the oxygen vacancy (VO) reservoir. The simulation utilizes dimensions of W = 40 nm, h = 10 nm, and d = 20 nm. Here, V1 represents the voltage applied to the CML while V2 represents the effective voltage applied to the memristor’s TE. b Measured and simulated dc I–V characteristics of the memristor device with ICC = 500 µA, illustrating the forming switching cycle. c 2D maps of nD were obtained in the model for forming and first RESET.

Full size image

In this research, we present a detailed physical model for TaOx-based memristors that advances beyond existing frameworks by simultaneously considering temperature evolution and oxygen vacancy concentrations49. Our model addresses previous reliability prediction limitations47 by incorporating compliance current (ICC) to control maximum programming current during CF formation. We validate our approach using a practical 1T1R device structure, where gate voltage enables precise programming current control for better management of conductance levels and oxygen vacancy arrangements48.

Our investigations reveal several key relationships between oxide properties and device performance. We demonstrate how electrical conductivity influences Joule heating and oxygen vacancy generation, while thermal conductivity affects heat dissipation and forming voltage requirements. These findings suggest that optimal CF uniformity can be achieved through careful selection of metal oxides with specific combinations of electrical and thermal conductivity. Following the Wiedemann-Franz law correlation between thermal and electrical conductivity in metals, we identify that transition metal oxides with reduced Lorenz numbers offer promising characteristics for RRAM applications50. These insights provide crucial guidelines for material selection to enhance electroforming processes and device reliability.

Results

Device structure and physical model

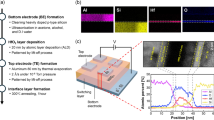
We investigate a bilayer device structure consisting of Ta2O5/TaOx, where a high-resistance Ta2O5 layer is positioned above a more conductive TaOx layer (Fig. 1a)51. The structure is enclosed between palladium (Pd)-based top electrode (TE) and bottom electrode (BE). The switching mechanism primarily depends on oxygen vacancy (VO) movement and redistribution between the low-resistance TaOx and high-resistance Ta2O5 layers47,52. Application of a negative voltage to the TE drives VOs from the TaOx layer, which acts as a VO reservoir, into the Ta2O5 layer, forming a conductive filament (CF) that connects the TE to the conductive TaOx layer. This SET process transitions the device to a low-resistance state. Conversely, applying a positive voltage during the RESET process repels VOs from the Ta2O5 layer, rupturing the conductive filament and returning the device to a high resistance state.

Fig. 2
figure 2

Parameters from measurements and assumptions. a Electrical conductivity pre-exponential factor \(\left( {{\sigma _0}} \right)\), b assumed thermal conductivity kth as a function of local Vo density nD, and c assumed activation energy for conduction (\({E_{AC}}\)).

Full size image
Table 1 Material parameters used in the proposed model.
Full size table
Table 2 Material constants used in the proposed model.
Full size table

Figure 1b demonstrates the measured and simulated DC I-V characteristics during the forming process with a compliance current (ICC) of 500 μA, while Fig. 1c shows the two-dimensional maps of VO concentration (nD) during the forming process. Our simulation results show excellent agreement with experimental measurements48.

In our analysis, we assume a uniform VO concentration of nD=1 × 1022 cm−3 and an electrical conductivity of 105 Sm−1 within the conductive TaOx layer, based on density functional theory calculations and experimentally measured conductivity values for TaOx films46. It is important to clarify that while reference46 utilized TaOx as the active switching layer, the structure of our device differs significantly. In our model, the Ta2O5 layer serves as the primary switching medium, with the TaOx layer functioning as a reservoir for oxygen vacancies. This structural distinction allows us to investigate the dynamics of oxygen vacancy migration from the reservoir layer to the switching layer and its impact on switching uniformity, forming voltage, and overall device performance. These VO defects are assumed to exhibit the same local conductivity (105 Sm−1) as the TaOx layer. Conversely, the stoichiometric Ta2O5 film is modeled with a significantly lower VO concentration (nD =1 × 1016 cm−3), making it highly resistive. In this framework, the electrical conductivity (σ) of the oxide material is expressed as a function of nD, temperature (T), and electric field (E). The relationship is described by the following equation:

$${\sigma _{T{a_2}{O_{5 - x}}}}={\sigma _0}\exp \left( { - \frac{{{E_{AC}}}}{{KT}}} \right)+{\sigma _{PF}}\left( {E,T} \right)$$
(1)

where σ0 is a prefactor, EAC is the activation energy for electron conduction, and \({\sigma _{PF}}\left( {E,T} \right)=exp(\frac{{293}}{T}.\left( {\alpha \sqrt E +\beta } \right)\) represents the Poole−Frenkel (PF) conduction term. To simulate the SETand RESET transitions, we solve three partial differential equations (PDEs) self-consistently: (1) a continuity equation for the drift and diffusion of VO, (2) a current continuity equation for electrical conduction, and (3) a Fourier equation to account for Joule heating. The drift and diffusion of VO migration are modeled using a simplified one-dimensional rigid point ion framework originally introduced by Mott and Gurney53. Although Mott and Gurney’s ion-hopping model was developed for oxygen ions, we extend its applicability to oxygen vacancies, with adjustments made to specific physical parameters. Based on Eq. (5), the diffusion and the drift velocity are described by \(D=\frac{1}{2}{a^2}fexp\left( { - \frac{{{E_a}}}{{KT}}} \right)\), \(\nu =afexp\left( { - \frac{{{E_a}}}{{KT}}} \right)sinh\left( { - \frac{{qaE}}{{KT}}} \right)\), respectively, where f is the attempt-to-escape frequency (1012 Hz)47, a is the effective hopping distance (0.32 nm), and Ea is the activation energy required for VO migration (0.85 eV). In reality, the effective hopping distance can vary within a range of a few nanometers (typically < 1 nm). However, the value of 0.32 nm is used in this study to best fit the experimental data. This discrepancy likely arises from the different physical properties of oxygen vacancies compared to oxygen ions. Incorporating both drift and diffusion, the time-dependent change in VO concentration (nD) is described by the following continuity equation:

$$\frac{{~\partial {n_d}}}{{\partial t}}=\nabla .\left( {D\nabla {n_d} - \nu {n_d}+DS{n_d}\nabla T} \right)$$
(2)

where D∇nD and vnD are the Fick diffusion flux and the drift flux terms, respectively47. The DSnD∇T term corresponds to the Soret diffusion flux, where S is the Soret coefficient (S = − Ea/ kT2 ). Soret diffusion describes the movement of particles along a temperature gradient, which contributes to the formation of stable conductive filaments (CFs) under high-temperature conditions. In the simulation, VOs migrate toward areas of higher temperature, particularly within the filament region, when exposed to a temperature gradient. This migration occurs due to the enhanced diffusivity of oxygen ions at elevated temperatures. As a result, the process facilitates the development of a stable CF composed of VO particles, even in high-temperature environments. To model this behavior, Eq. (2), which governs Soret diffusion, is solved in conjunction with Eq. (3), the continuity equation for electrical conduction, and Eq. (4), the Fourier equation for Joule heating. This self-consistent approach follows the methodology proposed by Ielmini et al.54.

$$\nabla .\sigma \nabla \Psi =0$$
(3)
$$\rho {C_p}\frac{{\partial T}}{{\partial t}} - \nabla .{k_{th}}\nabla T=J.E$$
(4)

These equations are solved simultaneously using numerical methods (COMSOL) to calculate electrical conductivity (σ), electric potential (Ψ), oxygen vacancy concentration (nD), and temperature (T). The simulated structure has a width of 40 nm, a depth of 20 nm, and consists of layers with the following thicknesses: a 35 nm palladium bottom electrode (BE), a 30 nm VO reservoir layer (TaOx) a 5 nm switching layer (Ta2O5), and a 50 nm palladium top electrode (TE). These dimensions and layer compositions are designed to replicate the physical properties of the system under study. Parameter definitions and values are detailed in Tables 1 and 2 and illustrated in Fig. 2, as referenced in prior works54,55.

To solve Eqs. (3) and (4), models for both electrical conductivity (σ) and thermal conductivity (kth) are essential. We consider these properties to be dependent on nD, as illustrated in Fig. 2a and b. Following Eq. (5), σ0 increases linearly from 10 to 940 Ω⁻¹ cm⁻¹ with increasing nD. Figure 2c presents the conduction activation energy EAC used in our calculations, which is − 0.006 eV at high nD and increases linearly to 0.05 eV with decreasing nD, corresponding to measured data for LRS and HRS, respectively.

Furthermore, a linear relationship between kth and nD is assumed, as shown in Fig. 2b. The minimum value for nD = 0 is associated with the thermal conductivity of insulating Ta2O5, \({K_{T{a_2}{O_5}}}=0.12~\) Wm−1 K−1 at T0 =300 K. Additionally, the thermal conductivity \({K_{T{a_2}{O_5}}}\) is assumed to have a linear temperature dependence, expressed as:

$${K_{T{a_2}{O_5}}}=0.12(1+\lambda (T - T0)$$
(5)

where λ = 0.1 is the linear thermal coefficient. The maximum kth value at high nD is equivalent to that of metallic CF, represented by the thermal conductivity of tantalum, kTa =57.5 W m⁻¹ K⁻¹.

Fig. 3
figure 3

Forming process. a Schematic of the device during pulse forming. b Evolution of the oxygen vacancy concentration (nD) across the Ta2O5 layer thickness (Z) at different times. c Temperature distribution across the Z over time. d 2D maps of oxygen vacancy concentration and temperature at different times during the forming process and Post-forming process.

Full size image

For boundary conditions, we maintain a constant temperature (300 K) at the surfaces of BE, TE, and the current modulation layer (CML). While this represents an idealized thermal boundary condition that assumes perfect heat dissipation at the electrodes, it allows us to focus on the thermal effects within the oxide layers where the primary switching phenomena occur. The BE remains grounded throughout the simulation, while voltage is applied to the CML’s top surface. To implement ICC during forming and SET processes, we define the CML conductance through Eqs. (6), (7), and (8):

$${\sigma _{CML}}=\frac{{{I_{CC}}.h}}{{\left| {{V_1} - {V_2}} \right|.w.d}}{\text{~if~}}{E_{CML}} \geqslant {E_{max}}$$
(6)
$${\sigma _{CML}}={I_{CC\_Sigma}}{\text{~if~}}{E_{CML}} \leqslant {E_{max}}$$
(7)
$${E_{max}}=\frac{{{I_{CC}}}}{{{I_{CC\_Sigma}}.w.d}}$$
(8)

Here, V1 denotes the voltage applied to the top surface of the CML, while V2 represents the effective voltage at the memristor’s TE, as depicted in Fig. 1a. When the electrical field applied to the CML is below Emax, the CML conductance maintains ICC_Sigma (105 Sm−1). For fields exceeding Emax, the conductance follows Eq. (8). During RESET process, σCML remains constant at ICC_Sigma = 105 Sm−1.

While the model is specifically developed for Ta2O5/TaOx, it is generalizable to other oxide materials by adjusting key material-specific parameters. These include the pre-exponential factor for electrical conductivity (σ0), activation energy for conduction (EAC), thermal conductivity (kth), and other constants such as density, heat capacity, and diffusion coefficients, which must be recalculated based on the new material’s properties. The general equations governing electrical conductivity, Poole-Frenkel conduction, and vacancy migration remain the same; however, their material-specific parameters need to be updated using experimental or computational methods for the material of interest. This ensures the flexibility and broad applicability of the model to various oxide-based materials beyond Ta2O5/TaOx.

The conductive filament (CF) growth behavior during the electroforming process

Figure 3 illustrates the detailed dynamics of CF formation in our device. Figure 3a depicts the applied voltage pulses during forming and RESET operations, with fixed amplitudes of − 2.1 V for the forming voltage and 1 V for the RESET voltage, each lasting 10 ms. The forming voltage refers to the initial electroforming step, during which the conductive filament (CF) is formed for the first time in the device. During this process, the high-resistance Ta2O5 layer initially allows minimal current flow due to its insulating properties. Before CF formation, Poole–Frenkel (PF) emission dominates conduction through defect-free regions of the Ta2O5 layer. In subsequent cycles, the device transitions between high-resistance (HRS) and low-resistance (LRS) states using the SET voltage to transition to LRS and RESET voltage to return to HRS. The first SET operation, following the initial forming and RESET operations, is where the HRS and LRS values are reliably measured and reported.

The evolution of oxygen vacancy concentration (nD) across the device thickness (Z) over time (2.12–12 ms) is shown in Fig. 3b. We observe a progressive increase in nD, particularly near the Ta2O5/TE interface. This increase is driven by the applied electric field, which generates localized heating and promotes VO migration toward the TE, facilitating CF formation within the oxide layer.

Figure 3c presents the temporal evolution of temperature distribution across the device. As the forming pulse continues, Joule heating leads to significant temperature elevation, particularly near the TE where filament formation occurs. Local temperatures exceed 500 K in specific regions, further facilitating VO migration. Upon voltage removal, temperature decreases, marking the completion of the forming process.

Figure 3d features consistent minimum and maximum values for the temperature scale, ensuring clear visualization of the temperature evolution. The forming process has been divided into two stages: (1) the forming process, characterized by significant Joule heating and oxygen vacancy migration, and (2) the post-forming process, where the device begins to cool after the voltage is removed. These stages are distinctly visualized to better represent the dynamics of the process.

The 2D maps in Fig. 3d provide spatial visualization of both nD and temperature distributions at various time points during the forming process. These maps demonstrate the progressive concentration of heat and VO migration in specific regions, leading to controlled CF formation. The spatial and temporal evolution of these parameters reveals the complex interplay between electrical and thermal effects during the forming and post-forming stages. This analysis highlights how localized heating and vacancy migration contribute to the structural evolution of the conductive filament during and after the forming pulse.

Resistive switching mechanism

While RRAM technology shows promising memory characteristics, resistance variability and the incomplete understanding of switching mechanisms remain critical challenges for practical applications. Both the Low Resistance State (LRS) and High Resistance State (HRS) exhibit resistance variability, manifesting as temporal and spatial fluctuations that impact the stability of the memory window. Figure 4a presents I–V curves from 20 consecutive DC switching cycles, demonstrating resistance variations in both the LRS and HRS. These variations reduce the memory window, resulting in a decreased HRS-to-LRS ratio. As the memory window shrinks, the device becomes less robust and more susceptible to noise and errors during read/write operations. However, cycles 7–20 show minimal variation in the hysteresis curve uniformity, leading to overlapping characteristics. This indicates a degree of stabilization in the switching behavior after the initial cycles.

Fig. 4
figure 4

a Current–voltage curves of all 20 consecutive switching cycles. b Cumulative cycle-to-cycle resistance distribution of Pd/ Ta2O5/TaOx /Pd RRAM device. Both LRS and HRS show resistance variability. The uniformity of resistance states is quantified using the standard deviation-to-mean ratio (\(\bar {\sigma }/\bar {\mu }\)), with HRS showing \(\bar {\sigma }/\bar {\mu }\)= 0.028 and LRS exhibiting \(\bar {\sigma }/\bar {\mu }\)= 0.0355. The LRS and HRS are measured at V = − 0.1 V. c Endurance curve for LRS and HRS.

Full size image

Figure 4b shows the cumulative probability distributions of resistance states for 500 switching cycles, with a standard deviation-to-mean ratio (\(\bar {\sigma }/\bar {\mu }\)) of 0.028 for HRS and 0.0355 for LRS. The higher variability in LRS and the overlapping resistance regions underscore the challenges in achieving consistent device performance. These findings highlight the need for a deeper understanding of the mechanisms governing filament formation and rupture, as well as advancements in material engineering and device optimization to minimize such variations.

Figure 4c shows the endurance and stability of the RRAM device over 500 switching cycles. Throughout this extended operation, both the LRS and HRS remain clearly distinguishable, with average resistance values of approximately 2 kΩ and 220 kΩ, respectively. Although slight resistance fluctuations occur, particularly during the initial cycles, the subsequent cycles demonstrate stable switching behavior with minimal variation, confirming the stability of the memory window. This long-term consistency indicates reliable filament formation and rupture dynamics, validating the endurance performance of the device.

Effect of oxide properties on the CF growth behavior

Our simulation results reveal that the local electric field and temperature are key factors influencing the movement of oxygen vacancies and the subsequent growth of CF. Following Eqs. (3) and (4), the electrical and thermal conductivity properties of host metal oxides, significantly influence these processes. Given that σ and kth values for metal oxides are substantially lower than their metallic states, we simplify our analysis by assuming uniform initial σ and kth for various pristine oxides (such as Ta2O5, HfO2, etc.). These properties are linearly extrapolated to their metallic state values as nD increases, with the slopes defined by parameters K1 and K2.

In metal oxide-based RRAM devices, oxygen vacancies act as n-type donors, creating distinct behavioral regimes. For regions with lower oxygen vacancy density (nD < 5 × 1027 m−3), semiconductor-like behavior dominates, with EAC increasing linearly from 0.0 eV to 0.05 eV as nD decreases, matching reported values for TaOx RESET states. At higher concentrations (nD >5 × 1027 m−3), EAC becomes 0.0 eV, indicating Fermi level pinning in the conduction band - characteristic of the CF’s metallic nature. The relationship between kth and nD follows the Wiedemann-Franz Law54,56, providing theoretical justification for our linear approximation approach. This framework enables systematic analysis of how electrical and thermal properties influence CF growth through the tuning of K1 and K2 parameters.

Figure 5 demonstrates electrical conductivity’s effect on CF growth. The total current evolution with different electrical conductivities (K1 = 6.2, 9.5, and 18.8 Sm−1) shows that while initial current patterns remain similar, the forming voltage (Vf) decreases monotonically with increasing K1. The 2D maps in Fig. 5c and corresponding 1D profiles in Fig. 5b provide additional insights into potential competing filament formation. At lower electrical conductivity (K1 = 6.2 Sm−1), multiple localized regions of enhanced nD are observed near the TE/Ta2O5 interface, suggesting the possibility of initiating parallel filament nucleation sites. These regions emerge due to the sharp resistivity contrast between the matrix and emerging filamentary paths, which creates multiple localized high-field regions. As K1 increases to 18.8 Sm−1, the nD distribution exhibits more consistent spatial gradients, resulting in a single uniform CF morphology, indicating that higher conductivity suppresses competing filament formation through more uniform field distribution.

The 1D electric field distributions near the Ta2O5/TaOX interface (Y = 0 and Z = 0 nm), shown in Fig. 5d, provide crucial insights into the forming process. At low electrical conductivity (K1 = 6.2 Sm−1), the high resistivity contrast between emerging filamentary regions and the surrounding oxide matrix creates sharp local electric field enhancements (Fig. 5d, pink curve). This concentrated field drives preferential VO migration paths, leading to localized CF formation. As electrical conductivity increases (K1 = 9.4 Sm−1), the reduced resistivity contrast results in more gradual potential drops across the device, shown by the decreased field enhancement (Fig. 5d, red curve). At the highest conductivity (K1 = 18.8 Sm−1), enhanced heat generation leads to the lowest electric field (Fig. 5d, blue curve), while elevated local temperatures (exceeding 500 K, as shown in Fig. 5e) exponentially enhance oxygen vacancy mobility through reduced activation barriers, consistent with the thermally-accelerated ionic transport mechanism established for filamentary VCM systems57. Additionally, at lower conductivities, a positive feedback mechanism emerges where initial VO accumulation creates localized conductive regions, further concentrating the electric field and accelerating VO migration to these sites. This self-reinforcing process explains the sharp spatial variations in the nD profile observed at K1 = 6.2 Sm−1 (Fig. 5b, pink curve). In contrast, higher conductivity disrupts this feedback loop and enables thermally-dominated transport, resulting in more uniform vacancy distribution and filament formation, despite the reduced electric field. This interplay between electrical conductivity, local electric field, and temperature demonstrates how these parameters collectively influence CF formation dynamics.

Fig. 5
figure 5

Effect of electrical conductivity on the CF growth. a Current characteristic with different electrical conductivity (by K1). b Horizontal 1D nD profiles for different K1 at final state. The Y = 0 position is the center of the filament. c 2D maps of distributions of nD at final state. d Calculated 1D profiles of local electric field (E) near the Ta2O5/TaOx interface (Y = 0 and Z = 0 nm). e Temperature (T) along the center of CF (Y = 0, Z = 0–4 nm) at final state.

Full size image

Figure 6 illustrates the effect of kth (by slope K2) on the CF growth. Here, we apply the same boundary conditions of electrical bias as the electrical conductivity case. Figure 6a shows the temporal evolution of total current with different kth (represented as K2 = 2.5, 5.75, and 11.5 Wm−1 K−1). The lower kth (K2 = 2.5 Wm−1K−1) results in a higher temperature (pink curve in Fig. 6e) which promotes the nD generation at a reduced forming voltage of − 1.62 V (Fig. 6a). In this case, the induced nD migrates to the TE and the drift flux from TaOx to Ta2O5 is suppressed due to the decreasing local electrical field (pink curve in Fig. 6d). As the kth (K2) increases, the heat generated by the Joule heating effect can be easily dissipated and the local temperature decreases (red curve in Fig. 6e), which inhibits the nD generation and increases the CF forming voltage up to −1.78 V (Fig. 6a). When kth further increases (K2 = 11.5 Wm−1 K−1), the induced nD migration from TaOx to Ta2O5 becomes much easier under a higher local electrical field (blue curve in Fig. 6d). Thus, more nD accumulation near the TE and a larger nD width near the TE are observed (Fig. 6c and blue curve in Fig. 6b).

Figure 7 provides a comprehensive analysis of how K1 and K2 influence the forming voltage and the resistance ratio (RHRS/RLRS). Figure 7a presents the forming voltage as a function of K1 and K2, while Fig. 7b shows the corresponding resistance ratio under similar conditions. From Fig. 7a, it is evident that a low electrical conductivity needs a stronger forming voltage (higher negative value), especially at higher thermal conductivities. Forming voltage decreases with increasing electrical conductivity and decreasing thermal conductivity. This trend can be attributed to the Joule heating effect: increased electrical conductivity generates more localized heat, facilitating oxygen vacancy generation and reducing the energy required for CF formation. Conversely, higher thermal conductivity enhances heat dissipation, suppressing vacancy generation and necessitating an elevated forming voltage. This relationship highlights the critical balance between electrical and thermal properties for achieving efficient forming processes.

Figure 7b demonstrates that the RHRS/RLRS ratio, a crucial performance metric for RRAM devices, strongly depends on these parameters. The resistance ratio shows distinct regions of behavior across the K1–K2 parameter space. A high RHRS/RLRS ratio (> 250) is observed in the region where 11 Sm−1 < K1 < 18 Sm−1 and 5 Wm−1 K−1 < K2 < 6 Wm−1 K−1, corresponding to moderate forming voltages (− 1.75 V to − 1.65 V). This optimal region can be explained by two key physical mechanisms. In this regime, the moderate electrical conductivity (K1) provides sufficient current flow to form stable conductive filaments during SET operation while allowing effective rupture during RESET. The balanced electrical transport prevents excessive Joule heating that could lead to uncontrolled filament growth or incomplete rupture. Additionally, the relatively low thermal conductivity (K2) in this region helps maintain localized heating during switching operations. This localization is crucial for achieving high RHRS/RLRS ratios as it enables complete filament rupture during RESET, leading to higher HRS resistance, while ensuring controlled filament formation during SET, maintaining stable LRS resistance. Conversely, lower resistance ratios are observed in regions with lower electrical conductivity and higher thermal conductivity. This reduction occurs because lower electrical conductivity limits the completeness of filament formation during SET, resulting in higher LRS resistance. Simultaneously, higher thermal conductivity leads to rapid heat dissipation, preventing efficient local heating needed for complete filament rupture during RESET, resulting in lower HRS resistance. These results indicate that optimal RHRS/RLRS ratios require careful balancing of Joule heating (controlled by K1) and heat dissipation (controlled by K2) to achieve both efficient filament formation and complete rupture during switching operations. This balance is critical for maintaining the large memory window necessary for reliable and energy-efficient device resistive switching operation.

Fig. 6
figure 6

Effect of thermal conductivity on the CF growth. a Current characteristic with different thermal conductivity (by K2). b Horizontal 1D nD profiles for different K2 at final state. The Y = 0 position is the center of the filament. c 2D maps of distributions of nD at final state. d Calculated 1D profiles of local electric field (E) near the Ta2O5/TaOx interface (Y = 0 and Z = 0 nm). e Temperature (T) along the center of CF (Y = 0, Z = 0–4 nm) at final state

Full size image
Fig. 7
figure 7

a Contour plot of the forming voltage dependence on the electrical conductivity (K1) and thermal conductivity (K2) of the oxide layer. b Contour plot illustrating the ratio of high resistance state (HRS) to low resistance state (LRS), RHRS/RLRS, as a function of K1 and K2.

Full size image

The graphs in Fig. 8 illustrate the uniformity analysis of resistive switching characteristics, mapping the standard deviation (\(\bar {\sigma }\))-to-mean (\(\bar {\mu }\)) ratio as a function of electrical conductivity (K1) and thermal conductivity (K2). This analysis is crucial for understanding device reliability and optimization58. Figure 8a shows the HRS uniformity map with two distinct regions of optimal performance. The first occurs at mid-range K1 (≈ 8.2 Sm−1) and low K2 (≈ 5.5 Wm−1 K−1), achieving excellent uniformity (\(\bar {\sigma }/\bar {\mu }\) ≈ 0.045). In the first region, the moderate electrical conductivity combined with low thermal conductivity creates ideal conditions for filament rupture. The moderate electrical conductivity prevents excessive current flow that could cause irregular rupture patterns, while the low thermal conductivity ensures heat remains localized. This localized heating leads to consistent temperature profiles during RESET, resulting in reproducible filament rupture locations and dimensions. In the second region (K1 ≈ 12 Sm−1, K2 ≈ 9.5 Wm−1 K−1), the physics is different. Higher electrical conductivity enables more efficient oxygen vacancy movement due to stronger electric fields, while moderate thermal conductivity provides balanced heat distribution. This combination allows oxygen vacancies to migrate more uniformly during RESET, leading to consistent filament rupture despite the higher thermal dissipation.

Figure 8b reveals that LRS uniformity has a simpler dependency on electrical conductivity and thermal conductivity, exhibiting the optimal uniformity of \(\bar {\sigma }/\bar {\mu }\) ≈ 0.009. For LRS uniformity, the physics is governed by filament formation dynamics. When either K1 or K2 is low, or both, the SET process becomes more controlled as low thermal conductivity concentrates Joule heating, ensuring consistent filament formation locations and low electrical conductivity limits current flow, preventing random branching of filaments during formation. However, when both conductivities are high, excess current flow combined with widespread heat distribution leads to less controlled filament formation, reducing uniformity. The interesting case of high LRS uniformity at high K1 (≈ 14 Sm−1) and low K2 actually results in poor HRS uniformity because the same conditions that enable consistent filament formation (high electrical conductivity) make controlled rupture more difficult, highlighting the inherent trade-off between SET and RESET processes in these devices.

The relationship between these parameters fundamentally affects the switching mechanisms through several physical processes: Joule heating distribution throughout the device, dynamics of filament formation and rupture, oxygen vacancy migration patterns, and the development of local temperature gradients. These findings emphasize that achieving optimal device performance requires precise tuning of both electrical and thermal conductivities to maintain uniform switching characteristics. Understanding these relationships provides crucial insights for material engineering and device optimization, particularly for applications requiring high reliability and consistency in resistive switching behavior.

Fig. 8
figure 8

Contour plots illustrating the standard deviation-to-mean ratio (\(\bar {\sigma }/\bar {\mu }\)) for a HRS and b LRS as a function of electrical conductivity (K1) and thermal conductivity (K2).

Full size image

Design guidelines for oxide-based RRAM devices

Our comprehensive analysis of transport properties in oxide-based memristors reveals that the balance between electrical conductivity and thermal conductivity is central to optimizing device performance. The following guidelines summarize key design strategies, incorporating both quantitative targets and qualitative insights for achieving low forming voltages, high resistance ratios, and uniform switching behavior:

  1. 1.

    Optimizing Forming Voltage.

    • High Electrical Conductivity: Materials with higher electrical conductivity (e.g., σ > 15 S/m) promote oxygen vacancy generation through enhanced Joule heating, which can reduce the forming voltage (target forming voltage < − 1.65 V).

    • Low Thermal Conductivity: Lower thermal conductivity (kth< 6 W/m·K) helps retain localized heat, further facilitating vacancy formation.

    • Design Insight: The synergistic effect of a high σ and low kth minimizes the energy barrier for conductive filament (CF) formation while ensuring that localized heating is sufficient to drive oxygen vacancy migration without excessive dissipation.

  2. 2.

    Maximizing Resistance Ratio (RHRS/RLRS).

    • Balanced Transport Properties: To achieve a high resistance ratio (> 250), materials should ideally have moderate-to-high electrical conductivity (approximately 11–18 S/m) paired with low-to-moderate thermal conductivity (around 5–6 W/m·K).

    • Trade-Off Consideration: While higher conductivity lowers the forming voltage by promoting vacancy generation, it must be balanced against thermal dissipation to ensure that CF rupture during the RESET operation is complete, thereby maintaining a high HRS resistance.

  3. 3.

    Achieving Uniform Switching Behavior.

    • HRS Uniformity—Two Approaches:

    • Approach A: Moderate electrical conductivity (≈ 8.2 S/m) combined with low thermal conductivity (≈ 5.5 W/m·K) yields stable and reproducible CF rupture by concentrating Joule heating in localized regions.

    • Approach B: Alternatively, higher electrical conductivity (≈ 12 S/m) together with moderate thermal conductivity (≈ 9.5 W/m·K) can also provide uniform high resistance states, though the underlying mechanism shifts toward more efficient vacancy migration under stronger electric fields.

    • LRS Uniformity: For the low resistance state, high uniformity (\(\bar {\sigma }/\bar {\mu }\) ≈ 0.009) is best maintained when either electrical or thermal conductivity is low, as controlled Joule heating promotes consistent filament formation without random branching.

  4. 4.

    Additional Practical Considerations.

    • Device Geometry and Electrode Compatibility: The physical dimensions of the oxide layers and the nature of the electrode materials can strongly influence both heat dissipation and vacancy migration. Designers should ensure that the geometry supports uniform temperature gradients and that electrode materials are compatible with the targeted transport properties.

    • Temperature Dependence: As device operation involves significant local temperature variations, it is important to account for the temperature dependence of both electrical and thermal conductivities. Materials should be characterized over the anticipated operating temperature range to ensure robust performance.

    • Layered and Bilayer Structures: Employing bilayer configurations—where one-layer acts as a controlled reservoir for oxygen vacancies (e.g., TaOx) and the other serves as the primary switching medium (e.g., Ta2O5)—can decouple vacancy supply from switching dynamics. This approach offers additional flexibility in tuning both the forming process and the uniformity of resistance states.

    • Simulation-Guided Tuning: Given the complex interplay between Joule heating, electric field distribution, and vacancy dynamics, designers are encouraged to utilize physics-based simulations (similar to the models presented in this work) to fine-tune material parameters and device architecture before fabrication.

Conclusion

This research provides comprehensive insights into how electrical and thermal conductivities fundamentally influence the operation of oxide-based RRAM devices. Through detailed physical modeling and simulation, we demonstrate that the interplay between transport properties critically influences key device characteristics such as forming voltage, resistance ratio, and uniformity of resistance states. Our analysis reveals several important findings. First, the forming voltage exhibits a clear dependence on both conductivities: higher electrical conductivity promotes oxygen vacancy generation and reduces forming voltage, while higher thermal conductivity leads to increased forming voltage through enhanced heat dissipation. Second, we identify an optimal region for achieving high resistance ratios at moderate conductivity values, where balanced Joule heating and heat dissipation enable both efficient filament formation and complete rupture. Our finding shows two distinct pathways for achieving optimal HRS uniformity, each governed by different physical mechanisms: one at moderate electrical and low thermal conductivity, and another at higher values of both conductivities. For LRS, high uniformity can be maintained when either conductivity is low, offering greater flexibility in material design. These findings provide crucial guidelines for oxide material selection in RRAM devices, suggesting that materials with carefully tuned transport properties can significantly enhance device performance and reliability. The existence of multiple pathways to achieve optimal uniformity offers flexibility in material engineering while highlighting the importance of balanced transport properties. This understanding paves the way for designing more efficient and reliable RRAM devices for large-scale integration in next-generation memory and neuromorphic computing applications.