Introduction

As urbanization emerges and vehicle utilization becomes more extensive, transportation challenges become increasingly complex. Since, smart cities evolve managing urban traffic congestion effectively remains a major challenge1. Challenges like traffic congestion, frequent accidents, and a deteriorating traffic environment are becoming essential2. As a result, enhancing road network capacity has become a major fact for many researchers. A general model to address these issues is to build additional highways and extend existing road lanes. Traffic congestion on roads significantly contributes to pollution and deteriorates air quality in an urban environment3. This in turn raises morbidness in densely populated cities. Effectively addressing congestion through intelligent systems is adequate for smart transportation and sustainable city evaluation. Due to the emergence of technologies like edge computing, Internet of Things (IoT), 5G networks and Artificial Intelligence (AI) have been a growing interest in research focused on smart traffic congestion4,5.

Predicting traffic congestion is essential to evaluate Intelligent Transportation Systems (ITS). Accurate congestion forecasts enable traffic management systems to carefully adjust signal controls and implement preventive measures to mitigate congestion6. In addition, users can plan their routes more efficiently by avoiding congested areas on the basis of the real-time predictions7,8,9. Despite numerous traditional models for congestion prediction, accurately predicting traffic conditions across an entire road network remains complex10. Different works focused on congestion prediction at particular locations making it difficult to use these models in different parts of the network11. Congestion tends to propagate both upstream and downstream along a road segment and showing the importance of spatial correlations between road sections. Unfortunately, most location-based prediction models overlook these spatial relationships and leads to suboptimal performance12.

Furthermore, many approaches based on data from probe vehicles and requires map matching to correctly position these vehicles on the network. This process is complex and leads to errors, because of the noise inherent in GPS13,14,15. The recent works have utilized neural networks with promising results, the lack of interpretability in these models poses a significant challenge for traffic prediction applications. Hence, developing an efficient approach that can predict congestion across the entire road network is essential16.

ITS play a crucial role in smart cities by gathering real-time data on traffic conditions and vehicle information. These systems enable the development of extensive travel services that can continuously monitor vehicles’current locations, travel durations, and driving speeds17,18,19,20. Deep Learning (DL) approaches offer substantial benefits in traffic flow prediction and dynamic conditions within urban environments. Further, it offers powerful tools for processing and analyzing the data and makes more accurate congestion forecasting and dynamic traffic management21. Techniques such as Convolutional Neural Network (CNNs), Deep Belief Network (DBN), and Long Short-Term Memory (LSTM) have demonstrated remarkable success across different applications22,23,24. Hence, utilizing DL approaches holds high potential for improving traffic flow forecasting and mitigating urban congestion in smart cities. The foremost contributions are:

  • To present traffic congestion forecasting in smart cities using Reinforcement Learning (RL) with Bi-LSTM based adaptive Secretary Bird optimization (ASBO) in IoT environment.

  • To capture spatial and temporal patterns of the road using RL with Bi-LSTM networks.

  • To enhance the prediction performance by ASBO by considering state-of-the-art parameters

The subsequent sections are organized as follows: Part 2 reviews recent studies on traffic congestion prediction; Part 3 discusses the materials and the methods used in this work; Part 4 elaborates the proposed traffic congestion prediction methodology; Part 5 discusses the results with experimental setup and the results drawn; and finally, Part 5 concludes the work.2.

Related works

Wu et al.25 suggested an integration of Graph Convolutional Networks(GCN) and Bi-LSTM (Bidirectional Long Short-Term Memory) with multi-layer to accurately capture the spatio-temporal data with real time traffic patterns. This helps in analyzing the traffic patterns and predict the congestion on weekly pattern basis which supports urban planning but this requires an accurate, clearly maintained datasets and cannot accommodate dynamic traffic changes. To extract spatial patterns, the CNN processes the traffic flow data and the RNN captures the temporal dependencies. The features were combined and passed through a regression layer for generating the final traffic flow prediction26.

Chen et al.27 suggested an ensemble model for forecasting traffic flow with data denoised framework. Three different denoising models like Empirical Mode Decomposition (EMD), Ensemble EMD (EEMD) and Wavelet (WL) were considered. At last, the LSTM was exploited for traffic flow prediction.

Wang et al.28 suggested the Multi-task Time series with Graph Network model that combines CNN with Temporal features as TCN and Graph Attention Networks (TCN – GAT) to get the temporal-based traffic data and the dynamic correlations in congestion between regions. This could produce better results in predicting traffic but highly relies on the input data quality and also challenges arise when input given from multiple data sources.

Multi-task Recurrent (MR) Graph Convolutional Network (GCN) for traffic congestion process. Author’s considered multi-task model using four stages like region flow encoding that captures region, a transition flow encoding term that identifies correlations among transition flows, a context module that fuses these two kinds of traffic flow information, and a task-based decoding designed for traffic flow prediction29. Finally, Dual Attention Graph Convolutional Gated Recurrent Unit (DG-CGRU) to effectively model both spatial and temporal dependencies30.

Bai et al.31 presented an approach called the Relative Positioned Congestion Tensor for forecasting traffic congestion. Initially, the congestion matrices within regional traffic networks and utilized the relative positions concept of road nodes. These matrices were then transformed into 3D spatio-temporal tensors. Finally, the CNN with LSTM was used for estimating future congestion levels over every location on the road network.

Majumdar et al.32 explored the application of LSTM network for predicting congestion spread using observed and forecasted vehicle speeds. This existing work considered univariate LSTM and multi-variate LSTM for predicting congestion. The univariate LSTM considered the observed speed only with respect to the prior five minute as the input and the multi-variate LSTM considered the vehicle headway and traffic flow rate. Here, the accuracy value achieved was 84.5% (North) and 92.3% (South) directions33,34.

Alsubaiet al.35 presented the CNN with LSTM model for predicting traffic congestion. The algorithm Improved Arithmetic Optimizer (IAO) was used for parameter enhancement. The performance was demonstrated on road traffic dataset and achieved better accuracy and error rate of 98.03% and 1.97% respectively.

Chen et al.36 suggested DBN for predicting traffic congestion in smart cities. Initially, the primary methods and procedures for collecting traffic data were described and aimed to capture real-time traffic conditions over the road network. The next phase focused on data pre-processing and at last the DBN algorithm was applied for predicting traffic flow and considered key performance measures for assessing the accuracy and reliability of the prediction models.

Ata et al.37,38 introduced a model to manage smart road traffic congestion using Artificial Back-propagation Network (ABPN). This existing work provided efficiency, better transparency, and availability for individuals. The system utilizes a back-propagation for training the model and makes proper congestion prediction. This predictive capability aimed for improving traveler comfort by empowering them for making more informed and intelligent transportation decisions.

Zhai et al.39 focused on utilizing a BiLSTM for traffic flow prediction and aimed at effectively managing and optimizing urban traffic congestion. A short term traffic state prediction model was developed by BiLSTM by considering gathered traffic flow data. The memory unit’s internal model was refined for enhancing performance and the model undergoes rigorous training to ensure it delivers accurate and reliable traffic predictions40.

Elfaret al.41 investigated the application of three ML models for predicting short-term traffic congestion utilizing vehicle trajectory data. The data was sourced from the Next Generation SIMulation program (NGSIM). The predictive models like offline and online approaches were considered. The offline approaches were trained using historical data and re-calibrated only when substantial variation updated and then, the online approaches were initially trained with historical data42.

Mohanty et al.43 demonstrated that a DL approach utilizing LSTM can effectively address neighbourhood traffic congestion within a broader area. Simulations revealed that the predicted output, represented as neighbourhood congested value, responds to region traffic condition and can be accurately forecasted using 4 real-time signals that act as proxies for these conditions. Enhancements to the model included the inputs representation as weighted undirected graphs which lead to provide accuracy through the Graph-CNN-LSTM model44,45. Table 1 states the advantages and limitations of the existing works.

Table 1 Advantages and limitations of the existing works.
Full size table

Research gaps

  • The conventional approaches lack the ability to adapt quickly to dynamic changes in traffic pattern.

  • Conventional ML models fail to capture long-range temporal dependencies in traffic flow data.

  • Although numerous studies have explored the application of DL models in smart city contexts, most of them primarily focus on traffic flow prediction to enable ITS. However, the strategies and mechanisms for alleviating congestion once it has occurred remain insufficiently addressed.

To tackle the abovementioned challenges, the suggested work integrates Bi-LSTM into the RL framework to bring better accuracy in congestion prediction with fluctuations in input data and direction of traffic flow. This model captures both short-term and long-term temporal dependencies in traffic data and provides more accurate forecasting. Further, the algorithm ASBO is taken into account for highly reducing the overfitting chances and adjust the hyperparameters dynamically when compared to other metaheuristic optimization algorithms like GA, PSO and DE etc. It provides better trade-off between the exploration and exploitation. The combination of RL, Bi-LSTM, and ASBO improves congestion management and address the major limitations of existing models.

Materials and methods

Materials

The data considered in this work is Traffic Prediction Dataset46 and it was collected from Kaggle. The data is collected on December 2024 and the approach detected 4 categories of vehicles like buses, trucks, bikes, and cars. The size of the dataset is 393.11 kB. The data was saved in a CSV file and has columns like time in date, days of the week, hours and counts for all kind of vehicles (Bus Count, Truck Count, Bike Count, Car Count). The Total column shows the entire count of each vehicle type identified within 15 min. In addition, the dataset has classes like 1 (Heavy), 2 (High), 3 (Normal) and 4 (Low) to indicate the traffic.

Methods

To handle the dynamic traffic patterns and to consider the congestion rate in place of the existing traffic flow rate, the Reinforcement Learning based Bi-LSTM model with ASBO is taken into account. This model captures both short-term and long-term temporal dependencies in traffic data and provides more accurate forecasting. Further, the algorithm ASBO provides better trade-off between the exploration and exploitation. The combination of RL, Bi-LSTM, and ASBO improves congestion management and address the major limitation of existing models.

Proposed methodology

System model

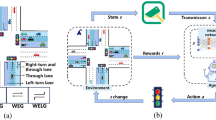
This research introduces an advanced traffic congestion prediction system in smart cities using RL with BiLSTM with ASBO. The RL captures spatial features and the Bi-LSTM captures the temporal dependencies of traffic flow. Then, the ASBO is used for fine-tuning the congestion prediction performance by considering Mean Square Error (MSE) as the fitness function. This hybrid model provides timely and accurate congestion forecasts and empowers smart city infrastructure with better traffic management potential. The suggested model enhanced the traffic flow efficiency and gave rise to sustainable urban mobility by reducing congestion and supporting ITS. Figure 1 shows the framework of the suggested traffic congestion prediction system.

Fig. 1
figure 1

Framework of the suggested traffic congestion prediction system.

Full size image

Architectural model

  • Pre-processing

Pre-processing stage is essential stage in developing proper and better traffic congestion prediction system. At first, the missing values are removed by mean imputation. Then, the outliers are removed by z-score normalization. This normalization is used for rescaling features and it is represented as:

$$z_{a} = \frac{{x_{a} - \mu }}{\sigma }$$
(1)

where \(x_{a} ,z_{a} ,\mu\) and \(\sigma\) are original value, normalized value, mean and standard deviation.

  • Traffic congestion prediction

In traffic congestion prediction, capturing spatial and temporal features is essential for proper forecasting. RL plays a key role in extracting spatial features over different road networks. This spatial feature makes the model for understanding congestion patterns and their geographic distribution in the city. Then, the Bi-LSTM with ASBO extracts temporal features using historical traffic data and identifying patterns with respect to time. This extraction process shows that the model captures the dynamic, complex relation between spatial road conditions and temporal traffic flow variations. Figure 2 shows the RL- BiLSTM model structure for traffic congestion prediction.

Fig. 2
figure 2

Structure of the RL- BiLSTM model.

Full size image

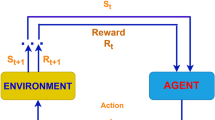
RLIn RL, the system has the components like Agent, Environment, State, Action and Reward that work together to make an agent to learn how to perform decisions in an environment for maximizing cumulative rewards.

State: The state ensures important features to the agent regarding the present condition of the environment. Here, the state has historical traffic data and allows the agent for understanding the road’s temporal dynamics. By incorporating past traffic conditions the state representation provides a contextual view of how traffic patterns have evolved over time, and enhances the agent’s ability for managing and predicting traffic dynamics effectively.

$$S_{l} = \left\{ {c_{l}^{j} |j \in \chi } \right\}$$
(2)

where \(S_{l}\) is the state at time step \(l\) and \(c_{l}^{j}\) is the vehicle count.

Agent: The traffic congestion prediction environment is set as a Markov Decision Process (MDP) and the major aim is to minimize traffic congestion and optimize the vehicles flow in a smart city. In this scenario, an agent interacts with the traffic environment and identifies decisions for minimizing congestion. The actions of the agents like traffic light control, and adjusting signal timings are guided by Q-values in a Deep Q-Network (DQN). These Q-values show the expected future rewards (such as reduced congestion, improved traffic flow, and minimized delays) accompanied with taking specific actions in particular traffic states.

Action: In the context of RL, the action space is a vital component and it allows the agent for interconnecting with the environment and influence future outcomes. The agent performs in a discrete action space and has three actions adjust signal, reroute traffic, and maintain current flow. All actions represent an opinion that the agent can make at any given condition within the traffic network. It is expressed mathematically as:

$$A_{l} = \left\{ {a_{l}^{j} |j \in \chi } \right\} = \left\{ {a_{l}^{0} ,a_{l}^{1} ,a_{l}^{2} ,.........,a_{l}^{\chi } } \right\}$$
(3)

where \(\chi\) is the various traffic control points, \(A_{l}\) is the action vector sent by the agent to the environment at time step \(l\).

Reward: The reward function provides essential feedback to the agent and guiding its decision-making process. In traffic prediction and management using RL, the reward function defines the agent’s actions effectiveness like adjusting traffic signals or rerouting vehicles. A reward function assists the agent learn for optimizing traffic flow by reducing congestion, travel time and delays. Here’s a typical mathematical expression for a reward function in this context:

$$R_{l} = - \left\{ {\beta_{1} \times We_{l} + \beta_{2} \times D_{l} + \beta_{3} \times Q_{l} } \right\}$$
(4)

where \(\beta_{1} ,\beta_{2} ,\beta_{3}\) is the weighting term, \(We_{l} ,D_{l}\) and \(Q_{l}\) are the average vehicle waiting time at step \(l\), Average travel delay at time step \(l\) and Queue length (number of vehicles waiting) at time step \(l\).

Bi-LSTM: This network is highly effective in extracting temporal features from traffic flow patterns. They capture dependencies from both past (prior traffic conditions) and future (anticipated traffic states) information, and it is essential for accurate traffic prediction. A Bi-LSTM has dual LSTM layers: one processes the input sequence forward, and the other processes it backward. The outputs of these layers are integrated for forming the final representation. Let the input vector at time step \(l\) is \(Z_{l}\); \(\mathop {h_{l} }\limits^{ \to }\) and \(\mathop {h_{l} }\limits^{ \leftarrow }\) are the hidden state of the forwarded and back warded LSTMs.

The forwarded LSTM is given as:

$$\mathop {h_{l} }\limits^{ \to } = LSTM_{for} \left( {Z_{l} ,\mathop {h_{l - 1} }\limits^{ \to } } \right)$$
(5)

The back warded LSTM is given as:

$$\mathop {h_{l} }\limits^{ \leftarrow } = LSTM_{back} \left( {Z_{l} ,\mathop {h_{l - 1} }\limits^{ \leftarrow } } \right)$$
(6)

The final representation is given as:

$$h_{l} = \mathop {h_{l} }\limits^{ \to } \oplus \mathop {h_{l} }\limits^{ \leftarrow }$$
(7)

where \(\oplus\) is the concatenation.

Optimal parameter selection

Hyperparameters like learning rate, batch size, and number of layers influence model performance. The data engineering methods such as spatio-temporal data and time-cropping method adopted in the time-series Augmentation view to build the model along with considered hyperparameters. The optimal set of hyperparameters is identified by the Adaptive Secretary Bird Optimizer (ASBO) for improving RL with Bi-LSTM efficiency and the value of the Mean Square Error (MSE) is considered as the fitness score for all hyperparameters configuration.

$$Fitness = Minimize\;(MSE)$$
(8)

ASBO is an improved version of SBO47 and it integrates the opposition based learning (OBL) and Chaotic Local Search (CLS).

ASBO mimics the behaviour of the survival behaviors of secretary birds (SB) in their natural habitat. These birds must constantly hunt for prey and evade predators. This makes their survival strategies ideal for designing a new metaheuristic approach for solving real-world optimization challenges. In the ASBO, the exploration stage mimics the hunting process and SB searches for snakes and it represents a broad search for potential solutions. The exploitation stage shows the bird’s evasion from predators, during which they carefully observe their surroundings and choose the safest path to refuge. These stages are iteratively executed, continuing until pre-defined ending conditions are met and the optimal solution.

Initialization: In ASBO, every SB represents an individual within the population. The position of every SB in the searching space corresponds to specific decision variable values. Therefore, in the ESBO, these positions are candidate solutions to the optimization challenge. During the initial phase, a randomized initialization process is applied for generating the positions of the SB in the searching space.

$$Y_{k,l} = lb_{l} + r \times (ub_{l} - lb_{l} )$$
(9)

where \(Y_{k,l}\) is the position of the \(k^{th}\) SB at \(l^{th}\) dimension. \(r,ub_{l}\) and \(lb_{l}\) is the arbitrary number, upper and lower bounds. In the ESBO, the process of optimization begins from the candidate’s solution population is given as:

$$\left[ \begin{gathered} y_{1,1} \quad y_{1,2} \quad \cdots \quad y_{1,l} \quad \cdots \quad y_{1,\dim } \hfill \\ y_{2,1} \quad y_{2,2} \quad \cdots \quad y_{2,l} \quad \cdots \quad y_{2,\dim } \hfill \\ \quad \vdots \quad \quad \vdots \quad \quad \ddots \quad \quad \vdots \quad \quad \ddots \quad \quad \vdots \hfill \\ y_{k,1} \quad y_{k,2} \quad \cdots \quad y_{k,l} \quad \cdots \quad y_{k,\dim } \hfill \\ \quad \vdots \quad \quad \vdots \quad \quad \ddots \quad \quad \vdots \quad \quad \ddots \quad \quad \vdots \hfill \\ y_{M,1} \quad y_{M,2} \quad \cdots \quad y_{M,l} \quad \cdots \quad y_{M,\dim } \hfill \\ \end{gathered} \right]$$
(10)

where \(Y_{k,l}\) is the \(k^{th}\) SB at \(l^{th}\) dimension, \(M\) is the number of SB and \(\dim\) is the dimensions.

Every SB shows the candidate’s solution for optimizing the problem. Hence, the fitness \(G\) can be defined with respect to the every SB and it is given as:

$$G = \left[ \begin{gathered} G_{1} \hfill \\ \vdots \hfill \\ G_{k} \hfill \\ \vdots \hfill \\ G_{M} \hfill \\ \end{gathered} \right]_{M \times 1} = \left[ \begin{gathered} G(Y_{1} ) \hfill \\ \vdots \hfill \\ G(Y_{k} ) \hfill \\ \vdots \hfill \\ G(Y_{M} ) \hfill \\ \end{gathered} \right]_{M \times 1}$$
(11)

where \(G_{k}\) is the fitness value of the \(k^{th}\) SB.

Exploration (hunting): There are three stages are involved in the hunting strategy of SB. They are prey search, prey consumption and prey attack. According to the biological term of SB’s hunting and the time taken for every stage, the overall hunting strategy is split into \(l < \frac{1}{3}L,\frac{1}{3}L < l < \frac{2}{3}L\), and \(\frac{2}{3}L < l < L\).

Prey search: The SB’s hunting strategy generally initiates by the prey search particularly snakes. These birds have long necks and legs which makes them to manage a safe distance to overcome from snack attack. This scenario occurs in the begging optimization iteration in which exploration is important and therefore this stage uses a differential evolution (DE) model. This DE utilizes variation among individual for generating new solutions. This improves global search and diversity and the differential mutation is incorporated. This improves the optimizer to overcome local optima. The prey search strategy is given as:

$$while\;l < \frac{1}{3}L,\;y_{k,l}^{new,Q1} = y_{k,l} + \left( {y_{rand\_1} - y_{rand\_2} } \right) \times R1$$
(12)
$$Y_{k} = \left\{ \begin{gathered} Y_{k}^{new,Q1} ,when\;G_{k}^{new,Q1} < G_{k} \hfill \\ Y_{k} ,\quad \quad elsewhere \hfill \\ \end{gathered} \right.$$
(13)

where \(l\), \(L,\)\(y_{k,l}^{new,Q1}\), and \(R1\) are the present iteration, maximum iterations, new stage of \(k^{th}\) SB and randomized array. \(y_{rand\_1}\) and \(y_{rand\_2}\) are randomized solution of candidates in the initial iteration.

Prey consumption: When a SB encounters a snake, it employs a unique hunting strategy. It uses its nimble footwork over the snake and it maintains a vigilant stance, carefully observing the snake’s each move from an elevated position. By skilfully assessing the snake’s behaviour, the bird alternates between hovering, jumping, and provoking the snake, and slowly depleting its energy. To model this behavior, Brownian motion (BM) is incorporated for representing the SB’s random motions. BM is described mathematically by Eq. (14) and introduces stochastic elements into the SB’s actions.

$$BM = rand(1,Dim)$$
(14)

where \(rand(1,Dim)\) is the randomly created array with dimension \(1 \times Dim\) from the normal distribution.

The randomness in BM enhances the exploration of the solution space and facilitates to avoid local optima. This leads to improved performance in solving complex problems. Hence, the process of SB’s updating position during the Prey consumption is given by:

$$while\;\frac{1}{3}L < l < \frac{2}{3}L,\;y_{k,l}^{new,Q1} = y_{best} + \exp \left( {\left( {l/L} \right) \wedge 4} \right) \times \left( {BM - 0.5} \right) \times \left( {y_{best} - y_{k,l} } \right)$$
(15)
$$Y_{k} = \left\{ \begin{gathered} Y_{k}^{new,Q1} ,when\;G_{k}^{new,Q1} < G_{k} \hfill \\ Y_{k} ,\quad \quad elsewhere \hfill \\ \end{gathered} \right.$$
(16)

where \(y_{best}\) is the present best value.

Prey attack: If the snake shows signs of exhaustion, the SB senses the perfect opportunity and quickly strikes and utilizes its strong leg muscles for an effective attack. In the random search, the Lévy flight (LF) is incorporated for increasing the global exploration ability of the optimization. This approach minimizes the chances of the ESBO becoming trapped in local optima. This increases the entire convergence of the optimization.

$$while\;l> \frac{2}{3}L,\;y_{k,l}^{new,Q1} = y_{best} + \left( {\left( {1 - \frac{l}{L}} \right)} \right) \wedge \left( {2 \times \frac{l}{L}} \right) \times y_{k,l} \times LF$$
(17)
$$Y_{k} = \left\{ \begin{gathered} Y_{k}^{new,Q1} ,when\;G_{k}^{new,Q1} < G_{k} \hfill \\ Y_{k} ,\quad \quad elsewhere \hfill \\ \end{gathered} \right.$$
(18)

The weighted LF (WLF) is used for enhancing the optimization efficiency and it is given as:

$$WLF = 0.5 \times LF(Dim)$$
(19)

The value of the \(LF(Dim)\) is determined by:

$$LF(Dim) = x \times \frac{u \times \beta }{{|g|^{1/\sigma } }}$$
(20)

where \(x\) is a constant term, \(u\) and \(g\) are the random number which ranges between 0 and 1. \(\beta\) is the scaling term and the value of \(\sigma\) is 1.5.

Exploitation (Escaping process of SB): There are two mechanisms like Camouflage \(V_{1}\) and fly \(V_{2}\) are involved in exploitation. In the initial process, when SB detects a predator nearby, they first seek a proper environment for camouflage. When no safe hiding spot is available close by, they choose to escape either by flying or running quickly. Inspired by this behavior, a dynamic perturb term \(\left( {1 - \frac{l}{L}} \right)^{2}\) is introduced. It is expressed as:

$$y_{k,l}^{new,Q2} = \left\{ \begin{gathered} V_{1} :y_{best} + \left( {2 \times BM - 1} \right) \times \left( {1 - \frac{l}{L}} \right)^{2} \times y_{k,l} ,\quad when\;ra < r_{k} \hfill \\ V_{2} :y_{k,l} + R_{2} \left( {y_{rand} - P \times y_{k,l} } \right),\quad elsewhere \hfill \\ \end{gathered} \right.$$
(21)
$$Y_{k} = \left\{ \begin{gathered} Y_{k}^{new,Q1} ,when\;G_{k}^{new,Q1} < G_{k} \hfill \\ Y_{k} ,\quad \quad elsewhere \hfill \\ \end{gathered} \right.$$
(22)

where \(P\) is the random integer (1 or 2), \(y_{rand}\) and \(R_{2}\) are the randomized solution of candidates in the present iteration and randomized array.

OBL improves global exploration and CLS refines local searches, balancing the optimization capacity for exploration and exploitation. Combining OBL and CLS helps the algorithm converge faster and reduces the risk of getting trapped in local minima.

Let \(y\) is the real number and \(y \in \left[ {ll,ul} \right]\) and the opposite number \(\overline{y}\) is given as:

$$\overline{y} = ul + ll - y$$
(23)

where \(ul\) and \(ll\) are upper and lower boundaries.

When \(y = \left( {y_{1} ,y_{2} ,y_{3} ,.....y_{Dim} } \right)\), where \(y_{1} ,y_{2} ,y_{3} ,.....y_{Dim}\) is the real number and the value of \(\overline{y}_{k}\) is computed as:

$$\overline{{y_{k} }} = ul_{k} + ll_{k} - y_{k}$$
(24)

Then, the chaotic mapping considered is logistic mapping and it is utilized for generating the chaotic sequence.

$$a^{w + 1} = Ca^{w} (1 - a^{w} )$$
(25)

The value of \(C\) is 4 and \(a^{w} = rand(0,1)\). The chaotic model is considered for obtaining a search operation and the operation is combined with the optimization. The solution created by the CLS is given as:

$$Cw = (1 - \alpha ) \times T_{a} + \alpha \overline{{C_{k} }} \quad k = 1,2,3,...,n$$
(26)

where \(Cw\) is the solution of the candidate, \(\overline{{C_{k} }}\) is the mapping term, and \(T_{a}\) is the targeting position. The value of the \(\alpha\) is given as:

$$\alpha = \frac{MaxI - currI + 1}{{Max_{k} I}}$$
(27)

where \(MaxI\) and \(currI\) are the maximum and present iterations. Algorithm 1 shows the pseudocode of the suggested ASBO for updating the parameters of the RL with BiLSTM.

Algorithm 1
figure a

Pseudocode of the suggested ASBO.

Full size image

Experimentation, result and analysis

Experimental setup

Experimentation of the Traffic Congestion prediction is performed on Python using libraries such as TensorFlow, and PyTorch for model development. It also considered the tools like NumPy and pandas for pre-processing of the data and analysis. Table 2 defines the hyper parameters considered for experimental purpose.

Table 2 Parameters.
Full size table

Performance measures

To verify the traffic congestion in smart cities the performance measures like Mean Square Error (MSE), Root MSE (RMSE), coefficient of determination (R2), Mean Absolute Percentage Error (MAPE) and mean absolute error (MAE) are compared.

MSE: It calculates average of the squared differences among forecasted \(\mathop {u_{j} }\limits^{ \wedge }\) and actual traffic \(u_{j}\) congestion values.

$$MSE = \frac{1}{v}\sum\limits_{j = 1}^{v} {\left( {u_{j} - \mathop {u_{j} }\limits^{ \wedge } } \right)}$$
(28)

RMSE: It calculates error metric in the same unit as traffic data values.

$$RMSE = \sqrt {\frac{1}{v}\sum\limits_{j = 1}^{v} {\left( {u_{j} - \mathop {u_{j} }\limits^{ \wedge } } \right)}^{2} }$$
(29)

R2: It calculates how all prediction approach match the \(u_{j}\) and it indicates the ratio of variance defined by the approach.

$$R^{2} = 1 - \frac{{\sum\limits_{j = 1}^{v} {\left( {u_{j} - \mathop {u_{j} }\limits^{ \wedge } } \right)}^{2} }}{{\sum\limits_{j = 1}^{v} {\left( {u_{j} - \overline{{u_{j} }} } \right)}^{2} }}$$
(30)

MAPE: This measure shows how large the prediction errors are related to actual traffic levels.

$$MAPE = \sum\limits_{j = 1}^{v} {\left| {\frac{{u_{j} - \mathop {u_{j} }\limits^{ \wedge } }}{{u_{j} }}} \right|}$$
(31)

MAE: It is measured by taking the absolute differentiation among the \(\mathop {u_{j} }\limits^{ \wedge }\) and the \(u_{j}\) values.

$$MAE = \frac{1}{v}\sum\limits_{j = 1}^{v} {\left| {u_{j} - \mathop {u_{j} }\limits^{ \wedge } } \right|}$$
(32)

where \(v\) is the overall data samples and \(\overline{{u_{j} }}\) is the average of the \(u_{j}\).

Ablation study

The ablation study is performed for methods like RL, deep Q learning (DQL), LSTM, BiLSTM and the suggested RL with BiLSTM-ASBO with respect to various traffic congestion measures.

Figure 3 presents the MSE comparison of the different approaches like RL, DQL, LSTM, BiLSTM48,49,50,51,52,53 and the suggested RL with BiLSTM-ASBO. Here, the performance is considered by varying the timesteps from 1.0 to 4.0. When the timestep is 1.0, the MSE values achieved by the RL, DQL, LSTM, BiLSTM and the suggested RL with BiLSTM-ASBO are 0.135, 0.116, 0.1, 0.05 and 0.017. Similarly, when the timestep is 4.0, the MSE values achieved by the RL, DQL, LSTM, BiLSTM and the suggested RL with BiLSTM-ASBO are 0.094, 0.09, 0.065, 0.04 and 0.012. The suggested RL with BiLSTM-ASBO attained better outcome because the RL obtains complex spatial features and the BiLSTM obtains complex temporal dependencies. When integrating RL with BiLSTM model into ASBO, the optimization process benefits from better convergence performance and adaptive parameter tuning. This proves that the suggested model identified better optimal parameter. This coordination allows the approach for capturing from diverse traffic scenarios more effectively. This provides better MSE values when compared to the other DL models.

Fig. 3
figure 3

MSE comparison.

Full size image

Figure 4 presents the RMSE comparison of the different approaches like RL, DQL, LSTM, BiLSTM and the suggested RL with BiLSTM-ASBO. Here, the performance is considered by varying the timesteps from 1.0 to 4.0. When the timestep is 2.0, the RMSE values achieved by the RL, DQL, LSTM, BiLSTM and the suggested RL with BiLSTM-ASBO are 0.353, 0.316, 0.282, 0.223 and 0.118. Similarly, when the timestep is 3.0, the RMSE values achieved by the RL, DQL, LSTM, BiLSTM and the suggested RL with BiLSTM-ASBO are 0.36, 0.34, 0.3, 0.244 and 0.130.The RL with BiLSTM-ASBO maintains lower RMSE even as the timestep increases. These outcomes define the superior ability of the suggested model for obtaining complex temporal patterns and optimizing learning by the ASBO algorithm. This enhances performance in traffic congestion prediction compared to other models.

Fig. 4
figure 4

RMSE comparison.

Full size image

Figure 5 presents the R2 comparison of the different approaches like RL, DQL, LSTM, BiLSTM and the suggested RL with BiLSTM-ASBO. If the value of the R2 is near to 1 means the model defines most of the variability in traffic congestion and a shows a better prediction capability. Here, the performance is considered by varying the timesteps from 1.0 to 4.0. When the timestep is 1.0, the R2 values achieved by the RL, DQL, LSTM, BiLSTM and the suggested RL with BiLSTM-ASBO are 0.875, 0.9, 0.93, 0.95 and 0.971. Similarly, when the timestep is 2.0, the R2 values achieved by the RL, DQL, LSTM, BiLSTM and the suggested RL with BiLSTM-ASBO are 0.887, 0.910, 0.930, 0.95 and 0.975. Finally, when the timestep is 3.0 and 4.0 the R2 values achieved by theRL with BiLSTM-ASBO are 0.979 and 0.981. Finally, the outcomes demonstrate that RL with BiLSTM-ASBO effectively captures complex traffic patterns and provides better congestion prediction performance when compared to other approaches.

Fig. 5
figure 5

R2 comparison.

Full size image

Figure 6 depicts the MAE comparison of the different approaches like RL, DQL, LSTM, BiLSTM and the suggested RL with BiLSTM-ASBO. It is observed from the graph that when the timesteps are increasing, the MAE values are also increasing for all DL models. The suggested RL with BiLSTM-ASBO attained better MAE values of 0.13 (timestep 1.0), 0.133 (timestep 2.0), 0.131 (timestep 3.0) and 0.14 (timestep 4.0). This performance highlights the proposed model’s robustness and superior performance in predicting traffic congestion when compared to RL, DQL, LSTM, and BiLSTM approaches.

Fig. 6
figure 6

MAE comparison.

Full size image

Figure 7 depicts the MAPE comparison of the different approaches like RL, DQL, LSTM, BiLSTM and the suggested RL with BiLSTM-ASBO. When the timestep is 1.0, the MAPE values achieved by the RL, DQL, LSTM, BiLSTM and the suggested RL with BiLSTM-ASBO are 6.16%, 5.99%, 5.72%, 5.4% and 5.12%. Similarly, when the timestep is 2.0, the MAPE values achieved by the RL, DQL, LSTM, BiLSTM and the suggested RL with BiLSTM-ASBO are 6.16%, 6%, 5.72%, 5.48% and 5.2%. Finally, when the timesteps are 3.0 and 4.0 the MAPE values achieved by the RL with BiLSTM-ASBO are 5.2% and 5.4%. This shows that RL with BiLSTM-ASBO consistently obtained lower MAPE values compared to the other models. This demonstrated its supremacy and reliability in predicting traffic congestion, even as the prediction timestep increases.

Fig. 7
figure 7

MAPE comparison.

Full size image

Figure 8 depicts the relation among the total vehicle arrived with respect to the simulation time. It is noted that when the simulation time is increased, the total vehicle arrived is also increasing. Total vehicle arrived in default path is very less and the total vehicle arrived in the DL models are higher. Hence, it is proved that even when the road is congested, the suggested RL with Bi-LSTM and ASBO can overcome the congestion in better way.

Fig. 8
figure 8

Comparison of total vehicle arrived.

Full size image

Figure 9 presents the analysis of the actual vs predicted traffic flow of the suggested RL with BiLSTM-ASBO. This analysis shows how closely the RL with BiLSTM-ASBO’s predictions fit with actual traffic flow data. By plotting actual and predicted values, the analysis highlights the correctness of the model in capturing traffic patterns.

Fig. 9
figure 9

Analysis of the actual vs predicted traffic flow.

Full size image

Figure 10 presents the convergence analysis of the SBO and ASBO. This analysis defines how rapidly and effectively the SBO and ASBO approach reach its optimal solution. Here, the performance is measured by plotting the fitness value (or error) against the number of iterations. It is noted that the suggested ASBO attained better optimal and this achievement is because of the integration of the OBL and CLS.

Fig. 10
figure 10

Convergence analysis.

Full size image

Table 3 suggests the comparison of inference and training time with respect to different approaches like RL, DQL, LSTM, BiLSTM and the suggested RL with BiLSTM-ASBO. It is noted that the suggested RL with BiLSTM-ASBO attained better inference time of 3.1 s and training time of 1.1 s.

Table 3 Comparison of inference and training time.
Full size table

The comparison points out a significant improvement in computing efficiency, training time, and real-time inference capacity with the Proposed RL with BiLSTM-ASBO model. Below is an overview of the major improvements:

1. Computing Efficiency

The proposed model performs inference in a mere 3.1 s, which is much faster than isolated RL (11.2 s), DQL (9.34 s), LSTM (9.12 s), and BiLSTM (8.3 s). This enhancement is due to the optimization of the ASBO and the interaction between RL and BiLSTM, which leads to efficient computation and optimal resource usage.

2. Training Time

The training time of 1.1 s for RL with BiLSTM-ASBO is the least among all the methods mentioned. This efficiency is due to the adaptive sine cosine algorithm (ASBO), which speeds up parameter optimization during training and minimizes convergence time.

3. Real-Time Inference Ability

Real-time systems need to have rapid and dependable prediction models. The model proves to be superior by merging RL’s decision-making capability with BiLSTM-ASBO’s strong sequential data handling.

Conclusion and future scope

Traffic congestion is a major challenging process in ITS, as it affects both sustainability and efficiency in modern cities. This work explored the use of a deep learning approach RL with BiLSTM-ASBO for predicting traffic congestion in urban road networks. Moreover, the algorithm ASBO improves the prediction performance. The experimentation was performed on the Traffic Prediction Dataset and attained better MSE and MAE values of 0.015 and 0.133, respectively. The outcomes showed that RL-BiLSTM with ASBO is robust in managing the complexities, and non-linear traffic patterns. This makes it a promising solution for congestion prediction and analysis and the suggested model can minimize air pollution and enhance the urban environment’s sustainability.

Traffic dataset and patterns might change according to the seasons as well as specific occasions like holidays, festive seasons, School/College vacation time etc. Accordingly, dataset size and patterns might change. In future, this needs to be addressed along with the biases that may arise due to peak hour and non-peak hour travel, vehicle types etc. to minimize the traffic congestion.