Explicit intent enhanced contrastive learning with denoising networks for sequential recommendation

Abstract

Sequential recommendation aims to accurately predict the users’ next preferences, where user interest is influenced by their intent. Utilizing intent contrastive learning, the sequential recommendation has achieved advanced performance. However, most contrastive learning models address the critical issue of data sparsity using data augmentation, which amplifies the noise present in the original sequences, resulting in learning biased user intent distribution functions, and deteriorating the modeling effectiveness of true intent. To address this issue, we propose a model named Explicit Intent Enhanced Contrastive Learning with Denoising Networks for Sequential Recommendation (EICD-Rec). In EICD-Rec, we design a contrastive learning recommender naturally sensitive to users’ true intents. The recommender can adaptively filter noise at different frequency scales in sequences in the frequency domain, thus obtaining purer representations of user intents. Moreover, to further enhance the accurate representation of users’ true intents, we model explicit intent. Integrating this explicit intent with implicit intent to construct high-quality self-supervision signals and maximize the joint probability distribution between items and explicit intent, thereby enhancing the accuracy of representing users’ true intent. Extensive experimental evaluations on three widely used real-world datasets demonstrate the effectiveness and generality of our proposed EICD-Rec model.

Introduction

Recommender systems are unique data filtering system that utilizes techniques such as data mining and deep learning to extract features from various aspects of user information, including historical behaviors and preferences, and leverage these features to predict users’ levels of preference for items¹. Nowadays, recommender systems have been widely applied in various domains, including social recommendations, product recommendations, music recommendations, and movie recommendations.

Sequential Recommendation (SR)^2,3,4,5 considers the item dependency relationships within a user’s historical behavior sequence, leveraging the correlations between data to model users’ dynamic preferences. SR not only takes into account the user’s current interests, but also considers the impact of their long-term historical interactions on their current interests, to accurately predict items that the user may be interested in at the next moment. Therefore, SR has found widespread applications in domains such as e-commerce. With the advancement of deep learning, SR models based on Convolutional Neural Networks^6,7, Recurrent neural networks^8,9,10, deep reinforcement learning¹¹, attention mechanisms^12,13,14, and graph neural networks¹⁵ have emerged. These Neural Network(NN)-based SR models adopt deep neural networks or their variants to model user behavior sequences, enabling the models to learn more complex and higher-level vector representations of users and items, while automatically learning users’ interest patterns and sequential dependencies from the sequences, thus helping the models make more accurate predictions.

Fig. 1

An example illustrating the necessity of denoising original sequences containing user intent.

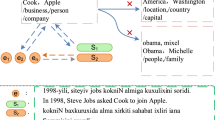
Typically, NN-based SR models assume that a user’s current interests depend on their historical interactions, which are often driven by the user’s intents and usually contain noisy information. As shown in the motivating example of the user’s original sequence in Fig. 1, the user engages in interaction with a shopping platform during a certain period, intending to engage in the activity of running, and ultimately purchases running shoes (including noisy interaction due to user misoperation). A model that doesn’t learn about the user’s intentions is more likely to recommend treadmills, socks, or sports kettles. If the model can infer the user’s intent to engage in running activities from historical behaviors, it can recommend items related to running to the user, such as his shopping goal: running shoes. However, existing research works^16,17,18 mostly model user intents through auxiliary information, which has limitations as it solely relies on item category information and fails to capture users’ true intentions fully¹⁹. Recently, methods that use Contrastive Learning (CL)^19,20 for sequence modeling have gradually become popular because they can effectively overcome data sparsity issues. Among them, some advanced works extract users’ latent intents from user behavior sequences and integrate them with SR models through contrastive learning, constructing a joint loss function for the SR task and the contrastive learning task to further learn user preferences precisely. ICL¹⁹ discovers users’ implicit intent representations through unsupervised methods and incorporates them into the contrastive learning loss function. IOCRec²⁰ obtains two augmented sequences for each user using two random augmentation operators and constructs a positive pair for each intent in each sequence, building a contrastive learning loss function.

On the other hand, it is typical for user behavior sequences to be contaminated with noise. For example, users may click on items that are different from their intent due to accidental clicks, item category labels may contain erroneous information, and models typically overfit to sequences containing noise, resulting in biased embedding representations of sequences, which can greatly impact the accuracy of SR models^21,22. In addition, the aforementioned CL-based models mainly address the critical issue of data sparsity through data augmentation, which amplifies any potential noise present in the original sequences, leading to biased user intent representations being learned. This constrains the performance of CL and consequently degrades recommendation performance.

To address the aforementioned issues, we investigated how to effectively mitigate the negative impact of noise on the contrastive learning task, thereby obtaining more accurate recommendations. Consequently, we propose a recommendation algorithm called Explicit Intent Enhanced Contrastive Learning with Denoising Networks for Sequential Recommendation (EICD-Rec). We designed a sequence encoder in EICD-Rec to more accurately represent users’ true intentions and address the potential issue of severe sparsity caused by item transitions within sequences. By combining Fourier transformation, we adaptively filter noise from the sequence at dual scales, and input the denoised representation into the encoder. Simultaneously, the encoder models categorical features to capture explicit intents. By incorporating explicit intents into the sequence representation and leveraging contrastive learning tasks, we enhance and construct high-quality latent intention self-supervised signals, reducing the noise’s impact on the intent contrastive learning. The main contributions of this paper are as follows:

• 1. To accurately extract users’ true intents from noisy sequences, we design a sequence encoder that can adaptively filter out noise at dual scales and apply it to the SR task in combination with intent contrastive learning.

• 2. We model the item category features to obtain the representation of the user’s explicit intent and incorporate it into the intent contrastive learning module to acquire more accurate representations of the true intents. Meanwhile, we enhance the model by maximizing the joint probability distribution between items and explicit intents.

• 3. We conduct extensive experiments on three widely used real-world datasets, and the experimental results demonstrate that the EICD-Rec model achieves advanced performance on the SR task, outperforming several state-of-the-art baseline models.

Related work

Shallow model for sequential recommendation

SR learns user interest changes based on their historical behavior sequences to predict their interactions with items in the next time step. Early SR algorithms often relied on matrix factorization^23,24,25. Singular value decomposition^26,27, widely used in recommendation algorithms due to its applicability to any matrix, unlike eigendecomposition which is limited to square matrices, was preferred. However, such shallow models struggled to handle complex user behaviors or data inputs, particularly in scenarios with sparse data.

Some other early SR models were based on Markov chains. The fundamental idea was to analyze the user’s historical behavior sequence, count the frequency of each item appearing in the sequence, construct a transition matrix, and establish the corresponding Markov chain model. Then, based on this model, predict the next item or action that might occur and recommend it to the user. Shani et al. proposed a Markov Decision Processes (MDPs) model²⁸ for recommender systems, viewing the recommendation prediction problem as a continuous optimization problem, but they did not fully utilize contextual information. Such shallow models based on Markov chains have advantages like simplicity and ease of implementation. However, they are sensitive to factors like sequence length.

Deep model for sequential recommendation

With the remarkable success of neural network in fields like computer vision²⁹ and natural language processing³⁰, introducing NN-based recommendation models into personalized recommendation problems has become the mainstream paradigm. Compared to shallow models, deep neural network models can learn more complex and higher-level latent factors and features of users and items. Currently, in NN-based SR models, models based on Convolutional Neural Network (CNN), Recurrent Neural Network (RNN), Multilayer Perceptro (MLP) architecture, and attention mechanisms dominate.

CNN-based SR models^6,7 use convolutional and pooling layers to extract and combine features, yielding satisfactory results, but they may not capture the correlations between sequences effectively. RNN-based SR models^8,9,10, on the other hand, can effectively utilize historical interaction item sequences to model long-term sequential dependencies, but they are greatly restricted when dealing with sparse sequences. He et al.³¹ proposed the Neural Collaborative Filtering model, which employs MLP to capture complex nonlinear relationships between users and items. Zhou et al.³² introduced a deep model with an all-MLP architecture to encode user historical sequences and accomplish recommendation tasks. Additionally, with the outstanding achievements of the Transformer in various fields, its powerful sequence modeling capability has been introduced into sequential recommendation systems. As a pioneering work, SASRec¹² first utilizes multi-head self-attention structure to model user sequences and achieves advanced performance. BERT4Rec¹³ adopts deep bidirectional self-attention to model user behavior sequences. MAN¹⁴ extracts global and local information through a hybrid attention network to infer user interests. While attention mechanism-based sequential models have shown advanced performance, they suffer from issues like susceptibility to noise and high computational complexity.

The recent application of intent modeling methods in NN-based SR models has attracted widespread attention^16,17,18. KA-MemNN¹⁶ directly constructs user intent representations through a neural network architecture with attention and aggregation functions. ASLI¹⁷ extracts user intents from the user’s multi-type behavior history records, but the acquisition of multi-type behavior is difficult, limiting its applicability. CocoRec¹⁸ learns the transition relationships between categories, i.e., it utilizes the most recent behavior categories to predict and obtain the category representation of the user’s next behavior, which is used as the intent representation.

Self-supervised learning for sequential recommendation

In recent years, self-supervised learning (SSL) has attracted significant attention as a new learning paradigm, which generates supervised signals from a large amount of unlabeled data and has shown superior performance in various deep learning downstream tasks. The idea of applying SSL to SR problems is to maximize the consistency between specific auxiliary tasks while enhancing the discriminative ability between positive and negative pairs. S3-Rec³³ proposed an SSL-based SR model based on the principle of maximizing mutual information, utilizing intrinsic data correlations to obtain self-supervision signals, and enhancing data representation through pre-training methods. DSSRec³⁴ introduced a training strategy based on latent self-supervision and decoupled training. ICLRec¹⁹ incorporated intent variables into SR models using contrastive learning. CL4SRec³⁵ introduced contrastive learning and constructed data-augmented sequences from different perspectives to learn the embeddings of user and item sequences. IOCRec²⁰ proposed a framework that combines local and global intent to create high-quality intent signals by selecting the main intent of users. Although models based on contrastive learning SSL can alleviate data sparsity issues, they also amplify noise in the original data, leading to learning biased user intent and thereby reducing model performance.

Overall, existing research has not effectively addressed the issue of amplifying sequence noise through data augmentation. Additionally, prior studies only constructed implicit intent self-supervision signals from user-item interaction sequences, without considering the explicit intent reflected by the item category transition patterns. In contrast, our proposed EICD-Rec can utilize the Fourier transform to denoise from different frequency scales, and integrate user’s explicit intent with implicit intent for contrastive learning. Therefore, our EICD-Rec not only reduces the impact of noise but also takes into account the user’s explicit intent information, aiding in understanding the user’s true intent.

Methods

Problem statement

This section elaborates on the proposed model named EICD-Rec, detailing its architecture, and mechanisms. Table 1. summarizes the key symbols and their respective descriptions.

Table 1 Key notations and descriptions.

Assuming the dataset comprises a large number of users, items, and categories, denoted respectively by U, I, and O, where the numbers of users, items, and categories are represented as $\left| \text {U} \right|$, $\left| \text {I} \right|$, and $\left| \text {O} \right|$ $(\left| \text {O} \right| \ll \left| \text {I} \right| )$. For sequential recommendation involving user latent intent, each user $u \in U$ has a sequentially ordered interaction item sequence $S_{u} = [s_{1}^{u}, s_{2}^{u},...,s_{t}^{u},...,s_{n}^{u}]$ , where n is the length of the sequence, and $s_{t}^{u} = (i_{t}^{u},o_{t}^{u})$ represents the interaction information of user u at step t. For each item $i_{t}^{u}$, there is a corresponding category representation $o_{t}^{u}$.

Based on the above notation, the task of SR can be defined as follows: for a given user u, based on their interaction item sequence $S_{u}$, item set I, and category set O, predict the item that the user is most likely to interact with at the next time step, i.e., the (n+1)th step.

Model framework

The overall framework of the model we propose is illustrated in Fig. 2

Fig. 2

Overview of the proposed EICD-Rec.

First, we employ a dual-scale adaptive denoising mechanism to filter out noise signals from the sequence. The denoised sequence representations are then combined with the explicit intent representations learned from the item category sequences. Through the MLP of the sequence encoder, explicit intents are leveraged to enhance the model’s perception of the user’s true intents, resulting in a sequence representation that includes explicit intents.

Then, we construct a pure user implicit intent supervision signal. By using clustering learning and the sequence representations with explicit intent output by the sequence encoder with a denoising network, we obtain the purer representation of the user’s implicit intent. Extracting this implicit information serves as auxiliary information for sequence modeling, and contrastive learning is utilized to maximize the consistency between the sequence representation and its corresponding implicit intent.

Finally, predictions are made based on the output of the sequence encoder and item embeddings. Training and optimization are performed through a multi-task joint loss function.

Explicit intent enhanced encoder with denoising networks

Embedding layer

We utilize a pre-trained embedding model³⁶ to convert each historical interaction of a user into a vector representation. Specifically, given the interaction sequence $S_u$ for user u, which includes an item sequence $S_{u}^{i} = [i_{1}^{u}, i_{2}^{u},...,i_{t}^{u},...,i_{n}^{u}]$ and an item category sequence $S_{u}^{o} = [o_{1}^{u}, o_{2}^{u},...,o_{t}^{u},...,o_{n}^{u}]$. For item set I, an embedding table $E^{i} \in {\mathbb {R}}^{\left| I\right| \times d}$ is constructed from all items, where d is the dimension of the embedding vectors. Similarly, for the set of item categories, an embedding table $E^{o} \in {\mathbb {R}}^{\left| O\right| \times d}$ is constructed from all item categories.

Given the item sequence $S_{u}^{i}$ of length n and the item category sequence $S_{u}^{o}$ for user u, we obtain their low-dimensional vector representations $M^{i}$ and $M^{o}$, calculate them as follows:

$$\begin{aligned} M^i=Embedding^i(S_u^i)=\begin{bmatrix}e_1^i+p_1^i\\ e_2^i+p_2^i\\ ...\\ e_n^i+p_n^i\end{bmatrix} \end{aligned}$$

(1)

and

$$\begin{aligned} M^o=Embedding^o(S_u^o)=\begin{bmatrix}e_1^o+p_1^o\\ e_2^o+p_2^o\\ ...\\ e_n^o+p_n^o\end{bmatrix} \end{aligned}$$

(2)

where $e_{x}^{i} \in {\mathbb {R}}^{d}$ represents the embedding of item $i_{x}$, $e_{y}^{o} \in {\mathbb {R}}^{d}$ represents the embedding of item category $o_{y}$, $P^{i} \in {\mathbb {R}}^{n \times d}$ and $P^{o} \in {\mathbb {R}}^{n \times d}$ are the position embedding matrices respectively.

Denoising networks module

The item embedding matrix may likely contain noise that could impact the performance of SR models. In our denoising networks, to better capture useful information in the sequences and obtain sequence representations that more accurately reflect user interests, we introduce a dual-scale adaptive denoising networks module.

Fig. 3

The framework of the denoising networks module.

The framework of the denoising networks module is shown in Fig. 3.

The Fast Fourier Transform (FFT) effectively extracts periodic features by transforming time-domain signals into the frequency domain, a property that facilitates its application in scenarios such as spectral analysis and noise filtering³². Its denoising principle relies on the energy distribution characteristics of signals in the frequency domain. According to signal processing theory, user behavior sequences can be regarded as discrete signals in the temporal dimension. Consequently, FFT can be employed to convert behavioral sequence signals from the time domain to the frequency domain for global spectral analysis, while decomposing the embedding vectors of user behavior sequences into linear combinations of different frequency components. Subsequently, in the frequency domain space, we leverage the distinction between low-frequency and high-frequency signals to design two learnable filters based on threshold mechanisms for signal processing. The filtered signals are then reconstructed into time-domain signals through inverse FFT. This process preserves the characteristic phase and amplitude representing stable behavioral patterns in user embeddings while eliminating noise disturbances. As illustrated in Fig. 1, the user behavior sequence includes: treadmill, athletic socks, accidental click on an electronic product, sports water bottle, and running shoes. Through Fourier Transform, the low-frequency components highlight the coherent purchasing patterns in the sequence, while the high-frequency components mark the anomalous click on the electronic product.

Given the item representation matrix or item category representation matrix $F^{q} \in {\mathbb {R}}^{n \times d}$ for the q-th layer (when q=0, we set $F^{0} = M^{i}$ or $F^{0} = M^{o}$), we first perform fast Fourier transform:

$$\begin{aligned} X^q={\mathcal {F}}(F^q) \end{aligned}$$

(3)

where ${\mathcal {F}}(\cdot )$ represents one-dimensional Fast Fourier transform, and $X^{q}$ represents the transformed frequency domain signal. We employ dual-scale learnable filters to modulate the spectrum, dividing low-frequency signals $X_{l}$ and high-frequency signals $X_{h}$ in the frequency domain based on the median frequency and setting corresponding learnable filters:

$$\begin{aligned} & X_l^q=W_l\odot X^q\cdot \mathbbm{1}_{\{f\le f_{\textrm{median}}\}} \end{aligned}$$

(4)

$$\begin{aligned} & X_h^q=W_h\odot X^q\cdot \mathbbm{1}_{\{f> f_{\textrm{median}}\}} \end{aligned}$$

(5)

$$\begin{aligned} & {\widetilde{X}}^q=X_l^q+X_h^q \end{aligned}$$

(6)

where $W_l,W_h\in {\mathbb {C}}^{n\times d}$ are learnable filters, and $\odot$ represents element-wise multiplication, f denotes the frequency, and $\mathbbm{1}_{\{f\le f_{\textrm{median}}\}}$ represents an indicator function that selects signals with frequencies less than or equal to the median frequency. Since different SR models may correspond to different and complex data distributions and embedding matrix features, the most suitable filtering algorithm may also differ. Therefore, using learnable filters with the ability to handle complex signal patterns allows the model to adaptively learn the most appropriate filtering algorithm. Additionally, study³² have shown that low-frequency signals in the frequency domain typically contain more meaningful key information, such as primary trends and temporal correlations, while high-frequency signals tend to carry noise-related information and may potentially encompass some detailed features.We introduce two learnable filters optimized by stochastic gradient descent to handle these two parts respectively, thereby adaptively representing any filter in the frequency domain, influencing the output of the filter, and improving the model ability to extract useful signals.

For the information after denoising, we utilize the inverse fast Fourier transform to convert the modulated spectrum ${\widetilde{X}}^q$ back to the time domain. Following the inverse fast Fourier transform, we update the sequence representation through residual connections, layer normalization, and dropout operations to stabilize the network training process and alleviate the gradient vanishing problem:

$$\begin{aligned} & {\widetilde{F}}^q={\mathcal {F}}^{-1}({\widetilde{X}}^q)\in {\mathbb {R}}^{n\times d} \end{aligned}$$

(7)

$$\begin{aligned} & {\widetilde{F}}^q=Layernorm(F^q+Dropout({\widetilde{F}}^q)) \end{aligned}$$

(8)

where ${\mathcal {F}}^{-1}(\cdot )$ represents one-dimensional inverse fast Fourier transform.

Explicit intent enhanced encoder

Existing SR models typically treat users’ historical records as a single long sequence, aiming to extract implicit information from the data. However, they often overlook the fact that the transformation patterns of explicit features within the sequence, such as item categories, also reflect user intents. These neglected category transformation patterns in the sequence also contain valuable user intent information, which we refer to as explicit intent. For example, for a given user, if transitions from clothing (category 1) to shoes (category 2) frequently appear in their history, it indicates that after viewing clothing items, the user is likely to have an intent to purchase shoes. Their next action is likely to be related to shoe items. Such explicit intent signals embedded in item category transitions can significantly enhance the prediction of the user’s next interaction item.

Current mainstream sequence encoders typically employ deep neural networks incorporating attention mechanisms^12,13,14 to encode user behavior sequences, model sequence patterns, and predict users’ next behaviors. Inspired by the Transformer-based SR model¹², we define a sequence encoder $f_\theta (\cdot )$, but our sequence encoder does not employ the computationally expensive self-attention mechanism, we train and capture features of item representation vectors using a multilayer perceptron architecture to reduce model computational costs and improve training efficiency³⁷.

The sequence encoder $f_\theta (\cdot )$ encodes users’ historical interaction item sequences $S_{u}$ and outputs user interest representations $H_u=f_\theta ({S}_u)$ at all time steps, where $h_{t}^{u}$ represents user interest at time t. The objective of this paper is to find the optimal encoder parameters $\theta$ that maximize the log-likelihood function of the expected next item at all time steps of a given sequence:

$$\begin{aligned} \theta ^*=\underset{\theta }{{argmax}}\sum _{S_u\in S_N}\sum _{1\le t\le n}lnP_\theta (i_t^u,o_t^u) \end{aligned}$$

(9)

where $S_N$ represents the batch size of the input model. Specifically, the core of the sequence modeling module is a Feed Forward Neural Network (FFN). According to previous studies¹², as the network depth increases, the increase in model capacity exacerbates the problem of overfitting, and the stability of the training process significantly decreases due to factors such as gradient vanishing. In this case, residual connections³⁸ have been shown to effectively propagate low-level features to high levels, allowing the network to better utilize these useful features. Additionally, layer normalization plays a stabilizing and accelerating role in the training process of neural networks by normalizing across features, contributing to the stability of the network. To address the overfitting problem in deep neural networks, the dropout regularization technique has been widely applied and shown effectiveness in various neural network architectures³⁹. Therefore, we incorporate residual connections, layer normalization, and dropout operations to alleviate the issues of gradient vanishing and instability, representing the output of the sequence modeling module of the q-th layer:

$$\begin{aligned} & {\widetilde{F}}^q=FFN({\widetilde{F}}^q)=(GELU({\tilde{F}}^qW_1+b_1))W_2+b_2 \end{aligned}$$

(10)

$$\begin{aligned} & {\widetilde{F}}^q=Layernorm({\widetilde{F}}^q+Dropout({\widetilde{F}}^q)) \end{aligned}$$

(11)

where $GELU(\cdot )$ is the activation function, $W_{1}$ and $W_{2}$ are trainable parameter matrices, and $b_{1}$ and $b_{2}$ are trainable bias vectors. We model both the item sequence and the item category sequence separately. Given the item embedding $F^{i}$ and the category feature embedding $F^{o}$, our encoder outputs $R^{i} \in {\mathbb {R}}^{n \times d}$ and $R^{o} \in {\mathbb {R}}^{n \times d}$ as representations of the item sequence and the explicit intent sequence, respectively. Considering that the current item sequence output $R^{i}$ mainly focuses on the most recent items, to incorporate long-term preferences and obtain prior knowledge from the explicit intent of uncommon items, we combine $R^{i}$ and $R^{o}$ to obtain the final representation $R^{S} \in {\mathbb {R}}^{n \times d}$:

$$\begin{aligned} R^S=R^i+R^o \end{aligned}$$

(12)

Then, we simultaneously use $R^{o}$ and $R^{i}$ to calculate the correlation $r_{j,t}^{o}$ and $r_{k,t}^{i}$ with the original embeddings at step t:

$$\begin{aligned} r_{j,t}^o=R_t^oE_j^{o^T},r_{k,t}^i=R_t^iE_k^{i^T} \end{aligned}$$

(13)

where $E_j^o,E_k^i\in {\mathbb {R}}^d$ respectively represent the embeddings of the j-th explicit intent and the k-th item in $E^{o}$ and $E^{i}$. Unlike previous SR models that only predict the next item based on historical items, the distinctiveness of our sequence encoder module lies in predicting by maximizing the joint probability distribution between previous items and explicit intents:

$$\begin{aligned} P(o_j,i_k|S_u^o,S_u^i,\Theta )=P(o_j|S_u^o,\Theta )P(i_k|o_j,S_u^o,S_u^i,\Theta )=\sigma (r_{j,t}^o)\sigma (r_{k,t}^i) \end{aligned}$$

(14)

where $\sigma (\cdot )$ is the sigmoid function, $\Theta$ represents the parameter set of the sequence encoder, $S_{u}^{o}$ and $S_{u}^{i}$ are the user’s explicit intent sequence and item sequence, respectively. We train using binary cross-entropy loss:

$$\begin{aligned} \begin{aligned}{\mathcal {L}}_{EDN}&={\mathcal {L}}_i+{\mathcal {L}}_o=-\sum _{S_u\in {S_N}}\sum _{1\le t\le n}\left[ log\left( \sigma \left( r_{y^i,t}^i\right) \right) +\sum _{i_k\notin {S}_u}log\left( 1-\sigma (r_{i_k,t}^i)\right) \right] \\ &-\sum _{S_u\in {S_N}}\sum _{1\le t\le n}\left[ log\left( \sigma (r_{y^o,t}^o)\right) +\sum _{o_i\notin {S}_u}log\left( 1-\sigma \left( r_{o_j,t}^o\right) \right) \right] \end{aligned} \end{aligned}$$

(15)

where $\sigma (\cdot )$ represents the sigmoid function. To train the model and maximize the log-likelihood function, we employ sampled softmax, as described in strategies^12,19, to sample a negative item at each time step of every sequence, allowing it to be compared with the positive item.

Pure intent contrastive learning

In addition to user-item interactions and item categories, user interests may also be influenced by latent factors¹⁹. These latent factors implicit in user behavior sequences can be regarded as the user’s implicit intent. Although some CL-based recommendation models^19,20 in recent years have been able to alleviate data sparsity issues and effectively utilize users’ implicit intent, they also amplify the deteriorating effect of sequence noise on the representation of user implicit intent. In our model, by combining the encoder with denoising network modules and explicit intent enhancement modules, we can effectively address this issue, enabling the model to learn more accurate representations of user implicit intent.Specifically, for the user intention information contained in the feature transition patterns of items, this paper terms it as “Explicit Intent”, such as the category attribute transition patterns utilized in this study. For instance, if a user behavior sequence contains multiple records like “steak (food category), black pepper (seasoning category), frying pan (kitchenware category)”, it indicates that after viewing food and seasoning items, the user likely exhibits an intention to purchase kitchenware. The subsequent interaction may potentially relate to kitchenware category items. Such explicit intentional signals embedded in category transitions significantly contribute to the learning of intention representations.

We denote by C the implicit intent set implied in the user behavior sequence $S_{u}$, assuming $S_{u}$ reflects Z implicit intents $\{c_i\}_{i=1}^Z$. Then, the optimization objective function for the interaction between a user and a certain item can be expressed as follows:

$$\begin{aligned} \theta ^*=\underset{\theta }{{argmax}}\sum _{S_u\in S_N}\sum _{1\le t\le n}ln{\mathbb {E}}_{(c)}[P_\theta (i_t^u,o_t^u,c_i)] \end{aligned}$$

(16)

Since the variables $\theta$ and implicit intent $c_{i}$ are both missing values, we follow strategy¹⁹, we construct a lower bound for the maximization of the expression Eq. (16) using the Expectation-Maximization (EM) algorithm. We assume the implicit intent follows the distribution Q(C), and $\sum \nolimits _{i=1}^{Z}Q(c_{i})=1 \& Q(c_{i})>0$, then the Eq. (16) can be constructed as the objective function of the lower bound function:

$$\begin{aligned} \sum _{S_u\in S_N}\sum _{1\le t\le n}ln{\mathbb {E}}_{(c)}[P_\theta (i_t^u,o_t^u,c_i)]=\sum _{S_u\in S}\sum _{1\le t\le n}ln\sum _{1\le i\le Z}Q(c_i)\frac{P_\theta (i_t^u,o_t^u,c_i)}{Q(c_i)} \end{aligned}$$

(17)

According to Jensen’s inequality and to reduce the complexity of the loss function calculation, we only consider the lower bound of each final step (i.e., the t-th step). Thus, the definition can be obtained as follows:

$$\begin{aligned} \sum _{S_u\in S_N}\sum _{1\le i\le Z}Q(c_i)\cdot lnP_\theta (S_u,c_i) \end{aligned}$$

(18)

In the above formula, $Q(c_i)$ and $P_\theta (S_u,c_i)$ are unknown. To learn the distribution of the user’s implicit intent Q(C), we utilize our proposed sequence encoder $f_\theta (\cdot )$ to encode all interaction sequences $\{S_u\}_{u=1}^{|U|}$. Through explicit intent enhancement and denoising networks module, it can output purer representations, which aids in extracting users’ true intents. Subsequently, K-means clustering operations are performed on the output representations $\{h_u\}_{u=1}^{|U|}$, resulting in ${Q}(c_i)=P_\theta (c_i|S_u)$:

$$\begin{aligned} Q(c_i)=P_\theta (c_i|S_u)={\left\{ \begin{array}{ll}1,& if \ S_u \ in\ cluster \ i\\ 0,& else.\end{array}\right. } \end{aligned}$$

(19)

Then, we employ the average pooling method to compute the mean of the representations in each cluster, obtaining the cluster centers as representations of the implicit intent $c_{i}$. After obtaining the distribution of implicit intent Q(C), to maximize the lower bound, it is necessary to calculate $P_\theta (S_u,c_i)$. We define its calculation formula as follows:

$$\begin{aligned} P_\theta (S_u,c_i)=P_\theta (c_i)P_\theta (S_u|c_i)\propto \frac{1}{Z}\cdot \frac{exp(h_u\cdot c_i)}{\sum _{j=1}^Zexp(h_u\cdot c_j)} \end{aligned}$$

(20)

where $h_{u}$ represents the vector representation of the sequence $S_{u}$. Maximizing equation (18) is equivalent to minimizing formula equation (21), which aims to maximize the mutual information between a behavior sequence and its corresponding latent intent (the MIM principle):

$$\begin{aligned} -\sum _{v=1}^Vlog\frac{exp(sim(h_u,c_i))}{\sum _{j=1}^Zexp(sim(h_u,c_j))} \end{aligned}$$

(21)

where, $sim(\cdot )$ represents the inner product. Following the principle of contrastive self-supervised learning, for each batch size of training sequences, we create two positive views, ${\tilde{h}}_1^u$ and ${\tilde{h}}_2^u$, use mainstream data augmentations^19,33 such as crop, mask, and reorder. To address the issue of false-negative samples, where different users’ identical intents are treated as negative samples, we follow the approach proposed by¹⁹ to mitigate this problem without contrastive operations, defining the loss function as follows:

$$\begin{aligned} & {\mathcal {L}}_{PICL}={\mathcal {L}}_{PICL}({\tilde{h}}_1^u,c_u)+{\mathcal {L}}_{PICL}({\tilde{h}}_2^u,c_u) \end{aligned}$$

(22)

$$\begin{aligned} & {\mathcal {L}}_{PICL}({\tilde{h}}_1^u,c_u)=-log\frac{exp(sim({\tilde{h}}_1^u,c_u))}{\sum _{v=1}^V\mathbbm {1}_{v \notin {\mathscr {C}}}exp(sim({\tilde{h}}_1^u,c_v))} \end{aligned}$$

(23)

$$\begin{aligned} & {\mathcal {L}}_{PICL}({\tilde{h}}_2^u,c_u)=-log\frac{exp(sim({\tilde{h}}_2^u,c_u))}{\sum _{v=1}^V\mathbbm {1}_{v \notin {\mathscr {C}}}exp(sim({\tilde{h}}_2^u,c_v))} \end{aligned}$$

(24)

where $c_{u}$ represents the vector representation of the implicit intent $c_{i}$, and ${\mathscr {C}}$ denotes the set of users who share the same intent as u, and $c_{v}$ is the vector representation of an implicit intent not in ${\mathscr {C}}$. Consequently, during the iterative execution of the EM-Step, both the intent distribution Q(C) and the model parameters $\theta$ will be continuously updated.

In addition to maximizing the mutual information between sequences and implicit intents as mentioned above, it is also necessary to consider the correlation between two sequences and maximize mutual information in contrastive learning. We define views within the same sequence as positive pairs, while views from different sequences are considered negative pairs. After encoding the behavior sequences under positive views to obtain their representations ${\tilde{h}}_1^u$ and ${\tilde{h}}_2^u$, we construct the loss function based on the principles of the InfoNCE⁴⁰ algorithm:

$$\begin{aligned} & {\mathcal {L}}_{Seq}={\mathcal {L}}_{Seq}({\tilde{h}}_1^u,{\tilde{h}}_2^u)+{\mathcal {L}}_{Seq}({\tilde{h}}_2^u,{\tilde{h}}_1^u) \end{aligned}$$

(25)

$$\begin{aligned} & {\mathcal {L}}_{Seq}({\tilde{h}}_1^u,{\tilde{h}}_2^u)=-log\frac{exp(sim({\tilde{h}}_1^u,{\tilde{h}}_2^u))}{\sum _{neg}exp(sim({\tilde{h}}_1^u,{\tilde{h}}_{neg}))} \end{aligned}$$

(26)

where ${\tilde{h}}_{neg}$ represents the sequence representation generated under negative views.

Prediction layer

In sequential recommendation, predicting the next item relies on the contextual information of the entire item set. In the final layer of EICD-Rec, we calculate the interest score of user u for item i at step (t+1) based on the user’s historical interaction sequence:

$$\begin{aligned} P(i_{t+1}=i|i_{1:t})=a_i^\textrm{T}h_t^u \end{aligned}$$

(27)

where $a_{i}$ represents the vector representation of item i, and $h_{t}^{u}$ denotes the output of the sequence encoder $f_\theta (\cdot )$ at step t, serving as the user’s intent representation. We train and optimize the model parameters using a multi-task joint loss function:

$$\begin{aligned} {\mathcal {L}}={\mathcal {L}}_{EDN}+\lambda _1\cdot {\mathcal {L}}_{PICL}+\lambda _2\cdot {\mathcal {L}}_{Seq} \end{aligned}$$

(28)

where parameters $\lambda _{1}$ and $\lambda _{2}$ respectively control the strength of the sequence-to-intent SSL task and the sequence-to-sequence SSL task.

Experiments and analysis

In this section, we will present the specific experimental settings, compare our proposed recommendation model EICD-Rec with several state-of-the-art methods on three real datasets, and evaluate its performance. We first describe the datasets, baseline methods, evaluation metrics, and implementation details used in the experiments, and then analyze the experimental results. Additionally, we explore the impact of noise ratio and hyperparameters on the model effectiveness.

Datasets

To evaluate the effectiveness of our proposed EICD-Rec model, we conduct experiments on three available real-world public datasets: Toys, Sports, and Beauty. They are from the three subcategory datasets of the Amazon dataset in study⁴¹, which contain user review actions on the items.

For all datasets, we follow the same preprocessing procedure¹⁹ to first filter out inactive users to improve data quality, ensuring that each user in the data used for training has interacted with at least five items. We then group the interactions by the user and sort them by timestamp. In the experiments, we split the training and test sets at an 8:2 ratio, using four historical interactions for training and one historical interaction for testing. The detailed statistics of the three datasets are shown in Table 2.

Table 2 Statistics of datasets.

Evaluation metrics

To evaluate the performance, we employ two commonly used evaluation metrics:Hit Ratio @k (HR@k)and Normalized Discounted Cumulative Gain @k (NDCG@k), where $k \in {5,20}$ represents the top-k items in the candidate set. While HR@k focuses on assessing the proportion of correctly predicted samples in the ground truth, NDCG@k considers the ranking of items in the recommendation results. The higher the predicted items are ranked within the candidate set, the higher the score they receive in NDCG@k.

Baseline methods

We compare our proposed method EICD-Rec with a series of state-of-the-art baselines, including the Non-sequential SR method, NN-based SR methods, SSL-based SR methods, and Intent-based SR methods, which are listed as follows:

Non-sequential method

• BPR-MF⁴²: It represents the interaction between users and items as a sparse matrix, then decomposes this matrix into two low-dimensional matrices through matrix factorization algorithms, optimizing the model by maximizing the accuracy of recommendation result ranking.

NN-based SR methods

• GRU4Rec⁸: A SR model based on RNN, using Gated Recurrent Unit (GRU) to capture long-term dependencies in behavioral sequences.

• Caser⁶: It adopts CNN-based sequence embedding techniques, applying convolution to extract sequential patterns from short-term sequences.

• SASRec¹²: Pioneering the use of self-attention mechanism to model user’s historical behavior information, thereby capturing dependencies between items in the sequence, and widely applied.

• BERT4Rec¹³: It uses bidirectional self-attention encoder representation from the BERT architecture to generate a series of hidden states to capture context and dependencies between items in the sequence.

SSL-based SR methods

• S3-Rec³³: It proposes a self-supervised learning method for sequential recommendation, encouraging the model to identify meaningful patterns in the data by maximizing the mutual information between input sequences and output predictions.

• DSSRec³⁴: It utilizes the idea of Disentangled Self-Supervision (DSS) and proposes a seq2seq training method to learn representations of separate input data, allowing the model to understand finer patterns in user consumption history.

• CL4SRec³⁵: The model introduces random data augmentation techniques to sequential recommendation and employs contrastive learning to learn user embeddings, alleviating data sparsity issues.

• CoSeRec⁴³: Building upon CL4SRec, it designs two superior data augmentation operators, insertion, and replacement, based on item correlations.

Intent-based SR methods

• ICLRec¹⁹: A SR model utilizing intent contrastive learning, distinguishing different user-item interaction pairs through training, even if users interact with items in different contexts but have similar latent intents, the model attempts to identify these users’ intents as similar.

• IOCRec²⁰: Also a SR model based on intent contrastive learning, proposing a framework for extracting primary and local intents to address the denoising problem in SR tasks.

Parameter settings

For our eleven baseline methods, all parameters are set according to the recommendations provided by their respective authors. Among them, Caser, BERT4Rec, S³-Rec, CoSeRec, ICLRec, and IOCRec are implemented using the source code provided by their authors, while BPR, SASRec, GRU4Rec, DSSRec, and CL4SRec are implemented based on publicly available resources.

Our method is implemented based on PyTorch. We set the number of layers in the learnable filtering network to 2, the maximum sequence length n to 50, the embedding size to 128, the batch size to 256, and the number of implicit intents Z to be within the range of {64, 128, ..., 2048}. Parameters $\lambda _{1}$ and $\lambda _{2}$ are varied within the range of {0.1, 0.2, ..., 0.6}. Our model uses the Adam optimizer⁴⁴ with a learning rate of 0.001, a dropout rate of 0.5, $\beta _{1}$ = 0.9, and $\beta _{2}$ = 0.999. We conduct an evaluation whenever there is an improvement in the model performance. If the NDCG@10 metric does not improve within 40 evaluations, the experiment is terminated early. All experiments are performed on a server with Intel(R) Xeon(R) Silver 4210 $\times$ 4 CPU, NVIDIA GTX 3090(24GB) GPU, and 256GB memory.

Performance comparison

To demonstrate the overall performance of our proposed model, we compare it with several state-of-the-art recommendation methods. The experimental results are shown in Table 3, where the best results are indicated in bold, the second-best results are underscored, and the last row show the relative improvements compared to the best baseline results. We have the following observations:

• (1) Generally, non-sequential methods like BPR perform worse than NN-based SR models. This is because they cannot effectively utilize the temporal order information in user behavior sequences, indicating the importance of capturing sequential patterns in constructing recommendation models.

• (2) For NN-based SR models, we find that SASRec and BERT4Rec, which use encoders based on self-attention mechanisms, outperform models without attention mechanisms like Caser (CNN-based model) and GRU4Rec (RNN-based model). This demonstrates the effectiveness of self-attention mechanisms in capturing sequential patterns.

• (3) For SSL-based SR models, we find that although S3-Rec introduces SSL to gain enhanced signals, its performance is worse than models based on attention mechanisms. This is because it uses a two-stage training strategy and requires sequences to provide sufficiently long contextual information, leading to decreased performance when facing datasets with mostly short sequences. DSSRec, by decoupling operations when selecting training samples for seq2seq and performing self-supervision in the latent space to promote convergence, achieves better performance than BERT4Rec on some datasets (e.g., Toys). CL4SRec and CoSeRec, by introducing contrastive learning and data augmentation, outperform models based on attention mechanisms overall, proving the superiority of introducing contrastive learning to enhance sequential representations.

• (4) For Intent-based SR models, we find that ICLRec and IOCRec, by introducing intent-level representation learning modules and contrastive SSL modules to enhance SR tasks, outperform most self-supervised SR models except for CoSeRec. In some cases, they are less effective than CoSeRec (e.g., NDCG@k in the Sports dataset), possibly due to the amplification of noise signals present in the original sequences by random data augmentation, resulting in decreased performance.

• (5) Finally, our proposed EICD-Rec can adaptively filter noise information at different frequency scales and model category features to explore the transformation information between explicit user intent and item categories, helping to obtain high-quality representations of the user’s true intent. By comparing our proposed method with all baseline methods, EICD-Rec outperforms other methods in most cases, demonstrating the effectiveness of EICD-Rec.

Table 3 Performance comparisons of different methods.

Ablation study

To thoroughly validate the effectiveness of each component of the model, we conducted ablation experiments on EICD-Rec and several variants. The experimental results are shown in Table 4, where (A) represents the complete version of our proposed EICD-Rec, (B) represents removing the denoising networks, (C) represents removing the explicit intent enhancement module obtained by modeling category features, and (D) represents removing the contrastive learning enhancement module for intent and sequences.

Table 4 The HR@20 and NDCG@20 performances achieved by EICD-Rec variants on three datasets.

According to the results of the ablation experiments, we found that our proposed EICD-Rec achieved the best performance on all datasets, indicating the effectiveness of each component of our model. Comparing the results between (A) and (B), our noise filtering network adaptively filters noise information at different frequency scales, aiding the model in learning representations of users’ true intent. Comparing the results between (A) and (C), modeling category feature information to obtain explicit intent representations of users can effectively improve the model accuracy. Comparing the results between (A) and (D), utilizing intent representation learning for contrastive SSL enhancement can significantly enhance the model performance.

Influence of the number of implicit intents

To explore the impact of the hyperparameter Z (i.e., the number of user implicit intents), we conducted experiments on Beauty and Toys datasets. Figure 4 shows the influence of different numbers of user implicit intents on model performance.

A larger number of implicit intent categories implies that users have more distinct intents. As shown in Fig. 4, taking the results on the Beauty dataset as an example, while keeping other parameters fixed, we can see that when Z increases to 2048, the EICD-Rec model achieves the best performance. This may be because when Z is very small, the number of users under each intent prototype could be large, causing the differences between users to become blurred. Consequently, it would introduce false negatives to the contrastive self-supervised learning task, where users with different intents are mistakenly treated as having the same intent, potentially leading to information loss in item representation learning and affecting the accuracy of recommendations. However, we found that for the Toys dataset, the EICD-Rec model achieves the best performance when Z increases to 512, and the performance starts to decline as Z further increases. This may be because when Z is too large, the number of data samples in each intent category could decrease, increasing data sparsity and adversely affecting model training. In the Beauty dataset, 2048 user implicit intent categories best cover the different behaviors of users, while in the Toys dataset, 512 user implicit intent categories best cover the different behaviors of users.

Fig. 4

The impact of different numbers of implicit intents Z.

In summary, excessively high or low numbers of implicit intent categories would affect the quality of item representation learning and the accuracy of recommendations. Therefore, when dividing implicit intent categories, an appropriate number of categories should be chosen to fully capture the differences between user behaviors.

Influence of implicit intent contrastive learning strength

We also conducted experiments on the influence of the contrastive learning strength $\lambda _{1}$ of implicit intents on Beauty and Toys datasets. Figure 5 illustrates the impact of different strengths of user implicit intent contrastive learning on model performance. We observed that as $\lambda _{1}$ increases, the model’s performance improves on both the Beauty and Toys datasets, indicating that introducing appropriate weights can enhance recommendation performance, thus demonstrating the effectiveness of EICD-Rec. The model $\lambda _{1}=0.2$ performance peaks when and then begins to deteriorate, possibly because excessively high implicit intent contrastive learning strength leads the model to overly rely on certain specific samples, thus affecting its generalization ability.

Fig. 5

The impact of implicit intent contrastive learning strength $\lambda _{1}$.

Noise robustness analysis

We conducted noise robustness experiments on the ICLRec model and EICD-Rec model across the three datasets to validate the stability of our proposed method against noise interference during the testing phase. Specifically, we randomly added a certain proportion (i.e., 5%, 10%, 15%, 20%) of negative items to the original sequences. From the Fig. 6, we can observe that as the ratio of added noise data increases, the performance of both models declines to a certain extent. This demonstrates the significant negative impact of noise data on recommendation effectiveness. However, the performance degradation rate of our proposed EICD-Rec model is lower than that of the ICLRec model in most cases, especially after adding 20% noise data, where the performance of the ICLRec model drops sharply while our proposed model still exhibits relatively good performance. This indicates that our dual-scale learnable filters can effectively filter out noise information, improving the model’s anti-interference ability. Moreover, from the Fig. 6, we can see that on the Toys, Sports and Beauty datasets, the performance of the EICD-Rec model with a 15% noise ratio is still better than that of the ICLRec model without noise data. This may be due to the introduction of category feature modeling of explicit user intent representations, which enhances the mutual information modeling between sequences and intents, enabling the model to learn more effective behavior feature semantics.

Fig. 6

The impact of noise ratio on model performance.

Conclusion

In this paper, we address the issue of noise amplification in users’ original interaction sequences caused by data augmentation and propose a novel CL-based SR model, EICD-Rec. First, we design a denoising network based on dual-scale adaptivity to denoise the data, enabling the acquisition of purer sequence and intent representations. At the same time, we explore the modeling of explicit intents embedded in item category transition patterns. By combining explicit and implicit intents, we construct high-quality self-supervised signals to more accurately represent users’ true intents. This approach not only enhances the model’s perception of category transition patterns but also mitigates the bias introduced by noise in sequence representations, thereby improving the performance of the intent contrastive learning task. Extensive experiments validate the effectiveness of EICD-Rec. In the future, we plan to analyze multiple types of user behaviors and improve the performance of SR models by modeling intents in user multi-behavior sequences.