Fault detection for Li-ion batteries of electric vehicles with feature-augmented attentional autoencoder

Abstract

The attainment of fault detection within battery packs is of paramount importance in ensuring the safe and reliable operation of electric vehicles. However, in the early stages of battery failure, its manifestations are often not obvious, making it difficult for conventional algorithms to detect them in time. Thus, this paper proposes a novel fault detection framework for battery packs to reduce detection time and eliminate false alarms. This framework employs a feature-augmented autoencoder that can effectively utilize the early-stage features for fault detection. The commonly used autoencoder is improved by applying a memory module to amplify the fault features between normal and abnormal cells and employing a similarity loss function to enhance the similarity of features for normal batteries. Then, the augmented features are input into the local outlier factor algorithm for battery fault detection. Real operational data from electric vehicles are used to train and test the autoencoder, covering the battery voltages, current, and temperature data. The results show that the proposed strategy can detect battery faults at most 10 hours earlier, and pinpoint the faulty battery without false alarms when compared to the existing methods.

Introduction

As the world increasingly seeks sustainable energy solutions to combat climate change, the development of efficient, high-capacity, and long-lasting battery technologies has become crucial for the automotive industry¹. Lithium-ion batteries, with their superior energy density, long cycle life, and low self-discharge rate, have emerged as the ideal choice for powering electric vehicles^2,3. However, due to abusive operations and complex working conditions, the performance of electric vehicles can be significantly impaired, leading to internal/external short circuits and even thermal runaway in on-board energy storage systems^4,5, potentially posing a serious threat to the safety of drivers⁶. Therefore, it is necessary to develop effective fault detection algorithms to identify battery anomalies at an early stage.

Over the past few years, numerous studies have been conducted on fault detection algorithm design, which can be roughly classified into model-based methods and data-driven methods⁷. Model-based methods detect anomalies by comparing the actual behavior of the battery with the behavior depicted by established electrochemical models or equivalent circuit models⁸. For example, a two-step equivalent circuit model was established to describe the process of external short-circuit faults⁹. Based on this model, an online fault detection scheme was developed. Ma et al.¹⁰ proposed a dual-Kalman filter detection method by analyzing the characteristics of external short-circuit faults in a series-connected battery pack. Considering the battery temperature as an indicator, an electro-thermal coupling model was established to predict the thermal and electrical properties of batteries under external short-circuit conditions¹¹. Yu et al.¹² proposed a fault detection method based on the voltage as input and current as output(VICO) to detect current sensor faults.

However, the main limitations of model-based methods lie in their reliance on the accuracy of the established models, which require time-consuming parameter validation and resource-intensive non-linear equation formulation¹³. Due to varying operating conditions and aging effects, the parameters and characteristics of the battery can change over time, leading to reduced accuracy and reliability in fault detection.

Data-driven methods treat the battery as a black box and analyze its behavior using information theory, expert prior knowledge, and machine learning techniques^14,15,16. Information-theoretic approaches quantify the degree of disorder in a time series through entropy and set a threshold to detect battery faults¹⁷. For instance, an enhanced multiscale entropy algorithm¹⁸ was introduced to identify the multiscale characteristics of pre-accident fault signals, thereby determining the fault level. By incorporating information fusion theory, a cost-effective battery diagnosis method¹⁹ was proposed for the early detection of minor faults. The proposed method combined three baseline anomaly detection methods to adjust the threshold adaptively, which can achieve high-precision and low-cost battery diagnosis.

Some studies leverage expert prior knowledge to design battery fault detection methods. Huang et al.²⁰ proposed an optimized data-driven method that incorporates the prior knowledge of battery degradation to estimate the long-term state of health of batteries. Additionally, Wang et al.²¹ presented an expert knowledge integration network that combines features from collected data and expert knowledge to enhance anomaly detection. Some studies further employ machine learning and deep learning methods to detect battery anomalies. For instance, a partitioned all-season coverage model that utilizes a spiral self-attention neural network was proposed to predict the real-time temperature of battery systems²². Moreover, Li et al.²³ combined a long short-term memory network with a convolutional neural network to train an abnormal heat generation model for predicting battery thermal runaway.

Although existed data-driven methods can detect battery anomalies, their performance is highly reliant on the quality of the collected dataset. In practical energy management systems, the collected data inevitably contains noise, which can lead to poor model generalization and unreliable fault detection, resulting in false negatives or false positives²⁴. Additionally, battery faults often have a minor impact on the battery management system’s performance (such as the voltage of the battery management system) when they first occur, but their detrimental effects can significantly escalate over time. Detecting battery faults at an early stage could strongly enhance the system’s safety, which requires the designed anomaly detection method to be sensitive to minor battery faults. Therefore, designing a noise-resistant and anomaly-sensitive fault detection method remains an open issue.

Recently, autoencoders (AEs) have gained significant attention in the field of anomaly detection due to their data reconstruction abilities^25,26. By encoding the input data into a lower-dimensional space and then reconstructing it, AEs can capture the essential features and patterns of normal data, even in high noise levels or poor dataset quality cases. Inspired by AE structure, a novel anomaly-sensitive memory-augmented autoencoder framework is designed in this paper to detect battery faults. The designed framework contains a self-attention AE module, a memory-augment module, and a local outlier factor module. Firstly, the AE module utilizes a multi-head attention mechanism to extract important features and refine them into a low-dimensional space. Subsequently, the refined features are passed through a feature-augmented memory module, which amplifies the differences between normal and anomalous battery features, and then these augmented features are used as input to the decoder for feature reconstruction. Finally, the reconstructed features are analyzed using the Local Outlier Factor (LOF) algorithm to identify which cells in the battery pack are at fault.

In summary, the main contributions of this paper are summarized as follows:

• 1. A novel attention-based autoencoder is proposed in this paper. By leveraging the attention mechanism to filter out irrelevant information and refine important features, the designed method can effectively reduce the false positive rate of anomaly detection algorithms.

• 2. A feature-augmented memory module is designed to enhance the detection sensitivity to minor battery faults. By employing feature similarity calculations and the local outlier factor algorithm, the designed detection method can quickly detect the faults at an early stage and locate the faulty cell in the battery pack.

• 3. Real operational data from electric vehicles, encompassing six months of data from a total of 480 electric vehicle battery cells, are utilized to verify the superiority of the proposed fault detection method. Compared to existing methods, the proposed method can detect battery anomalies 10 hours earlier without false alarms.

This paper is organized as follows: Section 2 introduces the fault detection framework. Section 3 presents the dataset and the training process of the proposed framework. The experiment setup and results are discussed in Section 4, and Section 5 concludes this paper.

Proposed fault detection framework

Fault detection framework overview

Fig. 1

Normal electric vehicle data is used to train the feature-augmented autoencoder. The trained model is used to extract features and the features are fed into the LOF algorithm for further fault detection.

We aim to improve the early detection of battery faults while reducing false alarms. As mentioned before, the key advantage of AEs is their unsupervised learning nature, which allows AEs to be trained on unlabeled datasets, making them particularly useful in poor data quality or scarce anomaly data cases. To fully leverage the advantages of autoencoders, a feature memory-augmented fault detection framework is proposed in this paper.

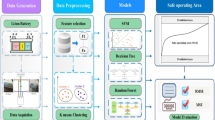
As shown in Fig. 1. The proposed framework comprises three core components: an attention-based autoencoder, a feature-augmented memory module, and a LOF fault detection module. The attention-based autoencoder filters out irrelevant information and extracts critical features from the input data. The feature-augmented memory module then amplifies the differences between normal and anomalous features, enhancing the sensitivity to minor faults. Finally, the LOF module applies the local outlier factor algorithm to identify and localize faulty cells within the battery pack based on the processed features.

In the following section, we will provide a detailed introduction to the core modules of the proposed fault detection framework.

Feature-augmented autoencoder of battery data

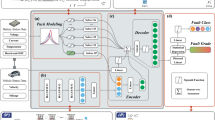
The basic autoencoder is a self-supervised learning neural network architecture consisting of an encoder and a decoder²⁷. The encoder compresses the high-dimensional original input into a low-dimensional hidden variable, and the decoder is responsible for reducing the encoder-compressed hidden variable to the original input. In this paper, a memory-augmented module is embedded between the encoder and decoder to amplify the differences between normal and anomalous battery features. The structure of the feature-augmented autoencoder is shown in Fig. 2.

The proposed attention-based autoencoder comprises an encoder, a decoder, and a memory-augmented module. Among these components, the encoder and decoder are constructed from two networks with identical architectures, as shown in Fig. 2.

In this paper the transformer encoder structure²⁸ is used to capture long-range dependencies in input data. The input data to the encoder comprises the features of a single battery cell from an electric vehicle over a past time window size $W_h$ denoted as

$$\begin{aligned} X^{i}_{\left[ t-W_h,t\right] } = \left[ x_{t-W_h}^{i},x_{t-W_h+1}^{i},\dots ,x_{t}^{i}\right] \end{aligned}$$

(1)

where $X^{i}_{[t-W_h,t]}$ denotes the features of battery cell i from time $t-W_h$ to time t, and $W_h$ is the sliding window size. For the features $x_t^i$ of battery cell i at time t, these include the cell’s voltage, current, state of charge (SoC), and temperature, which are represented as

$$\begin{aligned} x_{t}^{i} = (\hat{V}_{t}^{i}, I_{t}^{i}, \text {SoC}_{t}^{i}, \theta _{t}^{i}) \end{aligned}$$

(2)

where $\hat{V}_{t}^{i}$ represents the estimated voltage, $I_{t}^{i}$ the current, $\text {SoC}_{t}^{i}$ the state of charge, and $\theta _{t}^{i}$ the temperature of battery cell i at time t.

Fig. 2

The overall structure of the attention-based autoencoder, consists of an encoder, a decoder, and a memory-augmented module.

To extract hidden dependencies from battery features for fault detection, the encoder takes the battery cell’s features $X^{i}_{\left[ t-W_h,t\right] }$ as input data to refine and extract the hidden dependencies of battery features.

Due to the lack of convolutional and recursive structures, positional coding needs to be introduced to compute the positional information of the raw data. The positional encoding (PE) is computed as follows

$$\begin{aligned} & \operatorname {PE}_{(\textrm{pos}, 2 d)} =\sin \left( \textrm{pos} / 10000^{2 d / d_{\text{ model } }}\right) \end{aligned}$$

(3)

$$\begin{aligned} & \operatorname {PE}_{(\textrm{pos}, 2 d+1)} =\cos \left( \textrm{pos} / 10000^{2 d / d_{\text{ model } }}\right) \end{aligned}$$

(4)

where $\textrm{pos}$ represents the position of the data, d represents the dimension of the data, and $d_{\text{ model } }$ represents the total dimension after embedding.

In the proposed attention-based autoencoder, the input data $X^{i}_{[t-W_h,t]}$ first passes through a linear layer followed by positional encoding before being fed into the attention layer, which can be expressed as follows

$$\begin{aligned} X^{i}_{\text {att}\_\text {in}} = \left( \mathbf {W_1} X^{i}_{[t-W_h,t]} + \mathbf {b_1} \right) + \operatorname {PE} \end{aligned}$$

(5)

where $\mathbf {W_1}$ and $\mathbf {b_1}$ are the training weight and bias of the first linear layer. Subsequently, $X^{i}_{\text {att}\_\text {in}}$ will be the input of the attention layer to refine hidden dependencies.

In the proposed attention-based autoencoder, the attention mechanism is adopted to capture long-range dependencies in battery cell sequences better. For each head of attention calculation, the input vector $X^{i}_{\text {att}\_\text {in}}$ will be transformed into three different matrices represented as $\textbf{Q} = {\textbf{W}_q}X^{i}_{\text {att}\_\text {in}}$, $\textbf{K} = {\textbf{W}_k}X^{i}_{\text {att}\_\text {in}}$, and $\textbf{V} = {\textbf{W}_v}X^{i}_{\text {att}\_\text {in}}$ by multiplying three trainable weight matrices $\textbf{W}_q$, $\textbf{W}_k$, and $\textbf{W}_v$. Then the attention is calculated as

$$\begin{aligned} \operatorname {Attention}(\textbf{Q},\textbf{K},\textbf{V})=\operatorname {Softmax}\left( \frac{\textbf{Q}\textbf{K}^{T}}{\root \of {d_{K}}}\right) \textbf{V} \end{aligned}$$

(6)

where the $d_k$ is the dimension of $\textbf{K}$. Given the need to independently compute attention values for different battery features such as voltage, current, SOC, and temperature, the multi-head attention function is utilized for feature fusion, which can be represented as

$$\begin{aligned} \begin{aligned} \operatorname {MultiHead}(\textbf{Q}, \textbf{K}, \textbf{V})&=\operatorname {Concat}\left( \operatorname {head}_1,..., \operatorname {head}_n\right) \textbf{W}_h \end{aligned} \end{aligned}$$

(7)

where $\operatorname {head}_n=\operatorname {Attention}\left( \textbf{Q}_n, \textbf{K}_n, \textbf{V}_n\right)$, and $\textbf{W}_h$ is the trainable weight of attention head. After that, a residual normalization layer is used to mitigate the vanishing and exploding gradient during the deep network training process, which can be represented as

$$\begin{aligned} X_{\text {att}\_\text {out}}^{i} = \operatorname {LayerNorm}\left( X^{i}_{\text {att}\_\text {in}} + \operatorname {MultiHead}(\textbf{Q}, \textbf{K}, \textbf{V}) \right) \end{aligned}$$

(8)

where $\operatorname {LayerNorm}(\cdot )$ is feature normalize function, and $X_{\text {att}\_\text {out}}^{i}$ is the output of attention layer.

Subsequently, the attention layer output $X_{\text {att}\_\text {out}}^{i}$ are passed through a linear residual normalization layer to further refine the battery features, which can be calculated as

$$\begin{aligned} X_{\text {res}\_\text {out}}^{i} = \text {LayerNorm}\left( X_{\text {att}\_\text {out}}^{i} + \mathbf {W_2}\cdot X_{\text {att}\_\text {out}}^{i} + \mathbf {b_2}\right) \end{aligned}$$

(9)

where $X_{\text {res}\_\text {out}}^{i}$ is the output of linear residual normalization layer, and $\mathbf {W_2}$ and $\mathbf {b_2}$ are the training weight and bias of the linear residual normalization layer.

Finally, $X_{\text {res}\_\text {out}}^{i}$ is passed through a flattening function, denoted as $\operatorname {Flatten}(\cdot )$, to transform the input features into a lower-dimensional space, and a linear layer is applied to obtain the encoder output $X_{\text {enc}\_\text {out}}^{i}$, which can be given as

$$\begin{aligned} X_{\text {enc}\_\text {out}}^{i} = \mathbf {W_3}\operatorname {Flatten}(X_{\text {res}\_\text {out}}^{i}) + \mathbf {b_3} \end{aligned}$$

(10)

where $\mathbf {W_3}$ and $\mathbf {b_3}$ are the training weight and bias of the last linear layer.

Then, the refined features $X_{\text {enc}\_\text {out}}^{i}$ are processed through a feature-augmented memory module to amplify the differences between normal and anomalous battery features. After processing by the feature-augmented memory module, $X_{\text {enc}\_\text {out}}^{i}$ is enhanced and converted into feature $Z^{i}$, which serves as the input to the decoder. The principle and mechanics of the feature-augmented memory module will be elaborated in the next subsection.

The process of data reconstruction using the decoder is mirror-symmetric to that of the encoder. For the sake of brevity and to avoid redundant descriptions, we define the operations through an unflatten layer, linear layer, residual normalization layer, and attention layer as $\operatorname {Unflatten}(\cdot )$, $\operatorname {Linear}(\cdot )$, $\operatorname {Res-Norm}(\cdot )$, and $\operatorname {Multi-head}\, \operatorname {Attention}(\cdot )$, respectively. Then, the data reconstruction process can be expressed as

$$\begin{aligned} Y^{i}_{\left[ t-W_h,t\right] } = \operatorname {Linear}\left( \operatorname {Multi-head}\, \operatorname {Attention}\left( \operatorname {Res-Norm}\left( \operatorname {Unflatten}\left( \operatorname {Linear}\left( Z^{i}\right) \right) \right) \right) \right) \end{aligned}$$

(11)

where $Y^{i}_{\left[ t-W_h,t\right] }$ represents the reconstruct date from enhanced feature $Z^{i}$.

Finally, by training the network using normal battery data to optimize the trainable matrices in the equation (5)-(10), the proposed attention-based autoencoder minimizes the discrepancy between the original normal battery features $X^{i}_{[t-W_h,t]}$ and the reconstructed features $Y^{i}_{[t-W_h,t]}$. Through this process, the autoencoder learns the hidden dependencies of normal battery operations and captures the trends in performance variations, which enables the model to effectively distinguish abnormal data from normal operation patterns.

Between the encoder and decoder, a feature-augmented memory module is introduced to learn from normal battery cell data during the training process and store the learned hidden dependencies as memory vectors in a memory pool. Subsequently, during the testing phase, the refined features are compared with the stored memory vectors through similarity calculations, thereby amplifying the differences between normal and anomalous battery features.

The memory module is an implementation of the idea of sparse coding. It receives as input the hidden variables computed by the encoder and aims to learn a set of basis prototypical patterns from normal data. Based on the similarity between the hidden variables and the prototypical patterns, the input of the decoder will be obtained by combining several prototypical patterns.

In the feature-augmented memory module given in Fig. 2, the output data from the encoder $X_{\text {enc}\_\text {out}}^{i}$ is compared with each stored memory vector $m_k$ to compute similarity, which can be given as

$$\begin{aligned} q_{k}=\operatorname {Similarity}(X_{\text {enc}\_\text {out}}^{i}, m_{k}) \end{aligned}$$

(12)

where $m_k$ is k-th stored memory vectors from normal battery cells, $\operatorname {Similarity}(\cdot )$ is the dot product similarity function used to calculate the dot production of two input vectors, and $q_k$ is the similarity value between the encoder output and k-th stored memory vectors.

To prevent minor battery faults from being too similar to normal battery features during the similarity computation, it is necessary to apply sparsification to the similarity vuable $q_k$, which can be given as

$$\begin{aligned} \hat{q_{k}}=\frac{max(q_{k}-\lambda ,0)\cdot q_{k} }{\left| q_{k}-\lambda \right| + \epsilon } \end{aligned}$$

(13)

where $\lambda$ is a sparsity threshold designed to mitigate the influence of feature vectors with low correlation, and $\epsilon$ is defined as a very small constant to prevent the numerator from being zero. When $q_k$ smaller than $\lambda$, $\hat{q}_k$ is zero. When $q_k$ smaller than $\lambda$, $\hat{q}_k$ equal to $q_k$.

Finally, the enhanced hidden feature can be obtained through

$$\begin{aligned} Z^{i}=\sum _{k=0}^{M} \hat{q_{k}}m_{k} \end{aligned}$$

(14)

where M represents the size of the memory vectors pool, and $Z^{i}$ is the enhanced battery features used for fault detection and autoencoder training.

The role of the feature-augmented memory module is to enhance the characteristics of normal battery features and amplify the differences between anomalous and normal battery features. During the training phase, normal battery data serves as the training dataset, enabling the memory-augmentation module to store memory vectors that represent the features of normal operation. In the testing phase, the module compares the test battery data with the stored normal data, thereby amplifying the differences. This process enhances the accuracy of fault detection, particularly in identifying minor battery faults at an early stage.

Local outlier factor fault detection

The local outlier factor algorithm is a density-based outlier detection algorithm proposed by Breunig²⁹. The local outlier factor algorithm is widely used in unsupervised anomaly detection tasks because it does not require knowledge of the distribution of the dataset and can quantify the degree of anomaly for each sample point. The algorithm is also widely used for lithium-ion battery pack fault detection because it can adapt to datasets with different density distributions and can overcome the interference caused by the inconsistency of lithium-ion battery packs to some extent.

Given that battery cells within the same electric vehicle operate under identical conditions, their feature curves are more likely to be similar. Therefore, we can assess whether a particular battery cell is faulty by comparing its features at a given time with those of other battery cells in the same electric vehicle.

In this paper, the input of the local outlier factor algorithm is the features enhanced by the feature memory-augment module. Denote enhanced feature $Z^{i}$ as a sample point in the local outlier factor algorithm, the degree of anomaly is quantified by calculating the LOF value for each sample point.

The LOF algorithm begins with determining the k-distance for each sample point $Z^{i}$, which is defined as the distance to its k-th nearest neighbor. This k-distance serves as a threshold to identify the set of points within this distance, forming the k-distance neighborhood $N_k(Z^{i})$.

Subsequently, the reachability distance from $Z^{i}$ to any point $Z^{j}$ in its neighborhood is computed by

$$\begin{aligned} \text {reach-dist}_k(Z^{i}, Z^{j}) = \max \{k\text {-distance}(Z^{j}), d(Z^{i}, Z^{j})\} \end{aligned}$$

(15)

where $d(Z^{i}, Z^{j})$ represents the actual distance between $Z^{i}$ and $Z^{j}$. This ensures that points close together but not direct neighbors still influence each other’s LOF score.

Following this, the Local Reachability Density (LRD) for each point $Z^{i}$ is calculated as the inverse of the average reachability distance based on the points in its k-distance neighborhood:

$$\begin{aligned} \text {LRD}(Z^{i}) = \frac{|N_k(Z^{i})|}{\sum _{Z^{j} \in N_k(Z^{i})} \text {reach-dist}_k(Z^{i}, Z^{j})} \end{aligned}$$

(16)

where $|N_k(Z^{i})|$ denotes the number of points in the neighborhood of $Z^{i}$.

Finally, the LOF value of a point $Z^{i}$ is then determined as the average of the ratio of the LRDs of the points in its neighborhood to the LRD of $Z^{i}$ itself:

$$\begin{aligned} \text {LOF}_k(Z^{i}) = \frac{\sum _{Z^{j} \in N_k(Z^{i})} \frac{\text {LRD}(Z^{j})}{\text {LRD}(Z^{i})}}{|N_k(Z^{i})|} \end{aligned}$$

(17)

The LOF thus obtained reflects the degree to which a point $Z^{i}$ is an outlier relative to its neighbors. the battery cell features with a LOF significantly greater than 1 are considered outliers, indicating they have a high probability of being an anomaly, while battery cells with a LOF around 1 are likely normal.

In summary, the proposed battery fault detection framework detects battery faults through the following steps: (1) The proposed framework employs an attention-based autoencoder to learn the characteristic curves of normal battery cells. The refined features from the encoder are stored as memory vectors in the feature-augmented memory module; (2) The refined features of the battery cell under test are then compared with the stored normal battery memory vectors through similarity calculations, which enhances the representation of normal features and amplifies the differences between normal and anomalous features; (3) The enhanced features are analyzed using the local outlier factor algorithm, comparing them with the features of other battery cells in the same vehicle at the same moment. In this way, the battery cell exhibits abnormal behavior that can be detected.

Data pre-processing and model training

Data pre-processing

In this paper, we utilize six months of real operational data from five electric vehicles, encompassing a total of 480 battery cells, to validate the effectiveness of the proposed fault detection method. Since electric vehicles were not always in operation during data collection over six months, the raw dataset may contain periods of inactivity where the data remains unchanged for extended durations, as well as instances of sudden rises or falls in the battery features curve. To mitigate the detection performance degradation caused by the above cases, it is necessary to pre-process the raw dataset.

In the raw dataset, each electric vehicle contains 96 battery cells. Considering battery cells within the same vehicle exhibit similar characteristic curves, we first group the 480 battery cells according to their respective electric vehicles and designate these five vehicles as Vehicle No. 1 to Vehicle No. 5.

Since the electric vehicles were not always in operation during the six-month data collection period, we cut the dataset to exclude periods when the vehicles were not in operation and only data from operational states are included in the final dataset. Besides, sensor errors during data collection could cause sudden rises or falls in the battery operational feature curves (such as voltage and current), which will degrade the performance of the fault detection method. To mitigate noise, the battery feature curves are smoothed, which can be given as follows.

$$\begin{aligned} \hat{X_{t}^i} = \frac{1}{W_{s}} X^{i}_{\left[ t-\frac{W_s}{2},t+\frac{W_s}{2}\right] } \end{aligned}$$

(18)

where $\hat{X}_{t}$ is the smoothed feature vector of the $i_{th}$ cell in the battery pack at t time sampling period. $W_{s}$ is the filter window size. $\hat{X}_{t}$ is then normalized by the max-abs normalization method as the input features of the proposed fault detection framework.

The pre-processed voltage curves of the 96 cells from the five vehicles are plotted in Fig. 3. As illustrated in Fig. 3, vehicles No. 1 and No. 2 show no faults across all their battery cells, whereas vehicle No. 3 exhibits a minor internal short-circuit fault in cell No. 91. Meanwhile, vehicles No. 4 and No. 5 have minor internal short-circuit faults in cells No. 52 and No. 61, respectively, whose faults are initially minor but gradually worsen over time.

As observed in Fig. 3, for normal battery cells equipped with the same vehicle, the voltage curves of normal battery cells within the same vehicle follow a similar trend due to the consistent operating conditions they experience. However, the voltage curves of faulty battery cells gradually diverge from those of normal cells. This divergence motivates us to employ an attention-based autoencoder and a feature-augmented memory module to detect faulty battery cells.

Fig. 3

Cell voltage curves for all EVs. EV No. 1 and EV No. 2 are normal vehicles. EV No. 3 shows a minor internal short-circuit fault. EV No. 4 and EV No. 5 both show a severe internal short-circuit fault. The faulty cell is highlighted in red with its numbers labeled.

Fig. 4

Cell voltage curves from normal pack and faulty pack. The fault cell voltage curve is highlighted in red. (a) Normal cell voltage curve; (b) Faulty cell voltage curve.

Specifically, the local magnification of cell voltage curves is shown in Fig. 4, further illustrating the differences between normal cells and faulty cells. In this figure, all cell voltage curves of a battery pack are plotted together. For the normal battery pack, the voltage curves are highly consistent, with only minor deviations observed among them. In contrast, for the faulty battery pack, the voltage curve of the faulty cell with an internal short-circuit is highlighted in red. This curve shows a significant deviation from the other curves, clearly indicating the presence of a faulty cell.

Model training

As mentioned before, the proposed battery fault detection framework refines important features in normal battery cells using an attention-based autoencoder and then employs a feature-augmented memory module to obtain memory vectors from the refined hidden dependencies of normal battery cells. Therefore, to better train the designed model, the model loss function integrates three critical components: the reconstruction loss from the attention-based autoencoder to ensure accurate data reconstruction, the intra-battery diversity loss to capture differences between battery cells within the same vehicle, and the loss associated with the memory-augmentation module for preserving the refined features of normal batteries.

Firstly, to ensure that the attention-based autoencoder can effectively refine battery features, it is essential to guarantee its capability to accurately reconstruct the input data. Thus, the reconstruction loss is defined as

$$\begin{aligned} L_{r} = \left\| \hat{X_{t}}^{i}-Y_{t}^{i} \right\| ^{2} \end{aligned}$$

(19)

where $\hat{X_{t}}^{i}$ is the input data of encoder and $\hat{Y_{t}}^{i}$ is the output data of decoder.

Secondly, to avoid complex combinations of reconstructed out-of-memory anomalous samples, the addressing memory vector of the feature-augmented memory module should focus on a small number of certain memory blocks. Therefore, to preserve the refined features of normal batteries, the loss associated with the memory-augmentation module is designed as

$$\begin{aligned} L_{m}=\sum -q_{k}log(q_{k}) \end{aligned}$$

(20)

Finally, to capture the intra-battery differences between battery cells within the same electric vehicle, the input is no longer limited to data from a single cell but instead consists of data from two cells randomly selected from all cells within the current time window. The intra-battery diversity loss is defined as

$$\begin{aligned} L_{s} = \left\| Z^{i}-Z^{j} \right\| ^{2} \end{aligned}$$

(21)

where $Z^{i}$ and $Z^{j}$ are the enhanced feature from battery cell i and j.

In this paper, the three aforementioned loss components are equally important for training the model, they possess different scales in practical computation. Therefore, we unify them into a comparable range by introducing three weighting coefficients $a_1$, $a_2$, and $a_3$. The final loss function is obtained by summing these weighted losses, which can be given as

$$\begin{aligned} L = a_1L_{r}+a_{2}L_{m}+a_{3}L_{s} \end{aligned}$$

(22)

where coefficients $a_1$, $a_2$, and $a_3$ are chosen to balance the contributions of each loss component, ensuring that they are on a similar scale and thus facilitating effective training of the model.

The deployment of the proposed frameworks can be divided into two phases: offline training and online detection.

During the offline training phase, only features from normal battery cells are used for training. Training proceeds by randomly sampling 128 data records to form a training batch, with each record encompassing battery features over a 10-minute interval. Subsequently, the parameters of the attention-based autoencoder network are updated according to Eq. (19). Additionally, the parameters of the memory-augmentation module are updated based on Eqs. (20) and (21), and the refined features of normal battery cells are stored as memory vectors.

In the online detection phase, the features of the battery cells to be tested are input into the trained detection framework. Initially, these features pass through the encoder to be transformed into a lower-dimensional space, obtaining the refined features. Next, the refined features are compared with the memory vectors stored in the memory-augmentation module, which represent the normal battery characteristics. This comparison enhances the normal feature components of the battery under test and amplifies any anomalous features. Finally, the enhanced features of all batteries under test are treated as points in a LOF algorithm to detect the battery cell faults. Through this process, batteries exhibiting even minor faults can be identified by their deviation from the learned normal behavior.

Performance evaluation and discussion

In this section, experiments are conducted to verify the performance of the proposed fault detection framework. First, we introduce the experimental parameters and the neural network setting. Subsequently, the performance of the proposed fault detection framework is compared with that of state-of-the-art detection methods in terms of false positive rate (FPR) and fault alarm time.

Experiment settings

All experiments in this paper are conducted on a Win10 system computer equipped with Intel(R) Core(TM)2 Duo CPU T7700 processor and NVIDIA GeForce RTX 6000 graphics processor. The data-driven model is compiled in Python 3.8 with libraries Pytorch (1.11.0+cu113), Matplotlib (3.6.2), Numpy (1.19.2), Pandas(1.2.3), sciKit-learn (1.1.1).

We set the length of the filter window $W_{s} = 30$ and the length of the sliding window $W_{h} = 60$, i.e., ten minutes of data. The sliding step is set to 10 sampling intervals, i.e., 100s, and the weights of the loss function are set as $a_1= 1$, $a_2= 0.5$, and $a_3= 10000$, respectively. The reason for setting $a_3$ significantly larger than $a_1$ and $a_2$ is that battery cells within the same vehicle operate under very similar conditions, leading to refined features between two battery cells exhibiting minimal differences. However, faults typically manifest in these subtle discrepancies. To ensure that the intra-battery diversity loss associated with $a_3$ has an equal influence on the overall loss function and to amplify the distinctions between faulty and normal battery cells, $a_3$ is set substantially higher than $a_1$ and $a_2$.

Specifically, to determine an optimal value for $a_3$ in the context of $L_s$, we conducted a comprehensive comparison during model training using a range of $a_3$ values. The weight $a_3$ was varied from $10^2$ to $10^6$. For each value of $a_3$, the model was trained for an identical number of epochs to ensure consistent training conditions. The final losses of $L_r$, $L_m$, and $L_s$ are illustrated in Fig. 5. As shown, $L_s$ is significantly smaller than the other loss terms. As $a_3$ increases, $L_s$ rises, while $L_r$ and $L_m$ also exhibit an upward trend. Notably, when $a_3$ reaches approximately $10^4$, the decrease in $L_s$ becomes marginal, while $L_r$ and $L_m$ increase more rapidly. At this point, a balance among the three loss terms is achieved, ensuring that none of the terms are neglected. This balance is crucial for maintaining the overall effectiveness of the model.

Fig. 5

Impact of weight $a_3$ on balancing loss terms $L_s$, $L_r$, and $L_m.$.

Fig. 6

Statistical characteristics of the EV No. 1–5. (a) Pack voltage statistics; (b) Pack current statistics; (c) Pack temperature statistics; (d) Pack SOC statistics.

For EV pack data, data from two EVs are obtained from normal vehicles without faults, while data from three EVs are obtained from vehicles with faults. Among the three faulty EVs, the pack data from EV No. 3 exhibits a minor internal short-circuit, causing the faulty cell voltage to decrease gradually, indicating that the internal short-circuit is progressively worsening. Meanwhile, the pack data from EV No. 4 and No. 5 demonstrate a severe internal short-circuit, with the faulty cells showing abnormal behavior within a very short period of time.

The operation data of the EV No. 1 are used for model training, and the remaining operation data of EVs (No. 2 to No. 5) are used to evaluate the effectiveness of the proposed detection framework. Specifically, the operational data from Vehicle No. 2 is divided into two parts. The first part is used to calculate the threshold values for subsequent experiments, and the other part is used to calculate the FP to evaluate the robustness of the algorithm. Meanwhile, the statistical characteristics of the EVs are presented in Fig. 6. This figure collectively displays the main characteristics of voltage, current, temperature, and SOC for EV No. 1–5. According to the shown statistical characteristics, these five EVs experience similar operating conditions.

Table 1 The hyperparameters setting.

The hyperparameters setting of the neural network are shown in Table 1. The hidden size of the encoding linear layer is set to 40, and the hidden size of the attention layer is set to 320. The number of attention heads is set to 8. The hidden size of the res-linear layer and final linear layer are set to 32 and 8. The size of the memory module M is 4000 and the sparsity threshold $\lambda$ is 0.0004. For training, the batch-Size is 128.

Compared methods

Three battery fault detection methods are employed to evaluate the performance of the proposed fault detection framework. The Frechet and GDI methods can directly process time-series data while preserving key temporal information. Moreover, they provide stronger interpretability based on intuitive geometric and distance concepts, thus having a distinct advantage in handling such tasks. Two of these methods are designed by state-of-the-art works, while the remaining one uses the original autoencoder as the baseline method to validate the improvements achieved.

• Frechet: an online data-driven fault detection method that uses discrete Frechet distance and the LOF algorithm to detect faulty batteries³⁰.

• GDI: a generalized dimensionless indicator-based (GDI) battery fault detection method that uses a tolerance factor to map the battery features into 2-dimensional space, and uses the LOF algorithm to detect faulty batteries³¹.

• Autoencoder: a baseline fault detection method, which uses the original transformer autoencoder to refine battery features, and then uses the LOF algorithm to detect faulty batteries.

Since the compared methods use the LOF algorithm to detect faulty batteries, the LOF threshold needs to be defined. The LOF threshold value th is defined as $th = 0.5N$, where N is the smallest positive integer that makes the FP count equal to 0. The threshold value for the four methods are calculated as $th1 = 3$ (Frechet), $th2 = 2$ (GDI), $th3 = 1.5$ (Autoencoder), $th4 = 1.5$ (Proposed Method).

Evaluation metrics of fault detection

False alarm rate (FAR) and alarm time are two common performance metrics in fault detection tasks. The false alarm rate is defined as the probability that the algorithm incorrectly identifies a device as faulty when it is operating normally. For an all-negative sample set, the false alarm rate can be calculated using the following equation:

$$\begin{aligned} \text {FAR} = \frac{\text {FP}}{\text {FP} + \text {TN}} \end{aligned}$$

(23)

where FP denotes the number of false positives, i.e., instances where negative samples are misclassified as positive, and TN represents the number of true negatives, i.e., instances where negative samples are correctly identified as negative. Given that FP + TN constitutes a constant value equivalent to the dataset size for different methods, the number of FP can be used as a proxy for FAR in comparative evaluations.

The alarm time is defined as the earliest point at which the algorithm raises an alert for a faulty device. This metric can be formally expressed as:

$$\begin{aligned} T_{\text {alarm}} = \min \{ t \mid \text {Alarm}(t) = 1, t \ge t_{\text {fault}} \} \end{aligned}$$

(24)

where $T_{\text {alarm}}$ denotes the alarm time, $\text {Alarm}(t)$ is an indicator function that equals 1 if an alarm is triggered at time $t$. A lower $T_{\text {alarm}}$ indicates a more timely detection, which is crucial for mitigating potential damage and ensuring system reliability.

Verification with normal battery packs

Then the validation is performed on the second part data of EV No. 2 and the results are shown in Fig. 7. In the Frechet-based algorithm, the LOF scores of each cell show a more promiscuous trend. In the GDI-based algorithm, cell 92 and cell 93 show a strong inconsistency. In contrast, the original autoencoder produces false alarms on cell 39, cell 40, and cell 82. In contrast, the proposed method maintains good consistency throughout, with only two LOF scoring over 1.3, demonstrating the excellent robustness of the proposed method to the noise of the cells.

Fig. 7

The LOF results of the cells in the normal battery pack of EV No. 2 with the proposed method and three existing fault detection methods. (a) LOF score of cells with the Frechet-based method; (b) LOF score of cells with the GDI-based method; (c) LOF score of cells with the Autoencoder-based method; (d) LOF score of cells with the proposed method.

Fig. 8

The LOF results of the cells in the faulty battery pack of EV No. 3 with the proposed method and three existing fault detection methods. (a) LOF score of cells with the Frechet-based method; (b) LOF score of cells with the GDI-based method; (c) LOF score of cells with the Autoencoder-based method; (d) LOF score of cells with the proposed method.

Compared to autoencoder-based methods, the proposed method demonstrates significantly better consistency. This indicates that the incorporation of the memory augment module effectively enhances result consistency and minimizes the occurrence of false alarms. In addition to outperforming both the Frechet-based method and the GDI-based method, the proposed method excels particularly in terms of TN. This outstanding performance in TN enables it to stand out and compete effectively with other fault detection methods.

Verification with fault battery packs

Then, we tested each method on three EVs with faulty battery packs. Firstly, EV No. 3, which had a minor internal short circuit fault, was tested. As seen in Fig. 8, the Frechet-based algorithm performed the worst and did not detect any faults. The GDI-based method detected the fault at time point 1154, before which cell 22 showed strong inconsistency. The method based on the original autoencoder performs slightly worse than the GDI-based method, detecting fault only at time point 1367. The proposed method in this paper detects the cell fault at time point 777, which is about 10 hours earlier than the GDI-based method.

Fig. 9 and Fig. 10 show a comparison of the anomaly detection results for two EVs. The EV No. 4 and EV No. 5 had a severe internal short circuit failure. Since the faulty batteries of the two vehicles rapidly deviated from the normal voltage trend right after the fault occurred, all four algorithms easily detected the faulty batteries. However, the Frechet-based method was significantly less effective than the other three methods. Not only did it generate false alarms for cell No. 95, but the alarm detection for the faulty battery was also considerably delayed compared to the other methods. The GDI-based method detected the faulty cell, yielding results comparable to those of the other methods. The original Autoencoder-based method and the proposed method show similar trends in detecting faulty batteries. However, due to the absence of a memory module, the extracted features of the original method are unconstrained, resulting in unpredictable outcomes and several false alarms on normal batteries at EV No. 4.

Fig. 9

The performance comparison between the proposed method and three existing fault detection methods on gradually worsening faulty batteries of EV No. 4. (a) LOF score of the Frechet-based method; (b) LOF score of the GDI-based method; (c) LOF score of the autoencoder-based method; (d) LOF score of the proposed method.

Fig. 10

The performance comparison between the proposed method and three existing fault detection methods on serious faulty batteries of EV No. 5. (a) LOF score of the Frechet-based method; (b) LOF score of the GDI-based method; (c) LOF score of the autoencoder-based method; (d) LOF score of the proposed method.

Table 2 Comparison of FP count of different methods in EVs.

The results of the four methods on each vehicle are summarized in two tables. Table 2 shows the number of false alarms in the detection results of normal batteries in each vehicle. It can be seen that the original autoencoder generates false alarms for data other than the training set, which proves that its generalization ability and robustness are worse than the proposed method in this paper. The Frechet-based method also has false alarms. Both the GDI-based method and the proposed method do not generate false alarms.

Table 3 Comparison of earliest alarm time of different methods in fault EVs.

Table 3 shows the comparison of the alarm points for faulty batteries in faulty vehicles. For EV No. 4 and EV No. 5, the results of the proposed method and the GDI-based method are similar, both of them can detect the abnormality at the early stage of failure. In EV No. 3, the proposed method can detect the battery abnormality at least one hour earlier than other methods, which proves that the proposed method is more sensitive to minor battery failures than other methods.

Verification results of combined normal and fault battery packs

In order to eliminate the effect of the difference in magnitude between different features and thus better compare the effectiveness of the methods, we use the from normal vehicles shown in Fig. 7 as the training set to perform maximum-minimum normalization on other vehicles shown in Figs. 8, 9 and 10 and set 1.5 as the alarm threshold. It is worth noting that since there are several points with high anomaly scores in the Autoencoder method, we manually removed these points from the training set in order to eliminate this effect. Then we used LOF to evaluate the performance of four methods in fault detection in three faulty vehicles. The results are shown in Fig. 11.

Fig. 11

The LOF score comparison between the proposed method (shown as blue curve) and three compared battery fault detection methods. (a) The LOF score comparison on EV No. 3; (b) The LOF score comparison on EV No. 4; (c) The LOF score comparison on EV No. 5.

As can be seen from Fig. 11, after deflating the results to a consistent magnitude, the proposed method has a higher score than the other methods. The proposed method has the earliest detection times of all the methods, which proves that the features extracted by the proposed method are better able to distinguish between normal and faulty batteries.

In summary, the method proposed in this paper demonstrates the ability to rapidly detect faulty cells within a battery pack while significantly reducing the probability of false alarms. For normal battery cells in EV No. 2, the proposed method successfully avoids false alarms. Furthermore, for minor faults in EV No. 3, gradually worsening faults in EV No. 4, and severe faults in EV No. 5, the proposed method achieves faster detection without triggering false alarms.

Deployment of the proposed fault detection method

The battery fault detection method proposed in this paper can be readily applied to real-world scenarios. It can be deployed on a desktop computer, equipped with an Intel(R) Duo CPU T7700 processor and an NVIDIA GeForce RTX 6000 processor. In real-world applications, this method is integrated into a cloud platform that continuously collects time-sequence data from batteries and inputs it into our model for fault detection. Importantly, the model requires only normal operation data for training, which significantly reduces the workload associated with data labeling and enhances the model’s scalability. This enables it to adapt to fault detection in battery packs of various configurations. Through this approach, our method enables real-time monitoring of battery conditions, timely identification of potential faults, and provision of reliable fault warnings to the battery management system.

Conclusion

In this paper, a fault detection method for lithium-ion batteries is proposed. A feature-augmented autoencoder structure is introduced to address the challenge of detecting minor faults. The proposed method improves its ability to recognize normal and abnormal data in two ways: Firstly, introducing a memory module to expand the differences between normal and faulty batteries by memorizing typical feature patterns of normal data. Secondly, proposing a novel similarity loss to enhance the similarity between normal batteries by constraining the distance between normal battery features at the same moment. Finally, the trained encoder and memory enhancement module are deployed on real vehicles and the extracted features are fed into a local outlier factor algorithm for final fault detection. After extensive verification with a large amount of electric vehicle data, the proposed method can detect faulty battery cells 10 hours earlier than existing detection algorithms without false alarms.

This proposed method is designed to handle time-series data and requires less training data, making it more suitable for our current dataset and objectives. We acknowledge the potential of recent deep learning-based methods (e.g., graph neural networks for battery packs). In the future, we will explore hybrid approaches to further improve the accuracy of fault detection of battery pack.