Research on shale TOC prediction method based on improved BP neural network

Abstract

With the increasing attention to shale oil and gas in the field of oil and gas exploration and development, accurate prediction of TOC content has become the key to evaluating shale gas sweet spots. This paper studies a method for predicting shale TOC content using a BP neural network optimized by an improved cuckoo search algorithm. First, for the Longmaxi Formation shale, through logging sensitivity analysis, seven logging parameters sensitive to TOC content were determined: DEN, AC, RT, U, K, GR, and CNL. Using these parameters, a CSBP model was established and compared with the traditional BP neural network, multiple linear fitting method, and extended ∆lgR method. The results show that the CSBP model has higher prediction accuracy and generalization ability, with the mean absolute error and mean absolute percentage error being 0.38 and 15.00% respectively, which are significantly better than other methods. Further, the CSBP model was applied to predict the TOC content of Well W16 in the study area and verified by comparing with the measured TOC values. The correlation between the predicted and measured values is 0.89, and the change trends are consistent, confirming the applicability of the CSBP model. Finally, combined with the seismic waveform-guided simulation inversion technology, the planar and spatial distribution of TOC in the study area was predicted. The correlations between the predicted and measured values of four wells in the study area are all greater than 0.89. This method has high accuracy in the three-dimensional TOC content prediction of shale reservoirs and provides technical support for the evaluation of shale gas sweet spots in the work area.

Introduction

In recent years, the escalating demands of resources and energy in the modern economy and society have underscored the significance of shale oil and gas as pivotal energy sources and potential substitutes for conventional oil and gas reserves. Consequently, shale oil and gas exploration has emerged as a focal point in the energy sector¹. The total organic carbon (TOC) content serves as a critical geological parameter for assessing the viability of shale oil and gas reservoirs^2,3. Hence, investigating the TOC content distribution holds paramount importance in evaluating shale gas reservoirs and devising strategies for horizontal well placement^4,5.

Currently, the TOC logging prediction methods mainly include geochemical experimental methods, conventional logging simulation methods, mathematical statistical methods, and empirical formula methods⁶. Among them: ① Although the geochemical experimental method can accurately obtain TOC values, the obtained data are discrete, making it difficult to characterize the spatial distribution of TOC, and the cost is high^7,8; ② The conventional logging simulation method mainly uses the linear relationship fitted by TOC and logging curves such as acoustic time difference (AC), resistivity (RT), natural gamma (GR), and density (DEN) to predict TOC^9,10; ③ The mathematical statistical method mainly uses mathematical statistical methods to analyze and process logging data, so as to establish a statistical model and then realize the prediction of TOC^11,12; ④ The empirical formula method mainly realizes the prediction of TOC based on empirical formulas. For example, an empirical formula for predicting TOC is established based on the relationship between density and TOC⁵; the ∆lgR method¹³ and the improved ∆lgR method¹⁴ established based on acoustic time difference and resistivity are used to predict TOC.

In general, geochemical experimental methods, despite their high measurement accuracy, have difficulty in evaluating TOC across the entire work area. Conventional well-logging model methods are only applicable to TOC prediction at well locations. Mathematical statistical methods are suitable for strata with simple structures and shallow burial depths, and it is challenging to predict TOC in strata with complex structures and deep burial depths. Empirical formula methods are restricted by specific regions and conditions.

Seismic methods for predicting TOC: Predict TOC by establishing linear relationships between TOC content and parameters such as density, P-wave impedance, and Poisson’s ratio^5,15,16; Predict TOC using the pre-stack angle-divided seismic inversion method based on facies constraints¹⁷.

However, the above seismic methods mainly utilize pre-stack data, which are difficult to collect. Moreover, the accuracy of pre-stack data is subject to issues such as the incident angle and the requirement that the vertical variation of elastic parameters should tend to be stable¹⁸. In post-stack seismic data processing, seismic waveform-guided simulation is based on the principle of facies constraint, making full use of well logging and seismic data to improve the accuracy of inversion^19,20. This method can not only invert conventional parameters such as the wave impedance of the stratum, but also simulate various non-impedance parameters such as natural gamma and porosity, and has been widely used in thin reservoir prediction²¹.

To address the issues such as the lack of inter-well sample data and thin reservoir thickness in shale reservoirs, this paper proposes a TOC quantitative prediction method based on the BP neural network optimized by the Cuckoo Search (CS) algorithm. First, combined with the actual geological conditions of the study area, a correlation analysis is conducted between the well-logging data and the core TOC data. Then, the well-logging method for TOC prediction is used to predict the TOC of the Longmaxi Formation shale in the study area, so as to determine the method with the optimal prediction effect. Finally, an exploration is carried out to realize the prediction of the spatial distribution of the TOC of the Longmaxi Formation shale in the study area by combining the optimal well-logging method with the seismic waveform-guided simulation method, which can provide assistance for the exploration and development of shale oil and gas in the Longmaxi Formation of the study area.

Results

• (1) To address issues such as the lack of inter - well sample data and relatively thin reservoir thickness in shale reservoirs, this paper proposes a TOC quantitative prediction method based on a BP neural network optimized by the cuckoo search (CS) algorithm.

• (2) Through sensitivity analysis of various logging parameters of the Longmaxi Formation shale, seven parameters, namely DEN, AC, RT, U, K, GR, and CNL, were determined. Then, high-resolution inversion of sensitive parameters in the study area was carried out in combination with waveform indicator simulation. Finally, with the inverted parameter data as input, three-dimensional high-precision quantitative prediction of shale TOC was achieved.

• (3) This method is applicable to areas where there is a good response between well - logging parameters and TOC. Further research is still required for regions with complex and chaotic underground lithological and electrical characteristics.

Discussion

• (1) In this study, the prediction accuracy of the CSBP model is higher than that of the BP model, the multiple linear fitting method, and the extended ΔlgR method. Specifically, the mean absolute error (MAE) and mean absolute percentage error (MAPE) of the CSBP model are 0.38 and 15.00% respectively, which are significantly lower than those of other methods. This is because traditional TOC prediction methods, such as the multiple linear fitting method and the extended ΔlgR method, rely on simplified geological models and limited datasets, which restrict their prediction accuracy and generalization ability. In contrast, the CSBP model utilizes more geological parameters and combines advanced optimization algorithms, thereby improving the accuracy and reliability of prediction.

• (2) The CSBP model was used to predict Well W16 in the work area. The predicted TOC values showed a good correlation with the measured values, with a correlation coefficient of 0.89. Moreover, the MAE and MAPE were 0.47 and 37.57% respectively, indicating relatively small prediction errors.

• (3) Although the CSBP model performed excellently in this study, there is still room for further improvement and expansion. First, the prediction ability of the model is limited by the quality and integrity of the input data. For example, when predicting the TOC values across the entire work area, although there is a good correlation between the predicted TOC values and the measured TOC values for Well W16, the predicted MAE and MAPE reached 0.67 and 106.3% respectively. Future research can improve the model’s prediction ability by integrating more geological parameters and using more complex network structures. Second, the applicability of the CSBP model in different types of shale formations needs further verification.

Methodology

Sensitivity analysis of Toc logging in the study

The first sub-member of the first member of the Longmaxi Formation (S₁L₁) in the study area is close to the bottom of the Longmaxi Formation. It is currently the main target production interval for shale gas and also a high-quality shale interval. The measured minimum TOC value of the core is 0.08%, the maximum is 5.64%, and the average is 1.65% (Table 1), indicating that the TOC varies greatly vertically and the heterogeneity is strong.

Table 1 Basic data statistics of logging variables and core measured Toc.

In this study, various well-logging data of the first member of the Longmaxi Formation (S₁L₁) were collected, including acoustic travel time (AC), neutron porosity (CNL), compensated density (DEN), natural gamma ray (GR), potassium (K), photoelectric absorption cross-section index (PE), resistivity (RT), uranium (U), etc. In the following, the TOC logging sensitivity analysis of the S₁L₁ section will be carried out by combining the response mechanism and correlation analysis of logging parameters.

Analysis of the response mechanism between TOC content and logging parameters

The high organic matter content in shale leads to an increase in porosity, a decrease in density, and a reduction in velocity^22,23. Therefore, AC is directly proportional to the measured TOC content (Fig. 1A); DEN is inversely proportional to the measured TOC (Fig. 1C).

Neutron porosity tends to exhibit high values due to the hydrogen index. In high-TOC shales, organic matter may replace clay minerals with relatively high hydrogen content, resulting in a decrease in the overall hydrogen content of the formation. Consequently, the compensated neutron logging value decreases, showing a negative correlation. Additionally, high-TOC shales are often associated with pyrite (FeS₂). Its high density and neutron absorption characteristics may slightly suppress the neutron logging response. Therefore, the linear relationship between CNL and measured TOC is inverse (Fig. 1B).

When TOC is enriched, it can adsorb a large number of uranium ions. Source rocks rich in organic matter often have relatively high uranium contents and higher natural gamma values²⁴. Therefore, GR and U are positively correlated with the measured TOC (Fig. 1D,G).

In a quiet and anoxic sedimentary environment of water bodies, it is conducive to the enrichment of organic carbon, but not conducive to the precipitation and preservation of potassium-rich minerals. Therefore, K is inversely proportional to the measured TOC (Fig. 1E).

The conductivity of the kerogen matrix is extremely low, far lower than that of formation water or the bound water in clay minerals. In high-TOC formations, organic matter replaces some conductive minerals (such as clay) or occupies pore spaces, which reduces the overall conductivity of the formation and leads to an increase in resistivity. Therefore, RT is directly proportional to the measured TOC (Fig. 1F).

Fig. 1

Rendezvous of measured TOC with logging variables. (A) Rendezvous diagram of AC with TOC, (B) Rendezvous diagram of CNL with TOC, (C) Intersection plot of DEN with TOC, (D) Intersection plot of GR with TOC, (E) Rendezvous diagram of K with TOC, (F) Rendezvous diagram of RT with TOC, (G) Rendezvous diagram of U with TOC.

Correlation analysis between TOC content and logging parameters

The correlation coefficient (r) is used to measure the sensitivity of TOC and logging parameters, which is calculated as Eq. (1). The coefficient of determination, R², is used to measure the degree of fit of the two types of data. The positive and negative values of r indicate the correlation between the parameters, with the size of the absolute value of r showing the degree of correlation. A higher absolute value of r signifies a stronger correlation between the parameters, while a larger value of R² indicates a better fitting effect.

Table 2 Table of correlation coefficients between logging variables and measured Toc.

As can be seen from Table 2, among the selected logging parameters, seven logging parameters have a good correlation with the measured TOC. The absolute values of the correlation coefficients in descending order are DEN, AC, RT, U, K, GR, and CNL, all of which are above 0.45. Among them, DEN has the largest absolute value of the correlation coefficient, which is 0.83, while K and GR have the smallest, which is 0.46. According to R², it can also be seen that DEN has the best fitting effect, while K has a relatively poor fitting effect.

$${\text{r}}(in{x_q},d)=\frac{{\sum\limits_{{i=1}}^{n} {(in{x_{q,i}} - \overline {{in{x_q}}} )({d_i} - \overline {d} )} }}{{\sqrt {\sum\limits_{{i=1}}^{n} {{{(in{x_{q,i}} - \overline {{in{x_q}}} )}^2}{{\sum\limits_{{i=1}}^{n} {({d_i} - \overline {d} )} }^2}} } }}$$

(1)

where inx_q input logging parameters; d measured TOC; inx_{q, i} ith value of input logging parameters;$\:\stackrel{-}{\text{i}\text{n}{\text{x}}_{\text{q}}}$ average value of the input logging parameter; d_i i th value of the measured TOC; $\:\stackrel{-}{\text{d}}$ average value of the measured TOC.

Based on the above analysis, it is finally confirmed that seven logging parameters, namely DEN, AC, RT, U, K, GR, and CNL, are sensitive to TOC. These seven logging parameters are selected for subsequent research.

Analysis of prediction methods for shale TOC content

Conventional logging simulation method

After pre-processing the 195 sets of measured TOC data of cores collected in the work area and their corresponding DEN, AC, RT, U, K, GR, and CNL data, these 195 sets of data were divided into two categories: one was test data, and the other was training data. Among them, the test data accounted for 10% (20 sets of data), and the training data accounted for 90% (175 sets of data). The following formula of the multiple linear fitting model was obtained:

$$\begin{aligned} {\text{TOCDY}}\, & =\,0.0{\text{585}} \times {\text{AC}} - 0.{\text{153}} \times {\text{CNL}} - {\text{6}}.{\text{22}}0{\text{9}} \times {\text{DEN}}\,+\,0.00{\text{32}} \times {\text{GR}}\, \\ & +\,0.0{\text{83}} \times {\text{K}}\,+\,0.0{\text{528}} \times {\text{RT}}\,+\,0.0{\text{978}} \times {\text{U}}\,+\,{\text{13}}.{\text{5948}} \\ \end{aligned}$$

(2)

In the formula: TOCDY represents the TOC predicted by the multiple linear fitting method.

Empirical formula method

The traditional ∆lgR method uses the overlapping acoustic travel time (AC) and resistivity (RT) curves as the baseline, and the difference between the AC and RT curves is the ∆lgR value²⁵.

The formula for predicting TOC using the traditional ∆lgR method is as follows:

$$\Delta {\text{lgR}}={\text{lg(}}\frac{{{\text{RT}}}}{{{\text{R}}{{\text{T}}_{\text{b}}}}}{\text{)}}+{\text{0}}{\text{0.02}} \times ({\text{A}}C-A{C_{\text{b}}})$$

(3)

$$TOC=(\Delta {\text{lgR}}) \times {10^{2.297-0.1688 \times LOM}}$$

(4)

where TOC is the TOC predicted by the conventional ∆lgR method; LOM is the cheese root maturity; AC_b is the baseline AC curve value; RT_b is the baseline AC curve value.

Since the traditional ∆lgR method requires maturity data and is based on medium to shallow, normally compacted strata, it is not suitable for the Longmaxi Formation shale in this work area, which lacks maturity parameters and is deeply buried.

According to previous studies, GR is less affected by compaction and is more sensitive to deep source rocks²⁶. Therefore, GR can be considered to replace the maturity parameter. Based on this, the calculation formula of the extended ∆lgR method can be established:

$$\Delta {\text{lgRTOC }}={\text{ }}({\text{a}} \times {\text{GR}}\,+\,{\text{b}}){\text{ lgR}}\,+\,{\text{c}}$$

(5)

where ∆lgRTOC is the TOC predicted by expanding the ∆lgR method, and a, b, c are constants.

Expanded ∆lgR method model building again followed the same data division as in the multivariate linear fitting model building. The selected DEN, U, GR, AC, RT, and K logging parameters were used to build the expanded ∆lgR method model, and the following model equations were obtained:

$$\Delta {\text{lgRTOC}}=\left( {0.0{\text{149}} \times {\text{GR}}\,+\,{\text{3}}.{\text{4239}}} \right){\text{lgR}} - {\text{4}}.{\text{4746}}$$

(6)

BP neural network improved by CS algorithm

Currently, the emerging artificial intelligence methods are data-driven, and they search for the intrinsic mapping relationships among complex data through machine learning, which is highly suitable for handling such multi-dimensional mapping problems. Among numerous artificial intelligence methods, the BP neural network features a simple structure, strong anti-noise ability, and good generalization ability, making it well-suited for fitting various complex mappings. However, the BP neural network has the problem of easily converging to local minima instead of obtaining the global optimum²⁷. To address this issue, the cuckoo search (CS) algorithm is employed to optimize the BP neural network.

BP neural networks: In 1986, a research team led by Rumelhart, McClelland et al. proposed a multi-layer feed-forward network model called the BP neural network, which learns through the back-propagation algorithm. The learning process of this network mainly consists of two stages: forward propagation and back-propagation. Structurally, the BP neural network is composed of an input layer, a hidden layer, and an output layer. In the forward propagation stage, the input data starts to be transmitted from the input layer. If there is a deviation between the actual output of the output layer and the expected output, the back-propagation process is initiated, and the connection weights of each layer are adjusted according to the error²⁸. Thanks to this back-propagation ability, it is very easy to find the mapping relationship between the input and the output. The method to reduce the network output error is to adjust the weights and thresholds using the gradient descent method^29,30.

Figure 2 shows the structure of a BP neural network. Suppose the training data set V = (X₁, X₂, ..., X_m)^T contains m parameters. That is, the training set contains m logging parameters, with each parameter containing q elements. In other words, X_m =(x₁, x₂ ,... ,x_q).The number of nodes in the input layer is m, and the number of nodes in the hidden layer is h. The hidden layer input vector is Z = (z₁ ,z₂ ,... ,z_h)^T ; the number of nodes in the output layer is p, then the output layer vector is Y=(y₁ ,y₂ ,... ,y_q)^T, i.e., the predicted value of BP neural network about TOC TOC=(y₁ ,y₂ ,... ,y_q)^T ; the desired output vector is D=(d₁ ,d₂ ,... ,d_q)^T, i.e., the measured TOC. The weight matrix between the input layer and the hidden layer is W_mh =(w_1h ,w_2h ,... ,w_mh)^T, and the weights between the hidden layer to the output layer W_hp =(w_1p ,w_2p ,… ,w_hp)^T ; the threshold of the ith node of the hidden layer is θ_i, the threshold of the jth node of the output layer is θ_j, the activation function of the hidden layer is ξ(net), and the activation function of the output layer is φ(net), $\:{\upxi\:}\left(\text{n}\text{e}\text{t}\right)={\upphi\:}\left(\text{n}\text{e}\text{t}\right)=\frac{1}{1+{exp}^{-net}}$.

Fig. 2

Structural diagram of BP neural network.

The input layer signals input to the ith node of the hidden layer as:

$$ne{t_i}=\sum\limits_{{k=1}}^{m} {{w_{ki}}x_{{ki}}^{{}}+{\theta _i}} ,i=1,2,\ldots,h$$

(7)

$${z_i}=\xi (ne{t_i})$$

(8)

where x_ki is the input layer composition matrix element.

The jth node of the hidden layer sends input to the output layer as follows:

$$ne{t_j}=\sum\limits_{{i=1}}^{h} {{w_{ij}}{z_i}+{\theta _j}} ,j=1,2,\ldots,p$$

(9)

$${y_q}=\phi (ne{t_j}),j=1,2,\ldots,p$$

(10)

Equation (10) is the formula for calculating TOC using a BP neural network.

The error formula for sample q is as follows:

$${E^{}}=\frac{1}{2}\sum\limits_{{k=1}}^{q} {{{(d_{q}^{{}} - y_{q}^{{}})}^2}}$$

(11)

The weights from the input layer to the hidden layer and from the hidden layer to the output layer are adjusted by the gradient descent method to reduce the total error. The formulas for adjusting the weights and thresholds between the input layer to the hidden layer are respectively (in the formula $\eta \in (0,1)$ is the learning rate):

$$\Delta {w_{mh}}= - \eta \frac{{\partial E}}{{\partial {y_q}}}\frac{{\partial {y_q}}}{{\partial {z_i}}}\frac{{\partial {z_i}}}{{\partial ne{t_i}}}\frac{{\partial ne{t_i}}}{{\partial {w_{mh}}}}$$

(12)

$$\Delta {\theta _i}= - \eta \frac{{\partial E}}{{\partial {y_q}}}\frac{{\partial {y_q}}}{{\partial {z_i}}}\frac{{\partial {z_i}}}{{\partial ne{t_i}}}\frac{{\partial ne{t_i}}}{{\partial {\theta _i}}}$$

(13)

The weights and threshold adjustment formulas between the hidden layer and the output layer are as follows:

$$\Delta {w_{hp}}= - \eta \frac{{\partial E}}{{\partial {y_q}}}\frac{{\partial {y_q}}}{{\partial ne{t_j}}}\frac{{\partial ne{t_j}}}{{\partial {w_{hp}}}}$$

(14)

$$\Delta {\theta _j}= - \eta \frac{{\partial E}}{{\partial {y_q}}}\frac{{\partial {y_q}}}{{\partial ne{t_j}}}\frac{{\partial ne{t_j}}}{{\partial {\theta _j}}}$$

(15)

The final adjustment formulas for the weights and thresholds of the layers are obtained as:

$$\Delta {w_{mh}}= - \eta \sum\limits_{{k=1}}^{m} {\sum\limits_{{i=1}}^{h} {} ({d_q} - {y_q})} {\phi ^\prime}(ne{t_j}){w_{hp}}{\xi ^\prime}(ne{t_i}){x_{kq}}$$

(16)

$$\Delta {\theta _i}= - \eta \sum\limits_{{k=1}}^{m} {\sum\limits_{{i=1}}^{h} {({d_q} - {y_q}){\phi ^\prime}(ne{t_j})} {w_{hp}}{\xi ^\prime}(ne{t_i})}$$

(17)

$$\Delta {w_{hp}}= - \eta \sum\limits_{{i=1}}^{h} {({d_q} - {y_q}){\phi ^\prime}(ne{t_j}){z_i}}$$

(18)

$$\Delta {\theta _j}= - \eta \sum\limits_{{i=1}}^{h} {({d_q} - {y_q}){\phi ^\prime}(ne{t_j})}$$

(19)

Cuckoo (CS) Algorithm: The cuckoo search algorithm is a novel heuristic optimization algorithm proposed based on the breeding characteristics of cuckoos and the flight mode of fruit flies. This method has significant advantages over the particle swarm optimization and genetic algorithms, mainly manifested in aspects such as stronger global search ability, faster convergence speed, fewer parameter requirements, and better generality and robustness²⁸. Its concept originates from the Lévy flight behavior of birds and the parasitic behavior of cuckoos. The well-known scholar Yang from the University of Cambridge in the UK proposed the cuckoo search algorithm based on the following three assumptions: (1) Each cuckoo lays only one egg at a time and randomly selects a nest to lay the egg; (2) High-quality eggs in the best nests will be retained and hatch the next generation; (3) The probability that the host discovers a foreign egg is Pa. Once discovered, the host will directly abandon the egg or the nest. Under the above assumptions, the position update formula of the cuckoo search algorithm is proposed:

$$X_{{ij}}^{{t+1}}=X_{{ij}}^{t}+\alpha \times L(\lambda )$$

(20)

where $\:{\:\text{X}}_{\text{i+1}\text{j}}^{\text{t}}$ and$\:{\:\text{X}}_{\text{i}\text{j}}^{\text{t}}$ denote the i (i = 1,2 ,… ,m) nest at generation t and t + 1 in j (j = 1,2,… ,h)-dimensional positions;$\:\:\text{L}\left({\uplambda\:}\right)$ is the jump position of the Lévy ($\:\:{\uplambda\:}$ ) flight random search jump path.$\:{\upalpha\:}$ is the step size control quantity, this time set $\:{\upalpha\:}$ = 0.01.

Yang et al. simplified the $\:\text{L}\left({\uplambda\:}\right)$ distribution function was simplified and obtained by Fourier transform:

$$L(\lambda )\sim u={t^{ - \lambda }},1<\lambda <3$$

(21)

To facilitate programming needs, in 1992 Yang used Mantegna’s proposed simulation of the Lévy ($\:{\uplambda\:}$ ) flight jump path formula:

$$s=\frac{\mu }{{|\nu {|^{\frac{1}{\lambda }}}}}$$

(22)

where $\:\:{\uplambda\:}$ = 1.5, $\:{\upmu\:}$ and $\:{\upnu\:}$ obeys the normal distribution:

$$\left\{ {\begin{array}{*{20}{c}} {\mu \sim N(0,\sigma _{\mu }^{2})} \\ {\nu \sim N(0,\sigma _{\nu }^{2})} \end{array}} \right.$$

(23)

$${\left\{ {\begin{array}{*{20}{c}} {{\sigma _\mu }=\left[ {\frac{{\Gamma (1+\lambda )\sin (\frac{{\pi \lambda }}{2})}}{{\Gamma (\frac{{1+\lambda }}{2}){\lambda ^{\frac{{\lambda - 1}}{2}}}}}} \right]} \\ {{\sigma _\nu }=1} \end{array}} \right.^{\frac{1}{\lambda }}}$$

(24)

Thus Eq. (20) reduces to:

$$X_{{ij}}^{{t+1}}=X_{{ij}}^{t}+\alpha \times s$$

(25)

The CS algorithm enhances the performance of the BP neural network. The primary objective of integrating the CS algorithm with the BP neural network is to optimize the initial parameter settings of the gradient descent method, specifically the adjustment of the initial weights and bias values of the BP neural network. This integration is referred to as the CSBP neural network algorithm. The CSBP neural network algorithm is optimized at the end of the cuckoo after undergoing multiple iterations. The results obtained from the best search are then passed on to the BP neural network, resulting in a more accurate outcome with faster convergence and fewer errors.At the same time, it overcomes the dilemma of the traditional BP neural network that is trapped in local minima.

The flow of the whole algorithm is shown in Fig. 3. The basic idea is:

Firstly, the necessary pre-processing of the data (outliers removal, data normalisation) is carried out, and then the pre-processed data is used as input data to the CSBP neural network algorithm.

Randomly generate m bird nests with a given spatial extent. Each bird’s nest represents a set of weights and thresholds of the neural network to be optimised, the parameters of the algorithm are set, and then the optimisation training is performed and calculated according to the fitness function to find the current optimal bird’s nest location.

Retain the optimal bird nest position of the previous generation and update the position of n bird nests according to the Lévy flight pattern. Calculate the fitness value of the updated contemporary nests and compare it with the fitness value of the previous generation. If the updated position is better, then it is retained; otherwise, the position of the previous generation nests is kept.

To update the positions of all bird nests, generate random numbers k from the range (0,1) and set Pa = 0.25. If k is greater than Pa, the position of the original bird’s nest is retained; if k is less than Pa, update the position of the bird’s nest according to Eq. (25). At the same time, it is compared with the position of the original bird’s nest; if it is better, it is retained. Otherwise, the original bird’s nest is still used, and the updated m bird’s nest positions are obtained.

Finally, the optimal bird’s nest from many iterations is used as the optimal weights and thresholds for the BP neural network. The preprocessed data is inputted as the algorithm’s input data, and the prediction results are obtained in the output layer.

Fig. 3

Flowchart of CSBP neural network algorithm.

Normalization of data and development of CSBP prediction model: Logging data scales are usually different. Therefore, it is necessary to normalize the input parameters before algorithm training. Normalize the logging parameters DEN, AC, RT, U, K, GR, and CNL selected in this study. The normalization formula is:

$${\text{x}}_{i}^{*}=\frac{{{x_i} - {x_{\hbox{min} }}}}{{{x_{\hbox{max} }} - {x_{\hbox{min} }}}}$$

(26)

where x_i^* ith normalised data, x_i ith original data, x_max maximum value in the data, x_min minimum value in the data.

Establishment of the CSBP prediction model: The relevant program for the CSBP was written using MATLAB software. Then, the selected logging parameters DEN, AC, RT, U, K, GR, and CNL were normalized and input into the program to train the CSBP neural network algorithm. During the algorithm training process, certain evaluation indicators are required to assess the reliability of the model and the accuracy of the prediction results. Among them, the mean absolute error (MAE) can avoid the problem of error cancellation, thus accurately reflecting the actual prediction error. The mean absolute percentage error (MAPE) reflects the relative size of the error, and a smaller value indicates higher prediction accuracy³¹. Therefore, in this paper, MAE and MAPE were used as the evaluation indicators for the CSBP prediction model, and their calculation formulas are as follows:

$$MAE=\frac{{\sum\limits_{{{\text{i}}=1}}^{N} {\left| {{y_i} - {d_i}} \right|} }}{N}$$

(27)

$$MAPE=\frac{{\sum\limits_{{{\text{i}}=1}}^{N} {\frac{{\left| {{y_i} - {d_i}} \right|}}{{{d_i}}}} }}{N} \times 100\%$$

(28)

where N is the number of samples.

Establishment of the CSBP prediction model: Similarly, using the data division method adopted in the establishment of the multiple linear fitting model, the selected logging parameters of DEN, AC, RT, U, K, GR, and CNL were used to train the CSBP prediction model.

Table 3 Statistical table of prediction errors of different methods.

Fig. 4

Comparison of prediction results of different methods.

The prediction results of different methods are shown in Fig. 4: The results of the BP model, CSBP model, and multiple linear fitting method are basically consistent with the measured TOC, and their changing trends are quite similar.

The MAE and MAPE of the CSBP prediction results are 0.38 and 15.00% respectively, with the smallest prediction error. Its correlation with the measured TOC is also the highest, reaching 0.85. The MAE and MAPE of the extended ∆lgR method prediction results are 0.62 and 24.83% respectively, with the largest prediction error. Its correlation with the measured TOC is also the poorest, at 0.48 (Table 3).

By comparing the results of TOC prediction using different methods, it can be known that the prediction effect follows the order: CSBP model > BP model > multiple linear fitting method > extended ∆lgR method. Therefore, it can be confirmed that the CSBP neural network is the optimal method, and the CSBP prediction model established by it will be used in the subsequent research.

Application

Practical application of the CSBP prediction model

Based on the previous research, the accuracy of the CSBP prediction model has been verified. To further validate the applicability of this method, it is used to predict the TOC of other wells. The TOC content of the reservoir section (S₁L₁) of Well W16 in the study area was predicted and compared with the TOC measured from the core. After pre - processing the seven logging variables (DEN, AC, RT, U, K, GR, and CNL) of Well W16, such as removing outliers and normalizing, they were input into the CSBP prediction model. Figure 5 shows the prediction results of the TOC content of Well W16, where TOCCSBP represents the predicted value by CSBP.

The prediction results of Well W16 show that: the predicted CSBP values of Well W16 have a good correlation with the measured TOC values, with a correlation coefficient of 0.89 (Fig. 5). The MAE and MAPE are 0.47 and 37.57% respectively. The variation trend of the predicted CSBP values is the same as that of the measured TOC values (Fig. 6), indicating that the overall prediction effect of the predicted CSBP values is good, and the CSBP prediction model has good applicability.

The CSBP prediction results show that the thickness of the S₁L₁ layer in Well W16 is 34.75 m, with an average TOC of 1.77%. The prediction results for each sub-layer are as follows: The thickness of the S₁L₁² layer is 19.5 m, with an average TOC of 0.19%; the thickness of the S₁L₁^14c layer is 6 m, with an average TOC of 1.03%; the thickness of the S₁L₁^14b layer is 17 m, with an average TOC of 2.62%; the thickness of the S₁L₁^14a layer is 4.2 m, with an average TOC of 3.28%; the thickness of the S₁L₁¹³ layer is 5.4 m, with an average TOC of 3.07%; the thickness of the S₁L₁¹² layer is 4 m, with an average TOC of 3.14%; the thickness of the S₁L₁¹¹ layer is 2.4 m, with an average TOC of 2.93%. According to the reservoir classification standard based on TOC content in the work area: shales with TOC content ≥ 3% are Class I high-quality shales; shales with 2% ≤ TOC content < 3% are Class II high-quality shales; shales with TOC content < 2% are Class III ordinary shales. It can be seen that the S₁L₁² and S₁L₁^14c layers in Well W16 are Class III ordinary shales; the S₁L₁^14b and S₁L₁¹¹ layers are Class II high-quality shales; the S₁L₁^14a, S₁L₁¹³ and S₁L₁¹² layers are Class I high - quality shales.

Fig. 5

Crossplot of predicted TOC values and measured TOC values in Well W16.

Fig. 6

Comparison between the predicted TOC values and the measured TOC values in Well W16.

Fig. 7

Combined section of wells W3 and W9 in the study workings.

Application of CSBP prediction model and seismic waveform indicator simulation inversion

In the previous work, the CSBP prediction model was used to predict the TOC of a single well, yielding high-precision single-well prediction results. However, due to the limited drilling and logging data in the work area, it is impossible to obtain the TOC distribution characteristics of the entire work area. Therefore, in this study, an attempt was made to use the CSBP prediction model to predict the planar and spatial distribution of TOC in the study area based on the TOC-sensitive logging parameter volume obtained from high-resolution waveform indicator simulation inversion¹⁹.

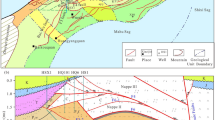
Basic principle of waveform-indicated simulation inversion: In the same sedimentary environment, seismic waveforms have similar characteristics. Similar-characteristic wells can be selected as effective samples for high-resolution well-seismic joint inversion³². Based on the above idea, a well-connected seismic section in the work area was selected for research (Fig. 7). There are two wells, W3 and W9, in the section. Then, the seismic waveforms of the well-side traces of the same layer in Wells W3 and W9 were extracted, and the seismic waveforms were compared by superposition (Fig. 8). The results show that the waveforms of the two are very similar, with a coincidence rate of over 95%. Therefore, the results of this study area show that the stratigraphic distribution areas with similar lithological combinations often have similar seismic waveform response characteristics, indicating that the seismic waveform-indicated simulation inversion is also applicable in this study area.

Fig. 8

Seismic waveform characteristics of wells W3 and W9 in the study work area.

The seven logging parameters, namely DEN, AC, RT, U, K, GR, and CNL, confirmed in the previous section, were inverted using the seismic waveform-guided simulation method. As shown in Fig. 9, the inversion results of DEN, AC, RT, U, K, GR, and CNL along Well W9 match the logging curves. Furthermore, the inversion coincidence rates of each logging parameter were statistically analyzed. Wells W3 and W9 were used for the seismic waveform-guided simulation inversion of sensitive logging parameters, and Well W16 was used as a posterior well to verify the inversion results.

The results show that the inversion coincidence rates of all logging parameters are above 75.3% (Table 4). The average inversion coincidence rates of the seven logging parameters range from 84.99 to 88.96%. Among them, Well W3 has the highest average inversion coincidence rate, reaching 88.96%. For the four logging parameters, the average inversion coincidence rates range from 82.95 to 93.23%. Among them, the inversion coincidence rate of DEN is the highest, with an average value of 93.23%, indicating high inversion accuracy. Meanwhile, the average inversion coincidence rate of the logging parameters in the verification well W16 is 87.94%. The inversion coincidence rate of DEN is the highest at 95.60%, and the lowest is 78.90% for K. Therefore, in this study, the inversion of sensitive logging parameters has high accuracy, and the results of the verification well also prove the high reliability of the inversion.

Table 4 Statistics of inversion compliance rate of logging parameters.

Fig. 9

Cross-sectional view of the well-logging sensitive parameter volume across Well W9 ((A) DEN section over W9 well, (B) AC section over W9 well, (C) RT profile over W9 well, (D) U profile over W9 well, (E) K profile over well W9, (F) GR profile over well W9,(G) CNL profile over well W9).

Therefore, the inverted data volumes of DEN, AC, RT, U, K, GR, and CNL were input into the CSBP prediction model to predict the planar and spatial distribution of TOC.

Figure 10 shows the slice map of TOC along the S₁L₁¹² layer. As can be seen from the figure, the overall TOC is greater than 2%. The areas where Wells W3, W9, and W16 are located have relatively high TOC values, while the area where Well W17 is located has a relatively low TOC value.

As can be seen from Table 5, there is a good correlation (above 0.89) between the predicted and measured TOC values of the four wells in the work area. Among them, Well W9 has the best correlation of 0.96, and its prediction error is also smaller than those of the other three wells. Well W16 has the lowest correlation of 0.89 and the largest prediction error.

Figure 11 shows the comparison between the predicted and measured TOC values of Wells W9 and W16. As can be seen from the figure, the changing trends of the predicted and measured values for the two wells are consistent.

Fig. 10

TOC slice map along the S1L112 layer.

Table 5 Statistical table of different logging prediction errors.

Fig. 11

Comparison between predicted and measured TOC values (A represents Well W9, B represents Well W16).