Abstract
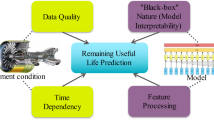
To address challenges in extracting health indicator (HI) curves and making accurate predictions with limited datasets in mechanical system prognostics, this study proposes a digital twin (DT)-driven framework for estimating remaining useful life (RUL). To minimize the deviation between simulated and measured data, we introduce a finite element model correction method using a stacked autoencoder–long short-term memory (SAE–LSTM) network. To reduce reliance on manual expertise and prior knowledge, the LSTM network is used to directly extract features from the frequency-domain vibration data and construct initial HI curves representing equipment performance degradation. Finally, this study employs a relevance vector machine (RVM) model to predict the HI curve trend by integrating failure criteria with twin data to establish the failure threshold. Experimental validation using the PHM2012 public dataset showed that the DT-based RUL prediction reduces the average relative error by 5.4% compared with traditional RUL prediction methods.
Similar content being viewed by others
Introduction
Centrifugal pump units are critical components in water treatment plants (often referred to as the ‘heart’), and their efficiency and reliability are essential for maintaining the safety and stability of the water supply system1. In the transmission system of a centrifugal pump unit, the rolling bearing is the primary wear component, and its condition directly affects the unit’s stable operation. Research indicates that over 60% of centrifugal pump unit failures are due to rolling bearing problems2. The reliability and lifespan of key components greatly influence the service life of the entire system, so analyzing their life data is an effective way to predict the remaining useful life (RUL) of the centrifugal pump unit3.
In recent years, researchers have proposed a range of methods—including time-frequency domain indicators, signal decomposition models, machine learning algorithms, and deep learning frameworks—to extract health indicator (HI) curves for performance degradation and predict device RUL through trend analysis4,5. For example, Antoni et al.6 proposed a spectral kurtosis state monitoring method based on short-time Fourier transform, which performs well in vibration monitoring. Clausen et al.7 developed an RMS-based method to extract HIs and applied a predictive model to estimate bearing RUL. Li et al.8 introduced an improved exponential model for predicting the RUL of rolling bearings. Son et al.9 proposed an RUL prediction technique based on constrained Kalman filters. Liu et al.10 used improved displacement entropy to identify monotonic trends in the observed data, supporting RUL prediction. Wang et al.11 proposed a model-free load softening prediction method using discrete wavelet transform.
Compared to time-frequency domain metrics and signal decomposition models, machine learning algorithms reduce reliance on manual expertise in predicting equipment RUL by eliminating the need for extensive understanding of underlying mechanical mechanisms12. Nielsen et al.13 proposed a method for predicting RUL by obtaining maximum likelihood estimates of transfer probabilities in Markov models through dynamic Bayesian networks. Chen et al.14 introduced a load softening prediction framework for aircraft engines using whole life cycle data and performance degradation parameters, based on similarity theory and support vector machines. Chen et al.15 proposed a hidden Markov model for RUL prediction. Singh et al.16 developed an adaptive data-driven model for predicting bearing RUL, using health state change point identification and k-means clustering.
In contrast to the above methods, deep learning effectively reconstructs and extracts data features through multiple hidden layers17. Zhou et al.18 proposed a method for predicting bearing RUL and diagnosing faults using short-time Fourier transform and a convolutional neural network (CNN). Li et al.19 proposed a multi-scale deep CNN for predicting RUL. CNNs can extract latent information from data, but they struggle to capture temporal dependencies within time series data20. Recurrent neural networks (RNNs) address this limitation by capturing temporal correlations in sequence data through their recursive structure21. Han et al.22 proposed a method for predicting bearing RUL by combining stacked autoencoders (SAEs) with RNNs. However, RNNs are prone to gradient vanishing and exploding gradients problems, particularly when handling long-term dependencies in modeling linear relationship parameters23.
To address this challenge, long short-term memory (LSTM) networks—a variant of RNNs—were introduced to mitigate long-term dependency issues in traditional RNNs24. Based on this, researchers have used LSTM networks to extract performance degradation HI curves and predict RUL25. Liu et al.26 further explored LSTM applications, and Wang et al.27 proposed a method that combines generalized learning systems and LSTM networks to enhance feature extraction and improve the correlation between prediction results and input data. Boujamza et al.28 introduced an improved LSTM with an attention mechanism and applied it to predicting the RUL of aircraft engines. Zhao et al.29 proposed a residual life prediction method combining local capsule neural networks with LSTM. Xiang et al.30 designed a multicellular LSTM to improve RUL prediction accuracy, addressing the difficulty most neural networks have in applying differentiated update strategies based on input data importance. Yusuf et al.24 developed an LSTM-based regression model to predict the load softening phenomenon in ring oscillator circuits. Hu et al.31 proposed a self-encoding LSTM-based method for predicting the RUL as part of predictive maintenance strategies in railway systems. Zhang et al.32 proposed a method for predicting the RUL and health status of lithium-ion batteries using differential thermal voltammetry and deep learning models.
A review of the literature shows that most prediction methods rely on full life cycle vibration signals—from operation to failure—to construct models of equipment performance degradation. Centrifugal pump units in water treatment plants typically have long degradation periods, high data density, and high acquisition costs, making it difficult to obtain full life cycle vibration signals in practical engineering settings—especially for newly installed or recently deployed units with limited degradation or failure data. This limits the applicability of existing research in real-world engineering practice.
In recent years, rapid advances in information technology have brought increased attention to digital twin (DT) technology in both industry and academia33,34,35,36,37. Building on prior research, this paper proposes a novel RUL prediction method based on DTs. This proposal provides an innovative framework for life prediction under limited datasets. To expand a limited dataset into a comprehensive simulation dataset covering the full life cycle, a finite element model (FEM) of the rolling bearings is established. To minimize deviation between simulated data and measured data, an FEM correction strategy combining SAEs and LSTM networks is proposed. To eliminate dependence on manual expertise and prior knowledge, the LSTM network is used to extract features directly from the frequency-domain vibration data, and an LSTM–HI curve is constructed to represent equipment performance degradation. On this basis, an extreme inflection point with slope (ES) model is introduced to smooth the LSTM–HI curves, producing LSTM–EHI curves incorporating ES points, which eliminate local fluctuations and enhance overall monotonicity. Finally, using failure criteria and twin data, the failure threshold is determined, and the relevance vector machine (RVM) is applied to predict the trend of the LSTM–EHI curve and estimate the RUL of centrifugal pump rolling bearings. The framework proposed in this paper is shown in Fig. 1. Its main contributions include:
-
[1]
A DT-based RUL prediction method for centrifugal pump rolling bearings that expands sample quantity and diversity under limited datasets and addresses the challenges of extracting performance degradation curves and accurately predicting lifespan.
-
[2]
A FEM correction method combining SAEs and LSTM networks, which reduces deviation between simulation data and measured data and improves alignment between twin data and measured data.
-
[3]
A smoothing approach based on the ES model, which reduces local fluctuations in the performance degradation curve and improves its overall monotonicity.
The remainder of this paper is organized as follows: Sect. 2 introduces the key techniques of the proposed method; Sect. 3 presents its theoretical verification using a public dataset; Sect. 4 discusses its application in engineering settings; and Sect. 5 summarizes the findings.
Key technology
Method of FEM correction based on the SAE–LSTM model
Because of uncertainties in the design, manufacture, and operation of rolling bearings (e.g., material variability, assembly errors, and environmental influences), the FEM, based on existing structural design specifications, cannot accurately represent the state of the physical system. In addition, discrepancies between the simulated response values of the FEM and actual measured values can affect the accuracy of load softening prediction. Therefore, a method is needed to minimize the deviation between the FEM’s simulated response and the actual measured values to within a given threshold, ensuring consistency between the DT model and the physical system.
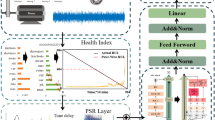
This paper proposes an FEM correction method based on the SAE–LSTM model, as shown in Fig. 2. First, the FEM simulation data are compared with the measured data of the physical system, and their consistency is evaluated by checking whether the deviation falls within the given threshold range (\(\:{T}_{p}\)). If the deviation value is within the acceptable range, the two are considered consistent; otherwise, adjustments are required. Once consistency is confirmed, the residuals can be combined with datasets from other devices operating under the same conditions as training data for the hybrid SAE–LSTM model. Finally, the output of the trained SAE–LSTM hybrid model is added to the FEM as a correction factor to generate DT vibration signals covering the device’s entire lifecycle. This increases the number of samples and keeps the DT model aligned with the dynamic response of the physical system.
Method of constructing degradation HI curves based on the LSTM–ES model
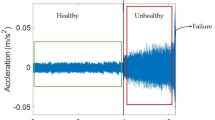
Raw vibration signals do not clearly show the trend of equipment performance degradation, as illustrated in Fig. 3a. This paper uses the fast Fourier transform (FFT) to convert the original vibration signal from the time domain to the frequency domain. Subsequently, the LSTM–HI curve is directly extracted from the frequency-domain signal using the LSTM model, reducing reliance on manual expertise and prior knowledge during HI curve construction (Fig. 3). As illustrated in Fig. 3b, the HI curve exhibits significant volatility before the 250 th data point and a slight upward trend afterward.
The mean-based exponential function method uses the average of all data points from the start time to the current time as a baseline and applies the monotonic property of the exponential function to smooth the raw data. Reference46 applied the mean-based exponential function method to smooth the health state curve of oil sand pumps and improve RUL prediction accuracy. To reduce the sharp fluctuations of the LSTM–HI curve in Fig. 3b and improve its monotonicity, this study also adopts the mean-based exponential function method to process the LSTM–HI curve. The results are shown in Fig. 3c. Compared with Fig. 3b, the LSTM–EHI curve in Fig. 3c shows improved smoothness and monotonicity. However, the region marked by the red dashed line still exhibits sharp fluctuations, which reduce the overall smoothness and monotonicity of the curve. Therefore, an effective technique is needed to smooth this part of the curve and apply appropriate adjustments. Based on these considerations, this study proposes an ES model to eliminate the fluctuation region of the curve in Fig. 3c while enhancing the overall monotonicity of the health state curve. The specific effect is shown in Fig. 3d. The calculation steps of the model are as follows:
Step 1: Identify all local minima points from the LSTM–EHI set and store them in the corresponding minima sequence MP={MPj} (1 < j < M < N), where M is the total number of minimum data points and N is the total number of LSTM–EHI sets.
Step 2: Calculate the slope of two adjacent minimum points in the sequence MP to obtain the slope sequence S. If any point Sj in the sequence S is 0 (a slope of 0 represents the horizontal axis), set Sj to 1.
Step 3: Arrange the points in sequence S in ascending order to obtain the slope data set sorta and the corresponding sequential subscript set sortb.
Step 4: Use the variable Temp to store the selected minimum extreme point P (xj, yj). The data point is obtained according to sorta and sortb. xj represents the lower corner of the corresponding data point, and yj represents the LSTM–EHI value. y1 represents the point with the lowest slope in the set sorta. The first value of Temp is P (x1, y1), and the second value of Temp is P (x2, y2). When the data point P (xj, yj) has the second-lowest slope, select the local extreme points P(xj−1, yj−1) and P(xj, yj). The linear line between these two points is then used to replace the segment of the HI curve with poor monotonicity.
Step 5: Repeat Step 4 until the slope of the current data point P (xj, yj) exceeds the slope of all previous data points. Once this condition is met, stop the process.
Methods for RUL prediction based on RVM models
RUL prediction refers to estimating the time between the current inspection moment and the failure threshold38, typically expressed as the time remaining until machine failure. It is defined as follows:
where Ti is the current inspection time specified by the user; Tf is the time when the predicted degradation HI curve first crosses the failure threshold; and RUL(Ti) is the RUL of the bearing predicted at time Ti, as shown in Fig. 4.
To reduce the parameter complexity of the lifetime prediction model and improve training speed, this study uses the RVM model to predict the HI curve trend, as shown in Fig. 5. Compared with SVM, RVM offers better sparsity and generalization, and it has been applied in trend prediction39.
Experimental verification and comparative analysis
Definition of evaluation indicators
(1) Monotonicity index
The monotonicity (Mon) index is used to evaluate the monotonicity of the constructed HI curve40. It is calculated as follows:
where dF = (HIt+1-HIt)/Δt (t = 1, 2, 3,…,T) is the difference between any two adjacent points. If the HI curve always increases monotonically, Number of dF > 0 will exceed Number of dF < 0. Mon = 0 indicates that the HI curve is smooth but non-monotonic. Mon = 1 indicates that when either Number of dF < 0 or Number of dF > 0 is 0, the HI curve will exhibit a monotonically increasing or decreasing trend.
(2) Prediction accuracy index
To quantitatively evaluate the effectiveness of the prediction model, RE41, RMSE41, Score42, and MAE42 are used as evaluation metrics for bearing RUL prediction. The evaluation formulas are as follows:
where \(\:{d}_{i}={\stackrel{\sim}{y}}_{i}-{y}_{i}\); n is the total number of data points; yi is the true value at time I; and \({\tilde {y}_i}\) is the predicted value at time i.
Introduction to experimental platform
The proposed method was validated using the IEEE PHM 2012 challenge dataset, derived from the PRONOSTIA platform (Fig. 6). This dataset includes vibration data from 17 roller bearings tested under three different operating conditions. Condition 1 and Condition 2 each contain data from seven bearings, while Condition 3 includes three bearings. The sampling frequency is 25.6 kHz. The details of this dataset are provided in Table 1.
Since the experimental platform only provided horizontal radial load data, the vibration data across the full life cycle of seven bearings—13#, 14#, 15#, 23#, 24#, 25#, and 31#—in the horizontal direction were selected as the observational dataset. The time-domain plot in Fig. 7c shows that most signals from bearing 15# exhibit minimal variation. This is due to the intrinsic nonlinearity and randomness of time-domain vibration signals in rolling bearings, making it difficult to directly observe performance degradation trends from the raw time-domain data.
To address amplitude inconsistencies in sensor signals, this study applies Layer Normalization to preprocess the raw time-domain vibration data. Following normalization, FFT is applied to convert the signals to the frequency domain, enhancing the identification of characteristic frequency components critical for downstream analysis43,44. Figure 8 shows that the eigenfrequencies of most bearings are concentrated around 113 kHz. The eigenfrequency of bearing 13# is 103 kHz, exactly four times the system operating frequency (25.6 kHz), indicating that the eigenfrequencies are predominantly concentrated near multiples of the operating frequency.
Experimental results and analysis of twin vibration data
(a) Experimental results and analysis of simulated vibration data of FEM
Figure 9 shows the simulated acceleration time-domain waveforms for bearings 13#, 24#, and 31# under three different working conditions, using FEM parameters set according to actual operating values. The corresponding frequency-domain waveforms are shown in Fig. 10.
As shown in Fig. 9, the acceleration simulation response of the rolling bearings shows a relatively stable trend. Compared with the measured signal in Fig. 7a and c, and 7e, the amplitude and fluctuations of the simulated vibration signals are significantly lower. The difference is especially noticeable during the initial stage of bearing operation, where the amplitude of the simulated signal is much smaller than that of the measured signal. This is because in the early stage of rolling bearing operation, the FEM uncertainty is relatively low, leading to lower simulated vibration amplitudes. As wear accumulates in the bearing components during the middle and later stages, the simulated vibration amplitude increases gradually. This increase reduces the influence of uncertain factors such as external noise and environment on the simulated vibration signal, causing the trend of the simulated and measured signals to gradually converge.
As shown in Fig. 10, the structure of the simulated vibration spectrum differs noticeably from the measured spectra in Fig. 8a and c, and e. This difference is mainly caused by discrepancies between the FEM and the actual operating conditions of the rolling bearings. These errors can be divided into two broad categories: errors in physical space and errors in twin space. Errors in physical space include slight fluctuations in radial force load and speed, sensor error, and abrupt changes in the working environment. Errors in twin space result from idealized parameter settings, improper FEM mesh division, and incomplete modeling of working conditions. As shown in Fig. 10b and c, the spectrum structure of the simulation signals for bearings 24# and 31# changes significantly, which negatively affects the construction of the subsequent performance degradation HI curve.
(b) Experimental results and analysis of twin vibration data based on the SAE–LSTM model
To verify the SAE–LSTM model effectively minimizes the deviation between simulation and measured data, simulation data are used as the input source and measured data as the target. The model is applied to modify the simulated response of the three datasets. The corrected vibration response signals are referred to as “twin vibration signals,” and their time- and frequency-domain waveforms are shown in Figs. 11 and 12.
The corrected time-domain waveforms of the twin vibration signals for bearings 13#, 24#, and 31# are illustrated in Fig. 11, with the corresponding spectrograms shown in Fig. 12. Compared with Figs. 9 and 10, the twin vibration signals closely match the measured data in Figs. 7 and 8 in both time-domain waveforms and spectral structure. This indicates that the SAE–LSTM model effectively reduces the deviation between the simulation and measured data. To further demonstrate the usability of the twin vibration signals, time-domain eigenvalues for the measured, simulated, and twin vibration signals were calculated for bearings 13# and 31#, as shown in Table 2.
As shown in Table 2, the amplitude of the simulated vibration signals is noticeably lower than that of the measured signals, with a mean value closer to 0. Compared with the measured vibration signals, the simulated signals show lower variance and standard deviation, as well as reduced skewness. A comparison of kurtosis, waveform factor, peak factor, and pulse factor indicates that the simulated vibration signal has a flatter waveform. Compared with the simulated signals, the corrected twin vibration signals show increased amplitude, a significantly higher mean value (no longer near 0), significantly improved skewness, and steeper waveforms. These changes bring the twin vibration signals closer to the measured signals, demonstrating that the DT model accurately reflects the dynamic response of the physical system.
(c) Experimental results and analysis compared with other correction methods
To evaluate the performance of the SAE–LSTM model in correcting vibration signals, this study conducted comparative experiments with Kalman Filter45 and Bayesian Optimization46 methods, using two evaluation metrics: time-domain feature matching and statistical bias index.
Table 3 shows that the amplitude errors (Max and Min) of the SAE–LSTM model are smaller than those of Kalman filtering and Bayesian optimization, indicating a stronger ability to compensate for nonlinear distortion in vibration signal amplitude. In addition, the reduction in the retention rate of transient features (skewness and kurtosis) for SAE–LSTM is 67–78% lower than with traditional methods. This suggests that the SAE component effectively extracts short-term transient features, such as impulse responses, through its layer-by-layer feature abstraction mechanism.
Table 4 shows that the MSE, RMSE, and R² error metrics of the SAE–LSTM model are improved compared with the Kalman filtering and Bayesian optimization methods. For example, the MSE and RMSE of SAE–LSTM for bearing 31# are 0.1399 and 0.3741, respectively. By contrast, Kalman filtering yields values of 0.1408 and 0.3752, while Bayesian optimization yields values of 0.1421 and 0.3769. SAE–LSTM shows a relative improvement of 55.3–65.7%, indicating stronger overall error suppression. The coefficient of determination (R²) reached 0.9899, demonstrating the effectiveness of deep networks in capturing the nonlinear coupling characteristics of vibration signals. These results indicate that SAE–LSTM achieves high-precision reconstruction of complex vibration signals through the synergistic effects of deep feature extraction and temporal dependency modeling. Its overall performance improvement provides a more reliable data correction approach for life prediction in industrial equipment.
Experimental results and analysis of performance degradation curves
(a) HI curve construction based on the LSTM–ES method
When extracting the LSTM–HI curves using the LSTM model, the initial learning rate was set to 0.01, and the maximum number of training iterations was 300. During training, RMSE was used as the loss function, and the adaptive moment estimation (Adam) was used as the optimizer. The internal architecture is shown in Fig. 13. The input to the LSTM model is the frequency-domain signal of a bearing in the i-th sample, and the target output is the degradation percentage in that sample. For example, if bearing 33# has 434 full life cycle samples, the ideal degradation percentage for the 292nd sample is 0.6728 when the maximum output value is set to 1. As shown in Fig. 13, to extract the performance degradation HI curve for a given bearing, measured vibration data from other bearings in the same condition group are selected as the training dataset for the LSTM model. This ensures that the LSTM model can learn and reflect the performance degradation characteristics of the target bearing. For example, when extracting the HI curve of bearing 31#, data from bearings 32# and 33# are used as the training data set. The HI curve extracted using the LSTM algorithm is referred to LSTM–HI curve, and the HI curve obtained by smoothing oscillations using the mean-based exponential function method is referred to as the LSTM–EHI curve, as shown in Fig. 14.
Figure 14 shows that the LSTM–EHI curve has a smoother trend than the LSTM–HI curve, with a significant reduction in oscillation amplitude. However, bearing 25# exhibits poorer smoothness in both its LSTM–HI and LSTM–EHI curves compared with the other bearings. In the blue dashed rectangular area before the first 300 data points (Fig. 14f), both curves show noticeable fluctuations. These oscillations obscure the gradual increase that occurs after the 300 th data point—a pattern consistent with the original vibration signal of bearing 25# in Fig. 7f. Therefore, the LSTM–EHI curves in the blue dashed area must be removed and replaced to ensure an overall smooth and monotonically increasing trend of the curves.
In the next step, the data are processed using the proposed ES model for two purposes: removing anomalies and oscillatory regions and improving the monotonicity of the LSTM–EHI curve (e.g., the blue dashed regions in Fig. 14f). The resulting LSTM–EHI with ES curves for different bearings are shown in Fig. 15.
In Fig. 15, the ES model replaces the oscillating regions in the LSTM–EHI curves of bearings 23# and 25#. Compared with the two blue dashed lines in the original LSTM–EHI curves, the red dashed lines in the LSTM–EHI with ES curves show a clear upward trend. In particular, for bearing 25#, the monotonicity is significantly improved: the original LSTM–EHI curve shows a decreasing trend before the first 500 data points and a sharp increase afterward. This indicates that the ES model enhances the monotonicity of the HI curve.
To evaluate the effectiveness of the ES model in enhancing the monotonicity of the LSTM–EHI curve, this study designed a comparative experiment of three classic smoothing algorithms: polynomial regression47, moving average filtering48, and Savitzky–Golay filtering48. As shown in Table 5, the ES model achieved the highest performance in the monotonicity metric (Mon value), with a retention rate of 100 ± 2–25.1% higher than the average Mon value of the other three classic smoothing algorithms.
(b) Comparative analysis with other HI construction methods
To verify that the LSTM–ES model is the most effective method for enhancing the monotonicity of HI curves, it was compared with other HI construction methods, such as RMS42, kurtosis42, EMD-SVD-k-means/k-medoids49,50, time-frequency methods45, and SAE–EHI46,51. Table 6 presents a comparative analysis of the Mon values (as defined in Eq. (2)) for these different models. The Mon values of all bearing HI curves constructed using the LSTM–ES model are significantly higher than those produced using the other methods.
Experimental results and analysis of RUL prediction
Section 3.3 validated the effectiveness of the twin vibration signals of the rolling bearing using both time-domain and spectral analyses. Section 3.4 presented a comparative analysis of HI construction methods to verify the LSTM–ES model’s ability to enhance the monotonicity of the HI curve. This section now evaluates the DT model’s ability to achieve accurate RUL predictions when confronted with a limited dataset.
Bearing 31# was selected as the experimental subject, and three groups of experimental tasks were designed. Different inspection moments, T (110, 256, 386), were selected to predict the RUL of bearing 31#, simulating life prediction using the finite dataset. The experimental tasks are summarized in Table 7. As indicated in Sect. 3.2, failure is defined as the point at which the peak of the acceleration time-domain signal reaches 20 g. Based on Figs. 7g and 11c, both the measured and twin signals exceed 20 g at data point 1,263,969. Therefore, the failure moment of bearing 31# in this experiment is set to 1,263,969/2560 = 493 (10 s) because a sample is collected every 10 s, and 2560 data points are recorded for each sample.
As shown in Table 7, the training set in Task 1 consists of the two other datasets from the same working condition group as bearing 31# in the public dataset, representing traditional RUL prediction. Task 2 uses the full-life twin dataset generated by the DT model as the training set, simulating RUL prediction under the limited dataset. Task 3 combines the training sets from Task 1 and Task 2 to evaluate whether the DT model improves RUL prediction accuracy.
(a) Effectiveness of the RVM model
In the RVM-based lifetime prediction experiments, the maximum number of iterations was set to 2500, the minimum error of the objective function was set to 10−3, and the Gaussian kernel width parameter τ was set to 0.1. Figure 16 shows the relative errors of the prediction results for different Gaussian kernel widths.
Figure 17 presents the prediction process and results obtained using the RVM model for the three tasks at different inspection moments (T).
Table 8 compares the predicted, actual, and relative errors of the RUL obtained using the RVM model for different tasks at different inspection moments (T).
As illustrated in Fig. 17; Table 5, the prediction outcomes for Task 2 are superior to those of Task 1. This is attributed to the physical characteristics of the FEM, which guide the degradation trend more accurately. This indicates that the DT model for bearing 31# reflects the degradation behavior of the physical bearing more effectively than data from other bearings in the same working condition group. Task 3 yielded significantly more accurate predictions than Task 2, primarily because the inclusion of twin data increased the number of training samples for the RVM model. By contrast, Task 2 had fewer samples, resulting in less stable fitting and prediction. With more available data, the RVM model achieved better prediction performance.
To further demonstrate the superiority of the RVM model in accurately predicting RUL, four methods (RVM, SVM52, BP52, and PSO53) were used to predict RUL values over the runtime interval [210, 493] for the datasets from Task 1 and Task 2. The relative error (RE) was used to evaluate the life prediction performance of each method, as shown in Fig. 18. For the SVM model, a Gaussian kernel function was used, with the penalty factor, kernel function parameters, and insensitivity coefficient set to 9, 0.002, and 1, respectively. In the BP neural network, the number of layers was set to 3; the neuron excitation function used the Sigmoid function; and the number of neurons in each layer of the input layer, hidden layer, and output layer was set to 10, 14, and 1, respectively. For the PSO method, the particle number, inertia weight, and learning factor were set to 50, 0.5, and 1, respectively. The maximum number of iterations, minimum error of the objective function, and failure threshold in the comparative models were set to the same values as in the RVM model.
Figure 19 shows that RVM achieved the best performance among all methods. The PSO method also produced accurate results, indicating that improving the monotonicity of HI supports more effective RUL prediction.
(b) Impact of data volume on RUL prediction results in limited datasets
To analyze the impact of sample size on RUL prediction accuracy under limited data conditions, this study used 30%, 60%, and 100% of the full lifecycle vibration data from bearing 31#. These samples were used to calibrate the simulated vibration signals generated by the FEM and then to perform RUL predictions. Figure 20 shows the time-domain waveforms of the corrected twin signals corresponding to different datasets.
As shown in Fig. 20, as more measured data are provided, the amplitude values of the time-domain waveforms of the twin vibration signals become closer to the measured amplitude values of the devices. In addition, the failure thresholds, which are determined by both the failure criterion and the time-domain data of the twin vibration, become closer to the real failure thresholds of the devices. The FEM is modified using the proposed method to generate full-life twin vibration signals for different quantities of measured data, and RUL is predicted. To assess the prediction performance more intuitively, RMSE was used as a qualitative metric, as shown in Fig. 18.
As shown in Fig. 18, when less than 20% of the full life cycle measured data are used to correct the FEM, the accuracy of the RUL prediction results improves significantly as the sample size increases. When more than 60% of the full life cycle measured data are used to modify the FEM, the RMSE stabilizes. Further increasing the amount of measured data for the modified FEM does not significantly improve RUL prediction accuracy. In addition, RUL prediction accuracy improves as equipment operation time increases and more data are accumulated. Therefore, in the absence of full life cycle vibration data, the DT-based RUL prediction method proposed in this study effectively improves prediction accuracy.
Comparative analysis with other data augmentation methods
To evaluate the robustness of the DT model under limited data conditions, bearing 31# was selected as the research subject. The dataset was constructed according to the sample ratio 30%/60%/100%, and its predictive performance was compared with two GAN models: AP-GAN-DNN54 and DCTC-GAN-DCNN55. To further assess the data augmentation abilities of the DT and GAN models in data-scarce scenarios, this study also constructed two composite models: AP-GAN-LSTM-RVM and DCTC-GAN-LSTM-RVM.
As shown in Table 9, across all sample ratios, the DT model outperforms the two GAN models in predictive performance. Specifically, the DT model yields lower RMSE and MAE values, indicating that its predicted results are closer to the measured vibration signals. In addition, after combining LSTM and RVM, the predictive performance of the two GAN models improved, but it still did not exceed that of the DT model. Especially at the 30% and 60% sample ratios, the DT model showed significantly lower RMSE and MAE values compared with the composite GAN model.
In summary, the results indicate that in data-scarce scenarios, the DT model shows better predictive performance and stronger data augmentation abilities compared with GAN models.
All experiments were conducted in a Windows 10 environment using an Intel Core (TM) I7-7700 CPU-2.80 GHz and 16 GB of memory. Table 10 lists the computation times of different models for bearing 31#.
As shown in Table 11, the computation time for the DT model (478.34 s) was lower than that of other GAN models, especially DCTC-GAN-DCNN, indicating a potential advantage in computational efficiency. However, this advantage was marginal and remained on the same competitive level as the other GAN models. In addition, the computation times of AP-GAN-LSTM-RVM (529.45 s) and DCTC-GAN-LSTM-RVM (528.56 s) were very similar, indicating that the combination of the LSTM–RVM framework and different GAN models may have similar computational efficiency characteristics. Notably, the CFD model used as the offline guidance module did not include the calculation time (minutes) in the total computation time of the DT model. Because the DT system in this study operates on the hourly time scale, covering the full equipment lifecycle, the offline nature of the CFD model does not conflict with the real-time requirements of the model’s online inference (response in seconds or minutes).
Engineering applications
In Sect. 3, the validity and superiority of the proposed method for RUL prediction under limited data conditions were verified using the PHM2012 public dataset. This section applies the proposed method to the secondary pump room of a water treatment plant to validate its feasibility in an actual engineering scenario. The two-stage pump room contains eight centrifugal pump units, each using a double-support structure for its rolling bearings. Since the rolling bearing supports the load of the centrifugal pump unit, many typical faults (such as unbalance, misalignment, loosening, gear failure, etc.) are transmitted to the bearing through vibration signals. Therefore, the vibration measurement point is placed primarily at the bearing seat (Fig. 21). In the experiment, the LZDSL1-930 vibration displacement sensor was used, with a displacement range of 0–100 mm/s. OPC UA technology was used to collect vertical and horizontal vibrations. The sampling frequency was 1 kHz, the collection time was 0.1 s, and 100 data points were collected at a time. Table 11 lists the relevant parameters of the centrifugal pump units in the secondary pump room.
Table 12 presents the vibration measurement and evaluation method from the national standard GB-10889-89 for centrifugal pumps. The failure criteria of the rolling bearings of the pump unit are established based on vibration amplitude. Based on the data in Tables 11 and 12, the vibration signal of the centrifugal pump reaches the upper boundary of zone D, indicating equipment failure. The failure moment is defined as the point at which the vibration amplitude exceeds 11.20 mm/s.
Because the vibration intensity in the horizontal direction is higher than that in the vertical direction, the horizontal vibration signal was chosen to predict the life of the centrifugal pump unit in the practical engineering application. The simulation parameters of the rolling bearings were set to match the actual operating conditions, and the DT model was used to generate the lifecycle twin vibration signals in the horizontal direction for all centrifugal pump units in the secondary pump room. The results are shown in Fig. 22. To predict RUL, the twin vibration data were grouped into 36,000 data points (60 × 60 × 10), converting the collected data into hours of operation. Then, the LSTM–ES method was used to extract their twin HI curves and measured HI curves. The twin failure threshold was determined according to the failure time identified from the twin time-domain vibration curve and the corresponding twin HI curve. Finally, using the current operating time as the starting point, the RVM model was applied to predict the trend of the measured HI curve and extrapolate it to the twin failure threshold, yielding the RUL of the rolling bearings for all centrifugal pump units (Fig. 23).
In this study, bearing 3# and bearing 4# are used as examples to illustrate the prediction process of the proposed method. As shown in Fig. 22c, the amplitude of the twin vibration curve for bearing 3# exceeds 11.20 mm/s at data point 747,518,896. Since one sample is collected every second and each sample contains 10 data points, the failure time corresponding to the twin curve is 747,518,896/10 = 74,751,889.6 s/3600 ≈ 20,764 h. As shown in Fig. 22d, the twin vibration curve amplitude exceeds 11.20 mm/s at data point 743,696,684, so the failure time corresponding to the twin vibration curve in the time domain is 743,696,684/10 = 74,369,668.4 s/3600 ≈ 20,658 h. As shown in Fig. 23c, the failure threshold of bearing 3# is 0.97967. Since the predicted HI curve for bearing 3# exceeds the failure threshold at 19,723 h, and the current operating time (inspection time) is 9870 h, the predicted RUL is 19,723–9870 = 9853 h. Figure 23d shows that the failure threshold of bearing 4# is 0.96854. Since the predicted HI curve for bearing 4# exceeds the failure threshold at 19,613 h, and the current operating time is 9870 h, the predicted RUL is 19,613–9870 = 9743 h. Table 13 presents the RUL of the front and rear rolling bearings of all centrifugal pump units using the method proposed in this study.
Conclusion
This study proposes an innovative DT-enabled prognostic framework designed to tackle the dual challenges of HI extraction and RUL prediction for centrifugal pump bearings, particularly under data-scarce conditions. Experimental validation on the PHM2012 benchmark dataset showed that the framework reduces MAPE by 5.4% compared to conventional approaches. Despite this advancement, two critical limitations remain for further exploration in future research: (1) reliance on high-fidelity simulation thresholds for accurate prognostic outcomes, and (2) susceptibility to environmental variability (e.g., temperature, load etc.), which introduces prediction uncertainty. Addressing these challenges would significantly improve the framework’s adaptability and practical applicability across diverse operational conditions.
Data availability
The datasets used and analyzed during the current study available from the corresponding author on request.
References
Hou, L. A. Creating smart waterworks to produce healthy drinking water. Engineering 5 (5), 826–827 (2019).
Nordmann, R. & Aenis, M. Fault diagnosis in a centrifugal pump using active magnetic bearings. Int. J. Rotating Mach. 10 (3), 183–191 (2004).
Baraldi, P., Di Maio, F., Al-Dahidi, S., Zio, E. & Mangili, F. Prediction of industrial equipment remaining useful life by fuzzy similarity and belief function theory. Expert Syst. Appl. 83, 226–241 (2017).
Guo, L., Yu, Y., Duan, A., Gao, H. & Zhang, J. An unsupervised feature learning based health indicator construction method for performance assessment of machines. Mech. Syst. Signal Process. 167, 108573 (2022).
Ye, Z. & Yu, J. A selective adversarial adaptation network for remaining useful life prediction of machines under different working conditions. IEEE Syst. J. 17 (1), 62–71 (2022).
Antoni, J. The spectral kurtosis: a useful tool for characterising non-stationary signals. Mech. Syst. Signal Process. 20 (2), 282–307 (2006).
Klausen, A., Huynh, K. & Robbersmyr, K. G. RMS based health indicators for remaining useful lifetime estimation of bearings. (2022).
Li, N., Lei, Y., Lin, J. & Ding, S. X. An improved exponential model for predicting remaining useful life of rolling element bearings. IEEE Trans. Industr. Electron. 62 (12), 7762–7773 (2015).
Son, J., Zhou, S., Sankavaram, C., Du, X. & Zhang, Y. Remaining useful life prediction based on noisy condition monitoring signals using constrained Kalman filter. Reliab. Eng. Syst. Saf. 152, 38–50 (2016).
Liu, L., Wang, S., Liu, D. & Peng, Y. Quantitative selection of sensor data based on improved permutation entropy for system remaining useful life prediction. Microelectron. Reliab. 75, 264–270 (2017).
Wang, Y., Pan, R., Yang, D., Tang, X. & Chen, Z. Remaining useful life prediction of lithiumion battery based on discrete wavelet transform. Energy Procedia. 105, 2053–2058 (2017).
Mansouri, S. S., Karvelis, P., Georgoulas, G. & Nikolakopoulos, G. Remaining useful battery life prediction for UAVs based on machine learning. IFAC-Papers Online. 50 (1), 4727–4732 (2017).
Nielsen, J. S. & Sørensen, J. D. Bayesian Estimation of remaining useful life for wind turbine blades. Energies 10 (5), 664 (2017).
Chen, Z., Cao, S. & Mao, Z. Remaining useful life Estimation of aircraft engines using a modified similarity and supporting vector machine (SVM) approach. Energies 11 (1), 28 (2017).
Chen, Z., Li, Y., Xia, T. & Pan, E. Hidden Markov model with auto-correlated observations for remaining useful life prediction and optimal maintenance policy. Reliab. Eng. Syst. Saf. 184, 123–136 (2019).
Singh, J., Darpe, A. K. & Singh, S. P. Bearing remaining useful life Estimation using an adaptive data-driven model based on health state change point identification and K-means clustering. Meas. Sci. Technol. 31 (8), 085601 (2020).
Wang, Y., Zhao, Y. & Addepalli, S. Remaining useful life prediction using deep learning approaches: A review. Procedia Manuf. 49, 81–88 (2020).
Zhou, S., Xiao, M., Bartos, P., Filip, M. & Geng, G. Remaining useful life prediction and fault diagnosis of rolling bearings based on short time fourier transform and convolutional neural network. Shock Vib. 2020(1), 8857307 (2020).
Li, H., Zhao, W., Zhang, Y. & Zio, E. Remaining useful life prediction using multi-scale deep convolutional neural network. Appl. Soft Comput. 89, 106113 (2020).
Wang, B., Lei, Y., Yan, T., Li, N. & Guo, L. Recurrent convolutional neural network: A new framework for remaining useful life prediction of machinery. Neurocomputing 379, 117–129 (2020).
Catelani, M., Ciani, L., Fantacci, R., Patrizi, G. & Picano, B. Remaining useful life Estimation for prognostics of lithium-ion batteries based on recurrent neural network. IEEE Trans. Instrum. Meas. 70, 1–11 (2021).
Han, T., Pang, J. & Tan, A. C. Remaining useful life prediction of bearing based on stacked autoencoder and recurrent neural network. J. Manuf. Syst. 61, 576–591 (2021).
Wu, S., Jiang, Y., Luo, H. & Yin, S. Remaining useful life prediction for ion etching machine cooling system using deep recurrent neural network-based approaches. Control Eng. Pract. 109, 104748 (2021).
Yousuf, S., Khan, S. A. & Khursheed, S. Remaining useful life (RUL) regression using Long–Short term memory (LSTM) networks. Microelectron. Reliab. 139, 114772 (2022).
Chen, X. & Liu, Z. A long short-term memory neural network based wiener process model for remaining useful life prediction. Reliab. Eng. Syst. Saf. 226, 108651 (2022).
Liu, Z. H. et al. A regularized LSTM method for predicting remaining useful life of rolling bearings. Int. J. Autom. Comput. 18, 581–593 (2021).
Wang, X., Huang, T., Zhu, K. & Zhao, X. LSTM-based broad learning system for remaining useful life prediction. Mathematics 10 (12), 2066 (2022).
Boujamza, A. & Elhaq, S. L. Attention-based LSTM for remaining useful life Estimation of aircraft engines. IFAC-Papers Online. 55 (12), 450–455 (2022).
Zhao, C., Huang, X., Li, Y. & Li, S. A novel cap-LSTM model for remaining useful life prediction. IEEE Sens. J. 21 (20), 23498–23509 (2021).
Xiang, S., Qin, Y., Luo, J., Pu, H. & Tang, B. Multicellular LSTM-based deep learning model for aero-engine remaining useful life prediction. Reliab. Eng. Syst. Saf. 216, 107927 (2021).
Hu, L. & Dai, G. Estimate remaining useful life for predictive railways maintenance based on LSTM autoencoder. Neural Comput. Appl. 1–12. (2022).
Zhang, L. et al. Remaining useful life and state of health prediction for lithium batteries based on differential thermal voltammetry and a deep learning model. Iscience, 25(12). (2022).
Tao, F., Xiao, B., Qi, Q., Cheng, J. & Ji, P. Digital twin modeling. J. Manuf. Syst. 64, 372–389 (2022).
Yun, J., Li, G., Jiang, D., Xu, M., Xiang, F., Huang, L., … Fang, Z., 2023. Digital twin model construction of robot and multi-object under stacking environment for grasping planning. Applied Soft Computing. 149, 111005.
Wang, B., Li, Z., Xu, Z., Sun, Z. & Tian, K. Digital twin modeling for structural strength monitoring via transfer learning-based multi-source data fusion. Mech. Syst. Signal Process. 200, 110625 (2023).
Parente, A. & Swaminathan, N. Data-driven models and digital twins for sustainable combustion technologies. Iscience, 27(4). (2024).
Cui, L., Xiao, Y., Liu, D. & Han, H. Digital twin-driven graph domain adaptation neural network for remaining useful life prediction of rolling bearing. Reliab. Eng. Syst. Saf. 245, 109991 (2024).
Xu, Z. et al. A novel health indicator for intelligent prediction of rolling bearing remaining useful life based on unsupervised learning model. Comput. Ind. Eng. 176, 108999 (2023).
Zhang, G., Liang, W., She, B. & Tian, F. Rotating machinery remaining useful life prediction scheme using Deep-Learning‐Based health Indicator and a new RVM. Shock Vib. 2021(1), 8815241 (2021).
Ren, L., Cui, J., Sun, Y. & Cheng, X. Multi-bearing remaining useful life collaborative prediction: A deep learning approach. J. Manuf. Syst. 43, 248–256 (2017).
Zhang, J., Wang, P., Yan, R. & Gao, R. X. Long short-term memory for machine remaining life prediction. J. Manuf. Syst. 48, 78–86 (2018).
Guo, J., Li, D. & Du, B. A stacked ensemble method based on TCN and convolutional bi-directional GRU with multiple time windows for remaining useful life estimation. Applied Soft Computing, 150, p.111071. (2024).
Guo, L., Li, N., Jia, F., Lei, Y. & Lin, J. A recurrent neural network based health indicator for remaining useful life prediction of bearings. Neurocomputing 240, 98–109 (2017).
Tse, P. W. & Wang, D. Enhancing the abilities in assessing slurry pumps’ performance degradation and estimating their remaining useful lives by using captured vibration signals. J. Vib. Control. 23 (12), 1925–1937 (2017).
Chumchean, S., Seed, A. & Sharma, A. Correcting of real-time radar rainfall bias using a Kalman filtering approach. J. Hydrol. 317 (1–2), 123–137 (2006).
Chen, J. et al. An error-corrected deep Autoformer model via Bayesian optimization algorithm and secondary decomposition for photovoltaic power prediction. Applied Energy, 377, p.124738. (2025).
Murray, L. & Bellhouse, D. WF Sheppard’s smoothing method: A precursor to local polynomial regression. Int. Stat. Rev. 87 (3), 604–612 (2019).
Liu, J. et al. The Life Prediction of PEMFC Based on Group Method of Data Handling with Savitzky–Golay Smoothing8pp.565–573 (Energy Reports, 2022).
Majali, A., Mulay, A., Iyengar, V., Nayak, A. & Singru, P. Fault identification and remaining useful life prediction of bearings using poincare maps, fast fourier transform and convolutional neural networks. Math. Models Eng. 8 (1), 1–14 (2022).
Rai, A. & Upadhyay, S. H. Bearing performance degradation assessment based on a combination of empirical mode decomposition and K-medoids clustering. Mech. Syst. Signal Process. 93, 16–29 (2017).
Xu, F. et al. Constructing a health indicator for roller bearings by using a stacked auto-encoder with an exponential function to eliminate concussion. Appl. Soft Comput. 89, 106119 (2020).
Ma, Y., Yao, M., Liu, H. & Tang, Z. State of health estimation and remaining useful life prediction for lithium-ion batteries by improved particle swarm optimization-back propagation neural network. Journal of Energy Storage, 52, p.104750. (2022).
Yao, F., He, W., Wu, Y., Ding, F. & Meng, D. Remaining useful life prediction of lithium-ion batteries using a hybrid model. Energy, 248, p.123622. (2022).
Yan, J. et al. AP-GAN-DNN based creep fracture life prediction for 7050 aluminum alloy. Engineering Fracture Mechanics, 303, p.110096. (2024).
Zhang, Z., Gao, H., Sun, W., Song, W. & Li, Q. Multivariate time series generation based on dual-channel Transformer conditional GAN for industrial remaining useful life prediction. Knowledge-Based Systems, 308, p.112749. (2025).
Acknowledgements
The first author and the corresponding author contributed equally. Financial support to complete this study was provided by the National Key Research and Development Program of China(NO.2023YFE0203200), the National Natural Science Foundation of China (NO.52205168, No. 52205575), the Natural Science Foundation of Hubei Province (No.2025AFD376), the Jingmen Science and Technology Burea (NO. 2024ZDYF004), Key Research and Development Program of Hubei Province: 2023BCB085, and Wuhan University of Technology 2024 Independent Innovation Research Fund for Undergraduate Programs: 104972024BKS0085. Supports from the Fundamental Research Funds for the Jingchu University of Technology (NO. YY202444) are also appreciated.
Author information
Authors and Affiliations
Contributions
Shengwen Zhou: Writing - original draft, Writing - review & editing. Li Zhang: Data curation, Validation, Visualization.XiaoMing Yang: Supervision.Ruiping Luo: Formal analysis. BaiGang Du: Funding acquisition, Supervision.Wenhui Zeng : Supervision.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Conflict of interest
We declare that we have no financial and personal relationships with other people or organizations that can inappropriately influence our work. There is no professional or other personal interest of any nature or kind in any product, service, and/or company that could be construed as influencing the position presented in, or the review of, the manuscript entitled.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Zhou, S., Zhang, L., Yang, X. et al. Remaining useful life prediction method of centrifugal pump rolling bearings based on digital twins. Sci Rep 15, 19513 (2025). https://doi.org/10.1038/s41598-025-03952-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-025-03952-2