Attention residual network for medical ultrasound image segmentation

Abstract

Ultrasound imaging can distinctly display the morphology and structure of internal organs within the human body, enabling the examination of organs like the breast, liver, and thyroid. It can identify the locations of tumors, nodules, and other lesions, thereby serving as an efficacious tool for treatment detection and rehabilitation evaluation. Typically, the attending physician is required to manually demarcate the boundaries of lesion locations, such as tumors, in ultrasound images. Nevertheless, several issues exist. The high noise level in ultrasound images, the degradation of image quality due to the impact of surrounding tissues, and the influence of the operator’s experience and proficiency on the determination of lesion locations can all contribute to a reduction in the accuracy of delineating the boundaries of lesion sites. In the wake of the advancement of deep learning, its application in medical image segmentation is becoming increasingly prevalent. For instance, while the U-Net model has demonstrated a favorable performance in medical image segmentation, the convolution layers of the traditional U-Net model are relatively simplistic, leading to suboptimal extraction of global information. Moreover, due to the significant noise present in ultrasound images, the model is prone to interference. In this research, we propose an Attention Residual Network model (ARU-Net). By incorporating residual connections within the encoder section, the learning capacity of the model is enhanced. Additionally, a spatial hybrid convolution module is integrated to augment the model’s ability to extract global information and deepen the vertical architecture of the network. During the feature fusion stage of the skip connections, a channel attention mechanism and a multi-convolutional self-attention mechanism are respectively introduced to suppress noisy points within the fused feature maps, enabling the model to acquire more information regarding the target region. Finally, the predictive efficacy of the model was evaluated using publicly accessible breast ultrasound and thyroid ultrasound data. The ARU-Net achieved mean Intersection over Union (mIoU) values of 82.59% and 84.88%, accuracy values of 97.53% and 96.09%, and F1-score values of 90.06% and 89.7% for breast and thyroid ultrasound, respectively.

Introduction

Ultrasonography represents a non-invasive imaging modality that is extensively employed in medical diagnostics. It operates by leveraging high-frequency sound waves, known as ultrasound, which penetrate human tissues and subsequently bounce back to the probe. This process generates an image that serves as a valuable tool for diagnosing, monitoring, and treating a diverse array of diseases. Possessing the advantages of being non-invasive, providing real-time imaging, ensuring safety, being cost-effective, and offering convenience, ultrasonography is frequently utilized in the diagnosis of cardiovascular disorders, obstetrics, and gynecology conditions, as well as in tumor screening procedures. Notwithstanding its crucial role in clinical practice, ultrasound imaging is not without its limitations. For instance, while ultrasound images are capable of visualizing numerous anatomical structures, their resolution falls short in comparison to that of CT¹ and MRI scans². When ultrasonic waves propagate in human tissues, reflection and scattering will occur when they encounter interfaces with different acoustic impedances. The fine structure and inhomogeneity of the tissues will lead to the irregularity of the scattered signals, thus forming noise. Moreover, during ultrasonic examinations, the respiratory movements of the thyroid gland or mammary gland, the conduction of the heartbeat, etc., will cause motion artifacts in the ultrasonic images, resulting in a decline in the quality of the images. In the context of traditional ultrasound image-based disease detection, the process hinges on manual labeling³, which is not only time-consuming but also demands significant manpower. Moreover, the outcomes of such studies are highly susceptible to subjective elements, including the experience and psychological state of the radiologist. However, with the advent of deep learning methodologies, the automatic segmentation of medical images has been experiencing rapid advancement within the domain of image analysis, presenting an effective solution to surmount the aforementioned limitations.

In the wake of the advancement of deep learning, numerous models have emerged and been applied in the medical domain, with U-Net⁴ being a prominent example. Renowned for its distinctive U-shaped⁵ architecture and skip connections⁶, U-Net has paved the way for the development of its variants. These variants address the challenge of noisy ultrasound images by devising novel network architectures. U-Net++⁷ allows the decoding layer to assimilate diverse levels of features through the establishment of multiple skip connections between each decoding layer and its corresponding encoding layer. Additionally, a deep supervision⁸ mechanism is incorporated into each decoding layer, thereby enhancing the model training process. Attention U-Net⁹ combines the architectures of the Transformer¹⁰ and U-Net, introducing an attention gate¹¹ within the skip connections. This modification enables the model to concentrate on the crucial regions¹² of the image, accentuating the features of the target object and mitigating the interference from irrelevant background areas. TransUnet¹³ integrates the Transformer with the U-Net architecture, enabling it to capture and extract global contextual information¹⁴ via the Transformer encoder. By leveraging the multi-attention mechanism, it accomplishes the task of handling long-distance dependencies effectively. SegNet¹⁵ is capable of better restoring the spatial information of images in the decoder section through pooling¹⁶ and unpooling operations. This characteristic renders it beneficial in fields such as autonomous driving and medical image segmentation. SAM¹⁷ represents an advanced image segmentation algorithm that attains high-precision image segmentation and exhibits excellent generalization capabilities.Additionally, PBPU-Net¹⁸ explicitly addresses the shift variance problem in CNNs, improving robustness to spatial inconsistencies in ultrasound images.

Despite the maturity of today’s image segmentation models, there are still many shortcomings in high-risk fields like medicine. For example, in the field of ultrasound image segmentation, the traditional U-Net model has a simple convolutional layer, which makes it difficult to obtain global information and is sensitive to noise¹⁹.U-Net++ improves feature fusion through dense jump connections, but its multilevel supervisory mechanism increases computational cost and is prone to overfitting on small datasets²⁰. Attention mechanism focuses on the target region, though Attention U-Net embeds an attention mechanism, a single attention gate is difficult to deal with multi-scale targets²¹.TransUnet combines a Transformer to extract global information, but its high demand for large-scale data and computational resources limits its application in medical scenarios²². SegNet recovers by pooling and repooling spatial information, but high-frequency details (e.g., tumor boundaries) are easily lost²³.

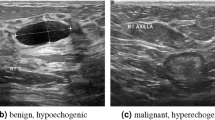
To address the aforementioned issues, scholars have introduced the CMUNeXt²⁴ module. This innovative module employs large kernel depth separable convolutions²⁵ in place of traditional convolutions to extract global information. In the current research, we propose the ARU-Net, which incorporates a spatial convolution fusion module. This module is designed to extract global information through a series of multiple convolution operations, to enhance the accuracy of image segmentation. Malignant tumors and nodules present a particular challenge due to the complexity of their boundaries and their tendency to blend with surrounding tissues. As illustrated in Figure 1, the segmentation of these boundaries is a highly intricate task.

Fig. 1

Sample ultrasound image. The red outline indicates the boundary of the tumor in breast ultrasound and the green outline indicates the boundary of the nodule in thyroid ultrasound.

Consequently, within this paper, we employ a novel self-attention²⁶ mechanism in conjunction with a channel attention module. This combination is strategically utilized to enhance the model’s ability to focus on and accurately identify the boundaries within patient data.Our proposed ARU-Net suppresses ultrasound noise through the combination of spatial attention + channel attention.The SpConvMixer module reduces computation through deeply separable convolution and prevents overfitting due to the small amount of data. Enhance the segmentation robustness for polymorphic lesions (e.g., lobulated tumors) by multi-convolution self-attention mechanism. Simulate long-range dependency through large kernel convolution to avoid Transformer’s self-attention matrix computation and reduce the demand of computational resources. Responding to the shortcomings of existing models from various aspects.

The present paper makes the following notable contributions:

• We use a residual structure instead of the traditional feature extraction structure in the U-Net model makes it is easier for the model to learn the advantages of constant mapping, which improves the ability of feature learning, and accelerates the convergence of the model also enhances the generalization ability of the model.

• We propose a channel attention mechanism and add it to the position of feature map superposition after the model can also be used as a tool for the development of a new model, which can expand the difference between channels, making the model more concerned about the feature maps on important channels, and can be used to construct interrelationships among the superimposed feature channels.

• We propose a multi-convolutional self-attention mechanism for use after the upsampling of the decoder part of the network, so that the model pays attention to the important parts of the feature map after recovering the features to size, and previously reduces the impact of the size recovery process on the feature map.

• We propose a spatial convolutional fusion module, which is used in the last layer of the encoder to deepen the network depth enhances the semantic information.

• In addition, this paper considers that tumors may only account for a small portion of breast ultrasound, and uses both the cross-entropy loss function and the Dice loss during model training to optimize the segmentation quality and improve the model performance.

• Finally, the comparison of the two publicly available datasets, as well as ablation experiments, demonstrates the effectiveness of our method.

Methods

The U-Net model is characterized by a symmetrical U-shaped architecture, comprising two parts on the left and right. The left portion represents the encoder structure, which is composed of four downsampling modules. Each of these modules contains a convolutional layer with a kernel size of 3$\times$3, followed by a Batch Normalization (BN)²⁷ layer, a Rectified Linear Unit (ReLU) layer²⁸, and a pooling layer. On the other hand, the right part constitutes the decoder structure, which also consists of four modules, namely the upsampling layer, the feature splicing layer, the convolutional layer, the BN layer, and the ReLU layer.

The encoder of the U-Net model is primarily responsible for extracting features from the input image. However, the successive downsampling operations during feature extraction result in the loss of numerous fine details. Unfortunately, the subsequent upsampling process fails to fully recover these lost details. In this paper, an ultrasound image segmentation model based on the attention mechanism and residual connection is proposed and illustrated in Figure 2.

Fig. 2

ARU-Net structure.

Encoder

For the input feature map $F_{\textrm{c}\times h\times w}$, the residual module undertakes the following processing steps. Initially, a convolution layer with a 3$\times$3 kernel is employed to conduct a dimension augmentation operation on the symmetric map. Subsequently, the output passes through a BN layer and a ReLU layer, resulting in an output feature size of $c_{1}\times h\times w$. Next, the residual connections are upgraded via a 1$\times$1 convolution operation, whereby the number of channels of the residual connections is also increased to $c_{1}$. Finally, an element-wise summation operation is performed with $F_{c_{1}\times h\times w}$, and the result is denoted as $F_{c_{1}\times h\times w}^{\prime }$. Subsequently, The preceding outcome is passed through a convolutional layer with a 3$\times$3 kernel. A BN layer and a ReLU layer are then applied to augment the network depth while maintaining the same number of channels. This result is then element-wise summed with the residual connection $F_{c_{1}\times h\times w}^{\prime }$ to yield the feature map $F_{c_{1}\times h\times w}^{\prime \prime }$. After the residual operation, the feature maps are downsampled via a pooling layer, reducing both the width and height to half of their original dimensions. Given that the input feature map measures 3$\times$512$\times$512, the size of the feature map obtained after encoder-based feature extraction is 1024$\times$32$\times$32. The encoder filters out crucial image information, such as the outlines of tumors or nodules, laying a significant foundation for subsequent precise image segmentation.

SpConvMixer block

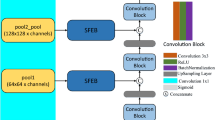
In this paper, we will use a spatial hybrid convolution module (SpConvMixer Block), whose structure is shown in Figure 3. The last layer of feature maps from the encoder part of the network is fed into the Spatial Hybrid Convolution Module, which is used to deepen the depth of the network and extract deeper semantic information.

Fig. 3

Spatial convolutional hybrid module.

The Spatial Hybrid Convolution Module is composed of a spatial attention mechanism²⁹ and five sets of hybrid convolution modules. In the spatial attention mechanism, the feature map is pooled using both maximum pooling³⁰ and average pooling³¹ operations. Subsequently, the pooled results are stacked and the number of channels of the feature map is restored through a convolutional layer with a 7$\times$7 convolutional kernel. The Sigmoid³² function is then employed to normalize the aforementioned results, thereby obtaining the spatial weights. These weights are then multiplied element-wise with the original feature map, leveraging the spatial attention mechanism to enhance the model’s learning capacity for spatial features. The hybrid convolution module comprises a deep convolutional layer with a kernel size of 3$\times$3 and a depth of 1024, along with a point-wise convolutional layer with a kernel size of 1$\times$1. Following each deep convolutional layer and point-wise convolutional layer are the GELU³³ activation layer and the BN layer, which are defined as illustrated in equations (1-3).

$$\begin{aligned} f_{t}^{\prime }&=BN(\sigma _{1}\{D e p t h w i s e C o n v(f_{t-1})\}) \end{aligned}$$

(1)

$$\begin{aligned} f_{t}&=BN(\sigma _{1}\{P o i n t w i s e C o n v(f_{t-1}^{\prime })\})+f_{t-1} \end{aligned}$$

(2)

$$\begin{aligned} \sigma _{1}&=x\cdot \phi (x) \end{aligned}$$

(3)

Where $f_{t-1}$ denotes the output feature map of layer t in the encoder, $f_{t}$ denotes the output feature map of layer t in the SpConvMixer module, $\sigma _{1}$ denotes the GELU activation function, and $\phi (x)$ denotes the cumulative distribution function of the standard normal distribution. The feature maps after spatial hybrid convolution remain unchanged in terms of channel dimensions and width and height dimensions, so the results of the last layer of the model encoder through the spatial hybrid convolution module can be directly input to the decoder for up-sampling and other feature recovery operations.

Decoder and attention mechanism

The decoder’s architecture primarily comprises an upsampling module, a feature stacking module, and a convolution block. The feature map generated by the spatial hybrid convolution module undergoes an upsampling process, which aims to restore the image size and transform the low-resolution feature map into a high-resolution one. For instance, if the output feature map from the spatial hybrid convolution module is sized 1024$\times$32$\times$32, after passing through the upsampling module, its size will be altered to 512$\times$64$\times$64. The feature map outputted from the upsampling module and the output feature map from the 5th layer of the encoder are combined along the channel dimension before the execution of the convolution operation. Subsequently, the resultant is fed into the next upsampling module to proceed with the feature restoration. This process is repeated, and after going through 4 upsampling modules and the feature stacking module, the feature map is restored to the dimension of the input. The number of channels in the output corresponds to the number of classifications required for the model to conduct subsequent classification tasks.

Multi-convolutional self-attention module

Given that the model is presumed to modify the resolution of the feature map during the upsampling procedure, leading to alterations in the distribution of feature information. Additionally, ultrasound image segmentation is essentially a semantic segmentation task, where the classification outcomes of the model for each pixel will directly impact the image segmentation efficacy. Consequently, this paper puts forward a multi-convolution self-attention mechanism. This mechanism extracts the spatial information of the feature map employing three convolutions with distinct receptive fields³⁴. This enables the model to focus on the target region and simultaneously enhance its attention to the global context. The specific structure of this mechanism is illustrated in Figure 4.

Fig. 4

Muti-convolution self-attention Block.

The multi-convolution self-attention module uses three different convolutions to process the feature maps. The standing convolution with a convolution kernel size of 1$\times$1 and a padding of 0 is used, which is used to extract feature information of smaller sizes; the normal convolution with a convolution kernel size of 3$\times$3 and a padding of 1 is used to extract feature information of medium sizes; and the null convolution with a convolution kernel size of 3$\times$3, a padding of 2, and a nulling rate of 2 is used to extract feature information of larger sizes. The feature map $F_{H\times W\times C}$ input to this module firstly goes through three convolutional layers to get $F_{H\times W\times C}^{\textrm{Pointwise}}$ , $F_{H\times W\times C}^{\textrm{Ordinary}}$ , $F_{H\times W\times C}^{\textrm{Dilation}}$ , and the three output features obtained are input to the BN layer for normalization. The feature maps $F_{H\times W\times C}^{\textrm{Pointwise}}$ and $F_{H\times W\times C}^{\textrm{Ordinary}}$ are stacked in the channel dimension, and the feature map obtained is $F_{H\times W\times 2 C}^{\prime }$ . The result of the previous step is input to the ReLU activation function layer to increase the nonlinear properties, and subsequently, the number of channels of the feature map is reduced using a convolutional layer with a convolutional kernel of 1$\times$1 to obtain the feature map $F_{H\times W\times C}^{\prime \prime }$ . The above results are normalized by a Sigmoid function to obtain the feature weights of the points of each pixel of the feature map, whose dimensions are consistent with the input dimensions, and then the feature weights obtained in the above steps are multiplied element by element with the feature map $F_{H\times W\times C}^{\textrm{Dilation}}$ . Finally, the result obtained in the above steps is added element by element with the feature map before inputting the multi-convolution module to obtain the final feature map $F_{H\times W\times C}^{\prime \prime \prime }$ . The expression is shown below:

$$\begin{aligned}&F_{H\times W\times 2 C}^{\prime }=\sigma _{2}(C o ncat\{{BN\{PointwiseConv(F_{H\times W\times C})}, BN\{OrdinaryConv(F_{H\times W\times C})\}\}) \end{aligned}$$

(4)

$$\begin{aligned}&F_{H\times W\times C}^{\textrm{Dilation}}=BN\{PointwiseConv(F_{H\times W\times C})\}\end{aligned}$$

(5)

$$\begin{aligned}&F_{H\times W\times C}^{\prime \prime \prime }=F_{H\times W\times C}^{\textrm{Dilation}}\times sigma_{3}(PointwiseConv(F_{H\times W\times 2C}^{\prime }))+F_{H\times W\times C})\end{aligned}$$

(6)

$$\begin{aligned}&\sigma _{2}={max}(0,x)\end{aligned}$$

(7)

$$\begin{aligned}&\sigma _{3}={\frac{1}{1+e^{-x}}} \end{aligned}$$

(8)

where $\sigma _{2}$ denotes the ReLU activation function and $\sigma _{3}$ denotes the Sigmoid function.

Channel attention module

In this research, it is contemplated that the quantity of channels within the feature map is subject to alteration following a skip connection. Hence, a channel attention mechanism is proposed herein. This mechanism serves the purpose of adaptively calibrating the significance of channel features and mitigating the interference caused by unproductive features, thereby enhancing the performance and precision of the model. The principal architecture of this mechanism is depicted in Figure 5.

Fig. 5

Channel attention mechanism.

The channel attention mechanism module performs maximum and average pooling of channel dimensions on the input feature map $F_{H\times W\times C}$ to obtain two sets of feature vectors, $F_{1\times 1\times C}^{M a x}$ and $F_{1\times 1\times C}^{A v g}$ respectively. Input the two feature vectors into a fully connected layer³⁵ and change the number of channels of the features to get two new feature vectors $F_{1\times 1\times C_{1}}^{M a x}$ and $F_{1\times 1\times C_{1}}^{A v g}$. The two feature vectors obtained above are multiplied element by element to obtain a new feature vector $F_{1\times 1\times C_{1}}^{F C}$ whose purpose is to increase the weight of the important channels. This feature vector is then fed into a new fully connected layer and the number of channels is recovered to obtain the feature vector $F_{1\times 1\times C}^{F C}$ . Finally, the above results are subjected to a Sigmoid function to obtain the feature weights of the feature map in the channel dimension and multiply it in the channel dimension with the original input feature map at the corresponding positions, so that the channel attention weights are mapped to the original feature channels. The new feature map with channel attention weights is finally obtained $F_{H\times W\times C}^{S}$. The expression is shown below:

$$\begin{aligned}&F_{1\times 1\times C_{1}}^{F C}=FC(Maxpooling(F_{H\times W\times C}))\times FC(Avgpooling(F_{H\times W\times C})) \end{aligned}$$

(9)

$$\begin{aligned}&F_{H\times W\times C}^{S}=\sigma _{3}(FC(F_{1\times 1\times C_{1}}^{F C}))\times F_{H\times W\times C} \end{aligned}$$

(10)

where FC denotes the fully connected layer and $\sigma _{3}$ denotes the Sigmoid activation function.

Loss function

In the ultrasound images of the data utilized for training in this paper, the majority of tumors and nodules possess a relatively small size and occupy only a minor portion of the overall ultrasound image area. Conversely, the background region constitutes a significant part of the ultrasound image. This imbalance between the foreground (tumors and nodules) and the background has the potential to impede the segmentation performance of the model. To address the aforementioned data imbalance issue, during the training process of the segmentation model in this paper, both the cross-entropy loss function³⁶ and the Dice³⁷ loss function are simultaneously employed to formulate the loss function. The calculation is carried out as detailed below:

$$\begin{aligned}&{\ L}={L}_{\scriptscriptstyle C E}+{\ L}_{\scriptscriptstyle D i c e} \end{aligned}$$

(11)

$$\begin{aligned}&{L}_{C E}=-[y\log (\hat{y})+(1-y)\log (1-\hat{y})] \end{aligned}$$

(12)

$$\begin{aligned}&{L}_{D i c e}=1-D \end{aligned}$$

(13)

$$\begin{aligned}&D=\frac{2\sum _{i}{p_{i}g_{i}}}{\sum _{i}{p_{i}^{2}}+\sum _{i}{g_{i}^{2}}} \end{aligned}$$

(14)

Where ${L}_{\scriptscriptstyle C E}$ is the cross-entropy loss function, which has better mathematical properties in binary classification tasks. ${L}_{D i c e}$ is the Dice loss function, which measures the degree of overlap between the predicted lesion region and the true region and is widely used in medical segmentation tasks. y is the true label of the sample, $\hat{y}$ is the probability that the sample belongs to the positive class, p is the prediction result, g is the true label, and D is the Dice coefficient.

Results and discussion

Datasets

This paper evaluates the proposed method by leveraging publicly accessible breast ultrasound images (BUSI)³⁸ and thyroid ultrasound (TUS)³⁹ images. BUSI collected 780 breast ultrasound images, including 437 images of benign tumors, 210 images of malignant tumors, and 133 images of normal breast tissue. We selected only images of benign and malignant tumors (647 images) for training. The TUS dataset consists of 627 thyroid ultrasound images that contain the segmentation results of benign and malignant thyroid nodules exhibiting various sizes and shapes.

This experiment is implemented within the PyTorch framework. The network is optimized using the Adam⁴⁰ optimizer with an adaptive learning rate, which is tuned via the cosine annealing strategy. The initial learning rate is configured as 0.0001, the batch size is set to 2, and the fp16 mixed precision training method is adopted.Both datasets were divided into training, validation, and test sets, and in the ratio of 7:1:2. For the BUSI dataset, we used stratified sampling to divide it, i.e., 70% (306 images) of the benign tumor images were extracted as the training set, 10% (44 images) as the validation set, and 20% (87 images) as the test set. Among the malignant tumor images, 70% (147 images) were taken as a training set, 10% (42 images) were taken as the validation set, and 20% (21 images) were taken as a test set. This prevents the generation of extreme cases. We use a loss function, a stopping-based approach to save the model with the lowest validation loss when the validation loss is not decreasing for a certain number of rounds. The number of stopping rounds is set to 15, and the threshold is 0.05.In addition, in this paper, online data enhancement is adopted to resize all the images to 512$\times$512, and random flip, rotate, and crop operations are performed on the dataset. Flipping is taken as random horizontal flipping, the angle of random rotation is set from -10$\phantom{0}^{\circ }$to 10$\phantom{0}^{\circ }$, and the cropping size is defined as 80% of the original size, which is subsequently resized to 512$\times$512. The generalization⁴¹ ability and robustness⁴² of the model are improved by the above data enhancement.

Evaluation indicators

This paper delves into the issue of ultrasound image segmentation. To thoroughly assess the model’s segmentation performance on images, a selection of evaluation metrics has been chosen for a comprehensive evaluation. These include Accuracy⁴³, Recall⁴³, mIOU (Mean Intersection over Union)⁴⁴, Precision⁴³, and F1-score⁴³. The mIOU represents the ratio between the intersection and the union of the predicted segmentation area and the ground truth area, serving as a measure of the model’s segmentation accuracy. Accuracy is defined as the proportion of correctly predicted samples to the total number of samples, indicating the overall correctness rate. Precision refers to the percentage of truly positive samples among all the samples that the model predicts as positive. Recall, on the other hand, represents the percentage of all samples with a true positive label that is accurately predicted. The F1-score, which is the harmonic mean of Precision and Recall, is utilized to holistically consider the model’s segmentation performance by balancing both precision and recall aspects.

Results

In this paper, we compare the segmentation performance of ARU-Net, U-Net, U-Net++, Attention U-Net, Segnet, and TransUnet for two datasets, BUSI and TUS, and the results are shown in Tables 1 and 2.

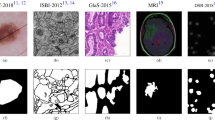
As shown in Table 1 and Table2, ARU-Net has better segmentation performance compared to several other image segmentation models. Especially on the BUSI dataset, ARU-Net achieves an accuracy of 96.74%, and the F1-score is improved by 12.54% compared to U-Net, which represents that ARU-Net has a good balance of Precision and Recall, and the model has a better performance in both accurately recognizing pixels and finding as many target pixels as possible. And the mIOU score is improved by 13.01% compared to U-Net++, which represents that ARU-Net has better segmentation performance for the boundary with the tumor. In addition, on the TUS dataset, ARU-Net also shows good performance and the mIOU score reaches 84.82%, which once again demonstrates the advantage of ARU-Net for global information processing and its importance for this task. Both HEAT-Net⁴⁵ and MicroSegNet⁴⁶ outperform the previous models in terms of performance. However, ARU-Net outperforms MicroSegNet in all aspects on the BUSI and TUS datasets, which suggests that the model proposed in this paper is more advantageous on images with multiple lesions or blurred boundaries, and is suitable for tasks that are more focused on recall. ARU-Net outperforms HEAT-Net in terms of precision, recall, and F1 scores, which suggests that it can recognize the target region more accurately in segmentation tasks and can recognize the target region more accurately. Recognize target regions and can achieve better results in more target regions. HEAT-Net, on the other hand, slightly outperforms HEAT-Net in mIoU, suggesting that it may perform more accurately in capturing region overlap and detail segmentation. ARU-Net’s strengths lie in the precision and F1 scores, and it is suitable for segmentation tasks that require higher precision and comprehensiveness, especially those that require higher details.From the table, it can be seen that some of the metrics of U-Net++ are lower than those of U-Net, which may be because the nested jump connections and deep supervision mechanism of U-Net++ significantly increase the model complexity, while the small number of datasets used in the experiments may not be sufficient to support the adequate training of complex models. Moreover, U-Net++ is prone to overfitting when the amount of data is limited, leading to its generalization ability on the validation set, while U-Net has a simpler structure and is more adaptable to small amounts of data. In addition, ultrasound images have fuzzy boundaries and significant noise, and the dense connectivity of U-Net++ may focus excessively on local details while ignoring the global context, resulting in inaccurate segmentation boundaries. The simple architecture of U-Net strikes a better balance between noise suppression and target localization, which is especially suitable for segmentation of small targets (e.g., tumors). This also reminds us that different models will produce different results on different datasets, and the model structure should be designed according to the task requirements. The segmentation outcomes of certain samples are illustrated in Fig. 6.

Table 1 Results for each indicator on the BUSI dataset.

Table 2 Results for each indicator on the TUS dataset.

Fig. 6

Ultrasound image segmentation results. Where the first to third rows are some of the samples in the BUSI dataset and the fourth to sixth rows are some of the samples in the TUS dataset.

As depicted in Fig. 6, it becomes apparent that the ARU-Net proposed within this paper exhibits superiority over the other five models in segmenting the boundary details of small targets. Moreover, its overall segmentation performance for large targets is also more favorable compared to the other models and, remarkably, even demonstrates greater accuracy than manual labeling in certain instances. The ultrasound image presented in the third row corresponds to that of a malignant breast tumor. Malignant tumors are typically characterized by indistinct boundaries and irregular shapes. It can be observed from Fig. 6 that the other five models do not perform optimally in segmenting malignant tumors. In contrast, the ARU-Net showcases a more proficient performance in this regard, incurring a relatively smaller loss. This outcome effectively underlines the significance and value of the ARU-Net proposed in this paper for this particular task.

We have trained and analyzed the loss function used in our model on the TUS dataset in comparison with the focal Tversky loss⁴⁷, training with the focal Tversky loss leads to faster convergence, but its performance in terms of performance is still a little bit inferior to the loss function we used, which is because the loss function we used is more applicable to our proposed model.Table 3 shows that the model obtained from training with focal Tversky loss has lower performance than the loss function we used. Although focal Tversky loss has a significant effect in dealing with data imbalance, the loss function we used has fewer parameters, and the combination of the two ensures global region matching and optimizes local pixel classification, which is especially suitable for boundary blurring ultrasound images. In contrast,$\alpha$ (false positive weight),$\beta$ (false negative weight), and $\gamma$ (difficult to separate the sample focusing parameters) need to be adjusted at the same time, with high parameter sensitivity, and improper settings can easily lead to unstable optimization or overfitting. This also confirms that different loss functions will show different effects under different models.

Table 3 The performance of the model under different loss functions.

Furthermore, within this paper, statistical analyses were conducted on both the training set loss and validation set loss of the model across the two datasets. This was done to evaluate the model’s performance by examining the convergence of the loss values. Figure 7 and Figure 8 respectively illustrate the variations in the training set and validation set losses of the model concerning the number of iterations on the BUSI and TUS datasets.

Fig. 7

Variation of the training set loss and validation set loss of the model on the BUSI dataset. Where the red curve is the change in training set loss value, the orange curve is the change in validation set loss, and the green and brown curves are the change in training set loss and validation set loss after the smoothing process, respectively.

Fig. 8

Variation of the training set loss and validation set loss of the model on the TUS dataset. Where the red curve is the change in training set loss value, the orange curve is the change in validation set loss, and the green and brown curves are the change in training set loss and validation set loss after the smoothing process, respectively.

Upon analyzing the figure above, it is evident that, on the BUSI dataset, the training and validation set losses of the other five models converge at a slower pace. By the 40th iteration, when the loss approaches 0.4, and ultimately, both losses converge to around 0.3. In contrast, the ARU-Net proposed in this study has already reached a loss value near 0.4 by the 20th iteration and finally converges to approximately 0.2 for both the training and validation set losses. This indicates that ARU-Net not only converges more rapidly than the other five models but also attains lower final loss values. Consequently, ARU-Net can achieve superior training results with fewer iterations. Moreover, on the TUS dataset, the convergence speed and final loss value of ARU-Net also outperform those of the other five models. Given the blurred boundaries of breast tumors and thyroid nodules in the dataset, the other five models exhibit significant fluctuations during the convergence process. For instance, the validation set losses of the Segnet and TransUnet models in the BUSI dataset exceed 0.2. This might be because these two models demand a substantial amount of training data, which is less than ideal for smaller datasets. However, due to the inherently limited size of medical datasets, ARU-Net is well-suited to deliver satisfactory segmentation performance even with small datasets. The overall loss fluctuations of the U-Net++ and Attention U-Net models in the TUS dataset are relatively large, whereas ARU-Net shows smaller fluctuations, suggesting better stability and robustness.

To prove that the difference in performance exhibited by the models is statistically significant, we performed a paired t-test on the mIOU and Accuracy of the models. First, we made the original hypothesis $H_0$: assuming that the mIOU and Accuracy of our proposed model are not higher than other models. Then, we made the alternative hypothesis $H_1$: the mIOU and Accuracy of our proposed model are higher than other models. The P-value was then determined by calculating the t-value of the test statistic, and the formula for calculating the t-value of the test statistic is shown below:

$$\begin{aligned}&t = \frac{\bar{d} - 0}{S_d / \sqrt{n}} \end{aligned}$$

(15)

where $\bar{d}$ is the mean of pairwise differences, $S_d$ is the standard deviation of pairwise differences; and n is the sample size.

Based on the calculated t-value, the P-value is calculated using the tool in Python’s scipy library, and we preset the level of significance to be 0.05. When the P-value is less than this level of significance, the original hypothesis is rejected, which indicates that the proposed model outperforms the other models. The performance of the model’s P-value on the BUSI and TUS datasets is shown in the table below:

Table 4 P-value between ARU-Net and other models.

According to Table 4, it can be seen that the P-value steer of mIOU and Accuracy of our model on BUSI and TUS is less than 0.05, then it proves that the difference of our model is statistically significant compared to several other models.

External validation

Due to the different ultrasound acquisition devices and scanning methods, many deep learning segmentation performances show poor generalization performance, resulting in poor performance on external test sets. To further validate the generalization and robustness of our model, we adopt an external validation dataset, “An open-access breast lesion ultrasound image database”⁴⁸. In this validation process, we directly use the training model parameters based on the BUSI dataset to generate segmentation results on the external validation set. Table 5 shows the segmentation results of different methods on the external dataset. It is worth noting that the proposed method also produces the most satisfactory segmentation results in the external test experiments.

Table 5 Results for each indicator on the external test dataset.

As can be seen from Figure 9, the other centralized models perform poorly on external data, indicating insufficient generalization ability. In contrast, our proposed model performs relatively well on external data, which indicates that our model has a good generalization ability.

Fig. 9

Segmentation results of the model on the external dataset.

Ablation experiments

The paper culminates with ablation experiments⁴⁹ designed to dissect the contribution of each module to the overall model performance. Specifically, Table 6 and Table 7 present two distinct sets of ablation experiments carried out on the BUSI dataset and the TUS dataset, respectively. These experiments serve the purpose of validating the efficacy of several key components, namely the residual edge encoder, the channel attention module, the multi-convolutional self-attention module, as well as the spatial hybrid convolution module proposed within this paper. Additionally, they aim to ascertain the impact of these modules on the accuracy of image segmentation, thereby providing valuable insights into the inner workings and optimization potential of the model architecture.

Table 6 Ablation experiments on the BUSI dataset.

Table 7 Ablation experiments on the TUS dataset.

As indicated by the data presented in Table 6 and Table 7, it becomes evident that upon the incorporation of the residual connection, along with the attention module and the spatial hybrid convolution module proposed in this research, there is a notable enhancement in the segmentation performance metrics of the model. In the context of the BUSI dataset, specifically, the F1-score exhibits improvements of 12.54%, 7.86%, and 3.37% respectively, when compared to the other three scenarios. Concurrently, the mIOU demonstrates respective enhancements of 12.94%, 9.72%, and 4.5%, while the Accuracy registers improvements of 1.31%, 0.64%, and 0.17% over the other three cases. Similarly, within the TUS dataset, the F1-score experiences augmentations of 14.13%, 6.2%, and 4.7%, the mIOU shows advancements of 18.93%, 8.57%, and 5.51%, and the Accuracy is elevated by 3.22%, 2.17%, and 1.31% respectively. Taking into account the experimental comparison outcomes and the preceding analyses, it can be concluded that the concurrent utilization of the residual edge encoder, the channel attention module, the multi-convolutional self-attention module, and the spatial hybrid convolution module proposed in this paper can further augment the segmentation performance of the model, thereby underlining their significance and effectiveness in the domain of image segmentation.

Conclusion

In this work, this paper introduces ARU-Net, a dedicated segmentation model designed specifically for medical ultrasound images. By integrating residual connections into the encoder architecture of the traditional U-Net network, the feature learning proficiency of the model is substantially enhanced, and its convergence rate is accelerated. This allows the model to attain the desired segmentation performance with a reduced number of iterations. Moreover, two innovative attention mechanisms are proposed in this paper: the channel attention mechanism and the multi-convolutional self-attention mechanism. These mechanisms not only augment the model’s learning capacity within the channel dimension but also bolster its ability to integrate global information. Consequently, the model is empowered to precisely locate and segment targets of diverse sizes and shapes. Finally, The paper concludes by proposing a spatial hybrid convolution module to deepen the longitudinal depth of the network and enhance the model’s extraction of semantic information from the images to obtain better image segmentation performance. In this paper, the feasibility of ARU-Net is verified on two ultrasound datasets, and it achieves better performance than other medical image segmentation models through experimental comparative analysis.

The model we propose still has the following shortcomings:

In terms of the dataset, we adopt publicly available datasets, which only include two types of ultrasound data: breast ultrasound and thyroid ultrasound. The dataset is relatively small, and thus it is impossible to know the performance of the model in other types of ultrasound imaging. Moreover, the publicly available dataset may not cover ultrasound images under different devices, operators, or imaging conditions. This may lead to insufficient generalization ability of the model in a wider range of clinical scenarios.

In terms of computational complexity, the model incorporates residual connections, hybrid convolutions, and attention mechanisms, which increases the complexity of the model. As a result, the computational speed will decrease, and the training time cost may increase.

In terms of practical applications, there is a lack of evaluation of the segmentation results by clinical doctors. The real-time requirements in practical applications (such as intraoperative ultrasound segmentation) or the integration issues with other medical systems have not been considered.