Introduction

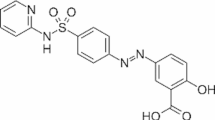
Sulfasalazine (SSZ) is a sulfonamide drug composed of 5-aminosalicylic acid and sulfapyridine, which is recognized for its anti-inflammatory properties, including the inhibition of the NF-κB pathway and proinflammatory cytokines. It is frequently utilized in the treatment of rheumatoid arthritis and inflammatory conditions, such as Crohn’s disease, in human patients. The formation of SSZ occurs through a chemical reaction between sulfapyridine and 5-aminosalicylic acid, resulting in the formation of an azo bond. This bond is subsequently broken down by the action of colonic bacteria. However, SSZ presents challenges, such as suboptimal pharmacokinetics and limited oral bioavailability due to extensive metabolism and limited solubility. While SSZ is generally effective, concerns have been raised regarding its long-term use due to the potential for adverse effects, including nausea, skin rashes, and hepatic dysfunction1,2,3. From a clinical perspective, SSZ, a class IV compound with a high log P (3.88), exhibits an absolute bioavailability of up to 15% when administered orally. This limited bioavailability is primarily attributable to its poor solubility and low permeability. These properties create significant obstacles for its topical delivery, even though it has a low molecular weight (398.39 g/mol). Consequently, the most effective approach for delivering this type of therapeutic agent topically may be the development of a dual delivery method. To enhance its therapeutic potential and mitigate toxicity, innovative drug delivery systems, including lipid-stabilized nanoparticles and micelles, have been developed and show promise in clinical applications1,4,5,6,7.

In recent decades, supercritical fluid (SCF) technology has endeavored to assume a significant role within the pharmaceutical industry, particularly with supercritical carbon dioxide (scCO2) for the production of drug particles. SCF is preferred due to its GRAS status, rendering it well-suited for the production of heat-sensitive drugs such as peptides and proteins. Furthermore, the rapid elimination of scCO2 from the solutes enhances the efficacy of the process. SCF has been demonstrated to enhance the solubility of lipophilic drugs, particularly those classified under BCS classes II and IV. The significance of solubility assessments in the realm of pharmaceutical development cannot be overstated, with gravimetric and chromatographic techniques being utilized to evaluate solubility. The process of producing particles using SCF as both a solvent and an anti-solvent involves a series of stages8,9,10,11,12,13,14,15,16,17,18,19,20. A substantial body of research has demonstrated that a significant challenge confronting the SCF process pertains to the limited capacity of CO2 to dissolve hydrophilic and polar solutes. While most medications are indeed polar molecules, their nonpolar characteristics mitigate their interaction with carbon dioxide. To address this limitation, the SCF technique is employed in conjunction with other solvents to enhance the solubility of carbon dioxide. These additional solvents, known as "co-solvents," modify the polarity of the solvent by interacting with the matrix or analyte. Consequently, the employment of these co-solvents is expected to enhance solubility in supercritical fluids, irrespective of their polarity. The solubility of compounds in scCO2 is a critical area of research, particularly concerning the use of cosolvents that may enhance extraction processes. Recent studies have explored various cosolvency effects on the solubility of different solutes in scCO2, revealing insightful trends and mechanisms21,22,23,24,25,26,27,28,29,30,31,32. Li et al.23 investigated the solubility of ammonium benzoate in supercritical carbon dioxide using several cosolvents, including ethanol, acetone, and ethylene glycol. The study was conducted within a temperature range of 308–328 K and pressures between 11.0 and 21.0 MPa. The solubility data were analyzed using semi-empirical models, and the Tang model was identified as the most accurate, with an average absolute relative deviation of 6.58%. Furthermore, the authors proposed a theoretical explanation grounded in density functional theory, providing a molecular perspective on the observed solubility enhancements.

Araus et al.25 focused on the solubility of trans-lutein, isolated from marigold petals, in pure CO2 and CO2 modified with ethanol. They conducted measurements at temperatures below 333 K and pressures under 34 MPa, noting a significant increase in solubility with rising temperature and pressure. The maximum recorded solubility of 4.02 × 10−6 mol mol−1 was achieved when 0.0211 mol mol−1 of ethanol was present, underscoring ethanol’s effectiveness as a cosolvent in improving lutein solubility. Gong et al.27 employed molecular dynamics simulations to assess how various cosolvents influence the dissolution of poly(vinyl acetate) in scCO2. Their findings indicated that PVAc can dissolve in CO2 at pressures exceeding 30 MPa. The incorporation of cosolvents led to a notable decrease in the transition points required for dissolution. The authors placed particular emphasis on Lewis acid-Lewis base interactions, noting that ethanol and acetic acid contributed new interaction dynamics that facilitate PVC solubility in supercritical environments. Zhan et al.28 measured the solubility of nitrendipine in scCO2 across a range of ethanol concentrations (1–7 mol%) and examined conditions at temperatures ranging from 308 to 328 K and pressures of 8–20 MPa. Their findings indicated that while solubility in pure scCO2 was relatively low, the addition of ethanol significantly enhanced solubility. The experimental data were successfully modeled using both the modified Méndez-Santiago and Teja (MST) models and other semi-empirical approaches, underscoring the role of ethanol as a cosolvent. In a subsequent study, Gurina et al.33 investigated the selective solvation of hydroxycinnamic acids through molecular dynamics and quantum-chemical calculations in methanol- and acetone-modified scCO2 at 328 K. Their analysis revealed that selective solvation occurs via the formation of hydrogen-bonded complexes, particularly in methanol solutions. The data suggested that larger clusters of hydrogen-bonded complexes are formed in the presence of methanol, leading to enhanced solvation efficiencies. In a related study, Tirado et al.34 employed the Hansen solubility theory to identify optimal cosolvents for the solubilization of oleic and linoleic acids in scCO2. Their findings identified short-chain alcohols, specifically ethanol and methanol, as the most effective cosolvents. Experimental validation confirmed the theoretical predictions, although the authors noted that temperature effects on solute vapor pressures necessitated further analysis for improved accuracy in solubility predictions.

Finally, Ting and Hsieh35 applied the PR + COSMOSAC equation of state to predict the solubility of solid solutes in scCO2 with organic cosolvents. Their study encompassed 23 solid solutes under pressures up to 40 MPa and temperatures ranging from 298.15 K to 353.15 K, yielding an overall average logarithmic deviation of 0.76. This accuracy suggests that the PR + COSMOSAC EoS has the potential to serve as a reliable tool for screening cosolvents in scCO2 systems.

To choose the best supercritical fluid process, you need to measure how well the drug substance can dissolve and how its solubility changes with temperature and pressure. This information is necessary for developing and designing any pharmaceutical process. There is no data about how well sufasalazine dissolves in scCO2 with ethanol. This study presents novel experimental data on the solubility of sulfasalazine in carbon dioxide and in supercritical mixed solvents of ethanol and CO2 at various pressures and temperatures. The primary objective of this study is to enhance our understanding of sulfasalazine’s solubility behavior under CO2 conditions, with a particular focus on the effects of ethanol as a co-solvent. The analysis focuses on several operational parameters, including pressure, temperature, and ethanol concentrations of 1 and 3 mol percent. To effectively correlate the solubility data, SRK and multiple density models were utilized: Méndez-Santiago and Teja (MST), Sodeifian-Sajadian, Soltani-Mazloumi, Jouyban et al., Madras, and González et al. Each model was meticulously evaluated for its predictive accuracy using statistical metrics such as the correlation coefficient (R2) and the average absolute relative deviation (AARD). The solubility data for sulfasalazine in scCO2 were measured experimentally across a wide range of temperatures and pressures, and these measurements were correlated using various semi-empirical models.

Materials and methods

Materials

Sulfasalazine with purity > 98% shown in Table 1. (CAS number 599-79-1), was acquired from Sigma-Aldrich, and carbon dioxide with a purity of over 99.5% was sourced from a local supplier.

Table 1 Properties of sulfasalazine.
Full size table

Methods

Solid solubility measurement:

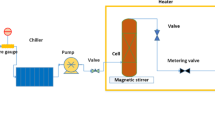
The solubility of the pharmaceutical compound was assessed using a method that integrated gravimetric techniques within a specially designed magnetic mixer apparatus (Fig. 1). This setup was engineered to function under pressures of up to 40 MPa and temperatures reaching 473 K, featuring an equilibrium cell with a capacity of 50 ml. The introduction of CO2 into the solubility cell was facilitated by a pump that gradually increased the internal pressure by increments of 0.1 MPa, reaching a maximum pressure of 40 MPa. Once the desired pressure was achieved, the CO2 flow into the cell was stabilized. Ethanol was then injected directly into the bottom of the cell at concentrations ranging from one to three percent by volume. A calibrated pressure gauge was employed to monitor the pressure within the cell, while a control system, including a PT-100 thermocouple, ensured temperature stability within a targeted accuracy of ± 0.1 K. Approximately 2 g of freshly compacted drug powder was molded into small tablets, each 6 mm in diameter. These tablets were exposed to supercritical CO2 for four hours (equilibrium state time). Preliminary tests were conducted to reach equilibrium state time (Supplementary Table S1). After the four-hour exposure, the cell underwent rapid depressurization to ambient atmospheric conditions. The remaining drug was weighed using an analytical balance with a precision of 0.01 mg, allowing for the calculation of solubility by determining the mole fraction of the drug using the initial masses (\({\text{m}}_{\text{i}}\)) and final masses (\({\text{m}}_{\text{f}}\)) of the sample.

Fig. 1
figure 1

The schematic representation illustrates the apparatus utilized in the measurement of solubility.

Full size image
$${\text{m}}_{\text{e}}={\text{m}}_{\text{i}}-{\text{m}}_{\text{f}}$$
(1)

The mole of drug was calculated by:

$$\text{Mole of drug}=\frac{{\text{m}}_{\text{e}}}{{\text{M}}_{\text{w},\text{drug}}}$$
(2)

The mole fraction and solubility of the drug were determined by Eqs. (3 and 4).

$${y}_{2}=\frac{\text{Mole of Drug }}{(\text{Mole of drug}+\text{Mole }{\text{of CO}}_{2})}$$
(3)
$$S=\frac{\rho \times {M}_{w, drug}{\times y}_{2}}{{M}_{w,C{O}_{2}}\times \left(1-{y}_{2}\right)}.$$
(4)

Modeling

Empirical models

Experimental and semi-empirical models including by K–J36, MST37, Bartle et al.38 and Chrastil39 were used in solubility of API in scCO2 (Supplementary Table S2). In addition, the various models developed to analyze the solubility of substances in scCO2 systems, particularly with the use of co-solvents.

  1. 1.

    Mendez-Santiago and Teja40 developed a correlation that combines the Clausius–Clapeyron equation with sublimation pressure, utilizing four adjustable parameters to analyze factors such as temperature, density, co-solvent composition, and solubility of ternary systems. This advancement enhances the predictive accuracy in supercritical fluid behavior.

    $$Tln\left(\frac{{y}_{2}^{\prime}P}{{P}_{ref}}\right) ={a}_{0}+{a}_{1}{\rho }_{1}+{a}_{2}T+{a}_{3}{y}_{3}$$
    (5)
  2. 2.

    Sodeifian-Sajadian41 developed a model correlating API solubility in CO2 with co-solvent addition, utilizing four parameters for effective calibration, building on prior research by Chrastil and González et al. who investigated solute behaviors in supercritical fluids.

    $$\text{ln}\left({y}_{2}^{\prime}\right) ={(a}_{0}+\frac{{a}_{1}{\rho }_{1}}{T})ln\left({\rho }_{1}\right)+{a}_{2}{\rho }_{1}+{a}_{3}\text{ln}\left({y}_{3}P\right)$$
    (6)
  3. 3.

    González et al.42 developed a thermodynamic model that links mole fraction and co-solvent concentration to solubility, emphasizing how strong solute-co-solvent interactions can enhance solubility, although higher temperatures can reduce it.

    $$ln\left({y}_{2}^{\prime}\right) ={a}_{0}ln\left({\rho }_{1}\right)+{a}_{1}ln\left({y}_{3}\right)+\frac{{a}_{2}}{T}+{a}_{3}$$
    (7)
  4. 4.

    Soltani-Mazloumi43 introduced a five-parameter experimental model for estimating solid solubility in scCO2 with co-solvents, identifying key relationships among temperature, density, and co-solvent mole fraction.

    $$ln\left({y}_{2}^{\prime}\right)={a}_{0}+\frac{{a}_{1}}{T}+\frac{{a}_{2}}{T}{\rho }_{1}-{a}_{3}\mathit{ln}\left(P\right)+{a}_{4}\mathit{ln}\left({y}_{3}{\rho }_{1}T\right)$$
    (8)
  5. 5.

    Jouyban et al.44 proposed a model that necessitates a minimum of six experimental data points to effectively estimate the solubility of organic compounds in scCO2. The model incorporates advanced interpolation techniques to enhance its precision and user-friendliness.

    $$\mathit{ln}\left({y}_{2}^{\prime}\right)={a}_{0}+{a}_{1}{y}_{3}+{a}_{2}{\rho }_{1}+{a}_{3}{P}^{2}+{a}_{4}PT+\frac{{a}_{5}T}{P}+{a}_{6}ln{\rho }_{1}$$
    (9)
  6. 6.

    In 2010, Garlapati and Madras45 extended the Jouyban et al. model by incorporating seven variables related to the solubility of high-molecular-weight substances in scCO2, considering both systems with and without co-solvents.

    $$\text{ln}\left({y}_{2}^{\prime}\right)={a}_{0}+{a}_{1}ln\left({\rho }_{1}\right)+{a}_{2}{\rho }_{1}+\frac{{a}_{3}}{T}+{a}_{4}ln\left(T\right) +{a}_{5}ln\left({y}_{3}\right)+{a}_{6}ln\left({y}_{3}{\rho }_{1}T\right)$$
    (10)

    In short, these contributions show how different factors affect solubility in supercritical fluid systems. This helps us predict how solubility will behave in practical applications.

Equation of state—SRK46

The Eq. (11) was used to calculate the solubility of SSZ (2) in scCO2 (1) at the different conditions of pressure and temperature:

$${y}_{2}=\frac{{P}_{2}^{sub}(T)}{P}\frac{{\varnothing }_{2}^{sat}(T)}{{\varnothing }_{2}(T,P,y)}exp\left[\frac{{v}_{2}^{s}(P-{P}_{2}^{sub}\left(T\right))}{RT}\right]$$
(11)

The sublimation pressure (\({P}_{2}^{sub}\)) of SSZ was determined using the Grain-Watson method. Concurrently, the Immirzi–Perini47 and the SRK were employed to calculate the molar volume (\({v}_{2}^{s}=421.4 \frac{{cm}^{3}}{mol}\)) and the saturation fugacity coefficient (\({\varnothing }_{2}^{sat}\)) of SSZ (Eq. 11), respectively.

$$RTln {\varnothing }_{i}=-RTlnZ+{\int }_{V}^{\infty }\left[{\left(\frac{\partial P}{\partial {n}_{i}}\right)}_{T,V,{n}_{j}\ne {n}_{i}}-\frac{RT}{V}\right]dV$$
(12)

The critical and physicochemical properties of SSZ were reported by Alghazwani et al.48. The thermophysical properties of SSZ were Tb = 844.5 K, Pc = 1.76 MPa, and Tc = 1177.3 K. Concurrently, the acentric factor (ω = 0.495) was estimated by the Ambros-Walton49 corresponding state method. The objective of this section is to provide a comprehensive description of the solubility data. Consequently, the SRK model has been selected for this study.

$$P=\frac{RT}{v-b}-\frac{a}{v\left(v+b\right)}$$
(13)

The attraction (a) and co-volume (b) constants were determined by applying the vdW2 as delineated in Eqs. (14) and (15), respectively.

$${a}_{m}=\sum_{i}\sum_{j}{x}_{i}{x}_{j}{a}_{ij}$$
(14)
$${b}_{m}=\sum_{i}\sum_{j}{x}_{i}{x}_{j}{b}_{ij}$$
(15)

The interaction parameters (aij and bij) were calculated using the Eqs. (16) and (17).

$${a}_{ij}={\left({a}_{i}{a}_{j}\right)}^{0.5}\left(1-{k}_{ij}\right)$$
(16)
$${b}_{ij}=\left(\frac{{b}_{i}+{b}_{j}}{2}\right)\left(1-{l}_{ij}\right)$$
(17)

Results and discussion

The present study investigates the solubility of SSZ in scCO2 + ethanol in two concentrations using a static solubility apparatus. The experiments were conducted at four different temperatures (308 K, 318 K, 328 K, and 338 K) and seven varying pressures ranging from 12 to 30 MPa. The measured solubility values are detailed in Tables 2 and 3, showing the mole fractions and solubility of SSZ and confirming the precision of the measurements through three repetitive trials, maintaining standard uncertainties below 5%. The solubility of SSZ was found to increase with higher pressure and CO2 density across all temperature settings. This finding suggests a discernible correlation between the operational pressure and the solubility of SSZ within the CO2 system. At constant temperatures, an increase in pressure leads to a substantial enhancement in SSZ solubility, particularly evident at higher temperatures. This phenomenon is attributed to the increased CO2 density and enhanced solvating power that characterizes higher pressures (Fig. 2). As evident in Table 2 solubility values exhibited substantial variation, ranging from 0.09 to 1.18 g/l. The study underscores that an increase in temperature can occasionally result in a decline in solubility within the crossover region, where temperature and pressure are approaching the critical state of the fluid. In this region, density emerges as a pivotal factor influencing SSZ solubility.

Table 2 The experimental of sulfasalazine solubility in scCO2.
Full size table
Table 3 Sulfasalazine solubility in scCO2 + 1 and 3mol % ethanol.{, 2008 #1058}.
Full size table
Fig. 2
figure 2

The sulfasalazine mole fraction in CO2 vs pressure and density.

Full size image

Furthermore, the investigation reveals a decline in solubility with isobaric temperature increases below 15 MPa. In this lower pressure regime, an increase in temperature leads to a decrease in CO2 density, resulting in reduced solvent power and decreased solubility. In this region, the impact of density reduction on solubility is more pronounced than the effect of increased sublimation vapor pressure. Conversely, at higher pressures and temperatures, the vapor pressure of SSZ increases, enhancing solubility due to enhanced molecular interactions within the supercritical fluid. The experimental findings have delineated the minimum and maximum conditions for precise measurement of SSZ solubility at 308 K and 12 MPa, and 338 K and 30 MPa, respectively.

As demonstrated in Fig. 2a,b, there is a consistent enhancement of SSZ solubility in scCO2 with increasing pressure at constant temperatures. This phenomenon is driven by increased CO2 density, which enhances the solvent capabilities. The solubility behavior of SSZ in scCO2 demonstrates a multifaceted interplay of temperature and pressure effects, aligning with observations from other solute-CO2 systems noted by various researchers50,51,52,53,54,55. The findings underscore the intricate relationship between pressure, temperature, and solubility of SSZ in scCO2, elucidating critical points in solubility measurements and enhancing the understanding of supercritical fluid processes.

The K–J model, with its three adjustable parameters, demonstrated notable efficacy in analyzing solubility data, as evidenced by its AARD values of 9.60 (Chrastil), 12.39 (Bartle), 6.20 (K–J), and 11.50 (MST). As illustrated in Figure S1, a clear correlation and consistency is observed for scCO2-solid solubility. To ensure the integrity of the models, a series of self-consistency checks were performed. These checks involved the application of linear regression to the experimental data, with the objective of establishing solubility relationships. This linearity enabled the evaluation of their self-consistency. The K–J model demonstrated the highest R2 value (0.990) among the MST (0.971), Bartle et al. (0.960), and Chrastil (0.989) models, suggesting its superior extrapolation ability (Supplementary Table S3). Based on the models, the solvation heat (∆Hsol) was calculated by subtracting the total mixing heat (∆Htotal) from Chrastil from the vaporization heat (∆Hvap) derived from the Bartle et al. The enthalpy values for SSZ in CO2 were found to be 36.43 kJ/mol using the Chrastil and 59.06 kJ/mol with the Bartle model. Consequently, the solvation heat (∆Hsol) was determined to be -22.63 kJ/mol, reflecting the difference between the vaporization and total heats.

As demonstrated in Table 3 and Fig. 3, the findings illustrate the alterations in SSZ solubility with respect to density and pressure at varying temperatures for both ethanol concentrations. Notably, the study established that the addition of ethanol notably enhances SSZ solubility under conditions of scCO2, a finding that underscores ethanol’s suitability for pharmaceutical-related applications due to its recognized safety profile. The enhancement factor (e) was calculated using the provided formula, thereby enabling the quantification of the impact of ethanol on solubility. The enhancement has been attributed to various factors, including polarity, the effect of temperature, and pressure.

Fig. 3
figure 3

The sulfasalazine mole fraction in CO2 + ethanol vs pressure and density.

Full size image
$$e=\frac{{y}_{2}^{\prime}}{{y}_{2}}\times 100=\frac{mole fraction of ternary}{mole fraction of binary}\times 100$$
(18)

The effect of the co-solvent on the solubility of materials in supercritical carbon dioxide has been investigated in a number of articles25,33,34,56,57, including the following.

Kloc et al.54 examined the dissolution of naproxen and indomethacin in a mixture of supercritical carbon dioxide (scCO2) and ethyl acetate. Their findings demonstrated that the incorporation of ethyl acetate significantly enhanced the solubility of these pharmaceutical agents. This research offers significant insights into the alterations in solubility that occur when diverse substances are combined. The study’s findings also provide a foundation for enhanced drug recovery and formulation methods.

Yang et al.58 focused on measuring the solubility of silymarin in scCO2, using co-solvents along with a combination of semi-empirical models and neural networks to analyze data. Their findings indicated that while traditional models adequately describe solubility, neural networks offer a superior capacity for predicting behavior. This study not only enhances methodologies for extracting silymarin but also proposes a framework for leveraging machine learning in other domains of pharmaceutical research.

Alghazwani et al.48 examined the impact of thermal conditions on the solubility of levetiracetam in a ternary system comprising scCO2 and ethanol. Their findings indicated that increasing temperatures significantly enhanced solubility and identified optimal extraction conditions. The thermodynamic analysis yielded pivotal insights, particularly concerning the formulation of levetiracetam for epilepsy treatment.

In a similar article, Razimanesh et al.59 conducted a comparative analysis of tacrolimus solubility in scCO2, employing both traditional and machine learning models. By exploring binary and ternary systems, their findings underscored the superior predictive capabilities of machine learning methodologies in comparison to conventional approaches. This innovative framework suggests improvements for tacrolimus formulations and demonstrates the broader applicability of machine learning techniques for predicting solubility behaviors in pharmaceutical processes.

In addition, the modeling of solubility in ternary systems involving scCO2, a co-solvent, and a solute is imperative for the design and optimization of various chemical processes. A range of methodologies have been employed by researchers, encompassing empirical correlations21,28,29,30,31,60, thermodynamic models (e.g., PR, SRK, Patel–Teja with Van Der Waals, Wong-Sandler mixing rules, and simplified cluster solvation model), artificial neural networks, and cosolvency models21,22,24. Each of these approaches possesses a unique set of advantages and limitations.

In this work, six distinct models grounded in current density have been employed to analyze the solubility of SSZ, each featuring a unique number of adjustable parameters. The models include Jouyban et al., MST, al., Garlapati- Madras, Sodeifian-Sajadian, Soltani-Mazloumi, and González et al. The study’s results, which include Average Absolute Relative Deviations (AARD%) and correlation parameters for each model, can be found in Table 4. To provide visual support for the findings, two graphs were created (see Figs. 3 and 4). The results indicate a strong correlation between SSZ solubility in scCO2, particularly for Madras et al., Soltani-Mazloumi, models, as demonstrated by their AARD% values.

Table 4 Results of the models of sulfasalazine in ethanol + scCO2.
Full size table
Fig. 4
figure 4

Modeling of sulfasalazine solubility in CO2 + ethanol: (a) Jouyban et al., (b) Madras et al., (c) Soltani-Mazlumi (d) Sodeifian-Sajadian (e) Gonzales et al., and (f) MST.

Full size image

Tables S4 and S5, as well as Figures S2, present the correlation analysis of EoS with two interaction parameters (vdW2) at temperatures of 308 K, 318 K, 328 K, and 338 K. The SRK equation with the vdW2 mixing rule yielded optimal results, attaining an AARD% of 12.46 and an R2 of 0.994 for binary and an AARD% of 05.88 and an R2 of 0.995 for ternary systems. The adjustable parameters of the models have been estimated by simulated annulling algorithm.

The parameters of correlations were then derived using Simulated Annealing (SA). SA is a statistically based search technique. SA has several advantages in optimization. It has a simpler structure and requires fewer parameters to tune, making it easier to implement. SA effectively explores the solution space by allowing uphill moves, which helps escape local minima61. In addition, it operates on a single candidate solution, avoiding the overhead of population management seen in other techniques such as GAs. SA can be applied to both discrete and continuous problems without extensive customization, and has theoretical convergence guarantees to global optima, often leading to faster discovery of good solutions in certain.

Conclusion

The aim of this investigation was to determine the solubility of sulfasalazine, a pharmaceutical compound, in scCO2, both independently and with ethanol as a co-solvent. Experiments were conducted at temperatures from 308 to 338 K and pressures of 12–30 MPa. The solubility of sulfasalazine in pure scCO2 was found to be low (between 0.094 and 1.213 g/l), indicating its ineffectiveness as a solvent for this drug. However, the solubility of sulfasalazine was notably enhanced upon the introduction of ethanol into the system. Within the ternary system (scCO2 + ethanol), the mole fraction of the drug exhibited an increase from 0.533 to 3.833 g/l and from 1.134 to 8.408 g/l with 1% and 3% ethanol, respectively. This solubility enhancement was attributed to favorable intermolecular interactions, including dipole–dipole and dipole-induced dipole interactions, between sulfasalazine and ethanol. The most increase of the solubility conditions manifested at 338 K and 12 MPa with 1% and 3% ethanol, respectively. These conditions resulted in solubility enhancements of 5.62 and 11.95 times, with a maximum mole fraction of 11.45 × 10−4 attained under these specific conditions. This highlights ethanol’s significant role as a co-solvent in boosting solute solubility in supercritical fluid systems. The findings are of considerable significance for enhancing the solubility of drugs with limited solubility, such as sulfasalazine. These findings are congruent with the outcomes of other studies that have demonstrated that modest quantities of polar co-solvents can substantially augment solubility. These findings bear implications for the development of more efficient sulfasalazine formulations using supercritical fluid technology, which could result in enhanced drug delivery methods, including the production of sulfasalazine nanoparticles with improved effectiveness.