Introduction

Recently, UAVs and their applications have been given increasing importance and attention in numerous regions, such as framework exploration, search and rescue, and reconnaissance and surveillance1. Detecting land cover is one of the main elements of UAV use, and it is a more complex task to make completely autonomous approaches. The recognition of object procedure is complicated, and the need for decreasing prices is problematic2. The images are fuzzy with noise frequency due to the actions in UAV since the onboard cameras regularly produce the lowest resolution images. In many UAV tasks, the detection procedure is complicated due to the requirement for real-time performance3. Many examinations are executed on UAVs to discover and track exact objects such as people, vehicles, landmarks, and landing places (including pedestrians’ actions). However, there arise some challenges that reflect many object recognitions since it is essential for numerous applications of UAVs4. The gap between the needs of utility and technical capacity happens via dual critical limits like (i) it is highly complex for building and keeping numerous techniques of directed objects and (ii) more considerable computation ability has been desired for actual object detection and also for a separate object. AIC of acts categorizes the derived aerial images into sub-areas by casing many ground objects and land cover kinds into numerous semantic types5. Various labels of AIC are completed using the projected method and can resolve complex issues. Integrating UAV aerial imagery and DL recognition techniques is one of the current research topics6.

Due to the features of flexibility and manoeuvrability and the capability to overcome the limits of natural situations like environment and land, UAV monitoring has enormous benefits such as extensive observing area, higher efficacy, and lowest cost. However, DL approaches were very challenging in real-world UAV object recognition tasks. It is because they are generally owing to dual points: in the first case, aerial photography UAV images are dissimilar from ground photography and contain features of smaller objectives, multi-scale, more significant scenes, complex backgrounds, and overlapping obstructions7. It is very complex to discover exact objects precisely, so such recognition tasks frequently need an awareness of inference procedures in embedded gadgets and have stronger desires for accuracy and present solutions. Complex object recognition techniques are more problematic to use in edge devices, and lightweight detectors of objects have trouble enhancing accuracy8. The growing demand for UAVs in various sectors, such as environmental monitoring, disaster response, and military surveillance, has emphasized the requirement for more effectual and accurate image classification systems. The complexity of classifying diverse land cover types from aerial images needs advanced algorithms capable of handling challenges like low-resolution, noisy images and real-time processing9. Conventional methods mostly face difficulty with these issues, necessitating innovative approaches that can enhance classification accuracy and computational efficiency. Integrating DL methods into UAV networks gives promising solutions for these challenges, allowing for more precise and faster aerial imagery analysis. This motivates the development of advanced algorithms tailored to improve UAV-based image classification tasks10.

This study proposes a Snake Optimization Algorithm with Deep Learning for Multi-Class Aerial Image Classification (SOADL-MCAIC) methodology on UAV Networks. The main purpose of SOADL-MCAIC methodology is to recognize the presence of multiple classes of aerial images on the UAV networks. To accomplish this, the SOADL-MCAIC technique utilizes Gaussian filtering (GF) for pre-processing. In addition, the SOADL-MCAIC technique employs the Efficient DenseNet model to learn difficult and intrinsic features in the image. The SOA-based hyperparameter tuning process is used to enhance the performance of the Efficient DenseNet technique. Finally, the kernel extreme learning machine (KELM)-based classification algorithm is implemented to identify and classify the presence of various classes in aerial images. The simulation outcomes of the SOADL-MCAIC method are examined under the UCM land use dataset. The key contribution of the SOADL-MCAIC method is listed below.

  • The SOADL-MCAIC model utilizes GF to input images to mitigate noise effectively and improve image quality. This pre-processing step plays a crucial role in enhancing the accuracy of the feature extraction process. Refining the input data ensures more reliable outputs in the subsequent stages of the model.

  • The SOADL-MCAIC technique employs the Efficient DenseNet model to extract high-quality features from the input images, ensuring the capture of critical information for accurate classification. This approach enhances overall performance by choosing the most relevant features. It improves the method’s capability to differentiate between classes effectively.

  • The SOADL-MCAIC method uses the SOA technique to fine-tune model parameters, optimizing feature selection and hyperparameters. This ensures the model operates with the most efficient configuration, improving overall performance. The tuning process assists in attaining higher accuracy and efficiency in classification tasks.

  • The SOADL-MCAIC methodology implements the KELM classifier for the final classification, providing a fast and effective approach for multi-class aerial image classification. Its capability to handle complex datasets confirms accurate and reliable classification results. This method improves the model’s robustness, delivering high performance in real-world applications.

  • The SOADL-MCAIC model uniquely incorporates the SOA for parameter optimization with Efficient DenseNet-based feature extraction, blending DL with advanced optimization techniques. This integration improves multi-class aerial image classification by ensuring optimal feature selection and hyperparameter tuning. The novelty is in the synergy of SOA and Efficient DenseNet, resulting in superior classification performance in complex aerial image tasks.

Related works

Selvam11 develops an Earthworm Optimizer with the Deep TL Enabled AIC (EWODTL-AIC) technique. This method first uses the AlexNet method as a feature extractor to make the optimum feature vector. The AlexNet method’s parameter is definite using the EWO model. Finally, the extreme gradient boosting (XGBoost) technique has been used for the AIC. Li et al.12 present an aerial image recognition method. Firstly, the concept of Bi-PAN-FPN has been proposed to enhance the neck part in YOLOv8-s. Next, the GhostblockV2 framework is employed as a benchmark technique to swap portion of the C2f. unit; lastly, WiseIoU loss is utilized as bounding box reversion loss, joined with a dynamic non-monotonic directing device, and the excellence of anchor boxes has been estimated by employing outlier. The authors13 developed an ensemble of DL-based multimodal land cover classification (EDL-MMLCC) techniques. Besides, an ensemble of DL approaches such as Capsule Network (CapsNet), VGG-19, and MobileNet is utilized to extract features. Furthermore, the training procedure is enhanced by applying a hosted cuckoo optimizer (HCO) approach. Lastly, the SSA with regularized ELM (RELM) approach is used for detection. Meng and Tia14 suggest building a UAV dataset affording dissimilar UAV shape structures. Then, depending upon the transfer learning model, experimentation contrast is made among 3 classic deep CNN (DCNNs) detection techniques like ResNet 101, Inception V3, and VGG16 and dual classic DCNNs detection methods such as Faster RCNN and SSD. Lastly, an experimentation assessment is directed at the collected UAV dataset. Minu and Canessane15 present an effectual DL-based AIC utilizing Inception with Residual Networkv2 and MLP (DLIRV2-MLP). The Inception with ResNet v2-based feature extraction is used. Lastly, aerial images employing the resultant feature vectors are detected using the MLP technique.

The authors16 project a novel meta-heuristic with an ANFIS for decision-making termed the MANFIS-DM approach. This technique includes a dual main phase: ANFIS-based classification and a different quantum evolution-based clustering (QDE-C) approach. The QDE-C model mainly consists of a fitness function design. Also, the classification of the image method contains a set of sub-processes like ANFIS-based classification, Adadelta-based hyperparameter optimizer, and DenseNet-based feature extractor. Pustokhina et al.17 present a new energy-effectual cluster-based UAV system with a DL-based scene detection system. The developed model comprises clusters using the parameter-tuned residual networks (C-PTRNs) method. Firstly, the UAVs are grouped by employing the T2FL approach. Then, a DL-based ResNet50 model has been used for scene classification. The water wave optimization (WWO) technique is employed for tuning. Eventually, the kernel ELM (KELM) method was utilized for classification. The authors18 develop a new optimum Squeezenet with a DNN (OSQNDNN) technique. The OSQN approach has been used as a feature extraction to originate a beneficial group of feature vectors. Still, the coyote optimizer algorithm (COA) has been utilized to select the parameters related to the traditional SqueezeNet method. Furthermore, the DNN technique has been applied as a classification algorithm whose primary goal is to assign appropriate classes to the applied images of the input aerial. Liu et al.19 present a transformer-based framework (TransUNet) methodology, improving the UNet model with a transformer encoder to enhance feature extraction in complex environments. Coletta et al.20 propose the A2-UAV framework to optimize task execution at the edge by addressing routing, data pre-processing, and target assignment. A polynomial-time solution is provided for the Application-Aware Task Planning Problem (A2-TPP). Al-Masri et al.21 propose an effectual malware classification methodology by utilizing dual CNNs, integrating a custom structure extraction branch with a pre-trained ResNet-50 model for improved image classification. Fu et al.22 introduce the Red-billed Blue Magpie Optimizer (RBMO) approach, a metaheuristic inspired by the predation behaviours of red-billed blue magpies, modelling their searching, chasing, and food storage behaviours.

The existing methods in AIC, UAV task optimization, and malware classification illustrate crucial improvements, but they have certain limitations. Several techniques, such as EWODTL-AIC, Bi-PAN-FPN, and EDL-MMLCC, often depend on a single dataset, limiting their generalization across diverse real-world scenarios. Additionally, some models lack scalability and computational efficiency when applied to massive datasets or complex environments, like the TransUNet19 and MANFIS-DM16. Further, the efficiency of hybrid models, such as those integrating CNNs and metaheuristics, remains underexplored, specifically in real-time applications. Moreover, the influence of environmental factors (e.g., lighting or fog) on UAV image classification performance remains an open issue. There is also a requirement for more robust frameworks addressing edge computing constraints in UAV networks and malware detection, as shown by approaches such as A2-UAV and RBMO. Future research should address these gaps, optimize models for broader applications, and enhance real-time processing capabilities.

The proposed method

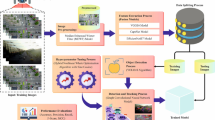
This study presents a novel SOADL-MCAIC method for UAV networks. The main aim of the method is to recognize the presence of multiple classes of aerial images on the UAV network. The method contains different types of processes, namely pre-processing, feature extractor, hyperparameter tuning, and classification. Figure 1 represents the workflow of the SOADL-MCAIC model.

Fig. 1
figure 1

Workflow of SOADL-MCAIC approach.

Full size image

Pre-processing

Primarily, the SOADL-MCAIC technique undergoes GF as a pre-processing stage23. This model is chosen for its efficiency in mitigating noise and improving image quality, which is significant for aerial image classification. Unlike other filtering methods, GF is simple, computationally efficient, and capable of smoothing out high-frequency noise while preserving the crucial features of the image. This makes it specifically appropriate for UAV images, which often suffer from low resolution and environmental noise. The capability of GF to improve image clarity directly contributes to improved feature extraction in subsequent stages of the model. Additionally, the flexibility of the GF model allows it to be easily adapted to diverse types of noise, making it a versatile and reliable choice compared to more complex techniques like median or bilateral filtering. Therefore, it strikes an ideal balance between efficiency and effectualness for multi-class aerial image classification tasks.

GF is a fundamental image-processing technique renowned for its effectiveness in smoothing and noise reduction. GF attenuates high-frequency noise and sharpens edges by convolving the image with a Gaussian kernel, rendering it especially valuable for improving image quality. The core of GF lies in its capacity to provide a weighted average of adjacent pixel values, where the Gaussian distribution defines the weight. This imparts a blurring effect, suppressing random variation while retaining crucial image structure. GF finds wide application in different fields, namely medical imaging and computer vision, where noise reduction without compromising image details is vital. Its simplicity, coupled with its ability to create immediate improvement in image analysis and aesthetics, underscores GF as a versatile tool in the pre-processing toolkit of feature extraction and image enhancement methods.

Feature extractor

At this stage, the SOADL-MCAIC technique involves the Efficient DenseNet model to learn complex and intrinsic features from the image24. This model is chosen because it can effectively capture high-level features while maintaining a relatively low computational cost. DenseNet’s unique architecture, which establishes direct connections between layers, allows for enhanced gradient flow and reduces the vanishing gradient problem, resulting in improved feature propagation. This benefits aerial image classification, where complex patterns and subtle details must be extracted. Compared to other CNNs, DenseNet needs fewer parameters for similar or better performance, making it computationally efficient. Furthermore, dense connectivity promotes better feature reuse, accuracy, and model robustness. Its performance in handling complex and multi-class image data makes it a more appropriate choice for UAV-based image classification tasks than conventional CNN architectures like VGG or ResNet. Figure 2 demonstrates the framework of the Efficient DenseNet model.

Fig. 2
figure 2

Architecture of Efficient DenseNet technique.

Full size image

Huang et al. 2017 presented that a DenseNet model depends on a deep layer structure having a direct connection, thereby obtaining a better data flow. The data increases and flows to each succeeding layer through a feature map. Every mapping feature of the existing layer is coupled with the mapping feature of the prior state. This FC layered architecture, named DenseNet, applies fewer parameters than typical CNNs. Rather than the new DenseNet, the reason behind using Efficient DenseNet is that the suggested framework is more effective because of a more transition layer after the 4th Dense Block.

Assumed an input image \(I_{0}\), provided as the input state. This structure has overall \(N\) layers with non-linear functions for individual transformation, viz., \(F_{n} \left( \cdot \right)\). Once the nth layer has a mapping feature from the prior layer using \(I_{0} ,I_{1} ,I_{2} , \ldots \ldots ,I_{n - 1}\), the network has an \(N\left( {N + 1} \right)/2\) count of layers. The resultant at \(the n^{th}\) layer is represented as:

$$I_{n} = F_{n} \left( {\left[ {I_{0} ,I_{1} ,{ }I_{n - 1} } \right]} \right),$$
(1)

In Eq. (1), \(I_{n}\) indicates the nth layer, \(F_{n} \left( \cdot \right)\) refers to the transformation function for ReLu and \(I_{0} ,I_{1} ,I_{2} , \ldots \ldots , and I_{n - l}\) denotes the feature map of the layer from 0 to n − 1.

Rectified Linear Unit (ReLu), Batch Normalization (BN), and convolution of 3 × 3 filters can 3 processes in the transition state. Once the mapping features differ in size, this process does not provide accurate output. Accordingly, the layer with the difference in mapping feature sizes is down-sampled. The transition state with 2 × 2 average pooling and 1 × 1 convolutional are supplied to the middle of the Dense convolution block. The initial convolutional state has a 7 × 7 convolutional and stride of 2. Lastly, the transition state, dense convolutional block, and the resultant state have the softmax classifier and global average pooling. The mapping feature has done the correct classification. Hence, the classifier layer with \(Z\) neurons provides accurate correspondence with \(Z\) diseases.

Pooling decreases the mapping feature size from the output. \({\text{Max}}\) and average are two ways to pool. The former takes the maximal values from the improved mapping feature, whereas the latter splits the input amongst the areas and proceeds to the average value from all the regions. The convolution function controls the sample matrix and filter. There is a BN‐ReLU convolutional sequential at the Conv layer. ReLU is employed for the output of the convolutional, which has been accomplished on the mapping feature. Thus, the non-linear ReLu function is given as.

$$f\left( {I_{0} } \right) = {\text{max}}\left( {0,{ }I_{0} } \right)$$
(2)

Hyperparameter tuning using SOA

The SOA-based parameter tuning process is used to improve the performance of the Efficient DenseNet technique25. This model is chosen due to its efficiency in exploring complex search spaces and optimizing continuous and discrete variables. SOA replicates the predation behaviour of snakes, giving a balance between exploration and exploitation, which is significant for fine-tuning hyperparameters. It is specifically effectual in avoiding local minima and converging to global optima, making it ideal for complex models like Efficient DenseNet. Compared to conventional optimization techniques like grid or random search, SOA is computationally more effectual and less prone to overfitting, particularly in high-dimensional spaces. Its flexibility in adapting to diverse optimization problems makes it appropriate for UAV-based multi-class aerial image classification, where parameter tuning is crucial in improving the model’s performance. Additionally, the nature of the SOA method ensures better generalization by exploring diverse regions of the solution space. Figure 3 illustrates the SOA framework.

Fig. 3
figure 3

Overall structure of the SOA model.

Full size image

The SOA is a metaheuristic optimizer technique that stimulates the behaviours of snakes seeking prey. This method searches for the optimum subset of features by fine-tuning the snake’s place iteratively within the search range. The steps for the SOA are discussed below:

  1. (1)

    Initialization

    In this phase, the random population was initialized in the search range, which allowed the optimization process to begin. An initial population has been attained by using Eq. (3):

    $$P_{j} = P_{{{\text{min}}}} + R \times \left( {P_{{{\text{max}}}} - P_{{{\text{min}}}} } \right)$$
    (3)

    whereas \(R\) signifies the random number between \({\text{zero}}\) and one, \(P_{j}\) denotes the position of \(a j\)th element, \(and P_{{{\text{max}}}}\) and \(P_{{\text{ min}}}\) are the upper and lower bounds of the problem.

  2. (2)

    Population splitting into two equivalent fractions like males and females

    An assumption is complete during this stage, but an equivalent distribution of males and females, each having 50% of the overall population, is accomplished. Then, the population was divided into female and male groups. The following equation is applied to execute the swarm division,

    $$I_{m} \approx I/2$$
    (4)
    $$I_{f} = I - I_{m}$$
    (5)

    \(I_{m}\) denote the count of male individuals. \(I_{f}\) represents the count of female individuals, and \(I\) describe the total individual counts.

  3. (3)

    Evaluating the two groups and creating the optimum temperature and food quantity supplies.

    • Recognize the top individual in every set and find the better female and male and their related places from the food order.

    • The temperature (T) is represented by applying Eq. (6),

      $$T = exp\left( {\frac{{i_{c} }}{{i_{T} }}} \right)$$
      (6)

      where \(i_{c}\) describes the existing iteration, \(i\tau\) is the maximum iteration count.

    • The Food quantity \(\left( F \right)\) must be found through the given expression:

      $$F_{q} = C_{1} \times \left( {\frac{{i_{c} - i_{T} }}{{i_{T} }}} \right)$$
      (7)

      where \(C_{1}\) is a constant value fixed as 0.5

  4. (4)

    Exploration Stage (Lack of food)

    When \(F <\) Threshold, snakes arbitrarily search for food and upgrade its position based on Eq. (8):

    $$P_{{\left( {j,m} \right)}} \left( {i_{c} + 1} \right) = P_{{\left( {rand,m} \right)}} \left( {i_{c} } \right) \pm C_{2} \times M_{ab} \times \left( {P_{{{\text{max}}}} - P_{{{\text{min}}}} } \right) \times rand + P_{{{\text{min}}}}$$
    (8)

    Now, \(P_{j,m}\) and \(P_{rand,m}\) are the positions of jth male and randomly selected male, \(rand\) represents the random number within [0, 1], and \(M_{ab}\) represents the male’s capability to search for food. Likewise, for the females, the position is upgraded using Eq. (9).

    $$P_{{\left( {j,f} \right)}} \left( {i_{c} + 1} \right) = P_{{\left( {randf,} \right)}} \left( {i_{c} } \right) \pm C_{2} \times F_{ab} \times \left( {P_{{{\text{max}}}} - P_{{{\text{min}}}} } \right) \times rand + P_{{{\text{min}}}}$$
    (9)

    Here, \(P_{j,f}\) and \(P_{randf}\) are the positions of \(j^{th}\) female and randomly elected female, \(rand\) describes a random number within zero and one, and \(F_{ab}\) indicates the female’s capability to search for food.

    The female or male ability to search for food is formulated by:

    $$\frac{{M_{ab} }}{{F_{ab} }} = \exp \left( {\frac{{ - f_{rand,m/randf} }}{{f_{j,m/j,f} }}} \right)$$
    (10)

    where \(f_{rand,m/randf}\) specifies the fitness of \(P_{rand,m} lP_{randf}\), \(f_{j,m/j,f}\) signifies the fitness of the \(j\) th individual from the female or male group, and \(C_{2}\) denotes a constant fixed as 0.05.

  5. (5)

    Exploitation Stage (Food is existing)

    When \(F_{q}\) and T > Threshold, snakes only search for food and upgrade their place based on Eq. (11).

    $$P_{{\left( {j,k} \right)}} \left( {i_{c} + 1} \right) = P_{food} \pm C_{3} \times T \times rand \times \left( {P_{food} - P_{{\left( {j,k} \right)}} \left( {i_{c} } \right)} \right)$$
    (11)

    where \(P_{j,k}\) represents the individual position (female and male), \(P_{food}\) denotes the best individual place, and \(C_{3}\) refers to a constant by a set value of 2.

T < Threshold (\(0.6)\) activates the mating or fighting mode of the snake.

Fight mode

$$P_{{\left( {j,m} \right)}} \left( {i_{c} + 1} \right) = P_{{\left( {j,m} \right)}} \left( {i_{c} } \right) + C_{3} \times MF_{ab} \times rand \times \left( {F_{q} \times P_{best,f} - P_{{\left( {j,m} \right)}} \left( {i_{c} } \right)} \right)$$
(12)

Now, \(P_{j,m}\) and \(P_{best,f}\) are the positions of jth male and best female individuals, \(rand\) denotes a random number ranging from zero to one, and \(MF_{ab}\) indicates the male’s capability for fighting.

Likewise,

$$P_{{\left( {j,f} \right)}} \left( {i_{c} + 1} \right) = P_{{\left( {j,f} \right)}} \left( {i_{c} + 1} \right) + C_{3} \times FF_{ab} \times rand \times \left( {F_{q} \times P_{best,m} - P_{{\left( {j,f} \right)}} \left( {i_{c} + 1} \right)} \right)$$
(13)

where \(P_{j,f}\) indicates the place of the jth female,\(FF_{ab}\) refers to the female’s capability to fight, if \(p_{best,m}\) has been the best individual male’s place, and the \(rand\) is a random number from 0 to 1.

Mating mode

$$P_{{\left( {j,m} \right)}} \left( {i_{c} + 1} \right) = P_{{\left( {j,m} \right)}} \left( {i_{c} } \right) + C_{3} \times MM_{ab} \times rand \times \left( {F_{q} \times P_{{\left( {j,f} \right)}} - P_{{\left( {j,m} \right)}} \left( {i_{c} } \right)} \right)$$
(14)
$$P_{{\left( {j,f} \right)}} \left( {i_{c} + 1} \right) = P_{{\left( {j,f} \right)}} \left( {i_{c} } \right) + C_{3} \times FM_{ab} \times rand \times \left( {F_{q} \times P_{{\left( {j,m} \right)}} - P_{{\left( {j,f} \right)}} \left( {i_{c} } \right)} \right)$$
(15)

Now, \(P_{j,m}\) and \(P_{j,f}\) describe the place of the jth female and male, and \(MM_{ab}\) and \(FM_{ab}\) represent the female and male’s capability for mating.

The least performing female and male are chosen and replaced when an egg hatches,

$$P_{worst,m} = P_{{{\text{min}}}} + rand \times \left( {P_{{{\text{max}}}} - P_{{{\text{min}}}} } \right)$$
(16)
$$P_{worst,f} = P_{{{\text{min}}}} + rand \times \left( {P_{{{\text{max}}}} - P_{{{\text{min}}}} } \right)$$
(17)

where \(P_{worst,m}\) and \(P_{worst,f}\) are the poor performance of male and female population groups.

Fitness choice is the main factor that influences the performance of the SOA technique. The hyperparameter choice system contains the performance of the encoded method to estimate the effectiveness of candidate results. The SOA approach considers accuracy as the signification condition for designing the FF, as follows.

$$Fitness = {\text{ max }}\left( P \right)$$
(18)
$$P = \frac{TP}{{TP + FP}}$$
(19)

Meanwhile, \(TP\) and \(FP\) denote the true and false positive rates.

KELM-based classification

At last, the KELM-based classification algorithm is utilized to identify and classify the presence of multiple classes in aerial images26. This model is chosen due to its superior computational efficiency and capability to handle non-linear data with minimal parameter tuning. KELM integrates the simplicity of extreme learning machine (ELM) with the power of kernel methods, allowing it to classify complex, high-dimensional aerial images effectually. Unlike conventional methods like support vector machines (SVM) or deep neural networks, KELM presents faster training times while maintaining high accuracy, making it appropriate for real-time UAV applications. Its capability to handle multi-class classification tasks with robust generalization to unseen data is another advantage over other techniques. Furthermore, KELM does not require iterative optimization, significantly mitigating computational cost and time, making it ideal for large-scale datasets like multi-class aerial image classification. Its inherent flexibility in mapping input data to higher-dimensional spaces improves its performance in complex image classification tasks.

KELM is developed based on ELM, a single-layer FFNN model composed of hidden, input, and output layers. The kernel function has the advantages of generalization ability and performance. Compared to other prediction methods, it shows faster processing speed. It successfully resolves the problem of handling a massive amount of data based on the variation mode decomposition, improving the demand‐side load forecasting response-ability. Therefore, KELM is preferred for load forecasting in this study.

The basic model function of ELM is formulated by:

$$f_{L} \left( x \right) = \mathop \sum \limits_{i = 1}^{L} h_{i} \left( x \right)\beta_{i} = H\beta$$
(20)
$$H = g\left( {W \cdot X + B} \right)$$
(21)
$$g\left( x \right) = \frac{1}{{1 + e^{ - x} }}$$
(22)

In the equation, the weight matrix from HL to the output layers is represented as \(\beta\); the output of ELM is \(f_{L} \left( x \right)\); the number of HL nodes represented is expressed as \(L\); \(W\) and \(B\) are input and output weights, correspondingly; \(X\) refers to the input vector; the amount of nodes from the resultant layer shows \(M\); \(g\left( x \right)\) refers to the sigmoid function. After presenting the regularization term \(L_{2}\), the optimizer procedure is:

$${\text{min}}_{{\beta \in R_{L \times M} }} \frac{{\beta^{2} }}{2} + \frac{C}{2}H\beta - T^{2}$$
(23)

In Eq. (23), the regularization parameter is \(C\), and the target matrix of the training dataset is \(T\). The optimum solution is attained by:

$$\beta^{*} = H^{T} \left( {\frac{I}{C} + HH^{T} } \right)T$$
(24)

The primary input weight impacts the optimum performance. The KELM is used to resolve these problems. The result of KELM is:

$$f_{L} \left( x \right) = \left[ {k\left( {x,x_{1} } \right) \ldots k\left( {x,x_{{\text{n}}} } \right)} \right]\left( {\frac{I}{C} + \Omega } \right)^{ - 1} T$$
(25)
$$\Omega = HH^{T} ,\Omega_{i,j} = k\left( {x_{j,} x_{j} } \right)$$
(26)

The radial basis kernel function (RBF) is adopted in this study. \(k\left( {x_{i} ,x_{j} } \right)\) is kernel function:

$${\text{exp}}\left( { - \frac{1}{{2\sigma^{2} }}x_{i} - x_{j} } \right)$$
(27)

Experimental validation

The performance evaluation of the SOADL-MCAIC approach undergoes the UCM land use dataset27. The dataset encompasses a total of 2100 images and 21 classes (buildings, agricultural, baseballdiamond, sparseresidential, airplane, beach, tenniscourt, runway, chaparral, overpass, storagetanks, forest, parkinglot, river, mediumresidential, freeway, intersection, mobilehomepark, harbor, denseresidential, and golfcourse) as represented in Table 1. Figure 4 illustrates the sample images.

Table 1 Details of the dataset.
Full size table
Fig. 4
figure 4

Sample images.

Full size image

Figure 5 illustrates the confusion matrices accomplished by the SOADL-MCAIC approach with 70% of TRPH under the UCM dataset. The achieved outcome represents the effective identification with all 21 classes.

Fig. 5
figure 5

Confusion matrix of SOADL-MCAIC model with 70% of TRPH under UCM dataset.

Full size image

Table 2 illustrates the classification performance of the SOADL-MCAIC approach on the applied 70% of TRPH. The outcomes demonstrate that the SOADL-MCAIC approach can appropriately recognize 21 classes. With 70% of TRPH, the SOADL-MCAIC methodology offers average \(accu_{y}\), \(prec_{n}\), \(reca_{l}\), \(F_{score}\), and \(G_{mean}\) values of 99.75%, 97.52%, 97.41%, 97.43%, and 98.62%, respectively.

Table 2 Classification outcome of the SOADL-MCAIC model under 70% of TRPH.
Full size table

Figure 6 demonstrates the confusion matrices generated by the SOADL-MCAIC method with 30% of TSPH under the UCM dataset. The accomplished findings represent the effectual recognition with all 21 classes.

Fig. 6
figure 6

Confusion matrix of SOADL-MCAIC model with 30% of TSPH under UCM dataset.

Full size image

Table 3 exhibits the classifier examination of the SOADL-MCAIC technique with 30% of TSPH. The experimental findings denote that the SOADL-MCAIC technique can correctly recognize 21 classes. Based on 30% of TSPH, the SOADL-MCAIC model provides average \(accu_{y}\), \(prec_{n}\), \(reca_{l}\), \(F_{score}\), and \(G_{mean}\) values of 99.67%, 96.36%, 96.42%, 96.31%, and 98.07% correspondingly.

Table 3 Classification analysis of the SOADL-MCAIC model with 30% of TSPH.
Full size table

The \(accu_{y}\) curves for training (TR) and validation (VL) shown in Fig. 7 for the SOADL-MCAIC method at the UCM dataset offer an appreciated understanding of its solution at diverse epochs. It could be a dependable improvement from the TR \(accu_{y}\) and TS \(accu_{y}\) with raised epochs, signifying the ability of the learning model to recognize patterns from both data. The improvement trend in TS \(accu_{y}\) accentuates the model’s adaptability for the TR set and skills to produce correct predictions under unobserved data, emphasizing proficiencies of robust generalization.

Fig. 7
figure 7

\(Accu_{y}\) curve of the SOADL-MCAIC model under UCM dataset.

Full size image

Figure 8 demonstrates a widespread analysis of the TR and TS loss rates for the SOADL-MCAIC method with the UCM dataset through several epochs. The TR loss always declines as a model improves weights to decline classifier errors in both data. These loss curves expose the method’s association with the TR set, demonstrating its proficiency for capably capturing patterns. Noteworthy is the incessant refinement of parameters in the SOADL-MCAIC technique, which is aimed at reducing discrepancies among real and forecast TR labels.

Fig. 8
figure 8

Loss curve of the SOADL-MCAIC model under UCM dataset.

Full size image

With respect to the PR curve shown in Fig. 9, the findings approve that the SOADL-MCAIC approach under the UCM dataset always accomplishes a better PR value in every class. These outcomes point out the model’s capability to differentiate among various classes, representing its solution in exactly distinguishing classes.

Fig. 9
figure 9

PR curve of the SOADL-MCAIC technique with UCM dataset.

Full size image

Also, the ROC curves produced by the PLDD-IDMODL methodology are illustrated in the UCM dataset in Fig. 10, demonstrating its ability to distinguish between classes. These curves provide valuable suggestions into how the trade-off between TPR and FPR differs in diverse classification thresholds and epochs. The simulation findings underscore the model’s accurate classification proficiency in distinct classes, illustrating their solution in overcoming several classifier tasks.

Fig. 10
figure 10

ROC curve of the SOADL-MCAIC method with UCM dataset.

Full size image

Table 4 and Fig. 11 comprehensively compares the SOADL-MCAIC technique concerning diverse measures 19,20,28. The table shows that the SOADL-MCAIC technique boosts performance. Based on \(accu_{y}\), the SOADL-MCAIC technique offers an increased \(accu_{y}\) of 99.75%. In contrast, the ResNet152, DenseNet201, MobileNet-v2, YoloV4, transformer encoder (TransUNet), SIDTLD-AIC, SIDTLD + SSA, DL-C-PTRN, DL-MOPSO, DL-AlexNet, DL-VGG-S, and DL-VGG-VD19 exhibit decreased \(accu_{y}\) of 96.33%, 95.33%, 97.54%, 95.60%, 97.55%, 99.60%, 99.10%, 99.09%, 95.89%, 94%, 95.76%, and 94.69%, respectively. According to \(prec_{n}\), the SOADL-MCAIC technique presents an increased \(prec_{n}\) of 97.52%. In contrast, the ResNet152, DenseNet201, MobileNet-v2, YoloV4, TransUNet, SIDTLD-AIC, SIDTLD + SSA, DL-C-PTRN, DL-MOPSO, DL-AlexNet, DL-VGG-S, and DL-VGG-VD19 models illustrate diminished \(prec_{n}\) of 93.85%, 94.76%, 95.76%, 95.77%, 94.91%, 95.89%, 93.95%, 93.23%, 94.26%, 94.01%, 93.15%, and 94.09%. Based on \(reca_{l}\), the SOADL-MCAIC methodology gains improved \(reca_{l}\) of 97.41%. Still, the ResNet152, DenseNet201, MobileNet-v2, YoloV4, TransUNet, SIDTLD-AIC, SIDTLD + SSA, DL-C-PTRN, DL-MOPSO, DL-AlexNet, DL-VGG-S, and DL-VGG-VD19 models acquire reduced \(reca_{l}\) of 95.25%, 94.91%, 96.72%, 95.20%, 95.98%, 95.86%, 94.29%, 92.91%, 95.08%, 93.47%, 94.48%, and 94.41%, respectively. Likewise, based on.

Table 4 Comparison outcome of the SOADL-MCAIC approach with other models 19,20,28.
Full size table
Fig. 11
figure 11

Comparison outcome of the SOADL-MCAIC approach with other models.

Full size image

\(F_{score}\), the SOADL-MCAIC methodology attain slightly reduced values of 93.62%, 95.54%, 95.27%, 96.33%, 94.52%, 95.85%, 94.47%, 93.45%, 93.60%, 94.62%, 93.02%, and 94.89%, subsequently. Similarly, based on \(G_{mean}\), the SOADL-MCAIC methodology reach moderate values of 93.84%, 95.58%, 95.50%, 94.80%, 94.69%, 97.80%, 93.13%, 93.56%, 93.88%, 93.14%, 93.05%, and 94.95%, respectively.

The computational time (CT) investigation of the SOADL-MCAIC approach compared with other approaches in Table 5 and Fig. 12. These acquired findings illustrate that the SOADL-MCAIC method achieves higher performance. According to \(CT\), the SOADL-MCAIC technique gives a decreased \(CT\) of 0.75 s. However, the SIDTLD-AIC, SIDTLD + SSA, DL-C-PTRN, DL-MOPSO, DL-AlexNet, DL-VGG-S, DL-VGG-VD19, ResNet152, DenseNet201, MobileNet-v2, YoloV4, and TransUNet models obtain increased \(CT\) of 1.60 s, 3.10 s, 2.09 s, 2.89 s, 3 s, 1.76 s, and 2.69 s, correspondingly.

Table 5 CT outcome of the SOADL-MCAIC approach with other methods.
Full size table
Fig. 12
figure 12

CT outcome of the SOADL-MCAIC approach with other methods.

Full size image

Table 6 and Fig. 13 demonstrates the ablation study of the SOADL-MCAIC technique with the existing models. The SOADL-MCAIC method outperforms all other techniques with an \(accu_{y}\) of 99.75%, \(prec_{n}\) of 97.52%, \(reca_{l}\) of 97.41%, an \(F_{score}\) of 97.43%, and a \(G_{mean}\) of 98.62%. The KELM method follows closely with an \(accu_{y}\) of 99.06% and similarly high values across other metrics. The SOA method shows a slightly lesser performance compared to KELM, with an \(accu_{y}\) of 98.40%, while Efficient DenseNet and GF exhibit slightly mitigated performance, with accuracies of 97.63% and 97.03%, respectively. Despite these variations, all methods demonstrate strong results, with SOADL-MCAIC clearly leading in all key performance indicators.

Table 6 Result analysis of the ablation study of the SOADL-MCAIC technique.
Full size table
Fig. 13
figure 13

Result analysis of the ablation study of the SOADL-MCAIC technique.

Full size image

Therefore, the SOADL-MCAIC methodology is performed to identify aerial image classes accurately.

Conclusion

In this study, a novel SOADL-MCAIC methodology on UAV networks is presented. The main aim of the SOADL-MCAIC methodology is to recognize the presence of multiple classes of aerial images on the UAV networks. To accomplish this, the SOADL-MCAIC technique utilizes GF for the pre-processing process. In addition, the SOADL-MCAIC technique involves the Efficient DenseNet model to learn complex and intrinsic features in the image. The SOA-based hyperparameter tuning process is used to boost the solution of the Efficient DenseNet technique. Finally, a KELM-based classification algorithm is employed to identify and classify the presence of several classes in aerial images. The simulation outcomes of the SOADL-MCAIC method are examined under the UCM land use dataset. The experimental analysis of the SOADL-MCAIC method portrayed a superior accuracy value of 99.75% over existing models. The SOADL-MCAIC method’s limitations include reliance on a single UAV network and dataset, which may not fully represent the diversity of real-world scenarios in aerial image classification. Furthermore, the model’s performance could be impacted by varying environmental conditions, such as lighting, weather, or image quality, which were not extensively addressed. The model also needs substantial computational resources, which may limit its scalability for large-scale, real-time applications. Future work could explore the incorporation of more diverse UAV datasets to improve generalization, as well as the integration of more advanced transfer learning techniques to enhance robustness in diverse environmental conditions. Optimizing the model for edge computing applications, where computational resources are constrained, would make it more appropriate for real-time UAV operations. Unsupervised learning or semi-supervised methods could also be explored to reduce the reliance on labelled data.