Introduction

The method of drug processing via supercritical solvents such as carbon dioxide has been recently assessed by extensive theoretical and experimental works to optimize the process. It is of great importance to evaluate this process as it has great potential to prepare drug nanoparticles in continuous operation1,2,3,4,5. Different methods based on supercritical approach can be adopted for production of nano-sized drug particles, however the solubility of drug in the solvent is the most important parameter which should be calculated via different methods. Before utilization of supercritical process for a drug, its solubility must be determined to ensure the suitability of process for that drug, otherwise the process might not be suitable for that particular drug and other methos need to be evaluated.

Some computational techniques have been reported in previous research on evaluation of drug solubility in supercritical CO2 (SC-CO2)6. Given the equilibrium nature of the solubility phenomenon, thermodynamics of solid-liquid equilibrium can be utilized for this analysis. Some previous thermodynamic approaches have shown acceptable accuracy for correlation of drug solubility in solvent as function of input parameters7,8,9. An important parameter which should be considered for solubility is the temperature which impacts the solubility significantly. However, for supercritical solvents, pressure can also affect the solubility of drug by compressing the solvent, as it is in the supercritical state. As such, the density of solvent varies with both pressure and temperature in supercritical processing. Although thermodynamic models perform well in estimating solute solubility in solvents, they are challenging to be generalized for wide variety of solutes such as vast majority of medicines. So, other simpler models such as Machine learning (ML) techniques can be applied for this area to calculate solubility of medicines in supercritical solvents at wide range of pressure and temperature to build a holistic model of process10,11,12.

ML has become increasingly important in many areas as a means of analyzing complex data patterns and producing reliable predictions13,14. Using statistical algorithms and computational techniques, ML algorithms can learn from existing data to make educated decisions and generate valuable insights for pharmaceutical solubility in supercritical solvents15. The methods of ML are based on learning the dataset, and therefore measured data is required for building robust models. For increasing the accuracy of models for drug solubility prediction, hybrid models integrated optimizer should be developed, which is a research gap in this area for developing reliable models in supercritical processing of medicines with enhanced solubility. Previously, simple ML models were employed in estimation of drug solubility which do not offer enough robustness in development of holistic modeling framework for pharmaceutical manufacturing16,17,18.

In this research, we applied AdaBoost regression in combination with three distinct models of Automatic Relevance Determination (ARD), Gaussian Process Regression (GPR), and Bayesian Ridge Regression (BRR). Additionally, we employed the use of BWOA (Black Widow Optimization Algorithm) for optimizing these models to enhance their performance. The mating behavior of black widow spiders inspires the BWOA. Females attract males with pheromones and mate, often consuming some males afterward. They lay eggs in their webs, and the hatchlings, being cannibalistic, compete for survival—with even the mother sometimes preying on them. This natural selection process forms the basis of the BWOA.

The AdaBoost Regression is a powerful and flexible ensemble learning method known for its strong performance in solving regression problems. When multiple weak learners are combined, complex data patterns can be captured effectively, and accurate predictions can be made19,20. The adaptability and resilience to outliers exhibited by this method have contributed to its widespread adoption across diverse industries and domains that prioritize precise regression analysis21. AdaBoost’s appeal as a reliable and efficient regression technique lies in its ability to handle non-linear relationships with minimal need for hyperparameter tuning22. Therefore, the main contribution of this study is to develop hybrid ML models and integrate the models into a novel optimizer for reliable prediction of drug solubility in supercritical CO2 as well as density of solvent.

Dataset of solubility

The dataset used in this study, obtained from23, has four variables: Temperature, Pressure, Density of SC (supercritical) solvent, and Solubility of drug. The Temperature and Pressure values represent the experimental conditions, while the Solvent Density and Solubility of niflumic acid provide the corresponding measurements. The Correlation heatmap of variables is displayed in Fig. 1. It should be pointed out that the density was considered as the variable to quantitatively estimate its variations with pressure and temperature during the process. Given that the density of solvent, which is kept in its supercritical state, can vary with pressure, it is of great importance to evaluate pressure as well as temperature effects on the density variations.

Fig. 1
figure 1

Visualization of four variables using Correlation Heatmap analysis.

Full size image

Table 1 presents the statistical summary of these variables, including their minimum, maximum, mean, and standard deviation values, providing a concise overview of the data’s range and distribution. Temperature spans from 313 K to 343 K, Pressure from 16 MPa to 40 MPa, Solvent Density from 595 kg/m³ to 1000 kg/m³, and Solubility from 0.657 to 6.06. The data of solubility for drug was divided into training, validation, and testing groups, with 20 data points used for training and validation and 7 allocated for testing, ensuring a robust evaluation of the machine learning models’ performance.

Table 1 Dataset statistics.
Full size table

Methodology

Black widow optimization algorithm (BWOA)

BWOA draws inspiration from the mating behavior of black widow spiders, where female spiders create webs at night and release pheromones to attract male spiders for mating. As the males are lured into the web, they become vulnerable to being consumed by the female subsequent or concurrent to mating. After the female black widow spins her web, she lays her eggs there. Eleven days later, the young cannibalistic spiders emerge from the eggs. Interestingly, the mother might consume some of the young spiders, favoring the survival of the fittest offspring, which serves as the underlying motivation for this novel algorithm24.

In BWOA, each candidate solution is represented by a black widow spider, and an initial population of spiders is formed in a random manner. The algorithm is divided into three stages: procreation, cannibalism, and mutation. During reproduction, pairs of spiders are chosen at random to mate and produce offspring. During the cannibalism phase, three distinct behaviors emerge: (i) the mother spider consuming the father spider, (ii) sibling spiders preying on each other, and (iii) offspring feeding on the mother spider. Ultimately, during the mutation phase, two randomly selected parts of a single spider are swapped, achieving a happy medium between discovery and exploitation. The reproduction process of BWOA can be represented by the following Eqs24,25:

$$\:{Y}_{i,d}=\beta\:\times\:{X}_{i,d}+(1-\beta\:)\times\:{X}_{j,d}$$
$$\:{Y}_{j,d}=\beta\:\times\:{X}_{j,d}+(1-\beta\:)\times\:{X}_{i,d}$$

where, i and j denote random numbers within the range [0, 1], while \(\:{\upbeta\:}\) is another random number within the range [1, N], where N is a predefined value. Additionally, \(\:{Y}_{i,d}\) and \(\:{Y}_{j,d}\) represent the offspring generated from this process. The mutation operation, in addition to reproduction, is defined as follows26:

$$\:{Z}_{k,d}={Y}_{k,d}+\alpha\:$$

In the above equation, \(\:{\upalpha\:}\) indicates a random mutation, Z stands for the spider that has undergone the mutation, and Y is the spider that has been chosen at random to undergo the mutation.

Adaptive boosting (adaboost)

AdaBoost regression is an iterative algorithm that sequentially builds a committee of weak regression models, assigning weights to each model considering their performance. These models are combined to create a robust and accurate regression model27. In AdaBoost regression, weak regression models are typically simple and computationally efficient. Examples of weak regression models include decision stumps and linear regression models. The models are often used as building blocks in the AdaBoost regression algorithm19.

The weighted error of a weak regression model quantifies its performance on the training data, taking into account the weights assigned to each sample. It is calculated by summing the weights of the misclassified samples and dividing it by the total sum of the weights. Mathematically, the weighted error can be represented as28:

$$\epsilon_{t}=\frac{{\sum\:}_{i=1}^{N}{w}_{i}\cdot\: 1\left({h}_{t}\left({x}_{i}\right)\ne\:{y}_{i}\right)}{{\sum\:}_{i=1}^{N}{w}_{i}}$$

In the above equation, t represents the current iteration, N stand for the total number of training samples, \(\:{w}_{i}\) is the weight assigned to sample \(\:{x}_{i}\), \(\:{h}_{t}\left({x}_{i}\right)\) represents the prediction of the weak regression model for sample \(\:{x}_{i}\), \(\:{y}_{i}\) denotes the true label of sample \(\:{x}_{i}\), and \(\:1\left(\cdot\:\right)\) stands for the indicator function.

The weight update process can be formulated as29:

$$\:{w}_{i}\leftarrow\:{w}_{i}\cdot\:\text{exp}\left(-{{\upalpha\:}}_{t}\cdot\:{y}_{i}\cdot\:{h}_{t}\left({x}_{i}\right)\right)$$

where \(\:{{\upalpha\:}}_{t}\) is the weight assigned to the weak regression model at iteration t. The weight \(\:{{\upalpha\:}}_{t}\) is determined based on the performance of the weak regression model, with better-performing models assigned higher weights.

The final regression model in AdaBoost regression is obtained by combining the weak regression models in the committee, assigning weights to each model according to their performance. The weights of the weak models are used to determine the contribution of each model to the final prediction. The final regression model can be represented as28:

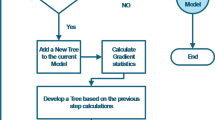
$$\:F\left(x\right)={\sum\:}_{t=1}^{T}{{\upalpha\:}}_{t}\cdot\:{h}_{t}\left(x\right)$$

where F(x) is the prediction of the final regression model for input x, T is the total number of weak regression models in the committee, \(\:{{\upalpha\:}}_{t}\) is the weight assigned to the weak regression model at iteration t, and \(\:{h}_{t}\left(x\right)\) is the prediction of the weak regression model \(\:t\) for input x. An overall flowchart for AdaBoost is shown in Fig. 2.

Fig. 2
figure 2

A Workflow Schema for AdaBoost.

Full size image

ML models

In this section, we present three distinct regression techniques: ARD Regression, Bayesian Ridge Regression, and Gaussian Process Regression. These base models serve as fundamental components in ensemble learning and play a pivotal role in the AdaBoost regression algorithm.

ARD Regression is a Bayesian regression technique designed to automatically select relevant features from the input data while simultaneously estimating their respective coefficients30. ARD Regression utilizes a sparse prior on the feature weights, allowing it to identify and discard irrelevant features during the learning process. This capability makes ARD Regression particularly useful for high-dimensional datasets, as it helps mitigate the curse of dimensionality and reduces the risk of overfitting. By effectively selecting the most informative features, ARD Regression yields a more interpretable and efficient regression model.

BRR is a Bayesian probabilistic model that provides a flexible approach to linear regression. This technique introduces prior distributions on the regression coefficients, allowing it to account for uncertainties in the model’s parameters. By incorporating prior knowledge or assumptions about the data, Bayesian Ridge Regression improves the model’s generalization capabilities and enhances its resilience to noise. Moreover, this Bayesian framework enables Bayesian Ridge Regression to handle multicollinearity in the input features, resulting in a stable and robust regression model19.

GPR is a non-parametric Bayesian regression technique that models the data as a collection of Gaussian processes. Unlike traditional regression methods that assume a fixed functional form, GPR considers the data as a distribution of functions and infers the underlying function that best fits the data31,32,33. GPR is particularly advantageous in scenarios where the relationship between input and output variables is complex and non-linear, as it offers a flexible and expressive modeling approach. Additionally, GPR provides a probabilistic framework, allowing for uncertainty quantification in predictions, which is essential in decision-making processes under uncertainty34.

Results and discussion

The models including ADA-ARD, ADA-BRR, and ADA-GPR were evaluated for predicting the properties of supercritical carbon dioxide (SC-CO2) density as well as the solubility of niflumic acid. The models were trained using the given dataset, and their predictions were compared against the actual values.

Table 2 Performance metrics for SC-CO2 density prediction.
Full size table
Table 3 Performance metrics for Niflumic acid solubility prediction.
Full size table

From Table 2, it is clear that all three models demonstrate strong capabilities in predicting SC-CO₂ density, with test R-squared values exceeding 0.94. Among them, ADA-GPR again stands out, achieving a superior test R² score of 0.9867, accompanied by the lowest RMSE (13.662) and AARD% (1.325%). Notably, ADA-GPR also showed excellent 10-fold cross-validation performance with an R² of 0.98292 and RMSE of 15.342, indicating both high predictive accuracy and robustness. Meanwhile, ADA-ARD and ADA-BRR delivered respectable results, with 10-fold CV R² values around 0.936 and 0.939, respectively. Overall, ADA-GPR exhibits the most consistent and precise performance across training, cross-validation, and test phases, confirming its superiority among the evaluated models.

Similarly, Table 3 shows that all three models provide reasonable predictive performance for niflumic acid solubility. However, ADA-GPR again clearly outperforms the others, achieving an impressive test R² of 0.98661, along with the lowest RMSE (0.14014) and AARD% (9.14587). Its robustness is further highlighted by its 10-fold cross-validation results, where it attained an R² of 0.98309 and an RMSE of 0.15066, significantly better than ADA-ARD and ADA-BRR, whose 10-fold CV R² values were 0.81025 and 0.75038, respectively. These findings reaffirm the ADA-GPR model’s high precision, consistency, and generalization ability for solubility prediction tasks.

Overall, ADA-GPR showed to be as the most robust model for both SC-CO2 density and niflumic acid solubility predictions. Figures 3 and 4, which are comparison of actual and predicted values using this model, show that most of test cases are predicted with errors near to zero. Its exceptional performance, coupled with the utilization of the BWOA for hyper-parameter tuning, showcases the potential of ML techniques in calculating essential properties of SC-CO2.

Fig. 3
figure 3

Cross Plot: Actual and Predicted Solvent Density using ADA-GPR model.

Full size image
Fig. 4
figure 4

Cross Plot: Actual and Predicted Solubility using ADA-GPR model.

Full size image

Figures 5, 6, 7 and 8 are two-dimensional plots showing the effect of each single input on outputs and their dual effects on outputs are shown in Figs. 9 and 10 in a three-dimensional manner. The results show agreement and similar variations to the results reported in35. The ML models which are optimized, are able to describe the behavior of solvent in terms of density variations as well as solubility of drug. Only the density of solvent is decreased with rising temperature, while other parameters are enhanced with pressure and temperature. As expected, density is a strong function of pressure and temperature, so that the solvent is suitable to be optimized for increasing the solubility of drug in it.

Fig. 5
figure 5

Effects of Pressure as input on Solvent Density as output (Constant Temperature Levels).

Full size image

As illustrated in Fig. 5, SC-CO2 density increases significantly with rising pressure at each constant temperature level, reflecting the compressibility of the supercritical fluid35. Indeed, more compressible fluid can accommodate more drug molecules for dissolving at higher pressure which in turn increases the drug solubility. As such, for supercritical solvents both temperature and pressure can alter the density and consequently the solubility. This trend is consistent with experimental findings, which demonstrated that supercritical CO2 behaves similarly to a dense gas, where density is highly sensitive to pressure changes due to the fluid’s proximity to its critical point. At higher pressures, the increased molecular interactions lead to a more compact fluid structure, thereby enhancing density35.

Figure 6 reveals that SC-CO2 density decreases as temperature increases at fixed pressure levels, a behavior typical of fluids where thermal expansion outweighs other effects35. This inverse relationship aligns with the experimental observations, which noted that in supercritical fluids, higher temperatures lead to greater kinetic energy, causing molecules to spread apart and thus reducing density. The rate of density decrease is more pronounced at lower pressures, where the fluid is less compressed.

Fig. 6
figure 6

Effects of Temperature as input on Solvent Density as output (Constant Pressure Levels).

Full size image
Fig. 7
figure 7

Effects of Pressure on Solubility (Constant Temperature Levels).

Full size image
Fig. 8
figure 8

Effects of Pressure on Solubility (Constant Temperature Levels).

Full size image
Fig. 9
figure 9

The Response surface of solvent density based on ADA-GPR model.

Full size image
Fig. 10
figure 10

The Response surface of solubility based on ADA-GPR model.

Full size image

This study, while showcasing the potential of ADA-GPR in predicting SC-CO2 density and niflumic acid solubility, is constrained by its use of a single, specific dataset, which may limit the generalizability of the results to other drugs or supercritical fluid conditions. The small dataset size and reliance on BWOA for hyper-parameter tuning could further restrict the model’s broader applicability and optimization potential. These factors may impact the findings’ external validity and practical utility in diverse pharmaceutical settings. Future work should incorporate larger, varied datasets and explore alternative optimization methods, such as genetic algorithms, to enhance model robustness and accuracy for wider applications.

Our ADA-GPR model outperforms Li et al.35 PR model in predicting niflumic acid solubility, as demonstrated by both R² and RMSE metrics. They used the same dataset for prediction of density and solubility. Specifically, our model achieves a test R² of 0.98661, indicating it explains more variance in the data, and an RMSE of 0.14014, reflecting lower prediction error, compared to the PR model’s R² of 0.969 and RMSE of 0.256. This superior performance highlights our model’s greater accuracy and reliability for practical use in supercritical fluid processes. Additionally, our use of 10-fold cross-validation (yielding an R² of 0.98009 ± 0.01024) ensures consistent results across data subsets, a robustness check not reported in Li et al.‘s study. By integrating ensemble methods and rigorous validation, our approach provides a more precise and generalizable tool for pharmaceutical applications involving drug solubility in SC-CO₂.

Conclusion

This study demonstrates the effectiveness of advanced machine learning models—ADA-ARD, ADA-BRR, and ADA-GPR—optimized via the BWOA for predicting supercritical carbon dioxide (SC-CO2) density and niflumic acid solubility. The ADA-GPR model significantly outperformed ADA-ARD and ADA-BRR, achieving high R-squared (R²) scores of 0.98670 and 0.98661 for density and solubility, respectively, with lower Root Mean Squared Errors (RMSE) and Average Absolute Relative Differences (AARD%). These results highlight the model’s superior accuracy and reliability compared to other approaches in recent literature. Our use of 10-fold cross-validation (R² = 0.98009 ± 0.01024 for solubility) further ensures model robustness and generalizability, marking a critical advancement over prior work lacking such validation.

By integrating ensemble methods and rigorous validation, this research provides a precise and reliable tool for optimizing SC-CO2-based processes, with significant implications for pharmaceutical and chemical industries. Unlike traditional thermodynamic models, which struggle with generalization, our approach offers scalable predictions across diverse conditions, advancing supercritical fluid technology. Future research could explore the incorporation of larger and more diverse datasets to enhance model performance across a broader range of compounds and conditions. Additionally, investigating alternative optimization algorithms, such as genetic algorithms or particle swarm optimization, could further improve computational efficiency and predictive accuracy. Expanding the models to real-time applications or integrating them with experimental workflows may also bridge the gap between theoretical predictions and practical industrial use.